Influence of Monolayer-Monolayer Coupling on the Phase Behavior of a Fluid Lipid Bilayer

Abstract

We suggest a minimal model for the coupling of the lateral phase behavior in an asymmetric lipid membrane across its two monolayers. Our model employs one single order parameter for each monolayer leaflet, namely its composition. Regular solution theory on the mean-field level is used to describe the free energy in each individual leaflet. Coupling between monolayers entails an energy penalty for any local compositional differences across the membrane. We calculate and analyze the phase behavior of this model. It predicts a range of possible scenarios. A monolayer with a propensity for phase separation is able to induce phase separation in the apposed monolayer. Conversely, a monolayer without this propensity is able to prevent phase separation in the apposed monolayer. If there is phase separation in the membrane, it may lead to either complete or partial registration of the monolayer domains across the membrane. The latter case which corresponds to a three-phase coexistence is only found below a critical coupling strength. We calculate that critical coupling strength. Above the critical coupling strength, the membrane adopts a uniform compositional difference between its two monolayers everywhere in the membrane, implying phase coexistence between only two phases and thus perfect spatial registration of all domains on the apposed membrane leafs. We use the lattice Boltzmann simulation method to also study the morphologies that form during phase separation within the three-phase coexistence region. Generally, domains in one monolayer diffuse but remain fully enclosed within domains in the other monolayer.

INTRODUCTION

One of the most challenging problems in membrane biophysics is to understand the influence of lipids on the lateral organization of biomembranes. Numerous experimental results point at the existence of lateral domains—membrane rafts—and their various functional roles (1,2). Yet, size, stability, and dynamic behavior of domains in biomembranes remain poorly characterized. This is in contrast to model membranes, consisting of only a few lipid species at well-characterized conditions, for which a wealth of detailed information on structural and phase behavior exists. Especially the ability of cholesterol to induce phase coexistence between two fluidlike lateral phases, the more condensed liquid-ordered (l_o) and the less condensed liquid-disordered (l_d) phase, has been well-characterized experimentally and through various subsequent modeling attempts (3–5).

An interesting problem concerns the coupling of coexisting liquidlike domains between the two leaflets of a lipid bilayer (6). Current evidence suggests matching of like-phase domains across a symmetric bilayer (7–10). That is, domains are observed to be in perfect registration, implying that some degree of composition-sensitive structural coupling must exist between the two apposed monolayers. The strength of this coupling could possibly be of importance for biomembranes. This is because the plasma membrane generally has an asymmetric lipid distribution, with domain-forming lipids enriched in the extracellular monolayer but depleted from the cytoplasmic monolayer (11). Indirect evidence (the colocalization of raft proteins with inner leaflet proteins (12) and the presence of inner leaflet proteins in detergent-resistant membranes (13)) could suggest the presence of domains in the cytoplasmic monolayer (12). The question arises whether domains in one monolayer can be imposed (imprinted) by the presence of domains in the other monolayer.

An experimental method to produce asymmetric membranes and to study their phase behavior is provided by combining the Langmuir-Blodgett/Schäfer method with fluorescence-based imaging. As the domains within the monolayer facing the solid support are immobile, they do not register with domains in the apposed monolayer (14,15). Yet, complete registration can be recovered by introducing a polymer cushion that sufficiently increases the substrate-membrane distance (16,17). The study by Garg et al. (16) clearly shows that domains in one monolayer can induce registered domains in the other monolayer, even if the latter monolayer has an insufficient tendency to phase-separate on its own. Kiessling et al. (17) also report cases where the domain-forming monolayer was unable to induce formation of registered domains in the apposed monolayer. In summary, present experimental evidence points to a composition dependence of a monolayer's ability to imprint its phase structure onto the apposed monolayer.

A number of recent theoretical studies have addressed consequences of a coupling between the two monolayers in a membrane (18,19). Two studies directly address the coupling of thermodynamic phase formation across the two membrane leaflets (20,21). Hansen et al. (20) have considered the coupling of two monolayers where each individual monolayer was modeled as having both a compositional and curvature degree of freedom. Based on Landau theory, the formation of a number of different phases, some of them flat and others with shape modulations, are predicted. In another study, Allender and Schick (21) also used Landau theory with two order parameters; again one was a compositional order parameter (an effective cholesterol concentration) but the other one described the thickness of a monolayer. The choice of this second-order parameter is common (22,23) and is well-motivated by the different chain ordering in the l_o and l_d phases (24). Monolayer-monolayer coupling was assumed to emerge only from a coupling between the thickness order parameters in each leaflet. Allender and Schick have specifically analyzed a situation where, without coupling, the outer leaflet of a membrane is unstable, whereas the inner one is stable. The coupling between the two monolayers then leads to a transition (though a weaker one) in the inner monolayer as well.

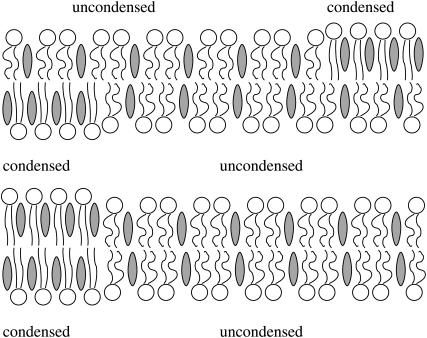
In this work, we analyze a minimal model of the coupling between monolayers and its influences on the phase behavior of a lipid bilayer. To this end, we shall employ only one single-order parameter, the composition of a binary monolayer. (Note that by merging two lipid species into a single effective one, we may, in principle, apply our results to a ternary lipid mixture that contains cholesterol; similar to Allender and Schick (21).) Each of the two individual monolayers will be described by the familiar regular solution model on the mean-field level (25,26). Without coupling between the two monolayers, each leaflet can independently undergo a lateral phase transition. We may, somewhat arbitrarily, refer to the two phases as condensed and uncondensed. Monolayer-monolayer coupling acts on the difference between the local compositions across the membrane. To suggest a physical mechanism we consider Fig. 1. It schematically displays two (initially symmetric) membranes that have undergone phase separation in both monolayers. Only in the lower membrane are the phases of the same type in registration. Despite being entropically unfavorable and creating a thickness mismatch (and corresponding line tension (27)) between the condensed and uncondensed regions, this is the experimentally observed scenario in a symmetric membrane (7–10). Various mechanisms such as van der Waals interactions or cholesterol flip-flop might contribute to the coupling (21). However, we speculate the main contribution has entropic origin and results from the conformational confinement of the lipid chains in the uncondensed phase when being opposite to a condensed monolayer. This confinement would concern predominantly the terminal segments of the lipid chains in the uncondensed monolayer. Facing a more condensed (i.e., more rigid) monolayer makes it more difficult for these segments to explore their conformational degrees of freedom by dynamically interpenetrating into the apposed monolayer. Note that the strength of this type of coupling would increase with the local compositional difference between the monolayers. This consideration motivates the simple expression for the coupling (see below in Eq. 2) that we use in this work.

FIGURE 1.

Schematic illustration of two mixed bilayer membranes. The two membranes have the same average composition in both monolayers. Each monolayer separates into two fluidlike phases, a condensed and an uncondensed one. A practical realization of this scenario could contain cholesterol and additional lipid species (in this case the phases would correspond to the l_o and l_d phases). In the upper membrane the condensed domains in one monolayer face the uncondensed ones in the apposed monolayer. We argue that this mismatch entails an energy penalty that is proportional to the square of the local compositional difference across the bilayer. The coupling between the two monolayers leads to complete registration of domains of the same kind, as illustrated for the lower membrane. Note that domain registration can be incomplete if the membrane is asymmetric; i.e., if there is a mismatch in composition between the two monolayers (this case is not shown but is part of our analysis).

We shall provide a complete thermodynamic analysis of our model as a function of the coupling strength. The results will be presented in phase diagrams. In addition, we analyze our model in terms of a Landau expansion which connects the present with previous work (20). The Landau expansion allows us to express the phase behavior in the limiting cases of small and large coupling analytically. Our model, despite being simple, would explain a range of possible observations, including the induction or suppression of phase separation due to the presence of monolayer-monolayer coupling and the formation of three-phase regions; i.e., incomplete spatial registration of domains between the monolayers. We finally use the lattice Boltzmann method to simulate possible morphologies during the process of phase separation in the three-phase region.

FREE ENERGY MODEL

Consider a planar, binary lipid membrane with the same lipid species but possibly different compositions in each of its two apposing monolayers. Assume the two lipid species exhibit nonideal mixing, with a tendency toward phase separation. We model this tendency using regular solution theory on the mean-field level which is also referred to as the Bragg-Williams or random mixing approximation (25,26). The free energy per lipid f_BW of a single two-component lipid monolayer can then be written as a function of its composition φ,

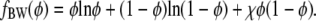(1)

Note that here and in the following, all energies are expressed in units of k_BT (Boltzmann's constant × absolute temperature). The nonideality parameter χ describes the effective strength of nearest-neighbor interactions. For χ > 0 this interaction is attractive, and for χ > χ_c it is able to induce phase separation. Mean-field theory predicts the critical point χ_c = 2. We note that in a more general approach each monolayer would have its own nonideality parameter. In view of our objective to formulate a minimal model, we assume that both monolayers have the same underlying energetics (namely, the same χ). What may be different are the average compositions of the two monolayers.

The main focus of this work is to investigate the consequences of the energetic coupling between the two apposed monolayers of a lipid bilayer. The coupling is local and likely reflects the dependence on composition of interactions between lipid tails across the bilayer midplane, such as interdigitation or, more accurately, dynamic interpenetration, as outlined in the Introduction. That is, any local compositional differences across the bilayer give rise to an extra energy penalty. If the compositional difference is sufficiently small this energy penalty must be proportional to (φ – ψ)² where φ and ψ denote the local compositions in the upper and lower monolayers, respectively. (Note that invariance of the free energy with respect to exchanging the upper and lower monolayer excludes the presence of the linear term φ – ψ.) Denoting the coupling strength by Λ (with Λ > 0), we can write for the local free energy of a lipid bilayer

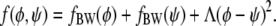(2)

The first two terms describe the free energies of each monolayer leaflet individually, and the last term accounts for the coupling between the apposed monolayers. To obtain the overall free energy F of a lipid bilayer we integrate f(φ, ψ) over the total lateral area A of the membrane,

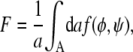(3)

where a denotes the cross-sectional area per lipid (which we assume to be the same for both species). Equations 1–3 form the basis of the present work. In the following, we theoretically analyze and discuss the implications of a nonvanishing coupling strength Λ.

PHASE BEHAVIOR

We characterize the phase behavior as a function of the two membrane compositions, φ and ψ, in the upper and lower monolayers, respectively. Let us first calculate the spinodal line that separates locally stable and unstable regions in the phase diagram. At the spinodal line, the determinant

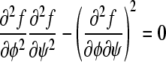(4)

of the stability matrix corresponding to f(φ, ψ) vanishes. Carrying out the derivatives using Eqs. 1 and 2 gives rise to the relation

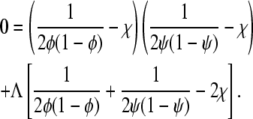(5)

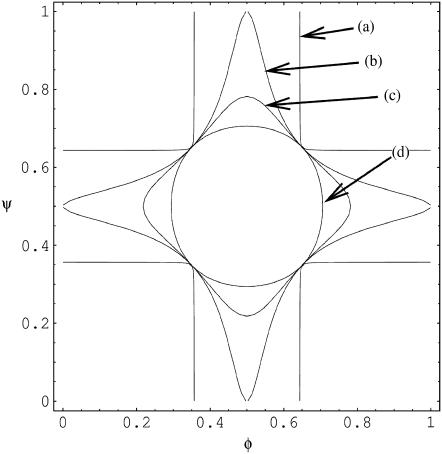
Solutions of that equation specify the spinodal lines for any given χ and Λ. Fig. 2 displays a number of representative examples of spinodals, derived for χ = 2.2 and different choices of the coupling parameter Λ. We note that sets of spinodals for values of χ different to χ = 2.2 (but with χ > 2) appear qualitatively equivalent to those shown in Fig. 2. Let us discuss the behavior of the spinodal lines: First, all spinodal lines exhibit fourfold symmetry about the two axes φ = ψ and φ = 1 – ψ. Second, the smallest χ for which Eq. 5 can be fulfilled is χ = χ_c = 2 with the corresponding compositions φ = ψ = 1/2. Hence, the coupling parameter does not affect the critical point. Also, close to the critical point, the behavior of the spinodals is independent of Λ. This becomes evident from an expansion of the spinodal up to quadratic order in φ and ψ in the vicinity of the critical point, leading to

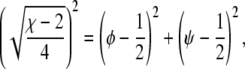(6)

which describes a circle of radius 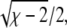independent of Λ. Third, for vanishing coupling parameter, Λ = 0, the spinodals consist of the two sets of straight lines,

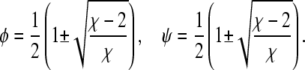(7)

The four points where these lines cross each other are part of the entire set of spinodals for fixed χ but variable Λ (see Fig. 2). What changes at these four points as a function of Λ (but fixed χ) is the curvature of the spinodal. For small Λ the spinodal is convex, and for large Λ it is concave. For the discussion below we note that the curvature vanishes at Λ = Λ_v with

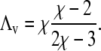(8)

For example, for χ = 2.2 this is the case at Λ ≈ 0.31 (a spinodal close to that, namely for Λ = 0.275, is shown in Fig. 2). And finally, note that for small Λ each spinodal (for fixed χ and Λ) consists of four individual segments. For sufficiently large Λ, the spinodal is described by a single closed curve in the φ,ψ-plane. The smallest Λ for which this appears to be the case is

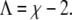(9)

For example, χ = 2.2 leads to Λ = 0.2; shown in Fig. 2. To summarize, a growing coupling parameter Λ restricts the regions of local instability of the bilayer but does not affect the critical point.

FIGURE 2.

Spinodal lines for χ = 2.2 and Λ = 0.02 (a), Λ = 0.2 (b), Λ = 0.275 (c), and Λ = 5 (d). The spinodals represent solutions of Eq. 5.

Let us now calculate the binodal phase behavior, with all multiphase regions and representative tie-lines included. To this end, we need to minimize the overall free energy F of the bilayer, defined in Eq. 3. Because the local free energy f(φ, ψ) depends on a single compositional degree of freedom in each of the two monolayers, the membrane can for any nonvanishing coupling Λ > 0, at most, separate laterally into three phases. (Of course, in each individual phase, the compositions of the upper and lower monolayer need not be the same.) Allowing for the coexistence of three homogeneous phases we may rewrite Eq. 3 as

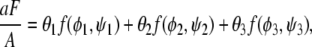(10)

where θ₁, θ₂, θ₃ are the area fractions of the three phases, φ₁, φ₂, φ₃ are the corresponding compositions of the upper monolayer, and ψ₁, ψ₂, ψ₃ are the corresponding compositions of the lower monolayer. Area fractions and compositions must fulfill the three conservation conditions θ₁ + θ₂ + θ₃ = 1, θ₁φ₁ + θ₂φ₂ + θ₃φ₃ = φ, and θ₁ψ₁ + θ₂ψ₂ + θ₃ψ₃ = ψ where φ and ψ are the fixed average compositions in the upper and lower monolayer, respectively, thus specifying a point {φ, ψ} in the phase diagram (see Fig. 3). (For brevity, we shall use the same symbols φ and ψ to denote local and average compositions; everywhere below the concrete meaning of φ and ψ is uniquely determined by its context).

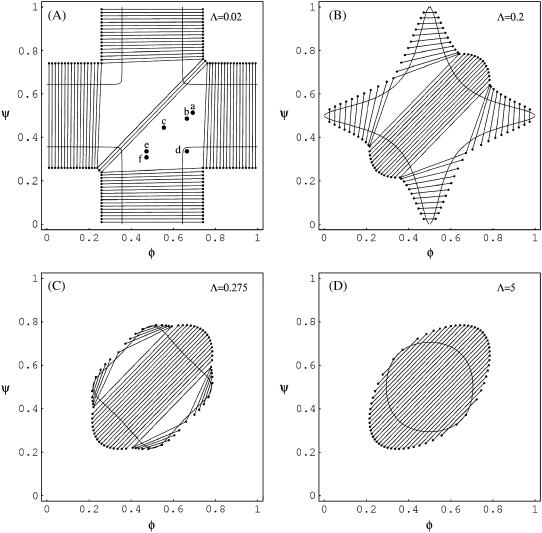
FIGURE 3.

Phase diagrams for Λ = 0.02 (top, left), Λ = 0.2 (top, right), Λ = 0.275 (bottom, left), and Λ = 5 (bottom, right). Three-phase regions are indicated by triangles. Representative tie-lines are displayed in regions of two-phase coexistence. Also shown are the spinodal lines (see also Fig. 2). Note that χ = 2.2 in all four diagrams. The points marked a–f in diagram A indicate systems for which we have carried out simulations of their morphological phase structure; see below in Fig. 4, A–F.

Owing to the three conservation conditions, only six variables in Eq. 10 are independent. In thermal equilibrium, the free energy F adopts its global minimum with respect to these six variables. The minimization can be carried out numerically; results of phase diagrams as functions of the fixed average compositions φ and ψ are shown in Fig. 3, derived for χ = 2.2 and various choices of Λ. Again, changing χ does not affect the qualitative features of the phase diagrams. Let us discuss the influence of the coupling parameter Λ.

In the absence of coupling, Λ = 0, the two monolayers, if unstable, phase-separate independently from each other. For example, if only the upper monolayer is unstable, then a tie-line parallel to the φ-axis of the phase diagram indicates the two coexisting compositions φ₁ and φ₂ = 1 – φ₁, which solve the equation ln [φ/(1 – φ)] = χ(2φ – 1). This last equation corresponds to the familiar common tangent construction. Instability of both monolayers would lead to a phase coexistence with compositions φ₁, φ₂ = 1 – φ₁ and ψ₁ = φ₁, ψ₂ = φ₂ in the upper and lower monolayer, respectively. Morphological phase structure and dynamic evolution toward the equilibrium structure in one monolayer is entirely independent from that in the apposed monolayer. Therefore phase morphologies in both monolayers are spatially uncorrelated in the limit Λ → 0.

For nonvanishing but still sufficiently small coupling parameter, Λ, we find both two-phase and three-phase coexistence regions. Let us first discuss two-phase coexistence. Consider, for example, Λ = 0.02 which is shown in Fig. 3 A. If only the upper monolayer is unstable, say at φ = 0.5 and ψ = 0.1, it will split into two phases. Yet, the corresponding tie-line is tilted with respect to the φ-axis, implying that a compositional difference is also induced in the lower monolayer. (The tilt of the tie-lines grows with the coupling parameter Λ.) Hence, if without coupling one monolayer is unstable and the other monolayer is stable, the coupling between them may induce phase-separation in both monolayers. In this scenario, the phases in both monolayers are in complete registration.

The phase diagrams in Fig. 3 also predict another possibility. A membrane with its two monolayers—one being stable and the other unstable without coupling—may not phase separate at all if coupling is present. This is evident from the decrease in size of the four symmetric two-phase regions with increasing Λ (see Fig. 3 B) for Λ = 0.2 and, even more pronounced, for Λ = 0.275 (see Fig. 3 C).

Three-phase coexistence is equivalent to incomplete phase registration across the bilayer. Yet, regions of three-phase coexistence only exist below a certain coupling strength Λ*. Above this maximal coupling strength, the membrane no longer exhibits three-phase coexistence. We can calculate Λ* by noting that along the spinodal ψ(φ) two critical points merge at position φ = φ_m with 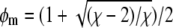(see Eq. 7). This can be written as

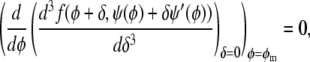(11)

where the prime in ψ′(φ) denotes the first derivative with respect to the argument. Solving Eq. 11 leads to the maximal coupling strength

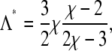(12)

above which three-phase coexistence does not exist. (It is interesting to note that Λ* = 3Λ_v/2; see Eq. 8.) For χ = 2.2, three-phase coexistence thus ceases to exist for Λ > 0.47.

The sizes of the three-phase regions shrink with growing coupling parameter, as is evident from Fig. 3, A–C. In fact, the three-phase regions are replaced by an additional two-phase region (absent for Λ = 0) that has all its tie-lines parallel to the diagonal φ = ψ, implying a constant compositional difference across the monolayers everywhere in the membrane. This is the most restrictive effect that the coupling between the monolayers can have. Hence, the additional two-phase region represents the strong coupling limit. Indeed, for large coupling parameter, Λ ≥ Λ*, the phase diagram has all its tie-lines with slope of 1 in the φ,ψ-diagram. Fig. 3 D displays this limiting case of large coupling.

Our final comment concerns the phase behavior of a membrane that has one of its two monolayers being a binary mixture whereas the other one contains only a single component. Assume the mixed monolayer is unstable for Λ = 0. Our phase diagrams show that with increasing coupling parameter the region of instability of the bilayer decreases until, eventually, a phase transition is completely absent. The strength of the coupling parameter beyond which phase separation ceases is Λ = χ – 2, corresponding to Eq. 9, for which the spinodal line starts forming a single closed curve in the phase diagram. With χ = 2.2, this happens for Λ = 0.2; shown in Fig. 3 B.

LANDAU EXPANSION

Close to the critical point it is convenient to expand the free energy into a series up to fourth-order in the order parameters. This often provides a means to characterize the phase behavior in terms of analytical expressions. Here, we shall also demonstrate the use of such a Landau expansion. The order parameter of the binary lipid membrane is the composition, φ in the lower monolayer and ψ in the upper monolayer. The critical point is adopted at φ = ψ = 1/2. It will be convenient to define the two new scaled compositions,

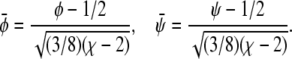(13)

We then expand the free energy f_L = (4/3)f(φ, ψ)/(χ – 2)² up to fourth-order in 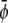and 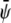at position 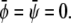The result can be written up to an irrelevant constant term as

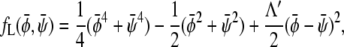(14)

where we have defined the normalized coupling strength Λ′ = Λ/(χ − 2). The reason for introducing scaled compositions is now evident: 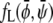depends on Λ and χ only through the normalized coupling strength Λ′. Hence, close to the critical point (where the Landau expansion is valid), the phase behavior only depends on one single parameter. This justifies presenting a sequence of phase diagrams in Fig. 3 as function of Λ for only one single value χ. Different choices of χ do not lead to qualitatively different behavior in the phase diagrams.

It is obvious that for Λ′ = 0 the free energy 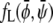decouples into two additive contributions. In this case, the binodal lines (representing solutions of the common tangent construction) are located at 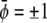and 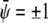with constant 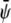and constant 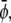respectively. The corresponding spinodal lines are 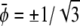and 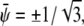which agrees with Eq. 7 for small χ – 2.

Let us first investigate the limit of small coupling Λ′. Here, the phase diagram contains both three-phase and two-phase regions. Using the case Λ′ = 0 as a reference state, we can perform an expansion of the phase coexistence equations with respect to small Λ′. For the three-phase region we then obtain the triangle, 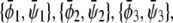of coexisting (scaled) compositions in the upper and lower monolayer. Our calculation yields 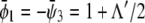and 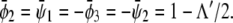This indeed describes the shift in the lower phase triangle (φ > ψ in Fig. 3) as a function of Λ. Analogous expressions are valid for the upper phase triangle (where φ < ψ).

A similar expansion of the coexistence equations with respect to the coupling parameter can be performed to obtain the tie-lines of the two-phase region in the limit of small Λ′. More specifically, we calculate the lower set of almost horizontal tie-lines in the phase diagram (see Fig. 3 A). Here the resulting two coexisting bilayer compositions 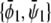and 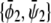define an almost horizontal tie-line (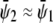) that crosses through the point 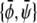of given (scaled) average compositions of the two monolayers. Our calculation leads to 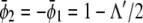and

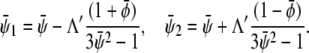(15)

Analogous expressions can be derived for the other almost horizontal and two almost vertical sets of tie-lines (see next paragraph for the remaining set of tie-lines that are parallel to the φ = ψ-diagonal of the phase diagram).

Let us now investigate the limit of large coupling parameter. (This analysis is valid for all tie-lines at Λ > Λ*, and also applies to the set of tie-lines parallel to the φ = ψ-diagonal of the phase diagram for 0 < Λ < Λ*.) As argued above, no three-phase coexistence region exists in this regime. Hence, the membrane can only exhibit two-phase coexistence. Whenever this is the case, the two monolayers have the same compositional difference between their respective phases. This fact can be used to solve the coexistence equations for any point of given (scaled) average compositions 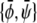within the two-phase region. 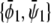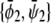The result for the two coexisting bilayer compositions and is

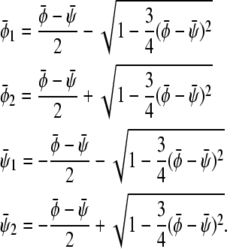(16)

Again, it can be verified that the corresponding tie-lines cross the point 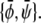The tie-lines described by Eq. 16 are indeed parallel to the diagonal ψ = φ of the phase diagram. In the φ, ψ-phase diagram, there are two critical points where the binodal and spinodal lines merge (see Fig. 3 D). These points are and 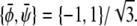The longest tie-line, extending along the 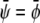-diagonal, connects the two points 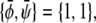and 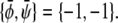We thus see that the binodal region in the regime Λ > Λ* corresponds to an ellipse with ratio 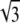between its long and short axis (see Fig. 3).

MORPHOLOGIES

We also simulated the dynamic phase-separation process using a lattice Boltzmann method (see Appendix for details) based on the Landau expansion of the free energy, Eq. 14. We simulated the following equations of motion. For the total density ρ we have the continuity equation

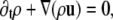(17)

where u denotes the mean fluid velocity, and the Navier-Stokes equation for the total momentum

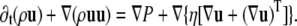(18)

Here P is the pressure tensor given by Eq. 24 and η is the viscosity. For the order parameters 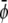and 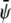the drift diffusion equation reads

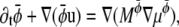(19)

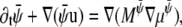(20)

where 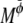and 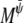are Onsager coefficients. The chemical potentials, 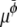and 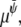are derived from the Landau free energy, Eq. 14, with the additional interfacial energy term, 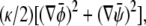given by Eq. 28 and Eq. 29.

Simulations for parameters leading to a two-phase region give rise to the usual morphologies seen for coarsening of two-phase systems (28). More interesting are the three-phase regions on which we focus here. In the following, it is sufficient to consider the case where the initial value of 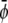(that is, the scaled average composition of the upper monolayer) is larger than the corresponding initial value of 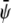(the scaled average composition of the lower monolayer). The three equilibrium phases are then 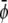-rich and 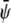-rich domains (condensed-condensed), 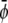-rich and 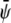-poor domains (condensed-uncondensed), and 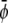-poor and 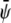-poor domains (uncondensed-uncondensed). In Fig. 4 these domains are shown as bright, gray, and dark domains, respectively. We initialized our simulations with homogeneous compositions 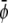and 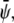modulated with small spatial disturbances to initiate spinodal decomposition.

FIGURE 4.

Dynamically formed membrane domain morphologies for different compositions of the upper and lower monolayers for parameters in the three-phase region of the phase-diagram. The three equilibrium phases are 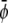-rich and 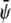-rich domains (bright, condensed-condensed), 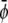-rich and 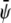-poor domains (gray, condensed-uncondensed) and 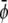-poor and 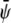-poor domains (dark, uncondensed-uncondensed). Generally, domains are in complete registration. That is, domains in one monolayer are fully contained in the domains of the other monolayer. Or, equivalently expressed, domain boundaries never cut each other. Simulations A–F correspond to the points a–f of the phase diagram shown in Fig. 3 A.

Six examples of typical morphologies are shown in Fig. 4 for Λ′ = 0.1. Note that for χ = 2.2 the choice Λ′ = 0.1 corresponds to Λ = Λ′(χ – 2) = 0.02. We thus simulate morphologies in the three-phase region of Fig. 3 A. The corresponding points are indicated in the phase diagram of Fig. 3 A. That is, point a in Fig. 3 A corresponds to the system simulated in Fig. 4 A, and analogously for points b–f. Note that for values of Λ′ an order-of-magnitude smaller (Λ′ ≤ 0.01) the domains begin to decouple dynamically, implying that domain boundaries start crossing each other. Morphologically, this is reminiscent of recent observations in solid-supported lipid bilayers where domains are not registered because domains in the substrate-facing monolayer are immobilized (14–16). In all simulations displayed in Fig. 4, the coupling parameter Λ′ = 0.1 is sufficiently high so that domains of one monolayer are always fully contained within domains of the other monolayer. In other words, the domains in the apposed monolayers are in full registration. All of the displayed morphologies are time-dependent and they continue to coarsen through the coalescence of domains (viscous hydrodynamic growth) and the occasional evaporation of very small domains (Oswald ripening).

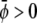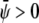If both average (scaled) compositions are larger than zero ( and ) the membrane will form predominantly the condensed phase in both monolayers. This is the case in Fig. 4 A, derived for 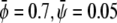where we indeed observe a large and continuous bright domain, enclosing gray domains that themselves each enclose one or more small dark domains. Recall that the upper monolayer, present with large composition, forms the uncondensed phase only within the dark domains. Decreasing both 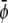and 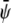(see Fig. 4 B) derived for 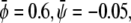favors formation of the gray phase; this phase then becomes the majority phase and contains distinct sets of bright and dark domains.

Symmetric systems, 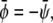are displayed in Fig. 4, C and D. For small absolute values of 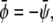the system resembles a familiar two-phase fluid where the gray phase decorates the interface of the dark and bright domains (see Fig. 4 C). For larger absolute values, the area fraction of the gray domains increases until there is a mixture of dark and bright domains suspended in a gray matrix (see Fig. 4 D).

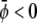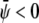If both and the membrane tends to form mostly the uncondensed phase in both monolayers (of course, more of it in the lower monolayer because we have assumed 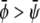). This is seen in Fig. 4, E and F, where we indeed observe mostly the dark phase. Because of the and 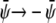symmetries this is roughly the complementary morphology to Fig. 4 A. Note for Fig. 4 E that we find only one single white domain enclosed in each gray one. The coarsening dynamics provides the reason for this observation: if the gray domains coarsen more slowly than the domains dispersed in them we will always end up with only one single domain suspended. If the gray domains coarsen faster than the domains dispersed in them we will end up with gray domains that contain an increasing number of smaller domains. Examples of the latter are shown in Fig. 4, A and F.

To discuss the dynamics of this simple model in relation to that observed in experiments it is important to compare several timescales. The first timescale refers to the phase-separation process which is roughly given by the time it takes to de-mix an initially homogeneous lipid layer and form small domains. The next two timescales are related to the coarsening of the domains. There are two coarsening mechanisms present: a diffusive coarsening mechanism dominating at small length scales and a hydrodynamic coarsening mechanism dominating for large domains. This is the case for all fluid mixtures.

In our special case there is an additional timescale involved. This timescale specifies the coupling of the hydrodynamics between the domains in both leafs of the membrane. If this coupling is small, or if one monolayer is prevented from hydrodynamic motion by being immobilized on a solid substrate, the domains may become spatially decoupled and registration of the domains can be lost. This is seen in experiments (14,15) using supported membranes where the hydrodynamic motion of the support-facing monolayer is inhibited or recovered by an additional polymer cushion (16,17).

CONCLUSIONS

This study investigates how the coupling between the two monolayers of a lipid membrane affects the phase behavior in each of the two membrane leaflets. Our model employs only one order parameter. In this respect it is simpler than previous theoretical studies (20,21). Still, it makes a number of nontrivial and experimentally verifiable predictions. First, if one monolayer leaflet is unstable it may induce phase separation in the apposed monolayer, even if this monolayer would be stable otherwise. A stable monolayer may also suppress phase separation in the apposed intrinsically unstable monolayer. If phase separation occurs, it always occurs in both monolayers, but is generally weaker in the more stable monolayer. This might be of relevance for the plasma membrane for which the extracellular leaflet typically contains a raft-forming lipid mixture whereas the cytoplasmatic one does not. Somewhat surprisingly, our simple model predicts that for low coupling strength the domains in the two monolayers are not always in registration. This is manifested by the presence of three-phase coexistence in the phase diagram. Here, each monolayer contains three phases of different compositions. The compositions of the two monolayers can be different but the three phases in each monolayer must be in perfect registration for thermodynamic reasons. Morphologically, the three-phase coexistence appears as two sets of domains, one contained in the other. Above a critical coupling strength (which we have calculated analytically; see Eq. 12) three-phase coexistence is no longer possible, and the membrane can only split into two phases in each monolayer that are always in perfect registration.

As our model is based on one single order parameter it should be the simplest model to investigate intermonolayer coupling. The simplicity of the model implies a considerable number of approximations. In particular, all effects related to other degrees of freedom beyond compositional changes are neglected. This includes curvature degrees of freedom (20), thickness changes of the membrane (21), and flip-flop (which could be particularly relevant for cholesterol (29).) In addition, we have considered a two-component system, thus neglecting the three components that are commonly used to produce fluid-phase coexistence (cholesterol and two lipid species with one of which cholesterol interacts more favorably). Note also that the coupling parameter between the two monolayers, Λ (see Eq. 2), was introduced phenomenologically; hence, it does not reveal the molecular origin of the coupling. At this point, further modeling studies might be useful to extract the source(s) of the coupling and to estimate the actual magnitude of Λ. Finally, we have assigned the same nonideality parameter, χ, to both leaflets of the membrane. A more general approach would allow for different free energy functions (and thus two different χ) in both monolayers. Still, the surprising variety of predicted phenomena makes us confident that our model captures some essential features of the coupling between the apposed monolayers and its thermodynamic implications.

APPENDIX: LATTICE BOLTZMANN

The application of the lattice Boltzmann method to the coupled leaflets of a lipid bilayer is presented here for the first time. It is based on a free energy in the spirit of the original Swift model (30,31) and consists of evolution equations for the densities 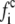for component c associated with a lattice velocity v_i

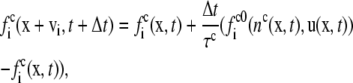(21)

where the density is 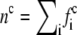and u denotes the mean fluid velocity. The equilibrium distribution is given by

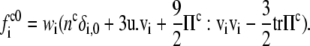(22)

We will use a standard D2Q9 velocity set of

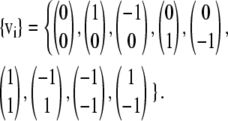(23)

For this velocity set the weights are w₀ = 1, w_1–4 = 1/9, and w_5–8 = 1/36.

We use three lattice Boltzmann equations to represent the total density ρ and the two order parameters 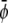and 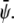The first density can then be used to define the mean fluid velocity through 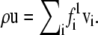The pressure tensor is given by

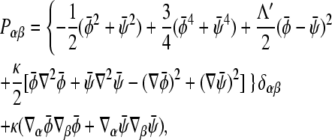(24)

and we choose

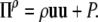(25)

For the other two Π we choose

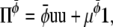(26)

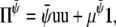(27)

where the chemical potentials are given by

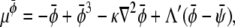(28)

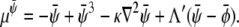(29)

A Taylor expansion method can then be used to derive the hydrodynamic equations simulated by this lattice Boltzmann method (28). The resulting equations are Eqs. 17–20 with η = n⁰(τ^ρ – 1/2)/3, 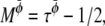and 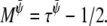We performed our simulations on a 250² lattice. The simulation parameters were κ = 0.5, 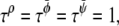Δt = 0.1, and Λ′ = 0.1.