Speeding the Recovery from Ultraslow Inactivation of Voltage-Gated Na⁺ Channels by Metal Ion Binding to the Selectivity Filter: A Foot-on-the-Door?

Abstract

Slow inactivated states in voltage-gated ion channels can be modulated by binding molecules both to the outside and to the inside of the pore. Thus, external K⁺ inhibits C-type inactivation in Shaker K⁺ channels by a “foot-in-the-door” mechanism. Here, we explore the modulation of a very long-lived inactivated state, ultraslow inactivation (I_US), by ligand binding to the outer vestibule in voltage-gated Na⁺ channels. Blocking the outer vestibule by a mutant μ-conotoxin GIIIA substantially accelerated recovery from I_US. A similar effect was observed if Cd²⁺ was bound to a cysteine engineered to the selectivity filter (K1237C). In K1237C channels, exposed to 30 μM Cd²⁺, the time constant of recovery from I_US was decreased from 145.0 ± 10.2 s to 32.5 ± 3.3 s (P < 0.001). Recovery from I_US was only accelerated if Cd²⁺ was added to the bath solution during recovery (V = −120 mV) from I_US, but not when the channels were selectively exposed to Cd²⁺ during the development of I_US (−20 mV). These data could be explained by a kinetic model in which Cd²⁺ binds with high affinity to a slow inactivated state (I_S), which is transiently occupied during recovery from I_US. A total of 50 μM Cd²⁺ produced an ∼8 mV hyperpolarizing shift of the steady-state inactivation curve of I_S, supporting this kinetic model. Binding of lidocaine to the internal vestibule significantly reduced the number of channels entering I_US, suggesting that I_US is associated with a conformational change of the internal vestibule of the channel. We propose a molecular model in which slow inactivation (I_S) occurs by a closure of the outer vestibule, whereas I_US arises from a constriction of the internal vestibule produced by a widening of the selectivity filter region. Binding of Cd²⁺ to C1237 promotes the closure of the selectivity filter region, thereby hastening recovery from I_US. Thus, Cd²⁺ ions may act like a foot-on-the-door, kicking the I_S gate to close.

INTRODUCTION

Voltage-gated Na⁺ channels are key players in the regulation of excitability in nerve and muscle. One mechanism by which excitability may be modulated is the entry of these channels into slow inactivated states upon depolarization. When slow inactivated channels are repolarized they do not recover until hundreds of milliseconds or even several hundred seconds have elapsed, thereby causing prolonged refractoriness.

Defective slow inactivation in voltage-gated Na⁺ channels has been associated with a number of disease states of the central nervous system (1–3), skeletal muscle (4–6), and the heart (7,8).

Many compounds alter the function of ion channels by modulation of their gating behavior (9). Modification of gating may arise from high-affinity binding to a specific state of the channel, resulting in stabilization of the high-affinity state with respect to low-affinity states (10,11). One possibility by which such stabilization may be envisioned on a molecular basis was first reported for quaternary ammonium compounds in voltage-gated K⁺ channels: Clay Armstrong proposed that a compound bound to the inner pore prevented normal closure of the activation gate (“foot-in-the-door”) and that channels could close only after the drug dissociated from its binding site (12). A similar mechanism can also be operative at the outer vestibule of ion channels: In Shaker-type K⁺ channels (Kv1) external tetraethylammonium and external K⁺ ions compete with an inactivation process (C-type inactivation) by a foot-in-the-door mechanism, giving rise to the idea that C-type inactivation is produced by a constriction or partial collapse of the outer vestibule of the channel (13–17).

μ-Conotoxin GIIIA (μ-CTX) interacts with voltage-gated Na⁺ channels by plugging the outer vestibule (18,19). Investigation of possible kinetic effects of this toxin has long been prevented by the slow off-rate of the compound. However, the construction of mutant derivatives of μ-CTX, which act as partial blockers, recently enabled assessment of the gating behavior in the blocked state (20–22). Using this approach we were able to demonstrate that μ-CTX R13Q interacts with a very stable inactivated state, which we refer to as “ultraslow inactivation” (I_US). Thus, when μ-CTX R13Q was bound, both the amplitude and the time constant of ultraslow recovery were significantly reduced (21). Superficially this mode of action was reminiscent of the interaction of K⁺ and of tetraethylammonium with Shaker K⁺ channels (15) suggesting that, similar to C-type inactivation in Shaker K⁺ channels, I_US results from a constriction of the outer vestibule. Other forms of slow inactivation in voltage-gated Na⁺ channels have also been associated with a closure of the outer vestibule (23–31).

On the other hand, the likelihood of entry into I_US was dramatically enhanced if a key residue in the selectivity filter of the rNa_V1.4 channel, K1237, was replaced by a glutamic acid (21). In addition to changing the gating behavior, mutations at this site also severely affected ion selectivity, allowing for the permeation of both K⁺ and Ca²⁺ ions as well as enabling the passage of large organic cations like choline (32–37). Hence, the mutation K1237E most likely increased the diameter of the selectivity filter rather than causing a constriction. This prompted us to propose a widening rather than a constriction of the outer vestibule as the molecular mechanism underlying I_US (38): If I_US is indeed produced by a widening of the outer vestibule, then inhibition of I_US by μ-CTX R13Q most likely results from a stabilizing action on the structure of the channel. Hence, the binding of the toxin to the external vestibule may impede the widening of the vestibule by acting as a “splint in the vestibule” (21). However, whereas the mutation which greatly enhanced the likelihood of entry into I_US was located at the selectivity filter of the channel (K1237E), μ-CTX has been shown to mainly interact with residues more external to this site (18,19,39–43), suggesting that I_US encompasses a broad rearrangement of the outer vestibule. In addition, widening of the outer vestibule fails to explain why the channel is nonconducting. A possible explanation is found in experiments showing that lidocaine bound in the inner pore also accelerates recovery from I_US (44). Perhaps the failure of conduction is a tilting of the pore lining such that the inner pore is blocked.

The aim of this study was to explore whether I_US can be modulated by a direct interaction between a molecule and the site 1237. For this purpose we tested the effect of binding Cd²⁺ ions to a cysteine engineered to this site. We found Cd²⁺ to substantially accelerate recovery from I_US without affecting entry into this state. We suggest that, during recovery, Cd²⁺ ions enter the pore in a voltage-dependent manner and bind in a coordinative manner to one or more sites at the level of the selectivity filter. This binding of Cd²⁺ promotes a constriction of the outer vestibule which, in turn, results in a weakening of the interaction between the selectivity filter and the S6 segment, thereby speeding recovery from I_US. Thus, rather than acting as a foot-in-the-door, Cd²⁺ ions may “kick the door” and close the gate responsible for I_US (“foot-on-the-door”).

MATERIALS AND METHODS

A detailed description of materials and methods is given in our previous work (22).

Site-directed mutagenesis

Detailed methods for the mutagenesis have been published previously (18,21,45).

Electrophysiological recordings

Two-microelectrode voltage clamp recording in Xenopus oocytes

All experiments except those summarized in Fig. 8 C were performed using the two-electrode voltage clamp technique in Xenopus laevis oocytes. Stage V and VI Xenopus laevis oocytes were isolated from female frogs (NASCO, Ft. Atkinson, WI), washed with Ca²⁺-free solution (90 mM NaCl, 2.5 mM KCl, 1 mM MgCl₂, 1 mM NaHPO₄, and 5 mM HEPES titrated to pH 7.6 with 1 N NaOH), treated with 2 mg/ml collagenase (Sigma, St. Louis, MO) for 1.5 h and had their follicular cell layers manually removed. As judged from photometric measurements, ∼50–100 ng of complementary RNA (cRNA) was injected into each oocyte with a Drummond microinjector (Broomall, PA). Either native or mutant α subunit cRNA was mixed with rat brain β₁ cRNA at a molar ratio of 1:1. Oocytes were incubated at 17°C for 12 h to 3 days before examination.

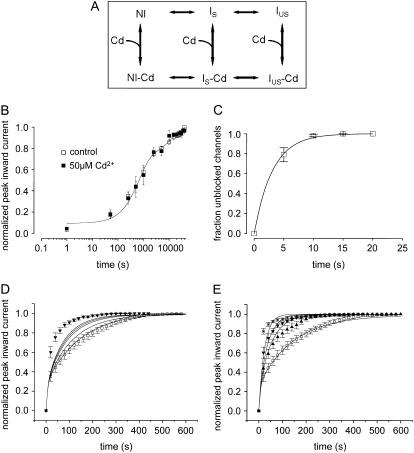
FIGURE 8.

(A) Kinetic modeling of the modulation of I_US by Cd²⁺. Hypothetical scheme of the proposed kinetic states and transitions. Upper row depicts Cd²⁺-free states: NI = noninactivated, I_S = slow inactivated, I_US = ultraslow inactivated. Lower row: Cd²⁺-bound states. (B) Time course of recovery from slow inactivation. From a holding potential of −120 mV, channels were depolarized to −20 mV for 25 s. Thereafter, the membrane potential was returned to −120 mV for the indicated time periods after which channel availability was tested by a 20-ms pulse to −20 mV. Peak inward currents were normalized to the value after full recovery. The time course of recovery was determined during a control period and during superfusion with 50 μM Cd²⁺. Data points were fitted with double exponential functions (Eq. 5). The parameters were drug free: A₁ = 0.62 ± 0.04, τ₁ = 573.2 ± 32.3 ms, A₂ = 0.30 ± 0.02, τ₂ = 6493.4 ± 56.3 ms; Cd²⁺: A₁ = 0.61 ± 0.07, τ₁ = 663 ± 64.3 ms, A₂ = 0.29 ± 0.03 (P = n.s.), τ₂ = 6828.5 ± 90.4 ms, n = 3; P = n.s. (C) Time course of relief from block by 50 μM Cd²⁺ in K1237C channels. K1237C channels were heterologously expressed in tsA201 cells and examined by the whole-cell patch-clamp technique. Cells were held at −120 mV, and inward currents were elicited by 10 ms depolarizations to −20 mV at 20-s intervals. Data points were fitted with a monoexponential function (Eq. 6). See text for fitting parameters. (D) Model A: Modulation of I_US by low-affinity binding of Cd²⁺ to the I_US state. Data points are time courses of recovery during control and during exposure to 20 μM Cd²⁺ (i.e., a concentration close to the K_D), taken from Fig. 2 C. Lines are model calculations assuming rates of unbinding of Cd²⁺ from the I_US state to be reduced with respect to the unbinding rates from the I_S and NI state by factors 0, 2, 5, 10, 100, and 1000 (lines in order from right to left). The lines representing model calculations assuming unbinding rates 100-fold and 1000-fold lower for I_US than for I_S and NI are superimposed. (E) Model B: Modulation of I_US by high-affinity binding of Cd²⁺ to the I_S state. The affinity of Cd²⁺ to the I_S state was assumed to be 10 times higher than the affinities for the NI and the I_US states. Data points are the same as in Fig. 2 D. Lines from right to left represent calculations assuming the following concentrations of Cd²⁺: 0 μM, 10 μM, 20 μM, and 50 μM.

Recordings were made in the two-electrode voltage clamp configuration using a TEC 10CD clamp (npi electronic, Tamm, Germany). For accurate adjustment of the experimental temperature (18°C ± 0.5°C) an oocyte bath cooling system (HE 204, Dagan, Minneapolis, MN) was used. Oocytes were placed in recording chambers in which the bath flow rate was ∼100 ml/h, and the bath level was adjusted so that the total bath volume was <500 μl. Electrodes were filled with 3 M KCl and had resistances of <0.5 MΩ. Using pCLAMP6 software (Axon Instruments, Foster City, CA), data were acquired at 71.4 kHz after low-pass filtration at 2 kHz (−3 dB). Recordings were made in a bathing solution that consisted of (in mM): 90 NaCl, 2.5 KCl, 1 BaCl₂, 1 MgCl₂, and 5 mM HEPES titrated to pH 7.2 with 1 N NaOH. BaCl₂ was used as a replacement for CaCl₂ to minimize Ca²⁺-activated Cl⁻ currents. In some experiments [Na⁺]_o was reduced by equimolar replacement with N-methyl-D-glucamine-chloride. Lidocaine was obtained from Sigma. The derivative of μ-CTX, R13Q, in which arginine 13 is replaced by a glutamine, was made as previously described (46). To examine the modification of K1237C channels by Ag⁺, AgNO₃ was added to the bathing solution at a concentration of 500 nM. Due to high concentration of Cl⁻ ions in the bath solution, the concentration of free Ag⁺ ions is limited by the low solubility of AgCl. To determine the final concentration of Ag⁺ we first considered the temperature dependence of the solution product (K_sp) of AgCl. Reported values of the K_sp are 2.54 × 10⁻¹¹, 7.05 × 10⁻¹¹, 1.78 × 10⁻¹⁰, 4.16 × 10⁻¹⁰, 6.17 × 10⁻¹⁰, and 1.32 × 10⁻⁹ mol² l⁻¹ at temperatures of 5°C, 15°C, 25°C, 35°C, 40°C, and 50°C, respectively (47). The temperature dependence of these K_sp values could be well fitted (R² = 0.99) by a single exponential equation of the form

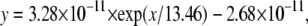(1)

which yielded a K_sp of 1.18 × 10⁻¹⁰ mol² l⁻² at 20°C. Furthermore, we considered the ionic activities (a_i) of the dissolved ions (i), which are given by

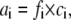(2)

where f_i is the activity coefficient of the ion i. f_i can be calculated following the equation of the Debeye-Hückel theory:

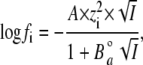(3)

where is the ion size parameter and I is the ionic strength (i.e., 103 mM for the bathing solution). For the calculation, the following values were used (47): A = 0.507, B = 0.328, (Ag⁺) = 2.5 Å,

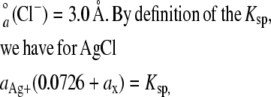(4)

because a_x is small in comparison to 0.0726 M, it can be disregarded. Also, 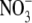ions were not considered because of their low concentration in comparison to Cl⁻ ions. Rearrangement of Eq. 4 yields an ionic activity of Ag⁺ of 2.19 nM. This low activity was sufficient for the irreversible modification of the thiolate group of the cysteine side chains.

Whole-cell patch-clamp recording

To determine the off-rate of Cd²⁺ from K1237C channels (see Fig. 8 C), experiments were performed using the whole-cell patch-clamp recording technique. TsA201 cells were grown in Dulbecco's modified Eagle's medium supplemented with 10% fetal bovine serum and 20 units/ml each of penicillin and streptomycin (Gibco, Gaithersburg, MD). Cells were maintained at 37°C in a humid atmosphere containing 5% CO₂. Before recording, cells were dissociated from their substrate by treatment with a 0.25% trypsin solution (Gibco) for ∼2 min, pelleted, resuspended in bath solution, and allowed to settle to the bottom of the recording chamber. Channel DNA was transiently transfected into tsA201 cells using a calcium phosphate transfection system (Gibco).

Na⁺ currents were recorded using an Axopatch 200B patch-clamp amplifier (Axon Instruments) as in Zebedin et al. (48). Recording was begun ∼10 min after whole-cell access was attained to minimize time-dependent shifts in gating. Pipettes were formed from aluminosilicate glass (AF150-100-10; Science Products, Hofheim, Germany) with a P-97 horizontal puller (Sutter Instruments, Novato, CA), heat polished on a microforge (MF-830; Narishige, Tokyo, Japan), and had resistances between 1 and 2 MΩ when filled with the recording pipette solution (105 mM CsF, 10 mM NaCl, 10 mM EGTA, 10 mM HEPES, pH = 7.3). Peak current amplitudes equaled −1.2 ± 0.4 nA. Series resistance was minimized (>80%–90%) using the Axoclamp 200B device. As such the uncompensated voltage error across the pipette was calculated to be 3.2 ± 0.3 mV. The bath solution consisted of (in mM) 140 NaCl, 2.5 KCl, 1 CaCl2, 1 MgCl2 10 HEPES. Voltage-clamp protocols and data acquisition were performed with pclamp 6.0 software (Axon Instruments) through a 12-bit A-D/D-A interface (Digidata 1200; Axon Instruments). Data were low-pass filtered at 2 kHz (−3 dB) and digitized at 10–20 kHz.

The external solution containing Cd²⁺ was applied via a DAD-12 drug application device (Adams & List, Westbury, NY). This superfusion system delivers buffers from 12 reservoirs under pressure (200–400 mm H₂O) via a capillary with an inner diameter of ∼100 μm and permits a complete exchange of solutions surrounding the cells under investigation within 100 ms (49).

Data evaluation. The time courses of recovery from I_US of normalized peak inward currents were fit with the double exponential function:

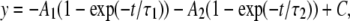(5)

where τ₁ and τ₂ are the time constants of distinct components of recovery, A₁ and A₂ are the respective amplitudes of these components, and C is the final level of recovery.

The time course of entry into I_US was fitted with the monoexponential function:

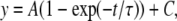(6)

where τ is the time constants of entry and C is the final level of entry.

To determine the dissociation constant (K_D) of Cd²⁺ from Na⁺ channels, 10-ms test pulses to −20 mV (Vh = −120 mV) were applied at 20-s intervals during Cd²⁺-free conditions and during superfusion with various concentrations of Cd²⁺. Data plots of the fractional block as a function of Cd²⁺ concentration were then fitted with the Hill equation:

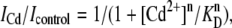(7)

where I_Cd and I_control are maximum inward currents during exposure to Cd²⁺ and during control, respectively, K_D is the midpoint of the curve, and n is the Hill coefficient.

Steady-state inactivation data were fitted with a Boltzmann function

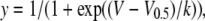(8)

where V is the voltage of the conditioning prepulse, V_0.5 is the voltage at which half-maximum inactivation occurred, and k is the slope factor.

To determine the voltage-dependence of block by Cd²⁺ ions, the following equation was fitted to the data points in the inset to Fig. 9 B (50):

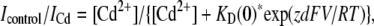(9)

where K_D(0) represents the apparent affinity at 0 mV, z the charge valence of Cd²⁺, d the fractional electrical distance, and F, R, and T have their usual meanings.

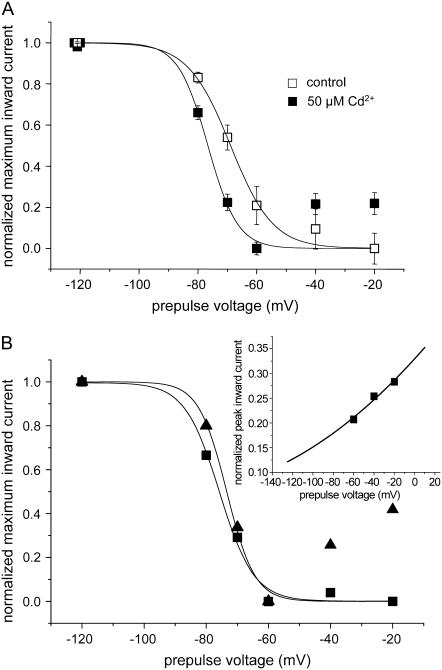
FIGURE 9.

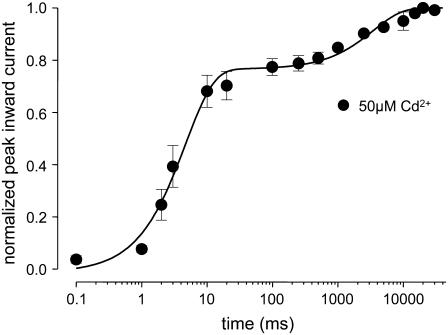
I_S is stabilized by Cd²⁺. (A) Steady-state availability curve for I_S. K1237C channels were depolarized for 25 s to different potentials, after which the membrane was hyperpolarized to −120 mV for 500 ms to allow for recovery of fast inactivated channels. Then a 20-ms test pulse to −20 mV was applied to open recovered channels. In each oocyte this protocol was performed under Cd²⁺-free conditions and after washin of 50 μM Cd²⁺. The minimum availability (−20 mV) was 0.48 ± 0.1 and was not changed by Cd²⁺. Data points were normalized for maximum and minimum availability and were fitted with a Boltzmann function (Eq. 8). The parameters were control: V_1/2 = −68.9 ± 0.8 mV, k = 7.2 ± 0.9 mV; Cd²⁺: V_1/2 = −76.6 ± 2.3 mV, k = 5.0 ± 2.2 mV, n = 6, P < 0.05). (B) Correction for voltage-dependent block left shifts the midpoint of availability and decreases its slope. Protocol, as in A, in a single oocyte exposed to 50 μM Cd²⁺. Triangles: uncorrected data points. Squares: data points corrected for voltage-dependent block. Inset: Voltage-dependent block by Cd²⁺. The data points for the voltages −60 mV, −40 mV, and −20 mV, shown in B were expressed as a fraction of the current before superfusion with Cd²⁺ and replotted. The line represents the fit of a Woodhull model (Eq. 9) to the data points. Fitting parameters were K_D(0) = 100.0 ± 6.9 μM, d = 0.13 ± 0.02, room temperature (20°C). This relationship was used to correct voltage-dependent availability (squares). Data points were normalized for maximum and minimum availability and were fitted with a Boltzmann function (Eq. 8). The parameters were uncorrected (straight line): V_1/2 = −73.4 ± 4.14 mV, k = 4.5 ± 3.6 mV; corrected (dotted line): V_1/2 = −75.8 ± 1.4 mV, k = 5.6 ± 1.2 mV.

Curve fitting was performed using ORIGIN 7.5 (MicroCal Software, Northampton, MA). Kinetic modeling was carried out using ModelMaker software (Cherwell Scientific, Oxford, UK). Data are expressed as mean ± SE. Statistical comparisons were made using the two-tailed Student's t-tests or one-way ANOVA for comparison of more than two groups. A P < 0.05 was considered significant.

RESULTS

A charge-altering mutation in the selectivity filter of rNa_V1.4 induces ultraslow inactivation

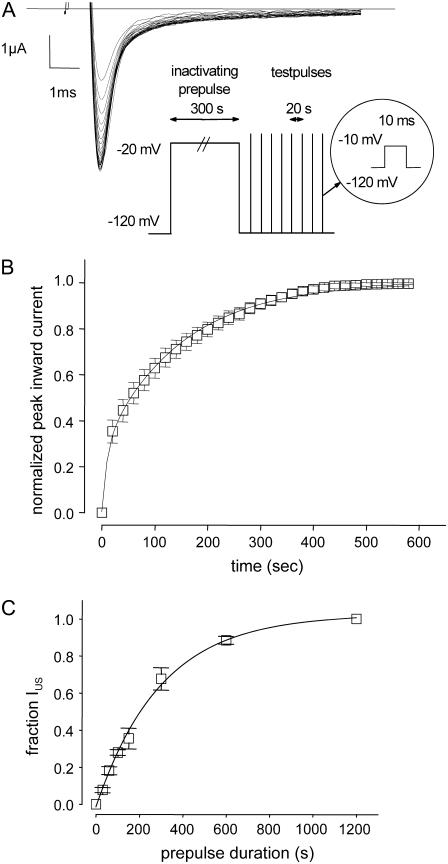
Amino acid replacement of the lysine at position 1237 in the selectivity filter of the rNa_V1.4 channel by glutamate, serine, and alanine substantially enhances the likelihood of entry into I_US during long depolarizations (>100 s; 21). To further explore the role of the nature of the amino acid and of charge at site 1237 in the modulation of I_US, we engineered a cysteine to site 1237. As shown in Fig. 1, A and B, recovery of peak inward currents from a 300-s conditioning pulse to −20 mV took several minutes. The time course of recovery could be fitted with two exponentials yielding time constants of ∼10 s and ∼100 s (Table 1, “0 μM”). The smaller time constant most likely represents recovery from slow inactivation (I_S; 51), whereas the larger time constant is typical for recovery from I_US. The amplitude of the ultraslow component of recovery (A₂ in Table 1) suggests that ∼70% of K1237C channels enter into I_US during the 300-s depolarization to −20 mV. These time constants and amplitudes are similar to those previously reported for the other mutations at site 1237, i.e., K1237E, K1237S, and K1237A (21,38). By contrast <20% of wild-type channels, or channels carrying the charge-conservative mutation K1237R, recover from I_US after a 300-s depolarization (21). Therefore, a positive charge at site 1237 appears to be essential for the prevention of entry into I_US.

FIGURE 1.

(A) Ultraslow recovery from inactivation in the mutation K1237C. Original traces of inward currents in an oocyte expressing K1237C channels. From a holding potential of −120 mV, the channels were inactivated by a depolarizing step to −20 mV of 300 s duration. After returning to −120 mV, recovery from inactivation was monitored by repetitive 20-ms steps to −10 mV at 20-s intervals. Peak inward currents were slowly rising approaching a maximum after several minutes. (B) Normalized time course of recovery from I_US. Peak inward currents from nine experiments as shown in A were normalized to the maximum current level after full recovery and plotted as a function of time after the conditioning prepulse. The time course of recovery was fitted with a double exponential function (Eq. 5). (C) Time course of development of ultraslow inactivation. The time course of recovery from I_US after varying prepulse durations was evaluated as in B (n = 4–12). The amplitudes of ultraslow recovery (A₂), as determined from fitting Eq. 5 to each time course of recovery, is plotted as a function of the duration of the conditioning prepulse. Data points were fitted with a monoexponential function (Eq. 6).

TABLE 1.

Parameters of recovery from I_US in K1237C

[Cd2+]	0 μM (n = 9)	10 μM (n = 7)	20 μM (n = 6)	30 μM (n = 6)	50 μM (n = 9)
τ1(s)	10.24 ± 1.0	6.9 ± 0.5	6.6 ± 0.7	5.2 ± 0.7*	8.4 ± 1.1
τ2 (s)	145.0 ± 10.2	70.2 ± 4.9†	55.6 ± 2.9†	32.5 ± 3.3†	—
A1	0.27 ± 0.07	0.26 ± 0.02	0.32 ± 0.03	0.76 ± 0.04†	0.87 ± 0.02†
A2	0.73 ± 0.07	0.74 ± 0.02	0.64 ± 0.02	0.24 ± 0.04‡	—

The values represent the results of fitting Eq. 5 to the data points in Fig. 2 D.

P-values vs. 0 μM: *P < 0.005. ^†P < 0.00001. ^‡P < 0.00005.

Development of I_US in K1237C was also extremely slow (τ = 299.0 ± 22.0 s), and I_US approached unity after ∼600 s, indicating that I_US is absorbing in K1237C (Fig. 1 C). Thus, replacement of lysine by cysteine at site 1237 strongly favored entry into I_US.

Recovery from I_US is modified by a mutant μ-CTX

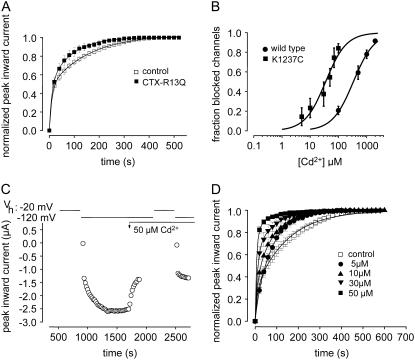
μ-CTX is a potent blocker of the outer vestibule of the skeletal muscle Na⁺ channel (18), but the mutant μ-CTX R13Q only partially blocks the outer vestibule, allowing for flow of ∼30% residual current in the blocked state (20). This property allows the investigation of kinetic changes when μ-CTX is fully bound to the channel. In an earlier report we presented evidence that binding μ-CTX R13Q to the outer pore substantially accelerated the time course of recovery from I_US after prolonged depolarizations in K1237E (21). Here, we test whether μ-CTX R13Q had a similar effect on I_US in K1237C. In the presence of 27 μM μ-CTX R13Q a significantly smaller fraction of K1237C channels appeared to be in I_US at the end of prolonged depolarizations (Fig. 2 A).

FIGURE 2.

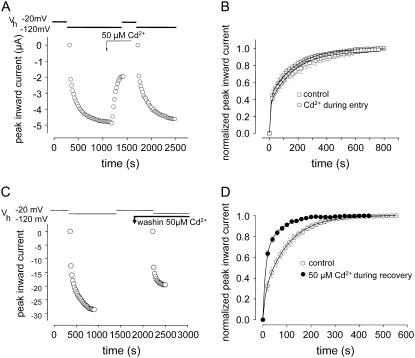
(A) The time course of recovery from I_US is modulated by a mutant μ-CTX. Experiments like those described in Fig. 1, A and B, were carried out before and after addition of 27 μM μ-CTX R13Q to the bath solution. μ-CTX R13Q significantly reduced both the amplitude and the time constant of ultraslow recovery (drug free: A₂ = 0.58 ± 0.01, τ₂ = 155.9 ± 4.3; μ-CTX R13Q: A₂ = 0.51 ± 0.01 (P = 0.03), τ₂ = 87.8 ± 2.6 (P = 0.002), n = 4). (B) Cysteine engineered to site 1237 creates a high-affinity binding site for Cd²⁺. Block by various concentrations of Cd²⁺ of maximum inward currents elicited by 20-ms depolarizations to −20 mV (Vh = −120 mV) at 20-s intervals was evaluated in wild-type (100 μM: n = 6, 500 μM: n = 5, 1000 μM: n = 4, 2000 μM: n = 3), and K1237C channels (5 μM: n = 5, 10 μM: n = 8, 30 μM: n = 5, 50 μM: n = 9, 70 μM: n = 5, 100 μM: n = 6). Data points were fitted with Eq. 3. The K_D for Cd²⁺ binding was significantly smaller in K1237C than in wild-type. (C) Speeding of recovery from I_US by Cd²⁺. Time course of peak inward currents during a typical experiment. Data points represent peak inward currents elicited by 20-ms step depolarizations to −20 mV from the indicated holding potential (Vh). During a Cd²⁺-free control, recovery from a 300-s prepulse to −20 mV was monitored analogously to the protocol described for Fig. 1 A. After recovery from ultraslow inactivation was complete, perfusion with 50 μM Cd²⁺ was started (arrow, “50 μM Cd²⁺”). After the reduction of peak Na current by Cd²⁺ had reached a steady-state level, the inactivation/recovery protocol was repeated. (D) Normalized time courses of recovery from I_US from several experiments at different Cd²⁺ concentrations. Data points were fitted with Eq. 5. The fitting results are presented in Table 1.

The binding site of μ-CTX involves residues in the P-loops located extracellularly to the selectivity filter (18,19). On the other hand, the mutation that gives rise to I_US is located within the selectivity filter ring (site 1237). The fact that μ-CTX interacts with I_US despite no direct interaction with site 1237 suggests that I_US involves a broad rearrangement of the outer vestibule. Therefore, it appeared of to be of interest whether an interaction at the level of the selectivity filter can also interfere with I_US.

Cysteine at amino acid position 1237 acts as a high-affinity binding site for Cd²⁺

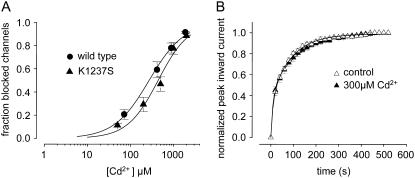
Cd²⁺ ions strongly interact with the sulfhydryl groups of cysteine residues (52). Therefore, we sought to investigate whether binding Cd²⁺ to C1237 results in a modulation of I_US. Such an interaction would tend to restore the positive charge to the selectivity filter that was lost when lysine was removed. First, we tested whether the construct K1237C binds Cd²⁺ ions with higher affinity than wild-type channels, as would be expected if the engineered cysteine formed a new binding site for Cd²⁺ ions. Oocytes expressing wild-type and K1237C channels were superfused with different concentrations of Cd²⁺, and the fractional block of maximal inward Na⁺ currents at holding potential −120 mV was determined. Short depolarizing steps were used at slow rates to avoid entry of channels into slow or ultraslow inactivated states. Plots of fractional block as a function of Cd²⁺ concentration were fitted with Hill equations (Eq. 7), yielding K_D values of 338.9 ± 10.3 μm for wild-type and 35.0 ± 1.8 μm for K1237C (P < 0.001; Fig. 2 B). The Hill factors were 1.2 ± 0.05 for wild-type and 1.2 ± 0.09 (not significant; n.s.) for K1237C, suggesting a 1:1 binding stochiometry. These dissociation constants are similar to those determined previously in this mutant (34,36). On the other hand, the low K_D of block by Cd²⁺ in the K1237C mutation could have been produced by a steric effect due to replacement of the lysine at site 1237 by a different amino acid. However, this appears unlikely because replacement of lysine 1237 by serine did not give rise to a high-affinity binding site for Cd²⁺ (see below, Fig. 3 A). Thus, the mutation K1237C created a high-affinity binding site for Cd²⁺ that resulted in block of current.

FIGURE 3.

(A) Binding of Cd²⁺ to C1237 mediates the kinetic effect on I_US. Concentration-dependent Cd²⁺ block in wild-type and in the mutant K1237S. Experimental protocol was analogous to Fig. 2 B. Data points were fitted with Eq. 3. The affinity of Cd²⁺ to K1237S channels was similar to wild-type (K_D = 440.1 ± 33 μm; n = 5; P = n.s. compared with wild-type). Data points and the fitted curve for wild-type are identical to Fig. 2 B. (B) Recovery from I_US in K1237S channels during control and after exposure to 300 μM Cd²⁺. Experimental protocol was analogous to Fig. 2 C. Data points were fitted with Eq. 5. Cd²⁺ did not change the time course of recovery from I_US (drug free: A₂ = 0.63 ± 0.04, τ₂ = 110 ± 15 s, n = 6; Cd²⁺: A₂ = 0.65 ± 0.07, τ₂ = 101 ± 17 s, n = 4; P = n.s.).

Cd²⁺ modulates the time course of recovery from I_US in the construct K1237C

To test whether I_US in K1237C is modulated by binding of Cd²⁺ ions, we monitored recovery from I_US during a Cd²⁺-free control and during subsequent superfusion with 50 μM Cd²⁺(Fig. 2 C). As shown in Fig. 2 D, Cd²⁺ dramatically altered the time course of recovery from I_US: both amplitude and time constant of recovery from I_US decreased as a function of the concentration of Cd²⁺ (Fig. 2 D, Table 1). At the highest concentration of 50 μM Cd²⁺, the time course of recovery after a 300-s depolarizing pulse to −20 mV of K1237 channels was indistinguishable from wild-type (data not shown, but see Hilber et al. 22).

Binding of Cd²⁺ to cysteine at position 1237 mediates the effect on ultraslow inactivation

The question arises, however, whether the modulation of I_US by Cd²⁺ ions resulted from interaction with C1237 or with some other superficial binding site. If the modulation of channel kinetics by Cd²⁺ resulted from interaction with site 1237, then Cd²⁺ should have had no kinetic effect on mutations at this site that do not increase binding affinity for Cd²⁺. Therefore, we tested the effect of Cd²⁺ ions on the mutant K1237S. When depolarized for 300 s, ∼60% K1237S channels entered into I_US as judged from the amplitude of the slower component of recovery (21). The affinity of Cd²⁺ ions to K1237S channels was similar to wild-type, suggesting that Cd²⁺ did not bind with high affinity to the selectivity filter of K1237S channels (Fig. 3 A). Superfusion with 300 μM Cd²⁺ did not affect the time course of recovery from I_US in K1237S (Fig. 3 B). This supports the interpretation that the modulatory action of Cd²⁺ ions on I_US in K1237C channels indeed occurs by interaction with C1237.

Acceleration of recovery is not caused by use-dependent inhibition by Cd²⁺

In the experiments shown in Figs. 1, 2, 3, 5, 6, and 7, we assessed the time course of recovery from I_US by repetitive 20-ms test pulses at 20-s intervals after the conditioning prepulse. Superfusion with Cd²⁺ reduced the time until currents reached steady-state conditions in K1237C channels in a concentration-dependent fashion (Fig. 2, C and D). However, such apparent acceleration of recovery could have been recovery from the cumulative use-dependent block by Cd²⁺ ions during the test pulses applied to monitor recovery from I_US. The combination of unchanged ultraslow recovery and cumulative block may have artifactually resulted in an acceleration of the recovery process. Therefore we tested whether K1237C channels exposed to 50 μM Cd²⁺ recovered completely during the interval between test pulses. We determined the time course of recovery from a 1-s depolarization to −20 mV. The duration of this depolarization was substantially longer than the test pulse duration in the protocols that tested recovery from I_US. Thus, even slow binding of Cd²⁺ to inactivated channels would be detected by this protocol. Fig. 4 shows that recovery from inactivation elicited by a single 1-s pulse was complete after ∼5 s. Thus, the interval of 20 s between test pulses was sufficient to avoid development of cumulative block during the recovery period.

FIGURE 5.

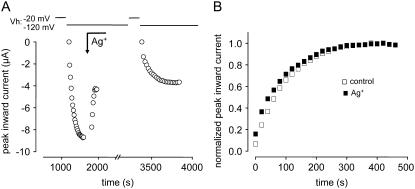
(A) Effect of Ag⁺ on I_US in K1237C. Time course of peak inward sodium currents during a typical experiment. The experimental protocol was analogous to Fig. 2 C. Because of the irreversible modification of the channels by Ag⁺, the exposure to Ag⁺ (∼2 nM) was terminated after the current was reduced to by ∼30%. (B) Normalized time course of recovery from I_US. Peak inward currents from the experiment shown in A were normalized to the respective maximum after full recovery. Superfusion with ∼2 nM Ag⁺ did not substantially affect the time course of recovery from I_US.

FIGURE 6.

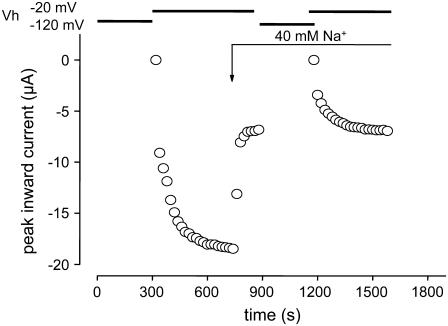
Lowering the concentration of Na⁺ does not affect the time course of recovery from I_US. Time course of peak inward sodium currents during a typical experiment. The experimental protocol was analogous to Fig. 2 C. At the time indicated by the arrow the bath solution was changed to a solution in which the 90 mM Na⁺ were replaced by 40 mM Na⁺ + 50 mM choline. The time course of recovery from I_US was not substantially changed by the solution exchange.

FIGURE 7.

Cd²⁺ has no effect on the development of I_US but selectively hastens the time course of recovery. To examine which phase of the inactivation process was modulated by Cd²⁺, the application of Cd²⁺ was restricted to either the development or the recovery process. (A) Selective application of Cd²⁺ during development of I_US. Time course of peak inward sodium currents during a typical experiment (voltage clamp protocol as in Fig. 2 C). Superfusion with Cd²⁺ was started 100 s before the conditioning prepulse to allow for steady-state Cd²⁺ concentrations to be established at the beginning of the conditioning prepulse. Exposure to Cd²⁺ was terminated 180 s before the end of the conditioning prepulse to allow for complete washout of Cd²⁺ before initiation of recovery. (B) Normalized time course of recovery. Four experiments as described in A. Data points were fitted by Eq. 5, yielding the following parameters: I_US (drug free: A₂ = 0.58 ± 0.02, τ₂ = 163 ± 6, n = 6; Cd²⁺: A₂ = 0.59 ± 0.03, τ₂ = 158 ± 4 (n.s.), n = 4). (C) Selective application of Cd²⁺ during recovery from I_US. Time course of peak inward sodium currents during a typical experiment (voltage clamp protocol as in Fig. 2 C). Superfusion with Cd²⁺ was started 120 s before the end of the conditioning prepulse to allow the bath concentration of Cd²⁺ to reach steady state at the time of the start of the recovery period. (D) Normalized time course of recovery. Four experiments as described in C. Data points were fitted to Eq. 5, yielding the following parameters: drug free: A₂ = 0.68 ± 0.04, τ₂ = 120.0 ± 5.9; Cd²⁺: A₂ = 0.64 ± 0.03 (P < 0.05), τ₂ = 64.2 ± 3.8 s, (P < 0.05).

FIGURE 4.

Cd²⁺ does not affect the time course of recovery from short depolarizations in K1237C. Oocytes were superfused with 50 μM Cd²⁺. From a holding potential of −120 mV channels were depolarized to −20 mV for 1000 ms. Thereafter, the membrane potential was returned to −120 mV for the indicated time periods, after which channel availability was tested by a 20-ms pulse to −20 mV. Peak inward currents were normalized to the value after full recovery. Data points were fitted with a single exponential function (Eq. 6). The time constant of recovery was 4.7 ± 0.2 s (n = 8).

The kinetic effect of Cd²⁺ is not due to selective block of a defined population of channels

As shown in Fig. 2, A and B, the time course of recovery of K1237C channels from a 300-s conditioning prepulse can be fitted with two exponentials, representing the recovery of at least two populations of channels (Table 1). If there is no interconversion between these populations (i.e., channels residing in slow and ultraslow inactivation, see above), the acceleration of recovery produced by Cd²⁺ may be the result of selective block of the fraction of channels determined to enter into I_US. To explore this question we tested the effect of irreversible block of the C1237 site on the time course of recovery from I_US. Ag⁺ ions react with sulfhydryl groups to form a strong Ag⁺-S bond (53). If the acceleration of recovery from I_US by Cd²⁺ resulted from simple elimination of the population of ultraslow inactivating channels, then irreversible block by Ag⁺ should have reproduced this phenomenon. As shown in Fig. 5, superfusion with ∼2 nM Ag⁺ did not affect I_US despite blocking ∼50% of channels.

Furthermore, as shown in Fig. 1 C entry into I_US approaches unity after ∼600 s. This indicates that all channels have the potential to enter into I_US, provided the conditioning pulse is long enough. This argues against the presence of distinct channel populations without interconversion. Thus, modulation of I_US results from dynamic interaction of Cd²⁺ ions with the pore of the K1237C channels. Cd²⁺ appears to bind and unbind faster than the rates of the inactivation processes, achieving an equilibrium with each inactivation state.

The kinetic effect of Cd²⁺ is not due to depletion of Na⁺ ions entering the pore

Lowering the concentration of Na⁺ ions in the pore has been shown to promote entry into slow (not ultraslow) inactivation (24,54). If we assume a linear kinetic scheme in which I_US is reached via a slow inactivated state (I_S), then lowering of the concentration of Na⁺ ions in the pore may stabilize slow inactivation and prevent further transitions from I_S to I_US. If binding Cd²⁺ ions in the pore results in depletion of Na⁺ ions from the pore, the reduction in I_US by Cd²⁺ may be a consequence of this depletion and the resulting stabilization of I_S. Therefore, we tested whether depletion of Na⁺ ions per se altered the likelihood of entry into I_US. Oocytes were first bathed in a solution containing 90 mM Na⁺ and the time course of recovery from I_US was assessed. Thereafter the concentration of Na⁺ was changed to 40 mM, which resulted in a reduction of the maximum inward current by ∼50%, which corresponds to the reduction of the Na⁺ current by ∼30–50 μM Cd²⁺. As shown in Fig. 6, bathing the oocytes in 40 mM Na⁺ affected neither the amplitude nor the time constant of recovery from I_US: τ₁: 10.4 ± 1.1 s, τ₂: 117.5 ± 18.5 s, A1: 0.22 ± 0.06, A2: 0.78 ± 0.07. Therefore, any Na⁺ depletion in the pore had no effect on entry into I_US.

Cd²⁺ ions do not prevent entry into I_US by a foot-in-the-door mechanism

In K⁺ channels C-type inactivation is considered to be prevented by K⁺ ions in the outer pore by a foot-in-the-door mechanism (15). Analogously, I_US may arise from a collapse of the outer vestibule and Cd²⁺ ions bound to the selectivity filter may prevent this constriction of the permeation pathway. If Cd²⁺ ions acted by a foot-in-the-door mechanism, then the time course of development of I_US at depolarized potentials should be prolonged by Cd²⁺. We tested this prediction by selectively exposing K1237C channels to Cd²⁺ either only during the conditioning prepulse or only during repolarization after the conditioning prepulse. If Cd²⁺ prevented I_US by a foot-in-the-door mechanism, then application of Cd²⁺ during the conditioning prepulse should have resulted in a substantial acceleration of the time course of recovery, whereas application of Cd²⁺ during recovery should have had no kinetic effect. As shown in Fig. 7, A and B, Cd²⁺ did not affect the time course of recovery from inactivation when applied during the conditioning prepulse (V_m = −20 mV) but dramatically accelerated recovery when applied during repolarization to −120 mV (Fig. 7, C and D). Therefore, the action of Cd²⁺ was exclusively during recovery from I_US, not during its development strongly arguing against a foot-in-the-door mechanism.

A kinetic model of the modulation of I_US by Cd²⁺

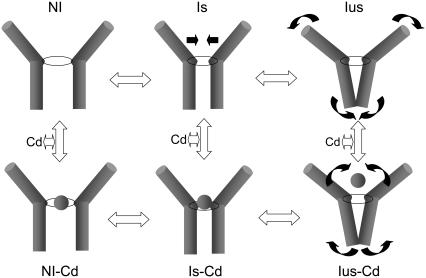
The experiment in Fig. 7 suggests that Cd²⁺ accelerates the time course of recovery from I_US at hyperpolarized potentials. During the 300-s conditioning prepulse K1237C channels enter into I_US even in the presence of Cd²⁺ ions, but after hyperpolarization Cd²⁺ ions may bind to and stabilize a conformation that is traversed during recovery, thereby speeding the time course of recovery from I_US. Therefore, a Cd²⁺-bound I_US state must recover at hyperpolarized potentials much faster than the unbound I_US state. To explore this concept we developed a gating model of recovery from inactivation at −120 mV. We considered three states: noninactivated (NI), slow inactivated (I_S), and ultraslow inactivated (I_US). Open, closed, and fast inactivated states were omitted because they are unlikely to contribute to time constants of recovery >1 s. We considered a serial gating model in which the I_US state is reached via the I_S state (Fig. 8 A).

During recovery from inactivation the backward rates leading into NI predominate those leading to inactivation. Therefore, the forward rates leading into inactivation were set two orders of magnitude smaller than the respective rates leading to the NI state. k_Ius→Is was defined as the reciprocal value of τ₂ during Cd²⁺-free conditions (0.0068 s⁻¹, Table 1). To determine k_Is→NI we evaluated the time course of recovery from inactivation produced by a 25-s conditioning prepulse to −20 mV. As shown in Fig. 8 B this time course could be well fitted by two exponentials. During depolarizations of longer durations than 25 s, recovery will be dominated by the larger time constant (τ₂ = 6493.4 ms). Hence, k_Is→NI was set to 1/τ₂ = 0.154 s⁻¹. Fig. 8, D and E (squares), shows that the modeled time course of recovery under Cd²⁺-free conditions fits well the experimental data.

To model recovery during block by Cd²⁺ we introduced a Cd²⁺-bound state for the noninactivated and both inactivated states (lower row in Fig. 8 A). To model the transitions between Cd²⁺-free and Cd²⁺-bound states we had to determine the on- and off-rates of Cd²⁺ with K1237C channels.

Determination of off-rates of Cd²⁺ from the noninactivated channel

Fast removal of a blocking agent in the bath solution will lead to dissociation from the binding site. Under this condition dissociation kinetics will only depend on the microscopic off-rate because the microscopic on-rate is zero. However, the two-electrode voltage clamp method in Xenopus laevis oocytes may not allow for bath exchange rates fast enough to faithfully monitor the off-rate of Cd²⁺ from K1237C channels. Therefore, we expressed K1237C channels in tsA201 cells and examined the washout of Cd²⁺ in the whole-cell patch-clamp configuration using a fast application system for rapid bath exchange. Cells were bathed in 50 μM Cd²⁺ until steady-state block was achieved (Fig. 8 C). Thereafter, Cd²⁺ was rapidly removed from the bath and the time course of unblock was monitored by sequential depolarizations at 0.2 Hz. We did not use higher test pulse frequencies to avoid possible contamination of the data by potential use-dependent unblock from open or fast inactivated states. Fig. 8 C shows that, upon washout of Cd²⁺, currents through K1237C channels recovered from block with a time constant of 3.2 ± 0.2 s (n = 8), yielding an off-rate of 0.3125 s⁻¹. Since the K_D of binding of Cd²⁺ to noninactivated channels is 35.0 ± 1.8 μM at −120 mV (Fig. 2 B), the association rate constant (k_on) of Cd²⁺ at that voltage was calculated to be 8930 M⁻¹s⁻¹.

Binding of Cd²⁺ does not alter the time course of recovery from I_S

Channels were exposed to 50 μM Cd²⁺ and the time course of recovery from a 25-s prepulse was determined. As shown in Fig. 8 B, the time course of recovery from I_S was not affected by Cd²⁺. Therefore, in the model k_{Is-Cd→NI-Cd} was set at the same values as the corresponding rates for the Cd²⁺-free transition (k_Is→NI).

Modeling modulation of I_US by low-affinity binding of Cd²⁺ to the I_US state (Model A)

For the inactivated states the on- and off-rates of Cd²⁺ cannot be determined directly. Therefore, we explored the effect of assuming different binding affinities to the I_US and I_S states as origin of the acceleration of recovery from I_US by Cd²⁺. Modulation of the rate constants of transition between states may result if the affinity of binding to a specific state differs from another connected state, resulting in stabilization of the high-affinity state with respect to the connected low-affinity state. Specifically, an acceleration of k_{Ius-Cd→Is-Cd} could result from either low-affinity binding of Cd²⁺ to the I_US state or from high-affinity binding of Cd²⁺ to the I_S state. We first considered low-affinity binding to the I_US state. For the I_S state we assumed on- and off-rates of Cd²⁺ to be equal to the corresponding values for the interaction with the NI state. Fig. 8 D shows the effect of increasing the rate of unbinding from the Cd²⁺-bound I_US state by factors of 0, 2, 5, 10, 100, and 1000. Microscopic reversibility required that k_{Ius-Cd→Is-Cd} be accelerated by the same factor by which the off-rate of Cd²⁺ from the I_US-Cd²⁺ state was increased (k_Ius-Cd→Ius). This procedure resulted in a speeding of the time course of recovery as a function of the decrease in affinity for Cd²⁺ of the I_US state. However, the increase in k_Ius-Cd→Ius causes channels to recover preferentially via the Cd²⁺-free states, setting an upper limit for recovery rate (upper row in Fig. 8 A). This effect produces a saturation of the speed of recovery at very high off-rates from the Cd²⁺-bound I_US state. Fig. 8 D shows that even with very low affinities of the I_US state for Cd²⁺, the experimental data cannot be faithfully reproduced.

Modeling modulation of I_US by high-affinity binding of Cd²⁺ to the I_S state (Model B)

In Fig. 8 E, we tested the hypothesis that the acceleration of recovery from I_US by Cd²⁺ resulted from high-affinity binding of Cd²⁺ to the I_S state. Such high-affinity binding during recovery could arise from a voltage-dependent increase in the on-rate to the I_S state at negative recovery potentials (−120 mV vs. −20 mV during the conditioning test pulse). We assumed the k_on of Cd²⁺ binding to the I_S state (see Model A) to be 10 times faster than the k_on of binding Cd²⁺ to the NI and I_US states. The off-rates of Cd²⁺ were defined to be equal for all Cd²⁺-bound states. The values for k_on of Cd²⁺ to the NI and to the I_US state were assumed to be equal. To preserve microscopic reversibility we accelerated k_{Ius-Cd→Is-Cd} and k_{NI-Cd→Is-Cd} by the same factor by which k_Is→Is-Cd was increased. This model is similar to a previously published model of mexiletine binding to the fast inactivated state of human skeletal muscle sodium channels. In this model the authors assumed high-affinity binding of mexiletine to fast inactivated channels to occur mainly by a 10-fold higher on-rate of binding to the inactivated state which, in turn, gives rise to a faster development of inactivation (55).

Fig. 8 E shows that Model B is able to reasonably reproduce the concentration-dependent acceleration of recovery from I_US. Thus, high-affinity binding of Cd²⁺ to I_S may account for the observed speeding of recovery from I_US.

Test of the prediction that Cd²⁺ ions bind with higher affinity to the I_S state than to the NI state

If Cd²⁺ binds to the I_S state with higher affinity than it does to the I_US state, then this should produce a depolarizing shift of the steady-state inactivation curve of the I_US state. However, as shown in Table 1, Cd²⁺ gives rise to a dramatic acceleration of the time course of recovery from I_US, such that the time constants of recovery from I_US and from I_S approach each other. Thus, the amplitude of I_US cannot be defined unequivocally at higher concentrations of Cd²⁺, which precludes the analysis of the effect of Cd²⁺ on the steady-state level of I_US at a given potential.

Another assumption of the model is that Cd²⁺ has a higher affinity to the I_S state relative to the NI state. This can readily be tested by determination of the steady-state inactivation for the I_S state (Fig. 9 A). To this end K1237C channels were depolarized for 25 s to different potentials, after which the membrane was hyperpolarized to −120 mV for 500 ms to allow for recovery of fast inactivated channels. Thereafter, a 20-ms test pulse to −20 mV was applied to open recovered channels. In each oocyte this protocol was performed under Cd²⁺-free conditions and during exposure to 50 μM Cd²⁺. Unfortunately, when exposed to Cd²⁺ during this protocol, currents through K1237C channels exhibited a high degree of rundown. To correct the data for rundown during superfusion with Cd²⁺ the degree of rundown was monitored at regular intervals during the experiment. In most experiments the maximum inward current decreased as a linear function of time, allowing the currents to be corrected for this linear trend in each experiment. Both the data during the Cd²⁺-free control and the data during application of Cd²⁺ were fit with Boltzmann curves.

As shown in Fig. 9 A the effects of Cd²⁺ on the availability of I_S were complex: First, Cd²⁺ produced an ∼8 mV hyperpolarizing shift of the availability curve, supporting the notion that Cd²⁺ binds with high affinity to the I_S state, thereby stabilizing this state. Second, the slope of the availability curve was increased by Cd²⁺, and, third, during exposure to Cd²⁺, availability did not saturate at depolarized voltages but increased at voltages positive to −60 mV. Both the increase in the slope of availability and the increase in availability at voltages positive to −60 mV may reflect the voltage-dependent unblock of Cd²⁺ from the channels at depolarized voltages. We assume that during the conditioning prepulse a fraction of the channels will enter into fast inactivation and will also be blocked by Cd²⁺ in a voltage-dependent manner. During the 500-ms interpulse at −120 mV these channels will recover from fast inactivation but may still be blocked by Cd²⁺ and will add to the nonavailable current produced by the channels in the I_S state. The steady-state availability curve may thus reflect a combination of voltage-dependent inactivation and voltage-dependent block. Therefore, we examined the effect of correcting availability for the influence of the voltage-dependent block. Fig. 9 B shows an availability curve in a single oocyte in which K1237C currents exhibited only minimal rundown during superfusion with Cd²⁺.

As in Fig. 9 A the slope of voltage-dependent availability negative to −60 mV was substantially steeper than in Cd²⁺-free solution (Fig. 9 A), and currents increased positive to −60 mV. To correct the steady-state availability curve for voltage-dependent block we fitted a Woodhull model (Eq. 9) to the measurements positive to −60 mV (inset of Fig. 9 B). Positive to −60 mV occupancy of I_S presumably is maximal, thus the change in availability in this potential range only reflects voltage-dependent block. The Woodhull model shown in the inset of Fig. 9 B was then used to calculate the contribution of voltage-dependent block at the potential range negative to −60 mV. Thereafter, the original data were corrected for the contribution of voltage-dependent block and replotted (squares in Fig. 9 B). If corrected by this procedure, the hyperpolarizing shift in availability imposed by 50 μM was increased and the slope factor of the availability curve was decreased. Hence, the complex effects of Cd²⁺ on voltage-dependent availability of I_S may have resulted from a combination of high-affinity binding to I_S with voltage-dependent block of fast inactivated channels. Taken together, the data support the notion that Cd²⁺ may bind with high affinity to the I_S state, thereby stabilizing this state.

I_US in K1237C channels involves a conformational change at the inner vestibule of the channel

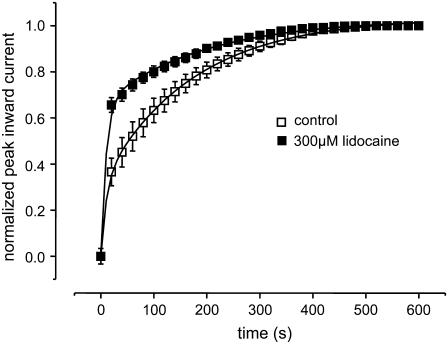
Local anesthetics modulate Na channel gating by binding to the inner vestibule of the channel. In a recent report we demonstrated that the local anesthetic lidocaine prevented channels in which K1237 was replaced by a glutamic acid from entering into I_US by a foot-in-the-door mechanism (44). A similar mechanism has recently been reported for the interaction of a pore blocker with the Kv1.5 channel (56). This suggested that I_US encompasses a conformational change of the inner vestibule of the channel and that binding of lidocaine may interfere with this conformational change. It appeared to be of interest whether a similar mechanism may account for I_US in K1237C. Fig. 10 shows that superfusion of K1237C channels with 300 μM lidocaine significantly decreased the fraction of channels dwelling in the I_US state at the end of a 300-s depolarizing pulse to −20 mV. Hence, I_US in K1237C may involve a conformational change of the inner vestibule of the channel.

FIGURE 10.

Modulation of I_US by lidocaine. The protocol was analogous to Fig. 2 A. After control oocytes were superfused with 300 μM lidocaine, which resulted in a significant acceleration of recovery from I_US. Data points were fitted with Eq. 5. Fitting parameters were drug free: A₁ = 0.29 ± 0.07, τ₁ = 9.8 ± 1.3 s, A₂ = 0.71 ± 0.07, τ₂ = 149.1 ± 6.8 s; lidocaine: A₁ = 0.64 ± 0.04 (P < 0.05), τ₁ = 10.0 ± 0.7 s, n.s., A₂ = 0.35 ± 0.04 (P < 0.05), τ₂ = 159.72 ± 16 s, n.s., n = 3).

DISCUSSION

The major finding of this study is that both the binding of a mutant μ-CTX to the outer vestibule and the binding of Cd²⁺ to a cysteine engineered into the selectivity filter of the voltage-gated Na channel dramatically accelerates recovery from ultraslow inactivation.

Previously, we reported that replacement of K1237 with E or S substantially increased the fraction of channels entering into I_US during long depolarizations (21). The same holds true for the replacement of K1237 by cysteine (Fig. 1). Also, similar to K1237E, binding of the mutant μ-CTX R13Q to K1237C decreases the fraction of channels recovering from I_US (Fig. 2 A). However, an even more dramatic effect is observed when K1237C channels are exposed to Cd²⁺. As shown in Table 1 and Fig. 2, C and D, Cd²⁺ reduces both the longer time constant (τ₂) and the amplitude of recovery with τ₂ (A₂) in a concentration-dependent fashion. τ₁ and τ₂ most likely represent the time courses of recovery from slow (I_S) and ultraslow (I_US) inactivation. The fact that Cd²⁺ reduced the fraction of channels recovering with τ₂ after a 300-s depolarization may indicate that the development of I_US is prolonged by Cd²⁺. However, the dramatic acceleration of τ₂ with a higher concentration of Cd²⁺ suggests that Cd²⁺ may exert most of its effect on the time course of recovery. Furthermore, given the dual action of Cd²⁺ on both amplitude and time course, the fitting procedure may be quite equivocal.

To clarify whether the time course of development of I_US is affected by Cd²⁺, we exposed K1237C channels to Cd²⁺ either during a depolarizing pulse (during which recovery develops) or during the following hyperpolarization (during which channels recover from I_US). Fig. 7 demonstrates that Cd²⁺ failed to affect recovery from I_US when the channels were exposed to Cd²⁺ only during the phase of development of I_US, whereas recovery from I_US was accelerated when channels were exposed to Cd²⁺ during recovery. The absence of an effect on development of I_US strongly argues against a static foot-in-the-door or a splint-in-the-vestibule mechanism as molecular underpinning of the modulation of I_US by Cd²⁺. Instead Cd²⁺ appears to act as a catalyst, decreasing the energy barrier which has to be surmounted to recover from I_US, resulting in an acceleration of the rate constants leading from the I_US to the NI state. A similar mechanism has recently been suggested for the hastening of recovery from inactivation of hERG K⁺ channels by Na⁺ ions (57). The authors presented a kinetic model in which both the rate constants of recovery from inactivation and entry into inactivation were accelerated by Na⁺.

Because the rate constants of recovery dominate those for entry at hyperpolarized potentials, such an acceleration of rate constants, although preserving microscopic reversibility, reproduces a speeding of recovery. Although such a model could formally reproduce our data, it falls short in elucidating the molecular mechanism of the acceleration of I_US recovery by Cd²⁺. Furthermore, the energy driving the catalytic activity of Cd²⁺ can only be derived from the energy of binding to the K1237C site, most likely to a state transiently occupied during recovery. Therefore, we considered two kinetic models in which a difference in binding energy to two distinct inactivated states is translated into the acceleration of the rate constants driving recovery from I_US. In Model A I_US is considered a low-affinity state by decreasing the off-rate of Cd²⁺ from the I_US state, and, to preserve microscopic reversibility, increasing the rate of transition from the Cd²⁺-bound I_US state to the Cd²⁺-bound I_S state (Fig. 8 D). Although the model can qualitatively reproduce the concentration-acceleration of recovery, the effect is only small and saturates if large differences in affinity of Cd²⁺ binding between I_US and I_S states are assumed. Model B tested the assumption that the I_S state has a 10-fold higher affinity for Cd²⁺ than the I_US and the NI states. Here, a higher affinity was the result of an increase in the association rate constant to the I_S state. Again, to preserve microscopic reversibility the rates of recovery from I_US to the I_S state were accelerated. As shown in Fig. 8 E this model closely reproduced the concentration-dependent acceleration of recovery from I_US.

For the reasons given above it is not possible to provide experimental evidence for a 10-fold difference in affinity for Cd²⁺ binding between the I_US and the I_S state. However, as shown in Fig. 9, 50 μM Cd²⁺ produce an ∼9 mV hyperpolarizing shift of the steady-state inactivation curve for the I_S state with respect to the NI, consistent with a higher affinity of the I_S state for Cd²⁺. According to Bean et al. (58), in the case of state-dependent binding to the inactivated state (in this case I_S) with respect to the noninactivated state, the amount of V_1/2 shift produced by this high-affinity binding is given by

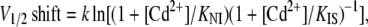(10)

where k represents the slope of the steady-state inactivation curve and K_NI and K_IS represent the respective affinities of the NI and the I_S state (58,59). If we consider values of 30 μM and 3 μM for K_NI and K_IS, respectively (i.e., a 10-fold higher affinity of Cd²⁺ to the I_S state as assumed in Model B), and a value of 7.2 mV for k (slope of the steady-state inactivation curve in Fig. 11 A), Eq. 10 yields a V_1/2 shift of −13.6 mV, which is larger than the experimentally observed shift by ∼−9 mV (Fig. 9). However, the data in Fig. 9 suggest that block by Cd²⁺ is voltage dependent. Thus, at −120 mV, i.e., the voltage at which the time course of recovery from I_US was assessed, block of channels in the I_S state would be enhanced by the negative voltage. This may explain why Cd²⁺ did not affect the time course development of I_US at −20 mV, whereas the recovery from I_US at −120 mV was dramatically accelerated (Fig. 7). Hence, upon recovery, Cd²⁺ ions may preferentially associate with channels in the I_US state, because the I_US state has a higher affinity for Cd²⁺ than other connected states and because of the negative voltage. This high-affinity binding to the I_S state may increase the rate constants leading into the Cd²⁺-bound I_S state (k_{Ius-Cd→Is-Cd}, k_{NI-Cd→IS-Cd}), resulting in an acceleration of recovery from I_US. It may be argued that Cd²⁺ should have accelerated the time course of recovery from I_S, which was not the case (Fig. 8 B). However, the time course of recovery from I_S is dominated by k_{IS-Cd→NI-Cd}, so that modifications of k_{NI-Cd→IS-Cd} have little effect on the time course of recovery from I_S.

FIGURE 11.

Molecular model of the interaction of Cd²⁺ with I_S and I_US. Shown are the S6 segments of two domains. The selectivity filter is indicated by a ring separating the outer vestibule (funnel-like shape) from the inner vestibule (central cavity). The kinetic scheme is analogous to Fig. 8 A. Slow inactivation (I_S) is considered to occur by a collapse of the outer vestibule at the level of the selectivity filter. A further rearrangement, consisting of a widening of the external vestibule and a simultaneous constriction of the inner vestibule, gives rise to I_US. The Cd²⁺-bound states are depicted in the lower row (Cd²⁺ is indicated by the ball). Cd²⁺ binds to all states, but the binding is strongest with the I_S state, producing a constriction of the selectivity filter ring. Hence, Cd²⁺ exposure during the I_US state (wide selectivity filter) promotes the formation of I_S (narrow selectivity filter) thereby speeding recovery from I_US.

A molecular model of the modulation of I_US by Cd²⁺

Which molecular events may underlie the modulation of I_US by Cd²⁺ ions? Recently we proposed a model of I_US in which I_US occurs by a conformational change of the cytoplasmic vestibule of the channel. This model was based on experimental findings showing that the binding of the inactivation particle to the cytoplasmic vestibule reduces the propensity of channels to enter I_US (60). Furthermore, lidocaine, by binding to residues in the cytoplasmic vestibule, opposes I_US by a foot-in-the-door mechanism (44). The modulation of I_US by lidocaine in the K1237C mutant suggests that in this construct I_US occurs by a similar mechanism as in K1237E. The experiment in Fig. 10 shows that lidocaine substantially reduced the fraction of channels recovering from I_US after a 300-s conditioning pulse without effect on the time course of recovery from I_US. This suggests that lidocaine prolonged entry into I_US, consistent with a foot-in-the-door mechanism, as reported for the mutation K1237E (44). Similarly, in Shaker K⁺ channels C-type inactivation—although initially thought to arise from a closure of the external vestibule—may also involve conformational changes at the internal side of the membrane (61). But how is the collapse of the internal vestibule, which presumably generates the I_US state, linked to the mutation at position 1237 in the selectivity filter?

We suggest that the mutations at site 1237 produce an increase in diameter of the selectivity filter, which is supported by ample experimental evidence demonstrating the fact that mutations of K1237 allow the permeation of cations which are substantially larger than Na (37). How is the widening of the selectivity filter transmitted to the internal vestibule to promote entry into I_US? Recently Cordero-Morales et al. presented electron paramagnetic resonance-spectroscopic evidence for an interaction between the selectivity filter and the adjacent pore helix in the KcsA channel (62). This interaction determines the propensity of the channel to inactivate. A similar interaction may account for the modulation of I_US by molecular events at the selectivity filter and in the internal vestibule in the K1237C mutation. We propose that the widening of the external vestibule associated with the replacement of K1237 with cysteine may result in an interaction of C1237 with the adjacent DIV S6 segment. Such an interaction between the selectivity filter and the adjacent S6 segment is supported by the finding that mutation of I1575 in DIV S6 to E abolishes I_US in K1237E (63). The interaction between C1237 and the adjacent S6 segment may result then in a conformational change of DIV S6 during inactivation.

This conformational change of DIV S6 then gives rise to the very stable I_US state. On the other hand, slow inactivation (I_S) has been suggested to result from a collapse of the outer vestibule (28). Structural evidence for the selectivity filter as inactivation gate has recently been found in the KcsA channel (64). In Fig. 11, we propose a model in which the idea that I_US and I_S represent drastically different molecular conformations is reconciled with the kinetic effects of Cd²⁺: To explain the acceleration of recovery from I_US in K1237C, we envision Cd²⁺ ions entering the pore during recovery from inactivation (lower row in Fig. 11). This entry may be favored by the negative holding potential of −120 mV during recovery from I_US. The development of I_US occurs at −20 mV, a potential at which a substantially smaller number of Cd²⁺ ions may enter the pore, accounting for the fact that washin of Cd²⁺ ions during the development of I_US does not prolong entry into I_US.

Group 12 ions are known to bind to cysteines, histidines, and aspartates (52). Cd²⁺ ions can coordinate at least three cysteines (65,66). In the absence of cysteines and histidines, glutamate and aspartates can serve as sites of action (52). Hence, it is possible that Cd²⁺ ions form coordinated binding with residues in the selectivity filter region. Candidate residues may be C1237, E755, D400, but also residues in the second ring of charge may be involved (E403, E758, D1241, D1532). This coordinated binding may result in a conformational change of the binding site, giving rise to a constriction of the pore and the formation of I_S (I_S-Cd²⁺ in Fig. 11). The reduction in the diameter of the pore at the level of the selectivity filter may then abolish the interaction between C1237 and the adjacent S6 segment, presumably with I1575, thereby accelerating recovery from I_US (Fig. 11). In the gating Model B (Fig. 8 D) the shaping of the outer vestibule by the Cd²⁺ ions entering the pore is reflected by the higher on-rate from the Cd²⁺-bound I_US state to the Cd²⁺-bound I_S state. A similar modification of the Cd²⁺ binding site by binding of Cd²⁺ to the channel pore has been suggested previously: in inwardly rectifying channels, the binding of Cd²⁺ to cysteines engineered into various sites within the pore was slowed down when the open state was stabilized by PIP₂.

The authors suggested that Cd²⁺ first enters the open channel, after which the helices collapse onto the ion in the process of coordination (67).

The idea that the outer vestibule of an ion channel adapts its structure to the ion in the permeation pathway is supported by recent crystallographic data obtained in the KcsA channel: The selectivity filter of the KcsA channel assumes a conductive conformation when exposed to high [K⁺] but becomes constricted in high [K⁺] (68). In the case of the interaction of Cd²⁺ ions with K1237C channels, we envision Cd²⁺ ions entering the pore during recovery from the I_US state, thereby producing an induced fit of the outer vestibule resulting in the formation of a high-affinity state (I_S), thereby speeding recovery from I_US. As shown in Fig. 7 D recovery from I_US was accelerated when the channels were exposed to Cd²⁺ ions during the recovery phase. This suggests that C1237 is accessible for Cd²⁺ ions when channels dwell in the I_US state, supporting the contention that I_US is not associated with a collapse of the external vestibule.

The modulation of recovery from slow inactivated states by cations may not be confined to voltage-gated Na channels. In voltage-gated K⁺ channels recovery from slow inactivation is modulated by cation binding to both extracellular sites (14,69–71) and to more intracellular sites (72,73) along the pathway of permeation. One of the modulatory sites is located at the intracellular end of the selectivity filter, i.e., at a site close to the homologous position of K1237 in the rNa_V1.4 channel (74). Hence the border between the external vestibule and the central cavity may be of pivotal importance for the regulation of slow inactivated states in voltage-gated ion channels.

As shown in Fig. 2 A, binding the mutant μ-CTX R13Q to K1237C channels resulted in a substantial acceleration of recovery from I_US. This effect was qualitatively similar to the hastening of recovery from I_US by Cd²⁺ ions. This suggests that binding of this large peptide toxin may produce a structural rearrangement of the outer vestibule, similar to the induced fit by Cd²⁺. Conformational changes in the toxin binding site in the outer pore of ion channels was previously suggested using computational methods (75,76) and was more recently confirmed by Lange and colleagues (77): Using high-resolution solid-state NMR spectroscopy, these authors demonstrated that high-affinity binding of the scorpion toxin kaliotoxin to a chimeric K⁺ channel was associated with significant structural rearrangements in both molecules.

Although both μ-CTX and Cd²⁺ produced a substantial acceleration of recovery from I_US, the effect was more dramatic with Cd²⁺ than with μ-CTX. This discrepancy may be explained by the fact that μ-CTX does not bind directly to the selectivity filter but has a more external binding site in the second ring of charge. Thus, the residue R13 of the toxin interacts with amino acid residues downstream of the selectivity filter (18,78,79). Interestingly, this region has recently been implicated in the generation of slow inactivation (80). Given the fact that the P-loops are highly flexible structures (81), it is conceivable that conformational changes due to toxin binding to residues may be transmitted downstream to site 1237. Furthermore, the fact that ligands at two different albeit close binding sites exert similar effects on the kinetics of I_US suggests that the conformational change which underlies I_US represents a broad rearrangement of the outer vestibule.

In summary, our data appear to be inconsistent with a collapse of the outer vestibule as the molecular mechanism of I_US. This seems at variance with the common notion that slow inactivation in Na channels as well as C-type inactivation in K⁺ channels result from a pore collapse. It is unclear, however, whether slow inactivation may have the same molecular underpinnings as ultraslow inactivation. As a matter of fact, in our proposed model Cd²⁺ ions favor a constriction of the outer vestibule corresponding to the formation of a slow inactivated state, thereby forcing channels to leave the ultraslow inactivated state. In other words, Cd²⁺ ions may act as a foot-on-the-door, “kicking” the I_S inactivation gate, thereby forcing the channels to leave I_US. Hence, slow inactivated states may represent an unexpected diversity of a quite heterogeneous class of molecular conformations.