Collective electrodynamics I

Abstract

Standard results of electromagnetic theory are derived from the direct interaction of macroscopic quantum systems; the only assumptions used are the Einstein–deBroglie relations, the discrete nature of charge, the Green’s function for the vector potential, and the continuity of the wave function. No reference is needed to Maxwell’s equations or to traditional quantum formalism. Correspondence limits based on classical mechanics are shown to be inappropriate.

But the real glory of science is that we can find a way of thinking such that the law is evident. – R. P. Feynman

Foundations of Physics

Much has transpired since the first two decades of this century, when the conceptual foundations for modern physics were put in place. At that time, macroscopic mechanical systems were easily accessible and well understood. The nature of electrical phenomena was mysterious; experiments were difficult and their interpretation was murky. Today, quite the reverse is true. Electrical experiments of breathtaking clarity can be carried out, even in modestly equipped laboratories. Electronic apparatus pervade virtually every abode and workplace. Modern mechanical experiments rely heavily on electronic instrumentation. Yet, in spite of this reversal in the range of experience accessible to the average person, introductory treatments of physics still use classical mechanics as a starting point.

Ernst Mach wrote (p. 596 in ref. 1), “The view that makes mechanics the basis of the remaining branches of physics, and explains all physical phenomena by mechanical ideas, is in our judgment a prejudice. … The mechanical theory of nature, is, undoubtedly, in a historical view, both intelligible and pardonable; and it may also, for a time, have been of much value. But, upon the whole, it is an artificial conception.”

Classical mechanics is indeed inappropriate as a starting point for physics because it is not fundamental; rather, it is the limit of an incoherent aggregation of an enormous number of quantum elements. To make contact with the fundamental nature of matter, we must work in a coherent context where the quantum reality is preserved.

R. P. Feynman wrote (p. 15–8 in ref. 2), “There are many changes in concepts that are important when we go from classical to quantum mechanics. … Instead of forces, we deal with the way interactions change the wavelengths of waves.”

Even Maxwell’s equations have their roots in classical mechanics. They were conceived as a theory of the ether: They express relations between the magnetic field B and the electric field E, which are defined in terms of the classical force F = q(E + v × B) on a particle of charge q moving with velocity v. But it is the vector potential A, rather than the magnetic field B, that has a natural connection with the quantum nature of matter—as highlighted by Aharonov and Bohm (3).

Hamilton’s formulation of classical mechanics was—and remains—the starting point for the concepts underlying the quantum theory. The correspondence principle would have every quantum system approach the behavior of its classical-mechanics counterpart in the limit where the mechanical action involved is large compared with Planck’s constant.

Although superconductivity was discovered in 1911, the recognition that superconductors manifest quantum phenomena on a macroscopic scale (4) came too late to play a role in the formulation of quantum mechanics. Through modern experimental methods, however, superconducting structures give us direct access to the quantum nature of matter. The superconducting state is a coherent state formed by the collective interaction of a large fraction of the free electrons in a material. Its properties are dominated by known and controllable interactions within the collective ensemble. The dominant interaction is collective because the properties of each electron depend on the state of the entire ensemble, and it is electromagnetic because it couples to the charges of the electrons. Nowhere in natural phenomena do the basic laws of physics manifest themselves with more crystalline clarity.

This paper is the first in a series in which we start at the simplest possible conceptual level, and derive as many conclusions as possible before moving to the next level of detail. In most cases, understanding the higher level will allow us to see why the assumptions of the level below were valid. In this stepwise fashion, we build up an increasingly comprehensive understanding of the subject, always keeping in view the assumptions required for any given result. We avoid introducing concepts that we must “unlearn” as we progress. We use as our starting point the magnetic interaction of macroscopic quantum systems through the vector and scalar potentials A⃗ and V, which are the true observable quantities. For clarity, the brief discussion given here is limited to situations where the currents and voltages vary slowly; the four-vector generalization of these relations not only removes this quasi-static limitation, but gives us electrostatics as well (5, 6).

Model System

Our model system is a loop of superconducting wire—the two ends of the loop being colocated in space and either insulated or shorted, depending on the experimental situation. Experimentally, the voltage V between the two ends of the loop is related to the current I flowing through the loop by

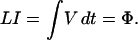1

Two quantities are defined by this relationship: Φ, called the magnetic flux*, and L, called the inductance, which depends on the dimensions of the loop.

Current is the flow of charge: I = dQ/dt. Each increment of charge dQ carries an energy increment dW = V dQ into the loop as it enters.† The total energy W stored in the loop is thus

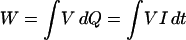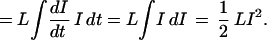2

If we reduce the voltage to zero by, for example, connecting the two ends of the loop to form a closed superconducting path, the current I will continue to flow indefinitely: a persistent current. If we open the loop and allow it to do work on an external circuit, we can recover all the energy W.

If we examine closely the values of currents under a variety of conditions, we find the full continuum of values for the quantities I, V, and Φ, except for persistent currents, where only certain discrete values occur for any given loop (7, 8). By experimenting with loops of different dimensions, we find the condition that describes the values that occur experimentally:

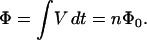3

Here, n is any integer, and Φ₀ = 2.06783461 × 10⁻¹⁵ volt-second is called the flux quantum or fluxoid; its value is accurate to a few parts in 10⁹, independent of the detailed size, shape, or composition of the superconductor forming the loop. We also find experimentally that a rather large energy—sufficient to disrupt the superconducting state entirely—is required to change the value of n.

The more we reflect on Eq. 3, the more remarkable the result appears. The quantities involved are the voltage and the magnetic flux. These quantities are integrals of the quantities E and B that appear in Maxwell’s equations, and are therefore usually associated with the electromagnetic field. Experimentally, we know that they can take on a continuum of values—except under special conditions, when the arrangement of matter in the vicinity causes the flux to take on precisely quantized values. In Maxwell’s theory, E and B represented the state of strain in a mechanical medium (the ether) induced by electric charge. Einstein had a markedly different view (p. 383 in ref. 9): “I feel that it is a delusion to think of the electrons and the fields as two physically different, independent entities. Since neither can exist without the other, there is only one reality to be described, which happens to have two different aspects; and the theory ought to recognize this from the start instead of doing things twice.” At the most fundamental level, the essence of quantum mechanics lies in the wave nature of matter. Einstein’s view would suggest that electromagnetic variables are related to the wave properties of the electrons. Quantization is a familiar phenomenon in systems where the boundary conditions give rise to standing waves. The quantization of flux (Eq. 3) is a direct manifestation of the wave nature of matter, expressed in electromagnetic variables.

Matter

To most nonspecialists, quantum mechanics is a baffling mixture of waves, statistics, and arbitrary rules, ossified in a matrix of impenetrable formalism. By using a superconductor, we can avoid the statistics, the rules, and the formalism, and work directly with the waves. The wave concept, accessible to intuition and common sense, gives us “a way of thinking such that the law is evident.” Electrons in a superconductor are described by a wave function that has an amplitude and a phase. The earliest treatment of the wave nature of matter was the 1923 wave mechanics of deBroglie. He applied the 1905 Einstein postulate (W = ℏω) to the energy W of an electron wave, and identified the momentum p⃗ of an electron with the propagation vector of the wave: p⃗ = ℏk⃗. Planck’s constant h and its radian equivalent ℏ = h/2π are necessary for merely historical reasons—when our standard units were defined, it was not known that energy and frequency were the same quantity.

The Einstein–deBroglie relations apply to the collective electrons in a superconductor. The dynamics of the system can be derived from the dispersion relation (10) between ω and k⃗. Both ω and k⃗ are properties of the phase of the wave function and do not involve the amplitude, which, in collective systems, is usually determined by some normalization condition. In a superconductor, the constraint of charge neutrality is such a condition.

The wave function must be continuous in space; at any given time, we can follow the phase along a path from one end of the loop to the other: the number of radians by which the phase advances as we traverse the path is the phase accumulation ϕ around the loop. If the phase at one end of the loop changes relative to that at the other end, that change must be reflected in the total phase accumulation around the loop. The frequency ω of the wave function at any point in space is the rate at which the phase advances per unit time. If the frequency at one end of the loop (ω₁) is the same as that at the other end (ω₂), the phase difference between the two ends will remain constant, and the phase accumulation will not change with time. If the frequency at one end of the loop is higher than that at the other, the phase accumulation will increase with time, and that change must be reflected in the rate at which phase accumulates with the distance l along the path. The rate at which phase around the loop accumulates with time is the difference in frequency between the two ends. The rate at which phase accumulates with distance l is the component of the propagation vector k⃗ in the direction dl⃗ along the path. Thus, the total phase accumulated around the loop is

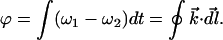4

We can understand quantization as an expression of the single-valued nature of the phase of the wave function. When the two ends of the loop were connected to an external circuit, the two phases could evolve independently. When the ends are connected to each other, however, the two phases must match up. But the phase is a quantity that has a cyclic nature—matching up means being equal modulo 2π. Thus, for a wave that is confined to a closed loop, and has a single-valued, continuous phase, the integral of Eq. 4 must be n2π, where n is an integer. The large energy required to change n is evidence that the phase constraint is a strong one—as long as the superconducting state stays intact, the wave function remains intact as well.

These relations tell us that the magnetic flux and the propagation vector will be quantized for a given loop; they do not tell us how the frequency ω in Eq. 4 is related to the potential V in Eq. 1. To make this connection, we must introduce one additional assumption: The collective electron system represented by the wave function is made up of elemental charges of magnitude q₀. By the Einstein relation, the energy q₀V of an elemental charge corresponds to a frequency ω = q₀V/ℏ.

Electrodynamics

Electrodynamics is the interaction of matter via the electromagnetic field. We can formulate our first relation between the electromagnetic quantities V and Φ and the phase accumulation ϕ of the wave function by comparing Eq. 1 with Eq. 4:

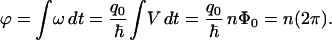5

From Eq. 5, we conclude that Φ₀ = h/q₀. We understand that the potential V and the frequency ω refer to differences in these quantities between the two ends of the loop. Equivalently, we measure each of these quantities at one end of the loop using as a reference the value at the other end of the loop. When we substitute into Eq. 5 the measured value of Φ₀ and the known value of h, we obtain for q₀ a value that is exactly twice the charge q_e of the free electron. The usual explanation for this somewhat surprising result is that each state in the superconductor is occupied by a pair of electrons, rather than by an individual electron, so the elemental charge q₀ should be 2q_e, rather than q_e. None of the conclusions that we shall reach depends on the value of q₀.

We have established the correspondence between the potential V and the frequency ω—the time integral of each of these equivalent quantities in a closed loop is quantized. The line integral of the propagation vector k⃗ around a closed loop also is quantized. We would therefore suspect the existence of a corresponding electromagnetic quantity, whose line integral is the magnetic flux Φ. That quantity is the well-known vector potential A⃗. The general relations among these quantities, whether or not the loop is closed, are

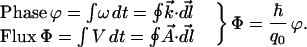6

Eq. 6 expresses the first set of fundamental relations of collective electrodynamics.

Coupling

Up to this point, we have tentatively identified the phase accumulation and the magnetic flux as two representations of the same physical entity. We assume that “winding up” the wave function with a voltage produces a propagation vector in the superconductor related to the motion of the electrons, and that this motion corresponds to a current because the electrons are charged. This viewpoint will allow us to understand the interaction between two coupled collective electron systems. We shall develop these relations in more detail when we study the current distribution within the wire itself.

Let us consider two identical loops of superconducting wire, the diameter of the wire being much smaller than the loop radius. We place an extremely thin insulator between the loops, which are superimposed on each other as closely as allowed by the insulator. In this configuration, both loops can be described, to an excellent approximation, by the same path in space, despite their being electrically distinct. As we experiment with this configuration, we make the following observations.

(i) When the two ends of the second loop are left open, its presence has no effect on the operation of the first loop. The relationship between a current flowing in the first loop and the voltage observed between the ends of the first loop follows Eq. 1, with exactly the same value of L as that observed when the second loop was absent.

(ii) The voltage observed between the two ends of the second loop under open conditions is almost exactly equal to that observed across the first loop.

(iii) When the second loop is shorted, the voltage observed across the first loop is nearly zero, independent of the current.

(iv) The current observed in the second loop under shorted conditions is nearly equal to that flowing in the first loop, but is of the opposite sign.

Similar measurements performed when the loops are separated allow us to observe how the coupling between the loops depends on their separation and relative orientation.

(v) For a given configuration, the voltage observed across the second loop remains proportional to the voltage across the first loop. The constant of proportionality, which is nearly unity when the loops are superimposed, decreases with the distance between the loops.

(vi) The constant of proportionality decreases as the axes of the two loops are inclined with respect to each other, goes to zero when the two loops are orthogonal, and reverses when one loop is flipped with respect to the other.

Observation i tells us that the presence of electrons in the second loop does not per se affect the operation of the first loop. The voltage across a loop is a direct manifestation of the phase accumulation around the loop. Observation ii tells us that current in a neighboring loop is as effective in producing phase accumulation in the wave function as is current in the same loop. The ability of current in one location to produce phase accumulation in the wave function of electrons in another location is called magnetic interaction. Observation vi tells us that the magnetic interaction is vectorial in nature. After making these and other similar measurements on many configurations, involving loops of different sizes and shapes, we arrive at the proper generalization of Eqs. 1 and 6:

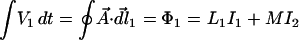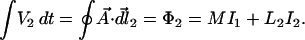7

Here, the line elements dl⃗₁ and dl⃗₂ are taken along the first and second loops, respectively. The quantity M, which by observation vi can be positive or negative depending on the configuration, is called the mutual inductance; it is a measure of how effective the current in one loop is at causing phase accumulation in the other. When L₁ = L₂ = L, the magnitude of M can never exceed L. Observations i–iv were obtained under conditions where M ≈ L. Experiments evaluating the mutual coupling of loops of different sizes, shapes, orientations, and spacings indicate that each element of wire of length dl carrying the current I⃗ makes a contribution to A⃗ that is proportional to I⃗, and to the inverse of the distance r from the current element to the point at which A⃗ is evaluated:

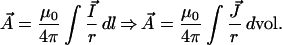8

The constant μ₀ is called the permeability of free space. The second form follows from the first if we visualize a distribution of current as carried by a large number of wires of infinitesimal cross section, and the current density J⃗ as being the number of such wires per unit area normal to the current flow. The 1/r form of the integrand of Eq. 8 is called the Green’s function; it tells us how the vector potential is generated by currents everywhere in space. It is perhaps more correct to say that the vector potential is a bookkeeping device for evaluating the effect at a particular point of all currents everywhere in space. Ernst Mach wrote (p. 317 in ref. 1), “We cannot regard it as impossible that integral laws … will some day take the place of the … differential laws that now make up the science of mechanics. … In such an event, the concept of force will have become superfluous.” Eqs. 6 and 8 and are the fundamental integral laws for collective electromagnetic interaction. The equivalent differential equation is ∇²A⃗ = −μ₀ J⃗ (5, 6).

We can express Eq. 2 in a way that gives us additional insight into the energy stored in the coil:

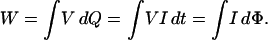9

Eq. 9 is valid for any A⃗; it is not limited to the A⃗ from the current in the coil itself. The integrals in Eq. 9 involve the entire coil. From them we can take a conceptual step and, using our visualization of the current density, imagine an energy density J⃗ ⋅ A⃗ ascribed to every point in space:

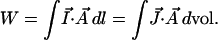10

Electrodynamic Momentum

Feynman commented on the irrelevance of the concept of force in a quantum context. At the fundamental level, we can understand the behavior of a quantum system using only the wave properties of matter. But we experience forces between currents in every encounter with electric motors, relays, and other electromagnetic actuators. How do these forces arise from the underlying quantum reality? We can make a connection between the classical concept of force and the quantum nature of matter through the concept of momentum. Using the deBroglie postulate relating the momentum p⃗ of an electron to the propagation vector k⃗ of the wave function, and identifying the two integrands in Eq. 6, the electrodynamic momentum of an elemental charge is

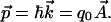11

We shall now investigate the electrodynamic momentum in one of our loops of superconducting wire. There is an electric field E along the loop, the line integral of which is the voltage V between the ends. From a classical point of view, Newton’s law tells us that the force q₀ E on a charge should be equal to the time rate of change of momentum. From Eq. 11,

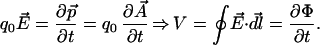12

Integrating the second form of Eq. 12 with respect to time, we recover Eq. 6, so the classical idea of inertia is indeed consistent with the quantum behavior of our collective system. Electrodynamic inertia acts exactly as a classical mechanical inertia: it relates the integral of a force to a momentum, which is manifest as a current. We note that, for any system of charges that is overall charge neutral, as is our superconductor, the net electromagnetic momentum is zero. For the −qA⃗ of each electron, we have a canceling +qA⃗ from one of the background positive charges. The electric field that accelerates electrons in one direction exerts an equal force in the opposite direction on the background positive charges. We have, however, just encountered our first big surprise: We recognize the second form of Eq. 12, which came from Newton’s law, as the integral form of one of Maxwell’s equations!

We would expect the total momentum P of the collective electron system to be the momentum per charge times the number of charges in the loop. If there are η charges per unit length of wire that take part in the motion, integrating Eq. 11 along the loop gives

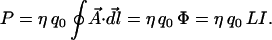13

The current I is carried by the η charges per unit length moving at velocity v; therefore, I = η q₀v, and Eq. 13 becomes

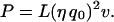14

The momentum is proportional to the velocity, as it should be. It is also proportional to the size of the loop, as reflected by the inductance L. Here we have our second big surprise: instead of scaling linearly with the number of charges that take part in the motion, the momentum of a collective system scales as the square of the number of charges! We can understand this collective behavior as follows. In an arrangement where charges are constrained to move in concert, each charge produces phase accumulation, not only for itself, but for all the other charges as well. So the inertia of each charge increases linearly with the number of charges moving in concert. The inertia of the ensemble of coupled charges must therefore increase as the square of the number of charges.

Forces on Currents

In our experiments on coupled loops, we have already seen how the current in one loop induces phase accumulation in another loop; the relations involved were captured in Eq. 7. In any situation where we change the coupling of collective systems by changing the spatial arrangement, mechanical work may be involved. Our model system for studying this interaction consists of two identical shorted loops of individual inductance L₀, each carrying a persistent flux Φ. As long as the superconducting state retains its integrity, the cyclic constraint on the wave function guarantees that the flux Φ in each loop will be constant, independent of the coupling between loops. Because M enters symmetrically in Eq. 7, the current I will be the same in both loops. Hence, L₀ and Φ will remain constant, whereas M and I will be functions of the spatial arrangement of the loops—M will be large and positive when the loops are brought together with their currents flowing in the same direction, and will be large and negative when the loops are brought together with their currents flowing in opposite directions. From Eq. 7, Φ = (L₀ + M)I. Substituting Φ into Eq. 9, and noting that the total energy of the system is twice that for a single coil,

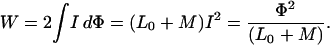15

The force F_x along some direction x is defined as the rate of change of energy with a change in the corresponding coordinate:

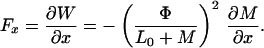16

The negative sign indicates an attractive force because the mutual inductance M increases as the coils—whose currents are circulating in the same direction—are moved closer. It is well known that electric charges of the same sign repel each other. We might expect the current, being the spatial analog of the charge, to behave in a similar manner. However, Eq. 15 indicates that the total energy of the system decreases as M increases. How does this attractive interaction of currents circulating in the same direction come about?

The electron velocity is proportional to I. As M is increased, the electrons in both loops slow down because they have more inertia due to the coupling with electrons in the other loop. This effect is evident in Eq. 15, where I = Φ/(L₀ + M). Thus, there are two competing effects: the decrease in energy due to the lower velocity, and the increase in energy due to the increase in inertia of each electron. The energy goes as the square of the velocity, but goes only linearly with the inertia, so the velocity wins. The net effect is a decrease in energy as currents in the same direction are coupled, and hence an attractive force. We can see how the classical force law discovered in 1823 by Ampère arises naturally from the collective quantum behavior, which determines not only the magnitude, but also the sign, of the effect.

Multiturn Coils

The interaction in a collective system scales as the square of the number of electrons moving in concert. Thus, we might expect the quantum scaling laws to be most clearly manifest in the properties of closely coupled multiturn coils, where the number of electrons is proportional to the number of turns. We can construct an N-turn coil by connecting in series N identical, closely coupled loops. In this arrangement, the current through all loops is equal to the current I through the coil, and the voltage V across the coil is equal to the sum of the individual voltages across the loops. If A₀ is the vector potential from the current in one loop, we expect the vector potential from N loops to be N A₀, because the current in each loop contributes. The flux integral is taken around N turns, so the path is N times the length l₀ of a single turn. The total flux integral is thus

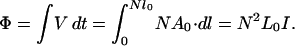17

From Eq. 17 we conclude that an N-turn closely coupled coil has an inductance L = N²L₀. Once again, we see the collective interaction scaling as the square of the number of interacting charges. We remarked that collective quantum systems have a correspondence limit markedly different from that of classical mechanical systems. When two classical massive bodies, each body having a separate inertia, are bolted together, the inertia of the resulting composite body is simply the sum of the two individual inertias. The inertia of a collective system, however, is a manifestation of the interaction, and cannot be assigned to the elements separately. This difference between classical and quantum systems has nothing to do with the size scale of the system. Eq. 17 is valid for large as well as for small systems; it is valid where the total phase accumulation is an arbitrary number of cycles—where the granularity of the flux due to ℏ is as small as might be required by any correspondence procedure. Thus, it is clear that collective quantum systems do not have a classical correspondence limit.

Total Momentum

To see why our simplistic approach has taken us so far, we must understand the current distribution within the superconductor itself. We saw that the vector potential made a contribution to the momentum of each electron, which we called the electrodynamic momentum: p⃗_el = qA⃗. The mass m of an electron moving with velocity v⃗ also contributes to the electron’s momentum: p⃗_mv = mv⃗. The total momentum is the sum of these two contributions:

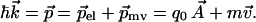18

The velocity v⃗ = (ℏk⃗ − q₀ A⃗)/m is thus a direct measure of the imbalance between the total momentum ℏk⃗ and the electrodynamic momentum q₀ A⃗. When these two quantities are matched, the velocity is zero. The current density J⃗ is just the motion of 𝒩 elementary charges per unit volume: J⃗ = q₀ 𝒩v⃗. We can thus express Eq. 18 in terms of the wave vector k⃗, the vector potential A⃗, and the current density J⃗:

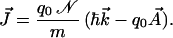19

Current Distribution

We are now in a position to investigate how current distributes itself inside a superconductor. If A⃗ were constant throughout the wire, the motion of the electrons would be determined by the common wave vector k⃗ of the collective electron system, and we would expect the persistent current for a given flux to be proportional to the cross-sectional area of the wire, and thus the inductance L of a loop of wire to be inversely related to the wire cross section. When we perform experiments on loops of wire that have identical paths in space, however, we find that the inductance is only a weak function of the wire diameter, indicating that the current is not uniform across the wire, and therefore that A⃗ is far from constant. If we make a loop of superconducting tubing, instead of wire, we find that it has exactly the same inductance as does a loop made with wire of the same diameter, indicating that current is flowing at the surface of the loop, but is not flowing throughout the bulk.

Before taking on the distribution of current in a wire, we can examine a simpler example. In a simply connected bulk superconductor, the single-valued nature of the wave function can be satisfied only if the phase is everywhere the same: k⃗ = 0. Any phase accumulation induced through the A⃗ vector created by an external current will be canceled by a screening current density J⃗ in the opposite direction, as we saw in observations iii and iv. To make the problem tractable, we consider a situation where a vector potential A₀ at the surface of a bulk superconducting slab is created by distant currents parallel to the surface of the slab. The current distribution perpendicular to the surface is a highly localized phenomenon, so it is most convenient to use the differential formulation of Eq. 8. We suppose that conditions are the same at all points on the surface, and therefore that A changes in only the x direction, perpendicular to the surface, implying that ∇²A = ∂²A/∂x².

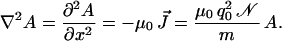20

The solution to Eq. 20 is

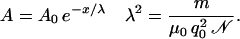21

The particular form of Eq. 21 depends on the geometry, but the qualitative result is always the same, and can be understood as follows: The current is the imbalance between the wave vector and the vector potential. When an imbalance exists, a current proportional to that imbalance will flow such that it cancels out the imbalance. The resulting screening current dies out exponentially with distance from the source of imbalance. The distance scale at which the decay occurs is given by λ, the screening distance, penetration depth, or skin depth. For a typical superconductor, 𝒩 is of the order of 10²⁸/m³, so λ should be a few tens of nanometers. Experimentally, simple superconductors have λ ≈ 50 nanometers—many orders of magnitude smaller than the macroscopic wire thickness that we are using.

Current in a Wire

At long last, we can visualize the current distribution within the superconducting wire itself. Because the skin depth is so small, the surface of the wire appears flat on that scale, and we can use the solution for a flat surface. The current will be a maximum at the surface of the wire, and will die off exponentially with distance into the interior of the wire. We can appreciate the relations involved by examining a simple example. A 10-cm-diameter loop of 0.1-mm-diameter wire has an inductance of 4.4 × 10⁻⁷ Henry (p. 193 in ref. 11): A persistent current of 1 Ampere in this loop produces a flux of 4.4 × 10⁻⁷ volt-second, which is 2.1 × 10⁸ flux quanta. The electron wave function thus has a total phase accumulation of 2.1 × 10⁸ cycles along the length of the wire, corresponding to a wave vector k = 4.25 × 10⁹ m⁻¹. Due to the cyclic constraint on the wave function, this phase accumulation is shared by all electrons in the wire, whether or not they are carrying current.

In the region where current is flowing, the moving mass of the electrons contributes to the total phase accumulation. The 1-Ampere of current results from a current density of 6.4 × 10¹⁰ Amperes per square meter flowing in a thin “skin” ≈λ thick, just inside the surface. This current density is the result of the 10²⁸ electrons per cubic meter moving with a velocity of v ≈ 20 meters per second. The mass of the electron moving at this velocity contributes mv/ℏ = 1.7 × 10⁵ m⁻¹ to the total wave vector of the wave function, which is less than one part in 10⁴ of that contributed by the vector potential. That small difference, existing in about 1 part in 10⁶ of the cross-sectional area, is enough to bring k⃗ and A⃗ into balance in the interior of the wire.

In the interior of the wire, the propagation vector of the wave function is matched to the vector potential, and the current is therefore zero. As we approach the surface, A decreases slightly, and the difference between k and Aq₀/ℏ is manifest as a current. At the surface, the value and radial slope of A inside and outside the wire match, and the value of A is still within one part in 10⁴ of that in the center of the wire. So our simplistic view—that the vector potential and the wave vector were two representations of the same quantity—is precisely true in the center of the wire, and is nearly true even at the surface. The current I⃗ is not the propagation vector k⃗ of the wave, but, for a fixed configuration, I⃗ is proportional to k⃗ by Eqs. 8 and 19. For that reason, we were able to deduce the electromagnetic laws relating current and voltage from the quantum relations between wave vector and frequency.

Conclusion

We took to heart Einstein’s belief that the electrons and the fields were two aspects of the same reality, and were able to treat the macroscopic quantum system and the electromagnetic field as elements of a unified subject. We heeded Mach’s advice that classical mechanics was not the place to start, followed Feynman’s directive that interactions change the wavelengths of waves, and saw that there is a correspondence limit more appropriate than the classical-mechanics version used in traditional introductions to quantum theory. We found Newton’s law masquerading as one of Maxwell’s equations. We were able to derive a number of important results using only the simplest properties of waves, the Einstein postulate relating frequency to energy, the deBroglie postulate relating momentum to wave vector, and the discrete charge of the electron. It thus appears possible to formulate a unified, conceptually correct introduction to both the quantum nature of matter and the fundamental laws of electromagnetic interaction without using either Maxwell’s equations or standard quantum formalism.