Abstract
The kinetics of Ca2+-dependent conformational changes of human cardiac troponin (cTn) were studied on isolated cTn and within the sarcomeric environment of myofibrils. Human cTnC was selectively labeled on cysteine 84 with N-((2-(iodoacetoxy)ethyl)-N-methyl)amino-7-nitrobenz-2-oxa-1,3-diazole and reconstituted with cTnI and cTnT to the cTn complex, which was incorporated into guinea pig cardiac myofibrils. These exchanged myofibrils, or the isolated cTn, were rapidly mixed in a stopped-flow apparatus with different [Ca2+] or the Ca2+-buffer 1,2-Bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid to determine the kinetics of the switch-on or switch-off, respectively, of cTn. Activation of myofibrils with high [Ca2+] (pCa 4.6) induced a biphasic fluorescence increase with rate constants of >2000 s−1 and ∼330 s−1, respectively. At low [Ca2+] (pCa 6.6), the slower rate was reduced to ∼25 s−1, but was still ∼50-fold higher than the rate constant of Ca2+-induced myofibrillar force development measured in a mechanical setup. Decreasing [Ca2+] from pCa 5.0–7.9 induced a fluorescence decay with a rate constant of 39 s−1, which was approximately fivefold faster than force relaxation. Modeling the data indicates two sequentially coupled conformational changes of cTnC in myofibrils: 1), rapid Ca2+-binding (kB ≈ 120 μM−1 s−1) and dissociation (kD ≈ 550 s−1); and 2), slower switch-on (kon = 390s−1) and switch-off (koff = 36s−1) kinetics. At high [Ca2+], ∼90% of cTnC is switched on. Both switch-on and switch-off kinetics of incorporated cTn were around fourfold faster than those of isolated cTn. In conclusion, the switch kinetics of cTn are sensitively changed by its structural integration in the sarcomere and directly rate-limit neither cardiac myofibrillar contraction nor relaxation.
INTRODUCTION
Ca2+ activation of cardiac contraction is regulated by the human cardiac troponin complex (cTn), consisting of the Ca2+-binding cTnC subunit, the inhibitory cTnI subunit and the tropomyosin (Tm)-binding cTnT subunit. During the systole, cytosolic [Ca2+] rises to ≥1 μM and binds to the low affinity Ca2+-binding site II of cTnC, the so-called regulatory binding site. This leads to a conformational change of the N-terminal domain of cTnC, which rearranges its interaction with the C-terminal regulatory region of cTnI (1). This structural rearrangement involves the C-terminal part and the inhibitory region of cTnI and leads to the removal of Tm from its blocking position on actin, allowing myosin to bind to actin in a force-generating manner. During the diastole, cytosolic Ca2+ falls to submicromolar concentrations. The systolic process is reversed: Ca2+ dissociation from cTnC induces a conformational rearrangement of the complex involving cTnI and cTnT, which immobilizes Tm on the thin filament (2). In this way, Tm prevents myosin from binding de novo to actin in a force-generating manner, and as the remaining cross-bridges detach, the heart relaxes (3).
Simultaneous measurements of force and intracellular [Ca2+] in intact cardiac trabeculae have shown that the rate of myoplasmic Ca2+ increase/removal does not rate-limit force development/relaxation (4,5). Thus, in principle, two mechanisms could determine the time course of the contraction/relaxation of myocardial force: 1), the cross-bridge turnover kinetics, and 2), the kinetics of thin-filament activation/inactivation after Ca2+ binding/dissociation.
Cross-bridge kinetics during activation/relaxation have been obtained from force transients induced either by flash photolysis of caged Ca2+ and caged-Ca2+ chelators in skinned cardiac fibers (6–9) or by rapidly changing the [Ca2+] in the environment of subcellular cardiac myofibrils (10,11). The observed rates of force increase/decrease and their dependence on interventions affecting cross-bridge mechanics indicated that cross-bridge turnover kinetics determine the time course of cardiac myofibrillar force development and relaxation. This implies, but does not prove, that the switch-on and switch-off kinetics of cTn are rapid processes compared to the time course of force changes.
Kinetics of thin filament activation/inactivation have been investigated extensively by measuring the Ca2+-induced conformational changes of cTn using isolated regulatory proteins like cTnC (e.g., (12–14)), or the whole cTn complex (15), as well as more complex systems, like reconstituted thin filaments (16,17). Comparison of the kinetics observed with isolated cTnC, cTnC·cTnI, cTn complex, and the cTn complex in reconstituted thin filaments showed that the kinetics depends on the complexity of the system (15,17). However, it had not yet been determined whether and how switch-on and switch-off kinetics of cTn are altered when the complex is incorporated into the functional environment of the contractile sarcomere. Therefore, direct measurements of the switch kinetics in the sarcomere are required to test for the possible role of cTn in rate-limiting force development/relaxation.
Recently, Bell et al. (9) measured simultaneously the kinetics of the switch-on of cTnC and force development in skinned fibers. Ca2+ activation was induced by flash photolysis of caged Ca2+ and switch-on kinetics was monitored with fluorescence polarization. Their fluorescence polarization signal was biphasic, which provided evidence for two conformational changes. The fast conformational change (∼120 s−1) was too fast to rate-limit the contraction of the cardiac muscle, whereas the slow conformational change (∼5 s−1) had the same rate constant as the kinetics of the force development. The fast change was interpreted to reflect the kinetics of Ca2+ binding to cTnC, though it was considerably slower than that measured for cTnC in solution. The slow change was interpreted to reflect a further activation of the thin filament when cross-bridges bind to it. However, it remained unclear whether the slow phase is a consequence of cross-bridge binding or represents an intrinsic part of thin filament activation that rate-limits the force increase. Thus, there is a need for an alternative technique to probe the Ca2+-induced thin filament activation in the sarcomere.
Furthermore, to fully understand the mechanism of cTn switch in the sarcomere, not only the kinetics of the switch-on but also that of the switch-off and its relation to force relaxation has to be determined. Such experiments are difficult to perform with skinned fibers because the Ca2+ affinity of available caged-Ca2+ chelators is limited (18). These problems can be overcome with myofibrils, which are functional contractile units of muscle. In comparison to skinned fibers, they are small enough to perform kinetic studies by rapid-mixing techniques such as stopped-flow (19,20) and rapid-solution-change techniques (10,21). These two techniques allow rapid and defined changes from initial to final [Ca2+] by the use of Ca2+ chelators such as 1,2-Bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid (BAPTA).
The main goal of this study was to elucidate whether the Ca2+-dependent conformational change of cTn rate-limits the kinetics of muscle contraction and relaxation. To determine the kinetics of conformational change of cTn, we labeled cTnC on Cys-84 with N-((2-(iodoacetoxy)ethyl)-N-methyl)amino-7-nitrobenz-2-oxa-1,3-diazole (IANBD), a fluorescence detector of protein conformational changes, and reconstituted it with cTnI and cTnT to form a heterotrimeric cTn complex (cTn labeled with IANBD at cysteine 84 cTnC (NBD-cTn)). NBD-cTn was then exchanged against the endogenous cTn in cardiac myofibrils. The stopped-flow technique allowed us to determine the switch-on and switch-off kinetics from the changes in NBD-Tn fluorescence, which occur after rapid increases and decreases in [Ca2+]. Because this technique can be applied in the same way to myofibrils and isolated proteins, it allowed us to investigate how the myofibrillar environment changes switch-on and switch-off kinetics.
In parallel to the stopped-flow measurements, myofibrillar force kinetics after rapid increase and decrease in [Ca2+] were measured to test whether the kinetics of force development and/or relaxation could be rate-limited by the Ca2+-dependent conformational changes of cTn.
METHODS
Expression, fluorescence-labeling and reconstitution of human cardiac troponin
The three human cardiac troponin (cTn) subunits cTnC, cTnT, and cTnI were separately expressed in Escherichia coli and isolated as described previously by Kruger et al. (22), with the modification of adding protease inhibitors (1 mM PMSF, 1 μg/ml pepstatin A, 0.5 mM 4-(2-aminoethyl)benzenesulfonyl fluoride hydrochloride, 10 μM leupeptin, 14.5 μM antipain, 5 μg/ml aprotinin) to the buffer for the lysis of E. coli cells. The plasmids of the three subunits were kindly provided by C. S. Redwood (University of Oxford, Oxford, UK). Site-directed mutagenesis of Cys-35-Ser on cTnC allowed us to label specifically the remaining Cys-84 in cTnC with the fluorescent dye IANBD. cTnC (2.5 mg/ml) was dissolved for 2 h at 4°C in urea buffer containing 25 mM MOPS (3-(N-morpholino)propanesulfonic acid, 4-morpholinepropanesulfonic acid), 0.2 M NaCl, 6 M urea, 0.5 mM CaCl2, 2 mM dithiothreitol (DTT), adjusted to pH 7.0 with NaOH, and then dialyzed (1:100) against buffer A but with 0.1 mM DTT for ∼3 h. IANBD was dissolved in dimethylformamide ([DMF] < 2%) and then added in a 5:1 molar ratio (IANBD/cTnC) to the protein solution. The mixture was incubated for 1 h at 4°C in the dark. The labeling reaction was stopped by adding ∼10 mM DTT. The labeled cTnC was then dialyzed (1:100 at 4°C for 2 h) against the same urea buffer containing 1 mM DTT to remove the free fluorescence label. Thereafter the labeled cTnC was reconstituted with cTnI and cTnT to the cTn complex, as described previously by Kruger et al. (22). Briefly, for reconstitution, the cTn subunits (weight ratio of cTnC/cTnT/cTnI = 2.5:1:1) were dialyzed in a series of buffers containing 25 mM MOPS, 0.5 mM CaCl2, and 1 mM DTT, adjusted to pH 7.0 with NaOH and decreasing in [NaCl] (buffer I, 1.0 M NaCl; buffer II, 0.75 M NaCl; buffer III, 0.5 M NaCl), with a final buffer (IV) containing 0.3 M KCl and no NaCl. Dialysis was performed three times in each buffer for 2 h respectively. After reconstitution, 20 mM DTT was added and the cTn solution was filtered (pore size 0.45 μm). The filtrate was then stored at −80°C. Before use, the cTn solution was thawed and then dialyzed (1:10 for 1 h at 4°C) against Ca2+-free rigor buffer containing 10 mM Tris, 132 mM NaCl, 5 mM KCl, 1 mM MgCl2, 1 mM NaN3, and 5 mM EGTA (pH 7.1 with NaOH).
Preparation of cardiac myofibrils
Guinea pigs (females of 1–4.5 months in age) were anaesthetized with isofluran before the heart was excised. The following steps were all carried out at 4°C. The heart (1.7–2.2 g in weight) was perfused for ∼10 h with the Ca2+-free rigor buffer. The ventricular walls were dissected into small pieces of ∼10 mm3 and homogenized in exchange buffer (100 mg/ml) for 5 s with a blender (Ultra-Turrax T25, Janke & Kunkel, Staufen, Germany). The homogenate was filtrated with meshes (pore sizes 40 μm and 20 μm), and then centrifuged (380 × g for 10 min at 4°C). The pellets were resuspended in an equal volume of a skinning buffer that contained 1% Triton X-100, 10 mM Tris, 10 mM NaCl, 15 0 mM KCl, 1 mM NaN3, 1 mM MgCl2, and 5 mM EGTA, adjusted with NaOH to pH 7.1. After incubation for 5 min, the myofibrils were centrifuged (380 × g for 10 min at 4°C) and the supernatant was discarded.
Incorporation of NBD-cTn into myofibrils
NBD-cTn was incorporated into myofibrils by replacing the endogenous cTn as a whole in the myofibrils according to the technique developed by Brenner et al. (23). To exchange the endogenous cTn in the myofibrils against NBD-cTn, the myofibril pellet was resuspended in Ca2+-free rigor buffer including protease inhibitors (0.5 mM 4-(2-aminoethyl)benzenesulfonyl fluoride hydrochloride, 10 μM leupeptin, 14.5 μM antipain, and 5 μg/ml aprotinin) and 1 mg/ml of NBD-cTn. The mixture was shaken gently for 1 h at room temperature. To prevent overcontraction of the myofibrils after transferring them from the Ca2+-free rigor buffer (0 mM ATP) to the ATP-containing relaxation buffer, 10 mM of the actomyosin ATPase inhibitor BDM (2,3-butandione-2-monoxime) was added before centrifugation of the myofibrils (380 × g for 10 min at 4°C). The pellet was then resuspended in approximately three volumes of one of two relaxation buffers. For switch-on kinetics, the buffer (single-mixed (SX) relaxation buffer, pCa >8) contained 10 mM imidazole, 3 mM MgCl2, 47.7 mM Na2CrP, 1 mM ATP, 3 mM BAPTA, and 20 mM DTT, adjusted to pH 7.0 with HCl plus 10 mM BDM. For switch-off kinetics, the buffer (double-mixed (DX) relaxation buffer, pCa >8) had the same constitution, but with 0.6 mM BAPTA instead of 3 mM BAPTA. The myofibrils were then washed twice by centrifugation (380 × g for 10 min at 4°C) and resuspension in the respective relaxation buffer containing no BDM to remove the excess cTn and the BDM.
To obtain myofibrillar suspensions with a reproducible density of the myofibrils, the concentration of myosin heads was determined at their absorption maximum at ∼280 nm as in Herrmann et al. (24). For switch-on kinetics (single mixing) the concentration of myosin heads was 3 μM, and for switch-off kinetics (double mixing) it was 6 μM.
The incorporation of NBD-cTn into myofibrils was monitored by sodium dodecyl sulfate polyacrylamide gel electrophoresis (SDS-PAGE). Therefore, samples of the myofibrils (∼10 μg total protein/slot) before and after the exchange were reduced with 30 mM DTT and alkylated with 75 mM iodoacetamide at pH 8.5, according to the procedure of Lane et al. (25). The samples were then transferred to Laemmli buffer, and the proteins were separated on a 12.5% SDS-PAGE and were visualized by Commassie-R250-staining. The different mobility of guinea pig and human cTnI made it possible to monitor the loss of endogenous guinea pig cTn and its replacement by the exogenous NBD-cTn.
Stopped-flow measurements
The Ca2+-dependent fluorescence change of cTn was measured using a stopped-flow apparatus of Bio-Logic (Claix, France) model SFM-400/S equipped with a TC 100/10F-cuvette (10-mm light path, dead time of 2.2 ms at 14 ml/s flow rate). The sample was excited by a 75-W Hg-Xe-Lamp (Hamamatsu, Hamamatsu, Japan) coupled to a monochromator (TgK Scientific, Bradford-on-Avon, UK) set to 482 nm and a band-with of ∼18 nm. Emission of fluorescence was monitored using an OG515 nm cut-off filter and a 530/40-nm band-pass filter in front of a custom-made photomultiplier system. All measurements were performed at 10°C. To determine the switch-on kinetics, myofibrils in SX relaxation buffer (pCa >8) were mixed 1:1 with SX activation buffer (like relaxation buffer but containing, in addition, different [CaCl2] up to 6 mM) using the single-mixing mode of the apparatus. The switch-off kinetics were determined by DX: myofibrils in DX relaxation buffer were first mixed 1:1 with DX activation buffer (like DX relaxation buffer, but with 1.2 mM CaCl2) to induce Ca2+ activation of the myofibrils at pCa 5.0. After an incubation time of 91 ms, the myofibrils were then mixed 1:1 with DX inactivation buffer (like DX relaxation buffer, but with 12 mM Na2BAPTA), which leads to an instantaneous drop in [Ca2+] to pCa >8.
To determine the kinetics of the fluorescence change after mixing rigor-myofibrils with 1 mM ATP, exchanged myofibrils were washed twice by centrifugation (380 × g for 10 min at 4°C) and resuspension with normal rigor buffer (as detailed above, but adjusted to pH 7.0 with HCl). These myofibrils were mixed 1:1 with rigor buffer containing 2 mM ATP using the single-mixing mode of the apparatus.
To determine the switch kinetics on isolated cTn, the procedure was exactly the same as for cTn in myofibrils, except that instead of myofibrils we used cTn. Before the measurements of the switch-on and -off kinetics cTn was dialyzed 1:10 against the respective relaxation buffer three times (1 h at 4°C). For switch-on and -off kinetics, the concentration of cTn was 75 μg/ml in the cuvette.
Measurements of myofibrillar force kinetics
Thin cardiac myofibril bundles (2.0–3.5 μm in diameter, 25–70 μm in length) with the incorporated NBD-cTn were mounted in an apparatus based on the principle of atomic force microscopy, as described previously by Stehle et al. (26). The myofibrils had slack sarcomere lengths of 1.96 ± 0.05 μm (mean ± SD), which is similar to that of native cardiac myofibrils (1.98 ± 0.04 μm). Bundles were prestretched by 15% of their slack length and then Ca2+-activated and thereafter relaxed by fast solution changes (10–30 ms), based on a technique used by Colomo et al. (27). Experiments were performed at 10°C. Activating or relaxing buffers were the same as for stopped-flow measurements.
Statistics and data analysis
For stopped-flow measurements with isolated cTn, typically three to four traces were averaged, and for incorporated cTn, typically four to eight traces were averaged. The averaged signals were then fitted by a monoexponential function with Biokine 32 (version V4.27, Bio-Logic, Mundelein, IL). The obtained parameters were analyzed and modeled with GraphPad-Prism (version 4.02), BioKine (version 4.41), and Berkeley Madonna (version 8.0.1).
Kinetic parameters of myofibrillar contraction (kACT) and relaxation (kLIN, tLIN, and kREL) were obtained as described previously (26). Transients of force relaxation were fitted to a function consisting of a linear (kLIN, tLIN) and an exponential term (kREL), starting at the time of Ca2+ removal.
If not otherwise specified, parameters are indicated as mean ± SE.
RESULTS
Incorporation of labeled cTn into cardiac myofibrils
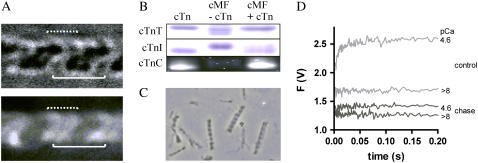
The NBD-cTn was incorporated to the myofibrils according to the method developed by Brenner et al. for skinned fibers (23), i.e., by replacing the endogenous cTn as a whole complex with the exogenous labeled NBD-cTn. The binding of NBD-cTn in the sarcomere after performing the cTn exchange was visualized by fluorescence microscopy. To test whether NBD-cTn had been bound to the actin and not to the myosin filaments, a myofibril was mounted in the mechanical setup and stretched to sarcomere length of 3.15 ± 0.05 μm. Thereby the actin filaments were pulled out partly from their overlap with the myosin filaments. Comparison of the fluorescence with the corresponding bright-field image (Fig. 1 A) shows that the fluorescence is preferentially localized along the I-band and the distal parts of the A-band. This fluorescence pattern suggests that NBD-cTn is predominantly bound to the actin filaments.
FIGURE 1.
Incorporation of NBD-cTn into guinea pig cardiac myofibrils. (A) Microscopic images (90× magnification) in bright-field (upper) and epifluorescence mode (lower) of a stretched myofibril bundle (consisting of two single myofibrils) exchanged with NBD-cTn. The solid lines indicate the position of a sarcomere limited by the two Z-lines and the dotted lines the position of the thin filaments on both sides of a Z-line. The width of solid lines corresponds to the sarcomere length (3.15 μm). (B) SDS-PAGE of guinea pig cardiac myofibrils (cMF) before and after the exchange with human NBD-cTn (for details, see Materials and Methods). Because endogenous guinea pig cTnC and exchanged NBD-cTnC have the same electrophoretic mobility the incorporation was proved by excitation of NBD-cTn with ultraviolet light. To obtain high enough fluorescence, a 12-fold higher myofibril- and NBD-cTn concentration was used than for cTnI and cTnT. (C) NBD-cTn exchanged myofibrils after being mixed in the stopped-flow apparatus. (D) Myofibrils exchanged with NBD-cTn were incubated either for 1 h with 10 mg/ml unlabeled cTn (“chase”) or in the same buffer but without exogenous cTn (“control”). Thereafter, myofibrils were washed in relaxation buffer (for further details, see Materials and Methods) and mixed with either relaxation buffer (pCa >8) or activation buffer (pCa 4.6). Though the chased myofibrils still exhibit a noticeable high basal fluorescence at pCa >8, the Ca2+-induced fluorescence increase is almost completely lost.
The exchange was probed by SDS-PAGE. Since endogenous guinea pig cTnI and exogenous human cTnI have different electrophoretic mobilities, they can be fully separated by SDS-PAGE and their amounts quantified. The gel showed that ∼68 ± 14% (SD, n = 6) of the endogenous cTnI was replaced by the exogenously added NBD-cTn (Fig. 1 B). The efficiency of our exchange correlates well with the exchange described for cardiac fibers (9,28,29). That the exchange is incomplete can be explained by the fact that under rigor conditions, in the absence of Ca2+, mainly the overlapping region is exchanged but not the nonoverlapping thin filament (30).
To test to what extent changes in NBD-Tn fluorescence induced by mixing myofibrils with the activator Ca2+ reflect specifically rather than unspecifically bound NBD-Tn, the fluorescent NBD-cTn in exchanged myofibrils was “chased” by incubating the myofibrils for 1 h in Ca2+-free rigor buffer with an excess (10 mg/ml) of unlabeled cTn. The myofibrils were then mixed in the stopped-flow apparatus with (pCa 4.6) or without Ca2+ (pCa >8), respectively. The recorded fluorescence traces were compared with those obtained with “unchased” myofibrils treated in the same way as the chased ones but without adding the unlabeled cTn to the Ca2+-free rigor buffer. Fig. 1 D shows that mixing of unchased myofibrils with Ca2+ induces an exponential fluorescence increase with a signal/noise ratio of >10. In comparison to the unchased myofibrils, chased myofibrils also exhibit a significant background fluorescence at pCa >8, suggesting that some of the NBD-cTn might be not specifically bound to the sarcomere and cannot reversibly be replaced by competitive binding of the unlabeled cTn. However, in contrast to unchased myofibrils, there was almost no change in fluorescence when the chased myofibrils were mixed with Ca2+. Thus, it is possible that NBD-cTn partly binds unspecifically, but if so, this does not appear to bias the interpretation of the fluorescence signal, as it seems not to significantly contribute to the Ca2+-induced fluorescence changes.
Effect of cTn exchange and the stopped-flow technique on the myofibrillar structure
We have investigated whether the exchange of cTn impairs myofibrillar structure by examining myofibrils before and after the exchange by phase contrast microscopy under 500× magnification. We could detect no effect of exchange on either sarcomere length or other characteristics of myofibrillar morphology (Fig. 1 C).
To test whether the exchange of the endogenous cTn in myofibrils by the human, recombinant NBC-cTn affects the contractile properties of myofibrils, we determined the kinetic parameters of force development and relaxation for NBD-cTn exchanged myofibrils and compared them with the parameters of native myofibrils which were treated as exchanged myofibrils but without NBD-cTn. In both exchanged and native myofibrils, Ca2+ induces a monoexponential force development with a rate constant kACT. The values of kACT were not significantly different between the two preparations (Table 1). In both preparations, Ca2+ removal induced a biphasic force decay described by an initial slow, seemingly linear decline with a rate constant, kLIN, lasting for a duration, tLIN, followed by a rapid exponential decay with a rate constant kREL. There were no significant differences in kLIN, tLIN, or kREL between native and exchanged myofibrils (Table 1). In summary, the cTn exchange and the IANBD label on cTnC appears not to alter significantly the kinetics of contraction or relaxation of the myofibrils.
TABLE 1.
Force kinetics during activation and relaxation of exchanged and native myofibrils
| Activation
|
Relaxation
|
||||
|---|---|---|---|---|---|
| Force/CSA (nN/μm2) | kact(s−1) | klin(s−1) | tlin(s) | krel(s−1) | |
| Native myofibrils | 101 ± 15 (5) | 1.1 ± 0.1 (11) | 0.6 ± 0.1 (11) | 0.2 ± 0.1 (11) | 3.4 ± 0.1 (11) |
| NBD-cTn exchanged myofibrils | 62 ± 8 (7) | 1.0 ± 0.1 (24) | 0.4 ± 0.1 (24) | 0.3 ± 0.1 (24) | 3.1 ± 0.1 (24) |
kact is the rate constant of force contraction, and klin, tlin, and krel describe kinetic parameters of force relaxation. For details, see text. Values given indicate the mean ± SE, with the number of experiments given in parentheses.
In contrast to this, a decrease in the force per cross-sectional area was observed in exchanged myofibrils by up to ∼1/3. A similar reduction of force upon cTn-exchange has been reported for skinned fibers (29,31).
We also determined the kinetics of ATP-induced cross-bridge detachment of native and NBD-cTn exchanged myofibrils by measuring the changes in their intrinsic tryptophan fluorescence induced by mixing myofibrils incubated under rigor conditions with Mg·ATP (32). The rate constant of the fluorescence increase induced by 1 mM Mg·ATP for NBD-cTn exchanged myofibrils (32 ± 7 s−1, n = 4) was not significantly different (p = 0.30) from that for native myofibrils (46 ± 11 s−1, n = 4). In conclusion, neither the exchange nor the labeling changes fundamental kinetics properties of the myofibrils, although maximal force can be decreased.
To test whether the high shear forces during the stopped-flow measurements could damage the myofibrils, we compared the sarcomere length and morphology of the myofibrils before and after being mixed in the stopped-flow apparatus: no change in sarcomere length or in the morphology before and after mixing of the myofibrils could be detected even if the maximum flow rate of 14 ml/s was used (Fig. 1 C).
Switch-on kinetics of isolated NBD-cTn and NBD-cTn incorporated into myofibrils
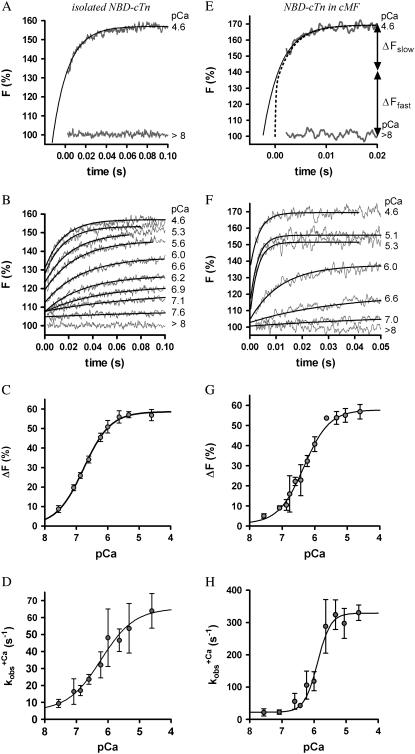
In a first series of experiments, we investigated whether the structural environment of the myofibrils changes the switch-on kinetics of cTn. For this, we compared the Ca2+-induced fluorescence increase of isolated and incorporated NBD-cTn after changing the pCa from >8 to different pCa (Fig. 2, A and E). In both isolated and incorporated cTn, the jump to saturating [Ca2+] induced a biphasic fluorescence increase with an initial fast phase that cannot be resolved (for details, see below) followed by a resolvable slow phase. At Ca2+ activation with pCa 4.6, the slow phase of the fluorescence increases monoexponentially with a rate constant of 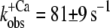 (n = 7) for isolated NBD-cTn and
(n = 7) for isolated NBD-cTn and 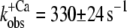 (n = 6) for incorporated NBD-cTn (Table 2). Thus, incorporation of the NBD-cTn increased the kinetics of the slow phase about fourfold at maximum Ca2+ activation.
(n = 6) for incorporated NBD-cTn (Table 2). Thus, incorporation of the NBD-cTn increased the kinetics of the slow phase about fourfold at maximum Ca2+ activation.
FIGURE 2.
Ca2+ dependence of fluorescence increase of isolated (A and B) and incorporated (C and D) NBD-cTn. (A) Fluorescence traces (gray lines) obtained after mixing isolated NBD-cTn (in relaxation buffer, pCa >8) at t = 0 s with activation buffer, leading to pCa 4.6. The first 2.2 ms of the traces cannot be shown because of the dead time of the stopped-flow instrument. The fluorescence trace at pCa 4.6 was fitted by a monoexponential function (solid lines) with the fit extrapolated to “negative” time. This emphasizes that within the dead time a very rapid fluorescence increase has to occur that precedes the signal, which can be fitted. (B) Same as A, but with NBD-cTn mixed with activation buffers, leading to different pCas. (C) Ca2+ dependence of the total fluorescence amplitude of isolated NBD-cTn. Symbols and error bars show means ± SE from five different preparations. The line shows a sigmoidal dose-response curve fitted to the averaged data. Corresponding fits of individual data from each of five preparations resulted in a pCa50 of 6.7 ± 0.1 and a nH of 1.0 ± 0.1 (mean ± SE). (D) Ca2+ dependence of the rate constant (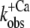 ) of the slow phase.
) of the slow phase. 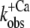 data were fitted as described for ΔF in B to yield a pCa50 of 6.2 ± 0.1 and a nH = 1.4 ± 0.4 (n = 5). (E) Same as A, but with NBD-cTn incorporated into myofibrils. The dotted line shows a biexponential simulation of the fluorescence increase, as shown in Fig. 6 A. The arrows indicate the signal amplitude of the fast phase (ΔFfast) and of the slow phase (ΔFslow). (F) Same as B, but with NBD-cTn incorporated into myofibrils. (G) Same as C, but data are from six different myofibrillar preparations, resulting in a pCa50 of 6.4 ± 0.1 and a nH of 1.1 ± 0.1 (mean ± SE). (H) Same as D, but with data from six different myofibrillar preparations, resulting in a pCa50 of 5.9 ± 0.1 and a nH = 2.3 ± 0.4 (n = 6).
data were fitted as described for ΔF in B to yield a pCa50 of 6.2 ± 0.1 and a nH = 1.4 ± 0.4 (n = 5). (E) Same as A, but with NBD-cTn incorporated into myofibrils. The dotted line shows a biexponential simulation of the fluorescence increase, as shown in Fig. 6 A. The arrows indicate the signal amplitude of the fast phase (ΔFfast) and of the slow phase (ΔFslow). (F) Same as B, but with NBD-cTn incorporated into myofibrils. (G) Same as C, but data are from six different myofibrillar preparations, resulting in a pCa50 of 6.4 ± 0.1 and a nH of 1.1 ± 0.1 (mean ± SE). (H) Same as D, but with data from six different myofibrillar preparations, resulting in a pCa50 of 5.9 ± 0.1 and a nH = 2.3 ± 0.4 (n = 6).
TABLE 2.
Ca2+ sensitivity and kinetic parameters of fluorescence changes of isolated and incorporated cTn
| ΔF(4.6) (%) pCa 4.6 | pCa50 |
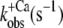 pCa 4.6 pCa 4.6 |
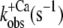 pCa 6.6 pCa 6.6 |
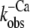 (s−1) (s−1) |
|
|---|---|---|---|---|---|
| Isolated NBD-cTn | 57 ± 3 (5) | 6,7 ± 0,1 (5) | 81 ± 9 (7) | 24 ± 3 (4) | 28 ± 3 (5) |
| Incorporated NBD-cTn | 57 ± 5 (6) | 6,4 ± 0,1 (6) | 330 ± 24 (6) | 56 ± 24 (6) | 39 ± 2 (10) |
Values given indicate the mean ± SE, with the number of experiments given in parentheses.
The kinetics of the fast phase of the fluorescence increase was too rapid to be resolved. The existence of the unresolvable fast phases with isolated and incorporated NBD-cTn is clarified in Fig. 2, A and E, respectively, where the monoexponential functions (black lines) fitted to the fluorescence transients (gray lines) are extrapolated to t = 0 s, i.e., the time of mixing with Ca2+. It is evident, that the extrapolations do not reach the baseline levels obtained by mixing isolated or incorporated NBD-cTn with the Ca2+-free buffer (pCa >8). After mixing isolated NBD-cTn with high [Ca2+] (pCa 4.6), already 50 ± 5% (SD, n = 5) of the total fluorescence increase occurred within the dead time of 2.2 ms provided by the standard mixing cuvette of the apparatus (Fig. 2 A). For incorporated NBD-cTn, 63 ± 14% (SD, n = 6) of the total fluorescence increase could not be resolved (Fig. 2 E). Even using a microcuvette with a shorter dead time of ∼250 μs did not allow us to record the initial fluorescence rise (data not shown). Thus, the rate constant of the fast phase has to be >2000 s−1. This could be explained if the fast phase represents the fast Ca2+ binding to cTnC. We have supported this hypothesis by modeling and simulation of the Ca2+-induced fluorescence changes (for details, see Discussion).
The fluorescence increase after activation with different [Ca2+] shows that the contribution of the fast phase to the overall fluorescence change is reduced with decreasing [Ca2+] (Fig. 2, B and F). At pCa <6.0, almost the whole signal is resolvable. This observation suggests that the fast phase and the slow phase report two sequentially coupled conformational changes (for details see Modeling, in Discussion) and thus supports the hypothesis that the label senses the fast Ca2+ binding to the regulatory Ca2+-binding site II, which then induces a slower, regulatory conformational change.
For isolated and incorporated NBD-cTn the Ca2+ dependencies of the steady-state fluorescence amplitudes (ΔF) and of the rate constants of the slow phase (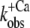 ) can be fitted by sigmoidal dose-response curves (Fig. 2, C, D, G, and H). For incorporated NBD-cTn, the Ca2+ dependence of ΔF gives a pCa50 of 6.4 ± 0.1 (n = 6) (Table 2) and a Hill slope of 1.1 ± 0.1 (n = 6), whereas the Ca2+ dependence of
) can be fitted by sigmoidal dose-response curves (Fig. 2, C, D, G, and H). For incorporated NBD-cTn, the Ca2+ dependence of ΔF gives a pCa50 of 6.4 ± 0.1 (n = 6) (Table 2) and a Hill slope of 1.1 ± 0.1 (n = 6), whereas the Ca2+ dependence of 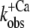 leads to a pCa50 of 5.9 ± 0.1 (n = 6) and a Hill slope of 2.3 ± 0.4 (n = 6). In comparison to this, the Ca2+ dependence of ΔF of isolated NBD-cTn has a pCa50 of 6.7 ± 0.1 (n = 5) and thus is ∼0.3 pCa units higher than incorporated NBD-cTn. As expected, the Hill slope is 1.0 ± 0.1 (n = 5). The Ca2+ dependence of the rate constant
leads to a pCa50 of 5.9 ± 0.1 (n = 6) and a Hill slope of 2.3 ± 0.4 (n = 6). In comparison to this, the Ca2+ dependence of ΔF of isolated NBD-cTn has a pCa50 of 6.7 ± 0.1 (n = 5) and thus is ∼0.3 pCa units higher than incorporated NBD-cTn. As expected, the Hill slope is 1.0 ± 0.1 (n = 5). The Ca2+ dependence of the rate constant 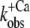 has a pCa50 of 6.2 ± 0.1 (n = 5) and thus is also ∼0.3 pCa units higher than incorporated NBD-cTn. The Hill slope is 1.4 ± 0.4 (n = 5).
has a pCa50 of 6.2 ± 0.1 (n = 5) and thus is also ∼0.3 pCa units higher than incorporated NBD-cTn. The Hill slope is 1.4 ± 0.4 (n = 5).
Switch-off kinetics of NBD-cTn in myofibrils after Ca2+ reduction
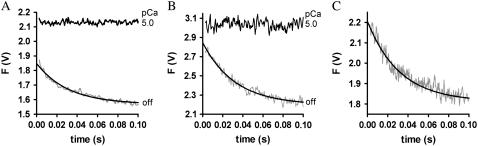
The kinetics of the conformational changes after Ca2+ removal from cTnC was determined also with isolated NBD-cTn and NBD-cTn incorporated into myofibrils. For this, the isolated NBD-cTn or the exchanged myofibrils were first Ca2+-activated for 91 ms at pCa 5.0 and then inactivated at pCa >8. The activation time was chosen to be sufficiently long to reach steady-state fluorescence during activation and, on the other hand, to be sufficiently short to prevent overcontraction of the myofibrils.
Fig. 3, A and B, shows that after the reduction in [Ca2+], the fluorescence decays biphasically for isolated and incorporated NBD-cTn. As for the switch-on kinetics, the first, fast phase cannot be resolved and is followed by a second slower phase. Compared to the switch-on kinetics, the amplitude of the missed signal for incorporated NBD-cTn comprises only 28 ± 15% (n = 10) of the total amplitude. For isolated NBD-cTn the missed signal is 40 ± 14% (n = 5). The decay of the slow phase was fitted by a monoexponential yielding a rate constant of 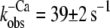 (n = 10) for incorporated NBD-cTn and
(n = 10) for incorporated NBD-cTn and 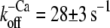 (n = 5) for isolated NBD-cTn.
(n = 5) for isolated NBD-cTn.
FIGURE 3.
Fluorescence changes after mixing of NBD-cTn with BAPTA or Mg·ATP. (A) Mixing of Ca2+-activated isolated NBD-cTn with BAPTA to induce a rapid decrease in [Ca2+] pCa from 5.0 to >8 causes an exponential fluorescence decay (gray line). This signal was fitted with a monoexponential decay (black line), yielding a rate constant of 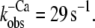 The black transient depicts the fluorescence baseline for steady-state activation at pCa 5.0. To obtain these baselines, NBD-cTn was mixed with the same buffers in which it was incubated before the mixing. (B) Same as A, but with NBD-cTn incorporated into myofibrils. The monoexponential fit of the decay yielded a rate constant of
The black transient depicts the fluorescence baseline for steady-state activation at pCa 5.0. To obtain these baselines, NBD-cTn was mixed with the same buffers in which it was incubated before the mixing. (B) Same as A, but with NBD-cTn incorporated into myofibrils. The monoexponential fit of the decay yielded a rate constant of 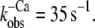 (C) Myofibrils exchanged with NBD-cTn in rigor buffer (pCa >8) were mixed with rigor buffer including ATP to rapidly increase [Mg·ATP] from 0 to 1 mM. The rate constant of the observed monoexponential fluorescence decay is 31 s−1.
(C) Myofibrils exchanged with NBD-cTn in rigor buffer (pCa >8) were mixed with rigor buffer including ATP to rapidly increase [Mg·ATP] from 0 to 1 mM. The rate constant of the observed monoexponential fluorescence decay is 31 s−1.
Fig. 3 C shows the fluorescence change of NBD-cTn after mixing rigor myofibrils with 1 mM ATP. The fluorescence decays with a rate constant of 33 ± 7 s−1 (n = 3) and is similar to the 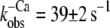 after Ca2+ inactivation.
after Ca2+ inactivation.
Force kinetics of Ca2+-dependent contraction/relaxation of myofibrils
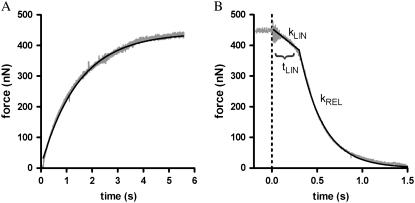
To find out whether the kinetics of the Ca2+-dependent switch-on/switch-off of cTn rate-limit the dynamics of myofibrillar force development and/or relaxation, force kinetics of myofibrils exchanged with NBD-cTn after rapid (within ∼10 ms) changes in [Ca2+] were determined in the mechanical setup. Fig. 4 A depicts the Ca2+-induced force development after a change in pCa from >8 to 4.6. Force rises in a monoexponential manner with a rate constant kACT = 1.0 ± 0.1 s−1 (n = 24). Thus, at saturating [Ca2+] the force develops ∼300-fold slower than the slow phase of the fluorescence increase, which is presumed to reflect the regulatory conformational change of cTnC.
FIGURE 4.
Force kinetics of cardiac myofibrils exchanged with NBD-cTn after rapid changes in [Ca2+]. (A) At t = 0 s, the [Ca2+] pCa was increased from >8 to 4.6. The Ca2+-induced force development (gray transient) is fitted by a monoexponential function (black line), which gives a rate constant of kACT of 0.7 s−1. (B) At t = 0 s, the [Ca2+] was rapidly decreased from pCa 4.6 to pCa >8. The force decay after the Ca2+ reduction (gray transient) is fitted by a biphasic function (black line) that includes a linear and an exponential term to obtain the three kinetic parameters kLIN = 0.35 s−1, tLIN = 0.38 s, and kREL = 3.8 s−1.
Fig. 4 B shows that the force decay after the Ca2+removal (changing pCa from 4.6 to >8) is faster than force development and, additionally, biphasic. First, during the “quasi-isometric” slow phase, the sarcomere lengthening is negligible. The rate constant of this slow phase is kLIN = 0.4 ± 0.1 s−1 (n = 24) and has a duration of tLIN = 0.3 ± 0.1 s (n = 24). The slow phase is followed by a rapid relaxation phase, which is induced by the rapid, sequential lengthening of sarcomeres (10). It has a rate constant of kREL = 3.1 s−1 ± 0.1 (n = 24). Thus kLIN is ∼80 times, and kREL ∼10 times, slower than the fluorescence decay presumed to report the regulatory conformational change of cTn.
DISCUSSION
The biphasic Ca2+-induced fluorescence changes obtained by selectively labeling Cys-84 in cTnC with IANBD reveals two conformational changes. The kinetics of the fast phase obtained here in cardiac myofibrils is at least one order of magnitude faster compared to those found in studies investigating kinetics of fast skeletal TnI or cTnC in skinned fibers (33,9). Thus, the kinetics of Ca2+ binding to cTnC in the sarcomere has to be very rapid, at least ∼10-fold faster than proposed previously. Consequently, our slow phase, which has rate constants similar to those found in the two fiber studies, reports a subsequent conformational change that is kinetically distinguishable from Ca2+ binding to cTnC. Furthermore, our results imply that the kinetics of the slow conformational change are increased by incorporation of NBD-cTn into the sarcomere. Finally, this study elucidates the dynamics of thin-filament inactivation after Ca2+ dissociation from cTnC in a contractile system. Comparison with force kinetics suggests that intrinsic kinetic properties of cTnC rate-limit neither the speed of cardiac myofibrillar contraction nor that of relaxation.
Labeling of cTnC
cTnC contains two reactive cysteines, which can be labeled Cys-35 and Cys-84. Cys-35 is located in the nonfunctional Ca2+-binding loop I. Labeling of Cys-35 does not sense the conformational change in skinned fibers (34) and in myofibrils (data not shown). To minimize structural disturbances by unnecessary labeling of site 35, we created a Cys-35-Ser mutant, which allows selective labeling of Cys-84. Cys-84 is located on the C-terminal end of helix D. Structural studies show that in the presence of Ca2+, helix D interacts with helix 3 in the regulatory region of cTnI (35). Several kinetic studies with isolated proteins (13,15,36) and studies on cTnC in skinned fibers performed under steady-state conditions (34,37,38) indicate that fluorescent probes coupled covalently to Cys-84 sense Ca2+-induced conformational changes of cTnC.
Kinetics of conformational changes with isolated and incorporated cTn
This study compares the kinetics of thin-filament regulation of isolated and incorporated cTn for the first time that we know of by using the same labeling and experimental approach. The Ca2+-induced kinetics with isolated NBD-cTn (Fig. 2, A and B) exhibit the same phases as NBD-cTn incorporated into myofibrils (Fig. 2, E and F): a fast phase, which was too rapid to be resolved by the stopped-flow technique, followed by a slow phase. These two distinct phases indicate that NBD located on Cys-84 of cTnC undergoes two conformational changes. The fast change is either directly or closely associated with Ca2+ binding to cTnC, which then triggers a subsequent slower change. Two distinct conformational changes of cTnI have also been proposed from analysis of the crystal structures of chicken cTnC (39). Ca2+ binding to the regulatory domain II of cTnC first induces the opening of the N-lobe of cTnC, which then triggers an interaction with the regulatory helix 3 of cTnI.
Such a two-step mechanism has been also proposed for the kinetics that occur after Ca2+ removal from isolated chicken cTnC by Hazard et al. (13). The authors showed that the rate constant of Ca2+ release from cTnC (700–800 s−1 at 4°C) determined with a fluorescent Ca2+ chelator is about threefold faster than the conformational change (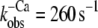 ) reported by the fluorescent probe IAANS on Cys-84. That the conformational change in Hazard's study is much faster compared to that given by the slow phase in our study (14 s−1 at 10°C for reconstituted human Tn complex) likely results from the assembly of cTnC with cTnI. This assembly is known to decrease the rate constant of the conformational change by a factor of 10–20 (15). In this study (15) of Dong et al., it has also been shown that addition of cTnT to cTnI-cTnC labeled at Cys-35 of cTnC with IAANS did not further change the kinetics induced by Ca2+ and Ca2+ removal. Therefore, the increased rate constant of the slow phase that we observed when cTn was incorporated into the myofibrils seems to be most likely due to a slight weakening of TnC-TnI interactions when the cTn complex is bound to actin in the myofibrils. The increase in kinetics for the myofibril-incorporated, compared to the isolated, cTn complex was similar (fourfold) for both Ca2+ activation and Ca2+ inactivation. It is noteworthy that if diffusion of Ca2+ or BAPTA into the myofilament lattice were to limit kinetics, one would expect slower, but not faster, kinetics in myofibrils. The faster inactivation of the incorporated complex is in qualitative agreement with biochemical studies showing that the association of Tn with actin and Tm to form reconstituted thin filaments accelerates the off-kinetics of skeletal Tn (40) and cardiac Tn (17). The fourfold faster kinetics in myofibrils might be related to a decrease in activation energy (∼3.5 kJ/mol) for the switch-on and the switch-off transition when cTn is incorporated in its native environment.
) reported by the fluorescent probe IAANS on Cys-84. That the conformational change in Hazard's study is much faster compared to that given by the slow phase in our study (14 s−1 at 10°C for reconstituted human Tn complex) likely results from the assembly of cTnC with cTnI. This assembly is known to decrease the rate constant of the conformational change by a factor of 10–20 (15). In this study (15) of Dong et al., it has also been shown that addition of cTnT to cTnI-cTnC labeled at Cys-35 of cTnC with IAANS did not further change the kinetics induced by Ca2+ and Ca2+ removal. Therefore, the increased rate constant of the slow phase that we observed when cTn was incorporated into the myofibrils seems to be most likely due to a slight weakening of TnC-TnI interactions when the cTn complex is bound to actin in the myofibrils. The increase in kinetics for the myofibril-incorporated, compared to the isolated, cTn complex was similar (fourfold) for both Ca2+ activation and Ca2+ inactivation. It is noteworthy that if diffusion of Ca2+ or BAPTA into the myofilament lattice were to limit kinetics, one would expect slower, but not faster, kinetics in myofibrils. The faster inactivation of the incorporated complex is in qualitative agreement with biochemical studies showing that the association of Tn with actin and Tm to form reconstituted thin filaments accelerates the off-kinetics of skeletal Tn (40) and cardiac Tn (17). The fourfold faster kinetics in myofibrils might be related to a decrease in activation energy (∼3.5 kJ/mol) for the switch-on and the switch-off transition when cTn is incorporated in its native environment.
In conclusion, the similar biphasic shapes and the similar [Ca2+] dependence of fluorescence transients for cTn incorporated in myofibrils and for isolated cTn indicate that their kinetic mechanism is similar but their switch kinetics of cTnC in situ and in vitro are different.
Implications of the fast phase for the kinetics of Ca2+ binding
That the fast phase represents the Ca2+ binding is demonstrated by the observation that mixing of isolated cTn and cTn incorporated into myofibrils with high [Ca2+] induces the fast phase, which increases the fluorescence by ∼60% within the dead time of the stopped-flow apparatus (2.2 ms) (Fig. 2, A and E). This fast conformational change must occur with a rate constant of >2000 s−1, because we were unable to resolve its kinetics at saturating [Ca2+] even when the dead-time was reduced to 250 μs by using a microcuvette (data not shown) instead of the standard mixing cuvette. This suggests, that at high [Ca2+], Ca2+ binding is too rapid (>2000 s−1) to be temporally resolved by stopped flow and only manifests itself in an offset of the initial fluorescence compared to the Ca2+-free control. Ca2+-binding could be therefore almost diffusion-controlled, as proposed by studies with isolated skeletal TnC (41). Different groups determined a second-order rate constant for Ca2+-binding (kB) to isolated skeletal and cardiac TnC of 100–200 μM−1 s−1 (13,41–43). This would yield a rate constant for Ca2+ binding of kB ≈ 2500–5000 s−1 at pCa 4.6 assuming that kB increases linearly with [Ca2+] in a nonsaturating manner, as for a diffusion-controlled reaction. Tikunova and Davis (44) showed that cTnC mutants can bind Ca2+ with even faster second-order rate constants, which indicates that the mechanism of Ca2+ binding may be not purely diffusion-controlled. Nevertheless, introducing a linear dependence of kB on [Ca2+] relation in a model simulation gives close agreement with our data (see modeling chapter).
We note that our interpretation of Ca2+-binding kinetics from phases in the fluorescence transients differs from those in previous studies of Dong et al. (15) on isolated cTn, and Bell et al. (9) on cTnC in skinned fibers. In neither of those studies did the authors notice a phase of similar fast kinetics. Dong et al. probed the kinetics of cTn by labeling the Cys-35 of cTnC with IAANS. In their study, they interpreted the fast phase to probe the mechanism of Ca2+ binding, but with a rate constant of 30–40 s−1 at 4°C—compared to our data—it kinetically corresponds to our slow phase of 80 s−1 at 10°C for the isolated cTn. Bell et al. (9) investigated the Ca2+-induced switch-on kinetics of rhodamine-labeled cTnC in skinned trabeculae from guinea pig by fluorescence polarization. They found two kinetic phases, of which they suggested that the first is associated with Ca2+ binding. Again, the kinetics of their fast phase is similar to that of our slow phase but not to that of our fast phase. Because they had to use caged Ca2+, they could neither activate at saturating [Ca2+] nor make a defined Ca2+ dependence. However, at ∼2/3 of maximum Ca2+ activation, their rate constant is ∼100 s−1, which correlates with a 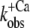 of the slow phase of 118 ± 29 s−1 (n = 5) at 65 ± 8% activation in our results for the incorporated cTn complex.
of the slow phase of 118 ± 29 s−1 (n = 5) at 65 ± 8% activation in our results for the incorporated cTn complex.
In conclusion, our fast phase represents the rapid conformational changes either directly or closely associated with an almost diffusion-limited Ca2+-binding process, whereas the fast phases observed by Dong et al. (15) and Bell et al. (9) clearly occur after Ca2+ binding. As the rate constants of the fast phases in the studies of Dong et al. and Bell et al. show striking similarities, in terms of magnitude and Ca2+ dependence, with that of our slow phase, for isolated and incorporated cTn, respectively, it seems very likely that all three refer to the same global conformational change of the cTn complex.
Relation of thin filament activation kinetics in the sarcomere to force development
Our slow phase indicates a ∼100-fold faster switch-on of cTnC compared to the kinetics of force development. The fast phase in the Bell et al. study is also ∼20-fold faster than Ca2+-induced force development. Thus from both studies, it is evident that the conformational change of cTnC will not rate-limit the time course of force development.
In addition, Bell et al. also detected a very slow phase, which had a rate constant (1–5 s−1) identical to that of the simultaneously measured Ca2+-induced force development. This phase indicates that cross-bridge binding can activate the thin filament beyond the level of activation induced by Ca2+ alone. Though we labeled the same site Cys-84 on cTnC as Bell et al., we could not detect this phase. This might be related to the absence of external load during myofibrillar contraction in our stopped-flow experiments. It is likely that during unloaded shortening only a few strongly bound cross-bridges are attached to the thin filament (45). Thus, the contribution of cross-bridges to the activation of the thin filament is negligible under our conditions. Therefore, we cannot exclude a possible feedback of cross-bridges on thin filament activation under isometric contraction. Consistent with the presence of such a positive feedback, Bell et al. found that the Ca2+ sensitivity of the overall fluorescence signal during contraction in the presence of Mg·ATP is markedly increased compared to Ca2+ sensitivity in the presence of the non-force-generating nucleotide analog ADP-vanadate.
Brenner and Chalovich (33) studied the kinetics of thin-filament activation probed by fluorescence of NBD-labeled troponin I in skinned rabbit psoas fibers. Their approach differs from ours and Bell's in that the [Ca2+] was kept constant and thin-filament kinetics were induced by changing cross-bridge attachment via mechanical perturbation. Like Bell et al., they found that slow fluorescence changes occurred in parallel with cross-bridge reattachment during force development. However, these fluorescence changes only occurred at intermediate Ca2+-activating levels and amounted to ∼20% of the total change observed between relaxing and fully-Ca2+-activating conditions. As Brenner and Chalovich (33) found no slow fluorescence changes during force redevelopment under high [Ca2+], their results indicated that cycling cross-bridges are able to additionally activate the thin filament at partial Ca2+ activation, whereas at saturating [Ca2+], Ca2+ alone is sufficient to fully activate the thin filament. When cross-bridge attachment was rapidly lowered by suddenly turning from isometric to unloaded shortening, fluorescence changed much faster, monoexponentially, with rate constants increasing from ∼10–15 s−1 at partial Ca2+ activation to 50–80 s−1 at full Ca2+ activation. Taking into account the lower temperature in their study (5°C), these values are in good agreement with those of the slow phase in our experiment (10°C), which increased from ∼20 s−1 to 330 s−1 with [Ca2+].
In conclusion, based on the results of these three different and complementary studies (ours and (9,29)), we propose that Ca2+ binding triggers two conformational changes, a fast one, induced directly by the Ca2+ binding, and a subsequent slower one, which is the major conformational change, involving at least TnC and TnI, and which is ∼1–2 orders of magnitude faster than force-development kinetics. Additional 10- to 100-fold slower changes in thin filament activation are likely occurring during the formation of force-generating cross-bridges, but these are not triggered by Ca2+ binding and might be restricted to intermediate levels of Ca2+ activation.
Further evidence that the slow phase in this study represents a global change of the Tn complex is given by the considerations about switch-off kinetics induced by Ca2+-independent relaxation from rigor (see below).
Kinetics of thin-filament inactivation in myofibrils
The fluorescence change after a rapid reduction of [Ca2+] from pCa = 5.0 to pCa > 8 consists of a slow phase with a rate constant of 39 ± 2 s−1 (n = 10). Based on our measurements, we cannot exclude the possibility that a minor fast phase precedes the slow phase (for details, see Results). Such a minor fast phase could also explain why the amplitude of fluorescence decay is smaller than expected, as determined from the difference between the steady-state fluorescence levels at pCa > 8 and pCa = 5.0.
The similar kinetics of the fluorescence decay induced by Ca2+ removal and that induced by mixing rigor myofibrils with Mg·ATP in the continuous absence of Ca2+ suggest that the conformational changes of cTnC are linked to the overall state of the thin filament. As is generally accepted, rigor bridges keep the thin filament in an activated state even in the absence of Ca2+ (46). They do so by causing Tm to move back to its off position, where it blocks the strong binding actomyosin interaction. That ATP-induced detachment of rigor bridges triggers a conformational change of cTnC with rate constants similar to those in the relaxation experiments suggests that this movement of Tm is mediated from Tm via cTnT and cTnI to cTnC. The slow conformational change induced by Ca2+ removal therefore not only represents the kinetics of a local change in the regulatory domain of TnC but is likely correlated to the kinetics of a global change of the thin filament involving the regulatory move of Tm.
Relating the kinetics of the conformational change of cTnC after Ca2+ inactivation to the kinetics of force relaxation is of special interest to determine whether the intrinsic kinetic properties of regulatory proteins determine the time course of force relaxation. The kinetics of the conformational changes of cTnC during inactivation is slower than during activation. Contrary to this, the force kinetics of myofibrillar relaxation is faster than for activation and, furthermore, occurs in two phases. The inital slow phase of myofibrillar force relaxation occurs when all sarcomeres remain isometric, whereas during the subsequent fast phase, cross-bridge detachment is accelerated by rapid lengthening of single sarcomeres (21,26). Correlation of the fluorescence decay with the force decays show that the switch-off is completed within the first ∼150 ms of the slow, linear phase of the force decay (Fig. 4 B). This indicates that the intrinsic switch-off kinetics of cTnC is much faster than the time course of force relaxation.
Nevertheless, the coupling between the switch-off of the thin filament and cross-bridge detachment during a physiological relaxation under load remains poorly understood. It remains difficult to predict how the fluorescence decay would occur under the isometric conditions under which the mechanical experiments were performed. In contrast, in the stopped-flow experiments, relaxation is likely initiated from very low levels of cross-bridge attachment because of the unloaded contraction of myofibrils preceding the Ca2+ removal. Under such conditions, the regulatory move of Tm to its off position is not allosterically inhibited by cross-bridges, and the conformational change of inactivation presumably occurs at a higher rate in most regulatory actin-Tm-cTn units than under isometric conditions where many cycling cross-bridges would be attached to actin. It has been shown that myosin Apo-S1—which is used to mimic the effects of strongly bound cross-bridges—decreases the rate of the switch-off of skeletal Tn and cTn in reconstituted thin filaments (17). These findings agree with structural and kinetic studies of regulated acto-S1 (47,48), implying that a regulatory unit will only be able to switch off after S1 detaches from it. If this also applies to cycling cross-bridges, Tn should switch off during loaded relaxation at a rate limited by cross-bridge detachment. Thus, even though the rate for the switch-off intrinsic to cTn (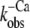 ) measured in the absence of cross-bridges is much faster than the rate of cross-bridge detachment, switch-off in the presence of cycling cross-bridges might be faster. However, this causes a new problem: if cycling cross-bridges are able to keep the thin filament activated even in the absence of Ca2+, like rigor bridges or Apo-S1, why should relaxation occur at all?
) measured in the absence of cross-bridges is much faster than the rate of cross-bridge detachment, switch-off in the presence of cycling cross-bridges might be faster. However, this causes a new problem: if cycling cross-bridges are able to keep the thin filament activated even in the absence of Ca2+, like rigor bridges or Apo-S1, why should relaxation occur at all?
Another possibility is that cycling cross-bridges, in contrast to Apo-S1, cannot permanently trap Tm in its on-position. The reason for such a mechanism could be that, e.g., the regulatory switch controls the probability of how many myosin heads enter force-generating states, but it would not control myosin heads, which already are generating force (as described in the steric blocking hypothesis). The argument for this is that cycling cross-bridges do not delay the kinetics of the force decay in isometrically held cardiac and skeletal myofibrils. In particular, the kinetics of the force decay is not altered if relaxation is initiated from different force levels of the preceding contraction (10,21,49). High phosphate concentrations greatly reduce the duration of the slow phase of force relaxation to <10 ms (10), which is less than half the time of the switch-off of cTn (t1/2 = 18 ms) determined in this study. This suggests that there might be alternative ways of cross-bridge detachment by rapid backward cycling and it emphasizes that cross-bridge kinetics are the main determinants of cardiac myofibrillar relaxation.
In summary, we can conclude from our data that the kinetics of conformational changes intrinsic to cTnC do not rate-limit the kinetics of the force decay during myofibrillar relaxation. However, the results presented here do not exclude the possibility that these changes could occur under loaded conditions briefly after the cross-bridge detachment, if it is presumed that force-generating cross-bridges allosterically hinder the switch-off. Future experiments using skinned fibers with incorporated fluorescently labeled regulatory proteins and caged Ca2+ chelators would help to elucidate the coupling mechanism of thin filament inactivation and cross-bridge detachment.
Modeling of cTn kinetics
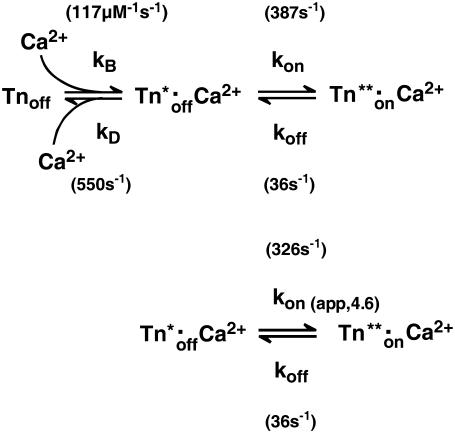
The minimal model that accounts for the observation of a fast and a slow phase in the “on” experiments is shown by the three-state model (Scheme 1, upper), where kB is the second-order rate constant of Ca2+ binding, kD the rate constant of Ca2+ dissociation, and kon and koff the rate constants of regulatory switch-on and switch-off, respectively. As discussed before, there are several reasons for us to assume that the 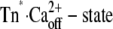 will be generated with kinetics according to a diffusion-limited, or approximately diffusion-limited, binding reaction with a rate constant kB[Ca2+] + kD that does not saturate at high [Ca2+] (41). Consequently, the fast conformational change would occur immediately with Ca2+ binding, i.e., there is no subsequent isomerization step whose kinetics can be distinguished from those of Ca2+ binding.
will be generated with kinetics according to a diffusion-limited, or approximately diffusion-limited, binding reaction with a rate constant kB[Ca2+] + kD that does not saturate at high [Ca2+] (41). Consequently, the fast conformational change would occur immediately with Ca2+ binding, i.e., there is no subsequent isomerization step whose kinetics can be distinguished from those of Ca2+ binding.
SCHEME 1.
Three-state model for thin-filament kinetics and its simplification to a two-state model. For the meaning of the rate constants and their calculation, see text.
We modeled the data in two steps: as a first approximation, the kinetics of Ca2+ binding and dissociation were treated as a rapid equilibrium. In this case, when kD ≫ koff and kD ≫ kon, the kinetic analysis can be simplified from a three-state model to a two-state model, as shown in the lower panel of Scheme 1. This approach has the advantage of yielding initial estimates for kon and koff, irrespective of the values for kD and kB. In this two-state model, fluorescence will increase monoexponentially depending on the rate constant 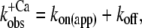 where kon(app) is an apparent Ca2+-dependent rate constant and koff is a fixed, Ca2+-independent rate constant with the same value as koff in the three-state model. The amplitude of the fluorescence change (ΔF) will be proportional to kon(app)/(kon(app) + koff). Defining ΔF and kon(app) at the highest [Ca2+] (pCa 4.6) as ΔF(4.6) and kon(app 4.6), respectively,
where kon(app) is an apparent Ca2+-dependent rate constant and koff is a fixed, Ca2+-independent rate constant with the same value as koff in the three-state model. The amplitude of the fluorescence change (ΔF) will be proportional to kon(app)/(kon(app) + koff). Defining ΔF and kon(app) at the highest [Ca2+] (pCa 4.6) as ΔF(4.6) and kon(app 4.6), respectively, 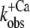 relates to the fluorescence change according to the equation given in Poggesi et al. (3):
relates to the fluorescence change according to the equation given in Poggesi et al. (3):
 |
(1) |
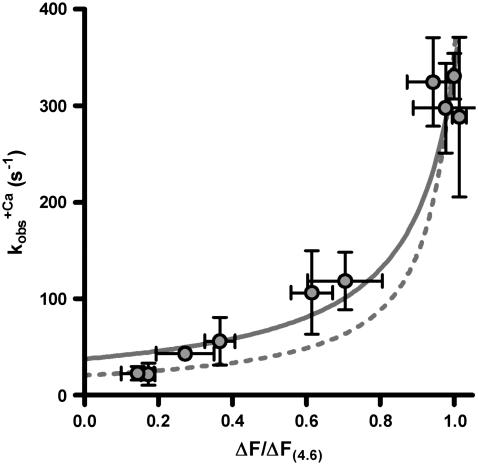
Therefore, the experimental data were plotted as 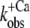 versus the corresponding relative fluorescence change (ΔF/ΔF(4.6)), and fitted by Eq. 1 (Fig. 5). The parameter koff corresponds to the value of the fit curve at ΔF = 0 and the parameter kon(app,4.6) to its total increment from ΔF = 0 to ΔF(4.6). Fitting of six experimental
versus the corresponding relative fluorescence change (ΔF/ΔF(4.6)), and fitted by Eq. 1 (Fig. 5). The parameter koff corresponds to the value of the fit curve at ΔF = 0 and the parameter kon(app,4.6) to its total increment from ΔF = 0 to ΔF(4.6). Fitting of six experimental 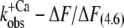 relations from six different myofibrillar preparations yields koff = 36 ± 5 s−1 and kon(app,4.6) = 326 ± 37 s−1 (n = 6). It is noteworthy that the koff value determined by this model is close to the rate constants determined from the fluorescent traces of the “off” experiments (
relations from six different myofibrillar preparations yields koff = 36 ± 5 s−1 and kon(app,4.6) = 326 ± 37 s−1 (n = 6). It is noteworthy that the koff value determined by this model is close to the rate constants determined from the fluorescent traces of the “off” experiments (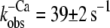 ). Furthermore, the curvature of the fit function—which is not a free parameter itself and only depends on the ratio of koff and kon(app,4.6)—agrees closely with the experimentally determined data shown in Fig. 5. Thus, the experimentally determined data are described well by the two-state model. However, an exception is seen at low Ca2+ activations (low ΔF) at which the experimentally determined
). Furthermore, the curvature of the fit function—which is not a free parameter itself and only depends on the ratio of koff and kon(app,4.6)—agrees closely with the experimentally determined data shown in Fig. 5. Thus, the experimentally determined data are described well by the two-state model. However, an exception is seen at low Ca2+ activations (low ΔF) at which the experimentally determined 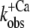 values are significantly lower than the koff values determined by the fit. This indicates that the initial assumption that kD ≫ kon for the two-state model is not completely fulfilled and that at low Ca2+ activations,
values are significantly lower than the koff values determined by the fit. This indicates that the initial assumption that kD ≫ kon for the two-state model is not completely fulfilled and that at low Ca2+ activations, 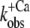 might be not solely determined by koff but also indirectly by kD. By determining the eigenvalues of the rate constants for the three-state model (Fig. 5, dotted line), it can be shown that if the value of kD were lowered to approach that of kon, then the kobs at low Ca2+ activations would be reduced below the koff determined initially in the approximation of the two-state model, e.g., when kD = kon, then
might be not solely determined by koff but also indirectly by kD. By determining the eigenvalues of the rate constants for the three-state model (Fig. 5, dotted line), it can be shown that if the value of kD were lowered to approach that of kon, then the kobs at low Ca2+ activations would be reduced below the koff determined initially in the approximation of the two-state model, e.g., when kD = kon, then 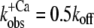 at ΔF/ΔF(4.6) = 0. Hence, by moving from the two- to the three-state model, we could estimate kD by keeping the values for kon and koff constant and changing the value of kD to match the kobs at low Ca2+ activations. By setting kD to 550 s−1, the eigenvalue of kobs in the ΔF/ΔF(4.6) region from 0–20% is lowered to 20–25 s−1, in better agreement with the corresponding experimental data. This estimated value of kD is in the same range as those for isolated human cTnC found by other groups (483 s−1 (50) and 1200 s−1 (44)).
at ΔF/ΔF(4.6) = 0. Hence, by moving from the two- to the three-state model, we could estimate kD by keeping the values for kon and koff constant and changing the value of kD to match the kobs at low Ca2+ activations. By setting kD to 550 s−1, the eigenvalue of kobs in the ΔF/ΔF(4.6) region from 0–20% is lowered to 20–25 s−1, in better agreement with the corresponding experimental data. This estimated value of kD is in the same range as those for isolated human cTnC found by other groups (483 s−1 (50) and 1200 s−1 (44)).
FIGURE 5.
Dependence of the rate constant of the observable slow fluorescence change (kobs) on the relative fluorescence amplitude. The relative amplitude of the total fluorescence change (ΔF/ΔF(4.6)) was obtained by normalizing the fluorescence changes induced by the different [Ca2+] to that induced by pCa 4.6 (ΔF(4.6)) in the particular experiment. kobs-(ΔF/ΔF(4.6)) obtained at the same [Ca2+]s were plotted as mean ± SE (circles and error bars). The solid line represents the kobs-(ΔF/ΔF(4.6)) dependence given by Eq. 1 according to the two-state model using the parameter means koff = 36 s−1 and kon(app.4.6) = 326 s−1, which were obtained from the six individual fits to the six experiments (see text). The solid line represents the dependence according to the three-state model to additionally specify the parameters for Ca2+ binding and dissociation (for details, see text).
Considering the three-state model, the equilibrium dissociation constant for Ca2+-binding (kB) is defined by
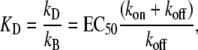 |
(2) |
where EC50 is the [Ca2+] required to yield the half-maximal fluorescence change (ΔF). The value of EC50 = 0.4 μM was obtained from the pCa50 = 6.4 of the experimentally determined ΔF-pCa relation shown in Fig. 2 G. The value of kon in the three-state model refers to the value of kon(app) in the two-state model at infinite [Ca2+], meaning that at 100% Ca2+ saturation of cTn they are the same. For <100% saturation, e.g., at pCa 4.6, their interdependence is:
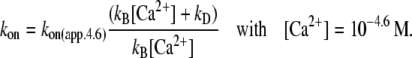 |
(3) |
Solving Eqs. 2 and 3 for the second-order rate constant for Ca2+ binding (kB) yields a value of 117 μM−1 s−1. This is similar to those determined in studies on isolated human cTnC (100 μM−1 s−1 (50) and 170 μM−1 s−1 (43)). The overall broad similarity of the values of kB and kD deduced from our modeling of cTn kinetics in myofibrils to those reported for isolated cTn suggests that Ca2+ binding/dissociation kinetics are primarily determined by cTnC and are hardly altered by cTnC-cTnI interactions or by integration of the cTn complex into the thin filament of myofibrils. This contrasts with the large changes in the kinetics of the regulatory switch, which are, as discussed above, slowed down ∼10-fold by interaction of cTnC with cTnI (15), and accelerated around fourfold by integration of the cTn complex to myofibrils.
The value of kon in the three-state model can be calculated from Eq. 3: at pCa 4.6, the pseudo-first-order rate constant of Ca2+ binding (kB[Ca2+]) is 2.900 s−1. With kD = 550 s−1 and kon(app,4.6) = 326 s−1, it follows that kon = 387 s−1. This is slightly higher than the kon(app,4.6), because a small fraction of cTn (∼1.6% of all cTnC states or 16% among the two cTn off-states) will not have bound Ca2+ at pCa 4.6.
It is noteworthy that in the three-state model, though kon and koff are fixed (Ca2+-independent) rate constants that do not directly rate-limit the regulatory switch, the observed kinetics of the regulatory switch are rate-modulated by the Ca2+-binding/dissociation step. As kB[Ca2+] is altered in relation to kD, the observed rate constant of the regulatory switch increases from values below koff at infinitesimal [Ca2+] to koff + kon at infinite [Ca2+]. In this way, the Ca2+-dependent rapid binding/dissociation equilibrium affects the observed rates of the switch kinetics.
A further implication of the model is that the Ca2+ sensitivity of the regulatory switch (EC50 in Eq. 2) is different from the Ca2+ affinity given by the Ca2+-binding/dissociation reaction (KD in Eq. 2). KD is the [Ca2+] at which kB[Ca2+] = kD, so that the equilibrium constant for the Ca2+-binding/dissociation step is unity. At [Ca2+] = KD, the two off-states (cTnoff and cTn*off·Ca2+) are equally occupied, i.e., half of them have bound Ca2+. Thus, KD is an indicator for the Ca2+ affinity of cTn if we would just focus on the isolated Ca2+-binding/dissociation reaction, i.e., as determined without the regulatory switch. Indeed, without the regulatory switch, half-maximal Ca2+ binding would occur at [Ca2+] = KD. However, due to the coupling to the regulatory switch, the ∼10-fold faster on- than off-transition of the regulatory switch shifts half-maximal Ca2+-binding from KD to EC50 according to Eq. 2. This kinetic coupling might explain why the Ca2+ affinity of cTnC·cTnI has been found to be about an order of magnitude higher than for isolated cTnC (51): when cTnI is absent, the regulatory switch on cTnC may not occur and Ca2+ affinity of cTnC remains low, being similar to KD in our model. When cTnI is present, Ca2+ binds to the N-lobe of cTnC to switch it on, and because the equilibrium constant for the regulatory switch is high (kon/koff ≈ 10), Ca2+ binding is promoted. The high ratio of kon/koff basically relates to our finding that the kinetics of the slow conformational change was strongly Ca2+-dependent, i.e., kobs increased >10-fold from low to high [Ca2+]. This also implicates a high fractional occupancy of Ca2+-activated sites: e.g., at pCa 4.6, in the steady state, most of cTnC (∼90%) will be switched on and only ∼10% will remain switched off (see Fig. 6 C).
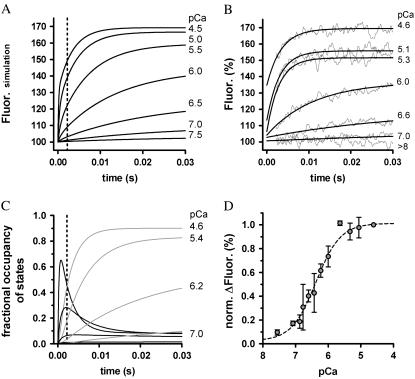
FIGURE 6.
Ca2+-induced fluorescence signals predicted by the three-state model involving Ca2+ binding and a subsequently coupled conformational change. (A) Simulated time course of fluorescence after instantaneous rises in [Ca2+] at t = 0 s to different pCa (indicated by the numbers). Kinetic parameters used for simulations were kB = 117 μM−1 s−1, kD = 550 s−1, kon = 387 s−1, and koff = 36 s−1 (for details, see text). The dotted line at 2.2 ms represents the dead time of the apparatus. (B) Same as in A, but with the fitted, experimentally determined transients to compare with the simulated curves predicted by the three-state model parameters. (C) Time courses of the transient fractional occupancies of the two Ca2+-binding states induced by different pCas. At high [Ca2+], the transient of the Tn*off·Ca2+ state (black traces) exceeds its steady state, which produces the large fast phase of the fluorescence increase depicted in A. The accumulation of the Tn*on·Ca2+ state (gray traces) is the major determinant of the observable slow phase after the dead time. (D) The experimentally determined total fluorescence increase in dependence of the activating pCa is compared with the theoretically determined total fluorescence increase predicted by the three-state model (black line).
To prove the correctness of the three-state model and its kinetic parameters, we correlated the experimentally determined traces against the traces we obtained by simulating the three-state model (Fig. 6, A and B). By appropriate setting of relative fluorescence for the three states, 100% for Tnoff, 135% for Tn*off·Ca2+, and 170% for 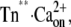 close agreement with experimental traces is obtained. A striking feature of the simulated traces is that not only do they reproduce the kinetics of the experimentally determined traces, but also the complex Ca2+ dependence of the contribution of fast and slow phases to the amplitude of the fluorescence change, i.e., the fast phase contributes significantly to the signal only at high [Ca2+] (pCa <6) (for illustration of ΔFfast and ΔFslow, see also Figs. 2 E and 6 C). The fast phase is generated by the formation of the Tn*off·Ca2+ intermediate state. Redistribution to this state is already rapid at low [Ca2+] due to the high kD, but a fast phase is not apparent at low [Ca2+] because of the low steady-state concentration of this state. This steady-state concentration never exceeds 10% of total cTn, even at very high [Ca2+] (Fig. 6 C). The real reason for the large fast phase at high [Ca2+] is a transient overshoot of the
close agreement with experimental traces is obtained. A striking feature of the simulated traces is that not only do they reproduce the kinetics of the experimentally determined traces, but also the complex Ca2+ dependence of the contribution of fast and slow phases to the amplitude of the fluorescence change, i.e., the fast phase contributes significantly to the signal only at high [Ca2+] (pCa <6) (for illustration of ΔFfast and ΔFslow, see also Figs. 2 E and 6 C). The fast phase is generated by the formation of the Tn*off·Ca2+ intermediate state. Redistribution to this state is already rapid at low [Ca2+] due to the high kD, but a fast phase is not apparent at low [Ca2+] because of the low steady-state concentration of this state. This steady-state concentration never exceeds 10% of total cTn, even at very high [Ca2+] (Fig. 6 C). The real reason for the large fast phase at high [Ca2+] is a transient overshoot of the 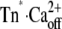 state whose concentration transiently rises above its steady-state level (Fig. 6 C). This overshoot comes up when kB[Ca2+] > kon and can become very large (e.g., sevenfold higher than its steady-state value at pCa 4.6). This transient kinetic phenomenon can therefore explain the observation that with increasing [Ca2+] the amplitude of the fast phase increases much more than the amplitude of the slow phase. The good reproduction of this observation by the model simulation (Fig. 6 B) is further proof that the fluorescence signals report two sequentially coupled processes. If, for example, fast and slow phases simply belong to two independent processes of fast and slower kinetics, their amplitudes should rise in proportion to each other when the [Ca2+] is increased.
state whose concentration transiently rises above its steady-state level (Fig. 6 C). This overshoot comes up when kB[Ca2+] > kon and can become very large (e.g., sevenfold higher than its steady-state value at pCa 4.6). This transient kinetic phenomenon can therefore explain the observation that with increasing [Ca2+] the amplitude of the fast phase increases much more than the amplitude of the slow phase. The good reproduction of this observation by the model simulation (Fig. 6 B) is further proof that the fluorescence signals report two sequentially coupled processes. If, for example, fast and slow phases simply belong to two independent processes of fast and slower kinetics, their amplitudes should rise in proportion to each other when the [Ca2+] is increased.
In conclusion, conformational changes of cTnC in its sarcomeric environment involve rapid Ca2+ binding and dissociation kinetics, which are similar fast as has been reported for isolated cTnC and a slower conformational change. Several lines of evidence suggest that the slow conformational change represents the kinetics of the regulatory switch. The Ca2+-controlled rates at which cTnC switches on and off are about two and one order of magnitude too fast to directly rate-limit cardiac myofibrillar contraction and relaxation, respectively. However, the results presented here cannot fully exclude the possibility that higher numbers of force-generating cross-bridges attached to actin during loaded contraction-relaxation cycles induce additional regulatory changes of regulatory proteins that modulate the force transient. Whether force-generating cross-bridges exert a feedback on the dynamics of thin filament activation and inactivation in loaded fibers/myofibrils remains to be resolved.
Acknowledgments
The authors thank Tom Barman (Institut national de la santé et de la recherche médicale (INSERM), Montpellier, France) for his critical reading of the manuscript and F. P. Kulozik for technical assistance.
This work was supported by grants from the Center of Molecular Medicine Cologne (grant: TV91), Köln Fortune (Faculty of Medicine, Cologne, grant 109/2003), and, in part, by the Deutsche Forschungsgemeinschaft (SFB 612-A2).
Editor: Shin'ichi Ishiwata.
References
- 1.Kobayashi, T., and R. J. Solaro. 2005. Calcium, thin filaments, and the integrative biology of cardiac contractility. Annu. Rev. Physiol. 67:39–67. [DOI] [PubMed] [Google Scholar]
- 2.Smith, D. A., and M. A. Geeves. 2003. Cooperative regulation of myosin-actin interactions by a continuous flexible chain II: actin-tropomyosin-troponin and regulation by calcium. Biophys. J. 84:3168–3180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Poggesi, C., C. Tesi, and R. Stehle. 2005. Sarcomeric determinants of striated muscle relaxation kinetics. Pflugers Arch. 449:505–517. [DOI] [PubMed] [Google Scholar]
- 4.Backx, P. H., W. D. Gao, M. D. Azan-Backx, and E. Marban. 1995. The relationship between contractile force and intracellular [Ca2+] in intact rat cardiac trabeculae. J. Gen. Physiol. 105:1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Janssen, P. M., L. B. Stull, and E. Marban. 2002. Myofilament properties comprise the rate-limiting step for cardiac relaxation at body temperature in the rat. Am. J. Physiol. Heart Circ. Physiol. 282:H499–H507. [DOI] [PubMed] [Google Scholar]
- 6.Palmer, S., and J. C. Kentish. 1994. The role of troponin C in modulating the Ca2+ sensitivity of mammalian skinned cardiac and skeletal muscle fibres. J. Physiol. 480:45–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Palmer, S., and J. C. Kentish. 1998. Roles of Ca2+ and crossbridge kinetics in determining the maximum rates of Ca2+ activation and relaxation in rat and guinea pig skinned trabeculae. Circ. Res. 83:179–186. [DOI] [PubMed] [Google Scholar]
- 8.Martin, H., M. G. Bell, G. C. Ellis-Davies, and R. J. Barsotti. 2004. Activation kinetics of skinned cardiac muscle by laser photolysis of nitrophenyl-EGTA. Biophys. J. 86:978–990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bell, M. G., E. B. Lankford, G. E. Gonye, G. C. Ellis-Davies, D. A. Martyn, M. Regnier, and R. J. Barsotti. 2006. Kinetics of cardiac thin-filament activation probed by fluorescence polarization of rhodamine-labeled troponin C in skinned guinea pig trabeculae. Biophys. J. 90:531–543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Stehle, R., M. Kruger, and G. Pfitzer. 2002. Force kinetics and individual sarcomere dynamics in cardiac myofibrils after rapid Ca2+ changes. Biophys. J. 83:2152–2161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Piroddi, N., A. Belus, B. Scellini, C. Tesi, G. Giunti, E. Cerbai, A. Mugelli, and C. Poggesi. 2006. Tension generation and relaxation in single myofibrils from human atrial and ventricular myocardium. Pflugers Arch. 454:63–73. [DOI] [PubMed] [Google Scholar]
- 12.Johnson, J. D., S. C. Charlton, and J. D. Potter. 1979. A fluorescence stopped flow analysis of Ca2+ exchange with troponin C. J. Biol. Chem. 254:3497–3502. [PubMed] [Google Scholar]
- 13.Hazard, A. L., S. C. Kohout, N. L. Stricker, J. A. Putkey, and J. J. Falke. 1998. The kinetic cycle of cardiac troponin C: calcium binding and dissociation at site II trigger slow conformational rearrangements. Protein Sci. 7:2451–2459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Strasburg, G. M., P. C. Leavis, and J. Gergely. 1985. Troponin-C-mediated calcium-sensitive changes in the conformation of troponin I detected by pyrene excimer fluorescence. J. Biol. Chem. 260:366–370. [PubMed] [Google Scholar]
- 15.Dong, W. J., C. K. Wang, A. M. Gordon, S. S. Rosenfeld, and H. C. Cheung. 1997. A kinetic model for the binding of Ca2+ to the regulatory site of troponin from cardiac muscle. J. Biol. Chem. 272:19229–19235. [DOI] [PubMed] [Google Scholar]
- 16.Shitaka, Y., C. Kimura, T. Iio, and M. Miki. 2004. Kinetics of the structural transition of muscle thin filaments observed by fluorescence resonance energy transfer. Biochemistry. 43:10739–10747. [DOI] [PubMed] [Google Scholar]
- 17.Davis, J. P., C. Norman, T. Kobayashi, R. J. Solaro, D. R. Swartz, and S. B. Tikunova. 2007. Effects of thin and thick filament proteins on calcium binding and exchange with cardiac troponin C. Biophys. J. 92:3195–3206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gordon, A. M., E. Homsher, and M. Regnier. 2000. Regulation of contraction in striated muscle. Physiol. Rev. 80:853–924. [DOI] [PubMed] [Google Scholar]
- 19.Ma, Y. Z., and E. W. Taylor. 1994. Kinetic mechanism of myofibril ATPase. Biophys. J. 66:1542–1553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lionne, C., M. Brune, M. R. Webb, F. Travers, and T. Barman. 1995. Time resolved measurements show that phosphate release is the rate limiting step on myofibrillar ATPases. FEBS Lett. 364:59–62. [DOI] [PubMed] [Google Scholar]
- 21.Tesi, C., N. Piroddi, F. Colomo, and C. Poggesi. 2002. Relaxation kinetics following sudden Ca2+ reduction in single myofibrils from skeletal muscle. Biophys. J. 83:2142–2151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kruger, M., G. Pfitzer, and R. Stehle. 2003. Expression and purification of human cardiac troponin subunits and their functional incorporation into isolated cardiac mouse myofibrils. J. Chromatogr. B Analyt. Technol. Biomed. Life Sci. 786:287–296. [DOI] [PubMed] [Google Scholar]
- 23.Brenner, B., T. Kraft, L. C. Yu, and J. M. Chalovich. 1999. Thin filament activation probed by fluorescence of N-((2-(iodoacetoxy)ethyl)-N-methyl)amino-7-nitrobenz-2-oxa-1, 3-diazole-labeled troponin I incorporated into skinned fibers of rabbit psoas muscle. Biophys. J. 77:2677–2691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Herrmann, C., C. Lionne, F. Travers, and T. Barman. 1994. Correlation of ActoS1, myofibrillar, and muscle fiber ATPases. Biochemistry. 33:4148–4154. [DOI] [PubMed] [Google Scholar]
- 25.Lane, L. C. 1978. A simple method for stabilizing protein-sulfhydryl groups during SDS-gel electrophoresis. Anal. Biochem. 86:655–664. [DOI] [PubMed] [Google Scholar]
- 26.Stehle, R., M. Kruger, P. Scherer, K. Brixius, R. H. Schwinger, and G. Pfitzer. 2002. Isometric force kinetics upon rapid activation and relaxation of mouse, guinea pig and human heart muscle studied on the subcellular myofibrillar level. Basic Res. Cardiol. 97(Suppl 1):I127–I135. [DOI] [PubMed] [Google Scholar]
- 27.Colomo, F., S. Nencini, N. Piroddi, C. Poggesi, and C. Tesi. 1998. Calcium dependence of the apparent rate of force generation in single striated muscle myofibrils activated by rapid solution changes. Adv. Exp. Med. Biol. 453:373–381. [DOI] [PubMed] [Google Scholar]
- 28.Morimoto, S., H. Nakaura, F. Yanaga, and I. Ohtsuki. 1999. Functional consequences of a carboxyl terminal missense mutation Arg278Cys in human cardiac troponin T. Biochem. Biophys. Res. Commun. 261:79–82. [DOI] [PubMed] [Google Scholar]
- 29.Neulen, A., N. Blaudeck, S. Zittrich, D. Metzler, G. Pfitzer, and R. Stehle. 2007. Mn2+-dependent protein phosphatase 1 enhances protein kinase A-induced Ca2+ desensitisation in skinned murine myocardium. Cardiovasc. Res. 74:124–132. [DOI] [PubMed] [Google Scholar]
- 30.She, M., D. Trimble, L. C. Yu, and J. M. Chalovich. 2000. Factors contributing to troponin exchange in myofibrils and in solution. J. Muscle Res. Cell Motil. 21:737–745. [DOI] [PubMed] [Google Scholar]
- 31.Takahashi-Yanaga, F., S. Morimoto, K. Harada, R. Minakami, F. Shiraishi, M. Ohta, Q. W. Lu, T. Sasaguri, and I. Ohtsuki. 2001. Functional consequences of the mutations in human cardiac troponin I gene found in familial hypertrophic cardiomyopathy. J. Mol. Cell. Cardiol. 33:2095–2107. [DOI] [PubMed] [Google Scholar]
- 32.Stehle, R., C. Lionne, F. Travers, and T. Barman. 2000. Kinetics of the initial steps of rabbit psoas myofibrillar ATPases studied by tryptophan and pyrene fluorescence stopped-flow and rapid flow-quench. Evidence that cross-bridge detachment is slower than ATP binding. Biochemistry. 39:7508–7520. [DOI] [PubMed] [Google Scholar]
- 33.Brenner, B., and J. M. Chalovich. 1999. Kinetics of thin filament activation probed by fluorescence of N-((2-(iodoacetoxy)ethyl)-N-methyl)amino-7-nitrobenz-2-oxa-1, 3-diazole-labeled troponin I incorporated into skinned fibers of rabbit psoas muscle: implications for regulation of muscle contraction. Biophys. J. 77:2692–2708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Putkey, J. A., W. Liu, X. Lin, S. Ahmed, M. Zhang, J. D. Potter, and W. G. Kerrick. 1997. Fluorescent probes attached to Cys 35 or Cys 84 in cardiac troponin C are differentially sensitive to Ca2+-dependent events in vitro and in situ. Biochemistry. 36:970–978. [DOI] [PubMed] [Google Scholar]
- 35.Takeda, S., A. Yamashita, K. Maeda, and Y. Maeda. 2003. Structure of the core domain of human cardiac troponin in the Ca2+-saturated form. Nature. 424:35–41. [DOI] [PubMed] [Google Scholar]
- 36.Dong, W. J., and H. C. Cheung. 1996. Calcium-induced conformational change in cardiac troponin C studied by fluorescence probes attached to Cys-84. Biochim. Biophys. Acta. 1295:139–146. [DOI] [PubMed] [Google Scholar]
- 37.Johnson, J. D., J. H. Collins, S. P. Robertson, and J. D. Potter. 1980. A fluorescent probe study of Ca2+ binding to the Ca2+-specific sites of cardiac troponin and troponin C. J. Biol. Chem. 255:9635–9640. [PubMed] [Google Scholar]
- 38.Putkey, J. A., H. L. Sweeney, and S. T. Campbell. 1989. Site-directed mutation of the trigger calcium-binding sites in cardiac troponin C. J. Biol. Chem. 264:12370–12378. [PubMed] [Google Scholar]
- 39.Li, Y., M. L. Love, J. A. Putkey, and C. Cohen. 2000. Bepridil opens the regulatory N-terminal lobe of cardiac troponin C. Proc. Natl. Acad. Sci. USA. 97:5140–5145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rosenfeld, S. S., and E. W. Taylor. 1985. Kinetic studies of calcium binding to regulatory complexes from skeletal muscle. J. Biol. Chem. 260:252–261. [PubMed] [Google Scholar]
- 41.Johnson, J. D., R. J. Nakkula, C. Vasulka, and L. B. Smillie. 1994. Modulation of Ca2+ exchange with the Ca2+-specific regulatory sites of troponin C. J. Biol. Chem. 269:8919–8923. [PubMed] [Google Scholar]
- 42.Davis, J. P., J. A. Rall, P. J. Reiser, L. B. Smillie, and S. B. Tikunova. 2002. Engineering competitive magnesium binding into the first EF-hand of skeletal troponin C. J. Biol. Chem. 277:49716–49726. [DOI] [PubMed] [Google Scholar]
- 43.Davis, J. P., J. A. Rall, C. Alionte, and S. B. Tikunova. 2004. Mutations of hydrophobic residues in the N-terminal domain of troponin C affect calcium binding and exchange with the troponin C-troponin I96–148 complex and muscle force production. J. Biol. Chem. 279:17348–17360. [DOI] [PubMed] [Google Scholar]
- 44.Tikunova, S. B., and J. P. Davis. 2004. Designing calcium-sensitizing mutations in the regulatory domain of cardiac troponin C. J. Biol. Chem. 279:35341–35352. [DOI] [PubMed] [Google Scholar]
- 45.Stehle, R., and B. Brenner. 2000. Cross-bridge attachment during high-speed active shortening of skinned fibers of the rabbit psoas muscle: implications for cross-bridge action during maximum velocity of filament sliding. Biophys. J. 78:1458–1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lehman, W., R. Craig, and P. Vibert. 1994. Ca2+-induced tropomyosin movement in Limulus thin filaments revealed by three-dimensional reconstruction. Nature. 368:65–67. [DOI] [PubMed] [Google Scholar]
- 47.McKillop, D. F., and M. A. Geeves. 1993. Regulation of the interaction between actin and myosin subfragment 1: evidence for three states of the thin filament. Biophys. J. 65:693–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Vibert, P., R. Craig, and W. Lehman. 1997. Steric-model for activation of muscle thin filaments. J. Mol. Biol. 266:8–14. [DOI] [PubMed] [Google Scholar]
- 49.Stehle, R., M. Kruger, and G. Pfitzer. 2003. Does cross-bridge activation determine the time course of myofibrillar relaxation? Adv. Exp. Med. Biol. 538:469–479. [DOI] [PubMed] [Google Scholar]
- 50.Brenkelmann, D., J. D. Potter, and P. R. Housmans. 2002. Effects of volatile anesthetics on kinetics of conformational changes after Ca2+ dissociation from human recombinant cardiac troponin C. Biophys. J. 82:387a. (Abstr.) [Google Scholar]
- 51.Niederer, S. A., P. J. Hunter, and N. P. Smith. 2006. A quantitative analysis of cardiac myocyte relaxation: a simulation study. Biophys. J. 90:1697–1722. [DOI] [PMC free article] [PubMed] [Google Scholar]