Conformations of Flanking Bases in HIV-1 RNA DIS Kissing Complexes Studied by Molecular Dynamics

Abstract

Explicit solvent molecular dynamics simulations (in total almost 800 ns including locally enhanced sampling runs) were applied with different ion conditions and with two force fields (AMBER and CHARMM) to characterize typical geometries adopted by the flanking bases in the RNA kissing-loop complexes. We focus on flanking base positions in multiple x-ray and NMR structures of HIV-1 DIS kissing complexes and kissing complex from the large ribosomal subunit of Haloarcula marismortui. An initial x-ray open conformation of bulged-out bases in HIV-1 DIS complexes, affected by crystal packing, tends to convert to a closed conformation formed by consecutive stretch of four stacked purine bases. This is in agreement with those recent crystals where the packing is essentially avoided. We also observed variants of the closed conformation with three stacked bases, while nonnegligible populations of stacked geometries with bulged-in bases were detected, too. The simulation results reconcile differences in positions of the flanking bases observed in x-ray and NMR studies. Our results suggest that bulged-out geometries are somewhat more preferred, which is in accord with recent experiments showing that they may mediate tertiary contacts in biomolecular assemblies or allow binding of aminoglycoside antibiotics.

INTRODUCTION

In the course of the life cycle of human immunodeficiency virus 1 (HIV-1), two copies of genomic RNA dimerize via loop-loop interactions. This process starts at the dimerization initiation site (DIS), located at the 5′ untranslated region of the viral RNA. The DIS stem-loop is nine-nucleotides-long (residues A₂₇₂-A₂₈₀) and contains a six-nucleotide (nt) self-complementary sequence in the loop that is flanked by one conserved adenine base at the 3′ side (residue A₂₈₀) and two conserved purines at the 5′ side (residues A₂₇₂ and R₂₇₃) (Fig. 1). The 6-nt sequence promotes genome dimerization by formation of a kissing loop-loop complex (Fig. 1) (1–3), which may be converted into a more stable extended duplex form at higher temperature (55°C) or in the presence of nucleocapsid protein (4–6). The conserved purines are key for formation and stability of kissing complexes (7,8). Kissing tertiary interaction has been also reported for TAR elements of HIV-1 (9) and H3 stem-loops of Moloney murine leukemia virus (10). Kissing complex motifs were also identified during replication of the ColE1 plasmid (11) and in the crystal of two tRNAAsp (between their anticodon loops) (12). In addition, large ribosomal subunit shows one kissing complex close to the ribosome exit site (regions 412–428 and 2438–2454 of Haloarcula marismortui) (13), in which flanking bases mediate tertiary contacts with neighboring part of the 23S rRNA.

FIGURE 1.

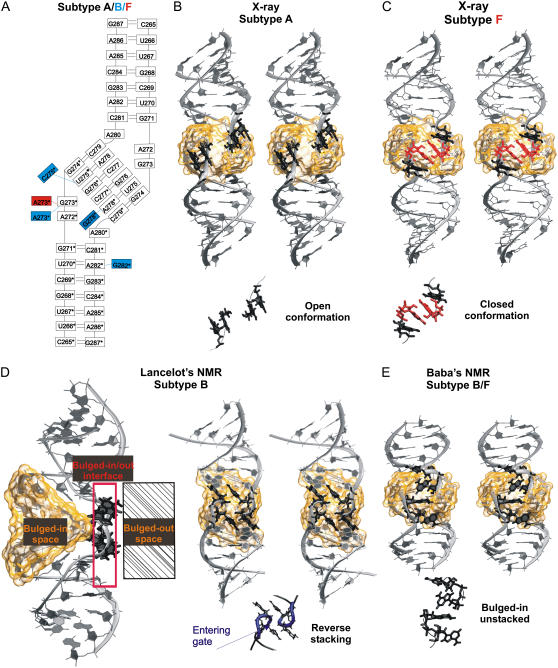
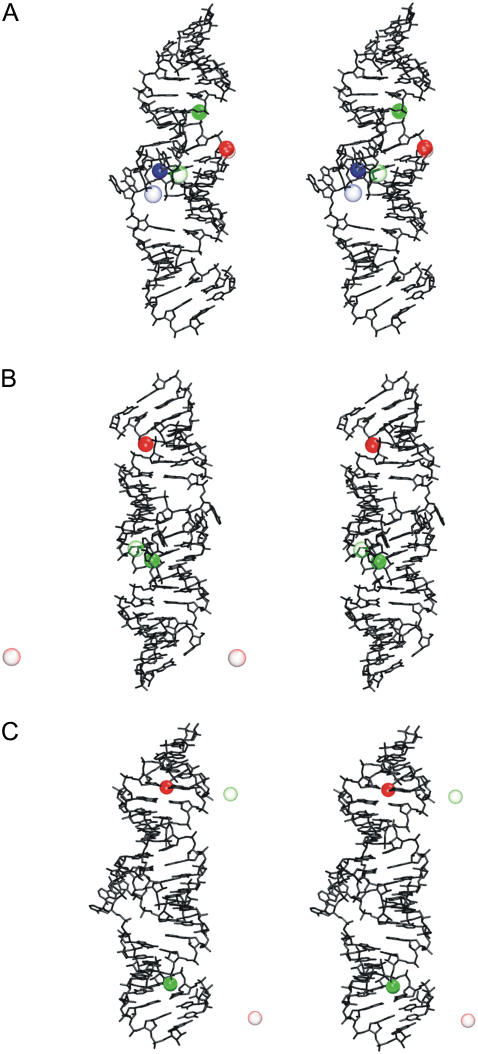
(A) Secondary structure of HIV-1 DIS subtype A kissing complex (PDB code 1XPF) (17), blue and red boxes indicate base mutations corresponding to subtypes B and F, respectively. (B) Stereo view of the x-ray subtype A structure (the subtype A, B, and F structures have identical overall geometry). Flanking bulged-out bases (A₂₇₂, A_272*, G₂₇₃, and G_273*) forming the open conformation (i.e., two separate two-base stacks) are highlighted in black. (C) Stereo view of the x-ray subtype F structure (PDB code 1ZCI) (17). The bulged-out bases A₂₇₂ and A_272* (in black) and A₂₇₃ and A_273* (in red) form the closed conformation (continuous four-base stack). (D) Lancelot's NMR structure of subtype B DIS (PDB code 2F4X) (18). (Left) Three-dimensional structure with cation-binding pocket highlighted as orange transparent surface and boxes marking regions of bulged-in, bulged-out, and bulged-in/out (intermediate) flanking base geometries. The flanking bases of this NMR structure are at the bulged-in/out interface. (Right) Stereo view showing reverse stacking of flanking bases; the bottom part shows detail of bulges with highlighted entering gate of the pocket (in blue). (E) Stereo view of the Baba's NMR structure of subtype B/F DIS (2D19) (20) with bulged-in bases (in black). Details of arrangement of flanking bases are visualized below the stereo views. The cation binding pocket in the central part of kissing-loop complexes is highlighted by transparent orange surface in panels B–E.

Crystal structures of HIV-1 subtype A and B DIS kissing-loop complex and extended duplex forms provided comprehensive views of this key region (14–16). Despite the difference in topology, both forms have similar overall shape but they differ in position of purine R273. Recently, kissing-loop complex structures were refined at higher resolution (17). In addition, two structures of HIV-1 subtype F DIS kissing-loop complex were obtained in distinct crystal environments, showing some variation in the conformation of bulged-out purines at the 5′ side (17) (see below). Additionally to x-ray structures, two NMR structures of HIV-1 subtype B DIS (18,19) and one NMR structure of HIV-1 subtype B/F DIS (20) were obtained. While Lancelot's (18) and Baba's NMR (20) structures are generally in agreement with the x-ray data, Mujeeb's NMR subtype B structure (19) shows substantial differences in the overall geometry compared to x-ray (17) and MD structures (21). However, all three NMR structures exhibit apparent differences in the positions of flanking bases (A₂₇₂ and R₂₇₃ and the symmetrical ones) compared to the x-ray structures. The x-ray structures consistently show the flanking bases to be in bulged-out arrangement while the NMR experiments suggest their bulged-in orientation.

The RNA atomic-resolution experiments can be complemented by computational molecular dynamics (MD) studies (22). Modeling is limited by the accuracy of the force field and simulation timescale but carefully executed MD simulations can be quite useful (23–49).

HIV-1 DIS kissing-loop complexes were studied using molecular dynamics methods (21,50–53). We have carried out a set of explicit solvent MD (AMBER force field (54), 33 ns of simulations for HIV-1 DIS kissing-loop complexes and 21 ns for other kissing systems) of HIV-1 DIS kissing-loop complexes assuming the earlier x-ray (PDB codes 1JJN and 1JJM) and NMR (1BAU) structures as start (21). The simulations predicted a novel four-adenine stack of the bulged-out bases (in the subtype B). This MD-predicted arrangement was subsequently confirmed by new x-ray structures of kissing-loop complex of subtype F and extended duplex form of subtype B (16,17), and termed “closed conformation.” The central pocket of the kissing complexes is characterized by a deep electrostatic potential (ESP) site. The simulations revealed that the pocket, in absence of divalent cations, is continuously occupied by 2–3 monovalent ions, a feature that was missed by the other MD studies. The ions smoothly exchange with the bulk solvent on a timescale ∼1–3 ns per ion while being delocalized in the pocket. Such flexible ion-binding sites are not likely to be captured by the x-ray technique which explains the absence of ions in many refined x-ray kissing-loop structures. The simulations revealed distortions of the oldest HIV-1 NMR DIS kissing-loop complex (19) and deformation of intermolecular basepairs in NMR kissing-loop complex of H3 stem loops of Moloney murine leukemia virus (9).

Beaurain and Laguerre (51) performed an MD (CHARMM force field (55), ∼15 ns total) study of both NMR and x-ray kissing-loop complexes of subtype B. In contrast to our work, they suggested that the starting NMR structure results in more stable trajectory than the x-ray structure. Aci et al. reported MD simulations (AMBER force field, ∼44 ns total) (52) of both structural forms of DIS. Extended duplex simulations (both NMR and x-ray) appeared stable while NMR kissing complex simulations showed large rearrangements at the stem-loop junctions. Surprisingly, this study reported rapid and peculiar destabilization (melting) of the stems when starting from the x-ray kissing complexes, which is in striking disagreement with our preceding results with the same force field (21). This is a quite unusual simulation behavior and to the best of our knowledge would be the only reported case where RNA x-ray structures are degraded in AMBER explicit solvent simulations. Another MD (AMBER) study of x-ray kissing complex of subtype A and B DIS was performed on a rather short timescale (400 ps) (50). Finally, the x-ray subtype B kissing complex (15) was recently merged in silico with the NMR structure of the internal loop in an attempt to obtain a complete SL1 stem-loop structure in dimer form (56).

In view of the discrepancies among the earlier MD studies, availability of new x-ray and NMR structures, and the continuing disagreement between positions of flanking bases seen in x-ray structures and predicted by NMR, we substantially extend the preceding theoretical studies on RNA kissing complexes. We report multiple extended MD simulations (AMBER code and force field, 30–50 ns trajectories, 583 ns in total) to study conformations of flanking bases in HIV-1 subtypes A, B, and F DIS crystal structures (17), in two recent DIS NMR structures (18,20), and in the ribosomal kissing complex (13). The simulations are carried out under variable ion conditions. The standard simulations are further supplemented by locally enhanced sampling (LES) MD technique (94 ns total) (40,57–59) to enhance the sampling of the flanking bases. The AMBER simulations are complemented by preliminary CHARMM (60–62) simulations (98 ns in total), to get insights into the dependence of the results on the force field.

Even with this considerable computational effort, we were unable to obtain a quantitative and converged description of the flanking base behavior (and other related studied should be viewed in this context). Nevertheless, our simulations quite clearly reveal that free flanking bases tend to self-associate via stacking while we identify several distinct substates (close in energy) that can be adopted by the flanking nucleotides. The LES technique considerably contributed to our ability to describe the conformational flexibility of the flanking bases, so we assume that our simulations identify essentially all substates that are sampled by them, albeit we cannot guarantee that their mutual balance is not affected by the force field and sampling limitations. The bulged-out geometry with consecutive stack of four bases, predicted first by our earlier simulations (21) and seen subsequently in new x-ray structures (17), is the most prominent substate. It is encouraging to see that AMBER and CHARMM force fields provide a qualitatively similar description of the flanking base substates, albeit CHARMM shows a visible tendency to a partial melting of the ARNA stem ends.

MATERIALS AND METHODS

Overview of all simulations is given in Table 1. X-ray structures of the subtypes A, B, and F (PDB codes 1XPF, 1XPE, 1ZCI, and 1YXP) (17) and NMR structures of the subtypes B and B/F (PDB codes 2F4X/model 1 and 2D19/model 11) were simulated using the AMBER program (63) version 8 (64) with parm99 (65) (simulations MD_A_1-2; MD_B_1-2; MD_F_1-2; and MD_nmr_1-2, respectively). Our preceding simulations (21) of x-ray subtypes A and B (PDB codes 1JJN and 1JJM (15)) using the AMBER-6.0 were extended up to 30 ns (simulations MD_A_3-4 and MD_B_3-4). Note that PDB files 1JJN and 1JJM have meantime been withdrawn from the PDB database and replaced as PDB 2B8R and 2B8S because of a reassignment of metal ions. Ribosomal kissing complex (regions 412–428 and 2438–2454) was extracted from the x-ray structure of the 50S subunit of H. marismortui (PDB code 1JJ2) (13).

TABLE 1.

Standard (MD) and LES simulations (LES) performed with the AMBER force field

Name of the simulation	PDB code (resolution)	Simulation length (ns)	RMSD (Å)	Ions in the simulations	Starting conformation of flanking bases
MD_A_1*	1XPF (2.30 Å)	30	3.1 ± 0.6	3 Mg2+, 38 Na+	open
MD_A_2	1XPF (2.30 Å)	48	4.7 ± 1.2	44 K+	open
MD_A_3†	1JJN (2.76 Å)	30	4.2 ± 1.2	14 Mg2+, 16 Na+	open
MD_A_4†	1JJN (2.76 Å)	40	5.6 ± 1.4	44 Na+	open
MD_B_1*	1XPE (1.94 Å)	50	4.7 ± 1.3	2 Mg2+, 40 Na+	open
MD_B_2	1XPE (1.94 Å)	50	5.1 ± 1.1	44 K+	open
MD_B_3†	1JJM (2.60 Å)	30	3.5 v 0.5	12 Mg2+, 20 Na+	open
MD_B_4†	1JJM (2.60 Å)	30	4.7 ± 1.2	44 Na+	open
MD_F_1	1ZCI (1.65 Å)	35	3.4 ± 0.8	44 K+	closed
MD_F_2	1YXP (2.40 Å)	10	4.0 ± 0.8	44 K+	open
MD_nmr_1	2F4X (N/A)	20	5.7 ± 1.0	46 Na+	reverse stacking
MD_nmr_2	2D19 (N/A)	20	2.5 ± 0.4	32 Na+	—
MD_nmr_2_1‡	2D19 (N/A)	20	2.1 ± 0.3	32 Na+	—
MD_nmr_2_2‡	2D19 (N/A)	20	2.4 ± 0.4	32 Na+	—
MD_ribosome	1JJ2 (2.40 Å)	50	2.4 ± 0.5	34 Na+	—
LES5_A§	1XPF (2.30 Å)	30 + 5**	5.1 ± 1.2	44 Na+	open
LES3_A¶	1XPF (2.30 Å)	10	3.9 ± 0.9	44 Na+	open
LES5_B§	1XPE (1.94 Å)	34 + 5**	4.3 ± 1.0	44 Na+	open
LES3_B¶	1XPE (1.94 Å)	10	6.4 ± 1.2	44 Na+	open
S_MD_A‖	1XPF (2.30 Å)	50	4.3 ± 0.9	5 Mg2+, 34 Na+	open
S_MD_B‖	1XPE (1.94 Å)	50	4.3 ± 0.9	5 Mg2+, 34 Na+	open

Instantaneous RMSD values are calculated along the trajectories with respect to the initial structures.

^*MD_A_1 and MD_B_1 simulations were carried out without considering the x-ray and Na⁺ ions.

^†Extended previous simulation (21).

^‡Control MD_nmr_2_1 and MD_nmr_2_2 simulations run with different random number seeds.

^§Five LES copies.

^¶Three LES copies.

^‖Supplementary AMBER simulation carried out with preliminary x-ray data; see explanation in the text and Supplementary Material.

^**Control 5-ns simulation without the initial heating to 500 K.

All systems were neutralized by Na⁺ or K⁺ ions using the Xleap module of AMBER. Ions that were placed initially into major groove or binding pockets were manually shifted 5 Å away from the solute to avoid any initial bias. Some simulations were carried out with x-ray Mg²⁺ and K⁺ ions. Box of TIP3P water molecules was added to a distance of 12 Å on each side of the solute. The following parameters were used: Na⁺ radius 1.868 Å and well depth 0.00277 kcal/mol; Mg²⁺ radius 0.7926 Å and well depth 0.8947 kcal/mol; and K⁺ radius 2.658 Å and well depth 0.000328 kcal/mol (66). Note that the parm99 DNA force field was very recently replaced by reparameterization of the α/γ backbone torsional profiles, presently known as parmbsc0 (67). The force-field refinement was necessitated by substantial imbalances occurring in B-DNA simulations with parm99 and parm94, which are eliminated by parmbsc0. In contrast to DNA, however, the parm99 force field shows a proper backbone behavior in RNA simulations (22,31,34,35), and in tests we performed so far, both parm99 and parmbsc0 are equally suitable for RNA simulations.

The standard simulations were carried out using the particle mesh Ewald technique (68) with 9 Å nonbonded cutoff and 2-fs integration time step. Equilibration started by 5000 steps of minimization followed by 200 ps of MD, with the atomic positions of the solute molecule fixed. Then, two series of minimization (1000 steps) and MD simulation (20 ps) were carried out with restraints of 50 and 25 kcal/(mol Ų), which were applied to all solute atoms. In the next stage, the system was minimized in five 1000-step rounds with restraints (20, 15, 10, 5, and 0 kcal/(mol Ų)) applied only to solute atoms. During the subsequent 100-ps unrestrained MD, the system was heated from 50 to 300 K. The production MD runs were carried out with constant pressure boundary conditions (relaxation time of 1.0 ps). Constant temperature of 300 K was maintained using the Berendsen weak-coupling algorithm with a time constant of 1.0 ps. SHAKE (69) constraints with a tolerance of 10⁻⁸ Å were applied to all hydrogens to eliminate the fastest X-H vibrations and allow a longer simulation time step. Translational and rotational center-of-mass motion was removed every 5 ps. Trajectories were analyzed using the Ptraj module of AMBER and structures were visualized using the VMD molecular visualization program http://www.ks.uiuc.edu/Research/vmd/ (70). The figures were prepared using VMD. Molecular ESP was calculated using the DELPHI program (71), which solves the nonlinear Poisson-Boltzmann equation. The present DELPHI calculations of ESP were carried out assuming the reference zero ionic strength, which simplifies comparison with minima of electrostatic potentials calculated for other RNA systems (21,25,35). (Inclusion of salt effects into the ESP calculations would change neither shapes nor positions of the ESP basins but would scale down the absolute values of the ESP minima.) Visualization of the potential maps was carried out using the program VMD.

To enlarge sampling of flanking bases we employed the LES technique (40,57–59) in AMBER-7.0 (72). The ADDLES module of AMBER was used to split the region of flanking bases (residues 272, 273 and symmetrical 272*, 273*) into five independent copies. We tested also MD LES simulations with only three copies. Force-field parameters for the copies were scaled, which results in lowering of the energy barriers on the potential energy surface (57). To provide an initial kick to the five copies, the structure was heated to 500 K. Moreover, a long relaxation phase appears vital to provide sufficient freedom for the copies to settle in different regions of the conformational space. Thus, the temperature was gradually decreased from 500 K to 300 K over 1.5 ns (during the first 750 ps, the pressure was set to 100 atm), and the flanking base region was maintained with flat-well restraints (R1 = 0.0, R4 = 6.0, RK2 = 10.0, and RK3 = 20.0; R2 and R3 depending on the actual distance R between the restrained atoms (R2 = R − 0.5 Å, R3 = R + 0.5 Å)) applied to heavy atoms forming H-bonds in basepairs. Control LES simulations were carried out without the initial kick, i.e., the heating was carried only up to 300 K.

CHARMM simulations were performed using the CHARMM program (62), with the CHARMM27 nucleic acid force fields (60,61) and using newly refined x-ray subtype A and B DIS structures (1XPF and 1XPE) with preliminary ion distribution (see Fig. S1 and Supplementary Material). Molecules were overlaid with a box of TIP3P water molecules (size of 95.2 × 52 × 52 Å for subtype A and 91.2 × 53.4 × 53.4 Å for subtype B) (73). Na⁺ ions were added to neutralize the system. Ions were placed by replacing the water molecules with the highest electrostatic energy and at the distance 3.5–4.8 Å to any RNA atom. The equilibration protocol started with 100 steps of steepest descent (SD) minimization followed by 10 ps of MD applied only to the water molecules whereas the RNA and ions were constrained. During the next 150 ps, the constraints placed on the ions are released allowing equilibration of the solvent around the RNA. The resulting system was subjected to five rounds of 100 steps of SD minimization with gradually reduced harmonic constraints on RNA (100, 20, 5, 2, and 1 kcal/(mol Ų)). Finally, the whole system was minimized without any restraints for 100 SD steps and heated from 50 to 300 K in 12 ps by 50 K increments. In contrast to AMBER simulations, CHARMM production runs were performed in constant volume ensemble. We do not expect this difference having any impact on the results. NVE conditions were used in our (Sarzynska and Kulinski) preceding studies with CHARMM. We kept all our standard protocols unchanged for the purpose of this article. Recent comparison of NVE versus NPT CHARMM simulations (74) did not reveal any differences. The particle mesh Ewald technique was used for treatment of electrostatic interactions (68). MD simulations were run with a 2-fs time step and SHAKE constraints were applied to all hydrogens (69).

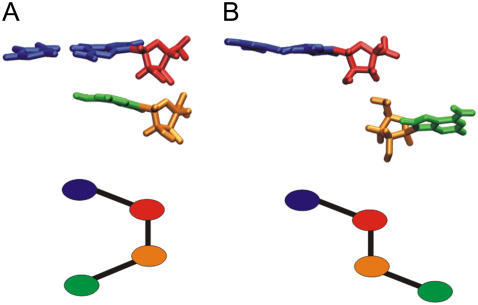
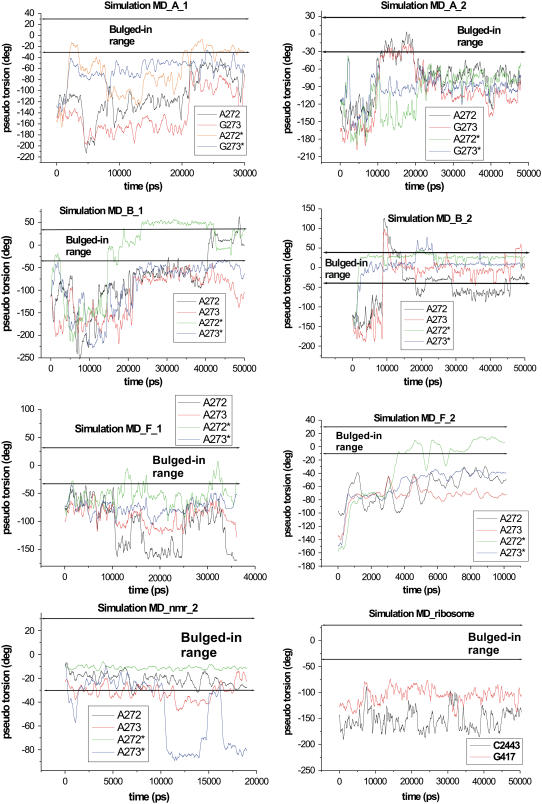
We defined θ-parameter (75) to monitor movement of the flanking bases (see Fig. 2 for definition). When flanking bases are bulged-in or at the gate of the kiss pocket the θ-angle falls into the bulged-in range, ±30°. Other θ-values correspond to the bulged-out states.

FIGURE 2.

The pseudo-dihedral angle used to describe flipping of flanking bases A₂₇₂ and A/G₂₇₃ is defined by center of mass of the basepair C₂₈₁-G₂₇₁ (blue), the G₂₇₁ sugar (red), the sugar of flanking base for which θ is calculated (A₂₇₂ or A/G₂₇₃) (orange), and the base itself (A₂₇₂ or A/G₂₇₃) (green). (A) Bulged-in and (B) bulged-out geometries of flanking bases.

Comment on inclusion of ions into simulations

Inclusion of ions is often a matter of controversy in assessment of simulation studies (22). These simulations were carried out in presence of neutralizing set of Na⁺ or K⁺ ions combined, in some cases, with a few x-ray divalent ions. This corresponds to ionic strength of ∼0.2 M (considering the number of ions and size of the water box). We suggest that this is a viable compromise to include ions in RNA simulations which can be justified in the following way. The nonpolarizable pair additive force field represents the ions as van der Waals spheres with atom-centered point charges. This simple force field is unlikely to exactly mimic the experimental ion conditions even when the ion concentrations match those in a given experiment. A meaningful description of divalent cations is fairly outside the applicability of the force field while sampling of divalent cations in simulations is very poor. Anions may posse a specific problem due to their polarizable nature. Monovalent ions, in contrast, sample quite well at a 50-ns simulation timescale. The simulations are, fortunately, too short to develop visible instabilities stemming from inexact salt conditions. For example, while RNA kink-turns unfold in solution experiments in absence of divalents they do not unfold in simulations (when starting from the folded structures). The computed kink-turn dynamics is independent of the type of ions used in simulations (45).

To compare the simulation behavior of ions with the experiments, the reader can consider the subsequent description of the common behavior of monovalent ions in the simulations. The monovalent ions readily sample the whole box and only part of them is interacting with the solute at a given time. Typically, <50% of the ions in the box are closer than 5 Å from any solute atom in the individual snapshots. The ion binding does not seem to substantially affect the local structure (groove width, etc.) (76). The solute-cation interactions are transient, except those of highly specific and structured ion binding pockets (see below). Extended simulations of B-DNA revealed that ions often sample electronegative sites in the double-helix grooves but direct (inner-shell) binding to DNA bases remains a rather rare event, with the highest site occupancies <13% (10% for phosphates) (77,78). In ∼50-ns simulations, the set of ions samples the complete space available during the simulation time very well, although a given ion still samples only approximately one-third of the simulation box. This is a common picture of ion binding to NA double-helical segments. In simulations of the Hepatitis Delta Virus ribozyme (HDVr) we noticed sites with up to ∼20% occupancies with individual inner shell binding events up to 2–4 ns in major grooves of A-RNA GpG and GpA steps (see Supplementary Material in (31)).

Occasionally, major monovalent cation-binding pockets are detected by simulations. Such pockets are not present around canonical double helices but are intimately associated with some noncanonical segments and RNA folds. They are continuously occupied often by multiple long-residency monovalent ions. Case examples are ion channels of guanine quadruplex molecules (79), the catalytic center of HDVr (31), and the major groove pocket of bacterial and spinach chloroplast 5S rRNA loop E (25,27). A prominent cation-binding site is also formed in the center of the kissing loop complex, as described below. Due to the extent of cation-solute interactions in these pockets and the rather acceptable accuracy of the force-field description of monovalent cations and their rather satisfactory sampling, MD simulation is a valuable tool to identify such ion-binding pockets. In many cases these predicted monovalent ion binding pockets coincide with divalent ion-binding sites, which are more difficult to capture by simulations in a realistic manner.

AMBER simulations were run on duals P4 XEON, 3.0 GHz (FSB 800 MHz) and XEON 2.4 GHz. CHARMM simulations were run on SGI Origin3800 and on 64-bit processors Intel Itanium2. Typical time for a run of 50 ns of standard simulation was approximately four-to-five months on two processors for both codes. Typical time for a run of 30 ns of LES simulation was approximately six months. LES method requires approximately twice more time compared with the standard simulation. LES simulations show transitions of the flanking base conformations approximately twice more frequently. The main advantage of the LES method is its ability to cross substantial barriers, so its application should guarantee that we do not miss some important conformations separated by too-high barriers from the starting geometries.

RESULTS

Starting structures and standard simulations

HIV-1 DIS kissing-loop complexes subtype A (PDB code 1XPF), B (1XPE), and F (1ZCI and 1YXP) (17) were studied using 30–50 ns standard explicit solvent simulations. Each hairpin contains three unpaired residues (A₂₇₂, A/G₂₇₃, and A₂₈₀) (Fig. 1 A). A₂₇₂ and A/G₂₇₃ are the flanking bases. Flanking bases in the subtype A and B x-ray structures are bulged-out and stacked in pairs, forming thus a base-grip with an empty space between the stacked pairs (Fig. 1 B), known as the “open conformation” (17). In the crystal unit, the gap is filled by a stacking pair from the adjacent kissing complex (Fig. 5 in (17)). The subtype F was solved in two different crystal forms. While the 1YXP structure shows the open conformation the 1ZCI structure has four continuously stacked bulged-out flanking bases (Fig. 1 C). This “closed conformation” is unaffected by the crystal packing (17) and has been predicted by simulations ahead of its observation in the x-ray structures (21).

FIGURE 5.

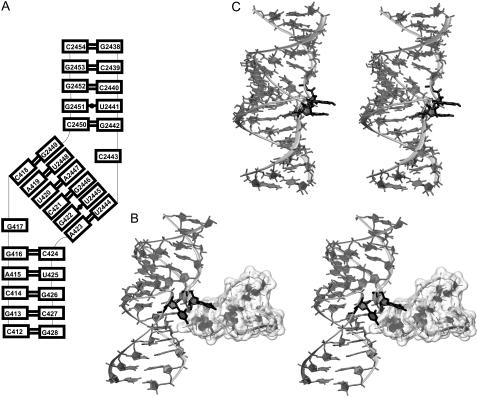
(A) Secondary structure and (B) stereo view of ribosomal kissing-loop complex from H. marismortui 50S subunit with bulged-out bases (highlighted in black) forming tertiary contacts to the adjacent part of the 23S rRNA (unfilled surface). (C) Averaged MD structure over the last 10 ns with stacked bulges (black).

We extended earlier (21) simulations of the original x-ray subtype A and B structures (15) (1JJN and 1JJM) to 30 ns (see Materials and Methods). Geometries of the original x-ray subtype A and B and newly refined structures are almost identical (RMSD of ∼0.2–0.3 Å), including positions of the unpaired bases. However, the new structures include a substantially reduced number of refined Mg²⁺ ions compared to the older structures where some divalent cations were misassigned. The new structures contain extra Na⁺ and 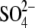ions (the subtype A structure shows also binding of spermine molecule and the subtype B structure suggests one Cl⁻ ion).

NMR subtype B DIS (18) and subtype B/F DIS (20) were simulated for 20 ns. In subtype B structure, flanking bases are at the entrance of the kiss ion-binding pocket (entering gate for ions) between bulged-in and bulged-out geometry and stack reversely than in the x-ray structure. We termed such an arrangement the “reverse stacking” conformation (Fig. 1 D). In subtype B/F structure, all flanking bases are entirely inside the pocket (bulged-in geometry) and do not stack (Fig. 1 E).

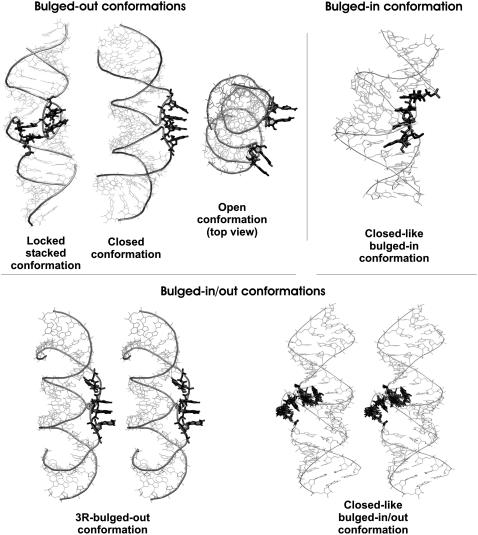
Fig. 3 summarizes the main conformations of flanking bases observed in at least two simulations or sampled for at least 30% in one simulation. Occupancy of individual conformations is listed in Table 2. PDB files with main conformations are provided in Supplementary Material.

FIGURE 3.

Main conformations of flanking bases of HIV-1 DIS kissing-loop complexes. Three distinct bulged-out, one bulged-in, and two bulged-in/out conformations are shown. Some conformations are visualized as a stereo view for clarity. Locked stacked conformation is stabilized by mutual stacking and H-bonding. In several conformations all four flanking bases are stacked but they may stay both bulged-out and bulged-in. Thus, closed conformation has all bulges bulged-out and we consider this conformation the most important substate (see the text), closed-like bulged-in conformation has all bulges bulged-in and closed-like bulged-in/out conformation has flanking bases both bulged-out and bulged-in. In open conformation, bulged-out bases stack in pairs from the same hairpin. 3R-bulged-out conformation is a variant of the closed conformation with three stacked bulged-out bases. PDB files with main conformations of flanking bases are provided in the Supplementary Material.

TABLE 2.

Main conformations (see Fig. 3) of flanking bases observed in MD and LES simulations

Simulation*	Open % (ns)	Locked stacked % (ns)	Closed % (ns)	Closed-like bulged-in % (ns)	Closed-like bulged-in/out % (ns)	3R-bulged-out % (ns)
MD_A_1	3(1)	67(20)	1.6(0.5)			20(6)
MD_A_2	21(10)	56(27)			23(11)
MD_A_3	43(13)					23(7)
MD_A_4	87(35)
MD_B_1	28(14)					36(18)
MD_B_3	3(1)		43(13)			53(16)
MD_B_4	33(10)
MD_F_1			80(28)			20(7)
MD_F_2	10(1)		25(2.5)			65(6.5)
MD_nmr_2				55(11)
LES5_A	2(0.5)		43(12.5)		20(6)
LES3_A	100(10)
LES5_B	1(0.5)		70(24)
LES3_B	85(8.5)		5(0.5)
S_MD_A	24(12)		16(8)			60(30)
S_MD_B	4(2)		36(18)			56(28)

Conformations are given as percent of time occupancy with the duration in nanoseconds in parentheses. For some simulations, the sum of occupancies is <100% due to minor or disordered conformations, fluctuations, and transitions. Note that closed and 3R-bulged-out geometries are closely related. Initial conformations are underlined and final conformations are in bold.

^*MD_B_2 simulation is not included since the flanking bases moved after 1 ns into the pocket and did not form any of the main conformations specified above. Similarly MD_nmr_1 simulation starting from the reverse stacking conformation did not sample the listed flanking conformations.

Conformation of flanking bases identified in MD simulations

HIV-1 subtype A DIS

Four simulations MD_A_1-4 were carried out (Table 1). Mg²⁺ ions, when present, were positioned based on the corresponding PDB files. At the beginning of the simulation MD_A_1, the flanking bases left the open x-ray conformation and formed intermediate “locked stacked” conformation. The bases mutually stacked and formed temporary H-bonds (G₂₇₃(O2′)-G_273*(N1), G₂₇₃(O2′)-G_273*(N2) and G₂₇₃(O2′)-A_272*(N7)). At 21 ns, the structure converted to the closed conformation with a continuous A₂₇₂G₂₇₃G_273*A_272* bulged-out stack (Fig. 3). Such a stack is formed by A₂₇₂A₂₇₃A_273*A_272* bases in the subtype F kiss crystal structure 1ZCI, Fig. 1 (17) and by A₂₇₃A₂₇₂A_272*A_273* bases in the subtype B extended duplex crystal (16). In the rest of the simulation, the A₂₇₂, G₂₇₃, and G_273* remained stacked (3R-bulged-out conformation, Fig. 3) while the A_272* was oscillating between bulged-in and bulged-out geometry. Three flanking bases are anti (χA₂₇₂ = −160°, χA₂₇₂* = −166°, and χG₂₇₃ = −108°) and one is syn (χG_273* = 65°) in the initial x-ray structure. Conformational changes of flanking bases during the simulation were mainly coupled with glycosidic torsion dynamics. After forming the AGGA stack, χA₂₇₂ is ∼−85°, χG_273* ∼50°, χG₂₇₃ fluctuates at ∼−122°, and χA_272* oscillates from −150° to 40°. Time course of the θ-angle (see Materials and Methods) is plotted in the Fig. 4 and shows that only the A_272* base was temporarily in bulged-in arrangement. Sugar pucker of majority residues is C3′-endo in the initial x-ray structure. Exceptions are nucleotides G₂₇₁, G₂₇₃, and the symmetrical nucleotides exhibiting C2′-endo conformations. During the simulation all nucleotides maintained the initial C3′-endo geometry except of G₂₇₁, A₂₇₂, G₂₇₃, and their symmetrical residues, which oscillated between C2′-endo and C3′-endo. Oscillations of pseudo-rotation angle P were seen also for the terminal bases (287, 265, and the symmetrical ones, data not shown). This was seen in all simulations and will not be further mentioned.

FIGURE 4.

Time course of parameter θ calculated for flanking bases in the simulations MD_A_1-2, MD_B_1-2, MD_F_1-2, MD_nmr_2, and MD_ribosome.

Simulation MD_A_2 in absence of Mg²⁺ ions exhibited similar behavior. During the first 10 ns, the flanking bases maintained the initial open conformation, which then converted to the closed conformation. However, in this case, closed conformation was formed by A₂₇₂/G₂₇₃ bulged-in and A_272*/G_273* bulged-out stacks (Fig. 4). Hence, we specified this arrangement the “closed-like bulged-in/out” conformation (Fig. 3). It was disrupted at 21 ns and replaced by the locked stacked architecture similar to that observed at the beginning of the simulation MD_A_1 (Fig. 3). We, however, observed different H-bonds; particularly, basepair with G₂₇₃(N7)-G_273*(N2) and G₂₇₃(O6)-G_273*(N1) H-bonds. This architecture was maintained until the end of the simulation. Glycosidic torsions of flanking bases fluctuated ∼−90° in the closed conformation except of base A_272*, whose χ fluctuated ∼−150°. In the locked stacked architecture, χ of A₂₇₂, G₂₇₃, A_272*, and G_273* were −80°, −50°, −150°, and 50°, respectively. Dynamics of puckering phase for G₂₇₁, G₂₇₃, G_271*, and G_273* was similar as in the previous simulation.

In simulation MD_A_3, the flanking bases kept the open conformation for 13 ns. Then A₂₇₂, G₂₇₃, and G_273* formed an AGG bulged-out stack (3R-bulged-out conformation, Fig. 3) while the fourth base A_272* moved toward the pocket similar to simulation MD_A_1. The 3R-bulged-out conformation was stable until 20 ns and then it was disrupted, resulting in formation of reverse stacking for 5 ns similar to NMR Lancelot's structure (Fig. 1 D). During the last 5 ns, the flanking bases did not adopt any ordered conformations. In simulation MD_A_4, the flanking bases stayed mainly in open conformation with A₂₇₂/G₂₇₃ and A_272*/G_273* stacks. Stacking of A₂₇₂ and G₂₇₃ was disrupted in the time period 27–30 ns and A₂₇₂ oscillated between bulged-out and bulged-in geometries. The other bases stayed bulged-out but the closed conformation was not reached.

HIV-1 Subtype B DIS

Four subtype B simulations (Fig. 1) were run (Table 1, simulations MD_B_1-4). In the simulation MD_B_1, the bases stayed in the open conformation until 14 ns and then A_272* fluctuated between bulged-in and bulged-out geometries (Fig. 4). The three remaining bulged-out bases A₂₇₂, A₂₇₃, and A_273* formed, at 22 ns, the 3R-bulged-out conformation (Fig. 3). At 40 ns, A₂₇₂ moved into the pocket and A_273* modestly shifted toward the gate of the pocket (Fig. 4); however, the stacking between A_273* and A₂₇₃ was maintained. The initial x-ray values of glycosidic torsions of A₂₇₂, A₂₇₃, A_273*, and A_272* were −165°, −118°, −113°, and −165°, respectively. When A_272* and A₂₇₂ moved inside, its χ changed to syn (65° and 40°, respectively). In 3R-bulged-out conformation, χ of bulges ranged from −80° to −100°. Similarly to the subtype A DIS, residues of the subtype B stayed in C3′-endo conformation except for G₂₇₁, A₂₇₂, A₂₇₃, and the symmetrical residues that sampled both C3′-endo and C2′-endo conformations. X-ray sugar pucker of G₂₇₁, A₂₇₃, and the symmetrical residues is C2′-endo, while that of A₂₇₂ and A_272* is C3′-endo.

In the simulation MD_B_2 lacking Mg²⁺, the flanking bases sampled bulged-in conformations. After 1 ns, A_272* and A_273* moved into the pocket and mutually stacked inside. In addition, A_272* formed a pair with opposite A_280* stabilized by an A_272*(N1)-A_280*(N6) H-bond. Symmetrical A₂₇₂ and A₂₇₃ stayed bulged-out until 10 ns, and then they occupied the cavity as well but they did not stack inside and were rather flexible. At 15 ns, the base A₂₇₂ flipped over its glycosidic bond and left the pocket. For the rest of the simulations it fluctuated between bulged-in and bulged-out conformations (see development of θ parameter Fig. 4). Its χ fluctuated, spanning the full range of 360°. Bases A_272*, A_273* were still stacked and their χ-torsions fluctuated at ∼−100°. A₂₇₃ changed to syn geometry (−52°) when this base moved inside. In the simulation MD_B_3, during the first two nanoseconds the flanking bases formed the complete four-adenine stack. Residue A₂₇₂ was, however, very dynamic and oscillated between bulged-out and bulged-in geometries. When being inside the cavity, A₂₇₂ forms a basepair with the opposite A₂₈₀ (A₂₇₂(N6)-A₂₈₀(N1) and A₂₇₂(N1)-A₂₈₀(N6) H-bonds). The simulation MD_B_4 carried out with Na⁺ ions exhibited a similar outcome to the simulation MD_B_2 run with K⁺ ions. Flanking bases stayed for the first 10 nanoseconds in the open conformation, and after that, they moved into the cavity but did not stack. Particularly, A_272* moved inside at 11 ns and created A_272*(N6)-A_280*(N1) and A_272*(N1)-A_280*(N6) H-bonds with unpaired adenine A_280*. The bases A_273*, A₂₇₂, and A₂₇₃ moved inside at 15, 17, and 17.5 ns, respectively, but did not form any contacts inside the cavity.

We, in addition, initially carried out two simulations (S_MD_A and S_MD_B) based on preliminary refined x-ray subtype A and B structures. While solute geometries are the same as in the final deposited files 1XPF and 1XPE, these preliminary x-ray structures had few incorrectly assigned ions. Specifically, the preliminary x-ray subtype A structure contained two incorrectly placed Mg²⁺ ions, and the subtype B structure, three such Mg²⁺ ions. These electron densities were later reinterpreted as 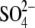or Na⁺ ions in the deposited PDB files. More details are provided in Supplementary Material Figs. S1 and S2. Both simulations are quite consistent with simulations MD_A_1-4 and MD_B_1-4 (Table 2).

HIV-1 subtype F DIS

The subtype F DIS differs by one base mutation (G₂₇₃A) from the subtype A (Fig. 1). The x-ray structure 1ZCI that shows the closed conformation of flanking bases was run with two x-ray K⁺ ions and added 42 K⁺ ions in 35-ns simulation MD_F_1. Flanking bases stayed in the initial closed conformation (see Fig. 1 C) for the majority of the simulation time (time periods 0–11, 14–16, 17–30, and 33–35 ns), except of base A_272*, which occurred three times inside the pocket (Fig. 4). The χ-torsions of A₂₇₂, A₂₇₃, A_273*, and A_272* in the closed conformation ranged from −80° to −100° while the initial x-ray values were −139°, −97°, −99°, and −136°, respectively. A_272* in bulged-in geometry adopted a syn geometry (χ ∼40°).

The x-ray structure 1YXP that shows the open conformation of flanking bases was run in 10-ns simulation (MD_F_2) with 44 K⁺ ions. The initially open conformation changed after 1 ns to closed conformation. At 3.5 ns, A_272* moved into the pocket, while other flanking bases stacked until the end of the simulation (3R-bulged-out conformation, see Fig. 3). The initial χ x-ray values of A₂₇₂, A₂₇₃, A_273*, and A_272* were −168°, −116°, −123°, and −163°, respectively. Similarly to the previous simulation in the closed conformation χ-torsions of bulges ranged from −80° to −100°. Bulged-in A_272* had χ-torsion in syn geometry (∼50°). X-ray subtype F DIS structure with open conformation has two residues with C2′-endo conformation, G₂₇₁ and A₂₇₃ of each strand. According to the experiment in the literature (17), formation of the closed conformation is coupled with C2′-endo → C3′-endo flip of the sugar of G₂₇₁. During the first two nanoseconds, we observed such repuckering. However, the sugar rings oscillated between C3′-endo/C2′-endo for the rest of the simulation. Interestingly, the x-ray density maps show some evidence of a population of C2′-endo conformations for G271 (E. Ennifar, unpublished data, 2007), although it was not reported in the original article (17).

NMR (Lancelot's) HIV-1 subtype B DIS

The 48-nt NMR subtype B DIS structure (PDB code 2F4X/model 1) (18) was simulated for 20 ns (MD_nmr_1). This NMR structure is in general agreement with the x-ray structure except for the area of flanking bases. First, these bases are placed at the gate of the central pocket, between bulged-out and bulged-in geometries (Fig. 1 D). Second, stacking is different than in the crystal—namely, A₂₇₂ stacks with A_273* from the opposite loop instead of the A₂₇₃. Likewise, symmetrical A_272* stacks with A₂₇₃ (Fig. 1 D). We termed this arrangement “reverse stacked” conformation (Fig. 1 D). The cross stacking attracts and twiddles the loops, resulting in closed entrance of the pocket and deformed backbone (the shortest distance between opposite phosphorus atoms at the gate of the pocket is only 3.8 Å compared with 7.5 Å in the x-ray structures). Due to the backbone distortion, we could not calculate the θ-parameters for the flanking bases. Within the first ns, A₂₇₂ and A_272* moved into the pocket. While A₂₇₂ stayed inside for the whole simulation and restored stacking with opposite A_273* base, A_272* flipped around its glycosidic bond and left the pocket. For the rest of the simulation, it fluctuated between bulged-in and bulged-out geometry. Bases A₂₇₃ and A_273* attempted to move inside as well, but the pocket entrance was obstructed by the reverse A₂₇₂/A_273* stacking, preventing A₂₇₃ and A_273* from moving in. It appears that 20-ns timescale is not sufficient to relax the central part of the complex and find optimal conformation. The starting NMR glycosidic torsions of A₂₇₂, A₂₇₃, A_272*, and A_273* were −24°, −18°, −24°, and −18°, respectively. During the simulations, they established values of −130°, −90°, −40°, and −140°, respectively.

NMR (Baba's) HIV-1 subtype B/F DIS

The second NMR structure (20) (PDB code 2D19/model 11) has 34-nt since it has both stems truncated by three basepairs. Sequence of the stem corresponds to subtype B while sequence of the loop corresponds to subtype F, so we call it “B/F structure” (Fig. 1 E). The overall geometry is in meaningful agreement with the x-ray structures. Area of bulges is not closed (the shortest distance between opposite phosphorus atoms at gate of the pocket is 11 Å) and not deformed. Baba's B/F structure predicts the flanking bases to be entirely bulged-in, i.e., inside the pocket. Initial NMR positions of flanking residues A₂₇₂ and A_272* slightly differ, so that only A₂₇₂ creates H-bonds with the unpaired A₂₈₀ (A₂₇₂(N1)-A₂₈₀(N6) and A₂₇₂(N6)-A₂₈₀(N1)) in the pocket, while the symmetrical base A_272* does not form any H-bond. At the beginning of the simulation (MD_nmr_2) the flanking bases stacked resulting in closed-like bulged-in conformation positioned at the gate of the pocket. It can be considered as a partly bulged-in arrangement (Fig. 3). This arrangement was then stable, except of several disruptions when A_273* moved entirely outside the pocket (Fig. 4). The H-bonds between A₂₇₂ and A₂₈₀ remained stable, while at 16 ns the A_272*-A_280* basepair formed. The new pair, however, exhibits different H-bonds (A_272*(N6)-A_280*(N1) and A_272*(N7)-A_280*(N6)). The initial values of glycosidic torsions χA₂₇₂ = −104°, χA_272* = −106°, χA₂₇₃ = −139°, and χA_273* = −71° changed to −25°, −145°, −88°, and 53°, respectively.

Two control 20-ns simulations (MD_nmr_2_1 and MD_nmr_2_2) were carried out using different random number seeds (Table 1). The first simulation sampled closed-like bulged-in conformation for ∼90% of the simulation time, similar to our primary simulation. In the second simulation, a three-adenine bulged-in stack of A₂₇₂, A₂₇₃, and A_273* was seen for only ∼7% of the simulation time. In other periods we observed the A₂₇₂/A₂₇₃ stack while A_273* oscillated nearby. A_272* was close to the stacked bases and involved in H-bonding with A_280*. The flanking bases nevertheless remained in the bulged-in conformation, so all three simulations appear to be reasonably mutually consistent. Note that the NMR starting structures are more difficult to relax by MD due to their lower accuracy compared to x-ray structures.

Kissing complex from the ribosome

The 412–428 and 2438–2454 regions of 23S rRNA of H. marismortui form a kissing-loop complex (Fig. 5 A). We extracted this complex from the x-ray structure of the large subunit (13) and carried out 50-ns-long MD simulation (MD_ribosome). Like the HIV-1 DIS kissing complexes, the ribosomal complex is formed by 6-nt complementary sequences (see Figs. 1 and 5 A). It has only two unpaired flanking bases (G₄₁₇ and C₂₄₄₃). These bulged-out bases are in the large ribosomal subunit of H. marismortui (13) (as well as in Deinococcus radiodurans (80), Escherichia coli (81), and Thermus thermophilus (82) ribosomal crystal structures) involved in tertiary contacts with bases of adjacent stem-loop of 23S rRNA (Fig. 5 B). During the first nanosecond of the simulation, the flanking bases formed a stack (Fig. 5 C) and remained in this arrangement until the end.

LES simulations

The LES method splits the selected part of the molecule into N (three-to-five) copies that move independently in the simulation. This allows us to overcome barriers that cannot be crossed during standard simulations. The LES method is optimally suited for loop regions but appears to be promising also for the flanking regions (83,84). LES can lead to wrong geometry when the force field itself is not sufficiently accurate and does not provide the correct global minimum (83). In addition, the LES method itself can poorly converge when struggling between competing minima. The experience with this technique so far is rather limited, but it is capable of providing striking insights. Thus, LES simulations were carried out for subtypes A and B DIS structures. We split regions of the flanking bases into five independent copies (see Materials and Methods) and run two 30-ns simulations LES5_A and LES5_B. In addition, two 10-ns simulations (LES3_A and LES3_B) with three copies were executed.

In the LES5_A simulation within the extended 1.5 ns equilibration phase (when the system is heated up to 500 K and cooled back to 300 K; see Materials and Methods), we observed conversion from the open x-ray conformation to the closed conformation, which was stable until 13 ns. Then the closed conformation was disrupted and the entrance of the pocket opened. Bases A₂₇₂ and G₂₇₃ moved into the pocket, and closed-like bulged-in/out conformation, with two bases bulged-in and another two bulged-out, formed (Fig. 3). This arrangement has been seen in standard simulation MD_A_2 for 11 ns. For the rest of the simulation, closed-like bulged-in/out conformation repeatedly disrupted and then restored itself (note that enhanced mobility is expected when applying LES). During a control 5-ns LES simulation performed without the initial 500 K heating, the closed conformation formed after the first two nanoseconds. Thus the initial heating did not affect the simulation outcome. During 10-ns LES3_A simulation (three copies), the flanking bases stayed in the open conformation.

Conversion to the closed conformation was observed during the 30-ns-long simulation LES5_B run. The closed conformation was then seen for the rest of the simulation, except for a few disruptions when A₂₇₂ or A_272* moved inside the pocket. Five-nanosecond control LES simulation, performed without the initial 500 K heating, resulted in formation of the closed conformation after the first three nanoseconds. In the 10-ns simulation LES3_B, closed conformation initially formed after 500 ps and was followed by open conformation until ∼9 ns. After that, three bases moved into the pocket and stacked, while the fourth adenine stayed bulged-out.

In summary, the LES simulations did not reveal any new geometry that would be missed by standard simulations, and, in general, gave some support to the closed bulged-out geometry.

Basepairing, backbone conformation, and cation-binding pocket

All simulated kissing complexes consist of six intermolecular pairs which are stable. Backbone torsion angles in simulated x-ray complexes exhibited common temporary α-γ flips (population ∼10%). They are discussed in detail elsewhere and do not affect the course of the simulation (34). In both NMR complexes (in area of bulges) we found deviations of phosphate backbone torsions from established RNA conformational families (85) (for instance, in Lancelot's complex, α = 97°, β = 243°, and γ = 75°, or in Baba's complex, α = 241° and β = 80°). In the simulations, the unusual torsions convert to the nearest-conformational family, while longer timescales would be needed to appropriately relax these distorted regions. We detected no visible distortions in structures during the simulation, indicating a good performance of the AMBER RNA force field (22,86,87).

The central part of kissing-loop complexes forms a pocket with deep minimum of ESP (21). The ESP minima of the subtype F DIS and the ribosomal complex (calculated for averaged MD structures) were −30 kcal/mol and −34 kcal/mol, respectively (Fig. 6). They are comparable with minima of subtype A and B (∼−30 kcal/mol) (21) or with the major and functionally important ESP minimum of the catalytic pocket of precursor structure of the Hepatitis Delta Virus ribozyme (HDVr, −37 kcal/mol) (31). All ESP values given above were calculated with identical procedure by the DELPHI program (71).

FIGURE 6.

Stereo views of subtype F (left) and ribosomal complex (right) with maps of electrostatic potential (in black) contoured at −25 kcal/mol. The cation-binding pocket is highlighted by transparent surface (in gray); detailed view is below.

The negative ESP central pocket of kissing complexes is a major binding site for cations, which may enter via the pocket gate (see Fig. 1 D) or through the major grooves. In presence of monovalent ions only, the pocket has the following features: 1), it is continuously occupied by two-to-three delocalized monovalent ions; 2), the ions easily enter the pocket from the bulk and exchange with the bulk on a timescale ∼1–3 ns (much faster than in the case of HDVr catalytic center where the ions are trapped for many nanoseconds (31)); and 3), while being in the pocket, the ions are dynamical and basically delocalized.

Changes of x-ray positions of Mg²⁺ and K⁺ ions in newly refined subtype A, B, and F structures

Newly refined x-ray subtype A DIS (PDB code 1XPF) contains 3 Mg²⁺. Two of them are in the major groove and the third one is positioned at the pocket gate (Fig. 7). After equilibration, the green Mg²⁺ ion escaped into solvent while the remaining two formed stable inner-shell contacts to adjacent O1P atoms (Fig. 7). Note that formation of the inner shell contacts in this case may reflect a force-field artifact. At 20 ns, the green Mg²⁺ ion appeared in the central pocket where it stayed until the end of the simulation without formation of any stable contacts (see Fig. 7).

FIGURE 7.

Stereo views of x-ray subtype (A) DIS (PDB code 1XPF) and subtype (B) DIS (PDB code 1XPE) structures with x-ray Mg²⁺ ions and (C) stereo view of subtype F DIS (PDB code 1ZCI) with x-ray K⁺ ions. Final positions of ions were obtained from the last nanosecond, and are represented by unfilled spheres.

X-ray subtype B DIS (PDB code 1XPE) shows 2 Mg²⁺ ions. One is positioned at the border of the central pocket (green) and the second one is in the major groove (red) (Fig. 7). The green ion sampled border of the pocket and appeared also inside while forming only temporary outer-shell contacts. The red ion left initial position at 24 ns and was released into solvent. At 27 ns, it appeared at the opposite side of the kissing complex, in relation to its initial position. Here it sampled major groove, border of the pocket, and at 43 ns, was released back to the solvent.

X-ray subtype F DIS (PDB code 1ZCI) was run with two x-ray K⁺ ions positioned in major groove (see Fig. 7). After 2 ns, the ions left their x-ray positions and were released into the solvent. They sampled RNA positions as well as the water box, and interestingly both K⁺ briefly visited the central pocket, which confirms satisfactory sampling for monovalent ions in simulations. Thus, the information about the initial position of the monovalent ions is lost very quickly.

Free energy calculations

To monitor free energy changes we employed the molecular mechanics, generalized Born, and surface area method. The results (see Supplementary Material) were inconclusive and the approach is too crude to meaningfully monitor the energetics of flanking bases (22,86,87).

CHARMM simulations

Newly refined HIV-1 subtype A and B DIS structures (1XPF and 1XPE) with preliminary ion distribution (see Supplementary Material) were simulated using CHARMM27 force field (Table 3). In CH_A (subtype A) simulations, flanking bases were observed both bulged-out and bulged-in in agreement with AMBER simulations. At the beginning of simulation CH_A_1, all flanking bases moved toward the pocket, which has been seen for subtype B but not for subtype A in AMBER simulations. The 12-ns-long CH_A_2 and CH_A_3 simulations sampled only the open conformation. In CH_B (subtype B) simulations, flanking bases were seen both bulged-out and bulged-in. Simulations CH_B_1 and CH_B_2 revealed formation of the consecutive A₂₇₂A₂₇₃A_273*A_272* closed stack that was frequently identified in AMBER simulations (see Fig. 3 and Table 2). Moreover, in CH_B_1 simulation, 3R-bulged-out and closed-like bulged-in conformation variants of closed conformation were sampled. Further, simulation CH_B_2 sampled locked stacked conformation seen in MD_A_1 and MD_A_2 simulations. More detailed analysis of CHARMM data will be given elsewhere, but qualitatively we can conclude that the CHARMM and AMBER data are, regarding the flanking base dynamics, quite consistent. However, CHARMM simulations revealed melting of 1–3 terminal basepairs, which could suggest underestimation of the duplex stability. In several cases the melting was, however, reversible.

TABLE 3.

Simulations performed with the CHARMM force field

Name of the simulation	PDB code (resolution)	Simulation length (ns)	RMSD (Å)	Ions in the simulations	Starting conformation of flanking bases
CH_A_1	1XPF (2.30 Å)	20	4.1 ± 0.6	5 Mg2+, 34 Na+	open
CH_A_2	1XPF (2.30 Å)	12	4.1 ± 0.6	5 Mg2+, 34 Na+	open
CH_A_3	1XPF (2.30 Å)	12	4.2 ± 0.6	44 Na+	open
CH_B_1	1XPE (1.94 Å)	30	3.9 ± 0.7	4 Mg2+, 36 Na+	open
CH_B_2	1XPE (1.94 Å)	12	4.8 ± 0.6	4 Mg2+, 36 Na+	open
CH_B_3	1XPE (1.94 Å)	12	4.2 ± 0.9	4 Mg2+, 36 Na+	open

Instantaneous RMSD values are calculated along the trajectories with respect to the initial structures.

DISCUSSION

We analyze structural dynamics of flanking bases in RNA kissing-loop complexes. The work is a major extension of our preceding study (21) considering the amount of simulations (775 ns) and the number of studied structures. We focus on conformations of flanking bases in the new x-ray HIV-1 DIS kissing complexes (subtypes A, B, and F) (17), in the NMR complexes of the subtype B and subtype B/F (18,20), and in the kissing complex from the large ribosomal subunit of H. marismortui (13). We test different ion conditions and two force fields (AMBER parm99 (65) and CHARMM27 (60,61)). In addition, we applied several long (up to 30 ns) LES runs to improve sampling of the flanking bases (57).

The crystal structures show bulged-out flanking bases, either four base stack (closed conformation, see Fig. 3) or two separate stacks (open conformation) depending on crystal packing (17). NMR studies suggest bulged-in positions of bases which, however, are mutually inconsistent (18,20).

The simulations identified six typical positions of the flanking bases as summarized in Table 2 and Fig. 3. The most prevalent arrangement predicted by the MD simulations is the closed conformation (closely agreeing with the respective x-ray arrangement) or related geometries where, e.g., three bases are stacked and the fourth one samples mostly bulged-in geometries. However, other substates are also nonnegligibly populated, including bulged-in geometries. Note that when assessing the Table 2, one needs to consider the starting and final structures separately (highlighted in Table 2), and also take into account that some structures are mutually structurally related. Vast majority of simulations started with the open bulged-out conformation, which then obviously dominates the overall percent of population. However, there is a clear trend to move toward the closed structures and related geometries. The simulations routinely achieve transitions from bulged-out starting x-ray geometries to bulged-in arrangements and even subsequent returns to bulged-out geometries. We have also evidenced bulged-out base excursion from a parent bulged-in NMR structure. All these movements indicate a meaningful sampling of movements of flanking bases in both directions.

Self-association of bulged bases was observed for all three subtypes when starting from x-ray structures. The simulations of subtype A DIS kissing complex show that the initial open bulged-out conformation (Fig. 1) tends to convert to the closed (bulged-out) conformation or related conformations such as closed-like bulged-in/out and 3R-bulged-out (Fig. 3, Table 2). Outcomes of simulations of the subtype A are not affected by presence or absence of Mg²⁺ ions. In contrast, for subtype B the conversion from the open conformation to the closed conformation occurred in presence of Mg²⁺ while in absence of Mg²⁺ ions we rather evidenced bulged-out→bulged-in conversion of all flanking bases. This could indicate that the subtype B bulged-out geometries are getting some stabilization by Mg²⁺ ions. Notably, the NMR structures were solved in presence of monovalent ions. Nevertheless, simulations with divalent ions should be taken with specific care due to a number of limitations (22) (see Materials and Methods). Note also that the divalent ions were considered by including only those ions seen in the crystal structures (see Fig. 7 and Supplementary Material).

Subtype F DIS kissing complex was investigated with the two different conformations of bulged-out residues observed in x-ray structures. The closed conformation showing weak crystal contacts was basically stable except of mobility of A_272*. Open conformation in which flanking bases mediate crystal contacts in asymmetric unit changed after the first nanosecond into the closed conformation. This observation is in agreement with the x-ray experiment (17), indicating that self-association of all four flanking bases is preferable, unless it is prevented by the crystal packing.

The two recent NMR DIS structures (subtype B (18) and subtype B/F (20)) show bulged-in geometry. We simulated these two NMR structures on a scale of 20 ns and found that they basically remained in their bulged-in conformations. Open question, however, is whether some structural deformations in the starting NMR structures (especially the local deformation of backbone area of bulges) are not affecting our simulations. For example, the Lancelot's structure exhibits visible local deformations, which are not repaired on our simulation timescale. Overall, there are substantial mutual differences among the three available NMR structures of the DIS kissing complexes (18–20). It also is not clear whether the NMR experiment would capture the bulged-out conformation, if coexisting. Flanking bases of the ribosomal kissing complex were essentially stable in bulged-out conformation.

All kissing complexes are associated with a very deep ESP minimum in the central pocket (see Fig. 6), which is continuously occupied by 2–3 monovalent ions (in absence of divalents), and these ions are delocalized (21). The RNA kissing complexes thus create one of the most intriguing cation-binding pockets visualized in RNA MD simulations so far.

CHARMM simulations (total 98 ns) essentially agreed with the picture from AMBER simulations. These simulations identified five of the six AMBER flanking base conformations and in addition with similar populations. This is a good agreement, taking into account the considerably shorter timescale of CHARMM simulations. No new substate was located. CHARMM simulations, however, revealed partial melting of stems (disruption of terminal 1–3 basepairs). Though some of the disruptions were reversible, such stem perturbations are most likely excessive. A recent study reported a difficulty with the CHARMM27 force field providing stable trajectories of folded Hammerhead ribozyme (88).

We also applied LES to enhance the sampling of the flanking bases. The MD and LES results were quite consistent, which gives us a confidence that no significant substate was missed. We also attempted to use the molecular mechanics, generalized Born, and surface area free energy method to characterize the free energies of various conformations seen in MD trajectories. This approximate method, however, was not capable of providing conclusive results (see Supplementary Material). Limitations of various methods that can supplement standard simulations are discussed elsewhere (22).

Several other MD studies have been performed with the aim of describing the subtype B DIS kissing complex on the nanosecond timescale (50–52). These studies did not report formation of the closed bulged-out conformation, which is seen in x-ray structures and is a major substate according to our simulations. It is likely caused by the short simulation timescales. Beaurain et al. (51) (using CHARMM) and Aci et al. (52) observed bulged-in geometries of flanking bases in the presence of Na⁺ ions similar to our corresponding simulations. Aci et al. also reported a peculiar instability of the AMBER simulations using x-ray starting structures, which was not observed in any of our kiss simulations and, in fact, in no other simulations starting from RNA x-ray structures.

CONCLUSIONS

Despite the substantial investment of computer time, the simulations were not sufficient to obtain a quantitatively converged picture of the flanking base positions. Nevertheless, the picture obtained from our full-scale investigation is considerably more complete compared to what would we see upon resting each simulation at 10 ns. Still, the variability of the results means that we are far from a timescale that could be considered as fully converged. Modest extension of the simulations would not solve the problem. MD investigations of flanking base positions are also complicated by the force-field approximations. This particular task can be rather sensitive to force-field imbalances (compared, for example, to studies of compact duplex regions), as we need to compare several competing substates with quite different geometries but presumably similar stabilities. The force-field approximations in RNA simulations are discussed in detail elsewhere (22). It would be a little too ambitious to expect quantitative accuracy for flanking base description with contemporary MD. Nevertheless, our study brings several valuable qualitative results. There is mutual agreement between AMBER and CHARMM force fields for the description of the flanking base behavior, which is a sign of robustness of the results. Besides the flanking base dynamics, we did not see any perturbation of the simulated structures that would indicate any significant misbalance of the AMBER force field. It confirms the known rather satisfactory performance of the AMBER parm99 force field for RNA molecules (22). We identified several typical classes of geometries that can be adopted by the flanking bases of the kissing complexes. The trend for self-association of the bases in the bulged-out conformation is clearly seen and may be supported by divalent cations. The simulations nicely capture transitions from the so-called open bulged-out geometry to the closed bulged-out arrangement with consecutive stretch of four stacked purine bases, seen in crystals where the packing is essentially avoided. In addition, once this geometry is formed, the overall agreement with the x-ray geometry is very good. The simulations are thus in qualitative agreement with the x-ray structural investigations. Besides that, the simulations also suggest that the bases can easily adopt typical positions either at the gate of the kissing pocket or inside the pocket. This result could reconcile the x-ray and NMR experiments. One additional argument in favor of the bulged-out conformation is the fact that x-ray structures (with bulged-out conformations) successfully predicted the binding of aminoglycoside antibiotics to the flanking region in the DIS kissing complex (89). This was confirmed with the x-ray structure of DIS/aminoglycoside complexes (90), although it is fair to admit that the bound ligand can shift the equilibrium in favor of the bulged-out geometry. The biological relevance of the closed bulged-out geometry is also supported by the conservation patterns of the flanking bases. The most conserved is A₂₇₂, while A₂₇₃ mutates to G for subtypes A and G (91,92). Nevertheless, the preference of evolution to have four adenines or alternating AGAG available for the stack is clearly visible, and these base combinations are expected to be the most favorable for stacking self-association (93,94). When replacing these purine bases by pyrimidines, a shift in favor of bulged-in geometry should occur simply due to reduced stacking (95). In addition, while bulged-out bases can be useful for molecular recognition, which can be seen for kissing complex in the ribosome where bulges mediate tertiary contacts with the adjacent part of 23S rRNA (Fig. 5 B), it is much less clear what functional role the bulged-in bases, hiding inside the pocket, could have. Perhaps bases in bulged-in geometries might be less likely targets of nuclease. However, there are many other highly exposed, single-stranded purines in the genomic RNA. The simulations indicate that the bulged-in and bulged-out states are close in energy and their balance can be affected by both sequence and environment, which is in accord with previous MD studies of flanking bases in RNA (96) and DNA duplexes (97). The dynamics of flanking bases of HIV-1 DIS kissing-loop complexes markedly resembles conserved adenines A1492 and A1493 of the decoding site in the ribosome. In bulged-in form, A1492 and A1493 are stacked in the stem of 16S rRNA helix 44, while in bulged-out form they contact the codon/anticodon complex of mRNA/tRNA (98). Previous modeling (30,34) and x-ray (or NMR) (98–102) experiments showed that these adenines are naturally dynamical and may adopt numerous substates. Based on current knowledge, flanking bases appear to be flexible mediators of tertiary contacts in molecular assemblies.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophys.org.