Analyzing for information, not activation, to exploit high-resolution fMRI

Abstract

High-resolution functional magnetic resonance imaging (hi-res fMRI) promises to help bridge the gap between the macro- and the microview of brain function afforded by conventional neuroimaging and invasive cell recording, respectively. Hi-res fMRI (voxel volume ≤ (2 mm)³) is robustly achievable in human studies today using widely available clinical 3-Tesla scanners. However, the neuroscientific exploitation of the greater spatial detail poses four challenges: (1) Hi-res fMRI may give inaccurate (i.e. blurred, displaced and distorted) images of fine-scale neuronal activity patterns. (2) Single small voxels yield very noisy measurements. (3) The greater number of voxels complicates interpretation and poses a more severe multiple-comparisons problem. (4) The functional correspondency mapping between individual brains is unknown at the fine scale of millimeters. Here we argue that these challenges can be met by shifting the focus of brain mapping and visualizing, not the activity patterns themselves, but the amount of information they convey about the experimental conditions.

Introduction

Neuroimaging has helped define the big picture of primate brain function at the systems level. Its macroview of functional regions activated in a given cognitive process has complemented the microview offered by invasive cell recording (Fig. 1a). However, with each blob of a neuroimaging map reflecting the averaged activity of hundreds of thousands of neurons over extended periods of time, macro- and microview are separated by many orders of magnitude. The gap between them represents one of the obstacles to forming a coherent overall account of primate brain function.

Figure 1. Four challenges of hi-res fMRI.

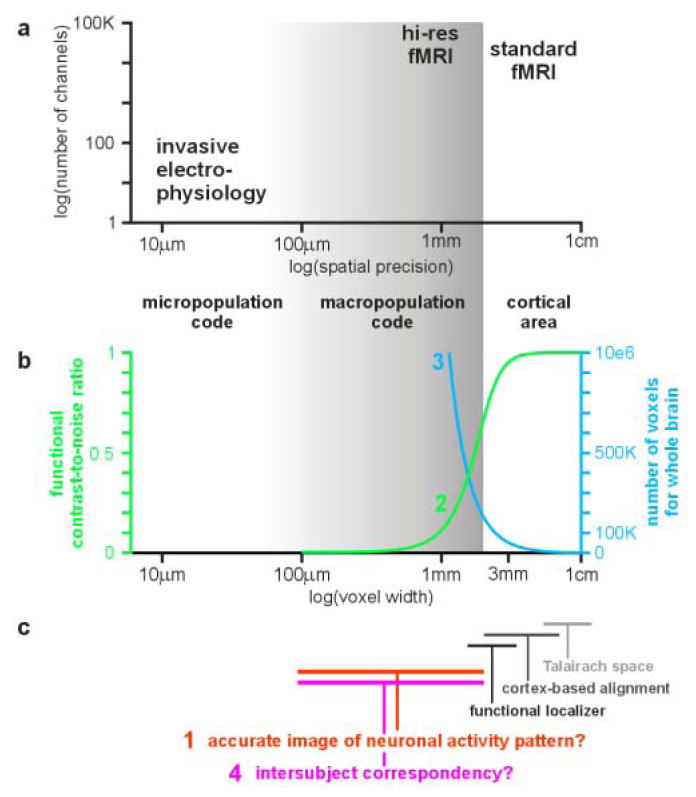
(a) Comparison of fMRI (standard and hi-res) and invasive electrophysiology in terms of spatial precision and number of channels, with which brain activity is simultaneously measured. The gray shading indicates the precision range of hi-res fMRI (≤ 2 mm voxel width). (b) The FCNR drops rapidly when fMRI resolution is increased (challenge (2), green). The curve depends on many parameters, but retains its sigmoid shape for realistic values. The curve shown (for a 3T scanner) is based on the physiological-noise model of Krüger et al. (2001) and on theory and measurements of Bodurka et al. (2007): we assume physiological effects with a standard deviation of 1.25% signal change (measured value for gray matter during resting state). Here we further assume that half this physiological variance is of interest (e.g. related to some experimental task, thus defining the functional contrast) and the other half is physiological noise. We consider gray-matter voxels reflecting physiological effects with no partial-volume sampling. We assume a spatial signal-to-noise ratio (SNR) of 100 for 2-mm-wide isotropic voxels. This SNR is intermediate between the values determined for a birdcage coil and a 16-channel receive-only array coil used with a 3T MRI scanner (Bodurka et al. 2007). The blue curve shows the rapid growth of the number of voxels needed to cover the brain as voxels become smaller (challenge (3), blue). (c) In the hi-res range (gray shading), fMRI may give an inaccurate (blurred, distorted, displaced) image of the neuronal activity pattern (challenge (1), red). Moreover, a voxel-to-voxel intersubject correspondency is very difficult to define and, in fact, may not exist (challenge (4), magenta). Standard fMRI, by contrast, operates at the spatial scale of cortical areas. At this coarser scale, hemodynamic blurring, distortion and displacement of neuronal activity patterns is less problematic and intersubject correspondency is roughly determined by the Talairach common space, and more precisely by cortex-based intersubject alignment or a functional localizer experiment.

Hi-res fMRI promises to help bridge the gap between the macro- and the microview of brain function. It offers greater spatial detail and a reduction of partial-volume effects (i.e. voxels averaging across different functional units or tissues). For convenience, we define hi-res to mean nominal voxel volumes ≤ (2 mm)³, but our argument here does not depend on this essentially arbitrary definition. A voxel volume of (2 mm)³ is robustly achievable in human studies today on widely available clinical scanners operating at 3 Tesla (T) (see Appendix for more detail). At high field (>3T; Uğurbil et al. 2003, Harel et al. 2006b, Formisano et al. 2003) and using parallel imaging (Prüssmann 2004, de Zwart et al. 2006), hi-res fMRI is invading the submillimeter range.

The neuroscientific exploitation of the greater spatial detail now available poses four challenges (Fig. 1b, c): (1) Fine-scale neuronal activity patterns are inaccurately represented in the functional MR images because of hemodynamic blurring, distortion and displacement. (2) Single small voxels yield noisy measurements (Fig. 1b, green curve). (3) The large number of voxels complicates the neuroscientific interpretation and poses a severe multiple-comparisons problem (Fig. 1b, blue curve). (4) The interindividual spatial correspondency mapping is unknown. This makes it difficult to combine data across subjects and to represent the functional layout of the brain in a standardized spatial model for humans or monkeys. These four challenges are substantial even at conventional resolution. They become severe as resolution increases.

Can advances in imaging technique alleviate the challenges? Challenges (1) and (2) are directly dependent on the imaging technique. Substantial progress has been made with regard to spatial specificity of fMRI (Harel et al. 2006b, Duong et al. 2001, Yacoub et al. 2003, Harel et al. 2006a, Uğurbil et al. 2003). For example, at high field strength it might be possible to obtain accurate single-condition maps at columnar resolution in cats (Duong et al. 2001). The optimization of existing MR imaging techniques and the search for novel contrast mechanisms will continue. This includes the nonhemodynamic approach of neuronal-current fMRI (Bodurka et al. 1999, Bodurka & Bandettini 2002, Petridou et al. 2006).

However, advances with respect to accurate hi-res imaging of neuronal patterns (challenge (1)) often come at a cost in terms of the functional contrast-to-noise ratio (FCNR, challenge (2)). For example, compared to the gradient-echo T2*-blood-oxygen-level-dependent (BOLD) fMRI technique widely used for cognitive studies (Ogawa et al. 1992), high-field Hahn-spin-echo T2-BOLD fMRI (Duong et al. 2002, Yacoub et al. 2003), initial-dip fMRI (Kim et al. 2000), and arterial-spin labeling (Kim 1995) all promise greater spatial specificity (Uğurbil et al. 2003). However, for all three approaches there is a penalty in terms of the contrast-to-noise ratio (thus exacerbating challenge (2)). More fundamentally, the accurate imaging of fine-scale neuronal activity patterns (challenge (1)) depends on the relationship between neuronal activity and the hemodynamic fMRI signal (Logothetis et al. 2001, see also Bandettini & Ungerleider 2001), which is still not fully understood (Logothetis & Wandell 2004). Despite continual progress, it appears unlikely that advances in imaging technique alone will lead to a simultaneous solution of challenges (1) and (2) for human studies.

Improving the imaging cannot at all address challenge (3), the complication of analysis and interpretation arising from the large number of voxels of hi-res fMRI, or challenge (4), the definition of a high-precision intersubject-correspondency mapping. The intersubject-correspondency problem is not purely a challenge to data analysis, either. Instead it concerns a fundamental neuroscientific question: To what level of spatial detail does a functional correspondency even exist between different individual brains?

If hi-res fMRI is to fulfill its promise, neuroscientists will need to learn how to extract the rich information about neuronal activity, which is present in the data despite the drawbacks of the measurement and the lack of a high-precision standard brain space defining intersubject correspondency. The conventional, activation-based approach to brain mapping analysis, however, is not suited for this endeavor.

Activation-based analysis

Conventional fMRI analysis is “activation-based” in that it is designed to detect the overall activation of functional regions (Worsley et al. 1992, Friston et al. 1994, Friston et al. 1995). Because cortical areas are much larger than even conventional voxels (3-5 mm width), the spatially smooth component of the data is considered signal and the fine-grained component is considered noise. This motivates smoothing of the data for mapping analyses, usually using a Gaussian kernel of 6-8 mm width. For region-of-interest (ROI) analyses, similarly, all time courses of a region are averaged (Fig. 2). Thus, under the activation-based paradigm, it is analysis, not measurement, that limits the effective resolution.

Figure 2. Activation- and information-based analysis.

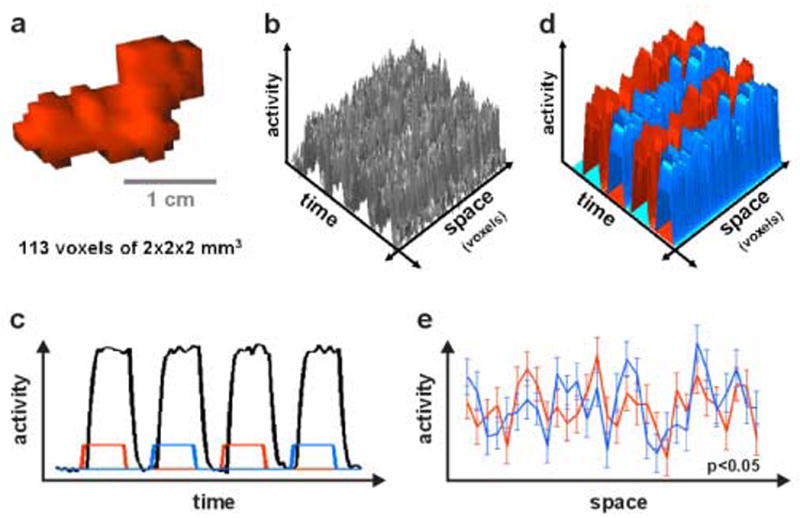
Toy simulation illustrating the potential benefits of analyzing for information in fine-grained activity patterns. (a) A region of interest (ROI) consisting of 113 voxels. (b) The fMRI data matrix (time by voxel) for the ROI. The voxels are lined up in arbitrary order along the space axis. (c) In a standard activation-based analysis of the ROI, all 113 time courses are first averaged across voxels, yielding an average time course (black line). This shows that there is little difference in the overall activation of the region during the two experimental conditions indicated by the rectangular reference functions (red for condition 1, blue for condition 2). (d) Modeling each voxel time course with a separate hemodynamic predictor for each trial suggests that each condition (red, blue) is associated with a replicable and distinct spatial activity pattern. (e) The average spatial patterns associated with the two conditions (red, blue) are plotted with standard-error bars. (Only 30 of the 113 voxels are shown.) For all voxels, the error bars overlap – indicating that the univariate effects are not significant in any voxel, even without correction for multiple comparisons. A mapping analysis would not mark any voxel in this toy simulation. However, a multivariate test performed on all voxels (multivariate analysis of variance here) demonstrates that the two activity patterns (red, blue) are in fact significantly different (p<0.05). For a similar example based on actual fMRI data, see Fig. 5.

The smoothing performed in activation-based analysis is well motivated and successful, precisely because it alleviates the challenges posed by fine-grained patterns: Smoothing locally integrates the signals, blurring out vascular artefacts to some extent (challenge (1)) and improving the FCNR for spatially extensive activations (challenge (2)). In mapping analyses, smoothing eases neuroscientific interpretation of the maps (which will show a smaller number of larger blobs) and reduces the effective number of multiple comparisons (challenge (3)), thus additionally improving statistical power. Smoothing also helps combine data from different subjects (challenge (4)) in Talairach space (Talairach & Tournoux 1988).

If smoothing is simply omitted, the four challenges are substantial, even at conventional resolution: Statistical sensitivity suffers and as a result much less of the activated volume is detected. If we abandon the idea of valid inferential mapping and lower the threshold (Fig. 6d), maps reveal salt-and-pepper patterns that are hard to distinguish from noise, inconsistent across subjects, and difficult to describe verbally or interpret in terms of systems-level brain theory. These problems all get worse as resolution increases. It appears questionable whether such patterns can form the basis of solid empirical neuroscience.

Figure 6. Information-based brain mapping using a multivariate searchlight.

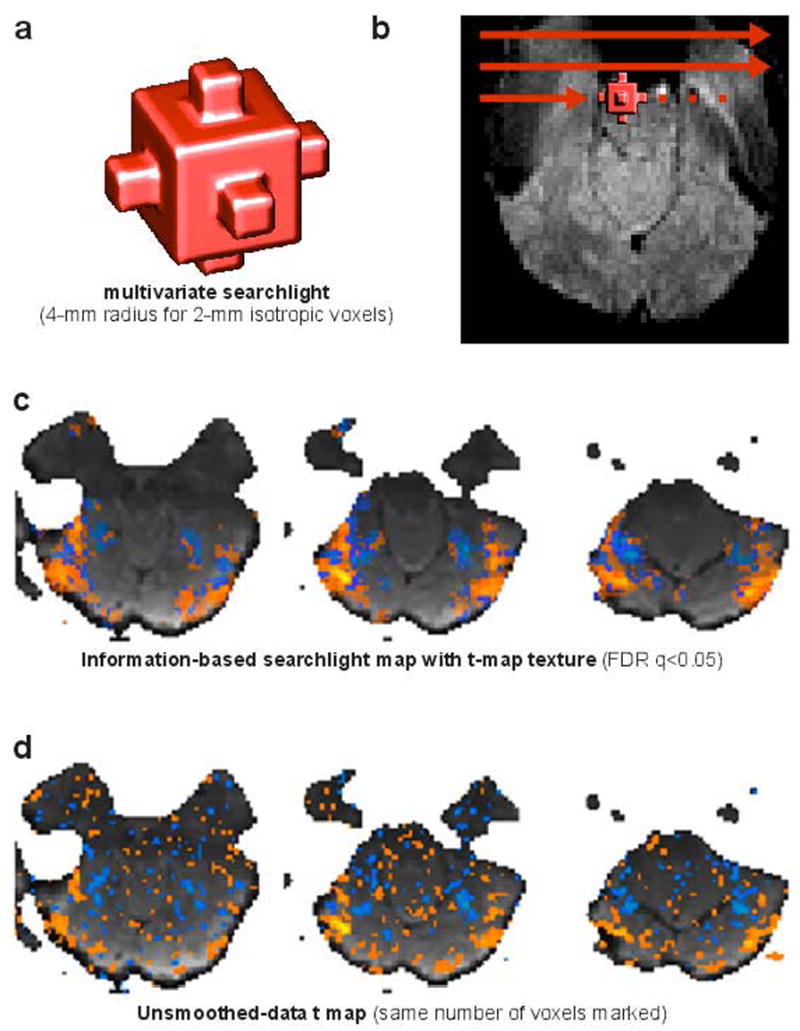
In order to map a neuroimaging volume for information in fine-grained activity patterns, a multivariate searchlight can be moved throughout brain space to obtain a continuous map of local pattern information (Kriegeskorte et al. 2006). (a) The searchlight, here, is a sphere of 4-mm radius illuminating 33 voxels (isotropic, 2-mm width). (b) The searchlight is centered on each voxel in turn (red arrows spaced more widely in the figure for visual simplicity) to select a spherical voxel cluster to be subjected to joint multivariate analysis. (c) The resulting map reveals, not activation, but information present in local activity patterns. Here the map shows regions, whose response pattern distinguishes two categories of visual objects. The information-based map has been thresholded at a false-discovery rate (FDR) of q<0.05 to select the voxels to be highlighted. The voxel color encodes the univariate t value, revealing the actual contrast pattern. Voxels below the information-based threshold but within the searchlight scope of a suprathreshold voxel are marked transparently. In this example, there are more suprathreshold voxels in the information-based map (nontransparently highlighted) than in the activation-based map, i.e. the t map from data smoothed by convolution with the a sphere of the same radius (not shown). (d) The t map from unsmoothed data (texture map in (c)), thresholded to highlight the same number of voxels as the information-based map, reveals salt-and-pepper patterns, whose significance is difficult to assess. When correctly thresholded (not shown), the unsmoothed-data t map highlights very few voxels, failing to detect the widespread pattern information evident in (c).

In essence, activation-based analysis evades the challenges of dealing with fine-grained patterns by removing all fine-grained patterns from the data (i.e. by spatial smoothing). This clearly defies the purpose of hi-res fMRI. The many advantages of smoothing derive from local combination of signals. So what is needed is a method that locally combines the signals, but is still sensitive to fine-grained pattern information. The challenges can be met by analyzing for the information that regional fine-scale fMRI activity patterns convey, rather than for overall activation of functional regions.

Information-based analysis

The idea of analyzing fMRI data for the information in local activity patterns (Fig. 2) has recently gained momentum as neuroscientists began to see spatial fMRI patterns as widely distributed codes or macropopulation codes (Haxby et al. 2001, Strother et al. 2002, Cox & Savoy 2003, Carlson et al. 2003, Mitchell et al. 2004, Hanson et al. 2004, Polyn et al. 2005, Kamitani & Tong 2005, Haynes & Rees 2005, LaConte et al. 2005, Mourao-Miranda et al. 2005, O’Toole et al. 2005, Davatzikos et al. 2005, Kriegeskorte & Goebel 2002, Kriegeskorte et al. 2006, Pessoa & Padmala 2006; for reviews see Haynes & Rees 2006, Norman et al. 2006). Although these studies did not use hi-res imaging (except Kriegeskorte et al. 2006), their approach to analysis naturally lends itself to hi-res fMRI.

Most of the cited studies used multivariate pattern-recognition techniques for decoding, i.e. they aimed to identify a perceptual representation or cognitive state on the basis of multivoxel regional fMRI signals (Fig. 5). When a perceptual representation can be decoded from the activity pattern, clearly the brain region studied contains information about the stimulus. In general, such “information-based” analysis requires multivariate techniques, but not necessarily decoding. (In the Appendix, we give a loose definition of “information-based analysis” and elaborate on the concepts “decoding”, “prediction” and “classification”.)

Figure 5. Even when single voxels are noisy, yielding insignificant effects, their joint spatial pattern can contain significant information about the experimental condition.

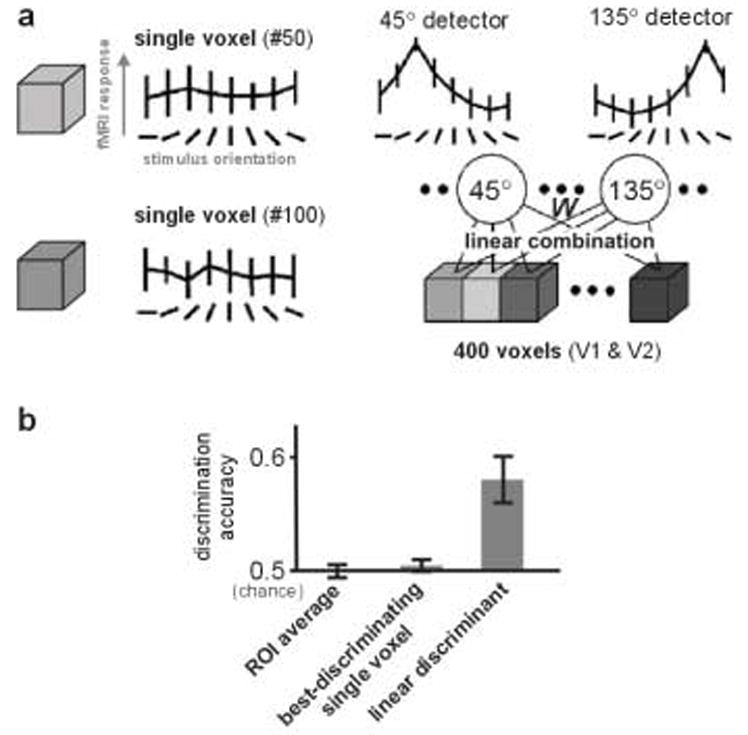
(a) Visual gratings of different orientations elicit very similar responses in single voxels (isotropic, 3-mm wide) within early visual areas V1 and V2 (left). However, when the responses of many voxels are linearly combined with appropriate positive and negative weights (determined using independent data), the resulting combined response can reveal that the region contains significant information about the orientation (right). Error bars indicate the standard deviation. Figure adapted from Kamitani & Tong (2005). (b) A linear combination of the voxel responses can discriminate conditions, even when both the best-discriminating single voxel and the average across all voxels (the regional activation level) do not show significant differences. Here 100 voxels in V1 were used to discriminate two stimulus orientations that were invisible to subjects due to masking. Error bars indicate the standard error of the mean. Figure adapted from Haynes & Rees (2005).

Multivariate techniques have been explored earlier in the neuroimaging analysis literature (e.g. Worsley et al. 1997). However, the current momentum of the information-based approach derives from a specific neuroscientific idea: the idea of revealing the information carried by a local macropopulation code. This idea motivates the joint multivariate analysis of contiguous functional regions in single subjects without smoothing of the data.

An information-based analysis determines whether there is a statistical dependency (i.e. mutual information) between the experimental conditions and the regional spatiotemporal activity patterns. Information undetected by activation-based mapping is often present in neuroimaging data (Kriegeskorte et al. 2006). If the information resides in the fine-scale pattern of the activity, the spatial average may be similar between conditions (Fig. 2c, Fig. 5b), so no effect may be found by conventional methods with the data spatially averaged for ROI analysis or smoothed for statistical mapping. Information-based analysis can be applied to predefined ROIs (Fig. 2, Fig. 5, e.g. Haxby et al. 2001, Kamitani & Tong 2005, Haynes & Rees 2005). Alternatively, a continuous information-based mapping¹ can be performed with a multivariate searchlight (Fig. 6, Kriegeskorte et al. 2006), in order to discover regions carrying a particular type of information.

Despite the four challenges, an information-based locally multivariate analysis can yield stable results of neuroscientific interest. Like conventional activation-based analysis, information-based analysis locally combines the signals to increase statistical power. In activation-based analysis, however, the local combination is achieved by smoothing the data and computing a univariate contrast statistic. In information-based analysis, local combination of signals is achieved by computing a multivariate contrast statistic from local unsmoothed data. If the local hemodynamic patterns differ across conditions, this indicates the presence of neuronal information about the experimental condition, even if the spatial structure of the patterns is greatly blurred, distorted and displaced (Fig. 4). If a macroscopic functional region can be defined as an ROI in each subject, a group analysis can be performed at the level of local information, even if the fine-grained activity patterns within the region are – like fingerprints – unique to each subject (Fig. 7). The remainder of the paper discusses each of the four challenges of hi-res fMRI and how to meet it with information-based analysis.

Figure 4. Despite blurring, distortion and displacement (challenge (1)), fMRI activity patterns may distinguish experimental conditions.

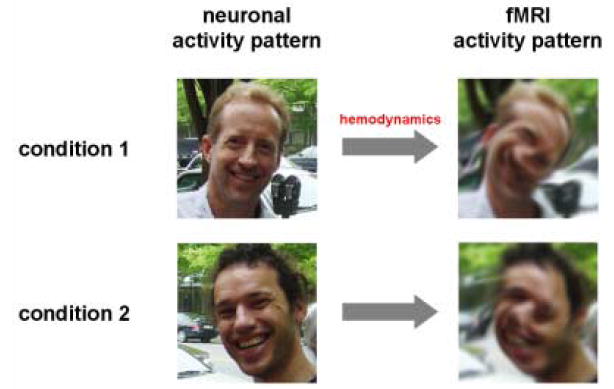
In this figure photographs serve as a stand-in for activity patterns. Even if the neuronal activity pattern is corrupted beyond recognition in the fMRI pattern, information distinguishing the experimental conditions will still be present, as long as the fMRI patterns are replicable and distinct for each condition. This would not be the case in a brain region displaying the same neuronal (and thus the same fMRI) activity pattern in both conditions. Information-based analysis detects differences between the spatiotemporal activity patterns present in a region in different experimental conditions. It can, thus, reveal fine-grained neuronal information, even when the underlying neuronal patterns cannot be accurately visualized with fMRI.

Figure 7. A voxel-to-voxel spatial correspondency mapping is not needed for group analysis, if single-subject local information effects are combined across subjects at the coarser scale of functional regions.

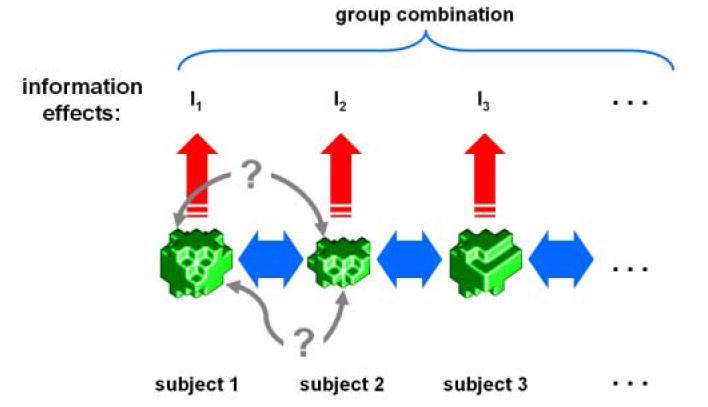
Corresponding functional regions (green ROIs) are defined (1) by a functional localizer experiment analyzed separately for each subject or (2) by selecting a region in Talairach space and projecting it back into the native space of each subject’s data or (3) by cortex-based intersubject alignment. Blue double arrows indicate the coarse correspondency defined by one of these three methods. ROIs will not in general have equal numbers of voxels. A precise voxel-to-voxel correspondency (gray double arrows) may not exist and is not needed. Each subject’s ROI undergoes individual analysis (red arrows) that estimates the information in its local activity pattern (e.g. the mutual information between stimulus and multivariate response). The information effect need not be quantified information-theoretically, but can be measured by any multivariate effect estimate (e.g. a t value obtained for independent data in a linear-discriminant subspace, or, similarly, the time course data projected onto that linear discriminant, as described in the text). Combination across subjects can then proceed at the level of the individual information effects in a fixed- or random-effects framework for group analysis.

Challenge (1): Neuronal activity patterns are inaccurately represented

Current fMRI does not directly measure neuronal activity. It measures the local hemodynamic response that delivers more energy to active neurons. Different fMRI techniques target different aspects of the hemodynamic response (i.e. blood flow, blood volume, blood oxygenation level). The spatial accuracy varies across techniques. However, all techniques share the basic limitation that the spatiotemporal patterns measured are transformed by the hemodynamics. First, the hemodynamic changes measured may be more extended than the site of neuronal activity. In other words, the hemodynamic activation unit may be larger than a single neuron or cortical column. Second, effects originating in the capillaries, where vessels interface with neurons, are washed out into venules and draining veins. This hemodynamic process blurs, distorts and displaces local effect patterns (e.g. Turner 2002). At the macroscopic level of low-resolution fMRI, these artefacts may be acceptable. At the finer scale of hi-res fMRI, they are usually substantial and cannot be ignored.

Cheng et al. (2001) used hi-res fMRI to reveal the pattern of ocular-dominance columns in human primary visual cortex (Fig. 3, see also Goodyear & Menon 2001). This is an example of successful visualization of neuronal activity patterns at the columnar scale. However, considering what was required to meet challenge (1) for the particular case of ocular-dominance columns illustrates that we cannot in general obtain accurate visualizations of neuronal patterns at the nominal voxel resolution.

Figure 3. Hi-res fMRI patterns may misrepresent neuronal activity (challenge (1)), but their difference is informative.

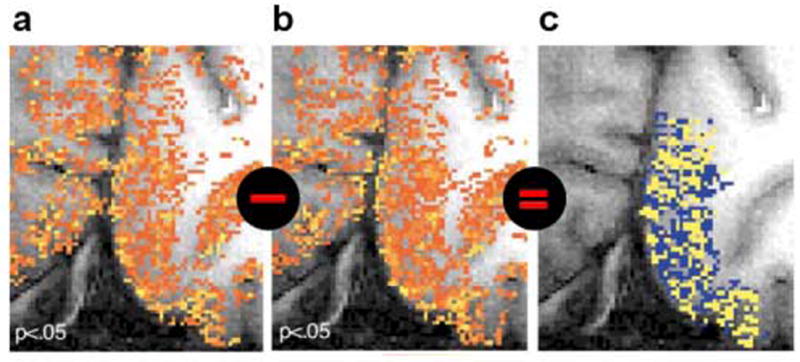
Results of Cheng et al. (2001) show that fMRI patterns elicited in V1 by left- and right-eye stimulation (a and b, respectively) are replicable and distinct, but corrupted by vascular artefacts obscuring the ocular-dominance pattern present in the neuronal responses. Because ocular-dominance domains are spatially complementary by definition, they could be visualized by subtracting the fMRI patterns (c). In general, we cannot rely on this assumption and hi-res fMRI patterns will misrepresent the fine structure of neuronal patterns (as seen in a and b). Cheng et al. performed gradient-echo echoplanar imaging at 4T using (0.47mm)² × 3mm voxels.

Ocular-dominance domains are regions of V1 responding primarily to stimulation from one eye. The two ocular domains form a zebra-like pattern of stripes, whose width ranges between 0.5 and 1 mm. Cheng et al. performed BOLD fMRI with 0.47 × 0.47 × 3 mm³ voxels using a gradient-echo multi-shot echoplanar-imaging technique at 4T. The activity patterns elicited by prolonged left- and right-eye stimulation (as compared to no visual stimulation) do not reveal the cortical ocular-dominance pattern (Fig. 3a, 3b). This demonstrates the inaccurate representation of neuronal activity patterns by the hemodynamic signal. The two conditions activate largely overlapping sets of voxels, suggesting that voxels do not respond specifically to neuronal activity occurring within their boundaries.

When the fMRI patterns for left- and right-eye stimulation were subtracted (Fig. 3c), however, significant differences were found between them. The V1 voxels clearly contained a lot of information about which eye was stimulated. This would not be expected in higher visual regions that do not have separate ocular domains.

Since ocular-dominance domains are nonoverlapping by definition, the authors managed to reveal them by mapping the difference between the left- and the right-eye pattern. The difference map (Fig. 3c) might be somewhat distorted, but it does reveal the ocular domains, correctly representing their shape and width.

Differential mapping can yield accurate visualizations of two neuronal activity patterns if (1) the contrasted conditions are associated with complementary neuronal activity patterns and (2) the artefacts corrupting the hemodynamic single-condition maps are additive and equal for both conditions, such that they cancel out in differential mapping. In general, we cannot make either of these assumptions. Differential mapping will not reveal what two noncomplementary neuronal activity patterns look like. In most studies, therefore, hi-res fMRI patterns will somewhat inaccurately represent neuronal patterns – just like the single-condition patterns obtained by Cheng and colleagues

Information-based analysis does not require accurate representation of neuronal activity patterns

Even if the fine-scale neuronal patterns cannot be recovered from the hemodynamic signals, a difference between the distorted fMRI patterns indicates that the two underlying neuronal patterns differ (Fig. 4). Information-based analysis targets such differences between activity patterns and reveals whether a given brain region distinguishes the experimental conditions.

Of course, the hemodynamic blurring and distortion could in principle obliterate the information about the experimental condition contained in a region’s neuronal activity. This might be expected if the information is known to be confined to the high-spatial-frequency band of the neuronal activity patterns. However, studies like that of Cheng et al. clearly indicate that neuronal pattern information at a scale as small as cortical columns is present in hi-res fMRI data.

Challenge (2): Small voxels yield noisy responses

Smaller voxels give noisier time series (Fig. 1b, green curve). If hi-res is not needed to resolve the pattern of activity (consider a large homogeneously activated region), it is advisable to image at a lower resolution, because the overall contribution of thermal and scanner noise will be smaller: Larger voxels will yield lower noise than smaller voxels locally averaged to give the same lower resolution. This is because MRI signal strength, and with it the spatial signal-to-noise ratio, is proportional to voxel volume (Edelstein et al. 1986). Local averaging of hi-res voxels, by contrast, yields a smaller gain in FCNR, because the noise-reduction factor is at best the square root of the volume factor.

In the conventional resolution range, however, imaging with larger voxel volume can yield diminishing returns in terms of the FCNR (Fig. 1b, green curve in the conventional resolution range), because thermal and scanner noise is already negligible relative to physiological noise, which does not get smaller as voxels get larger (Krüger et al. 2001, Bodurka et al. 2007). These considerations (and the green curve in Fig. 1b) assume that there are no partial-volume effects. When the functional contrast of interest is the difference between two fine-grained activity patterns, larger voxels may yield lower FCNR because they average over opposite effects. It may be optimal then to choose hi-res fMRI, even if thermal and scanner noise are substantial. At the resolution providing optimal contrast for reading a local macropopulation code, effects may be significant for the voxel ensemble, but not for any single voxel (see Fig. 2 for a toy simulation illustrating this situation, and Fig. 5 for actual fMRI data).

Information-based analysis reduces noise by locally combining signals without averaging

Two recent studies (Kamitani & Tong 2005, Haynes & Rees 2005) demonstrate how information-based analysis can reveal neuronal pattern information even when single voxels do not show significant effects (Fig. 5).

These authors imaged activity patterns in early visual areas while subjects viewed oriented gratings. Under these conditions, single voxels do not necessarily show significant effects of grating orientation. In both studies the information-based analysis involved using one portion of the data (the training set) to determine a weight for each voxel. The weight is a positive or negative real number and reflects how well the voxel distinguishes the viewed grating orientations. The weighted sum of the voxels then can be shown (using an independent portion of the data: the test set) to reflect the orientation viewed, demonstrating that the region in question (e.g. V1) contains orientation information. The orientation information is present, although the activity pattern across voxels does not accurately represent the orientation columns.

These studies did not use hi-res fMRI, but a more conventional resolution of 3 × 3 × 3 mm³. Nevertheless they demonstrate how information-based locally multivariate analysis can reveal effects invisible to conventional univariate analysis. This superiority of the information-based approach holds regardless of whether the univariate analysis is applied to each voxel separately or to the overall spatial average of a region (Fig. 5b).

Challenge (3): The greater number of voxels complicates interpretation and poses a more severe multiple-comparisons problem

Not only are smaller voxels noiser, they are also more numerous within the same volume. The greater spatial detail that defines hi-res fMRI presents a challenge to neuroscientific interpretation: What is the meaning of a complicated pattern of small activated patches? (See Appendix for a comment on the concept of patchy organization.)

Statistically, the large number of voxels entails a more severe penalty for multiple comparisons: a higher single-voxel threshold will need to be applied to smaller, noisier voxels. Challenges (2) and (3), thus, interact rather viciously, making hi-res mapping very difficult, unless we artificially reduce the resolution by smoothing or greatly increase the scan duration (Murphy et al. 2006) by performing many measurement sessions on the same subject.

As a practical example, one of the easiest localization exercises, finding the fusiform face area (FFA, Kanwisher et al. 1997), is not trivial at very high resolution (our own unpublished data). This can be seen in Fig. 3 of Grill-Spector et al. (2006), where the threshold was lowered to p<0.005 (uncorrected) to localize the FFA using a surface coil and (1 mm)³ voxels at 3T. Because the FFA comprises hundreds of voxels at this resolution, thresholding with correction for multiple comparisons, even just within the FFA, would likely fail to reveal face selectivity on the basis of the data used for those maps. It seems safe to say then, that localization of the FFA in a larger volume (e.g. the imaged slab) is truly a challenge at this FCNR. (In the cited study, replication of the uncorrected map and conventional-resolution fMRI do demonstrate that the hi-res clusters shown are within the FFA.)

Information-based analysis reduces complexity and the effective number of tests by locally combining signals without averaging

Local combination of signals, either within predefined ROIs (Fig. 2) or within a multivariate searchlight used for mapping (Fig. 6) reduces complexity. The use of predefined ROIs lends comfortable constraints to the interpretation: the number of regions is typically small and we can rely on prior knowledge about them from the literature. Information-based mapping with a multivariate searchlight provides a more open analysis with the potential of discovering information in unexpected regions. In contrast to univariate mapping, information-based mapping yields a smooth map of local pattern information. In place of innumerable small patches, the map will contain much fewer larger blobs indicating local distributed information. Because the spatial scale of the blobs is in the range of cortical areas, the map is more easily interpreted in terms of systems-level brain theory. For statistical inference, the smoothness implies a smaller effective number of multiple comparisons.²

Challenge (4): The fine-scale interindividual correspondency mapping is unknown

Neuroimaging group analysis is usually performed by projecting data into the Talairach standard space. Each subject’s data is first spatially smoothed (by convolution of each volume with a Gaussian of 4-8 mm full width at half maximum), because it is known that matching regions can be off by many millimeters between subjects in Talairach space. This approach is clearly unsuited for hi-res fMRI as it would obliterate the targeted information in fine-grained activity patterns.

Cortex-based intersubject alignment can provide a more precise correspondency than Talairach space (Fischl et al. 1999, Argall et al. 2006, Goebel et al. 2006). For a limited number of predefined macroscopic functional regions, localizer experiments analyzed for each subject, can also establish a more precise functional correspondency. However, none of these methods provide the spatial precision of hi-res fMRI. More importantly, the problem at hand is not merely a technical issue. Rather it concerns a fundamental neuroscientific question: To what level of spatial detail does a functional correspondency even exist between different human brains? The spatial precision of intersubject correspondency is likely to depend on the brain region studied.

For an example, consider primary visual cortex. Subjects’ brains could be matched up according to the individual retinotopic maps. This suggests a functional correspondency with at least millimeter precision. It seems questionable, however, if orientation columns can unambiguously be matched between subjects: At this finer scale, the organization may be unique to each subject like the fingerprint. A coarser intersubject correspondency than in retinotopic visual cortex might be expected for the functional regions of frontal cortex. For this part of the brain, it is unknown whether even the decomposition into cognitive component functions is consistent across subjects. Alternatively, one could argue that frontal cortex is merely less understood at present.

These considerations illustrate that the spatial precision of functional intersubject correspondency is an open neuroscientific question to be empirically addressed for each region. We know that each brain is structurally and functionally unique, giving rise to a unique personality. We also know that correspondency cannot exist at the single-neuron level, because the number of neurons varies across brains. A whole-brain high-precision standard space may, thus, never be available.

Information-based group analysis does not require fine-scale interindividual correspondency

Even if we cannot match activity patterns between subjects at the fine scale of hi-res voxels, we can still make use of established methods to define a coarser correspondency at the level of macroscopic functional regions (each comprising many voxels). We can then analyze the fine-scale pattern information separately in each subject and combine the single-subject information effects, instead of the raw activity patterns (Fig. 7). To make this more concrete, we describe two specific methods below. Because this information-based approach to group analysis has not previously been described to our knowledge, we provide greater methodological detail here than in the previous sections.

Localizer approach

One way to define a coarse-scale correspondency is by means of localizer mapping analyses. For example, the fusiform face area could be defined in each subject by the appropriate activation-based contrast mapping. Alternatively, we could also define functional regions in each subject using information-based mapping with a multivariate searchlight (Fig. 6). Once the ROIs are defined for all subjects, we can ask, at the group level, if the functional region carries a particular type of information in its fine-grained activity pattern. Let’s assume we are interested in whether the region’s activity pattern distinguishes two experimental conditions A and B. We need to integrate data across subjects, but do not know the voxel-to-voxel intersubject-correspondency mapping within the region. In fact the ROIs may have different numbers of voxels for different subjects. We must therefore first analyze the region separately for each subject.

One attractive method is to weight each voxel according to how well it distinguishes condition A from condition B. For this purpose, we could contrast the conditions (A-B) to obtain a t value for each voxel. If we linearly combine the voxel time courses, each weighted with its voxel’s t value, we have reduced the ROI’s multivariate activity pattern to a single combined time course that discriminates the two conditions. Intuitively, a voxel that does not discriminate the two conditions will have a weight (i.e. a t value) close to zero. A voxel responding more to A than B will have a positive weight and a voxel responding more to B than A will have a negative weight. As an alternative to using the t values, we could determine the weights by computing the Fisher linear discriminant (e.g. Duda et al. 2001) or by training a linear support vector machine (Vapnik 1996).³ These three options may all be reasonable for fMRI data and each is optimal under different assumptions.⁴

In order to test whether there is significant information in a single subject, we can use our linear model to perform a t test on the combined time course. However, in order to avoid circularity, we need to use separate replications of the experiment in the same subject for (1) defining the ROI and obtaining the weights and (2) computing the weighted sum of time courses and performing the test. After applying this procedure to each subject, we can perform fixed- or random-effects group analysis on the linearly combined time courses from the second data set by means of standard methods as described in Lazar et al. (2002). This approach works for block as well as slow and rapid event-related designs, utilizing the familiar framework of the general linear model.

Group-level information-based searchlight mapping in common space

Instead of using localizer mapping analyses to define corresponding functional regions at the coarse scale, we can make use of a common space, e.g. Talairach space. For a given location in the common space, we place a multivariate searchlight (Fig. 6) at corresponding locations in each subject. We can then perform a fixed- or random-effects test exactly as described above.The resulting p map in the common space could directly be subjected to false-discovery-rate thresholding (Genovese et al. 2002, Benjamini & Hochberg 1995). Alternative options include the use of randomization of condition labels (Nichols & Holmes 2002, Kriegeskorte et al. 2006) to obtain a simulated null distribution of whole brain maps in the common space. This approach would allow the use of any effect measure (including information-theoretic measures) and controlling the family-wise error rate for a whole map of locally dependent tests would be straightforward. Instead of Talairach space, cortex-based intersubject alignment could be used to define intersubject correspondency more precisely. It would be natural then to use a cortex patch, instead of a spherical voxel cluster, as a multivariate searchlight.

Conclusion

We argued that hi-res fMRI activity patterns can form the basis of solid empirical neuroscience even if they (1) do not accurately represent neuronal activity patterns, (2) are very noisy in single voxels, (3) are complex and fine-grained making them difficult to interpret and correct for multiple comparisons, and (4) do not match up between subjects. The four challenges can be met by abstracting from the regional fine-scale activity patterns themselves and instead asking how well they distinguish the experimental conditions. We can study the information carried by neuronal response patterns as reflected in the fMRI patterns, even if we forgo claims about the precise spatial structure of the neuronal activity patterns. Techniques of information-based, locally multivariate analysis, which have recently gained momentum in the analysis of standard-resolution fMRI data, can serve this purpose and will be crucial if hi-res fMRI is to fulfill its promise. Conceptually, information-based analysis targets the information a region carries, rather than its overall level of activation. Using standard imaging with activation-based analysis, we look at functional regions as black boxes and try to determine their level of involvement in a given component function. Hi-res fMRI with information-based analysis can help us look into the regions and illuminate their representational content.

Appendix

Choosing voxel size: are 2-mm voxels special?

The definition of hi-res fMRI in terms of voxels ≤ (2 mm)³ is essentially arbitrary, but appears useful at present, because (2 mm)³ voxels are still rarely used, although they are widely available to users of 3T scanners. Voxels of 2-mm width may sample the cortical ribbon without unreasonable loss of contrast caused by partial-volume effects, because the cortical thickness varies between 2 and 4 mm. In addition, voxel volumes just below (2 mm)³ have been suggested (Bodurka et al. 2007, see also Hyde et al. 2001) as a good choice at 3T in terms of the functional contrast-to-noise ratio (FCNR): Increasing voxel volume reduces the contribution of thermal and scanner noise. However, above about (2 mm)³, physiological noise dominates, so further reduction of thermal and scanner noise yields diminishing returns in terms of the FCNR (Fig. 1b, green curve). For very small voxels, on the other hand, thermal and scanner noise dominate and severely affect the FCNR. Recent standard-resolution studies probing orientation information in early visual cortex (Kamitani & Tong 2005, Haynes & Rees 2005) show that larger voxels (3-mm width, isotropic in both studies) can reflect columnar-level information. This could reflect a low spatial-frequency component in the selectivity maps or the way the venous vasculature samples the columnar-scale activity patterns.

Defining activation- and information-based fMRI analysis

By “activation” we mean the overall spatially averaged activity of a functional region. Activation-based analysis, then, determines whether a region becomes active as a whole. By contrast, information-based analysis determines whether a region’s activity pattern changes across experimental conditions. A change of activity pattern implies that the region carries information about the experimental condition. Clearly activation of a region as a whole also conveys information about the experimental conditions. In this sense, activation is a special case of information and information-based analysis is more general than activation-based analysis. Conversely, determining whether a region carries information is based on activity – albeit the activity pattern, not the overall average activity called “activation”.

With these complications in mind, we refer to an analysis as “information-based” if it meets the following two loose criteria: (1) An analysis is information-based if it is aimed at determining whether there is a statistical dependency (i.e. mutual information) between experimental condition and multivoxel spatiotemporal fMRI signal. Demonstrating a dependency does not require information-theoretic quantification. A significant test result on any effect statistic indicates a dependency between the experimental condition and the multivariate response. In many cases actual estimation of the mutual information (e.g. Kraskov et al. 2004) may not be the optimal method of detecting it, because the number of time points available is too small in relation to the number of voxels (i.e. multivariate dimensions). Functional MRI typically does not allow more than about 100 separate experimental events per run and provides no more than a few hundred time points. Restrictive assumptions can help by focusing sensitivity on a neuroscientifically motivated subclass of dependencies. For example, the cited studies all restrict the analysis to information in the spatial structure of the activity patterns, averaging over their temporal structure.⁵ This brings us to the second loose criterion defining information-based analysis: (2) The assumptions should not be too restrictive. For example, activation-based approach reduces a high-dimensional space of possible effects to a single dimension: the average across all voxels of a local cluster. This approach is a very successful when activation of whole regions is the sole target of the analysis. However, when such a small subset of all possible multivariate effects is targeted by an analysis, we do not refer to it as information-based.

The meanings of decoding, prediction and classification

Decoding

A particular form of information-based analysis is multivariate decoding. Decoding refers to the reading out of representational content from measured activity. The term decoding presupposes that something is encoded in the activity, that there is a neural code. Decoding, thus, implies a functional interpretation: that the activity serves to represent some mental content (Dennett 1987).

Prediction

A popular more general concept in neuroimaging analyses is “prediction”. Conventionally prediction denotes the foretelling of a future event based on a past event. By definition, then, (1) prediction proceeds forward in time and (2) the predicted event lies in the future relative to the act of prediction. The way the term is used in the neuroimaging literature is inconsistent with both of these criteria.

In neuroimaging, “prediction” usually denotes guessing the experimental condition (e.g. which stimulus has been presented) from the activity pattern or from a region’s overall activation. However, the “predicted” experimental condition occurs earlier in time and is the cause of the brain activity and subsequent hemodynamic response. This is like seeing a puddle and “predicting” that it must have rained. “Postdiction” might be a more appropriate term. Moreover, whether experimental conditions are “predicted” from brain activity or vice versa, the act of “prediction” is performed after the occurrence of the predicted events: in data analysis after the scanning session.

Why is it called “prediction”? The way the term is used in neuroimaging often relates purely to the temporal order, in which experimental information is revealed in an imaginary game: “I’ll give you the fMRI data and you are to predict the experimental-condition sequence, which I will reveal to you only later.” Because of these complications, we usually prefer the more general concept of “classification” to that of “prediction”.

Differences between the classification approach and conventional linear modeling

How does a “predictive” or classification approach to fMRI analysis relate to more conventional linear modeling based on an experimental design matrix? The difference that defines the classification approach is that it uses independent training and test data sets. The training data are used to fit the parameters of the classifier. The test data serve to determine the prediction accuracy and its statistical significance. In conventional linear modeling, by contrast, a single data set is used to estimate parameters and model the variability of those estimates for hypothesis testing. The statistical inference usually relies on assumptions (e.g. normal, uncorrelated errors).⁶ In this respect, the classification approach has an advantage: If classification accuracy (based on a truly independent test data sets) serves to demonstrate an effect, then the assumptions of the model are implicitly tested along with the effect of interest. Incorrect assumptions, in a classification approach, will cause false negatives, not false positives.⁷

Most examples of classification in fMRI studies (including Haxby et al. 2001, Cox & Savoy 2003, Carlson et al. 2003, Mitchell et al. 2004, Hanson et al. 2004, Polyn et al. 2005, Kamitani & Tong 2005, Haynes & Rees 2005, LaConte et al. 2005, and Mourao-Miranda et al. 2005) differ in two more respects from linear regression as conventionally applied in fMRI analysis. First, usually the experimental conditions are “predicted” from brain activity. The analysis, thus, proceeds in reverse to conventional linear regression, where activity is modeled using “predictors” based on the experimental design. However, the direction that the model operates in does not have any implications for a causal interpretation⁸ and either classification or conventional linear modeling could be performed in either direction in principle.⁹ Second, conventional linear modeling in fMRI relates multiple design time courses to a single voxel at a time (massively univariate multiple linear regression), whereas most classification approaches in the literature so far use multiple voxels as input to infer the experimental condition. The classification approach does not require using multiple voxels (for an example, see Pessoa & Padmala 2006), but it greatly benefits from the combination of evidence from multiple voxels. Conversely univariate linear regression could be replaced by the classical method of multivariate linear regression to relate multiple design time courses to multiple voxel time courses.¹⁰

The common feature: tests of statistical dependency

Whether a classification approach (with independent test data) or a single-data-set linear modeling approach is taken, and whether the model operates from experimental conditions to brain activity or in reverse, and whether multiple voxels are considered jointly or separately, all that is demonstrated in each case is a statistical dependency between brain activity and experimental design (or some other covariate, e.g. from behavior). The direction that the model operates in does not have any neuroscientific implications – unless temporal precedence is used to infer the direction of causality (Roebroeck et al. 2005), which isn’t the case in any of the cited studies using information-based approaches. That the direction of “prediction” has no implications for the interpretation is obvious when univariate regression is used to relate a single activity time course to a single covariate. It also holds when the model relates multiple design time courses to multiple activity time courses in either direction.

Moreover, “predictability” of experimental conditions from the data has no neuroscientific implications beyond the statistical dependency also demonstrated in a conventional linear-regression t test. Didactically, the concept of “predictability” works well, because the power to predict is an impressive concrete consequence of a statistical dependency. But this didactical advantage comes at the cost of falsely suggesting directionality and perhaps something more beyond a mere statistical effect. An activity difference between two experimental conditions (as tested by a conventional t test) necessarily implies that the experimental condition can be predicted from the activity (classification approach) with some accuracy greater than chance. Thus, the title of every fMRI study revealing an effect of experimental condition on brain activity (i.e. the vast majority of fMRI studies) could legitimately be changed to claim that the mental state associated with each condition can be predicted from measured brain activity.

The crucial factor in information-based analysis

It is not the classification approach or the common reversal of the direction of modeling or the notion of “prediction” associated with both that lends information-based fMRI analysis its power. The crucial advantage, instead, consists in the joint consideration of multiple voxels. Neuroscientifically, this is motivated by the concept of a spatially extended macropopulation code. Statistically, combining evidence across voxels can greatly enhance sensitivity, capitalizing on one of the great strengths of fMRI: the large number of measurement channels.

Prediction as a test of a causal model of brain function

In other scientific fields, such as weather forecasting, prediction involves a causal model of the temporal evolution of a system. Prediction of the future from the past, then, suggests that the model accurately captures some aspect of the system dynamics. In neuroscience, such prediction could involve a computational model of neuronal dynamics. An activity pattern measured at a given time would be used to predict a later activity pattern or behavior by simulating neuronal dynamics. We are not aware of any example of such prediction in the neuroimaging literature (but see Friston et al. 2003 for a related development). Rather “prediction” in neuroimaging has been used as a particular method of demonstrating a statistical dependency, where the algorithm for prediction (the classifier) is not thought of as a model of brain function.

Patchy organization, or noise?

Hi-res fMRI is likely to become a standard tool for studying the functional organization intrinsic to cortical areas. Cortical patterns of neuronal selectivity have generally been accommodated under the model of columnar organization (e.g. Mountcastle 1978) and are sometimes described as a “patchy organization”. The concept of “patchy organization” is intriguing, because patchiness suggests randomness, the very opposite of organization. The only obvious order in such patterns is that neighboring units exhibit similar selectivity. Such patterns of representation are plausible from the perspective of computational theory: A patchy organization could arise phylo- or ontogenetically through self-organization processes (e.g. Kohonen 1982). Such processes and the resulting maps are informed by a pronounced random element and locally correlated responses.

However, distinguishing patchy maps accurately reflecting the functional organization from patchy maps arising from measurement noise is not trivial. The feature of local clustering, which defines patchy patterns, is not very helpful in distinguishing them from noise: Local clustering can be caused by artefactual local correlation arising at the level of MR image construction and at the level of the hemodynamic response (Kriegeskorte et al., submitted). Hi-res fMRI will may tend to produce fine-grained somewhat patchy patterns of false positives, so there is a danger of mistaking noise for neuronal organization. If a valid inferential mapping is performed (correctly handling multiple comparisons and serial autocorrelation), we should be in control of false positives. However, in some published work, authors appear to be satisfied with less stringent criteria, perhaps because of challenges (2) and (3) described above.

Another way to assess whether a patchy selectivity pattern reflects neuronal organization, is to replicate its precise structure in the same subject (e.g. Cheng et al. 2001, Beauchamp et al. 2004). This requires an assessment of whether the similarity between the test and retest pattern is significant. Information-based analysis, which essentially provides formal tests of pattern replicability, can be helpful here. If patterns turn out to be replicable and distinct, this indicates neuronal pattern information about the experimental condition, which will be the essential finding in many studies (e.g. Kamitani & Tong 2005). Correct visualization of the neuronal activity pattern at high resolution is an independent further challenge that will often require prior assumptions about the patterns expected (e.g. complementarity), as well as imaging and analysis techniques that are customized for the brain region studied (e.g. Cheng et al. 2001).