Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Jan 1.
Published in final edited form as: J Biomech. 2007 Jul 19;40(15):3381–3388. doi: 10.1016/j.jbiomech.2007.05.008

Side-artifact errors in yield strength and elastic modulus for human trabecular bone and their dependence on bone volume fraction and anatomic site

Grant Bevill 1, Sarah K Easley 1, Tony M Keaveny 1,2
PMCID: PMC2099450  NIHMSID: NIHMS34225  PMID: 17659290

Abstract

In the context of reconciling the mechanical properties of trabecular bone measured from in vitro mechanical testing with the true in situ behavior, recent attention has focused on the “side-artifact” which results from interruption of the trabecular network along the sides of machined specimens. The objective of this study was to compare the magnitude of the side-artifact error for measurements of elastic modulus vs. yield stress and to determine the dependence of these errors on anatomic site and trabecular micro-architecture. Using a series of parametric variations on micro-CT-based finite element models of trabecular bone from the human vertebral body (n=24) and femoral neck (n=10), side-artifact correction factors were quantified as the ratio of the side-artifact-free apparent mechanical property to the corresponding property measured in a typical experiment. The mean (± SD) correction factors for yield stress were 1.32 ± 0.17 vs. 1.20 ± 0.11 for the vertebral body and femoral neck (p < 0.05), respectively, and the corresponding factors for modulus were 1.24 ± 0.09 vs. 1.10 ± 0.04 (p < 0.0001). Correction factors were greater for yield stress than modulus (p < 0.003), but no anatomic site effect was detected (p > 0.29) after accounting for variations in bone volume fraction (BV/TV). Approximately 30–55% of the variation in the correction factors for modulus and yield stress could be accounted for by BV/TV or micro-architecture, representing an appreciable systematic component of the error. Although some scatter in the correction factor-BV/TV relationships may confound accurate correction of modulus and yield stress for individual specimens, side-artifact correction is nonetheless essential for obtaining accurate mean estimates of modulus and yield stress for a cohort of specimens. We conclude that appreciation and correction for the differential effects of the side-artifact in modulus vs. yield stress and their dependence on BV/TV may improve the interpretation of measured elastic and failure properties for trabecular bone.

Keywords: cancellous bone, finite element modeling, bone quality, bone biomechanics, bone strength

Introduction

The elastic and strength properties of trabecular bone are widely studied due to their relevance in understanding structure-function relations, as well as their role in the pathophysiology of aging, disease, and treatment. These properties are typically obtained from experimental testing (Carter and Hayes, 1977) or finite element modeling (Homminga et al., 2003; Van Rietbergen et al., 1995) of excised specimens of trabecular bone. However, these measures all contain an unavoidable artifact due to the loss of connectivity at the periphery of the excised specimen, termed the “side-artifact” (Ün et al., 2006). Since the side-artifact is a connectivity-mediated mechanism (Andrews et al., 2001; Onck et al., 2001; Ün et al., 2006; Zhu et al., 1994), it may affect measures of strength differently than elastic modulus due to failure mechanisms such as large deformation bending and buckling (Bevill et al., 2006; Gibson, 1985), and may also depend on volume fraction or anatomic site for the same reasons. Understanding how the side-artifact affects measures of elastic modulus vs. strength and devising methods to correct for this artifact should therefore improve interpretation of biomechanical tests and may improve the fidelity of finite element models used to study whole-bone (Cody et al., 1999; Crawford et al., 2003; Homminga et al., 2001; Keyak et al., 2001) and bone-implant behavior (Huiskes and Chao, 1983; Keaveny and Bartel, 1995; Skinner et al., 1994).

The side-artifact mechanistically depends on trabecular spacing (or cell size in cellular foams) (Onck et al., 2001; Ün et al., 2006), and can result in underestimation of elastic modulus by as much as 50% in human vertebral bone (Ün et al., 2006). However, several fundamental questions remain unanswered. First, for human trabecular bone, errors due to the side-artifact have only been quantified for low-density anatomic sites. Theoretical analysis suggests that side-artifact errors should be less significant in high-density bone (Ün et al., 2006), but such predictions are confounded by the associated changes in micro-architecture with changing bone volume fraction (Hildebrand et al., 1999) as well as potential differences between anatomic site (Morgan et al., 2003). Second, side-artifact errors have only been quantified for elastic modulus in trabecular bone. However, interruption of connectivity and loss of lateral support at the sides of excised specimens (Fig. 1) could augment errors in measurements of failure properties (relative to elastic behavior) by facilitating local buckling or large bending deformations. The differences between elastic and failure behavior have previously been examined using cellular solid analysis (Onck et al., 2001) and experiment on metallic foams (Andrews et al., 2001), where it was found that errors in elastic modulus were greater than those for ultimate strength in cellular materials that fail by plastic hinging. While the differing failure mechanisms between trabecular bone and metallic foams make it difficult to extrapolate these results to human trabecular bone, they nonetheless highlight the importance of distinguishing between elastic and failure behavior in the context of side-artifact errors.

Figure 1.

Figure 1

Open in a new tab

Longitudinal cross-section (0.22 mm thick) of a core of vertebral trabecular bone with BV/TV = 0.16. The circled region at the right of the image illustrates a structure with complete loss of vertical connectivity due to the side-artifact. The circled region at the left of the image highlights a trabecula that has lost lateral support, but retained vertical load-bearing capacity. Such a structure may result in greater side-artifact errors in post-elastic measurements (e.g. yield and ultimate) than in elastic measurements due to large-deformation bending or buckling.

The overall goal of this study was to address the role of anatomic site and bone volume fraction on the side-artifact error and also the issue of differential errors for elastic modulus vs. yield stress and strain. Since quantification of side-artifact errors would be difficult in an experimental setting, we used experimentally-validated high-resolution finite element models. Focusing on human trabecular bone from the femoral neck and vertebral body, given the relevance of these sites to osteoporotic fracture and their combined wide range of bone volume fraction and architecture, our specific objectives were to: 1) compare the magnitude of the side-artifact errors for modulus vs. yield stress; 2) determine the dependence of these errors on bone volume fraction, micro-architecture, and anatomic site; and 3) establish a technique to correct for side-artifact errors in trabecular bone of any volume fraction. This study is unique in that it is the first to compare side-artifact errors for measurements of elastic modulus vs. yield stress for trabecular bone from multiple human anatomic sites.

Methods

Thirty-four “on-axis” (Morgan and Keaveny, 2001) cylindrical cores of human trabecular bone (14.4–17.3 mm long, ~8.2 mm diameter) were taken from L4 vertebral bodies (n=24 cadavers, BV/TV = 0.11 ± 0.04, age = 75 ± 13) and femoral necks (n=10 cadavers, BV/TV = 0.20 ± 0.40, age = 73 ± 11). A three-dimensional high-resolution image was obtained for each specimen using micro-CT scanning (Scanco μCT 20; Scanco Medical AG, Basserdorf, Switzerland) with an in-plane voxel dimension of 21 μm and out-of-plane dimension of 22 μm. Standard micro-architectural metrics were then measured from these images, including mean trabecular separation (Tb.Sp*, where * denotes a 3-dimensional measure made using a distance-transformation method), mean trabecular thickness (Tb.Th*), mean trabecular number (Tb.N*), degree of anisotropy (DA), connectivity density (CD) (Odgaard and Gundersen, 1993), and structure model index (SMI) (Hildebrand and Ruegsegger, 1997).

The effect of the side-artifact on apparent mechanical properties was assessed using a previously reported “inner-core” technique (Ün et al., 2006). Briefly, two concentric images were created directly from the micro-CT scan of each specimen—an 8 mm diameter core and an “inner” 6 mm diameter core—which were converted into voxel-based finite element meshes. Fully nonlinear (material and geometric) finite element analysis was conducted for each model to 1% compressive strain using roller-type boundary conditions. All tissue was assigned an isotropic elastic modulus of 18.5 GPa and a Poisson’s ratio of 0.3, and was modeled using a finite plasticity material model (Papadopoulos and Lu, 1998; Papadopoulos and Lu, 2001). Tension-compression asymmetry was included in the element via pseudo-kinematic hardening, and tissue level yield strains (compression = 0.81%, tension = 0.33%) were taken from a previous study (Bevill et al., 2006).

Apparent-level mechanical properties, with and without the presence of the side-artifact, were computed as follows. From the finite element analysis of the 8 mm core, mechanical properties were measured by only post-processing the tissue comprising the inner 6 mm diameter. It has been verified that the tissue comprising an inner core of this size is free from edge artifacts (Ün et al., 2006). Thus, the apparent properties derived from this inner core were considered to be free of the side-artifact, termed here as “true” or “in situ” properties. Next, finite element analysis was performed for only the inner 6 mm core by separating it from the 8 mm core and compressing it to 1% strain using the same roller-type boundary conditions as for the 8 mm models. Artifacts were present at the sides of these 6 mm specimens (since the entire cross-sectional area was used in post-processing), and thus the corresponding mechanical properties included the side-artifact error (referred to as “measured” or “in vitro” properties). In total, 68 finite element analyses were conducted using a highly scalable, implicit parallel finite element framework (Olympus, (Adams et al., 2004)) on a Cray-Dell PowerEdge Xeon cluster supercomputer (Dell, Round Rock, Texas). Model sizes ranged from 2.6–24.8 million elements, and the total CPU time for the analyses was approximately 53,953 hours.

The apparent mechanical properties were determined from standard analysis of the apparent stress-strain curve of each specimen using the 0.2% offset method. A separate correction factor (α) was determined for modulus, yield stress, and yield strain for each specimen, defined by the ratio of the true (artifact-free) to measured (with-artifact) property:

αE=EtrueEmeasured,ασ=σytrueσymeasured, and αε=εytrueεymeasured.

The correction factors for modulus and yield stress were compared for each anatomic site using a two-tailed paired Student’s t-test. Unpaired Student’s t-tests were performed to determine if separate correction factors were required for vertebral and femoral neck trabecular bone. Multivariate regression analyses (JMP, Version 5.0, SAS Institute Inc., Cary, NC) were performed on the correction factors for modulus, yield stress, and yield strain using bone volume fraction (BV/TV), anatomic site, and all micro-architectural measures as variates. These analyses served to elucidate the mechanisms of the side-artifact error and to establish the independent role of anatomic site after accounting for differences in micro-architecture and BV/TV.

Finally, we developed two techniques for correcting side-artifact errors in modulus and yield stress. In the first approach, the measured value of modulus or yield stress for each specimen was corrected by the mean value of the corresponding correction factor for that anatomic site. In the second approach, the measured properties were scaled by a specimen-specific value of α obtained from the corresponding regression of αE or ασ vs. BV/TV. Analysis of covariance (ANCOVA) and an overall test for coincidence (Glantz, 2002) were performed for the linear regressions of αE and ασ vs. BV/TV to determine whether separate regressions were required for each anatomic site.

Results

The side-artifact resulted in substantial differences between the true (artifact-free) and measured (with-artifact) elastic and yield properties for all specimens. The true stress-strain curve typically exhibited a larger elastic modulus (Fig. 2), and additional effects were observed for the post-elastic behavior in which the measured stress-strain curves exhibited premature yielding and softening relative to the true curves.

Figure 2.

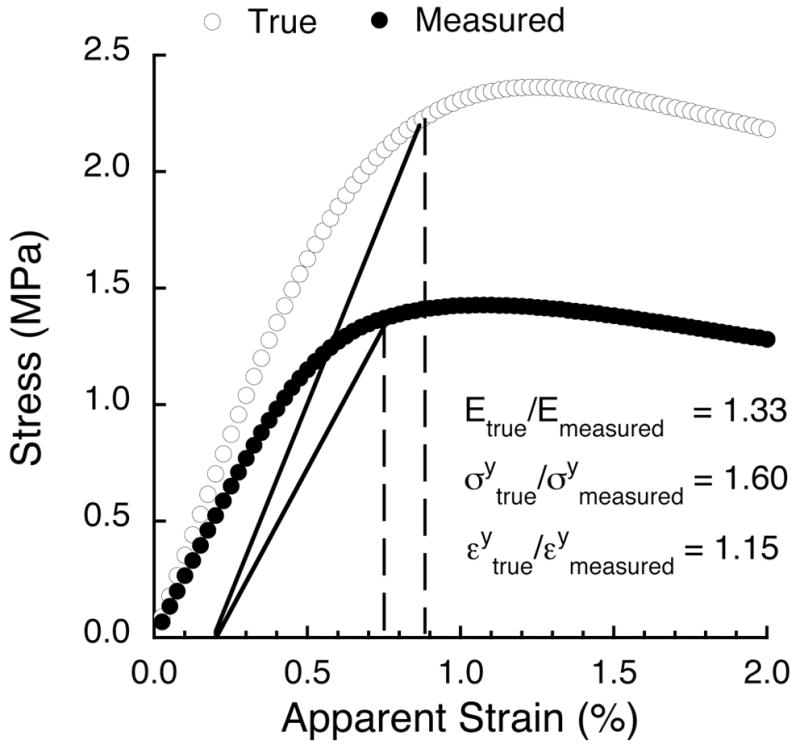
Figure 2

Open in a new tab

True (i.e. side-artifact-free) and measured stress-strain curves for the same specimen of vertebral trabecular bone (BV/TV = 0.08) loaded in compression to 2.0% strain. The correction factor for elastic modulus was 1.33 and increased to 1.60 for yield stress. The correction factor for yield strain was 1.15.

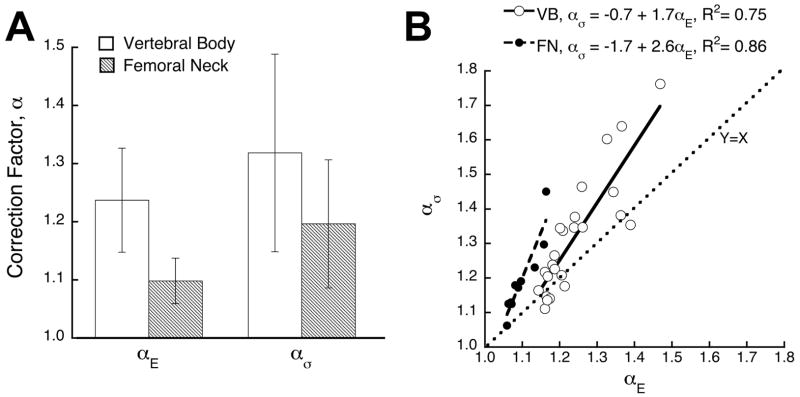
Without accounting for BV/TV, the correction factors depended significantly on anatomic site (modulus, p < 0.0001; yield stress, p = 0.045). The mean (± SD) correction factors for elastic modulus (αE ) were 1.24 ± 0.09 and 1.10 ± 0.04 for the vertebral body and femoral neck, respectively, and the corresponding correction factors for yield stress measurement (ασ ) were 1.32 ± 0.17 and 1.20 ± 0.11 (Fig. 3A). Within anatomic site, ασ was significantly greater than αE (Fig. 3B, vertebral body: p = 0.0006, femoral neck: p = 0.003). The correction factor for yield strain (αε) did not depend on anatomic site (p = 0.37) and had a mean value of 1.05 ± 0.05.

Figure 3.

Figure 3

Open in a new tab

(A) Mean values of the correction factor for modulus and yield stress for each anatomic site. Across anatomic site, the correction factors were significantly greater for vertebral vs. femoral neck trabecular bone both for modulus (p < 0.0001) and yield stress (p=0.045). (B) Linear regression of ασ versus αE. Intercepts were significantly different between anatomic site (p = 0.006, ANCOVA), but slopes were not (p = 0.16).

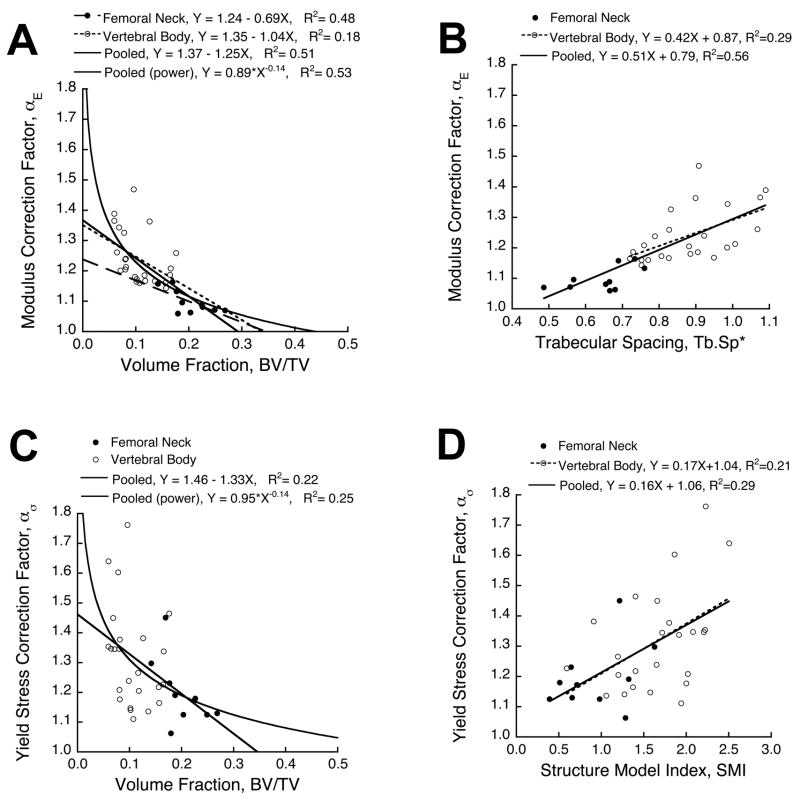
Correction factors did not depend on anatomic site after accounting for variations in BV/TV. ANCOVA indicated that neither the intercept nor slope depended on anatomic site for the linear regressions of αE vs. BV/TV (p > 0.24) and ασ vs. BV/TV (p > 0.84). This was confirmed by an overall test for coincidence, which showed that the pooled linear regressions were statistically equivalent to the site-specific regressions (Fig. 4A, C). The stepwise linear multiple regression analysis indicated that Tb.Sp* was the only significant predictor of αE (Fig. 4B, p < 0.0001, R2 = 0.56), SMI was the only significant predictor of ασ (Fig. 4D, p = 0.001, R2 = 0.29), and anatomic site was not a significant predictor of either correction factor (p > 0.84). The correction factor for yield strain was largely random, having no dependence on BV/TV (p = 0.86), and weak dependence on Tb.Th* (p = 0.04, R2 = 0.12).

Figure 4.

Figure 4

Open in a new tab

(A) Correction factor for elastic modulus as a function of bone volume fraction. The linear regressions for each site had statistically equivalent slopes and intercepts (p > 0.24, ANCOVA), indicating that anatomic site did not contribute to the side-artifact error after accounting for differences in BV/TV. The pooled data set was also well-described by a power law relationship. (B) Trabecular spacing was the only significant predictor of the correction factor for elastic modulus from stepwise multiple regression (p < 0.0001). (C) Correction factor for yield stress as a function of BV/TV. ANCOVA indicated that anatomic site did not significantly contribute to the correction factor for yield stress after accounting for differences in BV/TV (p = 0.84). (D) Stepwise multiple regression analysis showed that structure model index was the only significant predictor of the correction factor for yield stress (p = 0.001).

The comparisons of αE and ασ within and across anatomic site (Fig. 3) dictated that four distinct correction factors be used in the first technique for adjusting the measured values of modulus and yield stress (equations given in Table 1). The second correction technique used the pooled regressions for αE and ασ vs. BV/TV based on the results from the ANCOVA. Both correction techniques performed well at adjusting the measured values of modulus and yield stress into agreement with the true values (Table 2), although the specimen-specific techniques tended to have lower errors than did the constant correction technique. Within the specimen-specific techniques, the power law relationship performed as well as or better than the linear relationship for the pooled and vertebral body data, but tended to slightly over-predict modulus for the femoral neck bone (p = 0.06).

Table 1.

Constant, linear, and power law equations used for side-artifact corrections (VB = vertebral body, FN = femoral neck). The constants ‘A’ and ‘B’ represent the coefficients in the constant, linear, and power law equations as Ecorrect = A * Emeasured, Ecorrect = (A * BV/TV + B) * Emeasured, and Ecorrect = (A * BV/TVB ) * Emeasured, respectively. Values given in parentheses represent standard errors for the estimates.

Correction Technique Anatomic Site Measure (MPa) Equation Coefficients:
A B
Constant VB E 1.24 (0.02) NA
σy 1.32 (0.03) NA
Constant FN E 1.10 (0.01) NA
σy 1.20 (0.03) NA
Linear Pooled E −1.25 (0.21) 1.37 (0.03)
σy −1.33 (0.44) 1.46 (0.06)
Power Pooled E 0.89 (0.01) −0.14 (0.02)
σy 0.95 (0.02) −0.14 (0.04)
Open in a new tab

Table 2.

Comparison of techniques (constant, linear, power law, and no correction) used for correcting measured values of modulus and yield stress. Percent error and paired t-test are calculated for corrected vs. true (side-artifact-free) values. Slope (m), intercept (b), and coefficient of determination (R2) are reported for the linear regression of true vs. corrected values.

Correction Technique Anatomic Site Measure (MPa) Percent Error (mean ± S.D.) p-value (paired t-test) Linear fit: (vs. True values)
m b R2
None Pooled E −15.9 ± 6.7 < 0.001 1.04 85.8 > 0.99
σy −20.9 ± 9.1 < 0.001 1.10 0.6 0.99
VB E −18.8 ± 5.5 < 0.001 1.12 49.2 0.99
σy −23.0 ± 9.0 < 0.001 1.14 0.4 0.96
FN E −8.8 ± 3.2 < 0.001 1.03 90.8 > 0.99
σy −15.8 ± 7.1 < 0.001 1.07 0.8 0.99
Constant Pooled E 0.4 ± 6.0 0.11 0.97 15.4 > 0.99
σy 1.3 ± 10.9 0.09 0.93 0.2 0.99
VB E 0.5 ± 6.8 0.15 0.90 49.2 0.99
σy 1.5 ± 11.9 0.17 0.87 0.4 0.96
FN E 0.1 ± 3.5 0.47 0.94 90.8 > 0.99
σy 0.7 ± 8.5 0.33 0.90 0.8 0.99
Linear Pooled E 0.8 ± 5.5 0.28 0.99 −1.6 > 0.99
σy 1.0 ± 10.3 0.52 0.98 0.0 > 0.99
VB E 0.4 ± 6.1 0.67 0.98 7.5 0.98
σy 1.4 ± 11.4 0.45 0.93 0.2 0.95
FN E 1.7 ± 3.3 0.28 1.02 −56.8 0.99
σy 0.0 ± 7.4 0.92 0.98 0.2 0.98
Power Pooled E 0.3 ± 5.2 0.42 0.98 13.7 > 0.99
σy 0.6 ± 10.0 0.57 0.97 0.1 0.99
VB E 0.3 ± 6.0 0.68 1.01 −3.6 0.98
σy 0.8 ± 11.1 0.74 0.95 0.2 0.95
FN E 13.4 ± 5.8 0.06 0.98 0.5 > 0.99
σy 0.1 ± 7.5 0.65 0.95 0.5 0.99
Open in a new tab

Discussion

The results from this study demonstrate the need for separate side-artifact correction factors for yield stress and modulus measurements but show that, after accounting for bone volume fraction effects, anatomic site per se is not important. Unlike other artifacts in trabecular bone testing (Keaveny et al., 1997; Odgaard and Linde, 1991), side-artifact errors have an appreciable systematic component associated with BV/TV and micro-architecture and could thus directly affect the conclusions of any study involving excised trabecular bone. However, we found that errors for yield strains were small and largely random in nature. The necessity of these correction factors for yield stress and modulus is motivated by the fact that the side-artifact is an unavoidable problem that is equally present in experimental tests and finite element models of excised trabecular bone cores. Correction for the differential effects of the side-artifact in modulus vs. yield stress may have important implications regarding interpretation of elastic and failure properties, and may also help improve the fidelity of whole-bone and bone-implant finite element models.

A number of this study’s attributes support the validity of our results. First, our finite element modeling techniques have been validated against experimental data (Bevill et al., 2006) that was obtained for the same loading mode and anatomic sites as were used in the present study. All models included geometric nonlinearities, since this mechanism can appreciably affect measurements of mechanical properties for low-density bone, and also represents the primary mechanism by which the correction factors for modulus vs. yield stress differ. Second, the side-artifact error was quantified here using an inner-core technique, in which the apparent mechanical properties were measured from an artifact-free sub-region. The primary advantage of this method is that a specimen retains its in situ connectivity when measuring the side-artifact-free properties. However, this technique would be difficult to perform in a purely experimental setting given the delicate nature and substantial heterogeneity of human trabecular bone. Alternative techniques, such as confined compression (uniaxial strain) testing, may prove to be less sensitive to side-artifact errors and allow for a more representative characterization of trabecular bone properties from in vitro experimental testing, although this remains to be demonstrated.

The study limitations are mostly associated with extrapolation of our findings to other sites and different specimen geometries. Use of the correction factors for other anatomic sites requires the assumption that our trends hold for other types of trabecular bone. This assumption is likely reasonable for human bone since the vertebral and femoral trabecular bone display considerable differences in micro-architecture (Hildebrand et al., 1999) and span a large BV/TV range, yet we found no effect of anatomic site once differences in BV/TV were accounted for. However, our results may not be directly applicable to animal trabecular bone in which the BV/TV-micro-architecture relationships (particularly with respect to trabecular spacing) may differ substantially (Ding et al., 2003; Hildebrand et al., 1999). In that event, the key parameter for normalization would be mean trabecular spacing (Onck et al., 2001; Ün et al., 2006).

To adjust the correction factors reported here to larger or smaller specimens, we recommend using the theory of Ün et al. (2006) derived in the context of elastic behavior. This theory dictates that the magnitude of the correction factor is equal to the ratio of the apparent to the load-bearing cross-sectional area, in which a specimen’s trabecular spacing is the mechanistic factor that dictates the thickness of the unloaded region (approximately equal to 12·Tb.Sp∗). For example, based on the mean Tb.Sp* for the specimens in this study (0.81 mm), the correction factor for an 8 mm cylindrical specimen would be 7% less than the factor for an otherwise identical 6 mm specimen (i.e. α8 mm = 0.93 · α6 mm). We suggest that such a conversion should apply equally to the correction factors for yield stress, since no theory currently exists to account for the finite deformation effects that influence errors in strength beyond elastic modulus in trabecular bone. This effect of specimen size on the side-artifact error is an important caveat for previous studies that have compared elastic or strength properties from specimens of different size, since the properties measured from smaller specimens should be underestimated relative to the properties from larger specimens. A final caveat applies to the application of side-artifact correction to measures of modulus and yield stress from individual specimens. Scatter about the regressions between correction factor vs. BV/TV or micro-architecture (R2 ranging from about 0.22–0.55) may confound accurate correction of modulus and yield stress for individual specimens, particularly at low volume fractions. Nonetheless, side-artifact correction is essential for obtaining accurate mean estimates of modulus and yield strength for a cohort of specimens relative to in situ behavior (Figure 5, Table 2).

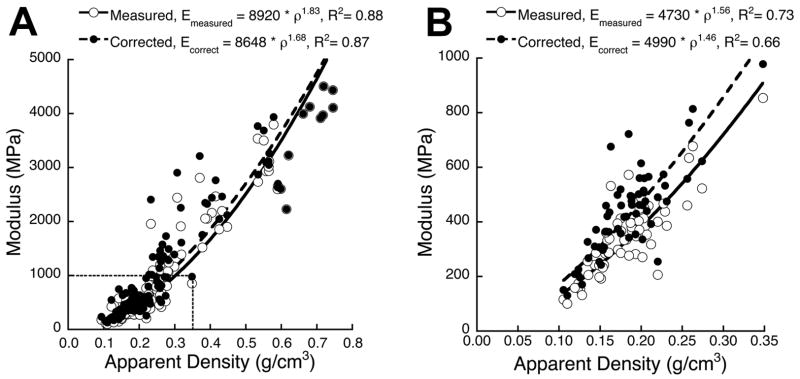
Figure 5.

Figure 5

Open in a new tab

Side-artifact correction (linear regression from Fig. 4A used assuming a constant tissue density of 2.0 g/cc) applied to the modulus-density data reported by Morgan et al. (2003). Side-artifact correction resulted in a substantial increase in modulus for data (A) pooled across multiple anatomic sites and (B) the vertebral body, but did not appreciably change the overall trends of the power law regressions. These data suggest that side-artifact correction can be very important for correcting the magnitude of modulus or yield stress, but may not change the interpretation of results when comparing structure-function relationships across groups (e.g. anatomic site or treatment).

While some previous studies have examined side-artifact errors in elastic modulus vs. ultimate strength for cellular solids and metallic foams (Andrews et al., 2001; Onck et al., 2001), the results from the current study provide insight into the applicability of such results to trabecular bone. For example, the theory of Onck et al. (2001) predicts elastic modulus correction factors of approximately 1.21 for vertebral trabecular bone (Tb.Sp* ranging from 70–110 μm) and 1.15 for femoral neck trabecular bone (Tb.Sp* ranging from 50–75 μm), which compare very well with our results. However, the correction factors for ultimate strength are lower than those for modulus (approximately 1.12 and 1.09, respectively), which highlights the importance of tissue-level deformation and failure mechanisms in the post-elastic behavior of the side-artifact and suggests that side-artifact errors in elastic modulus are only architecture-dependent, while those for strength may also be highly dependent on tissue material properties.

One of the most important and practical implications of the side-artifact concerns the mechanistic fidelity of whole-bone finite element models. To date, the only (preliminary) study to implement a side-artifact correction (Crawford et al., 2004) demonstrated that increasing the modulus and strength of the trabecular bone in models of human vertebrae by a constant factor of 28% brought strength predictions into statistical absolute agreement (Y=X) with experimental measures. It remains to be seen if these results hold up for larger studies and for different whole bones such as the proximal femur. The importance of the differential correction in modulus vs. yield stress is also unknown, as is the need to correct for BV/TV effects (as opposed to using a constant correction factor per site).

The results of this study may also have implications regarding assays of bone quality. For example, the structural efficiency at which trabecular bone carries load can be quantified by its strength-density relationship, in which bone with higher strength at a given density is more efficient at carrying load and might therefore be considered to be of higher biomechanical “quality” (Hernandez and Keaveny, 2006). However, the correlation between BV/TV and the side-artifact error for yield stress directly affects this measure of quality, whereby correction for the side-artifact would cause an increase in the strength-to-density ratio for low-density bone relative to high-density bone. Furthermore, if disease alters micro-architecture independently of BV/TV, then side-artifact errors may also affect non-normal bone differently than healthy bone. For these reasons, minimization of the effects of side-artifacts may be required to appropriately characterize—or even detect—the potentially subtle effects of treatment, aging, or disease on aspects of bone quality associated with trabecular micro-architecture.

Acknowledgments

Funding for this work was provided by grants from the National Institute of Health (AR43784 and AR49828). Cadaveric material was obtained from the NDRI and UCSF Willed Body Program. Super-computing resources were obtained from the National Partnership for Advanced Computational Infrastructure (NPACI UCB254 and UCB266). Micro-CT scanning was performed at Magnetic Resonance Science Center, University of California at San Francisco, under direction of Dr. Sharmila Majumdar. Dr. Keaveny has a financial interest in O.N. Diagnostics and both he and the company may benefit from the results of this research.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Adams MF, Bayraktar HH, Keaveny TM, Papadopoulos P. Ultrascalable implicit finite element analyses in solid mechanics with over a half a billion degrees of freedom. ACM/IEEE Proceedings of SC2004: High Performance Networking and Computing.2004. [Google Scholar]
  2. Andrews EW, Gioux G, Onck P, Gibson LJ. Size effects in ductile cellular solids. Part II: experimental results. International Journal of Mechanical Sciences. 2001;43(3):701–713. [Google Scholar]
  3. Bevill G, Eswaran SK, Gupta A, Papadopoulos P, Keaveny TM. Influence of bone volume fraction and architecture on computed large-deformation failure mechanisms in human trabecular bone. Bone. 2006 doi: 10.1016/j.bone.2006.06.016. In Press. [DOI] [PubMed] [Google Scholar]
  4. Carter DR, Hayes WC. The compressive behavior of bone as a two-phase porous structure. Journal of Bone and Joint Surgery. 1977;59-A:954–962. [PubMed] [Google Scholar]
  5. Cody DD, Gross GJ, Hou FJ, Spencer HJ, Goldstein SA, Fyhrie DP. Femoral strength is better predicted by finite element models than QCT and DXA. J Biomech. 1999;32(10):1013–20. doi: 10.1016/s0021-9290(99)00099-8. [DOI] [PubMed] [Google Scholar]
  6. Crawford RP, Brouwers J, Keaveny TM. Accurate Prediction of Vertebral Strength using Voxel-Based Non-Linear Finite Element Models. Trans Ortho Res Soc. 2004;29:1123. [Google Scholar]
  7. Crawford RP, Cann CE, Keaveny TM. Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone. 2003;33(4):744–50. doi: 10.1016/s8756-3282(03)00210-2. [DOI] [PubMed] [Google Scholar]
  8. Ding M, Day JS, Burr DB, Mashiba T, Hirano T, Weinans H, Sumner DR, Hvid I. Canine cancellous bone microarchitecture after one year of high-dose bisphosphonates. Calcif Tissue Int. 2003;72(6):737–44. doi: 10.1007/s00223-002-2066-6. [DOI] [PubMed] [Google Scholar]
  9. Gibson LJ. The mechanical behavior of cancellous bone. Journal of Biomechanics. 1985;18(5):317–328. doi: 10.1016/0021-9290(85)90287-8. [DOI] [PubMed] [Google Scholar]
  10. Glantz SA. Primer of Biostatistics. McGraw-Hill; New York: 2002. [Google Scholar]
  11. Hernandez CJ, Keaveny TM. A biomechanical perspective on bone quality. Journal of Bone and Mineral Research. 2006 doi: 10.1016/j.bone.2006.06.001. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hildebrand T, Laib A, Müller R, Dequeker J, Rüegsegger P. Direct three-dimensional morphometric analysis of human cancellous bone: microstructural data from spine, femur, iliac crest, and calcaneus. Journal of Bone and Mineral Research. 1999;14(7):1167–74. doi: 10.1359/jbmr.1999.14.7.1167. [DOI] [PubMed] [Google Scholar]
  13. Hildebrand T, Ruegsegger P. Quantification of Bone Microarchitecture with the Structure Model Index. Comput Methods Biomech Biomed Engin. 1997;1(1):15–23. doi: 10.1080/01495739708936692. [DOI] [PubMed] [Google Scholar]
  14. Homminga J, McCreadie BR, Weinans H, Huiskes R. The dependence of the elastic properties of osteoporotic cancellous bone on volume fraction and fabric. J Biomech. 2003;36(10):1461–7. doi: 10.1016/s0021-9290(03)00125-8. [DOI] [PubMed] [Google Scholar]
  15. Homminga J, Weinans H, Gowin W, Felsenberg D, Huiskes R. Osteoporosis changes the amount of vertebral trabecular bone at risk of fracture but not the vertebral load distribution. Spine. 2001;26(14):1555–61. doi: 10.1097/00007632-200107150-00010. [DOI] [PubMed] [Google Scholar]
  16. Huiskes R, Chao EYS. A survey of finite element analysis in orthopedic biomechanics: The first decade. Journal of Biomechanics. 1983;16:385–409. doi: 10.1016/0021-9290(83)90072-6. [DOI] [PubMed] [Google Scholar]
  17. Keaveny TM, Bartel DL. Mechanical consequences of bone ingrowth in a hip prosthesis inserted without cement. Journal of Bone and Joint Surgery American Volume. 1995;77-A:911–923. doi: 10.2106/00004623-199506000-00012. [DOI] [PubMed] [Google Scholar]
  18. Keaveny TM, Pinilla TP, Crawford RP, Kopperdahl DL, Lou A. Systematic and random errors in compression testing of trabecular bone. Journal of Orthopaedic Research. 1997;15:101–110. doi: 10.1002/jor.1100150115. [DOI] [PubMed] [Google Scholar]
  19. Keyak JH, Rossi SA, Jones KA, Les CM, Skinner HB. Prediction of fracture location in the proximal femur using finite element models. Med Eng Phys. 2001;23(9):657–64. doi: 10.1016/s1350-4533(01)00094-7. [DOI] [PubMed] [Google Scholar]
  20. Morgan EF, Bayraktar HH, Keaveny TM. Trabecular bone modulus-density relationships depend on anatomic site. J Biomech. 2003;36(7):897–904. doi: 10.1016/s0021-9290(03)00071-x. [DOI] [PubMed] [Google Scholar]
  21. Morgan EF, Keaveny TM. Dependence of yield strain of human trabecular bone on anatomic site. Journal of Biomechanics. 2001;34(5):569–577. doi: 10.1016/s0021-9290(01)00011-2. [DOI] [PubMed] [Google Scholar]
  22. Odgaard A, Gundersen HJ. Quantification of connectivity in cancellous bone, with special emphasis on 3-D reconstructions. Bone. 1993;14(2):173–82. doi: 10.1016/8756-3282(93)90245-6. [DOI] [PubMed] [Google Scholar]
  23. Odgaard A, Linde F. The underestimation of Young's modulus in compressive testing of cancellous bone specimens. Journal of Biomechanics. 1991;24(8):691–698. doi: 10.1016/0021-9290(91)90333-i. [DOI] [PubMed] [Google Scholar]
  24. Onck PR, Andrews EW, Gibson LJ. Size effects in ductile cellular solids. Part I: modeling. International Journal of Mechanical Sciences. 2001;43(3):681–699. [Google Scholar]
  25. Papadopoulos P, Lu J. A general framework for the numerical solution of problems in finite elasto-plasticity. Computer Methods in Applied Mechanics and Engineering. 1998;159(1–2):1–18. [Google Scholar]
  26. Papadopoulos P, Lu J. On the formulation and numerical solution of problems in anisotropic finite plasticity. Computer Methods in Applied Mechanics and Engineering. 2001;190(37–38):4889–4910. [Google Scholar]
  27. Skinner HB, Kim AS, Keyak JH, Mote CD. Femoral prosthesis implantation induces changes in bone stress that depend on the extent of porous coating. Journal of Orthopaedic Research. 1994;12(4):553–563. doi: 10.1002/jor.1100120412. [DOI] [PubMed] [Google Scholar]
  28. Ün K, Bevill G, Keaveny TM. The Effects of Side-Artifacts on the Elastic Modulus of Trabecular Bone. Journal of Biomechanics. 2006;39(11):1955–63. doi: 10.1016/j.jbiomech.2006.05.012. [DOI] [PubMed] [Google Scholar]
  29. Van Rietbergen B, Weinans H, Huiskes R, Odgaard A. A new method to determine trabecular bone elastic properties and loading using micromechanical finite element models. Journal of Biomechanics. 1995;28(1):69–81. doi: 10.1016/0021-9290(95)80008-5. [DOI] [PubMed] [Google Scholar]
  30. Zhu M, Keller TS, Spengler DM. Effects of specimen load-bearing and free surface layers on the compressive mechanical properties of cellular materials. Journal of Biomechanics. 1994;27(1):57–66. doi: 10.1016/0021-9290(94)90032-9. [DOI] [PubMed] [Google Scholar]

RESOURCES