Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Jan 1.
Published in final edited form as: J Biomech. 2007 Jul 5;40(15):3424–3431. doi: 10.1016/j.jbiomech.2007.05.013

A COMPUTATIONAL ASSESSMENT OF THE INDEPENDENT CONTRIBUTION OF CHANGES IN CANINE TRABECULAR BONE VOLUME FRACTION AND MICROARCHITECTURE TO INCREASED BONE STRENGTH WITH SUPPRESSION OF BONE TURNOVER

Senthil K Eswaran 1, Matthew R Allen 2, David B Burr 2, Tony M Keaveny 1,3
PMCID: PMC2099452  NIHMSID: NIHMS34227  PMID: 17618634

Abstract

This study addressed the effects of changes in trabecular microarchitecture induced by suppressed bone turnover — including changes to the remodeling space — on the trabecular bone strength-volume fraction characteristics independent of changes in tissue material properties. Twenty female beagle dogs, aged 1–2 years, were treated daily with either oral saline (n=10 control) or high doses of oral risedronate (0.5 mg/kg/day, n=10 suppressed) for a period of one year, the latter designed (and confirmed) to substantially suppress bone turnover. High-resolution micro-CT based finite element models (18-micron voxel size) of canine trabecular bone cores (n=2 per vertebral body) extracted from the T-10 vertebrae were analyzed in both compressive and torsional loading cases. The same tissue-level material properties were used in all models, thus providing measures of tissue-normalized strength due only to changes in the microarchitecture. Suppressed bone turnover resulted in more plate-like architecture with a thicker and more dense trabecular structure, but the relationship between the microarchitectural parameters and volume fraction was unaltered (p>0.05). Though the suppressed group had greater tissue-normalized strength as compared to the control group (p<0.001) for both compressive and torsional loading, the relationship between tissue-normalized strength and volume fraction was not significantly altered for compression (p>0.13) or torsion (p>0.09). In this high-density, non-osteoporotic animal model, the increases in tissue-normalized strength seen with suppression of bone turnover were entirely commensurate with increases in bone volume fraction and thus, no evidence of microarchitecture-related or “stress-riser” effects which may disproportionately affect strength were found.

Keywords: Trabecular bone, Bone strength, Suppressed bone turnover, Antiresorptive treatment, Microarchitecture, Bone quality, Stress risers

INTRODUCTION

It has been hypothesized that geometric changes to the remodeling space through bone turnover suppression-induced inhibition of trabecular perforation (Riggs and Melton, 2002), changes in microarchitecture and filling in of resorption cavities (Parfitt, 2002) may together reduce theorized “stress-riser” effects associated with remodeling cavities, thus strengthening the bone. Biomechanically, the effects of any such changes in trabecular bone quality can be quantified by analysis of the relationship between measures of biomechanical performance — such as strength — and bone density or bone volume fraction (Hernandez and Keaveny, 2006). However, because suppression of bone turnover results in simultaneous changes to the trabecular microarchitecture, mineralization, and/or collagen cross-linking (Boivin et al., 2000; Borah et al., 2004; Ding et al., 2003; Burr et al., 2003), it is difficult to quantify the independent effects on strength due only to microarchitectural changes. Understanding the contribution of suppression-induced changes in trabecular bone volume fraction and microarchitecture towards increased bone strength independent of tissue material properties may lead to improved means of evaluating treatment efficacy by providing insight into the biomechanical mechanisms by which antiresorptive treatments substantially reduce clinical fracture risk (Cummings et al., 2002; Delmas, 2000).

While the effects of suppressed bone turnover on the mineralization and the organic component of the trabecular tissue, and trabecular microarchitecture have been investigated through a number of clinical (Boivin et al., 2000; Borah et al., 2004; Borah et al., 2005; Roschger et al., 2001) and pre-clinical studies (Allen et al., 2006a; Allen et al., 2006b; Day et al., 2004; Ding et al., 2003; Ito et al., 2005; Mashiba et al., 2001; Muller et al., 2004), the independent contribution of suppression-induced microarchitectural changes alone to the improved mechanical properties remain unclear. Analysis of simulated microarchitectural changes have shown that inhibition of trabecular perforation (Guo and Kim, 2002; Riggs and Melton, 2002) and filling in of the remodeling space (Hernandez et al., 2006; Parfitt, 2002) may have a disproportionate effect on trabecular bone strength compared to the accompanying changes in bone volume fraction, particularly for low-density bone. It is also possible that the biomechanical effects of suppression-induced architectural changes may be sensitive to the loading mode, e.g. compression vs. torsion, since there is evidence that the failure mechanisms in trabecular bone depend on the loading mode (Niebur et al., 2002). Predominantly torsional loading, which can occur during non-habitual activities, would result in increased bending of trabeculae (Fenech and Keaveny, 1999), an effect that may accentuate strength changes due to alterations in microarchitecture and the remodeling space.

Our overall goal was to investigate the independent contribution of bone turnover suppression-induced changes to trabecular bone volume fraction and microarchitecture on bone strength by eliminating any changes to the tissue material properties. Given the dearth of large-animal models with trabecular bone volume fraction comparable to that of elderly human vertebral bone (Table 1), we analyzed trabecular bone cores taken from canine vertebrae from an ongoing animal experiment using high-resolution finite element modeling to gain early insight into this issue. Specifically, our objectives were to determine the effect of suppression of bone turnover by high-dose risedronate treatment on: 1) the trabecular microarchitecture-volume fraction relationships; and 2) the strength-volume fraction characteristics for both compressive and torsional loading. This study is unique in its focus on the mechanical consequences of suppression-induced microarchitectural changes and its use of fully nonlinear micro-CT based finite element models for strength predictions in two different loading modes.

Table 1.

Comparison of architectural parameters between various animal models and human trabecular bone obtained from vertebral bodies (Mean ± SD).

Sample Size BV/TV Tb.Sp. (mm) Tb. Th. (mm)
Canine (Ding et al., 2003) 11 0.22 ± 0.03 0.41 ± 0.06 0.099 ± 0.011
OVX Monkey (Muller et al., 2004) 13 0.26 ± 0.05 0.32 ± 0.06 0.111 ± 0.015
Sheep (Lill et al., 2002) 16 0.27 ± 0.09 0.37 ± 0.06 0.11 ± 0.04
Human (Ulrich et al., 1999) 58 0.08 ± 0.02 0.80 ± 0.13 0.123 ± 0.016
Open in a new tab

METHODS

Details of the experimental design have been published previously (Allen et al., 2006a). Twenty-four female beagle dogs, aged 1–2 years, were randomly assigned to two weight-matched groups — control and suppressed (turnover). Because some bone had been used for preliminary studies, only twenty of the dogs were available for the current study. X-rays obtained prior to the start of the study confirmed that the vertebral growth plates were closed. The control group (n=10 animals) was given oral saline and the suppressed group (n=10 animals) was given oral risedronate (0.5 mg/kg/day) daily for a period of one year and both groups were then sacrificed. This dosage of risedronate is five-fold higher than the clinical dose used to treat post-menopausal osteoporosis, is equivalent to the dose used to treat Paget’s disease, and, was chosen to ensure maximal suppression of bone turnover. Previously published data obtained from the second lumbar vertebrae of these same dogs showed that the activation frequency was 84% lower (p<0.0001) in the suppressed bone compared to the control bone (Allen et al., 2006a), confirming that the treatment substantially suppressed bone turnover.

The T-10 vertebral bodies obtained from the harvested dogs were scanned with micro-CT at 18 μm voxel size (Scanco 80, Basserdorf, Switzerland). An automated adaptive threshold algorithm (provided as part of the scanner) was used to select a global specimen-specific threshold to segment bone from any surrounding material. Two cylindrical cores (diameter = 3.5 mm, height = 6 mm nominal dimensions) were virtually removed from each scan such that the basivertebral foramen and the cortex were avoided (Figure 1). To satisfy the continuum assumption for analysis of trabecular bone, the minimum dimension is recommended to be greater than five trabecular spacings (Harrigan et al., 1988). For example, in human vertebral bone, the mean trabecular spacing is approximately 0.8 mm (Ulrich et al., 1999), so a 4 mm dimension is required to satisfy the continuum assumption. Since the mean trabecular spacing of canine bone is only about 0.4 mm (Ding et al., 2003), the continuum assumption requires a minimum specimen size of 2 mm. Visual inspection of the canine vs. human specimens confirms these calculations (Figure 2). The microarchitectural properties of the trabecular bone cores were determined from the segmented 3-D image data (Scanco; Scanco Medical AG, Basserdorf, Switzerland). Trabecular bone volume fraction (BV/TV), structural model index (SMI), connectivity density (CD), degree of anisotropy (DA), bone surface density (BS/BV), mean and SD of trabecular thickness (Tb. Th.), trabecular spacing (Tb. Sp.) and trabecular number (Tb. N) were calculated (Hildebrand et al., 1999).

Figure 1.

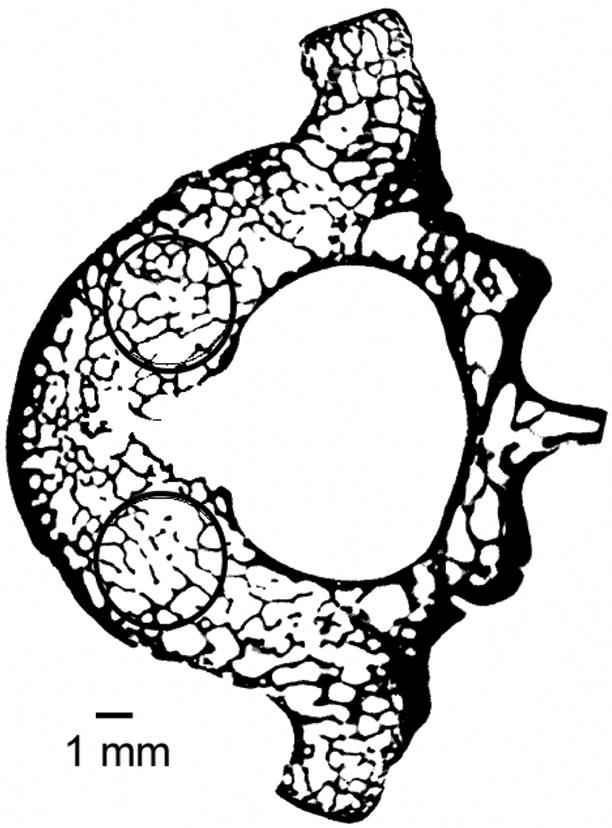
Figure 1

Open in a new tab

Mid-transverse slice from a canine vertebral body (scanned at 18-micron voxel size) shows the location of the cylindrical trabecular bone cores obtained such that the basivertebral foramen and the cortical shell were avoided.

Figure 2.

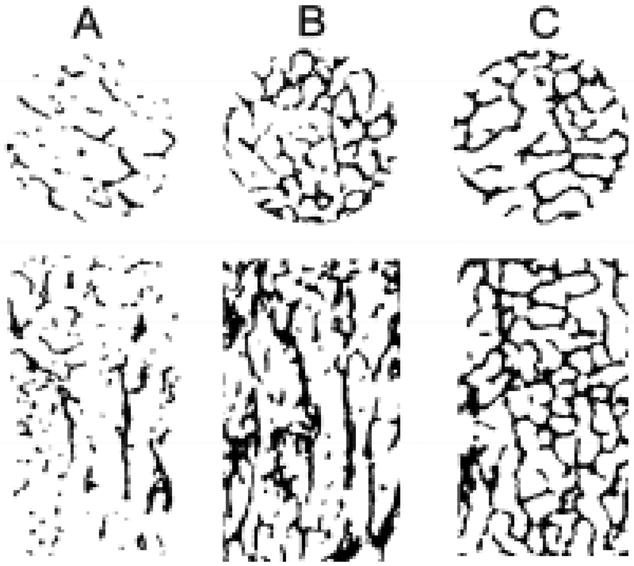
Figure 2

Open in a new tab

Transverse and vertical slices of cylindrical cores from (A) human vertebral body, (B) human femoral neck and (C) canine vertebral body showing that the canine cylindrical cores satisfies the continuum assumption. The specimen diameters for the human vertebral body (d=8 mm), human femoral neck (d=8 mm) and canine vertebral body (d=3.5 mm) were scaled to the same size for visual comparison.

To ensure that any observed changes in predicted strength were due only to changes in microarchitecture, the same tissue-level elastic and yield properties — a Young’s modulus of 18.5 GPa, Poisson’s ratio of 0.3, and tensile and compressive yield strains of 0.33% and 0.81%, respectively (Bevill et al., 2006) — were assigned to all specimens in both the control and suppressed groups. Using custom code with a parallel mesh partitioner and multigrid solver (Adams et al., 2004), two fully nonlinear finite element analyses — including material and geometric non-linearities (Bevill et al., 2006) — were performed on each model (n=80 total) using both compressive and torsional apparent loading. Each model had approximately 4 million degrees of freedom and analyses were run on an IBM-SP4 supercomputer (Datastar, San Diego) using 24 processors, requiring a total of approximately 12,000 CPU hours. This analysis technique has been previously validated for human trabecular bone (Bevill et al., 2006).

From the finite element analyses, apparent level strength (0.2% offset yield stress) was calculated for compression and torsional loading (Ford and Keaveny, 1996; Nádai, 1950). Since the predicted strength was independent of changes in the tissue material properties, this strength measure will be referred to as tissue-normalized strength. As expected, we found that the tissue-normalized strength was linearly correlated with bone volume fraction and this linear relation had a non-zero intercept. As a result, the slope of the relationship between tissue-normalized strength and volume fraction was different from the ratio of tissue-normalized strength to volume fraction (Hernandez and Keaveny, 2006). The ratio of tissue-normalized strength to volume fraction represents a measure of the structural efficiency of the bone (Hernandez and Keaveny, 2006), since for a given volume fraction, bone having a higher ratio of tissue-normalized strength to volume fraction will have higher strength. Thus, the strength-volume fraction characteristics were quantified by both the linear relationship between tissue-normalized strength and volume fraction, and the ratio of tissue-normalized strength to volume fraction.

Statistical analyses were performed to test for effects of suppressed bone turnover on the trabecular microarchitecture and tissue-normalized strength. A restricted maximum likelihood (REML) test was used in order to account for the replicate samples (n=2) taken from each specimen by including the specimen ID as a random effect (JMP, Version 5.0, SAS Institute Inc., Cary, NC). The treatment group and the specimen ID were the explanatory variables in the statistical comparison of the mean values of the microarchitectural parameters, tissue-normalized strength and the ratio of tissue-normalized strength to volume fraction between the control and suppressed groups. The microarchitecture- and tissue-normalized strength-volume fraction relationships (slope and intercept) of the control and suppressed groups were compared using the REML test with bone volume fraction, treatment group (corresponds to a change in the intercept), specimen ID and cross product between bone volume fraction and treatment group (corresponds to a change in the slope) as explanatory variables. The lower p-value among those for slope and intercept differences is reported. All statistical analyses were done separately for compression and torsion loading cases.

RESULTS

Suppression of bone turnover was associated with a more plate-like architecture having thicker and more dense trabecular structure. These changes were consistent with what would be expected in normal (control) bone of a higher volume fraction since the relationship between the microarchitectural parameters and volume fraction was not significantly different (p>0.05) between the control and suppressed groups (Table 2).

Table 2.

Comparison of architectural parameters between the control and turnover-suppressed groups (Mean ± SD, n=20 in each group).

Control Suppressed % Diff. ** p-value (Mean Values) † p-value (Arch.-BV/TV Relation) ††
BV/TV 0.20 ± 0.03 0.24 ± 0.01 23.9 <0.0001*
SMI 0.60 ± 0.32 0.21 ± 0.15 −65.2 0.0021* >0.26
Tb.Th (mm) 0.080 ± 0.007 0.091 ± 0.005 13.7 0.0005* >0.50
Tb.Sp (mm) 0.38 ± 0.03 0.36 ± 0.03 −7.4 0.04* >0.90
Tb.N 2.68 ± 0.26 2.86 ± 0.18 6.8 0.09 >0.67
BS/BV (mm−1) 29.6 ± 3.1 25.0 ± 1.3 −15.7 0.0002* >0.14
CD (mm−3) 35.8 ± 8.6 29.0 ± 5.1 −18.9 0.04* _‡
DA (Primary) 1.33 ± 0.08 1.32 ± 0.05 −0.5 0.82 _‡
DA (Secondary) 1.11 ± 0.06 1.08 ± 0.05 −2.2 0.29 _‡
DA (Tertiary) 1.20 ± 0.06 1.22 ± 0.04 1.7 0.29 _‡
Tb.Th.SD (mm) 0.024 ± 0.003 0.026 ± 0.002 7.3 0.11 _‡
Tb.Sp.SD (mm) 0.114 ± 0.007 0.108 ± 0.011 −5.4 0.13 >0.06
Tb.(1/N).SD 0.131 ± 0.006 0.124 ± 0.012 −6.0 0.07 >0.12
Open in a new tab
*

p<0.05 indicates statistically significant difference between the control and suppressed groups after accounting for replicate samples from each vertebral body.

**

Percent difference calculated with respect to the control means.

†

p-value for testing statistical change in mean values due to suppressed bone turnover

††

p-value for testing statistical difference in the microarchitecture-volume fraction relation (i.e. slope and intercept) for parameters that have a significant correlation with volume fraction. Lower p-value among the p-values for the slope and intercept differences is reported.

‡

The microarchitectural parameter did not have a statistically significant correlation with bone volume fraction.

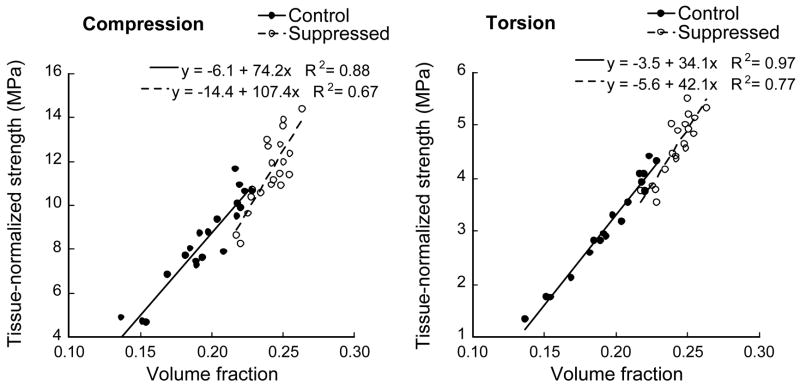
As with microarchitecture, changes in tissue-normalized strength seen with suppressed bone turnover were consistent with those expected with natural variations in bone volume fraction. The (linear) relationship between tissue-normalized strength and volume fraction (both slope and intercept) was not statistically different between the control and suppressed groups (Figure 3) for either compression (p>0.13) or torsion (p>0.09) load cases even though tissue-normalized strength increased much more on a percentage basis than did volume fraction (Table 3).

Figure 3.

Figure 3

Open in a new tab

Suppression-induced architectural changes did not significantly alter the relationship between tissue-normalized strength and volume fraction for either compression (p>0.13) or torsion (p>0.09) load cases.

Table 3.

Comparison of the finite element-predicted mechanical properties and bone volume fraction between the control and turnover-suppressed groups (Mean ± SD, n=20 in each group).

Control Suppressed % Difference† p-value*
Volume fraction, BV/TV 0.20 ± 0.03 0.24 ± 0.01 23.9 <0.0001
Compression:
 Tissue-normalized strength [MPa] 8.4 ± 2.1 11.5 ± 1.6 37.7 0.0009
 Tissue-normalized strength/(BV/TV) [MPa] 42.4 ± 5.9 47.6 ± 5.0 9.7 0.04
Torsion:
 Tissue-normalized strength [MPa] 3.1 ± 0.9 4.6 ± 0.6 46.0 0.0004
 Tissue-normalized strength/(BV/TV) [MPa] 15.7 ± 2.8 18.9 ± 1.7 20.0 0.0054
Open in a new tab
*

p<0.05 indicates statistically significant difference in the mean values of the control and suppressed groups after accounting for replicate samples from each vertebral body.

†

Percent difference calculated with respect to the control means.

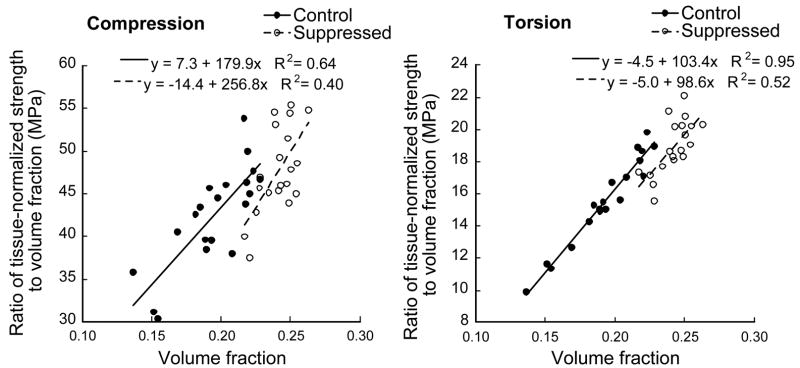
As a result of the natural dependence of the ratio of tissue-normalized strength to volume fraction (Figure 4), the mean value of this ratio for the suppressed group was significantly higher than that of the control group for both compression and torsion load cases (Table 3). The ratio of tissue-normalized strength to volume fraction depended (p<0.05) on volume fraction for both the control and suppressed groups, and for both loading modes.

Figure 4.

Figure 4

Open in a new tab

Variation of tissue-normalized strength:volume fraction ratio with volume fraction for the compression (Left) and torsion (Right) load cases.

DISCUSSION

The goal of this study was to investigate how changes in the canine trabecular bone volume fraction and microarchitecture induced by suppression of bone turnover affected the strength of trabecular bone independent of alterations in tissue material properties. The models, by design, eliminated any possible changes in hard tissue properties from affecting these comparisons, thus providing measures of tissue-normalized strength. We found no evidence of any increases in tissue-normalized strength with suppression of bone turnover that were not commensurate with the increases in bone volume fraction, and no evidence of any stress-riser effects. Thus, while there may be subtle differences between the control and suppressed bone in terms of microarchitecture, suppression of bone turnover did not fundamentally alter the trabecular microarchitecture- or tissue-normalized strength-volume fraction relations. As the bone increases in volume fraction, the ratio of tissue-normalized strength to volume fraction increases naturally. As a result, the higher mean ratio of tissue-normalized strength to volume fraction observed for the suppressed group was a direct consequence of the natural dependence of this ratio on bone volume fraction. Taken together, these results indicate that there were no appreciable microarchitecure-related bone quality effects — as defined in the context of this study — associated with suppression of bone turnover in this animal model.

A major feature of this analysis is that we quantified the biomechanical effects due only to changes in the trabecular microarchitecture, a technique that can also be applied to small-animal models provided the minimum dimension of the trabecular specimen satisfies the continuum assumption (Harrigan et al., 1988). We extended the technique utilized by Day et al. (Day et al., 2004) to isolate the effects of suppression-induced microarchitectural changes from any alterations in tissue material properties. The latter issue — including the effect of suppressed bone turnover on the mineralization and organic component of the trabecular tissue (Boivin et al., 2000; Burr et al., 2003; Roschger et al., 2001) — was not addressed in this analysis and it is possible that interactions between microarchitecture and tissue material properties could exist. Another notable feature was our use of two loading modes — compression and torsion — to test whether the effects of suppressed bone turnover depended on the choice of the loading mode. We had hypothesized that the biomechanical effects associated with the filling of remodeling cavities (Storm et al., 1993) might be accentuated for torsional loading, but no such effects were detected. A third important feature was our use of fully-nonlinear finite element analysis — previously validated for human trabecular cores (Bevill et al., 2006) — for our strength predictions.

One notable caveat of this study was the use of a non-osteoporotic, high-bone volume fraction animal model. Due to their low baseline estrogen levels, these dogs do not lose substantial trabecular bone with ovariectomy (Shen et al., 1992) and thus were not ovariectomized. There could be inherent differences in the physiological responses of canine and human bone. The high bone volume fraction and associated plate-type architecture in this model could affect the degree of response. For example, because of the relatively high bone volume fraction (0.20 ± 0.03) of the control specimens as compared to human vertebral bone (Figure 5), certain failure mechanisms such as large deformation bending (Bevill et al., 2006) or buckling (Gibson, 1985; Stolken and Kinney, 2003) may not be manifested in such a model (Bevill et al., 2006). Comparison of the trabecular microarchitectural parameters of different large-animal models shows a complete lack of large-animal models with trabecular bone volume fraction or trabecular spacing comparable to that of elderly human vertebral bone (Table 1). Care should be taken therefore, in extrapolating these results, or those from any current large-animal models, to elderly humans. For eventual clinical applications concerning the role of treatment-induced microarchitectural changes, one critical challenge will be to develop large-animal models having bone volume fraction and microarchitecture characteristics more akin to elderly human trabecular bone.

Figure 5.

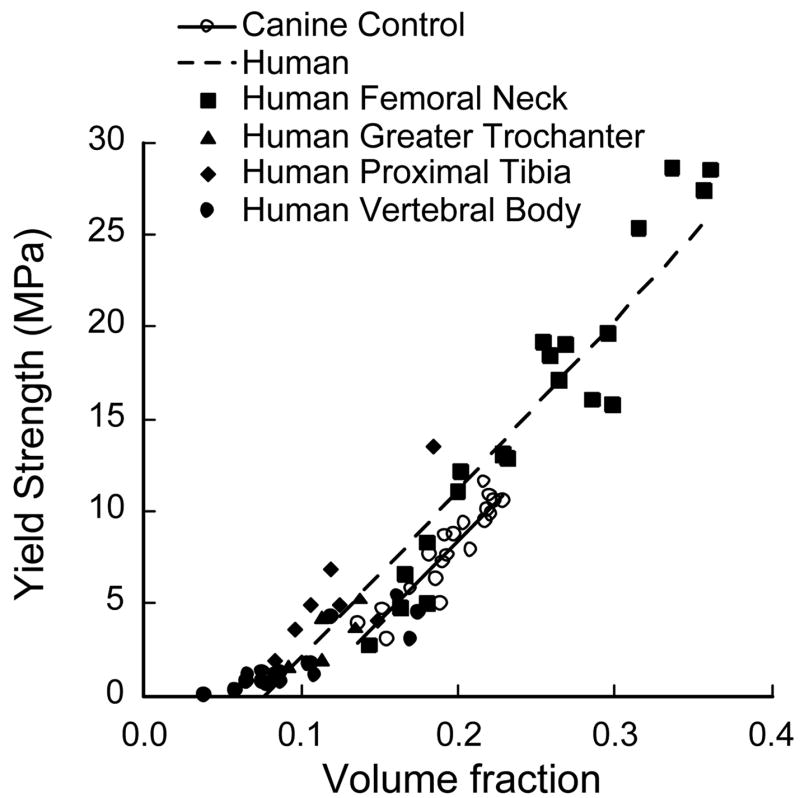
Figure 5

Open in a new tab

Comparison of finite element predicted strength-volume fraction characteristics of human and canine trabecular bone indicating that canine control bone volume fraction was comparable to that of human femoral neck bone. Previously published data on human trabecular bone is presented here (Bevill et al., 2006).

One numerical technical issue was the possibly limited spatial resolution of the finite element models as compared to the physical scale of the remodeling cavities. Since the reduction in resorption depth reported in humans with antiresorptive treatment is on the order of 10 microns (Storm et al., 1993), use of finite element models with a voxel size of 18 microns may have obscured the detection of real effects. Use of linear 8-noded elements might also obscure the modeling of large stress gradients over the scale of a few elements. Despite these limitations, evidence from a nonlinear analysis that we performed of a single individual trabecula having a resorption cavity showed that both the stress distribution as well as the overall strength predicted by a 20-micron model compared well with the outcomes of a 2-micron model (Figure 6). Moreover, strength predictions from finite element models of human vertebral trabecular bone cores (with voxel size of 20-micron) were well-correlated with experimental strength measurements (Bevill et al., 2006). These results suggest that the voxel size of 18 microns was sufficient to capture any differences in finite element-predicted strength between the control and suppressed groups in this study.

Figure 6.

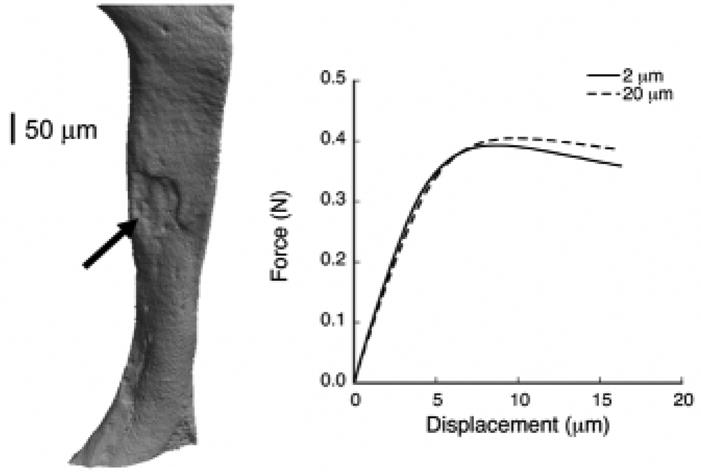
Figure 6

Open in a new tab

Left: “Nano-CT” 3D scan of an individual trabecula (480 nm resolution) obtained from a human vertebral body showing the presence of a resorption cavity (arrow). Right: Force-displacement curves at 2-μm and 20-μm for compressive loading of the individual trabecula showing that the coarse model with a 20-μm voxel size accurately captures the strength behavior predicted by the 2-μm model.

Our results are largely consistent with previous studies on similar canine models (Day et al., 2004; Ding et al., 2003). Though the specific values of architectural parameters and their change with suppressed bone turnover differ, the overall trends in these parameters were consistent with those reported by Ding et al. (Ding et al., 2003) except for connectivity density. Previous studies have reported that plate perforations without loss of trabecular elements tend to artificially increase connectivity (Borah et al., 2004), and this may explain why the connectivity density for the control bone tended to be higher than the suppressed bone in this study. The trends in architectural changes due to suppressed bone turnover are also consistent with previous clinical (Borah et al., 2004) and pre-clinical (Ito et al., 2005; Muller et al., 2004) studies which have shown that antiresorptive treatment preserves the trabecular architecture.

Previous animal studies have seldom compared the strength-density relationship of control and turnover-suppressed bone. The correlation coefficient of the strength-volume fraction relation reported in this study for the control group was comparable to that reported in previous animal studies (Ito et al., 2005; Muller et al., 2004) for the control group, but differs from that of various OVX (ovariectomy) groups. For example, a computational study on rat tibiae reported that the trabecular bone strength-volume fraction relation (Ito et al., 2005) was not statistically significant for the OVX-control group. However, those analyses involved trabecular specimens (OVX-control group) that were not large enough to satisfy the continuum assumption (Harrigan et al., 1988). Another study involving ovariectomy reported that the R2 value between whole-vertebral strength and bone mineral content was much lower for the OVX-control group as compared to the sham-control group (Muller et al., 2004). This is consistent with other studies that have observed an increase in whole-vertebral strength per unit areal BMD (measured by DXA) after treatment with SERM (selective estrogen receptor modulator) raloxifene but not with the antiresorptives (Allen et al., 2006b). The changes associated with estrogen deficiency or treatments on whole-vertebral strength may be a result of treatment effects on tissue-level material properties, or could be due to higher scale effects such as differential treatment effects on cortical vs. trabecular bone or periosteal remodeling (Allen et al., 2004; Delmas, 2000). In summary, although alterations in the remodeling space may have a disproportionate effect on strength in elderly human bone, particularly if the remodeling cavities occur predominantly in regions of high tissue-level stress (Hernandez et al., 2006), we found no such microarchitecture-related effects in this high-density canine model.

Acknowledgments

Funding was provided via an unrestricted gift by Procter and Gamble Pharmaceuticals Inc., and research grants provided by National Institute of Health (AR49828, AR47838) and the Alliance for Better Bone Health. Computational resources were available through grant UCB-266 from the National Partnership for Computational Infrastructure. All the finite element analyses were performed on an IBM Power4 supercomputer (Datastar, San Diego Supercomputer Center). We would like to thank Judd Day (Exponent Inc., Philadelphia) for micro-CT imaging the specimens. We would also like to thank Dr. Sharmila Majumdar and Andrew Burghardt for performing the microarchitectural analysis on the trabecular bone cores, and Skyscan for imaging an individual trabecula using the 2011 “Nano-CT” scanner. Dr. Keaveny has a financial interest in O.N. Diagnostics and both he and the company may benefit from the results of this research.

Funding Sources: Proctor & Gamble Pharmaceuticals Inc. (Unrestricted Gift), National Institute of Health Grant AR47838, AR49828, National Partnership for Computational Infrastructure UCB-266

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Contributor Information

Senthil K. Eswaran, Email: senthilk@me.berkeley.edu.

Matthew R. Allen, Email: matallen@iupui.edu.

David B. Burr, Email: dburr@iupui.edu.

Tony M. Keaveny, Email: tmk@me.berkeley.edu.

References

  1. Adams MF, Bayraktar HH, Keaveny TM, Papadopoulos P. Ultrascalable implicit finite element analyses in solid mechanics with over a half a billion degrees of freedom. ACM/IEEE Proceedings of SC2004: High Performance Networking and Computing.2004. [Google Scholar]
  2. Allen MR, Hock JM, Burr DB. Periosteum: biology, regulation, and response to osteoporosis therapies. Bone. 2004;35:1003–1012. doi: 10.1016/j.bone.2004.07.014. [DOI] [PubMed] [Google Scholar]
  3. Allen MR, Iwata K, Phipps R, Burr DB. Alterations in canine vertebral bone turnover, microdamage accumulation, and biomechanical properties following 1-year treatment with clinical treatment doses of risedronate or alendronate. Bone. 2006a;39:872–879. doi: 10.1016/j.bone.2006.04.028. [DOI] [PubMed] [Google Scholar]
  4. Allen MR, Iwata K, Sato M, Burr DB. Raloxifene enhances vertebral mechanical properties independent of bone density. Bone. 2006b;39:1130–1135. doi: 10.1016/j.bone.2006.05.007. [DOI] [PubMed] [Google Scholar]
  5. Bevill G, Eswaran SK, Gupta A, Papadopoulos P, Keaveny TM. Influence of bone volume fraction and architecture on computed large-deformation failure mechanisms in human trabecular bone. Bone. 2006;39:1218–1225. doi: 10.1016/j.bone.2006.06.016. [DOI] [PubMed] [Google Scholar]
  6. Boivin GY, Chavassieux PM, Santora AC, Yates J, Meunier PJ. Alendronate increases bone strength by increasing the mean degree of mineralization of bone tissue in osteoporotic women. Bone. 2000;27:687–694. doi: 10.1016/s8756-3282(00)00376-8. [DOI] [PubMed] [Google Scholar]
  7. Borah B, Dufresne TE, Chmielewski PA, Johnson TD, Chines A, Manhart MD. Risedronate preserves bone architecture in postmenopausal women with osteoporosis as measured by three-dimensional microcomputed tomography. Bone. 2004;34:736–746. doi: 10.1016/j.bone.2003.12.013. [DOI] [PubMed] [Google Scholar]
  8. Borah B, Ritman EL, Dufresne TE, Jorgensen SM, Liu S, Sacha J, Phipps RJ, Turner RT. The effect of risedronate on bone mineralization as measured by micro-computed tomography with synchrotron radiation: correlation to histomorphometric indices of turnover. Bone. 2005;37:1–9. doi: 10.1016/j.bone.2005.03.017. [DOI] [PubMed] [Google Scholar]
  9. Burr DB, Miller L, Grynpas M, Li J, Boyde A, Mashiba T, Hirano T, Johnston CC. Tissue mineralization is increased following 1-year treatment with high doses of bisphosphonates in dogs. Bone. 2003;33:960–969. doi: 10.1016/j.bone.2003.08.004. [DOI] [PubMed] [Google Scholar]
  10. Cummings SR, Karpf DB, Harris F, Genant HK, Ensrud K, LaCroix AZ, Black DM. Improvement in spine bone density and reduction in risk of vertebral fractures during treatment with antiresorptive drugs. American Journal of Medicine. 2002;112:281–289. doi: 10.1016/s0002-9343(01)01124-x. [DOI] [PubMed] [Google Scholar]
  11. Day JS, Ding M, Bednarz P, van der Linden JC, Mashiba T, Hirano T, Johnston CC, Burr DB, Hvid I, Sumner DR, Weinans H. Bisphosphonate treatment affects trabecular bone apparent modulus through micro-architecture rather than matrix properties. Journal of Orthopaedic Research. 2004;22:465–471. doi: 10.1016/j.orthres.2003.05.001. [DOI] [PubMed] [Google Scholar]
  12. Delmas PD. How does antiresorptive therapy decrease the risk of fracture in women with osteoporosis? Bone. 2000;27:1–3. doi: 10.1016/s8756-3282(00)00301-x. [DOI] [PubMed] [Google Scholar]
  13. Ding M, Day JS, Burr DB, Mashiba T, Hirano T, Weinans H, Sumner DR, Hvid I. Canine cancellous bone microarchitecture after one year of high-dose bisphosphonates. Calcified Tissue International. 2003;72:737–744. doi: 10.1007/s00223-002-2066-6. [DOI] [PubMed] [Google Scholar]
  14. Fenech CM, Keaveny TM. A cellular solid criterion for predicting the axial-shear failure properties of trabecular bone. Journal of Biomechanical Engineering. 1999;121:414–422. doi: 10.1115/1.2798339. [DOI] [PubMed] [Google Scholar]
  15. Ford CM, Keaveny TM. The dependence of shear failure properties of bovine tibial trabecular bone on apparent density and trabecular orientation. Journal of Biomechanics. 1996;29:1309–1317. doi: 10.1016/0021-9290(96)00062-0. [DOI] [PubMed] [Google Scholar]
  16. Gibson LJ. The mechanical behavior of cancellous bone. Journal of Biomechanics. 1985;18:317–328. doi: 10.1016/0021-9290(85)90287-8. [DOI] [PubMed] [Google Scholar]
  17. Guo XE, Kim CH. Mechanical consequence of trabecular bone loss and its treatment: a three-dimensional model simulation. Bone. 2002;30:404–411. doi: 10.1016/s8756-3282(01)00673-1. [DOI] [PubMed] [Google Scholar]
  18. Harrigan TP, Jasty M, Mann RW, Harris WH. Limitations of the continuum assumption in cancellous bone. Journal of Biomechanics. 1988;21:269–275. doi: 10.1016/0021-9290(88)90257-6. [DOI] [PubMed] [Google Scholar]
  19. Hernandez CJ, Gupta A, Keaveny TM. A biomechanical analysis of the effects of resorption cavities on cancellous bone strength. J Bone Miner Res. 2006;21:1248–1255. doi: 10.1359/jbmr.060514. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hernandez CJ, Keaveny TM. A biomechanical perspective on bone quality. Bone. 2006;39:1173–1181. doi: 10.1016/j.bone.2006.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hildebrand T, Laib A, Müller R, Dequeker J, Rüegsegger P. Direct three-dimensional morphometric analysis of human cancellous bone: microstructural data from spine, femur, iliac crest, and calcaneus. Journal of Bone and Mineral Research. 1999;14:1167–1174. doi: 10.1359/jbmr.1999.14.7.1167. [DOI] [PubMed] [Google Scholar]
  22. Ito M, Nishida A, Aoyagi K, Uetani M, Hayashi K, Kawase M. Effects of risedronate on trabecular microstructure and biomechanical properties in ovariectomized rat tibia. Osteoporos Int. 2005;16:1042–1048. doi: 10.1007/s00198-004-1802-3. [DOI] [PubMed] [Google Scholar]
  23. Lill CA, Gerlach UV, Eckhardt C, Goldhahn J, Schneider E. Bone changes due to glucocorticoid application in an ovariectomized animal model for fracture treatment in osteoporosis. Osteoporosis International. 2002;13:407–414. doi: 10.1007/s001980200047. [DOI] [PubMed] [Google Scholar]
  24. Mashiba T, Turner CH, Hirano T, Forwood MR, Johnston CC, Burr DB. Effects of suppressed bone turnover by bisphosphonates on microdamage accumulation and biomechanical properties in clinically relevant skeletal sites in beagles. Bone. 2001;28:524–531. doi: 10.1016/s8756-3282(01)00414-8. [DOI] [PubMed] [Google Scholar]
  25. Muller R, Hannan M, Smith SY, Bauss F. Intermittent ibandronate preserves bone quality and bone strength in the lumbar spine after 16 months of treatment in the ovariectomized cynomolgus monkey. Journal of Bone and Mineral Research. 2004;19:1787–1796. doi: 10.1359/JBMR.040809. [DOI] [PubMed] [Google Scholar]
  26. Nádai A. Theory of Flow of Solids. McGraw-Hill; New York: 1950. Torsion of a round bar. The stress-strain curve in shear. [Google Scholar]
  27. Niebur GL, Feldstein MJ, Keaveny TM. Biaxial failure behavior of bovine tibial trabecular bone. Journal of Biomechanical Engineering. 2002;124:699–705. doi: 10.1115/1.1517566. [DOI] [PubMed] [Google Scholar]
  28. Parfitt AM. High bone turnover is intrinsically harmful: two paths to a similar conclusion. The Parfitt view. Journal of Bone and Mineral Research. 2002;17:1558–1559. doi: 10.1359/jbmr.2002.17.8.1558. author reply 1560. [DOI] [PubMed] [Google Scholar]
  29. Riggs BL, Melton LJ., 3rd Bone turnover matters: the raloxifene treatment paradox of dramatic decreases in vertebral fractures without commensurate increases in bone density. Journal of Bone and Mineral Research. 2002;17:11–14. doi: 10.1359/jbmr.2002.17.1.11. [DOI] [PubMed] [Google Scholar]
  30. Roschger P, Rinnerthaler S, Yates J, Rodan GA, Fratzl P, Klaushofer K. Alendronate increases degree and uniformity of mineralization in cancellous bone and decreases the porosity in cortical bone of osteoporotic women. Bone. 2001;29:185–191. doi: 10.1016/s8756-3282(01)00485-9. [DOI] [PubMed] [Google Scholar]
  31. Shen V, Dempster DW, Birchman R, Mellish RW, Church E, Kohn D, Lindsay R. Lack of changes in histomorphometric, bone mass, and biochemical parameters in ovariohysterectomized dogs. Bone. 1992;13:311–316. doi: 10.1016/8756-3282(92)90075-8. [DOI] [PubMed] [Google Scholar]
  32. Stolken JS, Kinney JH. On the importance of geometric nonlinearity in finite-element simulations of trabecular bone failure. Bone. 2003;33:494–504. doi: 10.1016/s8756-3282(03)00214-x. [DOI] [PubMed] [Google Scholar]
  33. Storm T, Steiniche T, Thamsborg G, Melsen F. Changes in bone histomorphometry after long-term treatment with intermittent, cyclic etidronate for postmenopausal osteoporosis. Journal of Bone and Mineral Research. 1993;8:199–208. doi: 10.1002/jbmr.5650080211. [DOI] [PubMed] [Google Scholar]
  34. Ulrich D, van Rietbergen B, Laib A, Ruegsegger P. The ability of three-dimensional structural indices to reflect mechanical aspects of trabecular bone. Bone. 1999;25:55–60. doi: 10.1016/s8756-3282(99)00098-8. [DOI] [PubMed] [Google Scholar]

RESOURCES