A second-generation combined linkage–physical map of the human genome

Abstract

We have completed a second-generation linkage map that incorporates sequence-based positional information. This new map, the Rutgers Map v.2, includes 28,121 polymorphic markers with physical positions corroborated by recombination-based data. Sex-averaged and sex-specific linkage map distances, along with confidence intervals, have been estimated for all map intervals. In addition, a regression-based smoothed map is provided that facilitates interpolation of positions of unmapped markers on this map. With nearly twice as many markers as our first-generation map, the Rutgers Map continues to be a unique and comprehensive resource for obtaining genetic map information for large sets of polymorphic markers.

Accurate and comprehensive linkage maps continue to be critical for linkage analyses (Daw et al. 2000; Barber et al. 2006; Fingerlin et al. 2006; Dietter et al. 2007), positional cloning projects, and even for some aspects of genome-wide association analyses (Maniatis et al. 2002; Tapper et al. 2005). Previously, we constructed the first-generation combined linkage–physical map (Rutgers Map v.1; Kong et al. 2004) containing 14,759 markers, genotyped in a mixture of CEPH (Center d’Etude du Polymorphisme Humain) (Dausset et al. 1990) and deCODE (Kong et al. 2002) families. Now, we have pooled this data set with 13,666 single-nucleotide polymorphisms (SNPs) genotyped in the CEPH reference pedigrees at the companies Applied Biosystems, Affymetrix, and Illumina. We used the pooled data to construct a second-generation combined linkage–physical map (Rutgers Map v.2), which has nearly twice the number of markers and increased marker density relative to the Rutgers Map v.1. The physical positions of 28,121 markers were corroborated by recombination-based data, making the Rutgers Map v.2, to our knowledge, the most dense and accurate linkage map of the human genome.

The Rutgers Map v.2 also provides three novel features that are not generally offered by other publicly available maps. First, we have estimated approximate 95% confidence intervals for the size of all 24,145 map intervals, both on the sex-averaged and sex-specific maps. This feature may be useful for assessing sensitivity of an analysis to map uncertainty and for combining the information in the Rutgers Map v.2 with map estimates derived from independent studies. In addition, we have applied local regression to create a smoothed version of the Rutgers Map that separates all markers by non-zero map distances. Overall, this alternative map should provide better estimates of map distance since nearly half of the map intervals in the Rutgers Map v.2, while physically distinct, show no evidence of recombination. Third, the smoothed map facilitates interpolation of map positions for markers that are not on our map. For example, a cM-scale map position can be easily estimated for any of the millions of SNP markers that have not been genotyped in the CEPH reference pedigrees and hence are not present on any of the CEPH-based linkage maps.

Results

Markers and genotype data

The new SNP data were cleaned prior to distribution for genotyping errors using a variety of approaches specific to each company (Kennedy et al. 2003; Murray et al. 2004; Affymetrix, http://www.affymetrix.com/products/arrays/specific/10k.affx; Applied Biosystems, https://products.appliedbiosystems.com/ab/en/US/adirect/ab?cmd=catProductDetail&productID=4357150C&catID=600763&backButton=true; Illumina, http://www.illumina.com/pages.ilmn?ID=162). All of the data were cleaned of non-Mendelian inheritances. Some of the data were further cleaned by identification of close double-recombination events using the CHROMPIC function in CRIMAP (Lander and Green 1987), and some of the data were cleaned of likely errors using the error-detection routine in Merlin (Abecasis et al. 2002). Therefore our PedCheck analyses detected only a negligible number of non-Mendelian transmissions, which were cleaned from the data by removal of the culprit genotypes. Furthermore, we identified 210 markers that did not show significant linkage to their respective chromosomes. In most cases, this was due to low informativeness as evidenced by having only a small number of informative meioses. The number of informative meioses varies considerably among the markers, with an average of 301, and 550 markers show >1000 informative meioses. The marker set comprises 59% SNPs, 34% STRs, 5% RFLPs, and 2% markers whose type could not be identified.

Map construction

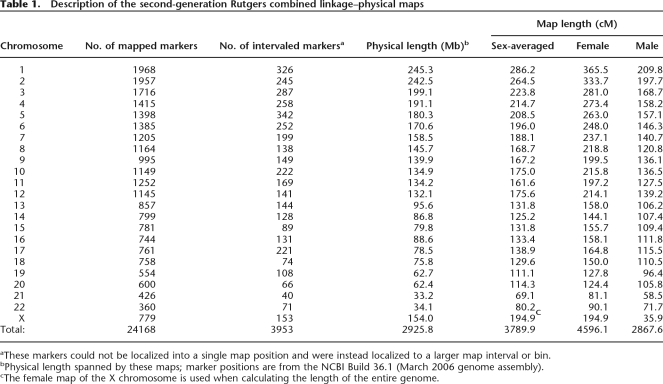
Upon completion of our mapping procedures, our Rutgers Map v.2 provided genetic map positions for 24,168 markers. The total sex-averaged map length is 3790 cM (Kosambi), with female and male map lengths of 4596 and 2867 cM, respectively (Table 1). The female map is 1.6 times as long as the male map, on average, and this size difference is consistent with previous studies. The average intermarker spacing is 117 kb and 0.16 cM. However, the average resolution increases to 0.52 cM when map intervals of length zero are excluded. Genetic map bin positions were determined for an additional 3953 markers for which unique positions could not be specifically determined. The physical position was inconsistent with the linkage-based position for 44 markers; and, for 50 markers with unknown physical positions, linkage analysis could not provide statistically significant evidence for a genetic map position. Therefore, these 94 markers were left off of the map.

Table 1.

Description of the second-generation Rutgers combined linkage–physical maps

^aThese markers could not be localized into a single map position and were instead localized to a larger map interval or bin.

^bPhysical length spanned by these maps; marker positions are from the NCBI Build 36.1 (March 2006 genome assembly).

^cThe female map of the X chromosome is used when calculating the length of the entire genome.

Rutgers Map v.2 spans a total of 2925.8 Mb (2,925,822,157 bases), covering 96.8% of the Build 36.1 assembled genome. The physical coverage varies by chromosome. While the average percentage of physical length spanned by these maps is 94.7%, 15 of the chromosomes have >99.5% coverage. The acrocentric chromosomes (13, 14, 15, 21, 22) have considerably lower coverage, ranging from 68.6% (chromosome 22) to 83.8% (chromosome 13), due to the presence of large regions of heterochromatin that result in sequencing gaps.

These maps are 7.5 Mb longer than our Rutgers Map v.1 (when compared to the B35 versions of our maps, which were updated on our website post-publication), indicating that the additional SNPs added to the mapping set provide greater coverage of most chromosomes. For example, the map coverage of chromosome 20 increased by 2.17 Mb due to the addition of 11 SNPs on the map’s q-telomere end. Similarly, map coverage of chromosome 13 increased by 1.19 Mb due to the addition of 12 SNPs at the beginning of the map.

Confidence intervals for intermarker map distance

The mean confidence interval lengths are 0.750, 1.090, and 0.760 cM for the sex-averaged, female, and male maps, respectively. Similarly, the corresponding values for the median confidence interval lengths are 0.605, 0.936, and 0.630 cM. An asymmetric distribution for confidence interval lengths is expected since the vast majority of our confidence intervals are truncated at zero. This is unavoidable since the map distance estimates for most intervals are relatively small in comparison to their standard errors. Furthermore, the median confidence interval lengths coincide with the adjusted Wald (see Methods) confidence interval lengths, which is not surprising since roughly one third of all confidence intervals are based on the adjusted Wald method.

Map smoothing and interpolation of marker position

The smoothed maps provide a unique map position, on the linkage-map scale, for every marker on the map. The median number of markers in the sliding smoothing window, determined by the value of the smoothing parameter (see Methods), was 45 over all chromosomes, with a range from 21 to 51. The smoothed maps result in determination of a “map function” that describes each region of each map, which can be easily used to identify interpolated positions for markers not present in our map. We provide an interface on our website (http://compgen.rutgers.edu/maps) that determines interpolated linkage-map positions for markers not on our map.

Discussion

This second-generation Rutgers combined linkage–physical map (Rutgers Map v.2) has almost double the number of markers as the previous version and provides a unique and valuable map for several types of genetic analysis. The data have been carefully cleaned, and the position of each marker on the map is supported by both physical and recombination-based data. The smoothed maps provide a non-zero map distance between all markers and facilitate interpolation of additional markers not already on the map.

We used CRIMAP (Lander and Green 1987), an extremely fast map estimation program, to estimate our linkage maps. However, CRIMAP can yield biased estimates in the presence of missing data (Stewart and Thompson 2006; Stewart 2007). To assess the accuracy of our map estimates, we used LM_MAP, a program that generates the maximum likelihood estimate (MLE) of the map in the presence of missing data, for comparison. Differences between our map and the MLE were negligible, confirming that the bias (if any) in our map is minimal.

The confidence intervals provided with this map could be used in two ways: (1) to quantify the effect of map uncertainty on a genetic analysis; and (2) to combine the information in the Rutgers Map v.2 with independent map estimates obtained from individual studies. First, in critical regions it may be helpful to repeat any genetic analysis using a small number of different maps, where the maps are selected so that their variance is representative of the sampling error of the map estimate. This is important since, despite the fact that many investigators ignore the effect of map uncertainty, several studies have shown the potential of incorrect map distances to negatively impact multipoint linkage analysis (Halpern and Whittemore 1999; Daw et al. 2000). Furthermore, many other analyses (e.g., genotype error detection and haplotype inference) could also be negatively affected by map uncertainty. Second, since LM_MAP provides direct estimates of variability for arbitrary linkage mapping datasets, the information in our Rutgers Map v.2 could easily be combined with the information in independent linkage mapping datasets via meta-analysis. Stewart (2007) showed that a meta-analysis of independent map estimates can yield less-variable maps with increased resolution, relative to the variability and resolution of any of the independent maps used in the meta-analysis.

This map contains virtually all of the polymorphic markers that have been genotyped in the CEPH standard reference pedigrees, and to our knowledge it is the most dense linkage map published to date. Other polymorphisms that investigators may be using can be localized onto our map using interpolation. Alternatively, as described above, meta-analysis could be used to combine our map with localized maps produced using genotype data from disease studies.

Files providing limited details about each marker (e.g., marker heterozygosity, number of informative meioses, Build 36 physical position) along with map positions (sex-averaged, female, male, smoothed) and confidence intervals are available on the Rutgers Map website at http://compgen.rutgers.edu/maps.

Methods

Markers and genotype data

Our working data set for this map contained 28,425 markers. Of these, 14,759 (51.9%) were on our Rutgers Map v.1 (Kong et al. 2004) and have been described previously in detail. For this Rutgers Map v.2, we received data for 14,565 additional SNP markers that were genotyped in CEPH pedigrees by Affymetrix, Applied Biosystems, or Illumina. Applied Biosystems provided genotypes for 3922 SNPs from their SNPlex System Human Linkage Mapping Set 4K, using 42 CEPH pedigrees (Applied Biosystems). Affymetrix provided data on 5969 SNPs from their precommercial Human Mapping 10K array, genotyped in 37 CEPH pedigrees (Kennedy et al. 2003). Illumina provided 4674 SNPs from their Linkage IV panel, genotyped in 28 CEPH pedigrees (Murray et al. 2004).

In total, 899 SNPs were genotyped by two or more companies. For each of the redundant SNPs, we retained only the genotypes that were assayed in the largest sample, leaving 13,666 nonredundant SNPs. The genotypes at the 13,666 nonredundant SNPs were analyzed for genotyping errors, identified using the PedCheck (O’Connell and Weeks 1998) program as non-Mendelian transmission events. We checked linkage groups using two-point linkage analysis to confirm that each SNP was linked to its corresponding chromosome with a lod score of ≥3.0, since unlinked markers cannot be used for map construction. We pooled the genotypes at the nonredundant SNPs with the genotypes that were used to construct the Rutgers Map v.1 to obtain our working data set that contains 28,425 markers.

Map construction

The combined linkage–physical maps were constructed using the same protocol as was previously published in detail (Kong et al. 2004). In brief, the procedure uses sequence assembly to order the complete set of markers and iterates between data cleaning and linkage map estimation to arrive at an overall estimate of the map. The CRIMAP program (Lander and Green 1987) is used for all likelihood calculations, and our own Perl scripts are used to automate the map construction procedure. First, linkage-based intermarker map distances are computed conditional upon the physical order, and a maximum likelihood analysis is applied to test the position of each marker. Markers for which the linkage evidence agrees with the corresponding physical order are retained. Then intermarker map distances are re-estimated, and probable genotyping errors are identified and removed. The entire process is repeated to maximize marker inclusion and minimize genotyping error. In the final step, markers without physical positions are analyzed by linkage analysis to determine whether they can be localized to statistically significant map intervals (or bins). Our Rutgers Map v.2 is based on the analysis of genotype data for 28,425 markers using this procedure. Marker physical positions on the current genome assembly (NCBI Build 36.1, March 2006) were determined from publicly available databases dbSNP, uniSTS, and the UCSC Genome Bioinformatics Site.

Confidence intervals for intermarker map distances

We used the percentile (Efron and Tibshirani 1993) and the adjusted Wald (Agresti and Coull 1998) methods to compute approximate 95% confidence intervals for the true map lengths for all 24,145 intervals. First, we generated a bootstrap distribution of the map based on 1000 nonparametric bootstrap samples and their corresponding map estimates. Then, for each interval, we used the observed order statistics (25th and 975th) to construct confidence intervals for the true map length. However, this procedure yielded degenerate confidence intervals of the form [0,0] for 7706 (32%) map intervals. For these map intervals, we used the adjusted Wald method to construct nondegenerate confidence intervals with approximate 95% coverage.

To understand the adjusted Wald method and how it applies to map estimation, consider a single map interval and a set of n independent, fully informative meioses. If nonrecombinant and recombinant intervals are labeled as zero and one, respectively, then the standard estimate of the recombination rate p is the sample mean x, and the standard 95% confidence interval for p is x ± 2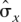/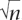. Note that 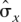(x) = x(1 − x) is a function of x, and that genetic distance is a function of p. The adjusted Wald method replaces x by (Σx_i + 2)/(n + 4), which permits construction of nondegenerate confidence intervals when x and 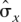(x) are both zero. Although most of the meioses in our linkage mapping data set are not fully informative, the information in our data is equivalent to some number of independent, fully informative meioses, denoted by n. In this sense, the degenerate confidence intervals have Σx_i = 0. We estimate the value of n separately, for the sex-averaged, female, and male maps using only the nondegenerate confidence intervals whose corresponding map distances are also non-zero.

In principle, our confidence intervals could be used in conjunction with Rutgers Map v.2 to posit realistic multivariate distributions for linkage maps, which would make it easy for investigators to quantify the effect of sampling error on their analyses. This is important since almost all multipoint genetic analyses contain an added, but often ignored, layer of variability that is attributable to uncertainty in the map.

Map smoothing and interpolation of marker position

Many of the map intervals have an estimated recombination-based size of 0 cM but have a non-zero physical size. The relatively small number of pedigrees genotyped does not provide enough power to allow detection of any recombination that may occur in these small map intervals. Undetected genotyping errors and variable marker informativeness may also lead to reduced observation of recombination. Therefore, we fit local quadratic curves to the map to produce a smoothed version of the map on which every marker has a unique linkage map (cM scale) position.

Map distances were smoothed with local regression using a quadratic fit, as implemented in the Locfit package in R (Loader 1999). The smoothed fit can be done to an arbitrarily dense grid; we used a grid with double the density of the number of markers on each chromosome map. The smoothing parameter, which determines the degree of smoothing applied to each chromosome, was selected by the Akaike information criterion (AIC) (Akaike 1974). Because of the desirability of applying the same degree of smoothing to the male and female maps, a common value for the smoothing parameter was selected as the one that minimized, over the two individual maps, the maximum increase of the AIC over its respective optima. Selection of the smoothing parameter is equivalent to selecting the number of markers used in the sliding window to determine the local smoothed fit. Under certain circumstances it was possible for the local regression to develop negative slope, an undesirable artifact of smoothing. Consequently, the next step was to monotonize the local regression fit as implemented in the monoproc package in R (Dette et al. 2006). The result was a dense, smoothed, nondecreasing map.

Map positions on the centimorgan scale can be interpolated for markers not present on our map. Given a marker’s physical position, linear interpolation from the dense grid is used to identify a corresponding cM map position.