Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2007 Dec;17(12):1787–1796. doi: 10.1101/gr.6554007

Sequence-based estimation of minisatellite and microsatellite repeat variability

Matthieu Legendre 1,4, Nathalie Pochet 1,2,4, Theodore Pak 1, Kevin J Verstrepen 1,3,5
PMCID: PMC2099588  PMID: 17978285

Abstract

Variable tandem repeats are frequently used for genetic mapping, genotyping, and forensics studies. Moreover, variation in some repeats underlies rapidly evolving traits or certain diseases. However, mutation rates vary greatly from repeat to repeat, and as a consequence, not all tandem repeats are suitable genetic markers or interesting unstable genetic modules. We developed a model, “SERV,” that predicts the variability of a broad range of tandem repeats in a wide range of organisms. The nonlinear model uses three basic characteristics of the repeat (number of repeated units, unit length, and purity) to produce a numeric “VARscore” that correlates with repeat variability. SERV was experimentally validated using a large set of different artificial repeats located in the Saccharomyces cerevisiae URA3 gene. Further in silico analysis shows that SERV outperforms existing models and accurately predicts repeat variability in bacteria and eukaryotes, including plants and humans. Using SERV, we demonstrate significant enrichment of variable repeats within human genes involved in transcriptional regulation, chromatin remodeling, morphogenesis, and neurogenesis. Moreover, SERV allows identification of known and candidate genes involved in repeat-based diseases. In addition, we demonstrate the use of SERV for the selection and comparison of suitable variable repeats for genotyping and forensic purposes. Our analysis indicates that tandem repeats used for genotyping should have a VARscore between 1 and 3. SERV is publicly available from http://hulsweb1.cgr.harvard.edu/SERV/.

Virtually all prokaryotic and eukaryotic genomes contain significant portions of tandem repeats, that is, stretches of DNA that are repeated head to tail. Tandem repeats are further classified into “microsatellites,” which have repeat units containing up to 9 nucleotides (nt), and “minisatellites,” with longer repeated units. The close proximity of multiple (nearly) identical DNA sequences causes frequent recombination or slippage events, generating new alleles that differ in the number of repeat units. Their instability makes tandem repeats ideally suited for fingerprinting, genotyping, and forensic analyses.

Because of their variability and their sequence simplicity, repeats have traditionally been considered as nonfunctional parasitic “junk” DNA (Orgel and Crick 1980). However, the recent sequencing of various genomes shows that repeats occur not only in intergenic gene deserts but often also in promoters and even coding regions (O'Dushlaine et al. 2005; Thomas 2005; Verstrepen et al. 2005). One particular category of intragenic repeats are the triplet repeats associated with neurodegenerative diseases, including Huntington’s disease, dentatorubro-pallidoluysian atrophy, spinobulbar muscular atrophy, and spinocerebellar ataxia (Gatchel and Zoghbi 2005). All of these disorders are progressive, with a strong correlation be|mtween disease onset and the number of triplet repeats in specific genes.

Apart from these negative consequences of repeat variability, hypermutable repeats may also have a beneficial role. Variable repeats located in certain key genes makes these genes hypervariable, allowing swift adaptive evolution of certain traits while maintaining low mutation rates in the rest of the genome (Rando and Verstrepen 2007). A genome-wide survey for tandem repeats located within coding regions in the Saccharomyces cerevisiae genome indicates that such intragenic repeats are mostly found within stress-induced and cell surface genes (Bowen et al. 2005; Verstrepen et al. 2005; Richard and Dujon 2006; Levdansky et al. 2007). The variability of these repeats may permit yeast cells to quickly adapt their cell surface properties to a changing environment. For example, variation in the repeats located in the FLO1 and FLO11 genes lead to gradual changes in the cell’s capacity to adhere to surfaces and form biofilms (Verstrepen et al. 2004, 2005; Fidalgo et al. 2006). Similarly, in dogs, variable repeats located within key developmental genes have been suggested to permit fast evolution of limb and skull morphology (Fondon and Garner 2004). These few known cases are presumably just the tip of the iceberg. Analyses presented in this study demonstrate that >30% of the genes in the human genome contain repeats in coding regions (exons). Hence, whereas the current focus of most large-scale genotype-to-phenotype mapping lies on single-nucleotide polymorphisms (SNPs), other phenomena such as repeat variation may also significantly contribute to genetic (and phenotypic) variation between organisms (Caburet et al. 2005; Rando and Verstrepen 2007; Stranger et al. 2007).

Whereas most tandem repeats are unstable compared with nonrepeated DNA, the mutation rates vary widely from repeat to repeat. Most repeat mutation rates are about 10- to 10,000-fold higher than those of nonrepeated regions and lie between 10−3 and 10−6 per cellular generation (Verstrepen et al. 2005). However, some tandem repeats appear to be nearly invariable, while others, most notably certain microsatellites in the human genome, show mutation rates >10−2 (Ellegren 2004). It has been shown that the majority of variation in both microsatellites and minisatellites is a consequence of homology-dependent double-stranded break repair, such as synthesis-dependent strand annealing (SDSA) or break-induced replication (Paques and Haber 1999; Lopes et al. 2006). For repeats that are prone to loop formation, replication slippage may be an additional source of variability (Viguera et al. 2001).

Repeats appear to be evenly distributed across the genome, and repeats located near meiotic hot spots are not noticeably more polymorphic than those located in recombination cold spots (Richard and Dujon 2006). This suggests that the mutation frequency of a repeat might mainly depend on its intrinsic properties rather than its genomic location. Hence, it might be possible to estimate a repeat’s variability from its basic features.

Several algorithms are available to detect tandem repeats, including ETANDEM (Rice et al. 2000), mREPS (Kolpakov et al. 2003), and Tandem Repeat Finder (TRF) (Benson 1999), the latter arguably the most used program to date. However, few tools are available to automatically detect “orthologous” repeats in different genomes (one notable exception is described in Denoeud and Vergnaud 2004). Similarly, only a handful of previous studies have developed models to predict repeat variability. First, Wren et al. (2000) described a set of “rules of thumb” to predict whether a given tandem repeat is hypervariable. More specifically, these authors postulated that for dinucleotide repeats, at least 8 units are needed to have a variable repeat. The minimal number of units drops to 7, 6, 5, and 4 for trimers, tetramers, pentamers to nonamers, and repeat units of 10 nt or more, respectively. Later, Denoeud et al. (2003) described a model aimed at classifying a specific category of minisatellite repeats (unit length 17, copy number >9, purity >70%) in the human genome. Recently, Näslund et al. (2005) used linear logistic regression to model variability of a limited set of minisatellite repeats in the human genome.

While these simple models are quite capable of accurately predicting the variability of repeats closely resembling the limited training data set, their performance has not been validated for other repeats or other species, making them of only limited use for genome-wide analyses (O'Dushlaine and Shields 2006). Moreover, repeat variability is not an all-or-nothing phenomenon, and a continuous scale seems more appropriate than a binary classification. Last but not least, a linear model may not be suitable to capture complex biological phenomena such as repeat variability. Adding one extra repeat unit to a repeat consisting of five units may, for example, have a relatively larger effect on mutation rates than adding a unit to a repeat that already contains 40 units.

Because of the large variation in repeat mutation rates, results obtained from repeat-based genotyping and forensics studies largely depend on the exact repeat(s) used. The lack of any standards makes it impossible to compare studies and sometimes even leads to flawed conclusions. Here, we describe the development of a general nonlinear model capable of predicting repeat variability for all types of tandem repeats (microsatellites and minisatellites) in a wide range of organisms spanning the major kingdoms of life. We demonstrate that the model outperforms existing models and that it can be used to identify and characterize potentially interesting (variable) repeats for genotyping, forensics, or functional studies.

Results

Genome-wide detection of variable tandem repeats

Existing models to predict repeat variability were based on small, specific data sets and used simple (linear) algorithms. As a result, while these models are quite capable of predicting variability for the limited data sets they were trained on, they are not suited as a general method to predict the variability of a broad range of repeats in a broad range of organisms. Therefore, we decided to use more complex models and large, unbiased training and validation data sets that represent the full spectrum of naturally occurring tandem repeats.

To obtain such expansive data sets, we first developed a method to detect and compare orthologous tandem repeats in large (whole-genome) sequences. Repeat data sets were assembled for yeast (Saccharomyces cerevisiae), primates (Homo sapiens), insects (Drosophila melanogaster), plants (Arabidopsis thaliana), and bacteria (Neisseria meningitides and Mycobacterium tuberculosis). For each data set, repeats were detected and compared between several closely related strains or species and subsequently categorized as variable (if the number of repeat units differed between the compared strains/species) or nonvariable (if the number of repeats was constant in all strains or species; see Methods for details).

As anticipated, this procedure generated large data sets containing an unbiased collection of naturally occurring repeats. For example, the S. cerevisiae data set comprises 2743 conserved repeat loci, of which 242 were categorized as variable between three S. cerevisiae strains. The data indicate just how different tandem repeats can be. The unit length ranges from 2 to 81 nt, with some repeats having as many as 80 units. Moreover, the repeats found by this procedure seem to agree very well with manually curated smaller data sets. For example, our M. tuberculosis data set comprised 20 out of 21 repeats found by Le Flèche et al. (2002), and all repeats are appropriately labeled as variable.

Generation of a predictive model for repeat variability

Our aim was to generate a predictive model that accurately estimates repeat variability from a set of basic repeat characteristics. We used multivariate analysis based on least square support vector machines (LS-SVMs) with nonlinear radial basis function (RBF) kernels to train a model that predicts repeat variability. This model was generated using a balanced training data set of 320 repeats comprising an equal number of variable and nonvariable repeats of all naturally occurring tandem repeats in the yeast genome and the 2423 remaining repeats as a validation data set (see Methods for technical details on how this model was developed and evaluated).

The final model (SERV; http://hulsweb1.cgr.harvard.edu/SERV/) uses three basic characteristics of a tandem repeat (number of units, unit length, and purity) as input variables. On the basis of these variables, SERV generates a continuous output (referred to as “VARscore”). The VARscore serves as a continuous estimation of repeat variability, with larger VARscores correlating with higher predicted repeat variability. Visualization of the model (Supplemental Fig. S1) shows the intuitive relation between the input variables and the predicted variability (VARscore) of the corresponding repeat. The single most important factor determining a repeat’s predicted variability is the number of units, with higher repeat units leading to increased predicted variability. Increased repeat purity or unit length also leads to higher predicted variability, although the effect is smaller. These intuitive conclusions are further supported by our experimental analyses (Fig. 1).

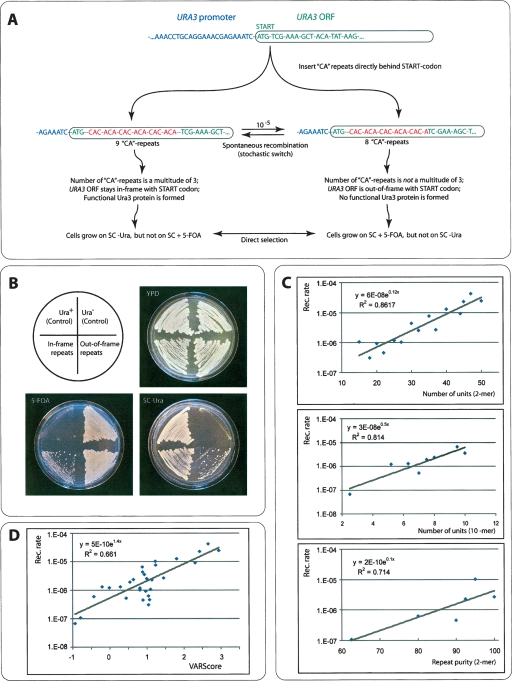
Figure 1.

Figure 1.

Open in a new tab

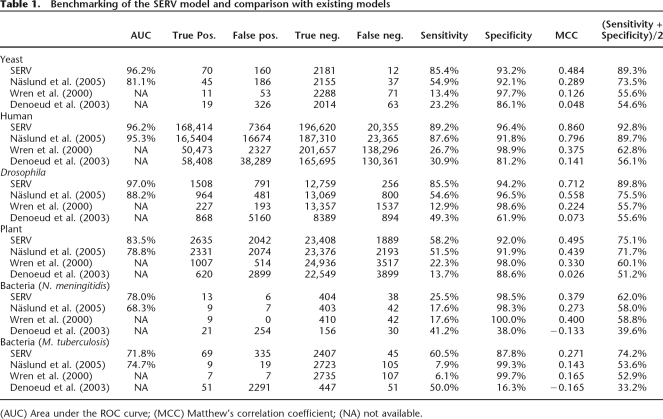
VARscore correlates with repeat mutation rates. (A) To evaluate the correlation between the VARscore and experimentally determined mutation rates, a series of 30 different artificial repeats was inserted right behind the START codon of the genomic URA3 gene of a haploid S. cerevisiae S288C yeast strain. Three classes of strains were constructed: (1) a series of “CA” dinucleotide repeats with varying number of units; (2) a series of CA repeats with a constant number of units, but varying repeat purity; (3) a series of strains with a 10-mer and 20-mer unit length and varying number of units. (B) Since the number of nucleotides in each repeat is not a multitude of three, changes in the number of repeats lead to shifts in the URA3 reading frame, so that some strains will be Ura+, and others Ura−, depending on the number of repeat units they contain. Moreover, because of the instability of tandem repeats, the number of repeats will change in a fraction of each mitotic division, resulting in frequent shifts between Ura+ and URA− phenotypes. This can be demonstrated by growing cells in either SC–Ura or 5-FOA medium, which selects for Ura+ and Ura− strains, respectively (see Methods for details). (C) Plotting the mutation rates in the various repeat classes shows an exponential increase in mutation events with increasing unit number and purity. (D) Plotting VARscores for each repeat against their experimental mutation rates shows the correlation between VARscore and mutation rates, indicating that VARscores can be used as a rough estimation of mutation rate.

SERV accurately predicts repeat variability in various genomes

To evaluate the performance of the model, we compared our tandem repeat variability predictions to the few other existing methods, using five whole-genome data sets obtained from different groups of organisms (human/primate, insects, plants, and two bacterial species).

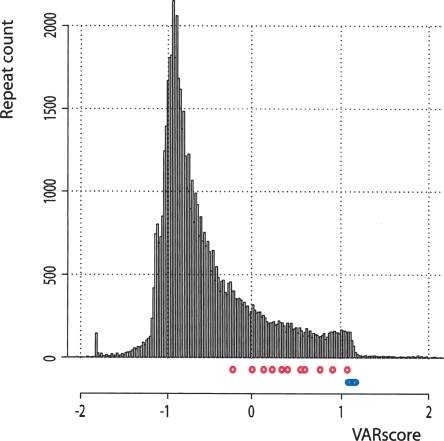
Since the models developed by Wren et al. (2000) and Denoeud et al. (2003) produce a binary output (variable/nonvariable), it is impossible to directly compare these predictions with our model, which has a continuous output value. To overcome this problem, we defined a VARscore cutoff based on the receiver operating characteristic (ROC) curve to differentiate predicted variable repeats from nonvariable repeats, so that the output of our model essentially becomes binary, classifying repeats as variable (VARscore above cutoff) or nonvariable (VARscore below cutoff). The cutoff score was set at the value that optimizes the sum of sensitivity and specificity of our model on the yeast training set and this same value (0.0273) was subsequently used to classify the repeats in the other data sets (see Methods for details and definitions). The results of these comparisons between all models are given in Table 1. On average, the method developed by Wren et al. (2000) has a slightly higher specificity but suffers from extremely low sensitivities. Sensitivity and specificity can be combined in a single measure, called Matthew’s correlation coefficient (MCC) (see formula in Methods), a value ranging from −1 to 1 (1 being a perfect prediction). On the basis of this value, SERV yields the best overall performance. One last way to compare the performance of the models is by calculating the sum of specificity and sensitivity. As the last column in Table 1 shows, our model systematically yields a considerably higher sum of specificity and sensitivity than the other models.

Table 1.

Benchmarking of the SERV model and comparison with existing models

graphic file with name 1787tbl1.jpg

Open in a new tab

(AUC) Area under the ROC curve; (MCC) Matthew’s correlation coefficient; (NA) not available.

The method developed by Näslund et al. (2005) produces a continuous output value, allowing a more rigorous comparison, using ROC curves (see Supplemental Fig. S2). Again, SERV shows a better average performance, with an area under the ROC curve (AUC) performance that is always significantly higher (P < 0.0001) than the Näslund model, except for the bacterial data sets, where no significant difference was found.

The model developed by Denoeud et al. (2003) shows high specificity but low sensitivity for higher eukaryotes and low specificity but high sensitivity for the tested prokaryotes. As shown in Supplemental Figure S3, yeast, plant, and human tandem repeats are relatively GC-poor, whereas bacterial repeats are relatively GC-rich. Interestingly, this GC content correlates with the performance of Denoeud’s model, which uses GC content as a main predictor for repeat variability. For a given species, the more GC-rich the repeats are, the higher the predicted variability, resulting in a higher sensitivity but a reciprocal decrease in specificity. This makes the performance variable between different species. Näslund et al. (2005) also use GC content as a predictive variable but with a low weight. SERV does not rely on nucleotide composition, which eliminates any sensitivity to compositional biases across different species.

Overall, these results show that SERV systematically outperforms existing methods on a wide spectrum of species. Moreover, instead of classifying repeats as variable or nonvariable, the model produces a continuous output (VARscore), allowing a complete ranking of all repeats in a data set according to their predicted variability. It is important to note that most existing models were not intended to predict repeat variability over a broad spectrum of repeat categories. Hence, our study does not discredit their usefulness for the goals for which they were developed. In fact, when SERV is used to predict the variability of the limited sets of repeats for which these other models were trained, the respective specific model always (slightly) outperform SERV, although the difference is not statistically significant (Supplemental Table S1).

VARscore correlates with experimental repeat mutation rates

The idea behind SERV was to generate a continuous VARscore that would correlate with the experimental variability of a given repeat. To investigate our model’s ability to accurately predict mutation rates in tandem repeats, we constructed a large set of different tandem repeats in the yeast genome and evaluated the correlation between the VARscore and the experimental mutation rates.

In total, we constructed 30 repeats that cover the parameter space of natural repeats found in the yeast genome (unit lengths of 2, 10, and 20 nt; number of units between 2 and 50; and purity between 62.5% and 100%) (Fig. 1). For each different repeat, we performed at least three independent fluctuation analyses to estimate the mutation rates. The results indicate that the three parameters used in our model (i.e., number of repeat units, unit length, and repeat purity) indeed influence mutation rates. Regression shows an exponential relation between these parameters and mutation rates (Fig. 1C). Furthermore, when all VARscores for these repeats are plotted against their mutation rates, it becomes clear that VARscores indeed correlate well with mutation rates, especially when taking experimental errors and the diversity of the set of artificial repeats into account (R2 = 0.66, P = 4 × 10−8; Fig. 1D).

In summary, the VARscore of a repeat correlates with its mutation rate, confirming that VARscores can be used to rank different repeats according to their predicted variability. We now explore a few different applications of this analysis.

VARscore as a benchmarking tool for variable repeats used as markers in fingerprinting

One major application of SERV is the selection and comparison of tandem repeats used in genotyping and forensic research. To be suited for genotyping purposes, it is essential that the repeat displays sufficient variability, thereby increasing the probability it will be able to discriminate between relatively closely related individuals. On the other hand, excessive hypervariability is unwanted as it would obscure genetic relatedness. Until now, the selection of suitable markers has been somewhat “hit or miss.” This is perfectly illustrated by comparing two recent papers that use variable tandem repeats to characterize Plasmodium vivax genetic diversity. In the first study, Leclerc et al. (2004) found very little diversity in a set of tandem repeats across a large set of isolates from eight geographical locations. Of the 13 repeat loci studied, only one was variable. Hence, they concluded that P. vivax likely underwent a series of recent selective sweeps or a major bottleneck event that all but eliminated existing genetic diversity. However, in a similar study, Imwong et al. (2006) found a plethora of diversity in tandem repeats, with markers having between 7 and 18 alleles per locus and many isolates being heterozygous for several loci. In an interesting perspective paper, Russell et al. (2006) suggested that these dramatically different conclusions may be due to differences in the chosen markers—the markers in Leclerc et al.’s study simply being less variable than those chosen by Imwong and coworkers.

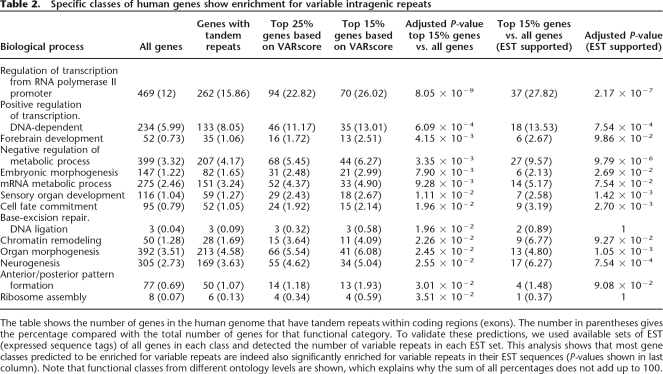
We decided to use SERV to check the predicted variability of both marker sets. As shown in Figure 2, there are striking differences in the VARscores for both sets of markers. Indeed, the scores for Leclerc et al.’s markers (Leclerc et al. 2004) are significantly lower than those for the repeats used by Imwong et al. (2006) (mean for Leclerc et al. is 0.46 compared with 1.1 for Imwong et al.; P = 4.8 × 10−5). Interestingly, the only exception is the one marker in the Leclerc data set that does show variability among the P. vivax isolates (VARScore for this marker is 1.1). We also determined the VARscores of some of the most frequently used tandem repeat markers for human forensics (Butler 2006) (Supplemental Table S2). The set of 15 markers shows a mean and median VARscore of 1. Hyper-unstable repeats often have VARscores above 3 (e.g., 5.8 for the human CEB1-1.8 repeat studied by Nicolas and colleagues; Lopes et al. 2006).

Figure 2.

Figure 2.

Open in a new tab

VARscore as a benchmarking tool for genotypic markers. All tandem repeats in the P. vivax genome were plotted according to their VARscore. The circles represent the VARscores of the markers used in two independent genotyping studies. The top row are the score for the markers used by Leclerc et al. (2004) who found very little variability in these markers, except for one marker, the one with the highest VARscore (far right point). The markers used by Imwong et al. (2006) (bottom row) have significantly higher VARscores, which agrees with the observed variability for these markers.

This analysis again demonstrated the correlation between a repeat’s VARscore and its instability. Hence, VARscores can be used as a criterion to select repeat loci suitable for genotyping and fingerprinting. On the basis of our analyses, we would recommend using repeats with a VARscore of at least 1, but lower than 2 (for divergent strains/species) or 3 (for closely related strains or individuals).

Human genes involved in transcriptional regulation and morphogenesis are enriched for variable repeats

As indicated, recent findings suggest that variable repeats may influence biological features. In particular, variable repeats located within protein coding regions introduce variability in the corresponding protein. This may allow these proteins to evolve faster and adapt swiftly to changes in selective pressure. In addition, uncontrolled variation in coding repeats is known to be associated with certain (human) diseases.

The authors of previous studies have already mapped the occurrence of coding repeats in the human genome (Denoeud et al. 2003; O'Dushlaine et al. 2005). However, these studies cannot predict which of these repeats will in fact be hypervariable and which are rather stable (and thus less likely to be involved in diseases or swift adaptation). We therefore performed our own analysis of the human coding regions and used SERV to rank the repeats according to their predicted variability (VARscore) and then determine which functional gene classes are enriched and depleted in this set.

We analyzed gene ontology for four groups of genes: (1) all human genes, (2) genes with tandem repeats, (3) top 25% ranked genes according to VARscore, and (4) top 15% genes according to VARscore. Results for functional categories that give significant enrichment in the top 15% of VARscores are reported in Table 2. The table shows a correlation between increasing VARscores and the proportion of genes belonging to every significant functional class. To validate these predictions, we used human EST (expressed sequence tags) data to investigate whether the repeats in these human genes indeed vary among transcripts isolated from different individuals (see Methods for details). The variability of the repeats in these EST sequences confirms the predictions made by SERV. As shown in the last column of Table 2, gene categories enriched for genes containing repeats with high VARscores also show significant enrichment in variable ESTs.

Table 2.

Specific classes of human genes show enrichment for variable intragenic repeats

graphic file with name 1787tbl2.jpg

Open in a new tab

The table shows the number of genes in the human genome that have tandem repeats within coding regions (exons). The number in parentheses gives the percentage compared with the total number of genes for that functional category. To validate these predictions, we used available sets of EST (expressed sequence tags) of all genes in each class and detected the number of variable repeats in each EST set. This analysis shows that most gene classes predicted to be enriched for variable repeats are indeed also significantly enriched for variable repeats in their EST sequences (P-values shown in last column). Note that functional classes from different ontology levels are shown, which explains why the sum of all percentages does not add up to 100.

Two main Gene Ontology (GO) classes that show enrichment for potentially variable repeats, stand out: transcriptional regulation and development. Highly polymorphic tandem repeats in genes involved in transcription regulation (such as transcription factors) could lead to modified transcription activities and thus swift evolution (Caburet et al. 2004, 2005; Fondon and Garner 2004). Genes involved in development are also enriched for variable repeats. Enrichment for these genes is perfectly in line with the work of Fondon and Garner (2004), which suggests that variable repeats in key regulators of morphological development can generate diversity in dog breeds.

Other development classes also emerge from our data set, including genes involved in neurogenesis and brain development. Genes containing intragenic trinucleotides repeats have indeed been linked to these phenomena (Karlin and Burge 1996), as well as neurodegenerative diseases (see below). In general, these findings agree with the previous observation of O’Dushlaine et al. (2005), who find enrichment for variable repeats in genes involved in morphogenesis and protein binding. However, the latter methodology does not allow proving the statistical significance of such enrichment, except for one GO category (protein binding). Moreover, the analysis depends on the availability of sufficient independent EST sequences. Clearly, classifying genes according to their VARscore and only working with a fraction of all genes that contain repeats increases the statistical power of such enrichment analyses.

VARscore allows identification of genes involved in repeat-based diseases

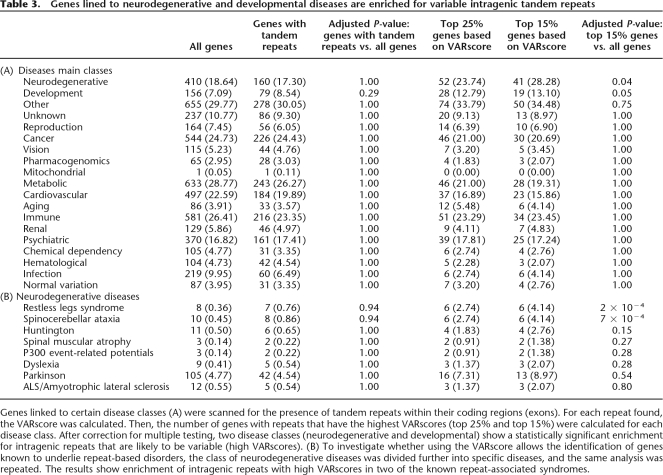
A last demonstration of the usefulness of SERV is its use as a tool to identify candidate genes underlying repeat-dependent diseases. Tandem repeats are known to be involved in various human genetic diseases. We therefore tested whether our model could identify genes known to be involved in repeat-based diseases. We used data from the Genetic Association Database (http://geneticassoiationdb.nih.gov) (Becker et al. 2004). As shown in Table 3, a simple search for genes containing tandem repeats does not show any statistically significant enrichment across the broad diseases classes. However, limiting the search to the subset of repeats in the top 15% of highest VARscores allows identification of specific disease categories and genes known to underlie repeat-related neurodegenerative diseases. In other words, using the VARscore helps to find statistically significant enrichment of potentially hypervariable tandem repeats linked to diseases.

Table 3.

Genes lined to neurodegenerative and developmental diseases are enriched for variable intragenic tandem repeats

graphic file with name 1787tbl3.jpg

Open in a new tab

Genes linked to certain disease classes (A) were scanned for the presence of tandem repeats within their coding regions (exons). For each repeat found, the VARscore was calculated. Then, the number of genes with repeats that have the highest VARscores (top 25% and top 15%) were calculated for each disease class. After correction for multiple testing, two disease classes (neurodegenerative and developmental) show a statistically significant enrichment for intragenic repeats that are likely to be variable (high VARscores). (B) To investigate whether using the VARscore allows the identification of genes known to underlie repeat-based disorders, the class of neurodegenerative diseases was divided further into specific diseases, and the same analysis was repeated. The results show enrichment of intragenic repeats with high VARscores in two of the known repeat-associated syndromes.

This prompted us to investigate whether SERV allowed us to identify other candidate genes that might be linked to genetic diseases. We therefore compiled a table of all repeat-containing human genes and ranked the list according to the VARscore of the repeats (Supplemental Table S3). Some of the highest-ranking genes are already known to contain polymorphic repeats, for example, the cartilage-specific proteoglycan gene AGC1. However, for many genes in the list, repeat polymorphisms and/or their possible phenotypic effect have not yet been described. One group of such candidate genes are the MUC (mucin) genes. Although they are currently not considered to underlie repeat-based diseases, size variation in MUC genes has been associated with progression of immunoglobulin A nephropathy (Li et al. 2006) and with certain eye disease (Berry et al. 2004). Moreover, elevated expression of MUC genes has been implicated in tumorigenesis (Schroeder et al. 2004) and is currently used as a marker for malignant tumors with a high risk for metastasis (Baldus et al. 2004). We have previously shown that an increase in coding repeats can affect transcriptional activity of the corresponding gene (Voynov et al. 2006), opening the exciting possibility that variation in the MUC repeats could underlie changes in expression observed during tumorigenesis.

Needless to say, not all genes containing hypervariable coding repeats will lead to disease. Supplemental Table S3 may therefore also allow the identification of specific genes involved in fast evolution of certain traits caused by the high mutation rates in these intragenic repeats.

Discussion

Our analysis shows that three basic characteristics of a given tandem repeat, namely number of repeated units, unit length, and repeat purity, are major determinants for its (in)stability. While other factors, such as GC content and entropy, may also exert some effect on repeat stability, the influence of the three factors used in our model is very intuitive. First and foremost, repeat variability increases exponentially with increasing number of repeat units. This observation confirms some of the pioneering work of Petes and coworkers, who found an exponential relation between number of units and mutation rates (Sia et al. 1997; Wierdl et al. 1997). The exponential increase in mutation rates with the addition of extra repeat units may indicate that repeats cannot only recombine with their direct neighbors but may, in fact, also be able to interact with more distantly located units. Second, repeat variability increases with increasing unit length, which probably reflects the effect of an increased “target” for homologous pairing during slippage, crossover, or SDSA. Third, repeat instability increases with increasing purity, which probably reflects an increased tendency for misalignment of the different repeat units.

The availability of a model to predict repeat variability has several applications, some of which were demonstrated in this paper. Despite the widespread use of variable tandem repeats in genotyping and forensics, results vary widely depending on which set of repeats is chosen. The lack of any standards makes it impossible to compare studies and sometimes even leads to flawed conclusions. Analysis of the VARscore of repeats used in different studies may help to compare and interpret paradoxical results and conclusions. Moreover, SERV also allows researchers looking for new microsatellite markers for genotyping or forensics to estimate if a given repeat would be a suitable marker and is likely to show variation between closely related (but nonidentical) individuals, strains, or species. From our analyses, it seems that only repeats displaying positive VARscores may be suited, with ideal markers showing VARscores above 1 but below 3.

Another use of the VARscore is the identification of hypervariable repeats in genomes for functional studies. As it becomes increasingly clear that changes in some repeats may have profound phenotypic consequences, researchers are trying to identify new examples of this phenomenon. The ability to discriminate between repeats with low and high variability may be an important tool to select specific repeats from the large pool of candidates in the genome. Our basic analysis of the human genome demonstrates the usefulness of the VARscore to identify the genes known to be involved in repeat-dependent diseases such as Huntington’s syndrome and ataxia, as well as to compile a list of candidate genes containing hypervariable repeats, which might lead to certain diseases.

Not all repeat variation leads to diseases. Instead, variation in repeat number might provide the basis for phenotypic diversity, thus allowing swift evolution of certain traits. While this has only been demonstrated for a limited number of examples, our analysis indicates that repeats may also play a role in humans. Here, repeats are enriched in genes involved in transcription and organismal development, including such key processes as brain development. Is it possible that so-called “junk DNA” underlies the swift evolution of the primate brain?

Methods

Data set assembly and analysis of repeat variability

To obtain an expansive and unbiased data set, the complete S. cerevisiae nuclear genome (S288C sequence 2006 from the Saccharomyces Genome Database [SGD]; E.L. Hong, R. Balakrishnan, K.R. Christie, M.C. Costanzo, S.S. Dwight, S.R. Engel, D.G. Fisk, J.E. Hirschman, M.S. Livstone, R. Nash, et al.; http://www.yeastgenome.org/) was scanned for tandem repeats using the TRF algorithm (Benson 1999). For an elaborate description of used parameters, thresholds, and sequence data, refer to the supplemental material online. Repeats that were conserved between all three strains were classified as variable if the number of units the three strains were different by at least one full unit (Supplemental Fig. S4). This procedure yielded 2743 conserved repeats (242 variable and 2501 nonvariable), of which 320 repeats (160 variable and 160 nonvariable) were used as training set to build the model. The rest of the repeats (2423) were used as a validation data set. Five test sets were generated from human/primate, plant, insect, and two bacterial genomes in essentially the same way as described for the yeast data set (see Supplemental material for details).

Model development

We used LS-SVMs (Suykens et al. 2002) with nonlinear RBF kernels to generate a multivariate model containing only the most relevant repeat characteristics that accurately predicts the variability of a repeat. Seven basic repeat characteristics (purity, unit length, number of units, TRF score, entropy, GC content, and GC bias) were considered for inclusion in the model. For a definition of these variables, see Näslund et al. (2005). LS-SVM models with RBF kernels (Suykens et al. 2002) were generated using the LS-SVMlab version 1.5 toolbox for MATLAB (http://www.esat.kuleuven.be/sista/lssvmlab/).

All models were trained on a balanced training data set comprising 320 of all naturally occurring repeats in the S. cerevisiae genome (training data set). To select the most relevant repeat characteristics for inclusion in the final model, we applied a forward variable selection procedure using LS-SVMs with an RBF kernel. The selection criterion we used was the AUC performance on the remaining 2423 repeats in the S. cerevisiae genome (validation data set). The model parameters, that is, the regularization parameter γ and the kernel parameter σ, were tuned by optimizing the “10-fold cross-validation” performance (generalization performance) on the 320 repeats in the yeast training data set. For details, refer to the supplemental material online. The final model, called SERV, as a typical LS-SVM classifier with RBF kernel, is formulated as:

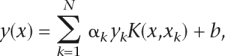graphic file with name 1787equ1.jpg

with training set 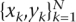Inline graphic (N = 320) containing 320 training tandem repeats characterized by three variables xk ∈ ℜd (d = 3; purity, unit length, and number of units), and corresponding binary class labels yk ∈ {−1,+1} (label “+1” in case of variable repeats; “−1” otherwise), model parameters α and bias term b, continuous predicted values y(x), and the kernel function using RBF kernel calculated as

graphic file with name 1787equ2.jpg

Since LS-SVMs generate continuous values (VARscores) for the predicted repeat variability, comparison of SERV to other models required us to convert SERV’s continuous output to a binary output. We therefore used the ROC curve to determine the cut-off point corresponding to the maximum value of the sum of sensitivity and specificity based on the training set (De Smet et al. 2006). The optimal cut-off value was 0.0273. All other model parameters are given at http://hulsweb1.cgr.harvard.edu/SERV/supplementalData/. For an overview of the benchmarking and statistical methods applied, refer to the Supplemental materials.

Analysis of human coding regions repeats

Coding sequences were gathered from Ensembl (human transcripts, version 42). These sequences were scanned for tandem repeats with TRF (for exact parameters see supplemental materials) and the VARscore was computed for each repeat. The genes were ranked according to the VARscore of their respective internal repeats and subsequently organized in different basic classes: genes without repeats, genes with repeats, and genes with repeats belonging to the top 25% and top 15% of highest VARscores. Functional annotations (gene ontology) were determined using the Babelomics tools (Al-Shahrour et al. 2005).

To identify variable repeats in EST sequences, we used UniGene clusters associated to each of these human transcripts. We then applied the methodology described in O'Dushlaine et al. (2005) to identify each EST associated to the detected tandem repeats and analyzed the differences in the number of units. We used Fisher exact tests corrected for multiple testing using the false discovery rate (FDR) (Benjamini and Hochberg 1995) to compute P-values for enrichment of variable ESTs for all genes in the top 15% VARscore category compared to all genes for which EST data is available.

Enrichment of variable repeats in genes that are associated with genetic diseases was calculated using the Genetic Association Database (Becker et al. 2004). Statistical significance of enrichment was calculated using the Fisher exact test. P-values were adjusted for multiple testing with the FDR function using the method developed by Benjamini and Hochberg (1995).

Analysis of P. vivax repeats

All tandem repeats present in P. vivax genome (TIGR, http://www.tigr.org/tdb/e2k1/pva1) were identified using TRF as described above. VARscores were computed for the repeats used in two previous studies (Leclerc et al. 2004; Imwong et al. 2006).

Experimental validation of model

The yeast strain used is a prototrophic variant of strain S288C (Brachmann et al. 1998). All PCR primers are listed in Supplemental Table S4. Yeast cultures were grown as described before (Sherman et al. 1991). YPD medium contained 2% peptone (Difco) and 1% yeast extract (Difco) and 2% glucose (Difco). Standard procedures and reagents for molecular biology were used. Mutation rates were estimated as described previously (Verstrepen et al. 2005). For a detailed overview of the strain construction and experimental procedures, see Supplemental materials.

Acknowledgments

We thank Gerald Fink, Marcelo Vinces, Chris Brown, Bodo Stern, Sharad Ramanathan, Amir Karger, William Ritchie, An Jansen, Frank De Smet, Xander Warnez, and Kathleen Marchal for their useful comments and suggestions. Research in the lab of K.V. is supported by NIH NIGMS grant 5P50GM068763-04 and the Human Frontier Science Program Young Investigator Award RGY79/2007. N.P. is a Henri Benedictus Fellow of the King Baudouin Foundation and the Belgian American Educational Foundation (BAEF). T.P. acknowledges the financial support of the Harvard College Research Program for undergraduate researchers (HCRP) and the Bauer summer program for undergraduate students.

Footnotes

[Supplemental material is available online at www.genome.org.]

Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.6554007

References

  1. Al-Shahrour F., Minguez P., Vaquerizas J.M., Conde L., Dopazo J., Minguez P., Vaquerizas J.M., Conde L., Dopazo J., Vaquerizas J.M., Conde L., Dopazo J., Conde L., Dopazo J., Dopazo J. BABELOMICS: A suite of web tools for functional annotation and analysis of groups of genes in high-throughput experiments. Nucleic Acids Res. 2005;33:W460–W464. doi: 10.1093/nar/gki456. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Baldus S.E., Engelmann K., Hanisch F.G., Engelmann K., Hanisch F.G., Hanisch F.G. MUC1 and the MUCs: A family of human mucins with impact in cancer biology. Crit. Rev. Clin. Lab. Sci. 2004;41:189–231. doi: 10.1080/10408360490452040. [DOI] [PubMed] [Google Scholar]
  3. Becker K.G., Barnes K.C., Bright T.J., Wang S.A., Barnes K.C., Bright T.J., Wang S.A., Bright T.J., Wang S.A., Wang S.A. The genetic association database. Nat. Genet. 2004;36:431–432. doi: 10.1038/ng0504-431. [DOI] [PubMed] [Google Scholar]
  4. Benjamini Y., Hochberg Y., Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. Roy. Statist. Soc. Ser. B. 1995;57:963–971. [Google Scholar]
  5. Benson G. Tandem repeats finder: A program to analyze DNA sequences. Nucleic Acids Res. 1999;27:573–580. doi: 10.1093/nar/27.2.573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Berry M., Ellingham R.B., Corfield A.P., Ellingham R.B., Corfield A.P., Corfield A.P. Human preocular mucins reflect changes in surface physiology. Br. J. Ophthalmol. 2004;88:377–383. doi: 10.1136/bjo.2003.026583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bowen S., Roberts C., Wheals A.E., Roberts C., Wheals A.E., Wheals A.E. Patterns of polymorphism and divergence in stress-related yeast proteins. Yeast. 2005;22:659–668. doi: 10.1002/yea.1240. [DOI] [PubMed] [Google Scholar]
  8. Brachmann C.B., Davies A., Cost G.J., Caputo E., Li J.C., Hieter P., Boeke J.D., Davies A., Cost G.J., Caputo E., Li J.C., Hieter P., Boeke J.D., Cost G.J., Caputo E., Li J.C., Hieter P., Boeke J.D., Caputo E., Li J.C., Hieter P., Boeke J.D., Li J.C., Hieter P., Boeke J.D., Hieter P., Boeke J.D., Boeke J.D. Designer deletion strains derived from Saccharomyces cerevisiae S288C: A useful set of strains and plasmids for PCR-mediated gene disruption and other applications. Yeast. 1998;14:115–132. doi: 10.1002/(SICI)1097-0061(19980130)14:2<115::AID-YEA204>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
  9. Butler J.M. Genetics and genomics of core short tandem repeat loci used in human identity testing. J. Forensic Sci. 2006;51:253–265. doi: 10.1111/j.1556-4029.2006.00046.x. [DOI] [PubMed] [Google Scholar]
  10. Caburet S., Vaiman D., Veitia R.A., Vaiman D., Veitia R.A., Veitia R.A. A genomic basis for the evolution of vertebrate transcription factors containing amino acid runs. Genetics. 2004;167:1813–1820. doi: 10.1534/genetics.104.029082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Caburet S., Cocquet J., Vaiman D., Veitia R.A., Cocquet J., Vaiman D., Veitia R.A., Vaiman D., Veitia R.A., Veitia R.A. Coding repeats and evolutionary “agility.”. Bioessays. 2005;27:581–587. doi: 10.1002/bies.20248. [DOI] [PubMed] [Google Scholar]
  12. De Smet F., De Brabanter J., Van den Bosch T., Pochet N., Amant F., Van Holsbeke C., Moerman P., De Moor B., Vergote I., Timmerman D., De Brabanter J., Van den Bosch T., Pochet N., Amant F., Van Holsbeke C., Moerman P., De Moor B., Vergote I., Timmerman D., Van den Bosch T., Pochet N., Amant F., Van Holsbeke C., Moerman P., De Moor B., Vergote I., Timmerman D., Pochet N., Amant F., Van Holsbeke C., Moerman P., De Moor B., Vergote I., Timmerman D., Amant F., Van Holsbeke C., Moerman P., De Moor B., Vergote I., Timmerman D., Van Holsbeke C., Moerman P., De Moor B., Vergote I., Timmerman D., Moerman P., De Moor B., Vergote I., Timmerman D., De Moor B., Vergote I., Timmerman D., Vergote I., Timmerman D., Timmerman D. New models to predict depth of infiltration in endometrial carcinoma based on transvaginal sonography. Ultrasound Obstet. Gynecol. 2006;27:664–671. doi: 10.1002/uog.2806. [DOI] [PubMed] [Google Scholar]
  13. Denoeud F., Vergnaud G., Vergnaud G. Identification of polymorphic tandem repeats by direct comparison of genome sequence from different bacterial strains: A web-based resource. BMC Bioinformatics. 2004;5:4. doi: 10.1186/1471-2105-5-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Denoeud F., Vergnaud G., Benson G., Vergnaud G., Benson G., Benson G. Predicting human minisatellite polymorphism. Genome Res. 2003;13:856–867. doi: 10.1101/gr.574403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Ellegren H. Microsatellites: Simple sequences with complex evolution. Nat. Rev. Genet. 2004;5:435–445. doi: 10.1038/nrg1348. [DOI] [PubMed] [Google Scholar]
  16. Fidalgo M., Barrales R.R., Ibeas J.I., Jimenez J., Barrales R.R., Ibeas J.I., Jimenez J., Ibeas J.I., Jimenez J., Jimenez J. Adaptive evolution by mutations in the FLO11 gene. Proc. Natl. Acad. Sci. 2006;103:11228–11233. doi: 10.1073/pnas.0601713103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Fondon J.W., Garner H.R., Garner H.R. Molecular origins of rapid and continuous morphological evolution. Proc. Natl. Acad. Sci. 2004;101:18058–18063. doi: 10.1073/pnas.0408118101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gatchel J.R., Zoghbi H.Y., Zoghbi H.Y. Diseases of unstable repeat expansion: Mechanisms and common principles. Nat. Rev. Genet. 2005;6:743–755. doi: 10.1038/nrg1691. [DOI] [PubMed] [Google Scholar]
  19. Imwong M., Sudimack D., Pukrittayakamee S., Osorio L., Carlton J.M., Day N.P., White N.J., Anderson T.J., Sudimack D., Pukrittayakamee S., Osorio L., Carlton J.M., Day N.P., White N.J., Anderson T.J., Pukrittayakamee S., Osorio L., Carlton J.M., Day N.P., White N.J., Anderson T.J., Osorio L., Carlton J.M., Day N.P., White N.J., Anderson T.J., Carlton J.M., Day N.P., White N.J., Anderson T.J., Day N.P., White N.J., Anderson T.J., White N.J., Anderson T.J., Anderson T.J. Microsatellite variation, repeat array length, and population history of Plasmodium vivax. Mol. Biol. Evol. 2006;23:1016–1018. doi: 10.1093/molbev/msj116. [DOI] [PubMed] [Google Scholar]
  20. Karlin S., Burge C., Burge C. Trinucleotide repeats and long homopeptides in genes and proteins associated with nervous system disease and development. Proc. Natl. Acad. Sci. 1996;93:1560–1565. doi: 10.1073/pnas.93.4.1560. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kolpakov R., Bana G., Kucherov G., Bana G., Kucherov G., Kucherov G. mreps: Efficient and flexible detection of tandem repeats in DNA. Nucleic Acids Res. 2003;31:3672–3678. doi: 10.1093/nar/gkg617. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Le Flèche P., Fabre M., Denoeud F., Koeck J.L., Vergnaud G., Fabre M., Denoeud F., Koeck J.L., Vergnaud G., Denoeud F., Koeck J.L., Vergnaud G., Koeck J.L., Vergnaud G., Vergnaud G. High resolution, on-line identification of strains from the Mycobacterium tuberculosis complex based on tandem repeat typing. BMC Microbiol. 2002;2:37. doi: 10.1186/1471-2180-2-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Leclerc M.C., Durand P., Gauthier C., Patot S., Billotte N., Menegon M., Severini C., Ayala F.J., Renaud F., Durand P., Gauthier C., Patot S., Billotte N., Menegon M., Severini C., Ayala F.J., Renaud F., Gauthier C., Patot S., Billotte N., Menegon M., Severini C., Ayala F.J., Renaud F., Patot S., Billotte N., Menegon M., Severini C., Ayala F.J., Renaud F., Billotte N., Menegon M., Severini C., Ayala F.J., Renaud F., Menegon M., Severini C., Ayala F.J., Renaud F., Severini C., Ayala F.J., Renaud F., Ayala F.J., Renaud F., Renaud F. Meager genetic variability of the human malaria agent Plasmodium vivax. Proc. Natl. Acad. Sci. 2004;101:14455–14460. doi: 10.1073/pnas.0405186101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Levdansky E., Romano J., Shadkchan Y., Sharon H., Verstrepen K.J., Fink G.R., Osherov N., Romano J., Shadkchan Y., Sharon H., Verstrepen K.J., Fink G.R., Osherov N., Shadkchan Y., Sharon H., Verstrepen K.J., Fink G.R., Osherov N., Sharon H., Verstrepen K.J., Fink G.R., Osherov N., Verstrepen K.J., Fink G.R., Osherov N., Fink G.R., Osherov N., Osherov N. Coding tandem repeats generate diversity in Aspergillus fumigatus genes. Eukaryot. Cell. 2007;6:1380–1391. doi: 10.1128/EC.00229-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Li G., Zhang H., Lv J., Hou P., Wang H., Zhang H., Lv J., Hou P., Wang H., Lv J., Hou P., Wang H., Hou P., Wang H., Wang H. Tandem repeats polymorphism of MUC20 is an independent factor for the progression of immunoglobulin A nephropathy. Am. J. Nephrol. 2006;26:43–49. doi: 10.1159/000091785. [DOI] [PubMed] [Google Scholar]
  26. Lopes J., Ribeyre C., Nicolas A., Ribeyre C., Nicolas A., Nicolas A. Complex minisatellite rearrangements generated in the total or partial absence of Rad27/hFEN1 activity occur in a single generation and are Rad51 and Rad52 dependent. Mol. Cell. Biol. 2006;26:6675–6689. doi: 10.1128/MCB.00649-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Näslund K., Saetre P., von Salome J., Bergstrom T.F., Jareborg N., Jazin E., Saetre P., von Salome J., Bergstrom T.F., Jareborg N., Jazin E., von Salome J., Bergstrom T.F., Jareborg N., Jazin E., Bergstrom T.F., Jareborg N., Jazin E., Jareborg N., Jazin E., Jazin E. Genome-wide prediction of human VNTRs. Genomics. 2005;85:24–35. doi: 10.1016/j.ygeno.2004.10.009. [DOI] [PubMed] [Google Scholar]
  28. O'Dushlaine C.T., Shields D.C., Shields D.C. Tools for the identification of variable and potentially variable tandem repeats. BMC Genomics. 2006;7:290. doi: 10.1186/1471-2164-7-290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. O'Dushlaine C.T., Edwards R.J., Park S.D., Shields D.C., Edwards R.J., Park S.D., Shields D.C., Park S.D., Shields D.C., Shields D.C. Tandem repeat copy-number variation in protein-coding regions of human genes. Genome Biol. 2005;6:R69. doi: 10.1186/gb-2005-6-8-r69. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Orgel L.E., Crick F.H., Crick F.H. Selfish DNA: The ultimate parasite. Nature. 1980;284:604–607. doi: 10.1038/284604a0. [DOI] [PubMed] [Google Scholar]
  31. Paques F., Haber J.E., Haber J.E. Multiple pathways of recombination induced by double-strand breaks in Saccharomyces cerevisiae. Microbiol. Mol. Biol. Rev. 1999;63:349–404. doi: 10.1128/mmbr.63.2.349-404.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Rando O.J., Verstrepen K.J., Verstrepen K.J. Timescales of genetic and epigenetic inheritance. Cell. 2007;128:655–668. doi: 10.1016/j.cell.2007.01.023. [DOI] [PubMed] [Google Scholar]
  33. Rice P., Longden I., Bleasby A., Longden I., Bleasby A., Bleasby A. EMBOSS: The European molecular biology open software suite. Trends Genet. 2000;16:276–277. doi: 10.1016/s0168-9525(00)02024-2. [DOI] [PubMed] [Google Scholar]
  34. Richard G.F., Dujon B., Dujon B. Molecular evolution of minisatellites in hemiascomycetous yeasts. Mol. Biol. Evol. 2006;23:189–202. doi: 10.1093/molbev/msj022. [DOI] [PubMed] [Google Scholar]
  35. Russell B., Suwanarusk R., Lek-Uthai U., Suwanarusk R., Lek-Uthai U., Lek-Uthai U. Plasmodium vivax genetic diversity: Microsatellite length matters. Trends Parasitol. 2006;22:399–401. doi: 10.1016/j.pt.2006.06.013. [DOI] [PubMed] [Google Scholar]
  36. Schroeder J.A., Masri A.A., Adriance M.C., Tessier J.C., Kotlarczyk K.L., Thompson M.C., Gendler S.J., Masri A.A., Adriance M.C., Tessier J.C., Kotlarczyk K.L., Thompson M.C., Gendler S.J., Adriance M.C., Tessier J.C., Kotlarczyk K.L., Thompson M.C., Gendler S.J., Tessier J.C., Kotlarczyk K.L., Thompson M.C., Gendler S.J., Kotlarczyk K.L., Thompson M.C., Gendler S.J., Thompson M.C., Gendler S.J., Gendler S.J. MUC1 overexpression results in mammary gland tumorigenesis and prolonged alveolar differentiation. Oncogene. 2004;23:5739–5747. doi: 10.1038/sj.onc.1207713. [DOI] [PubMed] [Google Scholar]
  37. Sherman F., Fink G.R., Hicks J., Fink G.R., Hicks J., Hicks J. Methods in yeast genetics. Cold Spring Harbor Laboratory Press; Cold Spring Harbor, NY: 1991. [Google Scholar]
  38. Sia E.A., Kokoska R.J., Dominska M., Greenwell P., Petes T.D., Kokoska R.J., Dominska M., Greenwell P., Petes T.D., Dominska M., Greenwell P., Petes T.D., Greenwell P., Petes T.D., Petes T.D. Microsatellite instability in yeast: Dependence on repeat unit size and DNA mismatch repair genes. Mol. Cell. Biol. 1997;17:2851–2858. doi: 10.1128/mcb.17.5.2851. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Stranger B.E., Forrest M.S., Dunning M., Ingle C.E., Beazley C., Thorne N., Redon R., Bird C.P., de Grassi A., Lee C., Forrest M.S., Dunning M., Ingle C.E., Beazley C., Thorne N., Redon R., Bird C.P., de Grassi A., Lee C., Dunning M., Ingle C.E., Beazley C., Thorne N., Redon R., Bird C.P., de Grassi A., Lee C., Ingle C.E., Beazley C., Thorne N., Redon R., Bird C.P., de Grassi A., Lee C., Beazley C., Thorne N., Redon R., Bird C.P., de Grassi A., Lee C., Thorne N., Redon R., Bird C.P., de Grassi A., Lee C., Redon R., Bird C.P., de Grassi A., Lee C., Bird C.P., de Grassi A., Lee C., de Grassi A., Lee C., Lee C., et al. Relative impact of nucleotide and copy number variation on gene expression phenotypes. Science. 2007;315:848–853. doi: 10.1126/science.1136678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Suykens J.A.K., Van Gestel T., De Brabanter J., De Moor B.L.R., Vandewalle J., Van Gestel T., De Brabanter J., De Moor B.L.R., Vandewalle J., De Brabanter J., De Moor B.L.R., Vandewalle J., De Moor B.L.R., Vandewalle J., Vandewalle J. Least squares support vector machines. World Scientific; Singapore: 2002. [Google Scholar]
  41. Thomas E.E. Short, local duplications in eukaryotic genomes. Curr. Opin. Genet. Dev. 2005;15:640–644. doi: 10.1016/j.gde.2005.09.008. [DOI] [PubMed] [Google Scholar]
  42. Verstrepen K.J., Reynolds T.B., Fink G.R., Reynolds T.B., Fink G.R., Fink G.R. Origins of variation in the fungal cell surface. Nat. Rev. Microbiol. 2004;2:533–540. doi: 10.1038/nrmicro927. [DOI] [PubMed] [Google Scholar]
  43. Verstrepen K.J., Jansen A., Lewitter F., Fink G.R., Jansen A., Lewitter F., Fink G.R., Lewitter F., Fink G.R., Fink G.R. Intragenic tandem repeats generate functional variability. Nat. Genet. 2005;37:986–990. doi: 10.1038/ng1618. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Viguera E., Canceill D., Ehrlich S.D., Canceill D., Ehrlich S.D., Ehrlich S.D. Replication slippage involves DNA polymerase pausing and dissociation. EMBO J. 2001;20:2587–2595. doi: 10.1093/emboj/20.10.2587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Voynov V., Verstrepen K.J., Jansen A., Runner V.M., Buratowski S., Fink G.R., Verstrepen K.J., Jansen A., Runner V.M., Buratowski S., Fink G.R., Jansen A., Runner V.M., Buratowski S., Fink G.R., Runner V.M., Buratowski S., Fink G.R., Buratowski S., Fink G.R., Fink G.R. Genes with internal repeats require the THO complex for transcription. Proc. Natl. Acad. Sci. 2006;103:14423–14428. doi: 10.1073/pnas.0606546103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Wierdl M., Dominska M., Petes T.D., Dominska M., Petes T.D., Petes T.D. Microsatellite instability in yeast: Dependence on the length of the microsatellite. Genetics. 1997;146:769–779. doi: 10.1093/genetics/146.3.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Wren J.D., Forgacs E., Fondon J.W., Pertsemlidis A., Cheng S.Y., Gallardo T., Williams R.S., Shohet R.V., Minna J.D., Garner H.R., Forgacs E., Fondon J.W., Pertsemlidis A., Cheng S.Y., Gallardo T., Williams R.S., Shohet R.V., Minna J.D., Garner H.R., Fondon J.W., Pertsemlidis A., Cheng S.Y., Gallardo T., Williams R.S., Shohet R.V., Minna J.D., Garner H.R., Pertsemlidis A., Cheng S.Y., Gallardo T., Williams R.S., Shohet R.V., Minna J.D., Garner H.R., Cheng S.Y., Gallardo T., Williams R.S., Shohet R.V., Minna J.D., Garner H.R., Gallardo T., Williams R.S., Shohet R.V., Minna J.D., Garner H.R., Williams R.S., Shohet R.V., Minna J.D., Garner H.R., Shohet R.V., Minna J.D., Garner H.R., Minna J.D., Garner H.R., Garner H.R. Repeat polymorphisms within gene regions: Phenotypic and evolutionary implications. Am. J. Hum. Genet. 2000;67:345–356. doi: 10.1086/303013. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES