Accurate gene-tree reconstruction by learning gene- and species-specific substitution rates across multiple complete genomes

Abstract

Comparative genomics provides a general methodology for discovering functional DNA elements and understanding their evolution. The availability of many related genomes enables more powerful analyses, but requires rigorous phylogenetic methods to resolve orthologous genes and regions. Here, we use 12 recently sequenced Drosophila genomes and nine fungal genomes to address the problem of accurate gene-tree reconstruction across many complete genomes. We show that existing phylogenetic methods that treat each gene tree in isolation show large-scale inaccuracies, largely due to insufficient phylogenetic information in individual genes. However, we find that gene trees exhibit common properties that can be exploited for evolutionary studies and accurate phylogenetic reconstruction. Evolutionary rates can be decoupled into gene-specific and species-specific components, which can be learned across complete genomes. We develop a phylogenetic reconstruction methodology that exploits these properties and achieves significantly higher accuracy, addressing the species-level heterotachy and enabling studies of gene evolution in the context of species evolution.

Comparative genomics of multiple related species has emerged as a powerful approach for the systematic discovery of evolutionarily conserved functional elements (Mouse Genome Sequencing Consortium 2002; Kellis et al. 2003; Ureta-Vidal et al. 2003; Miller et al. 2004; Richards et al. 2005), and for the identification of duplicated and rapidly evolving genes involved in the emergence of new functions (Jaillon et al. 2004; Kellis et al. 2004; Dehal and Boore 2005). Both types of analysis rely on an accurate mapping of orthologous and paralogous genes and regions across the species compared, accounting for all duplication and loss events (Fitch 1970).

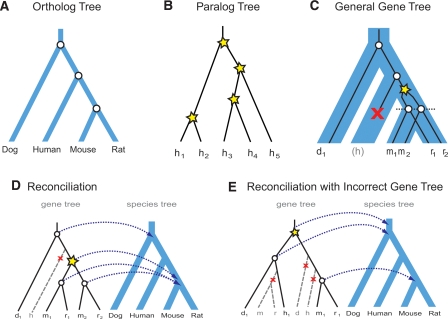
Phylogenetic trees provide a rigorous framework for genome comparison (Woese et al. 1990; Baldauf et al. 2000; Murphy et al. 2001), naturally capturing gene duplication and loss, and allowing varying rates of sequence divergence across evolutionary time (Goodman et al. 1979; Page 1994; Eisen 1998). Phylogenies of orthologous genes across species can be used to study species evolution, each internal node representing a speciation event (Fig. 1A). Similarly, phylogenies of paralogous genes within a species can be used to study gene-family expansions, each internal node representing a gene-duplication event (Fig. 1B). Phylogenetics in the context of multiple complete genomes, known as phylogenomics (Eisen 1998), combines multiple orthologs and paralogs across many species in a general gene tree (Fig. 1C) and enables a much richer set of questions than ortholog trees or paralog trees alone (Ma et al. 2000; Zmasek and Eddy 2002; Storm and Sonnhammer 2003; Arvestad et al. 2004; Dufayard et al. 2005; Durand et al. 2006; Li et al. 2006; Huerta-Cepas et al. 2007). Its internal nodes thus represent both speciation and duplication events, and their ordering dictates the evolutionary history of a gene family across the species compared (Goodman et al. 1979; Page 1994). Ortholog and paralog relationships can be readily inferred by mapping general gene trees to the known phylogeny relating the species (Fig. 1D), in a process known as reconciliation. Reconciliation assumes that the species tree is known, and that the gene tree is correct. However, these assumptions have been found to be frequently violated (Rokas et al. 2003; Li et al. 2006), and erroneous gene trees can lead to incorrect ortholog and paralog assignments and many extraneous duplications and losses (Fig. 1E), thus distorting inferred patterns of gene-family expansion and contraction (Hahn 2007).

Figure 1.

Relationship between gene trees and species trees. (A) Ortholog trees used to study species evolution. Each internal node represents a speciation event (circle). (B) Paralog trees used to study gene family expansions within a single species. Each internal node represents a duplication event (star). (C) General gene trees combine both orthologs and paralogs across multiple species to infer gene duplication (star), gene loss (×), and speciation (circle) events. Each gene is named with the first letter of the corresponding species. The gene tree (black lines) can be viewed as evolving inside the species tree (blue area), implying coordinated speciation events at branching points in the species tree (dotted line). (D) Gene duplication and loss events are inferred by reconciling a gene tree to a species tree, mapping each gene-tree node to its closest species-tree common ancestor node (arrows). (E) When the gene tree is incorrect, many spurious events will be inferred. In this example, a common misplacement of rodents due to long-branch-attraction leads to four spurious events (one duplication and at least three losses).

In this work, we use the 12 recently sequenced Drosophila genomes (Drosophila 12 Genomes Consortium 2007) and nine publicly available fungal genomes (Wolfe and Shields 1997) to study the properties and reconstruction of gene family evolution in the context of complete genomes. Our work has three key contributions:

• We show that many gene-tree incongruences in both flies and fungi are likely due to inaccuracies in phylogenetic reconstruction stemming from the lack of informative sites in the short alignments of individual genes. Indeed, we find that incongruences are most pronounced for short alignments and slow-evolving genes, and lead to the same alternate topologies as found in simulation due to reconstruction inaccuracies, suggesting that they are primarily methodological rather than biological.

• We show that the substitution rate of any gene can be expressed as the product of a gene-specific rate, dictated by the selective constraints on the gene’s function (Dickerson 1971; Bromham and Penny 2003), and a species-specific rate, dictated by the reproductive and population dynamics of each lineage (Ohta and Kimura 1971), and we provide specific distributions for the two. This decomposition provides a surprisingly good fit to actual phylogenies in both flies and fungi, and can be used for accurate gene-tree reconstruction.

• We present a probabilistic framework for distance-based gene-tree reconstruction in complete genomes, based on rate-distribution parameters learned from alignments of unambiguous orthologs and implemented in a publicly available tool, SPIDIR. We used SPIDIR to infer gene trees in both flies and fungi, and show that it leads to significantly higher reconstruction accuracies. In particular, we find that our strategy can address the long-branch attraction problem for species-level heterotachy (Bergsten 2005; Philippe et al. 2005), by learning to expect longer branches for faster-evolving lineages.

Results

Incongruences and inaccuracies of gene trees for syntenic orthologs

Numerous studies have addressed the accuracy of phylogeny reconstruction methods using mainly simulated alignments (Saitou and Imanishi 1989; Kuhner and Felsenstein 1994; Tateno et al. 1994; Philippe et al. 2005) and, in some cases, microevolution observed experimentally (Hillis et al. 1994; Bull et al. 1997; Woods et al. 2006). With multiple complete genomes, regions of conserved gene order (synteny) provide a natural test for phylogenetic methods (Rokas et al. 2003; Ciccarelli et al. 2006), since all genes within these regions are typically coinherited from a single gene in the common ancestor of the species (Fig. 2A). Therefore, in the absence of horizontal gene transfer, gene conversions, and incomplete lineage sorting (Avise et al. 1983; Koonin et al. 2001), their phylogenies should be perfectly congruent to the species phylogeny. However, recent studies have shown that phylogenetic trees obtained for different orthologs frequently disagree with the species phylogeny, resulting in large-scale incongruences (Rokas et al. 2003; Li et al. 2006; Hahn 2007; Huerta-Cepas et al. 2007).

Figure 2.

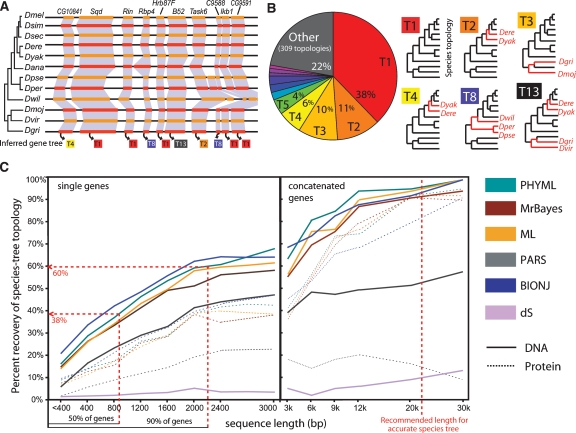
Large-scale gene-tree incongruence correlates with gene length. (A) Unambiguously orthologous genes in syntenic regions show diverse PHYML trees, even for consecutive genes (topologies numbered according to their genome-wide frequency). (B) Frequency and topology of most abundant ML gene trees for syntenic orthologs across 12 fly genomes. Discrepancies from the species topology (red branches) correspond to rotations of short internal branches. (C) Percentage of gene trees congruent to the species phylogeny correlates with gene length, regardless of the method used. DNA-based reconstruction, which uses threefold as many aligned positions, consistently outperformed protein-based reconstruction across all methods.

Indeed, using 5154 syntenic one-to-one orthologs across 12 Drosophila genomes and 739 syntenic one-to-one orthologs across nine fungal genomes (see Methods), we found that existing phylogenetic methods recovered the known species topology (Drosophila 12 Genomes Consortium 2007; Stark et al. 2007), denoted T1, for only a small minority of gene trees (Fig. 2B), between 24% and 42% for flies and between 22% and 31% for fungi. This was true across all methods tested, PHYML (Guindon and Gascuel 2003), DNAML (Felsenstein 2005), MrBayes (Ronquist and Huelsenbeck 2003), BIONJ (Gascuel 1997), Parsimony (Felsenstein 2005), for both protein-coding and nucleotide alignments, and using various substitution models (HKY) (Hasegawa et al. 1985), JTT (Jones et al. 1992), and synonymous-substitution dS (Yang 1997) (see Supplemental information). Moreover, no alternate topology was systematically favored: The next most frequent topologies for PHYML, denoted T2–T5, covered between 4% and 11% of fly trees, and an additional 305 topologies accounted for the remaining 31% of trees (Fig. 2B).

Biological mechanisms proposed for gene-tree incongruence, such as incomplete lineage sorting of pre-speciation alleles (Pollard et al. 2006; Wong et al. 2007), may be contributing to the observed incongruences, but are unlikely to explain all incongruent gene trees. Instead, we found multiple lines of evidence suggesting that algorithmic inaccuracies, rather than biological reasons, are likely responsible for a large fraction of the incongruent gene trees.

First, we found a clear, monotonic increase in recovery of congruent gene trees with the length of the corresponding genes (Fig. 2C), as expected for algorithmic accuracy based on simulation studies (Huelsenbeck 1995). For the length of a typical gene alignment (940 ungapped nucleotides), all methods showed accuracies around 40%. These were as low as 25% for shorter genes (<800 nt) and rose up to 60% for the longest genes (>2300 nt, corresponding to <10% of genes). The observed recovery vs. length correlation continued with increasing alignment lengths (90% for 20,000 nt, obtained by concatenating 20 randomly chosen genes) in agreement with lengths typically recommended to produce accurate species trees (Rokas et al. 2003; Ciccarelli et al. 2006). Of course, such lengths are unrealistic for individual genes, and concatenation is not an option for accurate gene-tree reconstruction.

Second, we found that genes with moderate divergence rates showed the highest performance, while most errors were found in very slow and very fast evolving genes. Reconstruction accuracy peaked for genes with 40%–50% sequence identity (reaching 48% accuracy), but was significantly reduced for slower evolving genes (25% accuracy for 70% identity) or faster evolving genes (35% accuracy for 20% identity; Supplemental Fig. S6). This can also be attributed to a lack of phylogenetically informative sites in slow-evolving genes (lacking sufficient events to resolve phylogenetic divergence order) and also in fast-evolving genes (as sites with many independent substitutions do not distinguish between different topologies). In contrast, incomplete lineage sorting is not expected to show such correlations.

Third, simulated phylogenies with the known species topology and similar branch lengths resulted in the same alternate topologies T1–T5 at comparable frequencies (e.g., 4%–11% vs. 3%–5% for PHYML in flies, Supplemental Fig. S3C), suggesting that even the most frequent incongruent topologies may result from reconstruction errors. In fact, the frequency of T2 + T4 corresponding to previously reported incomplete lineage sorting (Pollard et al. 2006; Wong et al. 2007) only differed by 8% between simulation and real data (9% vs. 17%), providing an estimate of the extent of incomplete lineage sorting. The correct phylogeny was recovered for 72% of simulated gene trees on average (an ∼30% increase over real data), potentially reflecting reduced discrepancies from model assumptions in simulated alignments (since the same model of evolution was used for reconstruction and simulation, while real alignments may violate this model), and potentially attributable to incomplete lineage sorting in true phylogenies. However, even if the increase is entirely due to incomplete lineage sorting in true phylogenies, it would only explain incongruences in, at most, 30% of trees, while 62% of fly trees and 76% of fungal trees were found to be incongruent. Thus, a significant portion of incongruences are likely due to reconstruction inaccuracies.

Lastly, if alternate topologies were due to biological reasons rather than methodological inaccuracies, we would expect them to be recovered with multiple methods, show high bootstrap support, and have significantly higher likelihood, neither of which was the case. In fact, the frequencies of T2–T5 were reduced from 4%–11% to 1%–5% when all methods were required to agree (Supplemental Fig. S3D), and the phylogenetic trees that disagreed with the species topology showed significantly lower bootstrap support values (Supplemental Fig. S17). In fact, amongst the 3102 gene trees where an alternative topology was selected by PHYML, only 5.7% of these had a significantly higher likelihood than the topology congruent to the species tree (SH test P < 0.01) (PAUP) (Shimodaira and Hasegawa 1999), suggesting that many of these alternative topologies have insufficient support.

We conclude that a significant fraction of observed phylogenetic incongruences are due to inaccuracies in phylogenetic reconstruction (attributable to a lack of informative sites in the typical gene), and that additional information is necessary to increase the accuracy of gene-tree reconstruction. When gene trees are studied in isolation, it is likely that such information may not exist. However, in the phylogenomic setting, where thousands of gene trees involve only a relatively small number of species, there is an opportunity to learn common features shared among different gene trees, which can be used to guide gene-tree reconstruction. In the following section, we study fly and fungal gene trees and propose a model capturing their common properties. We then develop a novel inference algorithm that can use this information for accurate gene-tree reconstruction in the phylogenomic setting.

Gene- and species-specific substitution rates in phylogenomics

To take advantage of the phylogenomic setting, we sought to capture the fact that thousands of gene trees all evolve within the same species tree, and explicitly model their common properties. We expressed the substitution rate b_i of each gene in each lineage as the product of two independent rates (Fig. 3A): a gene-specific substitution rate g dictated by the selective constraints imposed on the function of the gene (Bromham and Penny 2003), and a species-specific substitution rate s_i dictated by the time interval and evolutionary dynamics of each lineage i (e.g., population size, generation time, mating behavior, overall mutation rate). Our gene-specific rate is similar to site-specific scaling factors used in previous studies (Yang 1994; Felsenstein and Churchill 1996; Siepel et al. 2005; Kim and Pritchard 2007), and the independence of the two rates agrees with recently reported correlations in mammals and hominids (Cooper et al. 2003; Chimpanzee Sequencing and Analysis Consortium 2005).

Figure 3.

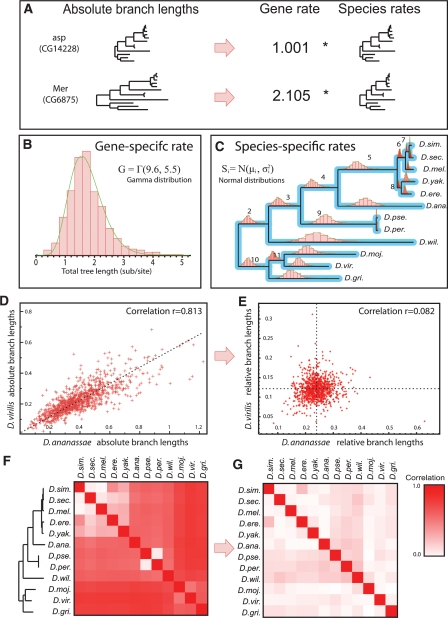
Evolutionary rates decoupled into gene-specific and species-specific components. (A) Syntenic ortholog trees appear as scaled versions of a common species tree, and can be expressed as the product of a gene-specific rate and species-specific rates. (B) Gene-specific rates of 5154 fly orthologs follow a gamma distribution. (C) Species-specific rates for each lineage follow normal distributions. Means and standard deviations shown in Supplemental Figure S7. (D) Unnormalized (absolute) branch lengths are highly correlated. Lengths for D. virilis and D. ananassae since their last common ancestor across the 5154 orthologs show correlation r = 0.813. (E) Relative branch lengths become independent after normalization by the gene-specific rate (r = 0.082). (F) Correlations are high for all species pairs before normalization, except for very closely related species. (G) Relative lengths are uncorrelated for all species pairs, showing that gene-specific rate accounts for their initial dependencies.

To derive the properties and specific distributions for gene- and species-specific substitution rates, we revisited our 5154 syntenic fly orthologs, this time requiring each gene-tree topology to be congruent to the species-tree topology, and inferring branch lengths from pairwise distances by maximum likelihood (see Methods). From our model definition, we expect the gene rate to be proportional to the total branch length for any tree. Thus, for each resulting gene tree, we can estimate the gene rate g as the sum of all “absolute” branch lengths b_i, (representing the overall substitution rate across the entire tree), and the species-specific rate s_i for each branch as its “relative” length b_i/g after normalization by the gene rate (representing the fraction of substitutions attributable to that lineage). We found that the gene rate g was distributed as a gamma distribution (Fig. 3B), as expected for a rate (Uzzell and Corbin 1971). We also found that each s_i was distributed as a normal distribution (Fig. 3C), reflecting small fluctuations around the expected mean rate μ_i for each branch, given the stochastic nature of nucleotide substitution. Relative branch lengths b_i/g showed tighter distributions than absolute branch lengths b_i (typically with standard deviations between 1/3 and 1/4 of the mean; Supplemental Figs. S7–S12).

Our model makes the assumption that species-specific rates are independent of each other and of the gene rate. This assumption implies specific properties of gene trees, which we found to hold in the fungal and fly genomes. First, we would expect gene trees to be uniformly longer or shorter across different orthologs, appearing as scaled versions of an average gene tree, due to the common species rates s_i across gene trees. Indeed, pairs of gene trees showed strong correlations to each other: For example, Merlin and abnormal spindle showed correlation r = 0.96 (Fig. 3A), and 93% of genes showed correlations above r = 0.8 to the average gene tree (tree with average branch lengths across all genes) (Supplemental Fig. S14). Second, we would expect strong correlations between the absolute branch lengths from any pair of species, stemming from the common gene rate g. Indeed, the average pairwise correlation of absolute branch lengths was 0.61 across all pairs of species (Fig. 3F). Lastly, we would expect relative branch lengths, representing species-specific rates, to be independent of each other if their correlation was truly due primarily to the common gene-specific rate g, and indeed, we found that the average pairwise correlation of relative branch lengths dropped to 0.09 after normalization by the gene rate (Fig. 3G). For example, the correlation between Drosophila ananassae and Drosophila virilis was r = 0.81 for absolute branch lengths and 0.082 for relative branch lengths after normalization (Fig. 3D,E). All of these relationships, reported here for flies, also held for mammals and fungi (see Supplemental material).

SPIDIR: A machine-learning framework for phylogenomic gene-tree reconstruction

Our results suggest that substitution rates can be decoupled into gene-specific and species-specific rates g and s_i, and that these are well approximated by independent gamma and normal distributions, respectively. Based on these properties, we develop a generative model for gene-tree evolution across multiple complete genomes: A gene tree is generated as the product of a gene-specific rate g, sampled from a gamma distribution g∼G = Γ(α, β), and a species-specific rate s_i for each lineage, sampled from a normal distrtibution s_i∼S_i = N(μ_i, σ_i²), each distributed independently of each other.

We used this generative model to develop a novel phylogenetic reconstruction method, called SPIDIR, for SPecies-Informed DIstance-based Reconstruction. Similarly to other likelihood-based methods, we search through a large number of gene tree topologies (Huelsenbeck and Ronquist 2001; Guindon and Gascuel 2003), evaluate the likelihood of each, and guide the search toward a maximum-likelihood tree. In contrast to existing methods, both phylogenetic (Gascuel 1997; Guindon and Gascuel 2003; Ronquist and Huelsenbeck 2003; Felsenstein 2005) and phylogenomic (Ma et al. 2000; Zmasek and Eddy 2002; Storm and Sonnhammer 2003; Arvestad et al. 2004; Dufayard et al. 2005; Durand et al. 2006), our algorithm works in two stages, first learning a model of gene and species evolution based on unambiguous orthologs, and then using this model for gene-tree reconstruction.

In the first stage (learning), we estimate the parameters of gene- and species-rate distributions based on alignments of unambiguous one-to-one orthologs across the species compared. As we focus on gene-tree reconstruction, we assume that the species tree is known, or can be reliably inferred using genome-scale information (e.g., using multigene analyses) (Rokas et al. 2003; Gadagkar et al. 2005; Ané et al. 2007; Edwards et al. 2007), or based on unique transposon insertion events (Kriegs et al. 2006). We also assume that a training set of genes with clear one-to-one orthology can be established, with phylogenies that are most likely congruent to the species tree (e.g., by using syntenic one-to-one orthologs, which, in the 12 fly species, include about one-third of all genes). Using the known species tree and multiple alignments of these unambiguous orthologs, we construct gene trees that are congruent to the species topology and estimate their absolute branch lengths b_i using least-square error (see Methods). As each gene tree has exactly one gene from each species, we use the total tree length Σ_i(b_i) as an estimate of the gene rate g, and the relative branch lengths b_i/g as estimates of individual s_i (see Methods). This results in thousands of g and s_i estimates, to which we fit gamma and normal distributions, respectively, to infer (α, β, μ_i, σ_i) parameters.

In the second stage (inference), we use our model to reconstruct phylogenies of the remaining genes, which may contain duplication and loss events (Fig. 4). In this work, we use our model for distance-based reconstruction, and thus, the input for the inference stage is a pairwise distance matrix M (Fig. 4A) inferred from multiple sequence alignments of the genes in question (extensions directly incorporating sequence characters are possible, but will be the subject of future work). We then search across many proposed topologies to find the maximum-likelihood gene tree. For each proposed gene-tree topology T, branch lengths b are estimated from the distance matrix M using least-square error (Bryant and Waddell 1998) (Fig. 4B,E), and the likelihoods of these branch lengths b_i are calculated according to our model, based on the learned parameters (α, β, μ_i, σ_i). When the proposed gene tree is congruent to the species tree (Fig. 4B–D), the rate estimation and probability calculation are straightforward: The probability of the observed branch lengths is simply the product of probabilities of the overall gene rate and the observed relative branch lengths: P(b|G,S) = P(g|G) ∏_i [P(b_i/g|s_i)], each gene-tree branch b_i uniquely mapping to a species-tree branch. When the proposed gene tree contains duplications and losses (Fig. 4E–G), our gene-rate estimate accounts for the missing data (see Methods), and the probability of relative branch lengths is estimated according to derived rate distributions, possibly spanning multiple species branches (see Methods). The nature of gene and species rate distributions within our model enables efficient likelihood computations for any gene-tree to species-tree reconciliation (see Methods).

Figure 4.

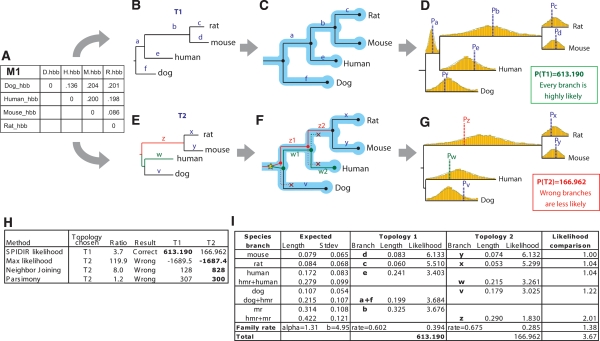
Evaluating gene-tree likelihood using learned rate distributions. (A) Observed distance matrix for mammalian orthologs of hemoglobin-β estimated from an HKY model based on multiple alignments of the four genes. (B–D) Likelihood evaluation for proposed topology T1. (B) Distance matrix M1 is mapped onto the proposed topology T1, resulting in branch lengths a–f. (C) Gene-tree branches are mapped to species-tree branches by reconciliation. Since the gene-tree topology is congruent to the species tree, each branch is mapped to exactly one lineage. (D) The probability of each branch length is evaluated based on species-specific rate distributions. T1 results in overall high-likelihood density, since the resulting relative branch lengths a–f fall near the average rate for the corresponding species-specific distribution (dotted lines). (E–G) Likelihood evaluation for proposed topology T2. (E) Distance matrix M1 is mapped onto the proposed topology T2, resulting in branch lengths v–z. (F) Reconciliation results in one gene duplication and three gene losses; gene-tree branches w and z now span two species-tree branches each and are evaluated based on accordingly longer species-tree rate distributions obtained by summing two normals. (G) The resulting branch lengths z, w, and v show large discrepancies from the average species-rate distributions, resulting in a 3.7-fold lower likelihood for branch lengths corresponding to the incorrect topology T2. (H) All other methods select the incorrect topology T2 due to long-branch attraction, even though the hemoglobin-β genes are unambiguous one-to-one orthologs and should follow the known mammalian phylogeny T1. (I) Branch-level comparison of likelihood scores shows consistently higher scores for T1, the correct topology. Notice that the gene-rate likelihood for T1 is different from that for T2, as the two topologies imply different gene family rates.

As each tree is evaluated according to the distributions learned across the genomes, this framework allows us to distinguish between gene trees with unlikely branch lengths and gene trees whose observed branch lengths fit the learned distributions. For example, the correct gene-tree topology T1 (Kriegs et al. 2006) for orthologous mammalian hemoglobin-beta genes showed more than a 3.5-fold higher likelihood than an alternative topology T2 (Fig. 4), each branch providing a much closer fit to the expected rate distributions, and thus resulting in consistently higher likelihood values (Fig. 4I): The ancestral rodent branch alone showed a twofold increase in likelihood for the correct topology, as the observed length b is much closer to the mean of the corresponding distribution, while the corresponding branch length z in the alternate topology is significantly shorter than would be expected if the gene-tree topology was truly T2. In contrast, all traditional methods systematically selected the incorrect topology T2 for the hemoglobin-beta genes because of long-branch attraction due to the faster-evolving rodent branch (tree rooted by fish ortholog): Neighbor-joining showed eightfold higher bootstrap support for T2, parsimony showed a slight preference for T2, and traditional maximum likelihood showed 100-fold higher likelihood for T2 (Fig. 4H; Supplemental Fig. S18). This effect has also been observed for other genes (Cannarozzi et al. 2006). Our method was able to resolve the correct topology T1 because it expected a longer branch for the rodent lineage, as they have an overall longer species-rate distribution S_i.

When paralogs were compared, and the correct gene-tree topology differed from the species-tree topology, our method again led to the correct answer (Supplemental Fig. S16): Comparing rodent hemoglobin-beta to the paralogous human and dog hemoglobin-alpha correctly resulted in T2, since hemoglobin-alpha and -beta are paralogs resulting from an ancestral duplication well before the mammalian speciation. In this case, the likelihood of topology T1 dropped 50-fold, while the likelihood of topology T2 increased, leading to 14-fold higher likelihood for T2. Thus, our method was not biased to always select the species topology when the correct gene-tree topology differed, and was able to resolve paralogous gene trees even in the presence of gene duplication and loss.

Learning species-specific rates leads to increased accuracy

We implemented and tested two versions of SPIDIR (available online at http://compbio.mit.edu/spidir), one using solely rate-based information to guide the reconstruction without penalizing duplication and loss, and one with an explicit penalty for duplication, similar in nature to those described elsewhere (Goodman et al. 1979; Page and Charleston 1997; Durand et al. 2006) and derived from previously reported gene duplication rates of 0.0023 and 0.0013 dup/gene/myr (Lynch and Conery 2000; Hahn et al. 2007) (see Methods).

We tested both versions extensively using the 12 fly and nine fungal genomes. We trained our evolutionary models using 500 randomly selected fly trees and 200 fungal trees, and used the remaining 4654 fly trees and 539 fungal trees to test our performance compared with existing algorithms. As the vast majority of these gene trees is likely congruent to the species tree, we evaluated accuracy as the ability to recover the expected gene tree in each case. We evaluated accuracy separately for the nine fly genomes with >7× sequence coverage from a single strain, and for the complete set of 12 fly species, which includes two species sequenced at 3× coverage and one mosaic genome assembled using seven different strains (Drosophila 12 Genomes Consortium 2007) (see Methods).

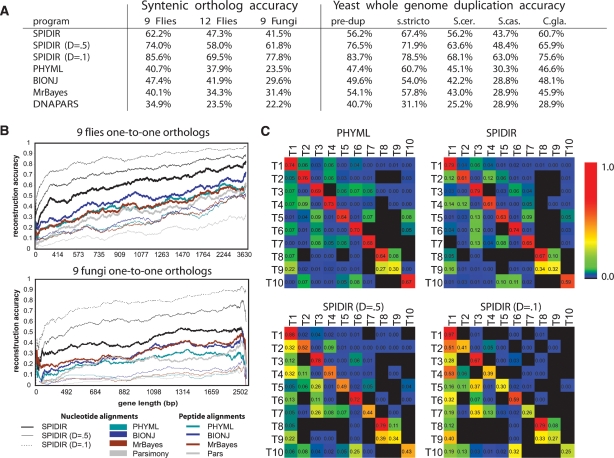
We found significantly increased performance over existing methods for both flies and fungi, and for both single-copy and duplicated genes (Fig. 5A). For the nine fly genomes, SPIDIR recovered the correct gene tree for 62% of genes, significantly higher than the leading existing reconstruction methods (BIONJ at 48% and PHYML at 40%); this increased to 74% and 86% with inclusion of an explicit parameter for a gene-duplication probability (0.5 and 0.1, respectively). For the full set of 12 genomes, SPIDIR also showed a clear improvement (5% over BIONJ and 9% over PHYML), although the low-coverage lineages showed increased reconstruction errors (Supplemental Fig. S3B), which may be due to sequencing errors affecting our rate estimates for the very short branches of low-coverage species. For the nine fungi, SPIDIR recovered the correct gene tree for 42% of orthologs, a 10% increase over MrBayes, and 18% increase over PHYML, the leading existing methods; again, this increased to 62% and 78% with use of an explicit duplication parameter of 0.5 and 0.1. Lastly, we used doubly syntenic orthologs arising from whole-genome duplication (“ohnologs”) (Wolfe and Shields 1997; Kellis et al. 2004), to test SPIDIR’s ability to capture gene duplication and loss, inferring model parameters from 739 single-copy syntenic genes and testing performance on 138 duplication-containing gene families; again, we found a 10% improvement on the correct placement of each duplicate pair, which increased by an additional 10% with inclusion of an explicit duplication parameter. Each of these performance improvements was also seen for partial correctness of the gene tree, measured using Robinson-Foulds error (Robinson and Foulds 1981) (Supplemental Fig. S5).

Figure 5.

SPIDIR learning methodology leads to significantly higher accuracy. (A) Comparison of SPIDIR and several popular phylogenetic methods for syntenic orthologs in nine flies, 12 flies, and nine fungi, and for duplicate genes arising from whole-genome duplication. “pre-dup” gives the accuracy of reconstructing the topology of the three preduplicated species, “s. stricto” is the topology accuracy of only the four sensu strict species, and “S. cer”, “S. cas”, and “C. gla” give the accuracy of placing annotated ohnologs of each species on opposing sides of the whole-genome duplication node. (B) Reconstruction accuracy for SPIDIR correlates with gene length, similarly to other methods, and is consistently higher. (C) Reconstruction accuracy for SPIDIR and PHYML for ROSE simulated fly alignments according to 10 most frequent topologies T1–T10 (left). Both methods are unbiased and recover alternate topologies at similar rates (top), although SPIDIR was trained on T1. With increasing duplication cost, T1 becomes favored by SPIDIR (D = 0.5 and 0.1).

Moreover, SPIDIR accuracy correlated with the number of informative sites, suggesting that it uses available information fully: Performance monotonically increased with increasing gene lengths (Fig. 5B), and peaked for genes with moderate sequence divergence (Supplemental Fig. S6), surpassing existing methods for all length and divergence intervals. In addition, we found that reconstruction accuracy was consistently high, regardless of the gene function: Of 3700 GO terms, SPIDIR had higher reconstruction accuracy than PHYML for 3469 (93%), and of the remaining 231 GO terms (7%), none showed significant enrichment for alternate topologies (P > 0.185 hypergeometric). This suggests that the evolutionary parameters learned in our training set held across all genes tested, regardless of their specific function.

Finally, we found that our method showed no systematic biases toward the species topology. We simulated evolution according to the 10 most frequent ML topologies T1–T10, and asked which topology was inferred by the different prediction algorithms, summarizing the results in a “confusion matrix” (Fig. 5C; Methods). We found that T1 constituted only 6.2% of the SPIDIR-inferred trees for simulated topologies T2–T10, which is similar to PHYML (also 6.2%), confirming that our method is not biased. With duplication and loss penalties, the percentage of T1 increased to 15% for D = 0.5 and 30% for D = 0.1, as expected, but this may be desirable when, in fact, the species tree is known. In addition, both SPIDIR and PHYML identified 62%–65% of all alternate topologies T2–T10 correctly, although SPIDIR was only trained on T1. These trends should be a necessary test for phylogenetic methods that use species-level information to ensure lack of systematic biases.

Discussion

We showed that gene trees are subject to two complementary forces of evolution: a gene-specific component, summarizing the selective pressures on individual gene functions, and a species-specific component, reflecting the divergence times and evolutionary dynamics of the species compared. We found gene- and species-specific substitution rates are independent and can be described by simple distributions that provide a very good fit to actual phylogenies. For both fly and fungal species, we found that a single gene rate was sufficient to model gene trees across the entire clades studied, although larger evolutionary distances and more diverse species groups may require modeling lineage-specific variations in this rate. More generally, we expect that the study of diverse groups of multiple complete genomes will reveal additional properties of gene and species phylogenies, enabling further increases in accuracy and potentially revealing new insights into gene evolution.

We used the decoupling of gene and species rates to introduce a novel approach for phylogenetic reconstruction that is specifically tailored for application in complete genomes. In contrast to existing methods, which treat each gene-tree reconstruction problem in isolation, our approach enables learning across hundreds of phylogenies to improve the accuracy of reconstructing any gene tree involving these species. We tested our method extensively and showed consistent improvements over existing methods for both flies and fungi, lack of bias with respect to the species topology, and increased performance across all lengths, functional categories, and in the presence of gene duplication and loss. Although we have applied our model solely for distance-based reconstruction, it is also applicable to character-based reconstruction. Specifically, our model can be viewed as specifying a prior probability on gene-tree branch lengths, which could replace the uniform branch length prior that is commonly used in maximum likelihood and Bayesian approaches, providing a promising direction for future development.

Several other models have been developed for modeling gene and species evolution simultaneously. One class of models has primarily addressed the inference of a species tree from many gene trees (Ané et al. 2007; Edwards et al. 2007), typically by considering only orthologous genes and assuming that every incongruent node is due to deep coalescence and incomplete lineage sorting. The second class of models has addressed gene-tree reconstruction, typically by assuming that the prevalent reasons for incongruences are gene duplication and loss (Ma et al. 2000; Zmasek and Eddy 2002; Storm and Sonnhammer 2003; Arvestad et al. 2004; Dufayard et al. 2005; Durand et al. 2006). Our model fits within the second class, demonstrating the effectiveness of learning branch-length distributions for gene-tree reconstruction in a generative model for gene tree evolution. A potential future direction for both types of work may be a joint modeling of deep coalescence and gene duplication/loss.

The methodology introduced here, although general, allowed us to address the problem of long-branch attraction at the species level (Bergsten 2005; Philippe et al. 2005). It is known that when fast-evolving lineages are intermixed with slowly evolving lineages, the longer branches tend to cluster together and join further back in evolutionary time, due to increased rates of homoplasy in rapidly evolving lineages. However, addressing long-branch attraction is still a major challenge in phylogenetics. Our decoupling of evolutionary rates allows us to capture heterotachy at the species level, since fast-evolving lineages are uniformly faster across the entire genome. As illustrated in our mammalian example, our model can learn to expect longer branches for faster-evolving lineages, thus recovering the true topology even when all existing methods suffer from long-branch attraction.

Although in this study we have focused our attention on phylogenetic reconstruction accuracy, decoupling gene-specific and species-specific rates can also be used to identify unusual cases of evolutionary change. In particular, it enables us to distinguish whether a long branch is due to simply an overall faster gene rate, a fast-evolving species, or specific acceleration for a particular gene in a given lineage. This is applicable at the level of individual genes, or for sets of genes within a functional category, to recognize evolutionary adaptation of individual genes or pathways. Such studies of acceleration or deceleration can be coupled with studies of positive selection (e.g., K_a/K_s), to detect lineage-specific changes in selective pressures.

The Saccharomycete and Drosophila groups are only the first two in an increasingly long series of groups of related species scheduled for dense sequencing, including 32 mammals, five worms, dozens of fungi, hundreds of bacteria, and thousands of viruses. The increasing number of species in comparative studies should lead to increased power, both for biological signal discovery and for evolutionary studies, but these will require increasingly rigorous methods for genome comparison, which can scale to many species. Single-gene phylogenetic methods are unlikely to scale reliably to dozens of species, while phylogenomic methods should benefit from the abundance of information in complete genomes. The methodologies presented here are general and likely to significantly contribute in the comparison and understanding of many complete genomes.

Methods

Genomic sequences

We selected the two largest groups of fully sequenced closely related species with long-range synteny across the entire group. The Drosophila genus includes D. melanogaster (Adams 2000), D. pseudoobscura (Richards 2005), and the 10 recently sequenced species D. sechellia, D. simulans, D. yakuba, D. erecta, D. ananassae, D. persimilis , D. willistoni, D. mojavensis, D. virilis, and D. grimshawi (Drosophila 12 Genomes Consortium 2007). Our fungal clade includes nine species: Saccharomyces cerevisiae, S. paradoxus, S. mikatae, S. bayanus, S. castellii (Cliften 2003; Kellis 2003), Candida glabrata, Kluyveromyces lactis (Dujon 2004), Ashbya gossypii (Dietrich 2004), and Kluyveromyces waltii (Kellis 2004).

Identifying syntenic orthologous genes

We constructed syntenic regions for the 12 flies by defining a syntenic block to be at least three genes within 200 kb of each other with no other blocks in between. For the fungal data set, we required at least three genes per block with a maximum uninterrupted gene separation of 20 kb. Syntenic blocks were filtered to keep only those containing exactly one gene from each species, thus removing potential segmental duplications. For our whole-genome duplication data set, we used S. cerevisiae, S. castellii, and C. glabrata ohnologs from the Yeast Gene Order Browser (YGOB) (Byrne and Wolfe 2005). Ohnologs were clustered by best reciprocal BLAST hits. Clusters were filtered such that exactly one ohnolog pair from each species is present. Clusters were extended to include genes from the remaining species using our syntenic alignments. Alignments were manually curated to remove possible gene conversion events.

Species phylogeny

The currently accepted fly species phylogeny (Drosophila 12 Genomes Consortium 2007) is shown in Supplemental Figure S1. The major features of the fungal phylogeny are also widely accepted (Rokas et al. 2003; Hittinger et al. 2004; Byrne and Wolfe 2005); however, there is less agreement on the branch orders of the preduplication species K. waltii, K. lactis, and A. gossypii. The branching order we used (Supplemental Fig. S1) is the most frequent topology for all methods (ML, MAP, MP) on nucleotide alignments.

Alignments

We study phylogenies of 5154 unambiguous fly orthologs and 739 unambiguous fungal orthologs. These genes are selected from regions of synteny that are filtered to be free of tandem duplications. For each of these ortholog sets, we produced multiple alignments of their protein sequences using MUSCLE (Edgar 2004). To attain nucleotide alignments, we map the nucleotide sequence on to peptide alignments, substituting every amino acid by the corresponding codon and every gap by a triplet of gaps.

Model parameter learning

For each ortholog alignment, a rooted tree congruent to the species was constructed and fitted with our implementation of least-square error on distances estimated by PUZZLE-TREE (Schmidt et al. 2002) using an HKY model. To be consistent, the root is placed at the midpoint of the rooting branch. The branches of each tree were normalized by the total tree length. To estimate the parameters of our model, the mean and variance of relative branches were calculated for each species (4n-2 parameters for n species), and the alpha- and beta-parameters for the gene-specific rate were calculated with maximum-likelihood estimates from the total absolute branch lengths.

Generative model of gene-tree evolution

To define a generative model for gene-tree evolution with an arbitrary number of duplications and losses, we use a more general definition of reconciliation than is commonly used (Goodman et al. 1979; Page 1994). We define a reconciliation R to be a mapping from gene nodes b_l to a species node i and duplication point k_l: R(b_l) = (i, k_l).

If gene node b_l is a duplication, k_l defines the fraction along the species branch at which the gene duplication occurred: k_l = ε if the duplication occurs immediately after speciation of species parent(R(b_l)), and k_l = 1-ε if the duplication occurs immediately before species R(b_l). If b_l represents a speciation, we define k_l to be 1. We define k_l to be distributed uniformly over (0,1), unless an ancestor b_l2 of b_l reconciles to the same species with duplication point k_l2, in which case k∼ Uniform(k_l2, 1).

For our model, we also define a reconciliation R_b that maps gene branches to species branches. One complication is that a gene branch may map to a path of species branches and may use only a portion of the starting and ending species branch. Thus, we define: R_b(b_l) = ((s₁, s_2,. . . , s_m), (p₁,p₂, . . . , p_m)), where the vector s₁, . . . , s_m defines the path of branches in the species tree and p₁, . . . , p_m defines the portion of each species branch used by R_b(b_l). Notice that the internal branch portions p₂, . . . , p_m-1, if they exist, are always 1. Defining duplication points k_l immediately imply the values of p_j, and vice versa (see Supplemental Methods).

Above, we have presented the generative model for a gene branch that reconciles to exactly one species branch ((s_i), (p₁ = 1)), namely, b_l ∼ G Si = Γ(α, β) N(μ_i,σ_i²), where G and S_i are the gene- and species-specific rates. Here, we specify how to generate a branch length b_l that reconciles across multiple species branches. We model such a b_l to be a product of a gene rate g and a relative rate x_l, that itself is the sum of m independent random variables y_j, each with the distribution: y_j ∼ N(p_j μ_j, p_j σ_j²). Thus, each branch b_l in a gene tree is distributed as: b_l ∼ G ∑_j y_j = Γ(α, β) ∑_j N(p_j μ_j, p_j σ_j²) = Γ(α, β) N(∑_j p_j μ_j, ∑_j p_j σ_j²).

In the Supplemental Methods, we present an algorithm that uses this generative model to search for the gene-tree topology with maximum likelihood given its branch lengths, based on a heuristic search over gene-tree topologies.

Performance comparison

We compared our algorithm against a variety of the most popular and successful phylogeny programs. For a maximum-likelihood method, we used PHYML v2.4.4 (Guindon and Gascuel 2003). Nucleotides substitutions were modeled with the HKY model and peptide substitutions were modeled with JTT. For parsimony methods, we used PHYLIP's DNAPARS and PROTPARS programs. MrBayes v3.1.1, a Bayesian-based method, was used to find the maximum a posteriori phylogenetic tree (Ronquist and Huelsenbeck 2003). We used four chains, an automatic stop rule, a 25% burn-in, sampled every 10 generations from a total of 10,000 generations, a fixed BLOSUM model for peptides, a 4by4 model for nucleotides, and we ensured MrBayes reported the most likely binary tree. Lastly, we used the Neighbor-Joining program BIONJ (Gascuel 1997) with a variety of substitution models, including HKY built with PUZZLE-TREE (Schmidt et al. 2002), JTT built with PROTDIST (Felsenstein 2005), and dS built with the YN00 program from PAML v3.15 (Yang 1997). For all programs, unless stated, default options were used. Parsimony methods perform consistently worse than other methods (parsimony is not statistically consistent) (Felsenstein 1978), as well as the synonymous-substitution metric dS, which unfortunately saturates at the evolutionary distances studied.

Duplication probability

Lynch and Conery (2000) and Hahn et al. (2007) estimated the rate of gene duplication to be 0.0023 dup/gene/myr and 0.0013 dup/gene/myr, respectively. Given that the fly tree has a depth of roughly 40 myr and a total length that is approximately six times that, we expect that a gene duplication occurs in any gene family with a probability of 0.5 (0.0023 * 40 * 6) and 0.312 (0.0013 * 40 * 6).

Simulation

We used simulated sequence evolution to evaluate the accuracy of all of the phylogenetic methods we tested. Unlike other phylogenetic methods, SPIDIR uses a generative model of gene-tree evolution to calculate the likelihood of a phylogeny. Therefore, we must simulate sequences such that they behave like real gene families. To do this, we combined an existing sequence simulation program, ROSE (Stoye et al. 1998), with our generative model of gene-tree evolution. If we use a model trained on fly one-to-one orthologs, we can create simulated fly gene trees that have the same gene-specific and species-specific substitution rates as real fly gene families.

For each simulation, we fix the desired topology (T1–T10). We then use our generative model to choose branch lengths for the topology as described in the generative model. In addition, if a negative branch length is generated, it is discarded and a new one is drawn from the distribution.

Once we have a tree with branch lengths, ROSE is used to simulate sequence evolution down each branch using the HKY model. Base frequencies (A = 0.258, C = 0.267, G = 0.266, T = 0.209), transition bias (3.18), gene length (861 bp), total tree length (1.82 sub/site), and alignment percent identity (0.368) are matched to that of real data.