A Fuzzy System for Helping Medical Diagnosis of Malformations of Cortical Development

Abstract

Malformations of the cerebral cortex are recognized as a common cause of developmental delay, neurological deficits, mental retardation and epilepsy. Currently, the diagnosis of cerebral cortical malformations is based on a subjective interpretation of neuroimaging characteristics of the cerebral gray matter and underlying white matter.

There is no automated system for aiding the observer in making the diagnosis of a cortical malformation. In this paper a fuzzy rule-based system is proposed as a solution for this problem. The system collects the available expert knowledge about cortical malformations and assists the medical observer in arriving at a correct diagnosis. Moreover, the system allows the study of the influence of the various factors that take part in the decision.

The evaluation of the system has been carried out by comparing the automated diagnostic algorithm with known case examples of various malformations due to abnormal cortical organization. An exhaustive evaluation of the system by comparison with published cases and a ROC analysis is presented in the paper.

1. Introduction

Malformations of the cerebral cortex are recognized as a major cause of neurologic abnormalities in children and adults. It is clear that these malformations have a strong relation with epilepsy, developmental delay, neurological deficits and mental retardation [5, 10, 17, 23, 29].

While clinical symptoms, past medical and family history are important in evaluating patients with cortical malformations, neuroimaging findings, especially, those seen with Magnetic Resonance Imaging (MRI), are the most common non-invasive means of arriving at a diagnosis. Unfortunately, the diagnostic process is often not simple. The difficulties in achieving an accurate diagnosis are due to a variety of factors including the existence of numerous classification schemes for cortical malformations, frequent disagreement on standard nomenclature even among specialists, and variability in the imaging features of the different types of malformations. As a result, the diagnosis of a specific cortical malformation is frequently based on a subjective interpretation of the neuroimaging findings. Clinically, uncertaintities in diagnosis may lead to under-recognition of a cortical malformation as the cause of a significant neurologic abnormality, thereby denying the patient potential treatment, or over-interpretation of the neuroimaging studies resulting in medical intervention that may be, at best, ineffective, or at worst, harmful.

Currently, there is no computerized system to help in this diagnostic problem. In this paper, a system for assisting physicians in the diagnosis of malformations of cortical development is proposed. The functions of this system are: first, to collect all the information that is usually analyzed in these cases by the expert, second, to study the relations between the different considered factors and the possible malformations, and third, to offer an automated diagnostic aide. The proposed system utilizes fuzzy logic. Fuzzy logic is an extension of classical logic. In some situations it is very difficult to use classical logic to model a system with the available knowledge. Classical logic does not allow working with uncertainty in the information when knowledge about the behaviour of the systems is imprecise.

One of the most important areas of application of fuzzy set theory as developed by Zadeh [35] is Fuzzy Rule-Based System (FRBS). These fuzzy logic systems constitute an extension of the classical rule-based systems, because they deal with “if-then” rules whose antecedents and consequences are composed of fuzzy logic statements, instead of classical logic ones.

In a broad sense, an FRBS is a rule-based system where fuzzy logic is used as a tool for representing different forms of knowledge about a problem, as well as for modelling the interactions and relationships that exist between its variables. Due to this property, fuzzy logic principles have been successfully applied to a wide range of problems in different domains for which uncertainty and vagueness emerge in varying ways. Fuzzy modelling [25], fuzzy control [12] and fuzzy classification [11] are the most common applications.

Since its inception fuzzy set theory has been regarded as a formalism suitable to deal with the imprecision intrinsic to many medical problems. For example, FRBSs have been applied in the classification of benign and malignant nuclei in cytological images [2, 13], diagnosis of myocardial infarction [14], medical data analysis [32], fuzzy control of anaesthesia [21], and others. The impact fuzzy set theory has had on the work in medical AI is investigated in [1, 19, 30].

Fuzzy sets have been recognized most for their ability to introduce notions of continuity into deductive thinking. Because it is continuous, the behavior of fuzzy systems is likely to be closer to medical reality than the behaviour of the classical systems. At the same time, fuzzy sets allow to use symbolic models. Fuzzy sets can bridge the gap between the discrete world of reasoning and the continuity of reality. In [30] this appears to be the main reason why they are considered useful. The “if-then” rules of the proposed RFBSs for helping diagnosis of malformations of the cortical development were derived from the input of a pediatric neuroradiologist experienced in the diagnosis of cortical malformations using MRI.

The paper is organized as follows: description of the diagnostic problem, an introduction to the principles of fuzzy logic and FRBSs, description of the proposed system for helping with this medical diagnostic problem, implementation of the system, results of the evaluation of the system, and finally, our conclusions.

2. Problem description

2.1. Classification of the malformations of cortical development

Although there is disagreement in the literature as regards the classification and nomenclature of malformations of the cerebral cortex [24, 16, 6, 18], in this work we have followed the classification proposed by Barkovich et al [4]. In this scheme, abnormalities of cortical development are considered to have their onset during one of three fundamental embryologic events of cortical formation:

1. Cellular proliferation in the germinal zones.

2. Migration of cells to developing cerebral cortex.

3. Vertical and horizontal organization of cells within the cortex.

Therefore, malformations of the cortical development are mainly classified in the following three categories:

1. Malformations due to an abnormal neuronal proliferation.

2. Malformations due to an abnormal neuronal migration.

3. Malformations due to an abnormal cortical organization.

Within each of these categories, hierarchical subsets of cortical malformations are recognized. As illustrated by category 3, malformations of cortical organization, there are two main subsets: generalized malformations and focal or multifocal malformations (table 1). Within each subset are a number of specific pathologic entities (i.e. polymicrogyria, schizencephaly, cortical dysplasia and microdysgenesis).

Table 1.

Malformations due to an abnormal cortical organization (extracted from [4]).

A. Generalized	1. Polymicrogyria (PMG)
B. Focal or multifocal	1. Polymicrogyria/Schizencephaly	Bilateral symmetric PMG Bilateral anterior PMG Bilateral perisylvian PMG Bilateral posterior PMG Asymmetric PMG Schizencephaly and mixed schizencephaly/PMG
	2. Focal or multifocal cortical dysplasia without ballon cells
	3. Microdysgenesis

2.2. Objective of the proposed system for helping diagnosis

The system as designed is used for helping in the diagnosis of malformations due to abnormal cortical organization (Barkovich et al, category three, see table 1). In addition to the malformations presented in table 1, primary porencephaly is also considered (see section 3.2.2).

3. Description of the proposed fuzzy system

3.1. Principles of Fuzzy Logic and FRBSs

It is impossible to cover all aspects of current developments in the field of the fuzzy logic. The aim of this section is to provide a summary of its basic concepts. A more complete summary can be found in [15].

The concept of fuzzy logic was first introduced by Zadeh in 1965 [35]. Fuzzy logic was proposed as an extension of classical logic. A classical logic set is a set with a crisp boundary. In contrast, a fuzzy set is a set without a crisp boundary. The transition from “belonging to a set” to “not belonging to a set” is gradual, and this smooth transition is characterized by membership functions that give fuzzy sets flexibility in modelling linguistic expressions.

For example, if X is a collection of objects denoted generically by x, then a fuzzy set A in X is defined as a set of ordered pairs:

$$A=\{(x,{\mu }_A(x))\mid x\in X\}$$ (1)

where μ_A(x) is called the membership function (MF) for the fuzzy set A. The MF maps each element of X to a membership grade between 0 and 1.

The central idea of the fuzzy logic is to model the imprecise aspects of the behaviour of the system through fuzzy sets and fuzzy rules. System variables are defined as linguistic variables and their possible values are linguistic terms (expressed as fuzzy sets). Fuzzy sets are used to represent linguistic variables. For example, if the temperature is a linguistic variable, its possible values could be {very cold, cold, medium, warm, hot, very hot}. These terms are called linguistic terms and each one is characterized by a fuzzy set. A possible interpretation of the linguistic variable “temperature” and its linguistic terms is shown in figure 1. In this example each linguistic term is represented by different fuzzy sets.

Figure 1.

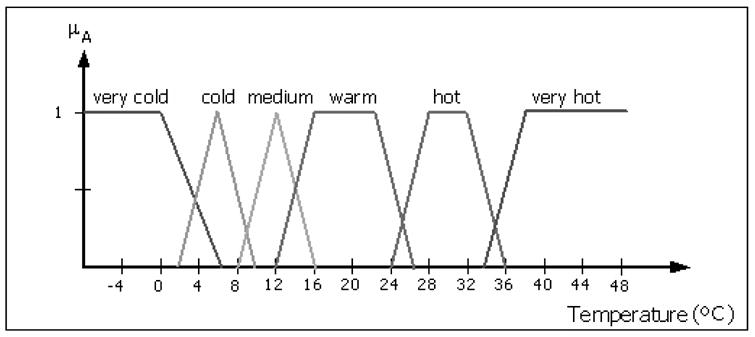
Definition of the linguistic variable “temperature” and its linguistic terms (very cold, cold, medium, warm, hot, very hot) expressed as different fuzzy sets (triangular and trapezoid shaped).

A fuzzy if-then rule has the form:

$$\text{if\hspace{0.28em}}x\mathrm{\hspace{0.17em} }\text{is\hspace{0.28em}}A\hspace{0.17em}t\text{hen\hspace{0.28em}}y\mathrm{\hspace{0.17em} }\text{is\hspace{0.28em}}B$$ (2)

where A₁, A₂,.. and B are linguistic values defined by fuzzy sets on universes of discourse X and Y respectively. Often “x is A” is called the antecedent while “y is B” is called the consequent. An example of fuzzy if-then rule could be: “if the pressure is high, then the volume is small”. We can employ fuzzy if-then rules to model and analyse a system. First we have to formalize what is meant by the expression “if x is A then y is B”, which is sometimes abbreviated as A → B.

Fuzzy reasoning, also known as approximate reasoning, is an inference procedure that derives conclusions from a set of fuzzy if-then rules and known facts. The basic rule of inference in traditional two-valued logic is modus ponens, according to which we can infer the truth of a proposition B from the truth of A and the implication A → B. This concept is illustrated as follows:

Premise 1 (fact):	x is A
Premise 2 (rule):	if x is A then y is B
Consequence (conclusion):	y is B

However, in much of human reasoning, modus ponens is employed in an approximate manner. This is written as:

Premise 1 (fact):	x is A’
Premise 2 (rule):	if x is A then y is B
Consequence (conclusion):	y is B’

where A’ is close to A and B’ is close to B. When A, B, A’ and B’ are fuzzy sets the foregoing inference procedure is called approximate reasoning or fuzzy reasoning. It is also called generalized modus ponens (GMP), since it has modus ponens as a special case.

In this work fuzzy implications are carried out with Mamdani’s fuzzy implication and the max-min composition rule. In figure 2, this process is explained on a rule with two antecedents and one consequent. First we find the degree of match w₁ as the maximum of the intersection of the membership functions that represent A (rule) and A’ (fact), μ_A ∧μ_A′ (x) (the shaded area in the antecedent part between A and A’ in figure 2). We repeat the same procedure for B and B’ (the second antecedent of the rule) to obtain the second degree of match w₂. The MF of the resulting consequence C’ is the shaded area in the consequent part (see figure 2), obtained with the lowest degree of match. Intuitively, w represents a measure of degree of belief for the antecedent part of a rule.

Figure 2.

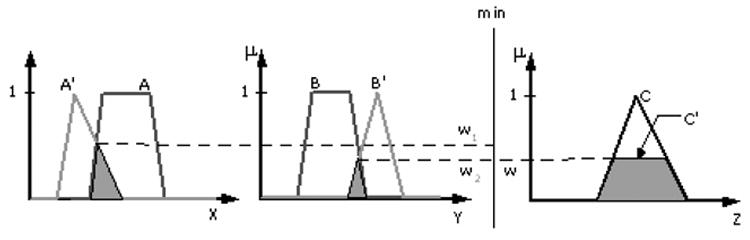
Graphic interpretation of GMP using Mamdani’s fuzzy implication and the max-min composition.

The interpretation of multiple rules is usually taken as the union of the fuzzy relations corresponding to the fuzzy rules, as shown in figure 3. The final consequence is the union of the obtained consequences for each rule.

Figure 3.

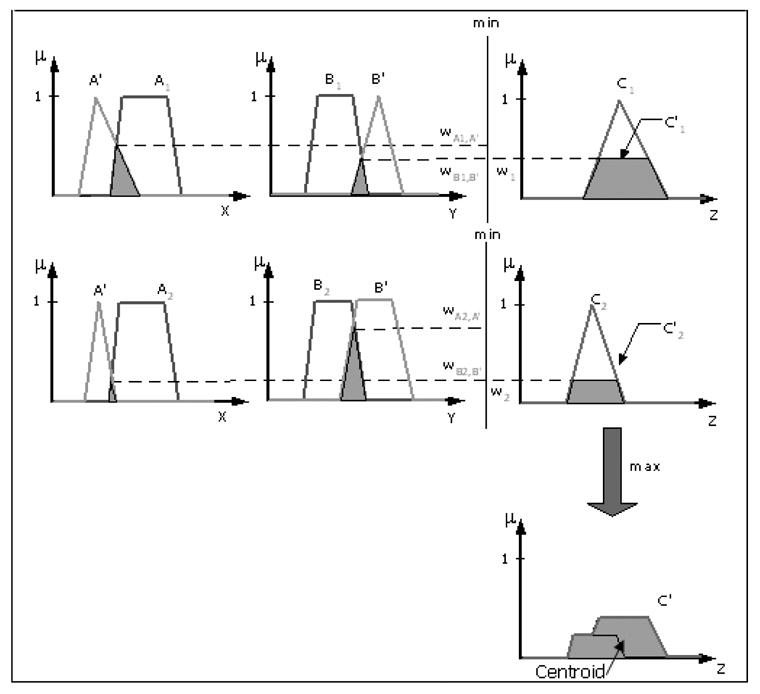
Fuzzy reasoning for multiple rules with multiple antecedents. Mamdani fuzzy system.

The fuzzy inference system is a computing framework based on the concepts of fuzzy set theory, fuzzy if-then rules and fuzzy reasoning. The basic structure of a fuzzy inference system consists of three conceptual components: a rule base, which contains a selection of fuzzy rules, a database, which defines the membership functions used in the fuzzy rules, and a reasoning mechanism, which perfoms the inference procedure (usually the fuzzy reasoning). The basic fuzzy inference system can take either fuzzy inputs or crisp inputs (which are viewed as fuzzy singletons), but the outputs it produces are fuzzy sets. Sometimes it is necessary to have a crisp output. Therefore, we need a method of defuzzification to extract the crisp value that best represents the resulting fuzzy set. In this work we have calculated the centroid of the area of the output fuzzy set. A fuzzy inference system with a crisp output (centroid of the area) is shown in figure 3. This kind of fuzzy system is called Mamdani fuzzy systems [20].

3.2. Design of the proposed FRBS

In this paper, a FRBS for assisting physicians in the diagnosis of malformations of cortical development is proposed. The functions of this system are: first, to collect all the information that is usually analyzed in these cases by the expert, second, to study the relations between the different considered factors and the possible malformations, and third, to offer an automated diagnostic aide. Rule-based systems have been successfully used to model human problem-solving activity and adaptive behaviour, where the classical way to represent human knowledge is the use of “if-then” rules. The fulfilment of the rule antecedent gives rise to the execution of the consequent. Conventional approaches to knowledge representation are based on bivalent logic, which is associated with a serious shortcoming: their inability to deal with the issue of uncertainty and imprecision. As a consequence, conventional approaches do not provide an adequate model for this mode of reasoning familiar to humans.

The general design of a FRBS includes:

1. Construction of the data base: the data base contains the linguistic term sets considered in the linguistic rules and the membership functions defining the semantics of the linguistic labels.

2. Construction of the rule base: collection of linguistic rules that model the problem.

3. Election of the fuzzy inference system.

There are several ways to design a FRBS:

1. Derivation from experts. In this first method, the composition of the data base and the rule base is made by means of the expert information available.

2. Derivation from automatic learning methods based on the existing numerical information. Due to the difficulties associated with the derivation of the data base and the rule base from experts, researchers developed inductive learning methods over the last few years for the different types of FRBSs. These design techniques are diverse. A complete summary can be found in [9].

In this research work, a neuroimaging specialist specified the linguistic labels associated to each linguistic variable, the structure of the rules and the meaning of each label. Linguistic variables represent the different factors that take part in the diagnostic problem (antecedents of the rules) and the possible malformations associated with the appearance of these factors (consequents of the rules). The fuzzy inference system selected was the Mamdani method [20]. In the next subsections, a complete description of the defined linguistic variables for antecedents and consequents is shown.

3.2.1 Rule antecedents

Four categories of factors have been considered for the construction of the antecedents:

1. Localization of the lesion.

2. Visual characteristics (MRI characteristics).

3. Symptoms.

4. Past medical/family history.

Each category is composed of a high number of linguistic variables, as shown in tables 2, 3, 4 and 5. These linguistic variables have been defined by the neuroimaging specialist. Rule antecedents have been constructed with different combinations of these variables.

Table 2.

Localization of the lesion: rule antecedents.

LOCALIZATION OF THE LESION
Linguistic variable	Linguistic label
1. Generalizad	Yes / No
2. Bilateral	Anterior / Perisylvian / Posterior
3. Unilateral	Anterior / Perisylvian / Posterior

Table 3.

Visual characteristics: rule antecedents.

VISUAL CHARACTERISTICS
Linguistic variable	Linguistic label
1. Number of cortical folds	Excessive / normal
2. Boundary gray/white matter	Fuzzy / sharp
3. Cortical folds depth	Shallow / normal
4.Periventricular cysts 5. Ventriculomegaly	Yes / no Severe / no
6. Abnormal cerebellum	Yes / no
7. Abnormal corpus callosum	Absent / intacto
8. Brainstem size	Small / normal
9. Abnormal clefts	Lined white matter/lined gray matter/ no
10. Calcification	Yes / no
11. Abnormal signal whitematter	Yes / no
12. Cortical folds wide	Too wide / normal
13. Heterotopic neurons	Yes / no
14. Microcephaly	Yes / no

Table 4.

Symptoms: rule antecedents

SYMPTOMS
Linguistic variable	Linguistic labels
1. Developmental delay	Severe / no
2. Seizures	Severe/moderate/no
3. Feeding difficulties	Yes /no
4. Breathing difficulties	Yes / no
5. Speech difficulties 6. Dysconjugate gaze	Severe/moderate/no Yes / no
7. Muscular problems in face, throat, tongue and/or jaw	Yes/no
8. Drooling	Yes/no
9. Joint deformities (arthrogryposis)	Yes/no
10. Delayed speech	Yes/no
11. Weakness	Complete/partial/no
12. Hypotonicity	Yes/no

Table 5.

Past medical/family history: rule antecedents

PAST MEDICAL/FAMILY HISTORY
Linguistic variables	Linguistic labels
1. Autosomal reccesive inheritence pattern	Yes/no
2. Intra-uterine infections (e.g. cytomegalovirus)	Yes/no
3. Problems with in utero-placental perfusion	Yes/no
4. Twin-twin transfusion syndrome	Yes/no
5. Degenerative disordes of the central nervious system (e.g. Zellweger)	Yes/no
6. Development disorders (e.g. Aicardi)	Yes/no
7. Other problems during pregnancy	Yes/no

The first category (“Localization of the lesion”) has 3 linguistic variables, the second one (“Visual characteristics”) adds 14 variables, the third one (“Symptoms”) adds 12 variables and the last one (“Past medical/family history”) has 7 variables. Therefore, there are 36 linguistic variables and 78 linguistic labels related to the rule antecedents in the data base. Membership functions used are Gaussian functions.

3.2.2 Rule consequents

The consequences of the rules are the system outputs: the “probability” (i.e., how likely it is) of suffering the studied abnormalities. The terms “probability of suffering …” are the linguistic variables for the system output. Note that the term probability does not correspond to the usual meaning. In our context, this term is only a linguistic variable that represents an intuitive measure of how close the patient is of suffering any considered cortical malformation. Rule consequents are shown in table 6.

Table 6.

System output: rule consequents

SYSTEM OUTPUT
Linguistic variables	Linguistic labels
1. Probability of having Generalized polymicrogyria (G-PMG)	No/low/high
2. Probability of having Bilateral symmetric anterior polymicrogyria (BSA-PMG)	No/low/high
3. Probability of having Bilateral symmetric perisylvian polymicrogyria (BSPe-PMG))	No/low/high
4. Probability of having Bilateral symmetric posterior polymicrogyria (BSPo-PMG)	No/low/high
5. Probability of having Asymmetric polymicrogyria (A-PMG)	No/low/high
6. Probability of having Porencephaly (P)	No/low/high
7. Probability of having Scizencephaly (S) 8. Probability of having Cortical Dysplasia without balloon cells (CD)	No/low/high No/low/high
9. Probability of having Microdysgenesis (M)	No/low/high

Therefore, there are 9 linguistic variables and 27 linguistic labels related to the rule consequents in the data base. Membership functions used are Gaussian functions.

3.2.3 Rule base design

The rule base design (construction and adjustment) has been developed with the direct supervision of a pediatric neuroradiologist. The expert knowledge available has been represented with 47 fuzzy rules. A rule example is presented in figure 4. In this example, only three possible antecedents and all the consequents are considered for the rule construction.

Figure 4.

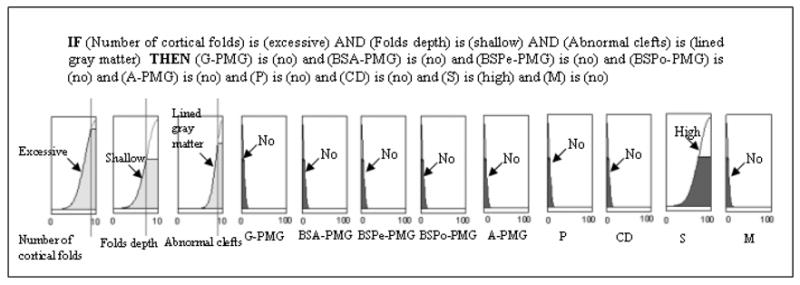
Rule example. The consequents are the probabilities of having G-PMG (Generalized polymicrogyria), BSA-PMG (Bilateral symmetric anterior polymicrogyria), BSPe-PMG (Bilateral symmetric perisylvian polymicrogyria), BSPo-PMG (Bilateral symmetric posterior polymicrogyria), A-PMG (Asymmetric polymicrogiria), P (Porencephaly), CD (Cortical Dysplasia), S (Schizencephaly), M (Microdysgenesis).

3.2.4 Design of the fuzzy inference systems

The total FRBS is composed of four subsystems. The fuzzy inference systems are Mamdani fuzzy systems [20]. Each subsystem is independent and extracts the conclusions from each one of the four considered categories of antecedents. Therefore, we have a different fuzzy system for the localization of the lesion, the visual characteristics, the symptoms of the patient and the past medical/family history of the patient.

There are several reasons to divide the global system in four subsystems:

1. This strategy facilitates the construction of the rules: if the information is divided in four categories the rules can also be divided in four categories. The number of antecedents to handle is lower and the structure of the rules can be simpler.

2. The relations between the variables can be better studied and the rule base is more interpretable.

3. This strategy simulates the human reasoning. Before making diagnosis, the human expert analyzes first these four categories of information separately.

4. This scheme provides additional flexibility to the final system and to the user since the neuroradiologist may not always have information about all the categories that are represented in the system. For example, it could happen that only the MRI or the past medical/family history are available. The system can be used in a partial way with this scheme.

Each subsystem contributes to the final consequence (probability of having a specific type of malformation) with a partial score. These partial scores are combined for obtaining the total score between 0 –100. If any subsystem is not used (there is no available information about that category), the final score is obtained by combining the partial scores of the used subsystems, therefore, the final score would be lower.

Not all the subsystems have the same significance. For example, for a given malformation, the information related to the visual characteristics of the lesion extracted from MRI may be more specific with regard to the type of cortical anomaly than the clinical symptoms. Therefore, the final system output (final score) is a weighted combination of the subsystems outputs (partial scores), where the output of the subsystem “Visual characteristics” carries more weight. This interaction between the four subsystems has been designed in close collaboration with the neuroradiologist. We have adjusted the weights in order to represent his expert reasoning.

4. Implementation of the proposed fuzzy system for assisting in medical diagnosis

The system has been implemented using Matlab [22]. If any researcher is interested in knowing more details about this software, please contact the first author.

In order to make the system more comprehensible and useful for the neuroradiologist, a visual interface was developed. This visual interface allows the user the direct utilization of the system. The interface was programmed with the tool GUIDE of Matlab.

Through this visual interface, the users can:

1. Input all of the information available about the problem.

2. Give a subjective valuation of each input variable.

3. Analyse the relationship between different input factors and how different combinations of input factors can modify the output of the system (probability of having a cortical malformation).

4. Obtain the probability of having any considered malformation (diagnostic).

The main window of the visual interface is shown in figure 5. It is composed of two different zones: the upper zone shows the four categories of input variables and the lowest zone shows the output variables (system diagnostic: probability of having the considered malformation).

Figure 5.

Main window of the visual interface of the proposed system for helping diagnosis.

The user can load an evaluated case, in order to consult or modify it, and create a new evaluation (study of a new case). The four input modules are independent (i.e. they can be used all at the same time or individually), however, the system result is more reliable as additional information is introduced and more modules are used together to obtain the final diagnosis.

There are different windows to input the information in each category. These secondary windows are shown in figure 6. The user introduces his subjective valuation of each variable with a numeric qualification: between 0–10. With this number, the user can indicate if the particular input factor has more or less weight in the analysed information.

Figure 6.

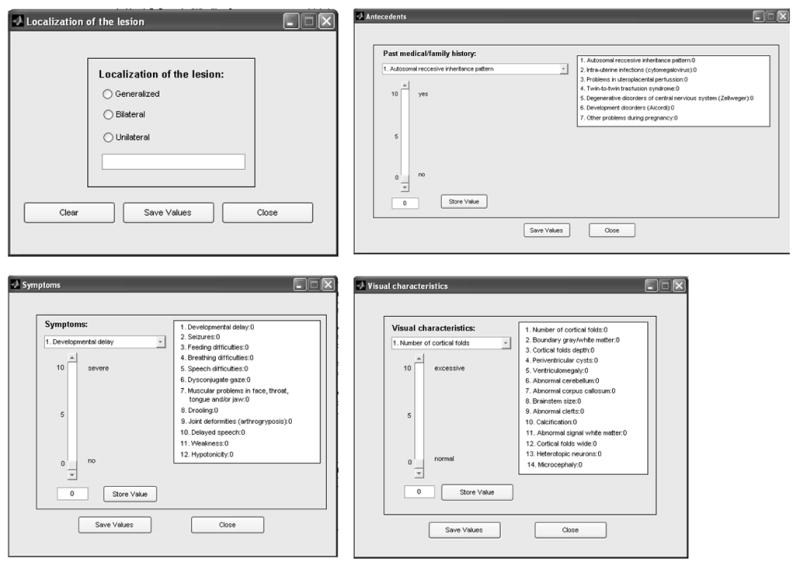
Secondary windows: Localization of the lesion, Past medical/family history, Symptoms and Visual characteristics.

5. Evaluation of the proposed fuzzy system for helping medical diagnosis

The first evaluation of the system was carried out by comparing the automated diagnostic algorithm with known case examples of various malformations due to abnormal cortical organization. As result of this evaluation, some adjustments in the rules were developed in order to improve the efficiency of the system. A pediatric neuroradiologist has collaborated in this evaluation process. A more exhaustive evaluation of the system by comparison with published cases was subsequently performed. We have selected two studies [5, 23] to test the system in similar clinical cases. These studies have been selected so that each one provides different types and amounts of information. This fact is important because we have two main purposes in this evaluation stage:

1. Evaluate the system response (how accurate it is).

2. Analyze the weight of the different subsystems that composed the final system. As more information is introduced to the system, the diagnostic accuracy of the system improves, because more subsystems and more variables can be used.

5.1. First study

The first selected study is [23]. In this study, 6 patients with Bilateral Symmetrical Perisylvian Polymicrogyria (BSPe-PMG) were reported.

The available information in that study includes age, sex, epilepsy, tongue and lip movements, finger movements, intellectual capacity, the location of the lesion and magnetoencephalographic (MEG) data for every patient. Our system cannot use all this information (i.e., age, sex and MEG data is not considered in the rules of the system). The information that can be used is presented in table 7. It is shown that the available information to test our system (extracted from [23]) can be classified in two categories used by our system: ‘Localization of the lesion’ and ‘Symptoms’.

Table 7.

Available information to test our system extracted from [14].

Patient	Localization of the lesion		Symptoms
	Bilateral perisylvian	Muscular problems in face, throat, tongue and/or jaw	Intellectual capacity	Seizures
1	Yes	Yes	Borderline	No
2	Yes	Yes	Normal	No
3	Yes	Yes	Mild disability	Yes
4	Yes	Yes	Normal	Yes
5	Yes	Yes	Borderline	No
6	Yes	Yes	Normal	Yes

In [23], the diagnostic of these 6 patients was Symmetrical Perisylvian Polymicrogyria (BSPe-PMG). We used the information of table 7 to test our system and obtain a diagnostic that could be compared with the one presented in [23].

In this case it is not possible to use the four subsystems of the total system because there is not enough information. But this fact does not represent a problem in using the system, because the program can be used in a partial way (see section 3.2.4). Using two subsystems (‘Localization of the lesion’ and ‘Symptoms’), we obtained different probabilities of having the considered malformations. We must remember that the terms “probability of having …” are the linguistic variables for the system output. The term probability means how likely it is (see explanation in section 3.2.2).

We obtained a probability between 33–39% of having bilateral perisylvian cortical malformation for all the patients, and these probabilities are the highest ones (see table 8).

Table 8.

Response of our system for helping diagnosis for the study [14]: probabilities (%) of having G-PMG (Generalized polymicrogyria), BSA-PMG (Bilateral symmetric anterior polymicrogyria), BSPe-PMG (Bilateral symmetric perisylvian polymicrogyria), BSPo-PMG (Bilateral symmetric posterior polymicrogyria), A-PMG (Asymmetric polymicrogiria), P (Porencephaly), S (Schizencephaly), CD (Cortical Dysplasia), M (Microdysgenesis). Highest probabilities for each patient are noted.

Patient	G-PMG	BSA- PMG	BSPe-PMG	BSPo-PMG	A-PMG	P	S	CD	M
1	4.26	4.26	37.41	4.26	4.26	4.26	4.26	4.26	4.26
2	4.26	6.67	33.11	6.67	4.26	6.60	6.64	6.61	4.26
3	4.10	4.15	39.00	4.15	4.10	7.25	7.26	7.25	4.15
4	4.26	4.26	37.41	4.26	4.26	4.26	4.26	4.26	4.26
5	4.26	6.64	33.34	6.63	4.26	6.57	6.60	6.57	6.62
6	4.26	4.26	37.41	4.26	4.26	4.26	4.26	4.26	4.26

In this test, there is not enough information for the system to offer higher probabilities, and the subsystem ‘Visual characteristics’, that has more weight in the decision (see section 3.2.4) is not used (there is no available information related to imaging features in the study). The system output could be improved with the inclusion of more information. This aspect is analyzed in the next section.

5.2. Second study

In a separate study presented in [5], 21 patients diagnosed with Bilateral Symmetric Polymicrogyria were presented. The available information in that study includes sex/age at most recent examination, the location of the lesion, seizures/EEG results and different neurologic findings. Similar to the first study, not all of the available factors in [5] are considered in our system. The information that can be used in this case is presented in table 9. It is shown that the available information to test our system (extracted from [5]) can be classified in three categories used by our system: ‘Localization of the lesion’, ‘Visual characteristics’ and ‘Symptoms’.

Table 9.

Available information to test our system extracted from [3]. Symbol ‘--' means ‘unknown’.

Patient	Localization of the lesion	Visual characteristics		Symptoms
	Bilateral symmetric	Number cortical folds	Cortical folds depth	Muscular problems in tongue	Weakness	Drooling	Hypotonicity	Motor Delay	Speech difficulties	Mental retardation	Seizures
1	Anterior	Excessive	Shallow	--	--	--	--	Yes	Yes	Mild	No
2	Anterior	Excessive	Shallow	--	Yes	--	--	Yes	Yes	Mild	No
3	Anterior	Excessive	Shallow	--	Yes	--	--	Yes	Yes	--	No
4	Anterior	Excessive	Shallow	--	Yes	--	--	Yes	Yes	--	No
5	Anterior	Excessive	Shallow	--	Yes	--	--	Yes	Yes	Mild	No
6	Anterior	Excessive	Shallow	--	Yes	--	--	Yes	Yes	Mild	No
7	Posterior	Excessive	Shallow	--	--	--	--	Normal	Yes	Normal	No
8	Posterior	Excessive	Shallow	--	--	--	Yes	Yes	Severe	Yes	Partial
9	Posterior	Excessive	Shallow	--	--	--	--	Mild	Yes	--	No
10	Posterior	Excessive	Shallow	--	Mild	Excessive	Yes	--	Yes	--	No
11	Posterior	Excessive	Shallow	--	Mild	--	--	--	Yes	--	No
12	Posterior	Excessive	Shallow	--	Mild	--	--	--	Yes	--	Partial
13	Perisylvian	Excessive	Shallow	--	--	--	--	Yes	--	--	No
14	Perisylvian	Excessive	Shallow	--	Yes	--	--	Yes	--	Yes	Yes
15	Perisylvian	Excessive	Shallow	--	--	--	--	Yes	Yes	--	Yes
16	Posterior	Excessive	Shallow	--	--	--	--	Yes	--	Normal	Partial
17 18	Posterior Perisylvian	Excessive Excessive	Shallow Shallow	-- Yes	-- --	-- --	-- Yes	Mild Severe	-- Yes	Mild Severe	Partial Partial
19	Perisylvian	Excessive	Shallow	Yes	--	Excessive	Yes	Severe	--	Severe	Partial
20	Posterior	Excessive	Shallow	Yes	--	--	Mild	Mild	Yes	Moderate	Partial
21	Perisylvian	Excessive	Shallow	Yes	Yes	--	Yes	--	Yes	Mild/moderate	Yes

The diagnostic presented in [5] of these 21 patients is shown in table 10. We used the information of table 9 to test our system and obtain a diagnostic that can be compared with the one presented in [5] (see table 10).

Table 10.

Diagnostic of the 21 patients (extracted from [3]). PMG – Polymicrogyria.

Patient	Diagnostic
1	Bifrontal PMG
2	Bifrontal PMG
3	Bifrontal PMG
4	Bifrontal PMG
5	Bifrontal PMG
6 7	Bifrontal PMG Bilateral Posterior PMG
8	Bilateral Posterior PMG
9	Bilateral Posterior PMG
10	Bilateral Posterior PMG
11	Bilateral Posterior PMG
12	Bilateral Posterior PMG
13	Bilateral Perisylvian PMG
14	Bilateral Perisylvian PMG
15	Bilateral Perisylvian PMG
16	Bilateral Posterior PMG
17	Bilateral Posterior PMG
18	Bilateral Perisylvian PMG
19	Bilateral Perisylvian PMG
20	Bilateral Posterior PMG
21	Bilateral Perisylvian PMG

Using our system gave a probability of between 75–82% of having bilateral symmetric polymicrogyria in different cerebral regions (see table 11). In this case, the study provides more information and the results obtained with our system are considerably better. Moreover, three subsystems (instead of two, as in previous example) are collaborating in this case to offer the final probabilities of having the different malformations.

Table 11.

Response of our system for helping diagnosis for the study [3]: probabilities (%) of having G-PMG (Generalized polymicrogyria), BSA-PMG (Bilateral symmetric anterior polymicrogyria), BSPe-PMG (Bilateral symmetric perisylvian polymicrogyria), BSPo-PMG (Bilateral symmetric posterior polymicrogyria), A-PMG (Asymmetric polymicrogiria), P (Porencephaly), S (Schizencephaly), CD (Cortical Dysplasia), M (Microdysgenesis). Highest probabilities for each patient are noted.

Patient	G-PMG	BSA- PMG	BSPe-PMG	BSPo-PMG	A-PMG	P	S	CD	M
1	4.10	81.43	5.12	7.22	4.10	7.27	7.28	7.22	4.11
2	4.11	81.72	5.15	7.25	4.11	7.23	7.24	7.23	4.12
3	4.10	79.46	5.27	7.02	4.10	7.37	7.39	7.01	5.26
4	4.10	79.46	5.27	7.02	4.10	7.37	7.39	7.01	5.26
5	4.11	81.72	5.15	7.25	4.11	7.23	7.24	7.23	4.12
6	4.11	81.72	5.15	7.25	4.11	7.23	7.24	7.23	4.12
7	4.27	6.67	6.66	73.66	4.27	6.60	6.63	4.27	4.27
8 9	4.10 4.11	7.27 7.25	7.27 7.25	80.23 80.00	4.10 4.11	7.25 7.23	7.26 7.24	7.25 6.80	4.15 5.86
10	4.10	7.27	7.27	80.23	4.10	7.25	7.26	4.10	4.10
11	4.14	7.12	7.11	78.52	4.14	7.08	7.10	4.15	4.15
12	4.10	6.84	6.84	80.22	4.10	7.25	7.26	7.26	4.15
13	4.18	7.00	76.50	7.00	4.18	6.95	6.97	6.95	6.92
14	4.10	4.20	80.23	4.20	4.10	7.25	7.26	7.25	7.26
15	4.14	6.18	78.61	6.18	4.14	7.09	7.11	7.09	7.02
16	4.15	6.64	7.05	75.72	4.15	7.05	7.07	7.06	7.08
17	4.10	7.27	4.55	81.99	4.10	7.25	7.26	7.25	7.20
18	4.10	7.27	80.30	7.27	4.00	7.25	7.26	7.25	7.26
19	4.10	7.27	80.30	7.27	4.00	7.25	7.26	7.25	7.26
20	4.10	4.20	4.20	80.23	4.10	7.25	7.26	7.25	7.26
21	4.10	7.27	80.30	7.27	4.00	7.25	7.26	7.25	7.26

The system results shown in table 11 are consisted with the published results in [5] (see table 10). The system response is highly dependent on the amount of available information. Because of this, the results are better for analysis of the study population in [5] than for that presented in [23].

5.3. System evaluation with ROC curves

It is important to evaluate our system from a medical point of view, specifically with an orientation to the diagnosis. ROC (Receiver Operating Characteristic) analysis, a methodology developed in Decision Theory in the 50’s and applied to the biomedical ambit [28, 31], is the framework for this study, where the diagnostic exactitude is measured in terms of sensitivity and specificity. ROC analysis is carried out through the construction of ROC curves, graphical representations of pairs (1-specificity, sensitivity) corresponding to different test cut values.

Test exactitude increases if the curve goes from diagonal to higher left vertex. An ideal classifier (100 % sensitivity, 100 % specificity) would result in a curve passing through that point.

We have used the obtained results in the second study (see section 5.2) to construct the ROC curves for our diagnosis system. In this study, 21 patients diagnosed with Bilateral Symmetric Polymicrogyria (BS-PMG) were presented: six patients with Anterior BS-PMG, six patients with Perisylvian BS-PMG and nine patients with Posterior BS-PMG. Pairs (1-specificity, sensitivity) for each response of the system for these malformations are calculated using different cut values.

The ROC curves obtained for the three cases are the same curve (see figures 7, 8 and 9). The ROC curve shows the ideal behaviour of the system: the curve passes through the higher left vertex. These ROC curves have been constructed with the data related to the output of the system shown in table 11 (Anterior BS-PMG: third column, Perisylvian BS-PMG: fourth column, and Posterior BS-PMG: fifth column).

Figure 7.

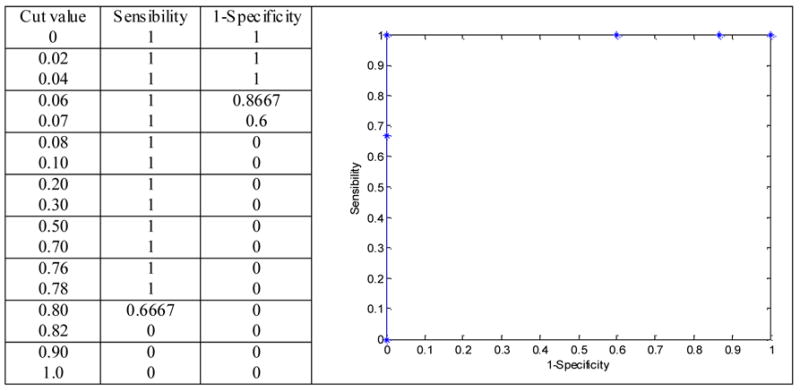
Roc curve for the BSA-PMG data (third column of table 11).

Figure 8.

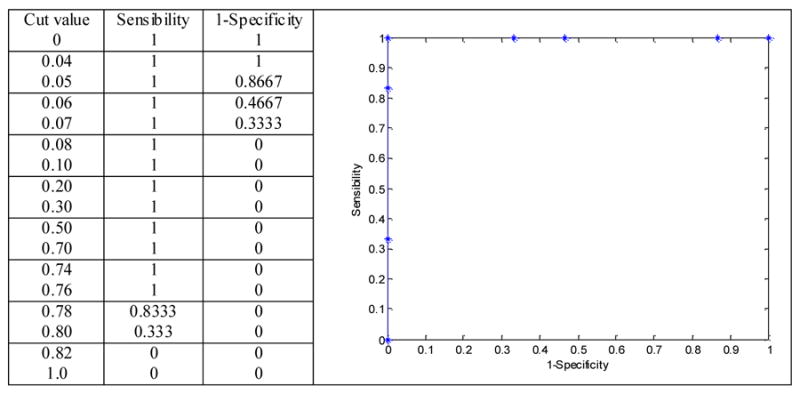
Roc curve for the BSPe-PMG data (fourth column of table 11).

Figure 9.

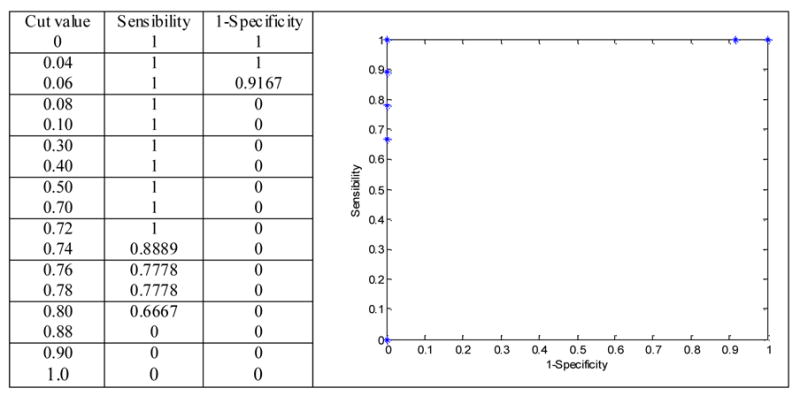
Roc curve for the BSPo-PMG data (fifth column of table 11).

6. Conclusions

Malformations of the cerebral cortex are an important cause of epilepsy, developmental delay, neurological deficits and mental retardation. Despite medical and imaging advances in recent years, the accurate, non-invasive diagnosis of a specific type of malformation is often illusive. The use of a fuzzy logic based, computer based diagnostic algorithm, as presented in this work, seeks to improve the accuracy in the diagnosis of a subset of cortical malformations by increasing the diagnostic confidence of the physician.

The proposed system allows one to:

1. Collect all the information that is usually analyzed in these cases by the clinician.

2. Study the relations between the different considered factors and the possible malformations.

3. Offer an automated diagnostic tool.

The proposed system is a Fuzzy Rule-Based System (FRBS). A FRBS was proposed because rule-based systems have been successfully used to model human problem-solving activity and adaptive behaviour, where the classical way to represent human knowledge is the use of “if-then” rules.

Machine learning techniques suiting computer-aided medical diagnosis should have good comprehensibility, i.e. the transparency of diagnostic knowledge and the explanation ability. In general, machine learning techniques can be categorized into two classes, that is, symbolic or connectionist learning techniques. Symbolic learning techniques such as rule induction are usually regarded as comprehensible techniques because the learned knowledge is expressed in forms such as production rules that are easy to be understood by the user. On the other hand, most connectionist learning techniques such as artificial neural networks are regarded as incomprehensible techniques because the learned knowledge is concealed in a lot of connections and is not transparent to the user.

For example, the neural network approach has proven useful for the development of artificial intelligence systems in the medical domain [7, 33]. However, a disadvantage with this approach is that the knowledge embedded in the neural network is opaque. Fuzzy logic can model the interactions and relationships that exist between different variables in a clearer way due to its symbolic formulation.

Decision trees have proven to be a valuable tool for description, classification and generalization of data. This is related to the compact and intelligible representation of the learned classification function, and the availability of a large number of efficient algorithms for their automated construction. A wealth of algorithms for the automatic construction of decision trees can be traced back to the ancestors ID3 [26, 27] or CART [8]. However, in many practical applications, the data used are inherently of imprecise and subjective nature. In theses cases, Fuzzy Logic performs better than decision trees.

The designed rules of the FRBS represent expert knowledge about the problem. Four categories of information are considered in the system: localization of the lesion, visual characteristics extracted from MRI, clinical symptoms and past medical/family history of the patient. The total FRBS is composed of four subsystems. There is a different fuzzy system for the localization of the lesion, the visual characteristics, the clinical symptoms and the past medical/family history. This scheme provides additional flexibility to the final system in that it can be used when only partial information is available.

The output of the system is the probability of having any considered malformation. The term probability does not correspond to the usual meaning. In our context, this term is only a linguistic variable that represents an intuitive measure of how close the patient is of suffering any considered cortical malformation. Each subsystem contributes to the probability of having any malformation in a different way. Therefore, the final system output is a weighted combination of the subsystems outputs, where the subsystem “Visual characteristics” carries more weight. This scheme makes it possible to use the system when only partial information is available.

In order to make the system accessible, a visual interface has been created. This interface allows the medical specialist to more easily use the system.

The evaluation of the system has been extensive. The first evaluation of the system was carried out by comparing the automated diagnostic algorithm with known cases. A pediatric neuroradiologist has collaborated with us in this validation stage. As result of this evaluation, some adjustments in the rules were developed in order to improve the efficiency of the system.

Subsequently, the system has been evaluated with data from published research studies related to the same diagnostic problem, and a ROC evaluation has been also carried out. Analysing these results, we conclude that the system offers a reliable aide to diagnosis when enough information is provided. Results are better for the second study carried out (see section 5.2), than for the first one (see section 5.1). More information about the patients was available in the second study.

One disadvantage of the system is the high dependency of its response on the amount of available information. When the available amount of information is high, the system response is useful for making diagnosis, because the probabilities of having any malformation are significant. When the available amount of information is not very high, these probabilities are low; therefore the system response is not so reliable. In this case, the system could be used as a screening tool.

The “if-then” rules of the proposed RFBSs for helping diagnosis of malformations of the cortical development were derived from the input of a pediatric neuroradiologist experienced in the diagnosis of cortical malformations using MRI. A fuzzy rule base design has two important objectives. One is to achieve a good approximation. The other is to reduce the number of rules. The main difficulty is that these two objectives are contradictory. Complexity reduction is therefore becoming a pertinent research topic of fuzzy theory [3, 34].

The rules have been formulated by the human expert and no study about the optimization of this rule base has been carried out. This study can improve the system response. But this reduction can also make worse the interpretability of the rules. The presented system is planned to be used in teaching tasks due to its ability to show the relations between different factors and how they can affect the resulting diagnosis. Therefore, the interpretability of the rules is very important in our case.

In future research work, we will try to expand the system to the other two categories of malformations of the cortex shown in [4]: malformations due to an abnormal neuronal proliferation and malformations due to an abnormal neuronal migration.