Cortical bone development under the growth plate is regulated by mechanical load transfer

Abstract

Longitudinal growth of long bones takes place at the growth plates. The growth plate produces new bone trabeculae, which are later resorbed or merged into the cortical shell. This process implies transition of trabecular metaphyseal sections into diaphyseal sections. We hypothesize that the development of cortical bone is governed by mechanical stimuli. We also hypothesize that trabecular and cortical bone share the same regulatory mechanisms for adaptation to mechanical loads. To test these hypotheses, we monitored the development of the tibial cortex in growing pigs, using micro-computer tomography and histology. We then tested the concept that regulatory mechanisms for trabecular bone adaptation can also explain cortical bone development using our mechanical stimulation theory, which could explain trabecular bone (re)modelling. The main results showed that, from the growth plate towards the diaphysis, the pores of the trabecular structure were gradually filled in with bone, which resulted in increased density and cortical bone. The computer model largely predicted this morphological development. We conclude that merging of metaphyseal trabeculae into cortex is likely to be governed by mechanical stimuli. Furthermore, cortex development of growing long bones can be explained as a form of trabecular bone adaptation, without the need for different regulatory mechanisms for cortical and trabecular bone.

Introduction

In adult bone, bone mass and architecture are believed to be adapted to the external loading conditions (Wolff, 1892; Lanyon & Bourne, 1979; Rubin & Lanyon, 1985; Lanyon, 1992; Rubin & McLeod, 1994; Leblanc et al. 1995; Petrtyl et al. 1996; Bailey et al. 1999). Bone density increases if the mechanical load increases by, for instance, physical activity (Bailey et al. 1999), and decreases by immobilization, bed rest (Leblanc et al. 1995) and under microgravity conditions (Collet et al. 1997). Bone trabeculae follow the principal stress directions, as described by Wolff (1892). In order to adapt to external loads, bone requires a load sensorial capacity in the form of ‘mechanosensors’. It is believed that osteocytes are the mechanosensors of bone (Skerry et al. 1989; Cowin et al. 1991; Weinbaum et al. 1994; Klein-Nulend et al. 1995; You et al. 2001). Based on this mechanosensory criterion, a mechanical adaptation theory for trabecular bone was developed (Mullender & Huiskes, 1995; Huiskes et al. 2000). The theory was implemented in a computer simulation model, which could explain modelling and remodelling of the trabecular structure, as well as its adaptation to alternative external loads (Huiskes et al. 2000). In the cortex, the organization of the Haversian system is also thought to be mechanically driven (Petrtyl et al. 1996; Smit & Burger, 2000; Skedros et al. 2001). For example, Petrtyl et al. (1996) showed that the principal stress direction under combined loading of bending and torsion corresponded to the direction of osteons in the diaphysis of the human femur. Alternatively, in unloaded cortical bone new osteons were rather unorientated (Petrtyl et al. 1996).

It is unclear if the regulatory mechanisms for cortical bone are different from or similar to those for trabecular bone. Many authors distinguish trabecular bone from cortical bone (Tobias et al. 1992; Alho et al. 1995; Mori et al. 2003; Heap et al. 2004). For example, Tobias et al. (1992) found opposite effects of insulin-like growth factor-I (IGF-I) on the formation of trabecular and cortical bone in adult female rats; IGF-I stimulated periosteal bone formation but reduced trabecular bone formation. Heap et al. (2004) found decreases in trabecular density, but not in cortical density in adolescents with type 1 diabetes mellitus. They suggested that physical activity protected the cortical bone, but not the trabecular bone, assuming different mechanisms for trabecular and cortical bone regulation. However, both trabecular and cortical bone are formed and resorbed by the same cells, the osteoblasts and osteoclasts. Moreover, it is believed that osteocytes are mechanosensitive through extracellular fluid flow, which in theory can be applied to both trabecular and cortical bone (Smit et al. 2002; Burger et al. 2003). In this study, we hypothesize that trabecular bone and cortical bone share the same regulatory mechanisms for adaptation to mechanical loads.

It has been proposed that not only adult bone but also bone during growth is governed by mechanical stimuli (Carter et al. 1991; Van der Meulen et al. 1993; Parfitt, 1994; Tanck et al. 2001). Growth plates cause longitudinal growth by producing new trabeculae that are subsequently resorbed or merged into the cortical shell. Considered in a longitudinal spatial–temporal context, the process of cortical bone development implies transition of trabecular metaphyseal sections into cortical diaphyseal sections. At the metaphyseal level, the cortex consists of younger bone compared with the cortex at diaphyseal level as a result of new bone production from the growth plate. This means that the cumulative number of loading cycles to which bone is subjected over time increases from the growth plate towards the diaphysis. In an earlier study, we suggested that trabecular bone density is adapted to external mechanical load from the early phase of growth, whereas the orientation of trabeculae is adapted to the principal loading direction only gradually (Tanck et al. 2001). In this study, we hypothesize that the development of cortical bone is also mechanically driven. Understanding the regulatory mechanisms of cortical bone development may help to elucidate the pathophysiology of growth disorders in children.

In summary, two hypotheses are addressed in this study: trabecular bone and cortical bone share the same regulatory mechanisms for adaptation to mechanical loads, and the development of cortical bone is governed by mechanical stimuli. To test these hypotheses, we monitored the (3D) development of the tibial cortex in growing pigs, using both micro-computer tomography (µCT) and histology. We then tested if regulatory mechanisms for trabecular bone adaptation can also explain cortical bone development by using our mechanical stimulation theory (Huiskes et al. 2000).

Materials and methods

Three right tibiae from three pigs at 6, 23 and 230 weeks of age (skeletally mature at about 100 weeks of age) from a Dutch farm were studied. Bone specimens of approximately 4 × 4 × 40 mm were sawn from the posterior cortex at three levels: just below the proximal growth plate, at one-third of the tibial length (metaphysis) and at one-half of the tibial length (diaphysis). The bone pieces were fixed for 1 week in a phosphate-buffered formaldehyde solution of 4%. Thereafter, they were rinsed with streaming water and kept in distilled water. From each specimen, a region of 5 mm in the longitudinal length of the bone was scanned via µCT (µCT20, Scanco Medical AG, Zürich, Switzerland) with a resolution of 12 µm. Three-dimensional reconstructions of the bone pieces were made and the 3D cortical development was evaluated. After scanning, the bone pieces were prepared for histology to obtain additional information regarding the structure of the bone matrix. For this, the specimens were stained en bloc in 2.5% basic fuchsin in 70% alcohol. Fuchsin discriminates newly formed bone tissue from older bone tissue. Subsequently, the specimens were rinsed with 96% and 100% alcohol and embedded in plastic (methylmetacrylate). Slices of about 50 µm were sawn with a sawmicrotome (Leica SP 1600). Five slices per specimen were analysed for the presence of primary or secondary osteons using transmitted light microscopy. The analyses of the specimens were performed at the same regions as the µCT scans.

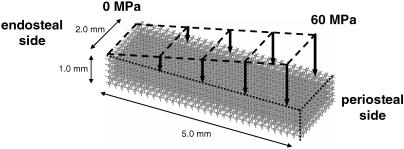
To analyse if regulatory mechanisms for trabecular bone adaptation could explain cortical bone development, the tendency of cortical bone development was simulated using our mechanical stimulation theory, which could explain bone (re)modelling of trabecular bone (Huiskes et al. 2000). Briefly, the theory assumes that when a bone is externally loaded, stress is transferred to the local trabecular bone, which results in a certain distribution of stresses and strains. A combination of these mechanical variables, i.e. the strain energy density (SED) rate (Huiskes et al. 2000; Ruimerman et al. 2001, 2005), is assumed to activate the osteocytes in the bone matrix to produce and transfer bone-formation stimuli to trabecular surfaces, through the canalicular network. The stimulus received at the surface depends on mechano-sensitivity, osteocyte density and signal decay by distance (Ruimerman et al. 2005). Bone is formed at the surfaces, where and while the stimulus exceeds a threshold value. Concurrently, osteoclasts are attracted to areas of microcracks. As microcracks could occur anywhere, and at any time, resorption is assumed to be spatially random as well. Bone formation and bone resorption influence the local trabecular architecture, which in turn changes the local distribution of SED rate. Coupling between osteoclastic and osteoblastic activities in remodelling is governed implicitly by the mechanics through stress concentrations around resorption cavities. This regulatory scheme was implemented in a 3D finite element analysis (FEA) for a section of cortical bone with dimensions of 2 × 5 × 1 mm, for its circumferential length, cortical thickness and longitudinal height, respectively (Fig. 1). The simulations were effected in an FEA model containing 60 × 150 × 30 cubic voxel elements, which can be bone or marrow. The initial structure of the model was a conceptual morphology, representing bone tissue at the post-mineralized fetal stage. The material properties and other parameter settings for the simulations were according to Ruimerman et al. (2005). The structure was loaded in the longitudinal direction with a distributed load that increased from 0 MPa endosteally to 60 MPa periosteally, cycling at 1 Hz (Fig. 1). This load distribution represented bending of the bone. The value of 60 MPa was arbitrarily chosen as we only study the phenomenon of cortical bone development at large. The simulation was continued to morphological homeostasis, where only remodelling still occurred.

Fig. 1.

The initial finite element model is a 3D rod-like structure. The model was loaded in the longitudinal direction with a distributed load that increased from 0 MPa at the endosteal side to 60 MPa at the periosteal side. The outer part of the model was not loaded to let the model create a natural bone surface.

Results

At 6 weeks, at growth plate level, the cortex consisted of trabecular bone (Fig. 2). At the metaphyseal level, a cortex was present, but it could barely be distinguished from trabecular bone. At the diaphyseal level, a cortex was clearly present; the endosteal surface was irregular owing to trabeculae merging into the cortex and osteoclastic bone resorption. At the periosteal side, circumferential plexiform plates were present, which were interconnected by radially orientated bone rods (Figs 2, 3A,B and 4). The pores in the cortical bone, mainly orientated longitudinally, could be visualized (Fig. 3C). They represented soft tissue. Histological examination showed that bone around the pores was plexiform; no secondary osteons were present (Fig. 3B).

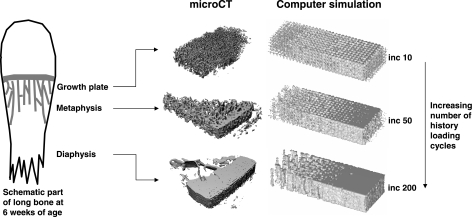
Fig. 2.

Results of µCT and computer simulations of cortical bone development. The number of history loading cycles that bone is subjected to increases from the growth plate towards the diaphysis. The left part of each picture is the endosteal side and the right part is the periosteal side. The computer simulation showed the tendency of cortical bone development. At increment 10, a trabecular structure has developed, which can be compared with the trabecular structure at growth plate level at 6 weeks of age. At increment 50, the structure corresponded with 6 weeks at metaphyseal level. At increment 200, the structure corresponded with 6 weeks at diaphyseal level.

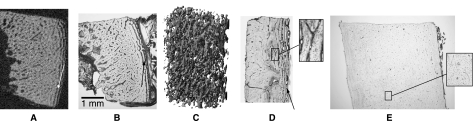
Fig. 3.

MicroCT section (A), histological slice (B) and 3D pore structure (C) of the diaphyseal cortex at 6 weeks (microCT); histological slice of the metaphyseal cortex at 23 weeks (D); and histological slice of the diaphyseal cortex at 230 weeks (E). The left part of each picture is the endosteal side and the right part is the periosteal side. At 6 weeks: at the periosteal side, circumferential bone plates are present (see arrows in A and B), which are interconnected by radially orientated bone rods. The 3D reconstruction of the pores (C) is made from a rectangular volume within the cortex. This means that the endosteal and periosteal surfaces are not shown. At 23 weeks (D), the endosteal surface had smoothened, but the circumferential plates were still present periosteally (see arrow). In the centre of the cortex, the plates had filled with plexiform bone (see detail). At 230 weeks (E), the inner and outer cortical surfaces were smooth, consisting of circumferential lamellar bone. Secondary osteons were present throughout the entire cortex (see detail).

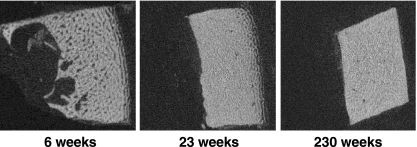
Fig. 4.

MicroCT sections of the cortical bone development at diaphyseal level. At 6 weeks, the inner surface is irregular due to merging trabeculae and bone resorption. The outer surface consists of the circumferential bone plates. At 23 weeks, the endosteal surface of the diaphysis has smoothened, but the circumferential plates are still present at the periosteal surface. At 230 weeks, inner and outer surfaces of the diaphysis are smooth.

At 23 weeks, at growth plate level, the situation was similar to that at 6 weeks. At metaphyseal (Fig. 3D) and diaphyseal (Fig. 4) levels, the endosteal surface had smoothened, but the circumferential plates were still present periosteally. In the centre of the cortex, the plates had filled with plexiform bone (Fig. 3D).

At 230 weeks, a porous cortex was present at growth plate level, in which trabeculae merged. The inner and outer cortical surfaces at metaphyseal and diaphyseal (Fig. 4) levels were smooth, consisting of circumferential lamellar bone (Fig. 3E). Secondary osteons were present throughout the entire cortex (Fig. 3E).

The computer simulation model showed the tendency of cortical bone development (Fig. 2). At remodelling increment 10, the initial homogeneous distribution of bone had developed into trabecular bone, a situation comparable with that at 6 and 23 weeks at growth plate level. At increment 50, the structure corresponded with that at 6 weeks at metaphyseal level, and at increment 200, the structure corresponded with that at 6 weeks at diaphyseal level and with 230 weeks at growth plate level. The model did not predict further cortical development, i.e. development of a smooth endosteal surface.

Discussion

The results of this study support the hypotheses that the development of cortical bone is governed by mechanical stimuli and that trabecular and cortical bone share the same regulatory mechanisms for adaptation to mechanical loads.

The cortical bone structure changed significantly during growth. The µCT scans visualized the 3D trabecular structure merging with the cortex. From the growth plate towards the diaphysis, the pores of the trabecular structure were gradually filled in with bone, which resulted in increased density and cortical bone. This observation is in agreement with the study of Cadet et al. (2003). They used oxytetracycline labelling and epifluorescence microscopy in growing rabbits and showed that metaphyseal cortical bone is indeed formed by coalescence of trabecular bone from the growth plate. Hence, metaphyseal cortex emerged from trabecular bone, which suggests that the regulatory mechanisms of trabecular and cortical bone are similar as well. This was confirmed by the results of the computer simulation model, largely predicting this morphological development, using the same bone regulatory theory that held for trabecular bone (Huiskes et al. 2000).

The trabecular fusion with the cortex could be visualized using µCT. In addition, µCT could be used to study the distribution and orientation of pores within the cortex. The pores in, for example, the diaphysis at 6 weeks were mainly orientated in the longitudinal direction; their structure was very irregular with many branches that were not perpendicular to each other. The pores, i.e. vascular canals being incorporated to form primary osteons, were mainly orientated parallel to the long bone axis, which agrees with the results of Hayes & Bouxsein (1997).

Pigs increase their weight from 12 kg at 6 weeks of age to about 200 kg at 230 weeks of age (Tanck et al. 2001). To withstand the increasing bending moment, it is efficient to form bone located far from the bone axis. The periosteal apposition plates, i.e. saltatory bone formation (Stover et al. 1992), illustrated this at 6 and 23 weeks of age. Another advantage of bone plates is that bone mass can be increased relatively rapidly as osteoblasts can form bone at both sides of the plates.

There were some limitations to the present study. First, the computer model did not predict the smooth surface at the endosteal side of the metaphyseal and diaphyseal cortices at 23 and 230 weeks; the surface remained trabecular-like. This was probably caused by the limited longitudinal dimension of the FEA model. In our model, load transfer goes through the entire cross-section, whereas in a model with a larger longitudinal length, stress transfer at the middle of the length would mainly go through the outside of the cortex. Despite this limitation, the computer simulation model largely predicted the morphological development of the cortex in a correct manner. Secondly, we only described the cortical development of three pigs with increasing age. A pilot study showed, however, that similar patterns could be found for cortical development in pigs at similar ages. Furthermore, the 2D histological slices did not completely match the µCT slices. This was probably caused by a slightly different sawing direction compared with scanning direction. Although it would be possible to manipulate the µCT slices to improve the matching somewhat, this would not affect the results and conclusions of this study.

Development of long bones depends on genetic, biological and biomechanical factors (Carter et al. 1991). The widely held hypothesis that the development of cortical bone is governed by mechanical stimuli does not preclude alternative explanations, such as those that assume that patterning results from the presence of threshold values for signalling molecules (Turing, 1952; Weinans & Prendergast, 1996; Lovejoy et al. 2002). Note that the basic assumption of our model is that mechanics and such mechanisms interact. Mechanical loading is not considered to be the direct stimulus for bone remodelling but rather the stimulus that determines the expression of biochemical signalling molecules. The local concentration of this biochemical factor is subsequently compared with a set-point value at the bone surface. Upon exceeding a certain threshold, local bone apposition occurs.

We conclude that merging of metaphyseal trabeculae under the growth plate into cortex is likely to be governed by mechanical stimuli. Furthermore, development of the diaphyseal cortex can be explained as a form of trabecular bone adaptation, without the need for different regulatory mechanisms for cortical and trabecular bone.