Skip to main content
PMC home page
Journal of Anatomy logoLink to Journal of Anatomy
. 2006 Jun;208(6):769–784. doi: 10.1111/j.1469-7580.2006.00576.x

Differences between sliding semi-landmark methods in geometric morphometrics, with an application to human craniofacial and dental variation

S Ivan Perez 1, Valeria Bernal 1, Paula N Gonzalez 1
PMCID: PMC2100233  PMID: 16761977

Abstract

Over the last decade, geometric morphometric methods have been applied increasingly to the study of human form. When too few landmarks are available, outlines can be digitized as series of discrete points. The individual points must be slid along a tangential direction so as to remove tangential variation, because contours should be homologous from subject to subject whereas their individual points need not. This variation can be removed by minimizing either bending energy (BE) or Procrustes distance (D) with respect to a mean reference form. Because these two criteria make different assumptions, it becomes necessary to study how these differences modify the results obtained. We performed bootstrapped-based Goodall's F-test, Foote's measurement, principal component (PC) and discriminant function analyses on human molars and craniometric data to compare the results obtained by the two criteria. Results show that: (1) F-scores and P-values were similar for both criteria; (2) results of Foote's measurement show that both criteria yield different estimates of within- and between-sample variation; (3) there is low correlation between the first PC axes obtained by D and BE; (4) the percentage of correct classification is similar for BE and D, but the ordination of groups along discriminant scores differs between them. The differences between criteria can alter the results when morphological variation in the sample is small, as in the analysis of modern human populations.

Keywords: dental and facial data, minimum bending energy, minimum Procrustes distance

Introduction

The analysis of human morphological variability has a long tradition in anthropological studies. Several recent analyses, usually based on craniometric data, support the existence of low morphological variation among modern humans (Howells, 1989; Relethford & Harpending, 1994; Relethford, 1994; Hannihara et al. 2003). Howells's (1989) study of worldwide craniometric variation established that differences among modern human populations are small based on the comparison of modern crania with several archaic forms. Likewise, Relethford (1994) and Relethford & Harpending (1994) found that the amount of morphological variation among geographical regions is relatively low with respect to intrapopulation variation. Such results are in agreement with those based on genetic data (Lewontin, 1972; Barbujani et al. 1997; among others). These craniometric studies have been based on traditional morphometric methods, which have been used widely in anthropology. However, given the low levels of morphological variation found among human samples, other techniques that allow the capture of subtle shape differences become necessary. Geometric morphometric methods (Rohlf & Marcus, 1993; Adams et al. 2004) have been increasingly applied to the study of human form over the last decade. These approaches focus on methods that capture the geometry of morphological structures and preserve this information throughout the analyses. More powerful morphometric analyses can be performed using these more comprehensive data (Rohlf, 1990, 2000a) and very subtle shape differences can be visualized (Rohlf & Marcus, 1993; Baylac et al. 2003). There are also theoretical reasons for the use of geometric morphometrics instead of traditional methods, including the rigorous statistical theory developed for shape analysis (see Adams et al. 2004). Concurrently, there is a considerable amount of empirical evidence demonstrating the ability of landmark-based geometric methods to provide new insights into patterns of biological shape variation that could not be evaluated by traditional methods (Monteiro & Abe, 1999; Monteiro et al. 2002; Reis et al. 2002; among others; cf. Lynch et al. 1996). For example, in some studies geometric morphometrics methods were able to discriminate groups (e.g. species, populations) that could not be separated by traditional methods (Adams & Funk, 1997; Monteiro-Filho et al. 2002; Baylac et al. 2003; Perez, 2003; Bernal, 2005). Given the above-mentioned theoretical and empirical reasons, geometric morphometrics techniques are useful for the study of intraspecific morphological variation, such as the variation among human populations.

The most widely used geometric morphometrics methods are landmark-based approaches that use sets of two- or three-dimensional coordinates of biological landmarks (Bookstein, 1996a,b, 1998). From a biological viewpoint, the use of landmarks may not be sufficient because they cannot describe some biological forms and patterns (Oxnard, 1978). Further information may be obtained by increasing the number of point coordinates. However, this cannot be done with points defined as landmarks because large areas of many biological objects, such as the human cranial vault or facial skeleton, have few or no landmarks and their structural information is represented only by surfaces, curves or outlines. Therefore, the sliding semi-landmark method was proposed, to capture and analyse outlines (Green, 1996; Bookstein, 1997). This operation extends the standard Procrustes superimposition procedure: in addition to translating, scaling, and rotating landmarks optimally, the semi-landmark points are slid along the outline curve until they match as well as possible the positions of corresponding points along an outline in a reference configuration (Adams et al. 2004). This is done because the curves or contours should be homologous from subject to subject, whereas their individual points need not be (Bookstein et al. 2002). Several criteria have been proposed to slide points along an outline. Two of the most widely used are minimum bending energy (BE; Bookstein, 1996c, 1997; Green, 1996; Bookstein et al. 2002) and perpendicular projection or minimum Procrustes distance (D; Sampson et al. 1996; Bookstein et al. 2002; Sheets et al. 2004). According to the first criterion, the positions of semi-landmarks along the contour of each specimen are allowed to slide along the direction locally parallel to the outline in order to minimize the bending energy necessary to produce the change in the outline relative to the reference form (Fig. 1a). The requirement that semi-landmarks of the mean shape deform smoothly to the shape of a particular specimen in a manner that minimizes bending energy is equivalent to the conservative assumption that the contour on a particular specimen is the result of the smoothest possible deformation of the corresponding contour on the reference form (Bookstein, 1996c; Sheets et al. 2004). The minimum Procrustes distance criterion removes the difference along the curve in semi-landmark positions between the reference form and each specimen by estimating the direction tangential to the curve and removing the component of the difference that lies along this tangent (Sheets et al. 2004). The semi-landmarks along the curve are aligned so that the semi-landmarks of each specimen lie along the lines perpendicular to the curve that passes through the corresponding semi-landmarks on the reference form (Fig. 1b; see Sampson et al. 1996). Owing to the fact that semi-landmark methods permit the generation of a representation of the overall shape of biological structures, they are destined to gain importance as morphometric tools. Thus, an understanding of the effects that the choice of sliding landmarks methods has on empirical studies of different biological problems becomes a fundamental issue for research.

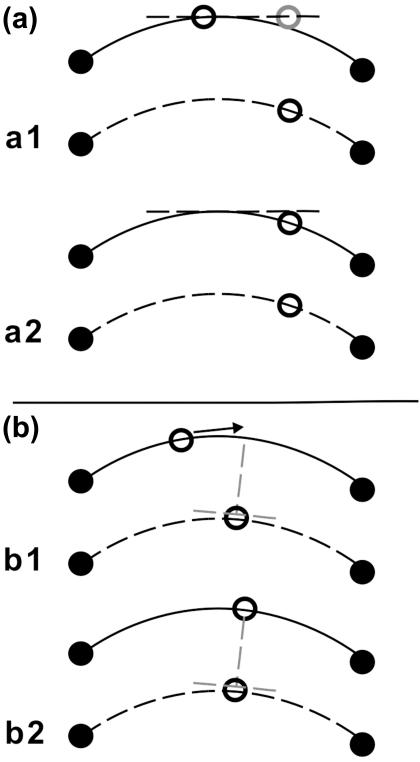
Fig. 1.

Fig. 1

Open in a new tab

(a) Minimum bending energy criterion. The figure shows a semi-landmark point slid along an outline tangent (a1) and projected onto the outline after the relaxation step (a2) (modified after Gunz et al. 2005). (b) Minimum Procrustes distance criterion. The figure shows a semi-landmark point before (b1) and after sliding it toward the line that is perpendicular to the edge at the corresponding semi-landmark of the reference (a2) (modified after Zelditch et al. 2004).

In this work we show the differences between the results obtained using semi-landmarks aligned by these two different criteria in the morphometric study of the biological relationships among human populations. Of particular concern is the possibility that the different methods of handling semi-landmarks might influence the estimated difference between the mean shapes of several different groups of specimens, or the variation within each group. These differences in the mean and variance might result in differences in principal components analysis (PCA) of patterns of variance or in the ability to discriminate among groups using discriminant function analysis (or canonical variates analysis, CVA). We also evaluate the extent to which the number of semi-landmarks used may influence these results. Finally, we discuss the implications that such differences have for the study of modern human populations characterized by low levels of morphological variation.

Materials and methods

Two structures differing in their intrapopulation variation and complexity were analysed: (a) the upper first molar, which varies little and can be described by means of a closed outline (Fig. 2a), and (b) the facial skeleton, which presents greater variation and can be described through a combination of landmarks with open and closed outlines (Fig. 2b). A total sample of 60 upper first molars of individuals from several geographical regions of Argentina (Bernal, 2004) and 66 male adult human skulls from the Chubut and Negro River valleys (Patagonia, Argentina) were analysed; the specimens are housed at División de Antropología in Museo de La Plata and at Museo Etnográfico ‘J. B. Ambrosetti’ in Buenos Aires, Argentina. The Chubut sample, which included individuals from Chubut Valley (CH, n = 20) and the neighbouring area (n = 10), corresponds to the later late Holocene (c. 500–1500 years bp), a subsample from Negro Valley (RNa, n = 17) corresponds to the same period, whereas the second subsample from Negro Valley (RNb, n = 19) corresponds to middle/late Holocene (c. 3000–4000 years bp; Barrientos & Perez, 2004, 2005).

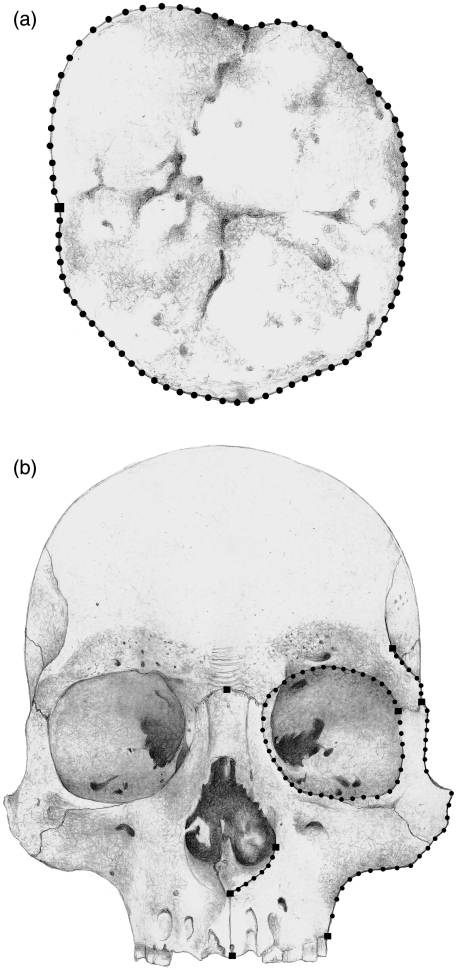
Fig. 2.

Fig. 2

Open in a new tab

Landmarks and semi-landmarks recorded on dental (a) and facial (b) structures. Drawing by Marina Perez.

The specimens were photographed with an Olympus Camedia C-3030 digital camera. The upper first molars were positioned with the occlusal surface parallel to the camera at 100 mm. The skulls were positioned in the Frankfurt plane and the camera lens was located in the coronal plane (Buikstra & Ubelaker, 1994). Frontal view images were taken at 250 mm from the prosthion point. Seventy-nine semi-landmarks and one landmark were obtained from the upper first molars (Fig. 2a); eight landmarks and 74 semi-landmarks were obtained from the facial skeleton (Fig. 2b). The semi-landmark coordinates corresponding to the upper first molars were automatically obtained using tpsDIG 1.40 (Rohlf, 2004). The application MakeFan6 (Sheets, 2003), which places alignment ‘fans’ at equal angular displacements along a curve, was used to ensure consistent placement of the facial semi-landmark coordinates. Both landmarks and semi-landmarks were then digitized using tpsDIG 1.40 software (Rohlf, 2004).

In landmark-based analysis shape can be defined as the information remaining in a configuration of landmark points after the differences due to location, scale and orientation are removed (Bookstein, 1991, 1996a). The effects of location, scaling and orientation are typically removed using generalized Procrustes analysis (Gower, 1975; Rohlf, 1990; Rohlf & Slice, 1990) to produce a set of specimens in partial Procrustes superimposition (Rohlf, 1999; Slice, 2001) with respect to a common reference form. In the partial Procrustes superimposition approximation, the set of x and y coordinates of any single specimen's digitized two-dimensional landmark points are first centred at the origin (0,0) by substracting the centroid or mean location of all landmarks from each (x,y) pair. After the specimen has been centred, the centroid size of the configuration (the square root of the summed square distance of all landmarks from the centroid) is set to 1 through division of the coordinates by the initial centroid size of the specimen. An iterative procedure is used to determine the mean form onto which all specimens are aligned. During this iterative procedure, all specimens are first aligned as a single specimen, and the mean shape of all specimens is calculated. All specimens are then rotated to minimize the added squared differences of landmark coordinates between each specimen and the estimated mean shape or reference form. This procedure is repeated until the mean shape does not change substantially after iteration of the orientation procedure (Rohlf, 1999). At this point, the specimens are said to be in partial Procrustes superimposition onto the reference form. A full Procrustes superimposition would allow the centroid size to vary from 1 to reduce further the distance between specimens and the reference, but the partial Procrustes superimposition is typically preferred (Rohlf, 1999; Slice, 2001).

When outlines are digitized at discrete points, a step is added to generalized Procustes analysis to minimize the variation tangential to the curve. In this case, individual points are not claimed to be homologous from specimen to specimen, and consequently only the coordinate normal to the outline bears information about differences between specimens or groups (Bookstein, 1997; Bookstein et al. 2002). There are various versions of the Procrustes method that slide the points along the tangential direction so as to remove this variation (Bookstein et al. 2002; Sheets et al. 2004). Here the semi-landmarks were aligned using both the minimum bending energy criterion (Green, 1996; Bookstein, 1997) and the minimum Procrustes distance criterion (Andresen et al. 2000; Sheets et al. 2004), the latter performed following Sampson et al. (1996). The algorithm for computing a Procrustes mean curve takes one of the original outlines Xi as an initial estimate of the mean curve Y, then translates, scales and rotates each of the outlines Xi into Procrustes superimposition on Y by the iterative closest point algorithm (Besl & McKay, 1992). Subsequently, new corresponding points on each of the outlines Xi are computed by projecting equally spaced points onto Y along the normals to the Y outline. A new estimate of the mean curve Y is computed as the average of these corresponding points on the superimposed Xi. Finally, each step can be iterated until Y has converged (Sampson et al. 1996) or just one cycle of adjustments can be made (F. J. Rohlf, personal communication).

Bookstein (1997) used the bending energy model of the thin-plate spline method to determine the criteria for sliding semi-landmarks along outlines. This approach places the semi-landmarks along the contour so as to minimize the bending energy required to deform the reference curve Y to match the target curve Xi (Gunz et al. 2004). The minimization of the bending energy is equivalent to seeking the smoothest possible deformation of one curve into the other, using a generally accepted mathematical definition of smoothness. Semiland6 software (Sheets, 2003) was used to slide the points by means of the minimum Procrustes distance criterion and tpsRelw 1.40 (Rohlf, 2004) was used to align semi-landmarks based on the minimum bending energy criterion.

To evaluate the influence of the number of semi-landmarks, 40 semi-landmark coordinates from molars and 38 semi-landmark coordinates from facial skeleton were deleted before performing the alignments. Every second coordinate was removed in each outline using the tpsUtil 1.29 software application (Rohlf, 2004).

Mean shapes of different groups of specimens (drawn from different localities aligned using different methods) were compared by computing group means from the superimposed coordinates using partial Procrustes superimposition. The differences in the relative positions of landmarks and semi-landmarks were then plotted and the partial Procrustes distances between the mean specimens of the different groups were calculated using the TwoGroup6 program (Sheets, 2003). Resampling-based (Bootstrap) Goodall's F-test (Goodall, 1991; Zelditch et al. 2004) was used to test the significance of the observed differences in mean shape between groups.

Morphological diversity or variation within each sample was evaluated using Foote's (1993) disparity measurement. This is defined as morphological disparity 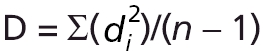Inline graphicwhere di represents the distance of the specimens to the group centroid. Disparity was measured using DisparityBox6 software (Sheets, 2003), which uses the partial Procrustes distance as a measure of di.

The partial warp scores plus the uniform components, derived using thin-plate spline decomposition of the bending energy matrix from the partial Procrustes-aligned landmark and semi-landmark coordinates, were used to perform a PCA of the specimens (Rohlf, 1993; Bookstein, 1996b; Dryden & Mardia, 1998). The partial warp scores are components along the orthogonal eigenvectors of the bending energy matrix and describe non-affine patterns of shape difference (Bookstein, 1989, 1991), whereas the uniform components describe affine shape differences (Bookstein, 1996d; Rohlf & Bookstein, 2003). Thin-plate spline decomposition has become a standard technique in geometric morphometrics because it yields a convenient set of variables to perform multivariate statistical analysis, as the partial warp plus uniform component scores express shape changes in the same number of variables as there are independent measurements. Additionally, the thin-plate spline method allows for use in the intuitive deformation grid diagrams to depict shape changes. A PCA of the partial warp plus uniform component scores, typically known as relative warp analysis, was performed using tpsRelw 1.40 (Rohlf, 2004). Discriminant function analysis was then performed on the first 50 principal component (PC) axes using the application CVAGen6n (Sheets, 2003). The deformation grids along the discriminant scores were obtained with tpsRegr 1.28 (Rohlf, 2004).

As PCA is often used as an exploratory analysis of the patterns of variation in a data set, we used Pearson's correlation and Procrustes analysis to compare the patterns of ordination produced by the two alignment procedures (Gower, 1971; Digby & Kempton, 1987; Peres-Neto & Jackson, 2001). The correlation of site scores along the first PC was used as a measure of consistency (Digby & Kempton, 1987). The ordinations in several dimensions were scaled and rotated in order to find an optimal superimposition to maximize their fit (see above). The sum of the squared residuals between configurations in their optimal superimposition can then be used as a measure of association (Gower, 1971). A permutation procedure (PROTEST) implemented by Jackson (1995) was then used to assess the statistical significance of the Procrustean fit (Peres-Neto & Jackson, 2001). Procrustes analysis was made using the vegan 1.4.4 package for R 1.9.1 (Ihaka & Gentleman, 1996).

Results

The differences in mean shape estimation and semi-landmark alignment between the two methods for both the molar and the facial data are shown in Figs 3 and 4. Goodall's F-test was used to compare the mean shapes of specimens from CH with those from RNa, and to compare RNb with RNa. The F-scores and P-values were similar for the minimum bending energy and minimum Procrustes distance criteria, whereas, not surprisingly, the estimated partial Procrustes distances between the means were larger under the minimum bending energy criterion (Table 1, Fig. 5). For comparison purposes, the same tests were run on the data without any semi-landmarks alignment (only partial Procrustes alignment). The F-scores obtained were smaller than those for the aligned semi-landmarks, and the partial Procrustes distances were similar to those produced applying the minimum bending energy criterion (Table 1).

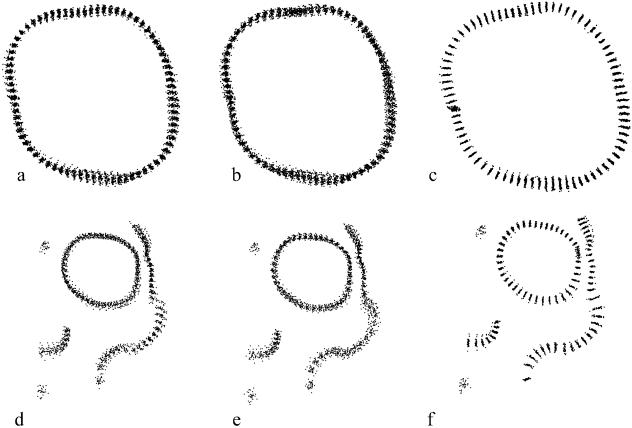
Fig. 3.

Fig. 3

Open in a new tab

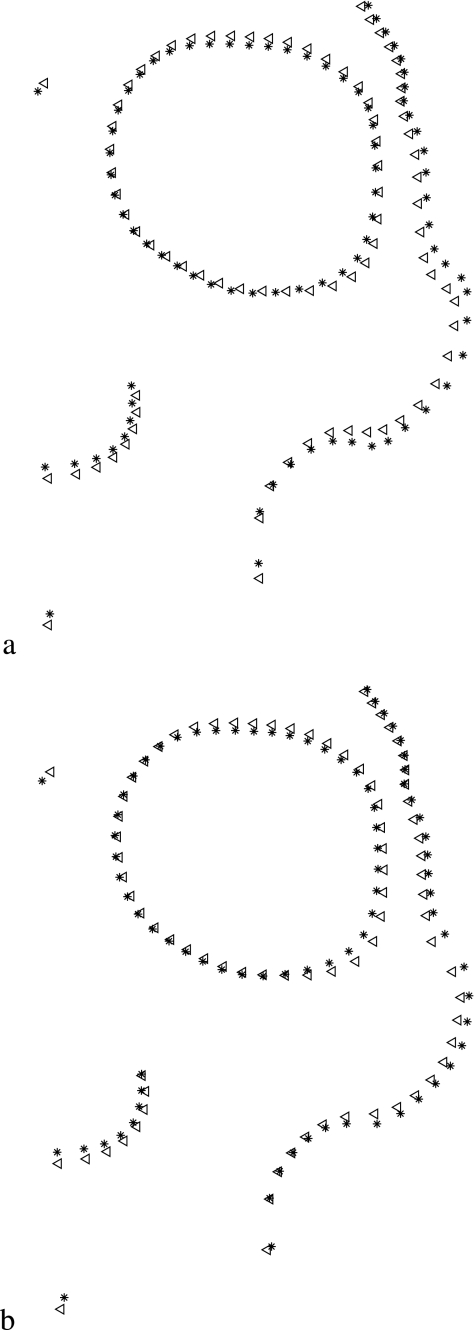
Procrustes superimposition of one landmark and 79 semi-landmarks on 60 molars without semi-landmark alignment (a), and aligned by minimum bending energy (b) and minimum Procrustes distance (c) criteria. Procrustes superimposition of 30 facial skeletons from Chubut with eight landmarks and 74 semi-landmarks without semi-landmark alignment (d), and aligned by minimum bending energy (e) and minimum Procrustes distance (f) criteria.

Fig. 4.

Fig. 4

Open in a new tab

Superimposition of group mean shapes of specimens aligned by BE and D criteria: (a) molar data with 80 points, (b) facial data with 82 points. The figure shows mean group shape, obtained after joint superimposition of both groups. Triangles = BE; stars = D.

Table 1.

Partial Procrustes distances, Goodall's F-scores and P-values (999 bootstraps) between Chubut and Negro valleys facial skeleton samples (82 points)

CH-RNa RNa-RNb RNb-CH
Method Distance F-score P Distance F-score P Distance F-score P
P 0.0220 1.54 0.148 0.0325 3.37 0.007 0.0398 5.92 0.001
BE 0.0246 2.13 0.038 0.0324 4.01 0.001 0.0439 7.82 0.001
D 0.0192 2.59 0.011 0.0246 4.30 0.001 0.0322 7.65 0.001
Open in a new tab

P, partial Procrustes superimposition without semi-landmark alignment; BE, minimum bending energy; D, minimum Procrustes distance.

Fig. 5.

Fig. 5

Open in a new tab

Superimposition of group mean shapes of specimens: (a) RNb sample vs. CH sample aligned by BE criterion; (b) RNb sample vs. CH sample aligned by D criterion. The figure shows mean group shape, obtained after joint superimposition of both groups. Triangles = RNb; stars = CH.

When within-groups variation was estimated using the two semi-landmark alignment procedures, the bending energy alignment produced changes in the estimated shape variation that were modest as compared with the shape variation obtained when no semi-landmark alignment was performed (Tables 2 and 3). The minimum Procrustes distance method consistently reduces within-group variation in comparison with either the bending energy-aligned data or the data without semi-landmark alignment.

Table 2.

Foote's measurement of within-sample disparity for the two sliding semi-landmarks criteria and the partial Procrustes superimposition of points

Method
Structure No. of points P BE D
Upper first molar 80 0.0009 0.0010 0.0006
40 0.0009 0.0011 0.0007
Facial skeleton 30 82 0.0026 0.0024 0.0013
(CH) 44 0.0025 0.0025 0.0013
Facial skeleton 56 82 0.0030 0.0028 0.0015
(CH, RNa and RNb) 44 0.0029 0.0027 0.0014
Open in a new tab

P, partial Procrustes superimposition without semi-landmark alignment; BE, minimum bending energy; D, minimum Procrustes distance.

Table 3.

Foote's measurement of disparity for the two semi-landmark sliding criteria and the Partial Procrustes superimposition of points for Negro and Chubut valleys facial skeleton samples (82 points)

Method
Structure Variance P BE D
Facial skeleton 56 Total 0.0030 0.0028 0.0015
(CH, RNa and RNb) Within CH 0.0031 0.0026 0.0014
Within RNa 0.0031 0.0026 0.0013
Within RNb 0.0025 0.0021 0.0013
Among 0.0005 0.0006 0.0003
Open in a new tab

P, partial Procrustes superimposition without semi-landmark alignment; BE, minimum bending energy; D, minimum Procrustes distance.

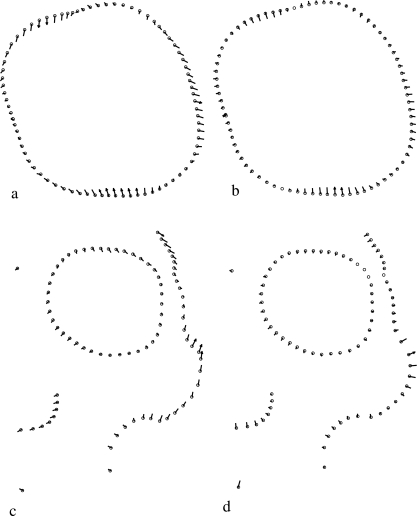
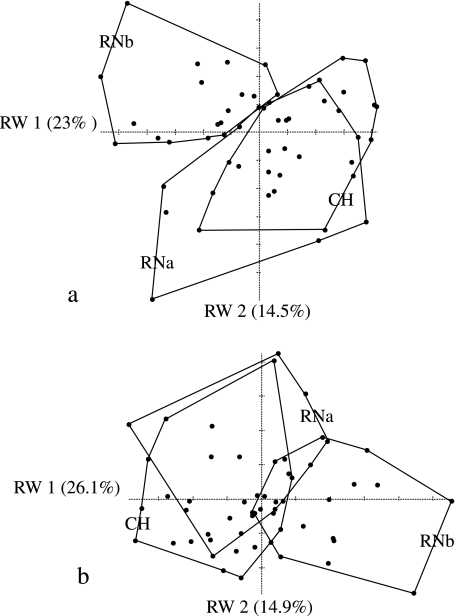
The correlation of specimen scores along the first PC and the Procrustes analysis of ordinations obtained from several PCs show several interesting features (Table 4). For the dental data, the correlation between scores along the first PC axes and between ordinations based on BE and D semi-landmark alignment is relatively high when all 80 semi-landmarks are used in the analysis, and decreases when the number of semi-landmarks is reduced to 40. The correlation does not appear to change substantially when computed along only the first PC or the first two PC axes. The ordinations obtained from semi-landmarks are highly correlated with the ordinations estimated using only partial Procrustes alignment of specimens. The correlation between the PC1 scores obtained with both criteria are lower for facial data than for dental data; they are particularly low and not significant for the CH sample (Table 4). The correlation of ordinations is lower for the facial data than for the dental data. Moreover, the values obtained for 30 specimens from the same sample (CH) are lower than those obtained for 56 specimens from the three samples (CH, RNa and RNb) (Table 4). A comparison of the variation explained by each of the PC axes shows little difference in the percentage explained between the minimum bending energy and minimum Procrustes distance methods (Table 5). By contrast, it does appear that the first two axes of the PCA of facial data do not explain as much variance as the first two axes of the dental data analysis. A significant percentage of the variation along the first PC axis is tangential to the outline when the specimens are aligned by minimum bending energy (Fig. 6a,c), whereas the variation is normal to the outline when the specimens are aligned by minimum Procrustes distance (Fig. 6b,d). Figure 7 shows the ordinations generated by BE (Fig. 7a) and D (Fig. 7b) using the three skull samples (RNa, RNb and CH). In the PCA obtained by minimum Procrustes distance alignment the RNb sample differs from the rest along axis 1, whereas in the case of the bending energy alignment this sample differs along the first two combined axes.

Table 4.

Correlation-like statistic derived from the symmetric Procrustes sum of squares (m12) and Pearson correlation. Unmarked values are significant at P < 0.001 (10 000 permutations)

Structure No. of points No. of PC BE – D P – BE P – D
Upper first molar 80 1 −0.99 −0.99 −0.99
80 2 0.97 0.98 0.98
80 all 0.96 0.96 0.98
40 1 −0.96 0.95 −0.99
40 2 0.94 0.95 0.99
40 all 0.95 0.94 0.98
Facial skeleton 30 (CH) 82 1 −0.32* 0.45* −0.18*
82 2 0.88 0.59 0.55
82 3 0.82 0.83 0.77
82 all 0.95 0.92 0.93
44 1 −0.37** −0.61* 0.22*
44 2 0.86 0.51 0.53
44 3 0.81 0.82 0.79
44 all 0.95 0.93 0.94
Facial skeleton 56 (CH, RNa and RNb) 82 1 −0.90 −0.14* 0.11*
82 2 0.94 0.73 0.68
82 3 0.75 0.86 0.67
82 all 0.94 0.92 0.92
44 1 0.90 −0.26* −0.09*
44 2 0.92 0.74 0.70
44 3 0.92 0.70 0.71
44 all 0.95 0.93 0.92
Open in a new tab

P, partial Procrustes superimposition without semi-landmark alignment; BE, minimum bending energy; D, minimum Procrustes distance.

*

Non-significant

**

significant at P = 0.05.

Table 5.

Distribution of variance explained for the first four PC axes

Percentage variance explained
Structure No. of points Alignment method No. of significant axes PC1 PC2 PC3 PC4
Upper first molar 80 BE 1 39 13  9  7
80 D 1 40 16  9  6
40 BE 1 38 14 11  9
40 D 1 40 16 10  6
Facial skeleton 30 (CH) 82 BE 0 21 15 13  9
82 D 0 19 16 15 10
44 BE 0 20 15 12  8
44 D 0 19 15 12  8
Facial skeleton 56 (CH, RNa and RNb) 82 BE 0 24 15 10  8
82 D 0 26 15 11  9
44 BE 0 24 19 10  9
44 D 0 18 16 13  9
Open in a new tab

BE, minimum bending energy; D, minimum Procrustes distance.

Fig. 6.

Fig. 6

Open in a new tab

Vectors of Procrustes fit of one specimen onto the reference along the first axis obtained by relative warps analysis of molar data (60 specimens and 80 points): (a) aligned by minimum bending energy and (b) aligned by minimum Procrustes distance criteria. Vectors of Procrustes fit of one specimen onto the reference along first axis obtained by relative warps analysis for facial data (30 CH specimens and 82 points): (c) aligned by minimum bending energy and (d) aligned by minimum Procrustes distance criteria.

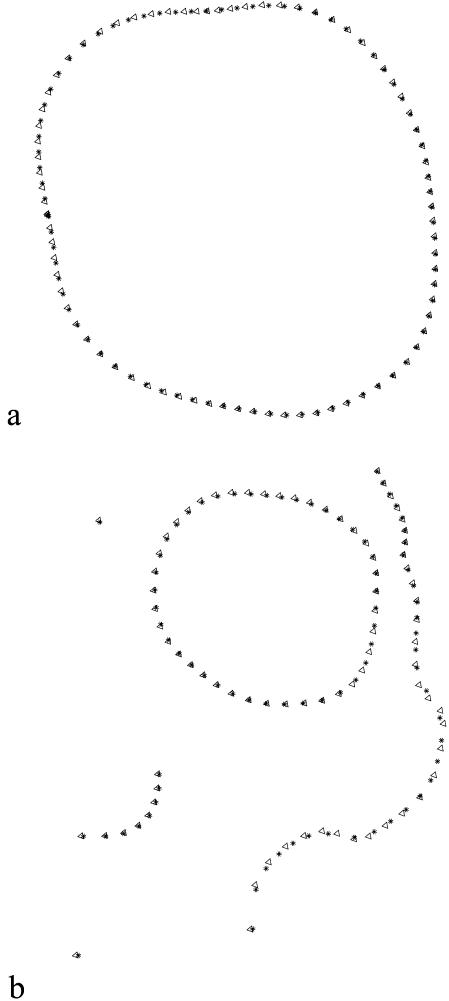
Fig. 7.

Fig. 7

Open in a new tab

Relative warps analyses performed using three samples of skulls (CH, RNa and RNb): (a) 82 points aligned by BE criterion; (b) 82 points aligned by D criterion.

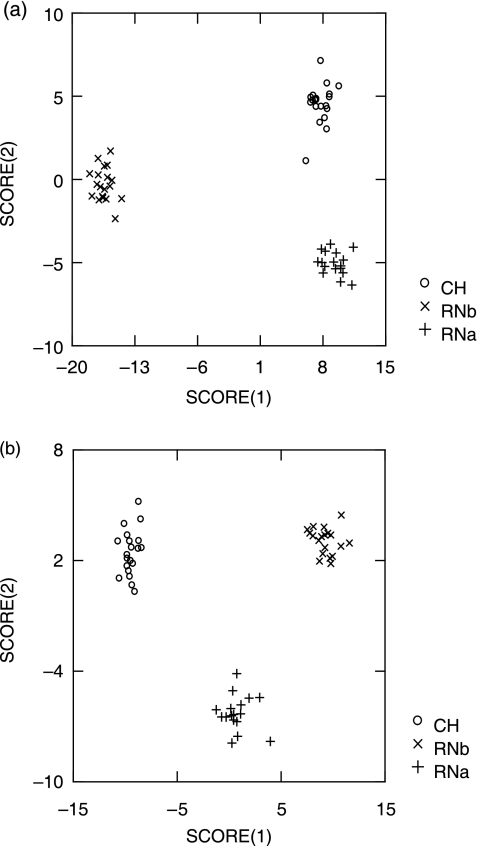
The discriminant function analyses of facial data performed on the first 50 PC axes obtained from the semi-landmarks aligned by the minimum bending energy and minimum Procrustes distance criteria also differ. The proportion of correctly classified specimens was 100% using either of the criteria. However, these proportions changed after jacknifing, with slightly higher values for minimum bending energy (64.29% for D and 67.86% for BE). When the number of points was reduced to 44, the proportion of correct classifications increased for both criteria (71.43% for D and 73.21% for BE). Although the number of correct classifications was very similar for BE and D, interpretation of the results varies when the relationships among the three groups along the discriminant scores are taken into account (Fig. 8). In the discriminant analysis of semi-landmarks aligned by the BE criterion, the RNa and CH samples have similar values along the first score (Fig. 8a). By contrast, in the discriminant analysis based on semi-landmarks aligned by the D criterion, the RNa sample shows an intermediate position along the first score but it is differentiated along the second score (Fig. 8b). Figure 9 shows the variation along the first and second scores of the discriminant analysis. When using the minimum bending energy criterion, a large proportion of the variation along the first axis is tangential to the outline, mainly in the orbital and nasal regions (Fig. 9a). In the second axis, this criterion shows tangential variation in the orbital and zygo-maxillary regions (Fig. 9c). By contrast, all the variation along these two axes is normal to the outline when using minimum Procrustes distance (Fig. 9b,d).

Fig. 8.

Fig. 8

Open in a new tab

Discriminant function analysis performed using three samples of skulls (CH, RNa and RNb): (a) 82 points aligned by BE criterion; (b) 82 points aligned by D criterion.

Fig. 9.

Fig. 9

Open in a new tab

Shape variation associated with the first two scores of discriminant analysis performed using three samples of skulls (CH, RNa and RNb): (a) score 1 aligned by BE criterion; (b) score 1 aligned by D criterion; (c) score 2 aligned by BE criterion; (d) score 2 aligned by D criterion. Procrustes vectors are exaggerated three-fold.

Discussion

Our results indicate that the two semi-landmark methods generate differences both in the mean group shapes and in the within-group variation. The minimum bending energy criterion results in larger within-group variances, but may also produce greater differences between groups (Tables 1–3). Although the overall mean sample shape does not change considerably according to the criteria employed, the position of semi-landmarks along the contours differs (Fig. 4). Nevertheless, such shifting of point coordinates along the curves cannot be interpreted as morphological differences. Likewise, the variation tangential to the outline was retained in the comparison between skeletal samples from different locations and chronological periods (RNb and CH samples) aligned by the minimum bending energy criterion. This variation increases the distance between mean sample shapes (Table 1) but cannot be interpreted as biological variation between them (Fig. 5). In particular, many of the differences between mean samples aligned by BE are due to the different location of points in the inferior orbital margin and zygomatic arch (Fig. 5a), but a substantial proportion of this variation is tangential to the contours. By contrast, the mean samples aligned using the D criterion are more similar, and the differences between them occur mainly in the left inferior orbital margin and zygomatic arch (Fig. 5b). These findings indicate that the use of BE can increase the distance between mean shapes. A significant point concerning the previous discussion is that the disparity within samples aligned by the minimum bending energy is similar to or greater than the disparity obtained by superimposing the points using the Procrustes method without sliding them. By contrast, when the points are slid by the minimum Procrustes distance, within-sample disparity is reduced by half (Tables 2 and 3). Similar results are achieved in the comparison of the disparity among samples, which is greater for minimum bending energy than for Procrustes superimposition and minimum Procrustes distance (Table 3).

Several studies include morphological traits with the purpose of comparing patterns of variation across human populations and morphological traits. In particular, analyses based on craniofacial data indicate that the action of genetic drift and gene flow are the main causes of differentiation among populations (Relethford, 1994; Roseman, 2004; González-José et al. 2005). In consequence, such studies examine within- and among-group variation of morphological traits to analyse the effects of these two evolutionary forces (Relethford & Lees, 1982), under the assumptions that the genetic and phenotypic variance–covariance matrices are proportional (Cheverud, 1988; Ackerman & Cheverud, 2000; Marroig & Cheverud, 2001) and that morphological traits have high heritability (Devor, 1987; Relethford & Lees, 1982; Relethford, 1994). The greater variation produced by BE could modify the patterns of within- and between-sample variation. In addition, the comparison of variation patterns across different types of biological data (e.g. dental and facial data) can be altered by using BE alignment (Table 2). Because the differences in variation among characters have been interpreted as reflecting differences in phenotypic plasticity (Wood & Lieberman, 2001; Lycett & Collard, 2005) the choice of sliding semi-landmark criteria can yield different interpretations.

When one sample is aligned by BE and D, the results of PCA show that the ordinations of two or more axes are similar for both criteria but the location of specimens along the first axis differs significantly (Table 4). The results of PCA can be discussed with regard to its two most common interpretations: (1) as the dimensions that best reproduce the observed distances between all the forms of the data set using linear combinations of the original variables (the interpretation as principal coordinates, see Reyment & Jöreskog, 1993); and (2) as the linear combinations of the shape variables that have the greatest variance in the data (Sokal & Rohlf, 1969). Based on the correlation-like statistic derived from the symmetric Procrustes analysis, it is apparent that PCA-based ordinations of the data represent the same pattern of relationships among the specimens as the entire set of measurements, so that the reduction in the number of variables achieved by PCA is reasonable (Table 4). The use of only two PC axes is adequate for the dental data, but not for the facial data. The analysis of the axis with greatest variation (PC1) for one sample of facial data (CH) shows significant differences between the ordinations obtained by the two alignment criteria (Table 4). The differences along the first PC among individuals aligned by D are due to the degree of zygomatic arch development and nasal height; all the variation is perpendicular to the contours (Fig. 6d). By contrast, the same individuals aligned by the minimum bending energy show variation tangential to the zygomatic and nasal outlines (Fig. 6c). Therefore, an important fraction of the variation described by the first PC axis obtained from the minimum bending energy criterion does not have a biological explanation.

The main craniofacial variation within human populations is due to sexual dimorphism; once this source of variation is controlled for, the second most important factor is the influence of environmental factors acting on the masticatory component (Hanken & Hall, 1993). These structures are recognized to be sensitive to non-genetic factors acting locally (Atchley & Hall, 1991; Hanken & Hall, 1993; Vogl et al. 1993; Lieberman, 1996; Wood & Lieberman, 2001; González-José et al. 2005; Lycett & Collard, 2005), which account for intrapopulation variation. In the CH male sample, the variation explained by the first PC calculated from D alignment can be attributed to differences in the masticatory component. By contrast, the first PC calculated from BE alignment expresses variation tangential to the zygomatic contour (Fig. 6c).

Our results indicate that the two alignment methods perform similarly in discriminant function analysis. The percentage of correctly classified cases is similar whether the semi-landmarks have been aligned by minimum Procrustes distance or minimum bending energy. In addition, this percentage increases slightly when fewer points are used. However, the relationships among samples change according to the criteria employed. In the analysis based on D alignment, the first discriminant score described variation at the zygomatic arch, nasal and orbital regions. In general, these variations represent a larger masticatory component in the CH sample but a smaller masticatory component in the RNa and RNb samples (Figs 8b and 9b). By contrast, the first discriminant score obtained by BE alignment described mainly the variation at the zygomatic arch, as well as tangential variation at the nasal and orbital regions. This analysis shows that the patterns for the CH and RNa samples are similar, whereas the RNb sample differs along the first axis; however, this differentiation is not entirely morphological (Figs 8a and 9a). These differences are due to the fact that the discriminant scores resulting from BE alignment reflected variation both tangential and normal to the outlines. In consequence, the similarity between CH and RNa samples along the first score calculated from BE is not morphological.

The differences between minimum bending energy and minimum Procrustes distance alignments become more noticeable when fewer semi-landmarks are used, indicating that the use of a large number of semi-landmarks might be advisable. An obvious disadvantage of this approach is the increased weight of the curves. In particular, the differences between our results for molars and facial skeleton are probably due to differences in the density of points used to describe either structure. For instance, 40 points were used for the orbit, with a density of 3 points cm−1, whereas 80 points were used for molars, i.e. 20 points cm−1.

Although several studies have found differences in the results achieved by traditional and landmark-based morphometric methods (Adams & Funk, 1997; Monteiro & Abe, 1999; Monteiro et al. 2002; Monteiro-Filho et al. 2002; Reis et al. 2002), other examples show that linear and landmark-based descriptors appear to be effective at capturing major shape features and describing intergroup differentiation (Lynch et al. 1996; Navarro et al. 2004). Accordingly, the effect of methods on results seems to be related to the type of analysis performed and the amount of within- and between-group variation (Navarro et al. 2004). When semi-landmarks are used, new information about biological shape is gained. Consequently, the incorporation of information about contours (i.e. semi-landmarks) can yield different results in analysis for which landmarks and linear measurements do not differ. In this respect, studies based on human facial and dental data show such results (Bernal, 2005; Perez, 2006). Because semi-landmarks incorporate information about morphological structures that is not included when using landmarks or traditional variables, they are highly useful for addressing some problems related to changes during ontogenetic development, functional aspects of structures, etc. (Atchley & Hall, 1991; Hanken & Hall, 1993; Gunz et al. 2004). Many such developmental changes affect large areas of the skeleton (e.g. zygomatic arch, neurocranium) rather than localized anatomical points (i.e. landmarks), and consequentially the area is better treated as a whole (Gunz et al. 2004). However, not all the information recorded at an outline is relevant, because only the variation that is perpendicular to the outline holds information regarding the differences between the structures; therefore, tangential variation must be removed (Bookstein, 1997). In this respect, this work demonstrates that the results obtained from the application of BE for sliding points along a contour correspond to variation that is not interpretable in biological terms because some of the tangential variation is retained. The minimum bending energy criterion is based on minimizing a part of the total variation corresponding to localized transformations, i.e. local changes, which are essentially differences in the vicinity of different points (Rohlf & Bookstein, 2003). By contrast, the minimization of Procrustes distances between outlines minimizes both the local (non-uniform) variation and the uniform variation, corresponding to the entire tangential variation between outlines. The different assumptions underlying each method and the empirical evidence presented in this work support the use of the minimum Procrustes distance criterion in the morphometric analysis of biological relationships among modern human populations.

Conclusion

In early morphometric studies, biological shapes were most often characterized by means of a single measurement or a small number of measurements (Howells, 1969; Oxnard, 1978). With the introduction of multivariate techniques, the number of measurements could increase. However, in practice such measurements are sometimes ineffective for solving real biological problems because they cannot describe most biological forms and patterns (Oxnard, 1978). With the use of two- or three-dimensional coordinates of landmarks, it becomes obvious that more information is obtained because the geometric relationships among landmarks are kept (Bookstein, 1991; Adams et al. 2004). Despite these advantages with respect to linear measures, biological structures frequently do not have enough homologous points or landmarks to permit a successful depiction of their shape. By increasing the number of coordinates along a homologous contour or surface, it is possible to obtain more information on the shape of a structure. In some instances, such as the case presented in this study, outline methods do not differ fundamentally from landmark methods in the way they handle biological homology (MacLeod, 1999; Sheets et al. 2004). When outlines are digitized as series of discrete points, individual points must be slid along the tangential direction so as to remove this variation for the purposes of averaging shapes and representing their variation and covariation (Bookstein et al. 2002). This tangential variation can be removed by minimizing bending energy with respect to an average (Bookstein, 1997, 1998) or by Procrustes distance (Andresen et al. 2000; Sheets et al. 2004). Because the two criteria make different assumptions about the processes involved, it is necessary to study how these differences modify the results obtained when either method is applied. When the morphological variation in the analysed sample is large, as in some ontogenetic (Sheets et al. 2004) or interspecific analyses, the differences between the results from different alignment criteria can be negligible (i.e. very small in relation to the variation in the sample). However, our results show that such differences can alter the results obtained when the morphological variation in the sample is small. This is especially relevant in the morphometric analysis of biological relationships among modern human populations, where D alignment is preferred because it removes all the tangential variation along outlines.

In this work the comparison of methods for semi-landmark sliding was addressed empirically using a set of actual dental and craniofacial data. However, new analyses based on simulated data (in which the underlying shape information is known instead of estimated) are necessary to compare the ability of these methods to capture the shape information of different biological objects.

Acknowledgments

We are sincerely grateful to David Sheets for his help and advice, which greatly improved the quality of the manuscript. Leandro Rabello Monteiro, F. James Rohlf and three anonymous reviewers provided helpful comments. We thank Hector M. Pucciarelli (División Antropología, Facultad de Ciencias Naturales y Museo of La Plata, Argentina), and Inés Baffi and Leandro Luna (Museo Etnográfico ‘J. B. Ambrosetti’, Buenos Aires, Argentina) for granting access to the human skeletal collections under their care. We also thank to Cecilia Morgan for help with the English version of the manuscript. Mariana Gonzalez constructed Fig. 1 and Marina Perez made the drawings in Fig. 2. This work was supported by a grant from the Fundación Antorchas (no. 14116-111); grant sponsorship Doctoral Fellowship Argentine Government (CONICET).

References

  1. Ackermann RR, Cheverud JM. Phenotypic covariance structure in tamarins (genus: Saguinus): a comparison of variation patterns using matrix correlation and common principal component analysis. Am J Phys Anthropol. 2000;111:489–501. doi: 10.1002/(SICI)1096-8644(200004)111:4<489::AID-AJPA5>3.0.CO;2-U. [DOI] [PubMed] [Google Scholar]
  2. Adams DC, Funk DJ. Morphometric inferences on sibling species and sexual dimorphism in Neochlamisus bebbianae leaf beetles: multivariate applications of the thin-plate spline. Syst Biol. 1997;46:180–194. [Google Scholar]
  3. Adams DC, Rohlf FJ, Slice DE. Geometric morphometrics: ten years of progress following the ‘revolution’. Ital J Zool. 2004;71:5–16. [Google Scholar]
  4. Andresen PR, Bookstein FL, Conradsen K, Ersbøll B, Marsh J, Kreiborg S. Surface-bounded growth modeling applied to human mandibles. IEEE Trans Med Imag. 2000;19:1053–1063. doi: 10.1109/42.896780. [DOI] [PubMed] [Google Scholar]
  5. Atchley WR, Hall BK. A model for development and evolution of complex morphological structures. Biol Rev. 1991;66:101–157. doi: 10.1111/j.1469-185x.1991.tb01138.x. [DOI] [PubMed] [Google Scholar]
  6. Barbujani G, Magagni A, Minch E, Cavalli-Sforza LL. An apportionment of human DNA diversity (genetic variation/microsatellite loci/restriction polymorphisms/racial classification) Proc Natl Acad Sci USA. 1997;94:4516–4519. doi: 10.1073/pnas.94.9.4516. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Barrientos G, Perez SI. La expansión y dispersión de poblaciones del norte de Patagonia durante el Holoceno tardío: evidencia arqueológica y modelo explicativo. In: Civalero MT, Fernández PM, Guráieb AG, editors. Contra Viento y MareaArqueología de Patagonia. Buenos Aires: INAPL; 2004. pp. 179–195. [Google Scholar]
  8. Barrientos G, Perez SI. Was there a population replacement during the late middle Holocene in the Southeastern Pampas of Argentina? Archaeological evidence and its paleoecological basis. Quaternary Int. 2005;132:95–105. [Google Scholar]
  9. Baylac M, Villemant C, Simbolotti G. Combining geometric morphometrics with pattern recognition for the investigation of species complexes. Biol J Linn Soc. 2003;80:89–98. [Google Scholar]
  10. Bernal V. Morfometría geométrica aplicada al estudio de la variabilidad morfológica dental. In: Tamagini M, Mendonca O, editors. Libro de Resúmenes del XV Congreso Nacional de Arqueología Argentina, Río Cuarto. Río Cuarto: Universidad Nacional de Río Cuarto; 2004. pp. 215–216. [Google Scholar]
  11. Bernal V. Size and shape analysis of Human molars: comparing traditional and geometric morphometric techniques. Homo. 2005 doi: 10.1016/j.jchb.2006.11.003. in press. [DOI] [PubMed] [Google Scholar]
  12. Besl PJ, McKay ND. A method for registration of 3-D shapes. IEEE Trans Patt Anal Mach Intell. 1992;14:239–256. [Google Scholar]
  13. Bookstein FL. Principal warps: thin-plate splines and the decomposition of deformations. IEEE Trans Patt Anal Mach Intell. 1989;11:67–585. [Google Scholar]
  14. Bookstein FL. Morphometric Tools for Landmark Data: Geometry and Biology. Cambridge: Cambridge University Press; 1991. [Google Scholar]
  15. Bookstein FL. Biometrics, biomathematics and the morphometric synthesis. Bull Math Biol. 1996a;58:313–365. doi: 10.1007/BF02458311. [DOI] [PubMed] [Google Scholar]
  16. Bookstein FL. Combining the tools of geometric morphometrics. In: Marcus LF, Corti M, Loy A, Naylor GJP, Slice DE, editors. Advances in Morphometrics. Vol. 284. New York: Plenum; 1996b. pp. 131–152. Nato ASI Series, Series A: Life Science. [Google Scholar]
  17. Bookstein FL. Applying landmark methods to biological outline data. In: Mardia KV, Gill CA, Dryden IL, editors. Image Fusion and Shape Variability. Leeds: University of Leeds Press; 1996c. pp. 79–87. [Google Scholar]
  18. Bookstein FL. A standard formula for the uniform shape component in landmark data. In: Marcus LF, Corti M, Loy A, Naylor GJP, Slice DE, editors. Advances in Morphometrics. Vol. 284. New York: Plenum; 1996d. pp. 153–168. Nato ASI Series, Series A: Life Science. [Google Scholar]
  19. Bookstein FL. Landmark methods for forms without landmarks: localizing group differences in outline shape. Med Image Anal. 1997;1:225–243. doi: 10.1016/s1361-8415(97)85012-8. [DOI] [PubMed] [Google Scholar]
  20. Bookstein FL. A hundred years of morphometrics. Acta Zool Hung. 1998;44:7–59. [Google Scholar]
  21. Bookstein FL, Streissguth AP, Sampson PD, Connor PD, Barr HM. Corpus callosum shape and neuropsychological deficits in adult males with heavy fetal alcohol exposure. Neuroimage. 2002;15:233–251. doi: 10.1006/nimg.2001.0977. [DOI] [PubMed] [Google Scholar]
  22. Buikstra J, Ubelaker D. Standards for Data Collection from Human Skeletal Remains. Fayetteville: Arkansas Archaeological Survey; 1994. Arkansas Archaeological Survey Research Series 44. [Google Scholar]
  23. Cheverud JM. A comparison of genetic and phenotypic correlations. Evolution. 1988;42:958–968. doi: 10.1111/j.1558-5646.1988.tb02514.x. [DOI] [PubMed] [Google Scholar]
  24. Devor EJ. Transmission of human craniofacial dimensions. J Craniofac Genet Dev Biol. 1987;7:95–106. [PubMed] [Google Scholar]
  25. Digby PGN, Kempton RA. Multivariate Analysis of Ecological Communities. London: Chapman & Hall; 1987. [Google Scholar]
  26. Dryden IL, Mardia KV. Statistical Shape Analysis. New York: John Wiley & Sons; 1998. [Google Scholar]
  27. Foote M. Contributions of individual taxa to overall morphological disparity. Paleobiology. 1993;19:403–419. [Google Scholar]
  28. González-José R, Ramírez-Rozzi F, Sardi M, Martínez-Abadías N, Hernández M, Pucciarelli HM. Functional-cranial approach to the influence of economic strategy on skull morphology. Am J Phys Anthropol. 2005;126 doi: 10.1002/ajpa.20161. in press. [DOI] [PubMed] [Google Scholar]
  29. Goodall CR. Procrustes methods in the statistical analysis of shape. J R Stat Soc Serie B. 1991;53:285–339. [Google Scholar]
  30. Gower JC. Statistical methods of comparing different multivariate analyses of the same data. In: Hodson FR, Kendall DG, Tautu P, editors. Mathematics in the Archaeological and Historical Sciences. Edinburgh: Edinburgh University Press; 1971. pp. 138–149. [Google Scholar]
  31. Gower JC. Generalized Procrustes analysis. Psychometrika. 1975;40:33–51. [Google Scholar]
  32. Green WDK. The thin-plate spline and images with curving features. In: Mardia KV, Gill CA, Dryden IL, editors. Image Fusion and Shape Variability. Leeds: University of Leeds Press; 1996. pp. 79–87. [Google Scholar]
  33. Gunz P, Mitteroecker P, Bookstein FL. Semi-landmarks in three dimensions. In: Slice DE, editor. Modern Morphometrics in Physical Anthropology. New York: Kluwer Academic/Plenum Publishers; 2004. pp. 73–98. [Google Scholar]
  34. Hanken J, Hall B. Mechanisms of skulldiversity and evolution. In: Hanken J, Hall B, editors. The Skull. Vol. 3. Chicago: University of Chicago Press; 1993. pp. 1–36. [Google Scholar]
  35. Hannihara T, Ishida H, Dodo Y. Characterization of biological diversity through analysis of discrete cranial traits. Am J Phys Anthropol. 2003;121:241–251. doi: 10.1002/ajpa.10233. [DOI] [PubMed] [Google Scholar]
  36. Howells WW. The use of multivariate techniques in the study of skeletal populations. Am J Phys Anthropol. 1969;31:311–314. doi: 10.1002/ajpa.1330310306. [DOI] [PubMed] [Google Scholar]
  37. Howells WW. Skull Shapes and the Map. Craniometric Analyses in the Dispersion of Modern Homo. Vol. 79. Cambridge: Harvard University; 1989. Papers of the Peabody Museum of Archaeology and Ethnology. [Google Scholar]
  38. Ihaka R, Gentleman R. R: a language for data analysis and graphics. J Computational Graphics Statistics. 1996;5:299–314. [Google Scholar]
  39. Jackson DA. PROTEST: a Procrustean randomization test of community environment concordance. Écoscience. 1995;2:297–303. [Google Scholar]
  40. Lewontin RC. The apportionment of human diversity. Evol Biol. 1972;6:381–398. [Google Scholar]
  41. Lieberman D. How and why recenthumans grow thin skulls: experimental data on systemic cortical robusticity. Am J Phys Anthropol. 1996;101:217–236. doi: 10.1002/(SICI)1096-8644(199610)101:2<217::AID-AJPA7>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
  42. Lycett SJ, Collard M. Due homoiologies impede phylogenetic analyses of the fossil hominids? An assessment based on extant papionin craniodental morphology. J Hum Evol. 2005;49:618–642. doi: 10.1016/j.jhevol.2005.07.004. [DOI] [PubMed] [Google Scholar]
  43. Lynch JM, Wood CG, Luboga SA. Geometric morphometrics in primatology: craniofacial variation in Homo sapiens and Pan troglodytes. Folia Primatol. 1996;67:15–39. doi: 10.1159/000157203. [DOI] [PubMed] [Google Scholar]
  44. MacLeod N. Generalizing and extending the eigenshape method of shape space visualization and analysis. Paleobiology. 1999;25:107–138. [Google Scholar]
  45. Marroig G, Cheverud JM. A comparison of phenotypic variation and covariation patterns and the role of phylogeny, ecology, and ontogeny during cranial evolution of new world monkeys. Evolution. 2001;55:2576–2600. doi: 10.1111/j.0014-3820.2001.tb00770.x. [DOI] [PubMed] [Google Scholar]
  46. Monteiro LR, Abe AS. Functional and historical determinants of shape in the scapula of xenarthran mammals: evolution of a complex morphological structure. J Morph. 1999;241:251–263. doi: 10.1002/(SICI)1097-4687(199909)241:3<251::AID-JMOR7>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
  47. Monteiro LR, Diniz-Filho JAF, Reis SF, Araújo ED. Geometric estimates of heritability in biological shape. Evolution. 2002;56:563–572. doi: 10.1554/0014-3820(2002)056[0563:GEOHIB]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  48. Monteiro-Filho ELA, Monteiro LR, dos Reis SF. Skull shape and size divergence in the genus Sotalia (Cetacea): a tridimensional morphometric analysis. J Mammal. 2002;83:125–134. [Google Scholar]
  49. Navarro N, Zatarain X, Montuires S. Effects of morphometric descriptor changes on statistical classification and morphospaces. Biol J Linn Soc. 2004;83:243–260. [Google Scholar]
  50. Oxnard CE. One biologist's view of morphometrics. Ann Rev Ecol Syst. 1978;9:219–241. [Google Scholar]
  51. Peres-Neto PR, Jackson DA. How well do multivariate data sets match? The advantages of a Procrustean superimposition approach over the Mantel test. Oecologia. 2001;129:169–178. doi: 10.1007/s004420100720. [DOI] [PubMed] [Google Scholar]
  52. Perez SI. Morfometría de poblaciones humanas prehistóricas: una comparación de técnicas Tradicionales y Geométricas. Intersecciones en Antropología. 2003;4:121–129. [Google Scholar]
  53. Perez SI. Argentina: Universidad Nacional de La Plata; 2005. El poblamiento holocenico del Sudeste de la Región Pampeana: un estudio de craneomorfometría geométrica. Doctoral thesis. [Google Scholar]
  54. Reis SF, Duarte LC, Monteiro LR, Von Zuben FJ. Geographic variation in cranial morphology in Thrichomys apereoides (Rodentia: Echimyidae). I. Geometric descriptors of shape and multivariate analysis of geographic variation in shape. J Mammal. 2002;83:125–134. [Google Scholar]
  55. Relethford JH, Lees FC. The use of quantitative traits in the study of human population structure. Am J Phys Anthropol. 1982;25:113–132. [Google Scholar]
  56. Relethford JH. Craniometric variation among modern human populations. Am J Phys Anthropol. 1994;95:53–62. doi: 10.1002/ajpa.1330950105. [DOI] [PubMed] [Google Scholar]
  57. Relethford JH, Harpending HC. Craniometric variation, genetic theory, and modern human populations. Am J Phys Anthropol. 1994;96:249–270. doi: 10.1002/ajpa.1330950302. [DOI] [PubMed] [Google Scholar]
  58. Reyment RA, Jöreskog KG. Applied Factor Analysis in the Natural Sciences. Cambridge: Cambridge University Press; 1993. [Google Scholar]
  59. Rohlf FJ. Rotational fit (Procrustes) methods. In: Rohlf FJ, Bookstein FL, editors. Proceedings Michigan Morphometrics Workshop. Michigan: University of Michigan; 1990. pp. 227–236. Special publication no. 2, Museum of Zoology. [Google Scholar]
  60. Rohlf FJ. Relative warps analysis and an example of its application to mosquito wings. In: Marcus LF, Bello E, García-Valdecasas A, editors. Contributions to Morphometrics. Madrid: Monografías del Museo Nacional de Ciencias Naturales; 1993. pp. 132–159. [Google Scholar]
  61. Rohlf FJ, Slice DE. Extensions of the Procrustes Method for the optimal superimposition of landmarks. Syst Zool. 1990;39:40–59. [Google Scholar]
  62. Rohlf FJ, Marcus LF. A revolution in morphometrics. Tree. 1993;8:129–132. doi: 10.1016/0169-5347(93)90024-J. [DOI] [PubMed] [Google Scholar]
  63. Rohlf FJ. Shape statistics: Procrustes superimpositions and tangent spaces. J Class. 1999;16:197–223. [Google Scholar]
  64. Rohlf FJ. Statistical power comparisons among alternative morphometric methods. Am J Phys Anthropol. 2000;111:463–478. doi: 10.1002/(SICI)1096-8644(200004)111:4<463::AID-AJPA3>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
  65. Rohlf FJ, Bookstein FL. Computing the uniform component of shape variation. Syst Biol. 2003;52:66–69. doi: 10.1080/10635150390132759. [DOI] [PubMed] [Google Scholar]
  66. Rohlf FJ. 2004. tps serie softwares. Available at http//life.bio.sunysb.edu/morph/
  67. Roseman CC. Detecting interregionally diversifying natural selection on modern human cranial form by using matched molecular and morphometric data. Proc Natl Acad Sci USA. 2004;101:12824–12829. doi: 10.1073/pnas.0402637101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Sampson PD, Bookstein FL, Sheehan H, Bolson EL. Eigenshape analysis of left ventricular outlines from contrast ventriculograms. In: Marcus LF, Corti M, Loy A, Naylor GJP, Slice DE, editors. Advances in Morphometrics. Vol. 284. New York: Plenum; 1996. pp. 131–152. Nato ASI Series, Series A: Life Science. [Google Scholar]
  69. Sheets HD. IMP-Integrated Morphometrics Package. Buffalo, NY: Department of Physics, Canisius College; 2003. [Google Scholar]
  70. Sheets HD, Keonho K, Mitchell CE. A combined landmark and outline-based approach to ontogenetic shape change in the Ordovician Trilobite Triarthrus becki. In: Elewa A, editor. Applications of Morphometrics in Paleontology and Biology. New York: Springer; 2004. pp. 67–81. [Google Scholar]
  71. Slice DE. Landmark coordinates aligned by Procrustes analysis do not lie in Kendall's shape space. Syst Biol. 2001;50:141–149. doi: 10.1080/10635150119110. [DOI] [PubMed] [Google Scholar]
  72. Sokal RR, Rohlf FJ. Biometry. San Francisco: W.H. Freeman; 1969. [Google Scholar]
  73. Vogl C, Atchley WR, Cowley DE, Crenshaw DE, Murray JD, Pomp D. The epigenetic influence of growth hormone on skeletal development. Growth Dev Aging. 1993;57:163–183. [PubMed] [Google Scholar]
  74. Wood B, Lieberman DE. Craniodental variation in Paranthropus boisei: a developmental and functional perspective. Am J Phys Anthropol. 2001;116:13–25. doi: 10.1002/ajpa.1097. [DOI] [PubMed] [Google Scholar]
  75. Zelditch ML, Swiderski DL, Sheets HD, Fink WL. Geometric Morphometric for Biologists: a Primer. London: Academic Press; 2004. [Google Scholar]

Articles from Journal of Anatomy are provided here courtesy of Anatomical Society of Great Britain and Ireland

RESOURCES