An allometric analysis of the number of muscle spindles in mammalian skeletal muscles

Abstract

An allometric analysis of the number of muscle spindles in relation to muscle mass in mammalian (mouse, rat, guinea-pig, cat, human) skeletal muscles is presented. It is shown that the trend to increasing number as muscle mass increases follows an isometric (length) relationship between species, whereas within a species, at least for the only essentially complete sample (human), the number of spindles scales, on average, with the square root rather than the cube root of muscle mass. An attempt is made to reconcile these apparently discrepant relationships. Use of the widely accepted spindle density (number of spindles g⁻¹ of muscle) as a measure of relative abundance of spindles in different muscles is shown to be grossly misleading. It is replaced with the residuals of the linear regression of ln spindle number against ln muscle mass. Significant differences in relative spindle abundance as measured by residuals were found between regional groups of muscles: the greatest abundance is in axial muscles, including those concerned with head position, whereas the least is in muscles of the shoulder girdle. No differences were found between large and small muscles operating in parallel, or between antigravity and non-antigravity muscles. For proximal vs. distal muscles, spindles were significantly less abundant in the hand than the arm, but there was no difference between the foot and the leg.

Introduction

In comparative studies of postcranial muscles considerable interest has attached to the relative abundance of muscle spindles since Sherrington (1894) first noted that some muscles appeared to be more richly supplied with them than others. For example, whereas there are on average 25 spindles in the Vth interosseus muscle of the cat's forelimb (Ip, 1961) and 114 in the semitendinosus muscle (Chin et al. 1962), the interosseus muscle is much smaller (0.21 vs. 6.41 g), resulting in a considerably higher concentration of spindles in that muscle (119 g⁻¹) than in the semitendinosus (18 g⁻¹). The relative abundance of spindles is almost always expressed as a density or concentration, the number per gram of muscle, in this way, from which we might naively suppose that spindles are about 6.5 times more abundant in interosseus than in semitendinosus.

Many data have now been accumulated in the form of tables attesting to the variation in numbers of spindles, both absolute and relative, in a wide variety of muscles (reviewed by Hosokawa, 1961; Voss, 1971; Barker, 1974). Smaller muscles are generally found to have higher spindle densities than larger muscles, and this has led to the frequent suggestion that the higher densities are functionally appropriate to small muscles involved in fine postural adjustment or manipulation (e.g. Matthews, 1972; Barker, 1974; Richmond & Abrahams, 1975; Brooks, 1986). This notion has been extended by Peck et al. (1984), who compared large and small muscles or groups of muscles acting in parallel and found that in humans the smaller member of each couple contained on average about 3.7 times the spindle density of the larger member. Peck et al. (1984) suggested that this difference is related to greater relative excursions of the smaller muscles, which are therefore appropriate locations for length sensors. However, the actual length changes of the spindles will depend on several features of the muscle architecture such as extrafusal fibre length, degree of pinnation and moment-arm length (Gans & Bock, 1965; McClearn, 1985), which are themselves complexly related to muscle function and not merely to size (Goslow et al. 1977; Muhl, 1982; McClearn, 1985).

Despite the widespread use of spindle density in comparative studies, it has never been demonstrated that muscle mass is an appropriate reference for spindle number. Consider, for example, the homologous muscles from four species of widely different body size given in Table 1. The trend to lower values of spindle density in larger species might tempt us to argue that we should only make comparisons between the different muscles of a single species (e.g. Cooper, 1966), but is it then merely coincidental that the soleus of the cat (2.4 g, 56 spindles, 23 g⁻¹; Chin et al. 1962) is so similar to the abductor pollicis brevis of humans (2.7 g, 80 spindles, 29.3 g⁻¹; Schulze, 1955)?

Table 1.

Spindle-capsule densities in homologous muscles of mouse, rat, cat and human

	Spindle density (g−1)
Species	Gastrocnemius (med. + lat. heads)	Flexor hallucis longus	Soleus	Lumbricalis III (hand)
Mouse			1750
Rat	40.3	50.0	309.1
Cat	6.5	23.1	22.5	173
Human	0.40	1.7	0.94	12.2

Cooper (1966) seems to have been aware of this difficulty with spindle density and she sought other comparisons that might be more informative. She found that the number of muscle spindles in a variety of muscles from three species was close to 10% of the total number of myelinated axons supplying the muscles, but her sample consisted mostly of hindlimb muscles. Nevertheless, there was evidence of functional specialization within the sample, as, following a suggestion of Swett & Eldred (1960), she also found that the ratio of the number of muscle spindles to the estimated number of alpha fibres varied between 1 : 1 and 1 : 6.

Compared with Cooper's approach to the problem of relative spindle number, that of spindle density has a major advantage, namely the ease of measuring muscle mass. Banks & Stacey (1988) used the allometric method to test the appropriateness of referring spindle number to muscle mass. The technique involves logarithmic transformation of the data, followed by regression analysis of the logarithm of spindle number against the logarithm of muscle mass. The best fitting linear relationship between the transformed data for a sample of 75 muscles, mostly from cat and humans, had a slope of 0.32, and Banks & Stacey (1988) suggested that the residual value for each muscle could be used as a convenient measure of the relative abundance of its spindle complement.

This paper presents the results of a much fuller study of muscle spindle number, again using the allometric approach. Particular attention is paid to the difference between intra- and interspecific variation in spindle number, and of the possible significance of the regression slopes and residual values. A preliminary account has been published in abstract form (Banks, 1998).

Materials and methods

Published sources

Most of the data used in this analysis have been obtained from various published sources as follows: human, Voss (1971); cat, Oshima (1938), Chin et al. (1962), Richmond & Abrahams (1975), Gonyea & Ericson (1977), Bakker & Richmond (1982), Richmond & Stuart (1985), Scott & Young (1987) and Eldred et al. (1998); rat, Arendt & Asmussen (1974), Maier (1979), Pfister & Zenker (1984) and van der Wal (1988); and guinea-pig, Martini & Palmieri (1970, 1971).

Original material

Additional data relating to various hindlimb muscles of the rat and to the soleus of the mouse have been obtained from serial sections prepared by final honours project students in Durham as follows: rat – extensor digitorum brevis (EDB), James Parker; flexor hallucis longus (FHL), Peter Himsworth; lumbricalis I, II, III and IV (LUM), and accessorius (or lumbricalis superficialis, ACC), Zoë Rogers; mouse soleus (SOL), Sally Howlett. The preparative techniques are given in Table 2.

Table 2.

Techniques used in the preparation of serial sections of rat and mouse muscles

Muscle	Fixation	Fixative	Embedding	Stain
rEDB	perfusion	cacodylate-buffered 2% formaldehyde +2.5% glutaraldehyde	epoxy resin	toluidine blue
rFHL	perfusion	phosphate-buffered 2% formaldehyde +2.5% glutaraldehyde	none (cryostat)	Weigert's haematoxylin + Van Giesen
rLUM + ACC	immersion	neutral buffered formalin	wax	Mallory's triple stain
mSOL	immersion	neutral buffered formalin	wax	Mallory's triple stain

mSOL, mouse soleus; rEDB, rat extensor digitorum brevis; rFHL, rat flexor hallucis longus; rLUM + ACC, rat lumbricalis I–IV and accessories.

Nature of the sample

In each case, the number of muscle spindles has been determined from serial sections of adult (some cat, rat, guinea-pig, mouse, some human), juvenile (some cat) or neonatal (most human) muscles and refers to the number of separately identifiable capsular expansions containing the sensory innervation, irrespective of any clustering or end-to-end (tandem) linkage (for general reviews of muscle spindle structure and function, see Banks & Barker, 2004; Banks, 2005). As section thickness was typically an order of magnitude smaller than the length of the capsular expansions, accurate determination of the number of capsules in an individual muscle is straightforward, if somewhat tedious (Voss, 1937).

In order to ensure comparability, muscle size always relates to the adult, fresh (i.e. wet) muscle. Although most authors refer to muscle weights, they all give the sizes in grams, so it is assumed that what was determined was in fact (wet) muscle mass, as for the original (Durham) material. Necessarily the values given by the various authors, both for numbers of spindles and for muscle masses, are treated as representative of the respective muscles and as having been obtained without systematic bias. Extensive use will be made of linear regression analysis, with the logarithm of muscle mass treated as the independent variable, so that any variability in spindle number or muscle mass, whether of biological or of experimental origin, will contribute to the residuals. It is necessary to consider the nature of that variability before presenting the results in detail because in many cases, especially in the human data, the spindle count for a specific muscle has been obtained from a single example and the counts for several such muscles often appear to have been obtained from a single individual.

Results

Variability in spindle number

I begin with the data given by Chin et al. (1962) on several limb muscles from the cat. Mean spindle counts varied from 25 (Vth interosseus of the hand) to 114 (semitendinosus), and overall the range of values for each muscle was close to 0.5 of its mean value (correlation coefficient = 0.99). Most of the muscles were multiply sampled as 20 pairs (left and right), and therefore represent the greatest number of replicates in the database. Chin et al. (1962) quoted means and standard deviations for the spindle counts of these muscles, from which the average coefficient of variation may be calculated as 13.0 (± 1.0 se)%. The bilateral counts were highly correlated, with an average correlation coefficient of 0.81. The mean left–right difference in spindle counts expressed as a proportion of the total range for each muscle varied from 0.08 to 0.20 (mean 0.13), so most of the variability for the muscle was, not surprisingly, due to differences between the muscles of individual animals rather than between the members of each pair of muscles from the same animal.

Despite the high correlation of the counts from homonymous pairs of muscles in the sample of Chin et al. (1962), no conclusion can be drawn about whether heteronymous muscles from single animals are similarly correlated, as the relevant primary data were not published. However, Martini & Palmieri (1970, 1971) did publish the necessary individual data for 76 fore- and hindlimb muscles of guinea-pig. From these it can be calculated that, as in the cat, the range of counts for particular muscles is highly correlated with their mean counts (correlation coefficient 0.77), although, on average, the range is only 0.3 of the mean. Probably, the range is a smaller proportion of the mean in the guinea-pig than in the cat because the muscles were derived from only three as against 20 animals. Conversely, but probably for the same reason, the average coefficient of variation is slightly higher (15.8 ± 0.8%). The spindle counts for homonymous muscles from the three animals were very highly correlated (correlation coefficients 1 vs. 2, 0.97; 1 vs. 3, 0.96; 2 vs. 3, 0.95), although there were differences among the three animals (anova, F₂ = 4.28, P < 0.05). The greatest mean difference (20.3–18.9) was that between animals 2 and 1, and, although small, is highly significant (Student's t₇₅ = −3.25, P < 0.002). This mean difference due to the individual animals, as a proportion of the grand mean, is much less than the average of the range, as a proportion of the mean count, for each muscle (0.07 vs. 0.30). The important preliminary conclusion is reached that most of the variability in a sample of heteronymous muscles attributable to stochastic deviations from the population mean will be present even if the sample is drawn from a single individual.

Homologous muscles

Selection of muscles included in the sample of Banks & Stacey's (1988) study was essentially arbitrary. Only one muscle (soleus) was represented by its homologues in all three species, although gastrocnemius was also represented as the complete muscle from human and the separate medial and lateral heads from cat and rat, reflecting the presentation of the data in the literature. Despite this limitation, and the small number of rat muscles included, the regression slope (0.32) was geometrically significant, suggesting an underlying isometric relationship in which the number of spindles scales in proportion to the dimension of length (Banks & Barker, 2004). As a working hypothesis I shall suppose that the relative abundance of spindles in a muscle is similar in its homologues in the different species, and, if so, that individual homologous series should have regression slopes close to 0.33 and intercepts that reflect their relative spindle abundances. Inclusion of data for the guinea-pig (Martini & Palmieri, 1970), of new data for the rat and mouse, and combination of the data for the separate heads of gastrocnemius, prior to logarithmic conversion, have now provided four homologous series. The results are summarized in Table 3. Least-squares regression analysis gives slopes ranging from 0.23 (gastrocnemius) to 0.52 (FHL), although only those for FHL and soleus are significantly different from 0. This may be at least in part because of the small number of data available for each series. The regression slope for the soleus series (0.33) is particularly notable because this is the only series that extends over approximately three orders of magnitude of body size, as it includes the mouse.

Table 3.

Regression analysis of logarithmic transformations of spindle counts against muscle mass for four homologous muscle series

Muscle						Statistics
	Species	Mass (g)	Spindle count	ln mass	ln spin count		Coefficients	t	P	Range of residuals
FHL	guinea-pig	0.02	2	−3.91	0.69	intercept	3.18	9.53	0.01
	rat	0.5	25	−0.69	3.22	slope	0.52	4.75	0.04
	cat	3.25	75	1.18	4.32					−0.48, 0.53
	human	89.4	152	4.49	5.02
GASTR	guinea-pig	1.3	33	0.26	3.50	intercept	3.76	16.97	< 0.01
	rat	1.44	58	0.36	4.06	slope	0.23	3.42	0.08
	cat	14.95	97	2.70	4.57					−0.32, 0.22
	human	390.1	156	5.97	5.05
SOL	mouse	0.008	14	−4.83	2.64	intercept	3.89	17.53	< 0.001
	guinea-pig	0.08	11	−2.53	2.40	slope	0.33	5.60	0.01
	rat*	0.11	34	−2.21	3.53					−0.66, 0.36
	cat	2.49	56	0.91	4.03
	human	434	408	6.07	6.01
SPLEN	rat	46	0.81	−0.21	3.83	intercept	4.22	10.03	0.06
	cat	170	2.92	1.07	5.14	slope	0.46	2.52	0.24
	human†	346	46.5	3.84	5.85					−0.29, 0.43

^*The spindle count for the rat soleus is that of Arendt & Asmussen (1974); Kucera et al. (1989) give a value of 21.

^†The spindle count for the human splenius is the sum of the counts for splenius capitis and splenius cervicis (Voss, 1971).

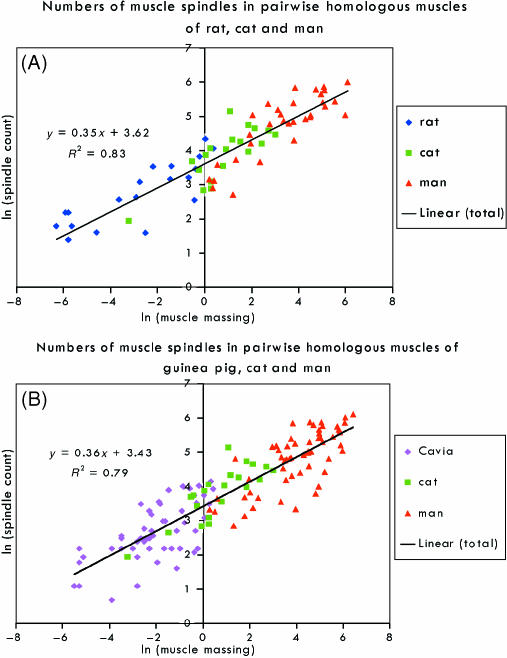
Because of somewhat different bodily proportions in the various species, in addition to other factors that have already been mentioned as contributing to residual values, it is inevitable that perfect isometry cannot in general be expected; however, averaging should reduce both specific and random variations. Simply taking the arithmetic mean of the best-fitting regression slopes for the four homologous series gives an average slope of 0.39 ± 0.06 (SE), whereas combining the data for the individual muscles that comprise the four series into a single sample for regression analysis gives a slope of 0.37, which is very highly significantly different from 0 (t = 6.95, P < 0.001) and has 95% confidence limits of 0.25 and 0.48. An alternative approach is to construct a sample consisting of all those muscles that are homologous with at least one other in a series of species differing in body size from each other by about an order of magnitude. This precludes the rat and guinea-pig from being included in the same sample, but allows two different samples (rat, cat and human; guinea-pig, cat and human) to be constructed. Scatter plots of these samples are shown in Fig. 1(A,B), and it may be noted that the data for the similarly sized rat and guinea-pig occupy essentially the same regions of their respective graphs. A summary of the statistical analysis of each sample is given in Table 4. The intercepts and slopes of the linear regressions all differ very highly significantly from 0, but are similar between the two samples. The isometric condition is within the 95% confidence limits of the slope, or at the lower limit, and in each case the slope is highly (rat, cat, human; t₆₈ =−3.33, P < 0.01) or very highly (guinea-pig, cat, human; t₁₃₀ = −4.01, P < 0.001) significantly different from 0.5 (see below).

Fig. 1.

Scatter plots of logarithmically transformed spindle counts against muscle mass for homologous muscles of three species differing in body mass. The least-squares regression of ln (spindle number) vs. ln (mass) is shown together with its equation. (A) Data from rat, cat and human. (B) Data from guinea-pig, cat and human.

Table 4.

Statistical summary of the regression analyses of two samples of logarithmically transformed spindle counts vs. muscle masses

Sample	n	Parameter	Coefficients	Standard error	t	P	Lower 95% CI	Upper 95% CI
Rat, cat, human	70	intercept	3.62	0.06	56.95	< 0.0001	3.50	3.75
		slope	0.35	0.02	17.92	< 0.0001	0.31	0.39
Guinea-pig, cat, human	132	intercept	3.43	0.05	64.18	< 0.0001	3.32	3.53
		slope	0.36	0.02	22.23	< 0.0001	0.33	0.39

Intraspecific variation

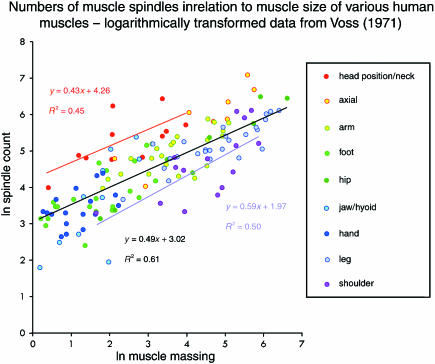
In order to examine the relationship between spindle number and muscle size in the various muscles of a single species, it is necessary to analyse the data summarized by Voss (1971), who has provided the only sample that is sufficiently large and comprehensive for the purpose. In his paper, Voss (1971) tabulates the muscles in alphabetical order, giving: (i) their mean weights in the adult (Voss, 1956); (ii) their spindle counts mostly from neonatal material; and (iii) their spindle densities (as ‘relative Spindelzahl’). For a small number of muscles, the spindle density does not correspond to the respective weight and spindle count, indicating the occurrence of a few arithmetical or typographical errors. In the present analysis the muscle weights and spindle counts have been accepted as primary data. The table has been edited to remove those muscles for which no spindle count is given, to take an average spindle count where more than one exemplar is listed, and to combine the weights of rhomboideus major and minor and of scalenus medius and posterior for which only a single spindle count is given in each case. Two muscles (mylohyoideus and pterygoideus lateralis) have also been omitted as Voss (1971) records spindle counts of 0 for both. A scatter plot of the logarithmically transformed data is given in Fig. 2, and a summary of the statistical analysis in Table 5. The slope of the best-fitting regression relationship is very close to the geometrically significant 0.5, indicating an underlying square-root function. Not only does it differ very highly significantly from 0 (see Table 5), but the slope also differs highly significantly from the isometric condition (i.e. the cube root function with exponent 0.33, t₁₃₅ = 2.85, P < 0.01).

Fig. 2.

Scatter plots of logarithmically transformed spindle counts against muscle mass for the complete sample of human muscles. The least-squares regressions of ln (spindle number) vs. ln (mass) are shown together with their respective equations, as follows: total sample in black; head position and neck muscles in red; shoulder muscles in purple.

Table 5.

Statistical summary of the regression analysis of logarithmically transformed spindle counts vs. muscle masses for a sample of human muscles (n = 137)

	Coefficients	Standard error	t	P	Lower 95% CI	Upper 95% CI
intercept	3.02	0.12	25.08	< 0.0001	2.78	3.26
slope	0.49	0.03	14.52	< 0.0001	0.42	0.55

At this point I shall hypothesize that, in other species, intraspecific variation in the abundance of spindles shows a similar relationship with muscle size to that in humans. The samples currently available are too small, too unrepresentative of the whole musculature, or both, to test the hypothesis directly, but an indirect test can be carried out using homologous pairs of subsamples for comparisons between rat and human, guinea-pig and human, and cat and human. A significant difference between the regression coefficients of any pair would be taken as evidence against the hypothesis. Having confirmed that the variances of the subsamples in each pair do not differ significantly (F-test, data not shown), I proceed to show that the regression slopes for the individual subsamples all differ very highly significantly from 0, whereas those of any pair do not differ significantly from each other (Student's t-test, statistical summary in Table 6).

Table 6.

Statistical summary of comparisons of the best fitting regression slopes for logarithmically transformed data from three samples of pairs of homologous muscles: rat vs. human; guinea-pig vs. human; and cat vs. human

	Rat	Human	Guinea-pig	Human	Cat	Human
slope	0.32	0.49	0.36	0.42	0.44	0.44
se	0.05	0.07	0.06	0.05	0.08	0.08
t	6.12	6.14	5.62	7.90	5.48	5.27
P	< 0.001	< 0.001	< 0.001	< 0.001	< 0.001	< 0.001
covariance	0.92		0.67		0.45
diff. in slopes	0.16		0.06		0.007
t	0.98		0.50		0.04
d.f.	34		96		30
P	NS		NS		NS

Information content of residual values

The regression analysis allows the extraction of a linear equation that implicitly relates spindle number in a particular muscle to the mass of the muscle. By the properties of logarithms, an equivalent, explicit, non-linear equation may also be written. For the human sample these are:

$$y=0.49x+3.02$$ (1)

and

$$S_{\text{pn}}=20.5m_{\text{n}}^{0.49}$$ (2)

respectively, where s_pn = ‘predicted’ or ‘theoretical’ number of spindles for muscle n; m_n = mass of muscle n; y = ln s_pn; and x = ln m_n. To avoid awkward units for the coefficient, the mass is taken to be the numerical value of the muscle's mass when measured in grams, or, equivalently, the ratio of the muscle's mass to a mass of 1 g. In this case the linear regression accounts for about 60% of the variability in the logarithmically transformed data space (Fig. 2). In reality, the observed number of spindles in a particular muscle, s_on, is likely to exceed or fall short of s_pn such that:

$$\text{In} S_{\text{on}}=y+{\text{r}}_{\text{n}}, \left|{\text{r}}_{\text{n}}\right| \ge 0$$ (3)

where r_n is the residual value for muscle n. In general, the residual values can be thought of as comprising two independent components: a stochastic component, itself compounded of the errors of measurement together with individual variability; and a systematic component, representing physiologically significant variation in the relative abundance of spindles in different muscles. Residual values show no correlation with ln muscle mass and so may be used to analyse differences in relative abundance of spindles, irrespective of the masses of the muscles concerned. Because the proportion of individual values due to the combined stochastic factors cannot be accurately estimated a priori, significant physiological variability is most easily demonstrated by statistical analysis of subgroups of the total sample, defined according to some rational principle.

The simplest such principle is probably that of grouping by regional location of the muscles (see Fig. 2). The results of a one-way anova carried out on nine regional groups (arm, axial muscles, foot, hand, head position + neck, hip, jaw + hyoid, leg, and shoulder) revealed the existence of very highly significant differences between groups (Table 7a). Mean residual values for the groups ranged from 1.09 (head position + neck) to −0.57 (shoulder) ln units; only three of the groups (arm, axial muscles, and head position + neck) had positive values; and five groups (foot, hand, hip, jaw + hyoid, and leg) had values between −0.1 and −0.17. Pairwise comparisons (Table 7b) of the mean residual values of selected groups using Student's t-test revealed a very highly significant difference between the head position + neck and the shoulder groups, as expected following the anova (regression relationships for these two groups are included in Fig. 2). In addition, two pairs of groups with adjacent mean values, ranked by magnitude, showed significant (leg vs. shoulder) or highly significant (axial muscles vs. arm) differences. The differences between the head position + neck and the axial muscles, and between the foot and the leg, were not significant.

Table 7(a).

One-way anova of the residual values for human muscles grouped by region

Groups	Count	Sum	Average	Variance
arm	22	3.41	0.15	0.16
axial	8	5.35	0.67	0.28
foot	20	−2.04	−0.10	0.26
hand	17	−2.94	−0.17	0.20
head position/neck	11	12.0	1.09	0.28
hip	8	−1.17	−0.15	0.24
jaw/hyoid	11	−1.70	−0.15	1.01
leg	25	−4.35	−0.17	0.11
shoulder	15	−8.58	−0.57	0.46

anova Source of variation	Sum of squares	d.f.	Mean square	F	F critical	P
Between groups	24.07	8	3.01	10.34	2.01	< 0.001
Within groups	37.25	128	0.29
Total	61.32	136

Table 7(b).

Pairwise comparisons of the mean residual values for selected regional groups of human muscles (Student's t-test, assuming equal* or unequal† variances according to preceding F-test)

	Head pos/neck	Shoulder	Head pos/neck	Axial	Arm	Axial	Shoulder	Leg
Mean	1.09	−0.57	1.09	0.67	0.15	0.67	−0.57	−0.17
Variance	0.28	0.46	0.28	0.28	0.16	0.28	0.46	0.11
Observations	11	15	11	8	22	8	15	25
Pooled variance	0.38		0.28		0.19
Hypothetical difference	0		0		0		0
d.f.	24		17		28		18
t	6.78*		1.72*		−2.84*		−2.14†
P	< 0.001		0.10 (NS)		< 0.01		< 0.05
t critical	2.06		2.11		2.05		2.10

Buxton & Peck (1990) examined three rational groupings of muscles in the forelimb of the dog for potential correlated differences in spindle densities, as measured by number of spindle profiles mm⁻² present in transverse sections. They also included similar analyses based on the spindle density data (no. g⁻¹) of Martini & Palmieri (1971) and Voss (1971). The three groupings were: (1) ordering by proximo-distal location in the limb; (2) antigravity vs. non-antigravity muscles (approximately equivalent to physiological extensors vs. physio−logical flexors); and (3) small vs. large muscles in ‘parallel muscle combinations’, a concept that had been introduced by Peck et al. (1984). Similar groupings, so far as possible containing the same muscles, have now been constructed exclusively from the human sample to facilitate comparison between the present allometric analysis and that based on spindle density of Buxton & Peck (1990). Results of the statistical analyses are summarized in Table 8a–c. Of the various comparisons made (arm vs. hand; leg vs. foot; antigravity vs. non-antigravity muscles; and small vs. large muscles in parallel muscle combinations) the only significant difference was between the arm and the hand, with the intrinsic muscles of the hand having relatively few spindles as assessed by mean residual values.

Table 8(a).

Pairwise comparisons of the mean residual values for distal vs. proximal groups of human limb muscles (Student's t-test, assuming equal* or unequal† variances according to preceding F-test)

	Hand	Arm	Foot	Leg
Mean	−0.17	0.15	−0.10	−0.17
Variance	0.20	0.16	0.26	0.11
Observations	17	22	20	25
Pooled variance	0.18
Hypothetical difference	0		0
d.f.	37		31
t	−2.40*		0.55†
P	0.02		0.59
t critical	2.03		2.04

Table 8(c).

One-way anova of the residual values for large vs. small muscles comprising ‘parallel muscle combinations’ (Peck et al. 1984) in the human upper limb

Groups	Count	Sum	Average	Variance
Large muscles	9	−3.07	−0.34	0.85
Small muscles	16	−4.08	−0.25	0.23

anova Source of variation	Sum of squares	d.f.	Mean square	F	F critical	P
Between groups	0.043	1	0.043	0.09	4.28	0.76
Within groups	10.34	23	0.45
Total	10.38	24

Table 8(b).

One-way anova of the residual values for antigravity (AG) vs. non-antigravity (N-AG) muscles of the human lower limb

Groups	Count	Sum	Average	Variance
AG muscles	30	−5.26	−0.18	0.11
N-AG muscles	18	−1.78	−0.10	0.22

anova Source of variation	Sum of squares	d.f.	Mean square	F	F critical	P
Between groups	0.066	1	0.066	0.43	4.05	0.52
Within groups	7.08	46	0.15
Total	7.15	47

Discussion

The problem of relative spindle abundance

If the functional organization of skeletal muscle is considered to arise from a system of controlled variables, including the number of motor units, their composition and the degree of pinnation, it is clear that one such variable is the number of muscle spindles present. This number is determined at an early stage of muscle organogenesis, remains essentially constant thereafter (Zelená, 1994) and is characteristic of a particular muscle. However, our inability to determine a priori the number of spindles in a given muscle, or even to provide a generally accepted explanation post hoc on the basis of its experimental determination, must surely reflect an incomplete kinematic and dynamic theory of motor control. The motivation behind comparative quantitative studies, like the present one, is therefore to provide empirical data that may contribute to a fuller such theory.

In comparing larger with smaller muscles (at least from the same species), it has long been supposed that smaller muscles may in some sense often possess a more ‘abundant’ complement of spindles than larger ones, despite having absolutely fewer of them. The notion seems to date back at least to Sherrington (1894) who, ever careful not to go beyond what was justified by the evidence, wrote: ‘Judging from my preparations I imagine the spindle-organs to be relatively more numerous in the intrinsic plantar muscles than in the large muscles of the thigh, though they are plentiful in both situations’. Although several classical authors expressed similar opinions about particular muscles, Gregor (1904) seems to have been the first to attempt a quantitative comparative study, based on three human fetuses from 25 to 29 mm long. The comparative measure used by Gregor was the ‘relative spindle quantity’ or ‘spindle density’ expressed as the number of spindles mm⁻² seen in cross-sections of each muscle. He drew up a table with the muscles arranged according to the maximum value of this measure, lumbricalis manus III emerging at the top. Clearly, the actual values of Gregor's ‘spindle density’ were only of use in establishing the relative order of the muscles according to this measure, as they would be subject to variation with growth. Few authors have subsequently used a similar measure, even when based on adult dimensions (Amonoo-Kuofi, 1983; Buxton & Peck, 1990).

The re-definition of spindle density to signify the number of spindles per unit mass of the adult muscle, introduced by Voss (1937), generates values that are characteristic of each muscle. Treating these values as though they can be placed on a linear scale naturally leads to the often repeated conclusion that small muscles assumed to be involved in fine control, such as the lumbricals of the hand, have a relatively rich supply of spindles. Such a notion has been extended by Peck et al. (1984), who have argued that the smaller member of a pair of muscles acting across the same joint could act as a ‘kinesiological monitor’, rather than a prime mover, given that in different pairs the smaller members consistently have greater spindle densities than the larger ones. Despite the accumulation of data on numbers of spindles in different muscles, culminating in the tabulated summary of the results for the human from by Voss (1971), it was not until Banks & Stacey (1988) that the non-linearity of the underlying relationship between spindle number and muscle size was pointed out. It surely follows therefore that comparison of the relative abundance of spindles in muscles of different sizes, based on linear treatment of spindle density, is invalid or at the very least misleading. Normalization of the data by logarithmic transformation greatly facilitates their statistical analysis (Smith, 1993), and has revealed the important underlying relationships described in the present paper.

It is also necessary at this point to look briefly at the fibre-type composition of muscles in relation to their spindle content, as Kokkorogiannis (2004) has recently suggested that the number of spindles, as well as their intramuscular distribution, is determined by the varying oxidative capacity of the muscles as measured by their oxidative index (OI). The OI is simply the proportion, usually expressed as a percentage, of extrafusal muscle fibres that exhibit an oxidative (type I, slow oxidative; and type IIA, fast oxidative glycolytic) as opposed to a purely glycolytic (type IIB, fast glycolytic) phenotype. More specifically, Kokkorogiannis's (2004) hypothesis is that the ‘number and intramuscular placement of muscle spindles are related to the oxidative angiotype supplying the muscle territories rich in oxidative fibers’. Thus, what appears to be important in this hypothesis is the total amount of the oxidative angiotype in a muscle, so that a large muscle with a low OI might still have a greater amount of oxidative angiotype, and therefore more spindles, than a small muscle with a very high OI. I shall set aside the question of the intramuscular distribution of spindles in relation to oxidative fibres, as it is not directly relevant to the present argument and I have considered it elsewhere (Banks & Barker, 2004). So far as the variation in the numbers of spindles between muscles is concerned, Kokkorogiannis (2004) seems to be relying, at least in part, on an assumption that the OI tends to increase with muscle mass. Although this is true for homologous muscles of different species of increasing body size (Fuentes et al. 1998), it does not appear to be true for muscles of increasing mass of a single species. So, for the sample of cat muscles given in table 2 of Kokkorogiannis (2004), there is a clear tendency for a decrease in OI with an increase in muscle mass (ln-transformed data: slope of linear regression = −0.18; anova: F₁ = 6.15, P < 0.05). The key test of Kokkorogiannis's (2004) hypothesis, however, is the relationship between relative spindle abundance and OI when the effects of muscle size have been removed. This is possible with the present analysis, using the residual values of the linear regression of ln spindle number against ln muscle mass. It is to be expected that there is a direct relationship between spindle abundance (residuals) and OI. Again using the data from table 2 of Kokkorogiannis (2004), it was found that there is, in fact, no such relationship (anova: F₁ = 2.33, P > 0.14).

Interspecific variation and isometry

Allometry, the analytical approach adopted here, is an established technique in general use in comparative physiological studies of differential growth of body structures as body size increases during development of individuals, or evolution of related forms (Schmidt-Nielsen, 1984), as well as in phylogenetic studies (Riska, 1991). For animals, or for solid (space-filling) organs such as skeletal muscles, that scale isometrically, mass increases as the cube of linear dimensions, assuming constant physical density. Analysis of the various homologous series of muscles presented above indicates that, on average, the number of spindles increases not, as we might have naively supposed, in proportion to muscle mass (which would have justified the use of spindle density as a comparative measure of relative abundance), but rather in proportion to increasing linear dimensions. Because the spindle is a length sensor (Banks, 2005), it is tempting to see in this relationship a direct coupling between scaling of the measured dimension and the number of sensors required for the measurement. If there is any merit in this argument, and it can be extended to other mechanoreceptors, we should expect a different relationship in the case of the Golgi tendon organ, which, as a tension transducer (Scott, 2005), might be expected to scale numerically in proportion to the square of linear dimensions. This is because tension (physically a stress) has dimensions M L⁻¹ T⁻², with mass again being proportional to L³ (assuming constant physical density) whereas time does not appear as a scaling variable. It would therefore be very interesting to obtain suitable comparative data that would bear on this problem.

Intraspecific variation

The sample of muscles used in the analysis by Banks & Stacey (1988) included most of the data then available for the rat and cat, together with a restricted and arbitrary subsample of the human data. The variation in spindle numbers between muscles from any one species was treated as though its relationship to muscle size was the same as that between muscles from the different species. The present analysis of the complete set of human data available in Voss's (1971) table has clearly shown that the intraspecific variation in spindle number, at least for humans, follows a different relationship with muscle size from that of the interspecific variation. The observed slope of the regression relationship for the human data is consistent with a theoretical scaling of spindle number in proportion to the square root of muscle mass. There is no reason to suppose that humans are peculiar in this respect, and the possibility that a similar relationship might apply to other individual species is certainly not precluded by analysis of the currently available data.

If the true intraspecific relationship is, indeed, the square-root function as seen for the human data, can this be coupled to the interspecific cube-root relationship so that spindle number is proportional to a common variable? I shall introduce a parameter, the characteristic width, W, which varies between muscles such that muscle mass M is proportional to W²L_f, where L_f is mean muscle-fascicle length (i.e. the overall mean for all muscles of a given species). Then for homologous muscles between species: suppose that spindle number is proportional to W and that W and L_f are proportional to some arbitrary length L. For any given set of homologous muscles, interspecific isometric scaling of L then leads to the 0.3(3) exponent of number vs. mass (M), as W and L_f covary and mass is proportional to L³ (assuming constant density, ρ = M L⁻³). For heteronymous muscles within a species: suppose that spindle number is again proportional to W but W and L_f no longer covary, as L is fixed and L_f is therefore constant. Individual muscle mass is now proportional to W² and spindle number is proportional to the square root of the mass. W itself is perhaps best thought of as proportional to the square root of the physiological cross-section. (W² is not identical to the physiological cross-section because mean fascicle lengths of individual muscles vary about the overall mean.)

Residual values and relative abundance of spindles

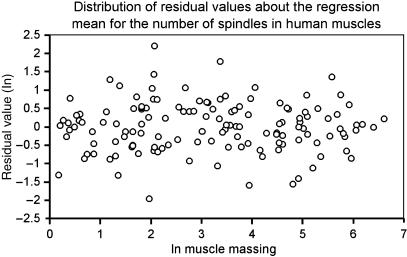
If we wish to compare the relative abundance of spindles in heteronymous muscles, we now see that at present we must restrict our attention to the human sample, because of the significant difference between the regression slopes of the inter- and intraspecific relationships and the incompleteness of the non-human samples. With the allometric method, the measure of relative abundance of spindles for a given muscle is provided by its residual value. For the complete human sample the residual values are homogeneously distributed with respect to muscle mass (Fig. 3), so that by this measure, in contrast to spindle density, there is no tendency for a systematic decrease in relative abundance as muscle size increases. Peck et al. (1984) have argued that the smaller members of pairs of muscles acting ‘in parallel’ about a joint might serve as ‘kinesiological monitors’ rather than prime movers, as they consistently have greater spindle densities than the corresponding larger members. They (Buxton & Peck, 1990) have since extended this study, demonstrating significant differences in spindle density between the members of such pairs of muscles, and also between the intrinsic muscles of the manus and pes as compared with more proximal muscles of the limbs. There were no differences between antigravity and non-antigravity muscles, nor was there a gradual increase in density from proximal to distal in the limbs. It is clear from the present allometric analysis, however, that the apparent differences between the small and large muscles of parallel pairs, and between intrinsic manus/pes and more proximal limb muscles, arise automatically from the underlying non-linear relationship between spindle number and muscle mass revealed by the fractional slope of the regression of ln number against ln mass. Statistical analysis of the allometric data for comparable rational groups of muscles to those used by Buxton & Peck (1990) failed to reveal any significant differences except that, in stark contrast to the picture derived from spindle density, intrinsic muscles of the hand have significantly smaller residual values than do those of the arm.

Fig. 3.

Distribution of residual values for the sample of human muscles showing their homogeneity.

Although the residual values are sufficient to establish a comparative ranking of muscles according to relative spindle abundance, it may be useful to express the relative abundance in linear rather than logarithmic values. In principle, this is simply done for each muscle by calculating s_pn by Eq. (2), the linear relative abundance then being given by s_on/s_pn. However, the coefficient (20.5) in Eq. (2) is an underestimate, as the intercept of the regression relationship (3.02) given in Eq. (1) is estimated from the arithmetic means of the logarithmically transformed data (Smith, 1993). It is therefore necessary to apply a correction to s_pn in order to calculate unbiased linear relative abundances. The data have been corrected using Snowdon's (1991) ratio estimator, and a table of human muscles ranked according to their unbiased relative spindle abundances is given in the Appendix.

Ranking the muscles by their residual values provides an objective comparison of relative abundance, although it must be recalled that the residual values contain both specific and non-specific (error) components, so for individual muscles the precise ranking should be treated with caution as the size of the error component is unknown. Nevertheless, the significant differences that emerge when regional groupings of muscles are compared demonstrate that on average the specific components are larger than the errors. Regionally, then, the greatest abundance of spindles is found in the axial muscles, including the neck and those controlling head position, whereas the least is found in the muscles of the shoulder girdle. Recognition of this large and significant difference in spindle abundance prompts us to seek the corresponding functional difference in the control strategies for these groups of muscles, and why they are exceptional in comparison with the more familiar limb muscles (particularly the hind limb). It is unlikely, however, that a simple correlation exists in view of the multifunctional role that any muscle or group of muscles is required to perform in different circumstances. For example, not only may a muscle contribute to both postural and kinetic actions, but the high-level neural control of these actions may also be different (Kurtzer et al. 2005). At the segmental and priopriospinal level, too, the central connections of spindle afferents are known to differ regionally; for example, despite the high relative abundance of spindles in neck muscles, monosynaptic reflexes are weak, whereas integration of the more complex vestibulo-collic and cervico-collic reflexes, so important for automatic adjustment of head position, is a prominent feature of motor control (Wilson, 1992). By contrast, the extreme mobility of the shoulder girdle at both the scapulo-thoracic attachment and the gleno-humeral joint may demand a more limited role for segmental and propriospinal stretch reflexes in the control of the relevant muscles, although they certainly do occur (Smeets & Erkelens, 1991).

Appendix

Appendix.

Muscle	n = 1 or –	Mass (g)	Actual no.	Predicted no. with correction	Relative abundance
longiss. capitis		8	507	67.6	7.5
semisp. capitis		29.1	619	126.5	4.9
obliq. capitis inf.		7.9	232	67.2	3.5
longiss. dorsi		266.8	1193	370.7	3.2
obliq. capitis sup.		3.3	131	44.0	3.0
rect. cap. post. maj.		4	122	48.3	2.5
transvers. abdom.		58.2	425	177.1	2.4
temporalis		14.73	217	91.0	2.4
pterygoideus med.		7.62	155	66.1	2.3
iliocostalis		317.1	796	403.2	2.0
obliq. ext. abdom.		161.2	569	290.4	2.0
scalen. med. + post.		32.3	254	133.1	1.9
ext. hallucis brevis	4	5.6	106	56.9	1.9
rect. cap. post. min.		1.5	54	30.0	1.8
sternocleidomast.		53.4	303	169.9	1.8
splenius capitis		29.1	222	126.5	1.8
scalenus anterior		7.8	117	66.8	1.8
serratus post. sup.		8.4	120	69.3	1.7
flex. digit. brevis	4	19.4	173	104.0	1.7
supinator		22.3	179	111.2	1.6
popliteus		22.8	179	112.4	1.6
flex. digit. superf.		95.2	356	224.9	1.6
iliopsoas		374.6	656	437.1	1.5
sternothyreoid.		6.2	86	59.8	1.4
extensor digitorum		42.8	219	152.6	1.4
pronator quadratus		12.9	120	85.3	1.4
omohyoideus		6.2	83	59.8	1.4
obliq. intern. abdom.		109.2	332	240.4	1.4
ext. digitorum brevis	4	6.8	86.25	62.5	1.4
adductor pollicis		5.3	75	55.4	1.4
trapezius		201.2	437	323.3	1.4
abd. pollicis brevis		6.2	80	59.8	1.3
flex. digit. prof.		112.4	326	243.8	1.3
ext. carpi ulnaris		25.2	157	118.0	1.3
pronator teres	5	38.8	187.6	145.5	1.3
splenius cervicis		17.4	124	98.6	1.3
quadratus plantae	4	14.2	112	89.3	1.3
masseter, p. superf.		15.95	118	94.5	1.2
lumbricalis man. I	5	3.08	52.8	42.6	1.2
flexor carpi ulnaris		36.5	175	141.2	1.2
rectus abdominis		157.3	354	286.9	1.2
lumbricalis man. II	5	1.83	38.6	33.1	1.2
pectoralis major		295.6	450	389.7	1.2
ext. digit. longus		50.9	190	166.0	1.1
lumbricalis ped. I	3	1.71	36	32.0	1.1
biceps brachii		163.8	320	292.6	1.1
flex. poll. longus		22.1	121	110.7	1.1
extensor indicis		7.1	68	63.8	1.1
tibialis anterior		140.8	284	271.9	1.0
ext. poll. longus		9.9	78	75.0	1.0
latissimus dorsi		246.2	368	356.6	1.0
gluteus max.		748	629	611.3	1.0
flex. carpi rad.		28.7	129	125.7	1.0
lumbricalis man. IV	5	1.31	27.6	28.1	1.0
inteross. dors. II (ped.)	2	1.8	32	32.8	1.0
brachialis		141	256	272.1	0.94
inteross. dors. III (ped.)	2	1.9	31.5	33.7	0.94
gluteus minimus		99	214	229.2	0.93
Inteross. dors. IV (ped.)	2	2.9	38.5	41.3	0.93
fl. poll. br. cap. superf.		2.34	27	29.5	0.91
masseter, p. prof		3.75	42	46.8	0.90
triceps brach. cap. lat.		94.2	200	223.7	0.89
extensor digiti minimi		6.2	53	59.8	0.89
adductor magnus		487.5	437	496.7	0.88
piriformis		33	117	134.5	0.87
soleus		433.9	408	469.4	0.87
peroneus brevis		35.6	120	139.5	0.86
lumbricalis ped. IV	3	1.23	23.33	27.3	0.86
coracobrachialis		39.8	123	147.3	0.83
flex. digit. longus		42.8	126	152.6	0.83
lumbricalis man. III	5	1.637	25.8	31.3	0.82
triceps brach. cap. long.		138.4	222	269.6	0.82
vastus lateralis		607.3	449	552.6	0.81
semitendinosus		151.5	222	281.7	0.79
gluteus medius		312.3	314	400.2	0.78
ext. carpi rad. brev.		32.1	102	132.7	0.77
lumbricalis ped. II	3	1.485	22.67	29.9	0.76
vastus medialis		427.5	350	466.0	0.75
abd. pollicis longus		20.5	78	106.8	0.73
fl. poll. br. cap. prof.		1.45	27	37.3	0.72
ext. pollicis brevis		4.5	37	51.2	0.72
flex. dig. min. br. ped.	4	5.2	39.5	54.9	0.72
ext. hallucis longus		30.6	92	129.7	0.71
flex. hallucis longus		89.4	152	218.1	0.70
peroneus longus		72.9	137	197.6	0.69
sternohyoideus		6.1	41	59.3	0.69
vastus intermedius		333.2	284	413.0	0.69
sartorius		164.8	198	293.5	0.67
tibialis posterior		89	146	217.7	0.67
gracilis		100.3	150	230.7	0.65
rectus femoris		254.9	232	362.6	0.64
inteross. plantaris I	2	4.4	32	50.6	0.63
lumbricalis ped. III	3	1.4	18.33	29.0	0.63
biceps femoris		343.3	264	419.0	0.63
levator scapulae		41.1	94	149.6	0.63
opponens pollicis		8.6	44	70.1	0.63
flex. hallucis brevis	4	12.6	49	84.3	0.58
adductor longus		137.7	155	269.0	0.58
abductor hallucis	4	24.5	65	116.4	0.56
inteross. dors. III (man.)	5	3.7	25.6	46.5	0.55
serratus post. inf.		18.8	56	102.4	0.55
serratus anterior		197.5	171	320.4	0.53
rhomboid. maj. + min.		93.6	119	223.0	0.53
pectoralis minor		50.5	87	165.3	0.53
inteross. palmaris II	5	2.4	19.6	37.7	0.52
adductor brevis		100.4	118	230.8	0.51
plantaris		10.5	39	77.2	0.51
inteross. plantaris II	2	5.2	27.5	54.9	0.50
subclavius		5.2	27	54.9	0.49
inteross. dors. II (man.)	5	5.1	26	54.4	0.48
ext. carpi rad. longus		44.3	74	155.2	0.48
quadratus femoris		34.3	65	137.1	0.47
inteross. plantaris III	2	8	32	67.6	0.47
inteross. dors. I (man.)	5	9.3	33.4	72.8	0.46
triceps brachii, cap. med.		92.5	98	221.8	0.44
pectineus		64.1	81	185.6	0.44
abd. dig. min. pedis	4	7.9	29	67.2	0.43
deltoideus		355.7	182	426.3	0.43
gemellus inferior		8.5	29	69.7	0.42
gemellus superior		5.8	23	57.9	0.40
inteross. palmaris I	5	2.4	14.8	37.7	0.39
inteross. palmaris III	5	2.1	13.8	35.4	0.39
inteross. dors. IV (man.)	5	3.7	17.4	46.5	0.37
brachioradialis		67.4	70	190.2	0.37
semimembranosus		213.2	122	332.5	0.37
gastrocnemius		390.1	156	445.8	0.35
thyreohyoideus		2	12	34.5	0.35
geniohyoideus		3.3	15	44.0	0.34
adductor hallucis	4	15.9	30.75	94.4	0.33
teres minor		27.7	35	123.6	0.28
subscapularis		182.8	83	308.6	0.27
stylohyoideus		1.2	6	26.9	0.22
inteross. dors. I (ped.)	2	3.9	10.5	47.7	0.22
infraspinatus		137.1	54	268.4	0.20
teres major		122.7	44	254.3	0.17
supraspinatus		51.8	28	167.4	0.17
digastricus	2	7.2	7.5	64.3	0.12