Abstract
Correlations between placental size and fetal mass during gestation fail to account for changes in composition that accompany placental growth and maturation. This study uses stereological data on the sizes of different tissue compartments in human placentas from 10 weeks of gestation to term and relates them to placental volume and to fetal mass by means of allometric analysis. In addition, tissue dimensions are used to calculate a physiological transport measure (diffusive conductance) for the villous membrane. Histological sections randomly sampled from placentas and analysed stereologically provided estimates of structural quantities (volumes, exchange surface areas, lengths, numbers of nuclei, diffusion distances). These data were combined with a physicochemical quantity (Krogh's diffusion coefficient) in order to estimate oxygen diffusive conductances for the villous membrane and its two components (trophoblast and stroma). Allometric relationships between these quantities and placental volume or fetal mass were obtained by linear regression analyses after log-transformation. Placental tissues had different growth trajectories: most grew more rapidly than placental volume and all grew more slowly than fetal mass. Diffusion distances were inversely related to placental and fetal size. Differential growth impacted on diffusive conductances, which, again, did not improve commensurately with placental volume but did match exactly growth of the fetus. Findings show that successful integration between supply and demand can be achieved by differential tissue growth. Allometric analysis of results from recent studies on the murine placenta suggest further that diffusive conductances may also be matched to fetal mass during gestation and to fetal mass at term across species.
Keywords: allometry, diffusive conductance, fetal mass, placental composition, placental volume
Introduction
Successful pregnancy outcome depends on the placenta allowing effective bi-directional transport between the mother and fetus to ensure regulated growth of the fetal–placental unit. Transport includes heat, waste products, gases, nutrients, hormones and other regulatory molecules. Placental size (mass or volume) is easy to determine and has been used as an indicator of placental development and a determinant of fetal growth (Anthony et al. 2003). Various species display positive correlations between placental size and fetal mass during gestation. However, placental size is not in general a reliable predictor of fetal mass, placental composition or placental function. For example, in ovine pregnancy, the placenta reaches its full size at a time when the fetus has attained only 10% of its final mass (Redmer et al. 2004). During normal gestation, human and murine placentas undergo substantial changes in tissue composition, which influence transport function (Mayhew et al. 1993a; Mayhew, 2002; Coan et al. 2004). In human adaptations to pregnancy associated with hypobaric hypoxia, maternal anaemia or maternal cigarette smoking, birthweights may be reduced while the placenta retains its size but alters its composition and oxygen transport capacity (Jackson et al. 1987a,b; Reshetnikova et al. 1994, 1995; Bush et al. 2000a,b; Larsen et al. 2002).
The human placenta is haemochorial in type and its functional (parenchymal) compartment comprises chorionic villi bathed by blood which percolates through the maternal (intervillous) vascular space. Villi are arranged as multiple arborizations, each consisting of a trunk (stem villus) bearing main branches (intermediate villi) and finer branches (terminal villi). Villi possess a stromal (connective tissue) core derived from extra-embryonic mesoderm within which the fetoplacental vascular bed develops and grows. Villous stroma is surrounded by a chorionic epithelium (trophoblast), which varies in depth, continuity and composition. In the first trimester, the trophoblast is relatively thick and uniform and arranged into two layers: a continuous inner layer of proliferative cells (cytotrophoblast) and an outer non-cellular differentiation layer (syncytiotrophoblast). During gestation, fetal capillaries become more peripheral and develop sinusoidal dilations while syncytiotrophoblast surface area expands disproportionately to volume and the underlying cytotrophoblast layer becomes discontinuous as its cells become more widely scattered over the expanded surface. These changes have three functional consequences: exchange surface areas increase while the trophoblast layer thins and intervascular distances decrease (Jackson et al. 1992; Benirschke & Kaufmann, 2000; Kingdom et al. 2000; Kaufmann et al. 2004).
A useful way of monitoring the relative growth trajectories of different tissue compartments of the placenta is by allometry (scaling). By this approach, it is possible to test whether tissue volumes, surfaces and lengths grow isometrically (i.e. by simple enlargement of the placenta) or anisometrically. The same approach can be used to assess the improvement of placental function. A valuable indicator in this context is diffusive conductance (see Laga et al. 1973; Mayhew et al. 1984). Oxygen and certain other gases and nutrients cross the placenta by passive diffusion and this process is influenced by various physiological and structural factors. The latter include exchange surface areas and effective diffusion distances, physical characteristics that vary during pregnancy as the different placental ingredients develop, interact and mature.
The principal aim of this study was to use allometry to relate structural and functional growth trajectories of different tissue compartments to placental volume and fetal mass. For functional development, the maternal–fetal oxygen diffusion pathway is partitioned into just two tissue compartments (villous trophoblast and stroma) arranged in series. Each contributes a partial resistance to oxygen diffusion and their sum determines total resistance and, hence, total diffusive conductance (expressed as cm3 min−1 kPa−1), across the villous membrane. Previously, this morphometric approach to estimating diffusive conductances for the villous membrane, or for the whole organ, has proved valuable in analysing functional adaptations of the placenta in normal and complicated pregnancies (Laga et al. 1973; Mayhew et al. 1990, 1993a,b; Reshetnikova et al. 1994, 1995; Ansari et al. 2003, 2004).
Materials and methods
Subjects and placental sampling
The present results are based on analysis of histological sections drawn from archival placental material fully described in an earlier report (Jackson et al. 1992). Altogether, placentas and fetuses from 90 singleton pregnancies were examined from a set collected at 10–24 weeks (from prostaglandin-induced terminations or spontaneous abortions due to cervical incompetence), 25–36 weeks (pregnancies associated with premature onset of labour) and 37–41 weeks (uncomplicated pregnancies). Fetuses showed no abnormalities and gestational ages were assessed from the date of last menstruation supported by ultrasound and clinical evaluation. Fetal mass and trimmed placental mass and volume (fluid displacement) were determined.
To meet sampling requirements for obtaining minimally biased stereological estimates of tissue volumes, surface areas, lengths, nuclearity and arithmetic and harmonic mean thicknesses, placentas were subjected to systematic uniform random sampling (Gundersen & Jensen, 1987; Mayhew, 1991a; Jackson et al. 1992; Howard & Reed, 2005). Full-depth placental samples were diced into cubes, fixed in buffered formalin and embedded haphazardly in paraffin wax. Tissues sectioned at 4–5 µm were stained by the Martius scarlet blue connective tissue procedure. Systematic uniform random microscopical fields were sampled from sections and viewed as black-and-white micrographs and colour slide transparencies. Final magnifications were calibrated using external (stage micrometer scale) standards.
Stereological estimations
Estimates were confined to the placental parenchyma, i.e. the intervillous space and peripheral (terminal and intermediate) villi. Growth of tissue compartments was evaluated in various ways. Expansion of the intervillous space was expressed as volumes (in cm3). Likewise, overall growth of villi was assessed in terms of the total volumes of their main compartments (trophoblast, stroma and fetal capillaries). To monitor the contribution of proliferation to villous growth, the numbers of nuclei in each compartment (trophoblast, stroma, vascular endothelium) were estimated. Growth of villi and capillaries was examined further by estimating total surface areas (cm2) and lengths (km). Villous maturity was assessed by estimating the arithmetic and harmonic mean thicknesses of trophoblast and stroma (both in µm). These layers collectively make up the villous membrane.
To secure minimally biased stereological estimates of the above quantities, sampling was randomized in terms of position and direction (Mayhew, 1991a, 1992; Howard & Reed, 2005). This was achieved by superimposing test lattices of points, lines and areas at random positions and orientations on suitably sampled microscopical fields (Jackson et al. 1992). Volume densities of tissues within placenta were estimated by counting test points and converted to absolute volumes after multiplying by corresponding placental volumes. Likewise, surface areas of villi and capillaries were obtained from surface densities determined by counting intersections with test lines, and lengths from length densities by counting profiles of villi and capillaries in unbiased counting frames. Numbers of nuclei were estimated from numerical densities by using physical disectors (volume probes comprising unbiased counting frames placed on parallel pairs of sections). Nuclear numerical densities were converted to total numbers of nuclei by accounting for placental volume (Simpson et al. 1992). Layer thicknesses were calculated from random intercept distances (Gundersen et al. 1978; Jackson et al. 1985) measured from sites determined by test line intersections with the maternal aspects of the trophoblast and stroma. The ratio of arithmetic to harmonic means was also calculated as this provides a measure of the uniformity of thickness of a layer. A ratio of 1 indicates that the layer is uniformly thick whilst values > 1 indicate increasing degrees of thickness irregularity (Jackson et al. 1985).
Diffusive conductance estimation
Although any diffusion model would suffice, the oxygen diffusion model was adapted from one described earlier (Laga et al. 1973; Mayhew et al. 1984, 1986). The pathway between oxyhaemoglobin in maternal erythrocytes and haemoglobin in fetal erythrocytes is divisible into six serially arranged tissue compartments, namely maternal erythrocytes, maternal intervillous blood plasma, villous trophoblast, villous stroma (including fetal capillary vascular endothelium), fetal capillary blood plasma and fetal erythrocytes. For the present purposes, I confined estimation of partial conductances to the two components of the villous membrane as this tissue layer is the most influential in determining the conductance of the placenta as a whole (Mayhew et al. 1984, 1986).
The partial conductances (D) of compartments can be calculated from a combination of stereological and physicochemical variables. The latter includes Krogh's diffusion coefficients (K), which is a measure of tissue solubility of oxygen. For the present purposes, the value adopted was 17.3 × 10−8 cm2 min−1 kPa−1 (see Mayhew et al. 1984). The key structural quantities were the surface areas of villi and fetal capillaries, and harmonic mean thicknesses of trophoblast and stroma. Because local thicknesses vary, harmonic means were estimated: these attach greater weighting to thinner areas and, consequently, represent more accurately effective diffusion distances (Jackson et al. 1985). Conductances of the trophoblast (Dtro) and stroma (Dstr) of peripheral villi were calculated from values of K and corresponding surface areas and diffusion distances. For each tissue compartment, maternal (upstream) and fetal (downstream) surfaces were included so as to avoid biases arising from assuming that both surfaces are equal. The relevant surfaces areas were maternal (Smtro) and fetal (Sftro) aspects of trophoblast and the luminal aspect of fetal capillaries (Sfc).
The tissue layers of the diffusion pathway are connected in series. Therefore, their partial resistances (equivalent to the reciprocals of partial conductances) were summed to obtain total resistance and, hence, total conductance of the villous membrane (Dvm).
Allometry
All structural variables were estimated separately for each placenta. These data, and corresponding placental volumes (Vp in cm3) and fetal masses (Mf in g), were subjected to log-transformation followed by linear regression analysis. This was used to examine relationships between the independent variable (Vp or Mf) and the various dependent (placental) variables. Log-transformation combined with linear regression establishes a regression equation of the form log Y =B · log X + log A, where log Y represents the dependent and log X the independent variable (either Vp or Mf), B is the slope of the regression line and log A the intercept on the log Y axis.
From log-transformed data, the following allometric relationship was obtained: Y = A · XB. In this equation, the term A now represents a constant determined by Y and X whilst B represents an exponent (a scaling or power factor), the value of which helps to define the growth relationships between Y and X. A value of B < 0 signifies that Y and X are inversely related. If Y grows more slowly than X, B < 1. By contrast, B > 1 if Y grows faster than X. Finally, B = 1 signifies that Y and X grow commensurately. On this convention, a placenta growing by simple enlargement would have the dimensions of all its compartments expanding isometrically (i.e. volumes would scale to  , surface areas to
, surface areas to  and lengths to
and lengths to  ).
).
By calculating values of B and their standard errors of means (SEM), it is possible to compare growth trajectories in different tissue compartments and to test whether B departs significantly from a given value (e.g. 0 or 1). All calculations and statistical evaluations were handled using Unistat commercial software (version 5.5, Unistat Ltd, London, UK).
Results
Growth of placental compartments
For each compartment, the main variables identifying allometric relationships with placental volume are summarized in Tables 1 and 2.
Table 1.
Allometric growth relationships between different tissue compartments and the volume, Vp, of human placenta during gestation. Values represent allometric exponents (B) and constants (A) calculated using the linear regression equation log Y = B · log Vp + log A where Y refers to the compartment variable and log A is the intercept on the log Y axis
| Compartment | Exponent B (SEM) | Constant A | P-value (B is not 1) |
|---|---|---|---|
| Volume IVS | 0.939 (0.0314) | 0.6538 | NS |
| Volume Villi | 1.002 (0.0286) | 0.4882 | NS |
| Volume Tro | 1.076 (0.0309) | 0.0821 | * |
| Volume Str | 0.916 (0.0279) | 0.3690 | ** |
| Volume FC | 1.544 (0.0460) | 0.0038 | *** |
| Surface Villi | 1.323 (0.0294) | 0.0032 | *** |
| Surface FC | 1.618 (0.0448) | 0.0005 | *** |
| Length Villi | 1.534 (0.0421) | 0.0071 | *** |
| Length FC | 1.622 (0.0502) | 0.0145 | *** |
| Number All | 1.069 (0.0143) | 0. 2005 | *** |
| Number Tro | 1.096 (0.0174) | 0.0684 | *** |
| Number Str | 1.026 (0.0233) | 0.1181 | NS |
| Number FCE | 1.135 (0.0312) | 0.0190 | *** |
| Arith thickness VM | −0.338 (0.0263) | 40.88 | *** |
| Arith thickness Tro | −0.333 (0.0230) | 20.97 | *** |
| Arith thickness Str | −0.340 (0.0353) | 19.48 | *** |
| Harm thickness VM | −0.177 (0.0147) | 2.097 | *** |
| Harm thickness Tro | −0.498 (0.0341) | 45.98 | *** |
| Harm thickness Str | −0.497 (0.0430) | 25.59 | *** |
| Ratio VM | 0.169 (0.0168) | 0.4651 | *** |
| Ratio Tro | 0.165 (0.0173) | 0.4561 | *** |
| Ratio Str | 0.157 (0.0234) | 0.7614 | *** |
IVS, intervillous space; Villi, terminal and intermediate villi; Tro, villous trophoblast; Str, villous stroma; FC, fetal capillaries; FCE, fetal capillary endothelium; Arith, arithmetic mean; Harm, harmonic mean; Ratio, index of thickness variability; VM, villous membrane (trophoblast + stroma).
NS, not significantly different from B = 1
P < 0.05
P < 0.01
P < 0.001.
Table 2.
Allometric relationships between villous membrane diffusive conductances and placental volume, Vp. Values represent allometric exponents (B) and constants (A) calculated from log-linear regression equations
| Conductance | Exponent B (SEM) | Constant A | P-value (B is not 1) |
|---|---|---|---|
| Villous trophoblast | 1.804 (0.0535) | 0.0014 | *** |
| Villous stroma | 1.905 (0.0621) | 0.0013 | *** |
| Villous membrane | 1.843 (0.0536) | 0.0007 | *** |
P < 0.001.
Placental growth is determined by its parenchyma
Exponents (SEM) for the volumes of the intervillous vascular space, 0.939 (0.0314), and peripheral villi, 1.002 (0.0286), were essentially the same and not significantly different from B = 1. This indicates that parenchymal volumes grow isometrically and that growth in placental volume, Vp, is determined primarily by its parenchymal compartments.
Growth of villous compartments is not concentric
Within villi, tissue compartments grew disproportionately to each other. Fetal capillary growth was fastest [B = 1.544 (0.0460)], trophoblast growth was intermediate [1.076 (0.0309)] and stromal growth was slowest [0.916 (0.0279)]. Estimates of the numbers of nuclei in these compartments revealed that all tissues exhibited mainly proliferative growth. While the total number of all nuclei within villi increased faster than Vp [B = 1.069 (0.0143)], differences between compartments were detected. For capillary endothelial cells, the exponent was 1.135 (0.0312) and this, compared with that for capillary volume growth, indicates that the increase in cell number (each endothelial cell has a single nucleus) did not match the increase in capillary volume. By contrast, trophoblast growth appeared to be exclusively hyperplastic [exponent 1.096 (0.0174) for nuclear number similar to that for volume] whereas proliferation of stromal cells seemed to be accompanied by a reduction in the volume of stroma per nucleus [exponent 1.026 (0.0233) for nuclear number].
Villi grow by linear expansion and calibre reduction
The volumes [B = 1.002 (0.0286)], surfaces [1.323 (0.0294)] and lengths [1.534 (0.0421)] of villi did not grow commensurately and this is inconsistent with the notion that villi grow merely by increases in total length. In fact, it implies that mean cross-sectional areas of villi gradually decline. Moreover, the expansion of villous surface area and length exceeded the increases in Vp and number of trophoblast nuclei.
Capillaries grow principally by linear expansion
The volumes [B = 1.544 (0.0460)], surfaces [1.618 (0.0448)] and lengths [1.622 (0.0502)] of fetoplacental capillaries increased more rapidly than Vp and in roughly the same manner. This indicates that capillaries grow mainly by increases in total length rather than by changes in mean calibre. The growth in capillary surface area also exceeded the increases in number of endothelial cell nuclei, suggesting that there was a change in the mean area of endothelial squames.
Villous membrane thicknesses decrease unequally and are inversely related to placental volume
Both arithmetic and harmonic mean thicknesses of the villous membrane were inversely proportional to Vp. However, the two thicknesses did not alter proportionately [B = −0.338 (0.0263) for the arithmetic and −0.177 (0.0147) for the harmonic mean]. This indicates that the decline in harmonic mean thickness outpaces that in the arithmetic mean. This was confirmed by analysing the arithmetic/harmonic thickness ratio, which was found to increase with Vp [0.169 (0.0168)]. In short, the villous membrane became more irregular in thickness.
Trophoblast and stroma contribute equally to villous membrane thickness changes
Villous membrane components acted in a congruent manner to alter mean thicknesses. Exponents, B, for the arithmetic mean thicknesses of trophoblast and stroma were −0.333 (0.0230) and −0.340 (0.0353), respectively. Corresponding values for the harmonic thicknesses were −0.498 (0.0341) and −0.497 (0.0430). Again, both layers became more irregular as Vp increased [exponents for arithmetic/harmonic thickness ratios were 0.165 (0.0173) and 0.157 (0.0234), respectively].
Villous membrane conductances are not matched to placental growth
Results are summarized in Table 2. The conductances of both components of the villous membrane increased faster than Vp [1.804 (0.0535) for trophoblast and 1.905 (0.0621) for stroma]. For the villous membrane as a whole, Dvm, expanded as the exponent 1.843 (0.0536).
Placental growth and its relationships to fetal growth
Allometric variables are given in Tables 3 and 4.
Table 3.
Allometric growth relationships between different placental compartments and fetal mass, Mf, during gestation. Values represent allometric exponents (B) and constants (A) calculated using the linear regression equation log Y = B · log Mf + log A where Y refers to the compartment variable and logA is the intercept on the log Y axis
| Compartment | Exponent B (SEM) | Constant A | P-value (B is not 1) |
|---|---|---|---|
| Volume placenta | 0.544 (0.0176) | 5.3358 | *** |
| Volume IVS | 0.518 (0.0226) | 3.0012 | *** |
| Volume Villi | 0.552 (0.0221) | 2.4912 | *** |
| Volume Tro | 0.593 (0.0238) | 0.4728 | *** |
| Volume Str | 0.496 (0.0232) | 1.7398 | *** |
| Volume FC | 0.862 (0.0315) | 0.0430 | *** |
| Surface Villi | 0.735 (0.0239) | 0.0266 | *** |
| Surface FC | 0.909 (0.0297) | 0.0066 | ** |
| Length Villi | 0.861 (0.0283) | 0.0770 | *** |
| Length FC | 0.912 (0.0320) | 0.1790 | ** |
| Number All | 0.584 (0.0199) | 1.1874 | *** |
| Number Tro | 0.601 (0.0201) | 0.4144 | *** |
| Number Str | 0.559 (0.0223) | 0.6569 | *** |
| Number FCE | 0.619 (0.0263) | 0.1255 | *** |
| Arith thickness VM | −0.203 (0.0133) | 26.45 | *** |
| Arith thickness Tro | −0.195 (0.0121) | 13.23 | *** |
| Arith thickness Str | −0.214 (0.0188) | 13.38 | *** |
| Harm thickness VM | −0.300 (0.0189) | 44.44 | *** |
| Harm thickness Tro | −0.290 (0.0181) | 22.89 | *** |
| Harm thickness Str | −0.296 (0.0226) | 13.26 | *** |
| Ratio VM | 0.097 (0.0094) | 0.5953 | *** |
| Ratio Tro | 0.095 (0.0096) | 0.5777 | *** |
| Ratio Str | 0.088 (0.0134) | 0.9741 | *** |
IVS, intervillous space; Villi, terminal and intermediate villi; Tro, villous trophoblast; Str, villous stroma; FC, fetal capillaries; FCE, fetal capillary endothelium; Arith, arithmetic mean; Harm, harmonic mean; Ratio, index of thickness variability; VM, villous membrane (trophoblast + stroma).
P < 0.01
P < 0.001
Table 4.
Allometric relationships between villous membrane diffusive conductances and fetal mass, Mf. Values represent allometric exponents (B) and constants (A) calculated from log-linear regression equations
| Conductance | Exponent B (SEM) | Constant A | P-value (B is not 1) |
|---|---|---|---|
| Villous trophoblast | 1.016 (0.0339) | 0.0222 | NS |
| Villous stroma | 1.079 (0.0367) | 0.0237 | * |
| Villous membrane | 1.040 (0.0334) | 0.0116 | NS |
NS, not significantly different from B = 1
P < 0.05.
Placental growth lags behind fetal growth
For placental volume, the allometric exponent amounted to 0.544 (0.0176), indicating that placental growth lagged behind fetal growth. The same was found for the intervillous space and for the various dimensions of peripheral villi, and their principal tissues (Table 3).
Partial diffusive conductances improve with fetal mass
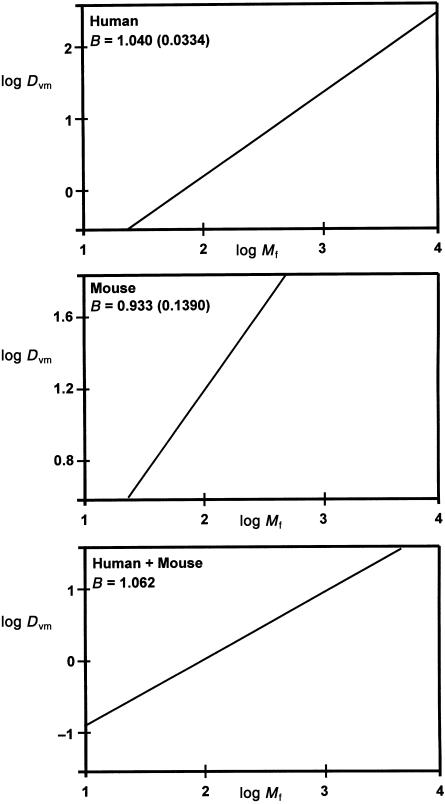
Results are summarized in Table 4. Interestingly, the conductances of both components of the villous membrane at least matched fetal growth and that of the stroma appeared to exceed it [1.016 (0.0339) for trophoblast and 1.079 (0.0367) for stroma]. In consequence, the conductance of the villous membrane was matched exactly to fetal growth (see also Fig. 1). The exponent had a value of 1.040 (0.0334) and this was not significantly different from B = 1.
Fig. 1.
Allometric relationships between villous membrane diffusive conductances and fetal mass. Graphs show log–log plots and the exponent B (SEM) for diffusive conductance (Dvm) relative to fetal mass (Mf) within and across species. Upper graph: relationship for human placentas (Mf in g; based on present data). Middle graph: relationship for murine placentas (Mf in mg; based on data in Coan et al. 2004). Bottom graph: relationship across both species (Mf in g; based on both studies).
Discussion
Allometric analyses have shed an interesting light on the way in which different placental tissues grow in order to secure a successful outcome for a critical transport function, namely the provision of oxygen to the developing fetus. The findings support an earlier finding that, by the second trimester, total placental diffusive conductance is matched to fetal mass (Mayhew et al. 1993a) but demonstrate clearly that this is achieved by different levels of development of the main tissue contributors to the diffusion pathway. The most influential tissue layer is the villous membrane (trophoblast and stroma). In terms of allometry, this is followed by the fetal vascular conductances and then the maternal vascular conductances (my unpublished data). All of the structural variables contributing to these changes grew at a slower rate than the fetus. Apart from the villous membrane thicknesses (which declined with placental and fetal size), the most dramatic growth changes involved the lengths of peripheral villi and the volumes, surfaces and lengths of their fetal capillaries.
Normal placental development, especially co-ordinated growth and differentiation of placental villi, are known to be determinants of continued fetal growth and well-being (Benirschke & Kaufmann, 2000; Kingdom et al. 2000; Kaufmann et al. 2004). In turn, villous development depends on fetal vascular morphogenesis. During early gestation, morphogenesis of the fetal vasculature in large-calibre, immature villi involves vasculogenesis and the creation of parallel arrangements of interconnecting capillary networks (branching angiogenesis). Later, a developmental switch occurs and growth effort is invested in producing smaller-calibre, more mature villi within which fetal capillaries grow mainly by elongation of existing segments (non-branching angiogenesis). This is accompanied by local dilation of capillaries to form sinusoids and by their apposition to the overlying villous trophoblast to produce shorter intervascular distances (vasculosyncytial membranes). Various growth factor ligands and receptors produced within villi regulate these events and may be perturbed in abnormal pregnancies to produce maldeveloped villous arborizations (Kingdom et al. 2000; Charnock-Jones et al. 2004; Kaufmann et al. 2004; Mayhew et al. 2004).
The present growth exponents are consistent with these observations. They show that growth of villi matches that of the maternal intervillous space and of the placenta as a whole, but falls behind that of the fetus. The increase in villous volume is outpaced by the expansion of villous surface areas and by longitudinal growth of villi. Within villi, fetal capillary volume grows faster than trophoblast and this, in turn, grows faster than stroma and can be explained by the production, after mid-gestation, of large numbers of mature terminal and intermediate villi characterized by small diameters, thinner trophoblast and reduced stromal connective tissue (Benirschke & Kaufmann, 2000; Kingdom et al. 2000). The volumetric growth of capillaries is roughly commensurate with the changes in surface area and length, emphasizing that growth is principally linear and not diametric (Mayhew, 2002). Moreover, this longitudinal growth is driven by vascular endothelial cell proliferation, although there is some increase in endothelial cell mean squame area towards term. By contrast, the volume of trophoblast per nucleus is maintained up to term and the volume of stroma per cell declines (Mayhew et al. 1994; Mayhew, 2002). Finally, thinning of the trophoblast, peripheralization of capillaries and reductions in stromal content affect both the arithmetic and the harmonic mean distances across trophoblast and stroma.
These structural changes impact on function. In particular, they partly dictate the changes seen in partial diffusive conductances along the oxygen pathway between maternal and fetal erythrocytes (Mayhew et al. 1993a). Those for the trophoblast and stroma are closely related to fetal growth and constitute the main determinants of total placental diffusive conductance which, from 10 weeks to term, exactly matches the gain in fetal mass. This is consistent with the constancy in mass-specific placental conductance reported previously (Mayhew et al. 1993a).
The present findings demonstrate that villous membrane diffusive conductance is related to fetal mass by the exponent 1.040 (0.0334). Recent studies on the mouse placenta from embryonic day (E) 12.5 to E18.5 have also provided estimates of fetal mass and the oxygen diffusive conductance of the labyrinthine intervascular membrane (Coan et al. 2004). This conductance roughly equates to that of the villous membrane of human placenta, which is the critical determinant of total resistance and, hence, total conductance. Using data provided by Coan et al. (2004), calculations suggest that murine intervascular membrane conductance is related to fetal mass by the exponent 0.933 (0.1390). As for human placenta, this value is not significantly different from B = 1 (see Fig. 1). This is achieved despite unequal growth trajectories in maternal and fetal vasculatures, both of which grow more slowly than fetal mass. Again, a critical determinant of diffusive capacity is the harmonic thickness of the intervascular membrane (Coan et al. 2004). It is also noteworthy that, despite differences in tissue composition between human and mouse placenta, combined allometric findings suggest that, for term fetuses, villous membrane diffusive conductance is also matched to mass in interspecies comparisons (estimated exponent, B = 1.062; see Fig. 1). Studies on further species are required to confirm or refine this suggestion.
The exponent relating total diffusive conductance to fetal mass allows for certain testable predictions about transplacental and intervillous oxygen tensions and gradients. Human term fetuses in this study had a mass of about 3.5 kg. Using allometric equations for predicting neonatal oxygen intakes from birthweights (Hofman, 1983; Bell et al. 1985), a 3.5-kg newborn is expected to consume oxygen at a rate of 27 cm3 min−1. The high metabolic activity of the trophoblast would increase the initial oxygen flux to 40 cm3 min−1 (see Bonds et al. 1986). With present conductances across the trophoblast and stroma, these consumption rates would predict an oxygen partial pressure gradient across the villous membrane of less than 1 kPa. To avoid the dangers of vasoconstriction of the umbilical arteries and ductus arteriosus, umbilical venous oxygen tension near term should not exceed about 6–7 kPa and so oxygen flux probably proceeds from a maternal intervillous partial pressure of no more than 8–9 kPa. Published values for oxygen tensions in the intervillous space at term are in the range 5–6 kPa (Metcalfe et al. 1967).
Another prediction consequent upon the discrepancy between exponents for fetal oxygen consumption (c. 0.88, Hofman, 1983; Bell et al. 1985) and placental diffusive conductance (c. 0.99, present study) is that oxygen partial pressure gradients across the placenta decline during gestation. In fact, analysis of gestational changes in intervillous oxygen tensions indicate a rise from 6–7 kPa to about 8 kPa between 12 and 16 weeks of gestation and then a gradual decline to roughly 6 kPa at term (Soothill et al. 1986; Rodesch et al. 1992; Jauniaux et al. 2001). These observed values are consistent with the present findings.
Although total placental diffusive conductance increases commensurately with fetal mass during gestation (Mayhew et al. 1993a) to maintain mass-specific conductance, responses vary in different complicated pregnancies. Several studies on complicated pregnancies have shown that the placenta can adapt to improve or maintain partial and total conductances. Mass-specific conductance increases at high altitude and in pregestational diabetes (Mayhew et al. 1990, 1993b) but in the former this is due mainly to a decrease in fetal mass and in the latter to an increase in total placental conductance. Mass-specific conductance does not alter in pregnancies associated with maternal cigarette smoking, sudden infant death or small-for-gestational-age (SGA) deliveries (Bush et al. 2000a,b; Ansari et al. 2003, 2004). In the former two pregnancies, neither fetal mass nor total conductance alter but, in SGA pregnancies, both variables decrease proportionately.
In pregnancies associated with fetal hypoxic stress (high altitude, maternal diabetes mellitus, anaemia and pre-eclampsia), changes in partial conductances are more variable and this may, to some degree, reflect the different origins of fetal hypoxia (Kingdom & Kaufmann, 1997). Being the cardinal contributors to total resistance, the villous membrane components are crucial. In all cases studied so far, villous membrane conductances are at least maintained or increased. They are maintained in maternal anaemia and pre-eclampsia (Reshetnikova et al. 1995; Burton et al. 1996) and increased at high altitude (Mayhew et al. 1990; Reshetnikova et al. 1994) and during maternal diabetes (Mayhew et al. 1993b). For those pregnancies in which other partial conductances have been analysed, increases are focused on the maternal side alone (high altitude) or on both maternal and fetal sides (diabetes mellitus). In both these types of pregnancy, the mass-specific conductance increases and, in high-altitude pregnancies, this is true whether or not the samples collected display group differences in birthweights (Mayhew et al. 1990; Reshetnikova et al. 1994). Comparisons suggest that the response pattern in pregnancies associated with maternal smoking differs from that seen in other pregnancies but resembles most closely that seen at high altitude. However, it differs in displaying no stromal response and no increase in mass-specific conductance. These findings should be assessed cautiously because observed changes may not be responses to hypoxia per se but to the presence of confounders (e.g. smoking is confounded by the toxic ingredients of tobacco smoke, diabetes by metabolic disturbances and altitudinal studies by ethnic and other factors).
Allometric analysis of high-altitude term pregnancies (Mayhew, 1991b) has also shown that partial and total conductances follow different growth trajectories and that these are slower than in low-altitude pregnancies. They are also consistent with current findings in that total conductances are determined primarily by partial conductances across the villous membrane and improve in a manner commensurate with fetal mass, although fetal mass at term is reduced in highland pregnancies. They also indicate that fetal conductances improve at a higher rate than maternal conductances (Mayhew et al. 1990).
In conclusion, the present findings demonstrate that different growth trajectories in the various tissue compartments of the human placenta may, nonetheless, combine to produce a functional outcome that serves the growing needs of the fetus and contributes to the maintenance of fetal well-being. The principle that placental oxygen diffusive conductance is matched to fetal weight may be true for other species and seems to hold for term fetuses in interspecies comparisons.
Acknowledgments
I am grateful to the Anatomical Society of Great Britain & Ireland and the Wellcome Trust for research support.
References
- Ansari T, Fenlon S, Pasha S, et al. Morphometric assessment of the oxygen diffusive conductance in placentae from pregnancies complicated by intra-uterine growth restriction. Placenta. 2003;24:618–626. doi: 10.1016/s0143-4004(03)00044-4. [DOI] [PubMed] [Google Scholar]
- Ansari T, Gillan JE, Condell D, Green CJ, Sibbons PD. Analyses of the potential oxygen transfer capability in placentae from infants succumbing to sudden infant death syndrome. Early Human Devel. 2004;76:127–138. doi: 10.1016/j.earlhumdev.2003.11.004. [DOI] [PubMed] [Google Scholar]
- Anthony RV, Scheaffer AV, Wright CD, Regnault TR. Ruminant models of prenatal growth restriction. Reproduction Suppl. 2003;61:183–194. [PubMed] [Google Scholar]
- Bell AW, Battaglia FC, Makowski EL, Meschia G. Relationship between metabolic rate and body size in fetal life. Biol Neonate. 1985;47:120–123. doi: 10.1159/000242100. [DOI] [PubMed] [Google Scholar]
- Benirschke K, Kaufmann P. Pathology of the Human Placenta. 4. New York: Springer; 2000. [Google Scholar]
- Bonds DR, Crosby LO, Cheek TG, Hagerdal M, Gutsch BB, Gabbe SG. Estimation of human fetal–placental unit metabolic rate by application of the Bohr principle. J Dev Physiol. 1986;8:49–54. [PubMed] [Google Scholar]
- Burton GJ, Reshetnikova OS, Milovanov AP, Teleshova OV. Stereological evaluation of vascular adaptations in human placental villi to differing forms of hypoxic stress. Placenta. 1996;17:49–55. doi: 10.1016/s0143-4004(05)80643-5. [DOI] [PubMed] [Google Scholar]
- Bush PG, Mayhew TM, Abramovich DR, Aggett PJ, Burke MD, Page KR. A quantitative study on the effects of maternal smoking on placental morphology and cadmium concentration. Placenta. 2000a;21:247–256. doi: 10.1053/plac.1999.0470. [DOI] [PubMed] [Google Scholar]
- Bush PG, Mayhew TM, Abramovich DR, Aggett PJ, Burke MD, Page KR. Maternal cigarette smoking and oxygen diffusion across the placenta. Placenta. 2000b;21:824–833. doi: 10.1053/plac.2000.0571. [DOI] [PubMed] [Google Scholar]
- Charnock-Jones DS, Kaufman P, Mayhew TM. Aspects of human fetoplacental vasculogenesis and angiogenesis. I. Molecular regulation. Placenta. 2004;25:103–113. doi: 10.1016/j.placenta.2003.10.004. [DOI] [PubMed] [Google Scholar]
- Coan PM, Ferguson-Smith AC, Burton GJ. Developmental dynamics of the definitive mouse placenta assessed by stereology. Biol Reprod. 2004;70:1806–1813. doi: 10.1095/biolreprod.103.024166. [DOI] [PubMed] [Google Scholar]
- Gundersen HJG, Jensen EB, Østerby R. Distribution of membrane thickness determined by lineal analysis. J Microsc. 1978;113:27–43. doi: 10.1111/j.1365-2818.1978.tb00091.x. [DOI] [PubMed] [Google Scholar]
- Gundersen HJG, Jensen EB. The efficiency of systematic sampling in stereology and its prediction. J Microsc. 1987;147:229–263. doi: 10.1111/j.1365-2818.1987.tb02837.x. [DOI] [PubMed] [Google Scholar]
- Hofman MA. Evolution of brain size in neonatal and adult placental mammals: a theoretical approach. J Theor Biol. 1983;105:317–332. doi: 10.1016/s0022-5193(83)80011-3. [DOI] [PubMed] [Google Scholar]
- Howard CV, Reed MG. Unbiased Stereology. Three-Dimensional Measurement in Microscopy. 2. Oxford: Garland Science/Bios Scientific Publishers; 2005. [Google Scholar]
- Jackson MR, Joy CF, Mayhew TM, Haas JD. Stereological studies on the true thickness of the villous membrane in human term placentae: a study of placentae from high-altitude pregnancies. Placenta. 1985;6:249–258. doi: 10.1016/s0143-4004(85)80054-0. [DOI] [PubMed] [Google Scholar]
- Jackson MR, Mayhew TM, Haas JD. The volumetric composition of human term placentae: altitudinal, ethnic and sex differences in Bolivia. J Anat. 1987a;152:173–187. [PMC free article] [PubMed] [Google Scholar]
- Jackson MR, Mayhew TM, Haas JD. Morphometric studies on villi in human term placentae and the effects of altitude, ethnic grouping and sex of newborn. Placenta. 1987b;8:487–495. doi: 10.1016/0143-4004(87)90077-4. [DOI] [PubMed] [Google Scholar]
- Jackson MR, Mayhew TM, Boyd PA. Quantitative description of the elaboration and maturation of villi from 10 weeks of gestation to term. Placenta. 1992;13:357–370. doi: 10.1016/0143-4004(92)90060-7. [DOI] [PubMed] [Google Scholar]
- Jauniaux E, Watson A, Burton G. Evaluation of respiratory gases and acid–base gradients in human fetal fluids and uteroplacental tissue between 7 and 16 weeks gestation. Am J Obstet Gynecol. 2001;184:998–1003. doi: 10.1067/mob.2001.111935. [DOI] [PubMed] [Google Scholar]
- Kaufmann P, Mayhew TM, Charnock-Jones DS. Aspects of human fetoplacental vasculogenesis and angiogenesis. II. Changes during normal pregnancy. Placenta. 2004;25:114–126. doi: 10.1016/j.placenta.2003.10.009. [DOI] [PubMed] [Google Scholar]
- Kingdom JCP, Kaufmann P. Oxygen and placental villous development: origins of fetal hypoxia. Placenta. 1997;18:613–621. doi: 10.1016/s0143-4004(97)90000-x. [DOI] [PubMed] [Google Scholar]
- Kingdom J, Huppertz B, Seaward G, Kaufmann P. Development of the placental villous tree and its consequences for fetal growth. Eur J Obstet Gynecol Reprod Biol. 2000;92:35–43. doi: 10.1016/s0301-2115(00)00423-1. [DOI] [PubMed] [Google Scholar]
- Laga EM, Driscoll SG, Munro HN. Quantitative studies of human placenta. I. Morphometry. Biol Neonate. 1973;23:231–259. doi: 10.1159/000240605. [DOI] [PubMed] [Google Scholar]
- Larsen LG, Clausen HV, Jonsson L. Stereologic examination of placentas from mothers who smoke during pregnancy. Am J Obstet Gynecol. 2002;186:531–537. doi: 10.1067/mob.2002.120481. [DOI] [PubMed] [Google Scholar]
- Mayhew TM, Joy CF, Haas JD. Structure–function correlation in the human placenta: the morphometric diffusing capacity for oxygen at full term. J Anat. 1984;139:691–708. [PMC free article] [PubMed] [Google Scholar]
- Mayhew TM, Jackson MR, Haas JD. Microscopical morphology of the human placenta and its effects on oxygen diffusion: a morphometric model. Placenta. 1986;7:121–131. doi: 10.1016/s0143-4004(86)80003-0. [DOI] [PubMed] [Google Scholar]
- Mayhew TM, Jackson MR, Haas JD. Oxygen diffusive conductances of human placentae from term pregnancies at low and high altitudes. Placenta. 1990;11:493–503. doi: 10.1016/s0143-4004(05)80195-x. [DOI] [PubMed] [Google Scholar]
- Mayhew TM. The new stereological methods for interpreting functional morphology from slices of cells and organs. Exp Physiol. 1991a;76:639–665. doi: 10.1113/expphysiol.1991.sp003533. [DOI] [PubMed] [Google Scholar]
- Mayhew TM. Scaling placental oxygen diffusion to birthweight: studies on placentae from low- and high-altitude pregnancies. J Anat. 1991b;175:187–194. [PMC free article] [PubMed] [Google Scholar]
- Mayhew TM. A review of recent advances in stereology for quantifying neural structure. J Neurocytol. 1992;21:313–328. doi: 10.1007/BF01191700. [DOI] [PubMed] [Google Scholar]
- Mayhew TM, Jackson MR, Boyd PA. Changes in oxygen diffusive conductances of human placentae during gestation (10–41 weeks) are commensurate with the gain in fetal weight. Placenta. 1993a;14:51–61. doi: 10.1016/s0143-4004(05)80248-6. [DOI] [PubMed] [Google Scholar]
- Mayhew TM, Sørensen FB, Klebe JG, Jackson MR. Oxygen diffusive conductances in placentae from control and diabetic women. Diabetologia. 1993b;36:955–960. doi: 10.1007/BF02374479. [DOI] [PubMed] [Google Scholar]
- Mayhew TM, Wadrop E, Simpson RA. Proliferative versus hypertrophic growth in tissue subcompartments of human placental villi during gestation. J Anat. 1994;184:535–543. [PMC free article] [PubMed] [Google Scholar]
- Mayhew TM. Fetoplacental angiogenesis during gestation is biphasic, longitudinal and occurs by proliferation and remodelling of vascular endothelial cells. Placenta. 2002;23:742–750. doi: 10.1016/s0143-4004(02)90865-9. [DOI] [PubMed] [Google Scholar]
- Mayhew TM, Charnock-Jones DS, Kaufman P. Aspects of human fetoplacental vasculogenesis and angiogenesis. II. Changes in complicated pregnancies. Placenta. 2004;25:127–139. doi: 10.1016/j.placenta.2003.10.010. [DOI] [PubMed] [Google Scholar]
- Metcalfe J, Bartels H, Moll W. Gas exchange in the pregnant uterus. Physiol Rev. 1967;47:782–838. doi: 10.1152/physrev.1967.47.4.782. [DOI] [PubMed] [Google Scholar]
- Redmer DA, Wallace JM, Reynolds LP. Effect of nutrient intake during pregnancy on fetal and placental growth and vascular development. Domestic Anim Endocrinol. 2004;27:199–217. doi: 10.1016/j.domaniend.2004.06.006. [DOI] [PubMed] [Google Scholar]
- Reshetnikova OS, Burton GJ, Milovanov AP. Effects of hypobaric hypoxia on the fetoplacental unit: the morphometric diffusing capacity of the villous membrane at high altitude. Am J Obstet Gynecol. 1994;171:1560–1565. doi: 10.1016/0002-9378(94)90402-2. [DOI] [PubMed] [Google Scholar]
- Reshetnikova OS, Burton GJ, Teleshova OV. Placental histomorphometry and morphometric diffusing capacity of the villous membrane in pregnancies complicated by maternal iron-deficiency anemia. Am J Obstet Gynecol. 1995;173:724–727. doi: 10.1016/0002-9378(95)90330-5. [DOI] [PubMed] [Google Scholar]
- Rodesch F, Simon P, Donner C, Jauniaux E. Oxygen measurements in endometrial and trophoblastic tissues during early pregnancy. Obstet Gynecol. 1992;80:283–285. [PubMed] [Google Scholar]
- Simpson RA, Mayhew TM, Barnes PR. From 13 weeks to term, the trophoblast of human placenta grows by the continuous recruitment of new proliferative units: a study of nuclear number using the disector. Placenta. 1992;13:501–512. doi: 10.1016/0143-4004(92)90055-x. [DOI] [PubMed] [Google Scholar]
- Soothill PW, Nicolaides KH, Rodeck CH, Campbell S. Effects of gestational age on fetal and intervillous blood gas and acid-base values in human pregnancy. Fetal Ther. 1986;1:168–175. doi: 10.1159/000262264. [DOI] [PubMed] [Google Scholar]