Morphometric analysis of facial landmark data to characterize the facial phenotype associated with fetal alcohol syndrome

Abstract

Procrustes analysis and principal component analysis were applied to stereo-photogrammetrically obtained landmarks to compare the facial features associated with fetal alcohol syndrome (FAS) in subjects with FAS and normal controls. Two studies were performed; both compared facial landmark data of FAS and normal subjects, but they differed in the number of landmarks chosen. The first study compared landmarks representing palpebral fissure length, upper lip thinness and philtrum smoothness and revealed no significant difference in shape. The second study added to the landmarks used in the first those affected by mid-face hypoplasia, and revealed significant differences in shape between the two groups, broadly confirming the FAS gestalt reported in the literature. Some disagreement in the characteristic FAS facial shape between our results and those reported in the literature may be due to ethnic variation.

Introduction

Fetal alcohol syndrome (FAS) is a clinical condition caused by excessive maternal consumption of alcohol during pregnancy and has come to be accepted as a leading identifiable and preventable cause of mental retardation and neurological deficit in the Western world (Burd et al. 2003). Diagnosis of FAS depends on evidence of growth retardation, central nervous system neurodevelopment abnormalities and a characteristic pattern of facial anomalies, specifically short palpebral fissure length, smooth philtrum, flat upper lip and flat midface (Astley & Clarren, 1995; Hoyme et al. 2005). Criteria have been published for the diagnosis of FAS as well as the broader spectrum of structural anomalies and neurocognitive and behavioural disabilities, known as fetal alcohol spectrum disorders, resulting from the exposure of the developing fetus to alcohol (Astley & Clarren, 2000; Hoyme et al. 2005). There are no biological markers for FAS. Clinical diagnosis of FAS from facial appearance in children has been emphasized (Smith, 1979; Astley & Clarren, 1996, 2001), but is variable, and experience and expertise in dysmorphology are required – many untrained paediatricians and a minority of dysmorphologists have difficulty in confidently confirming the disorder. Incorrect diagnosis can lead to stigmatization and be extremely damaging to the child and family. Attempts have been made to standardize the diagnosis of the characteristic FAS facial features by introducing a quantitative case definition derived both from direct anthropometric and indirect photogrammetric methods (Astley & Clarren, 1996, 2001).

Anthropometric measurements for diagnosis of FAS have traditionally been done using hand-held rulers, calipers, or a cloth retractable tape measure to obtain linear distances between facial landmarks. Two-dimensional (2D) photogrammetry to obtain landmark points from frontal photographs (Astley & Clarren, 2001) and stereo-photogrammetry to obtain landmark points in three-dimensional space (3D) from stereo photographs (Meintjes et al. 2002; Douglas, 2004) have been introduced as alternatives to direct anthropometry in FAS diagnosis. Other applications of facial anthropometry have used laser scanners (Hennessy et al. 2002, 2005; Buckley et al. 2005) and photogrammetric scanners (Hammond et al. 2004, 2005) to obtain 3D facial surfaces from which landmark and other surface points are obtained.

Most morphological studies to detect facial differences between groups have, until recently, concentrated on the delineation of characteristic features rather than on facial shape variation (Hammond et al. 2004). Facial shapes may be compared and averaged in terms of the relative positions of a set of landmarks, as demonstrated in an early study on the facial effects of fetal alcohol exposure (Clarren et al. 1987; Streissguth et al. 1991); these studies compared the mean shapes of triangles defined by sets of three landmarks in subjects more exposed or less exposed prenatally to alcohol. However, quantitative descriptions of the FAS phenotype since have been based on linear measurements (Astley & Clarren, 1995; Moore et al. 2001).

Shape is defined as all the geometrical information that remains when location, scale and rotational effects are removed from an object (Dryden & Mardia, 1998). Two shapes can be compared by adjusting for size and superimposing one shape on the other. The differences that remain are then due to shape dissimilarity. Statistical shape analysis or geometric morphometrics is a structured approach to the analysis of landmarks for shape variation (Kendall, 1984; Bookstein, 1997; Dryden & Mardia, 1998; Hammond et al. 2004). Although such studies have typically used a limited set of reproducible landmarks that are biologically homologous, the combination of statistical shape analysis with image processing methods allows interpolation of data between landmarks and hence more complete analyses of shape, as shown by Hammond et al. (2004).

This paper reports on the use of stereo-photogrammetric data to compare, in subjects with FAS and normal controls, the facial features clinically relevant in the diagnosis of FAS, using Generalized Procrustes analysis and principal component analysis. Two studies were performed, both comparing facial landmark data of FAS and normal subjects but differing in the number of landmarks chosen. The anatomical landmarks whose coordinates were extracted for the analyses were those that were clearly visible in stereo image pairs and that have been cited in the literature as clinically relevant for FAS diagnosis (Clarren et al. 1987; Astley & Clarren, 1995, 1996; Moore et al. 2002).

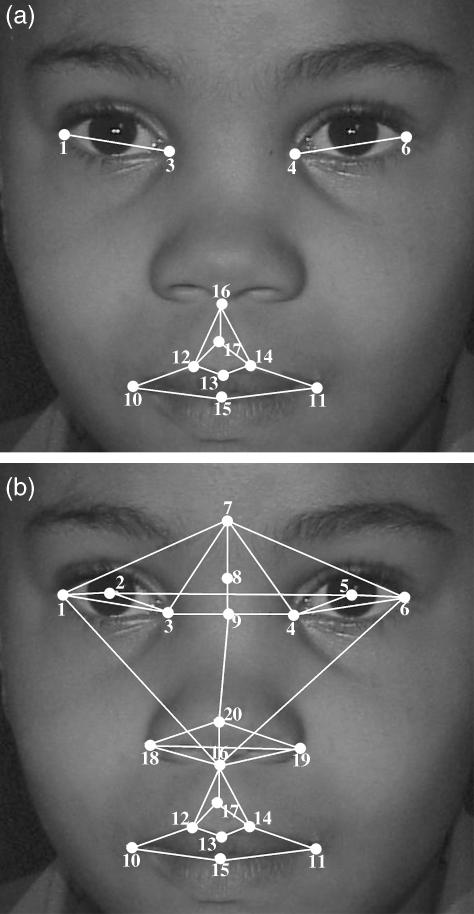
The first study included only those landmarks lying on features reported to be the most significant indicators of the FAS facial phenotype and used in diagnosis (Astley & Clarren, 1996), namely palpebral fissures (shorter in FAS), the philtrum (smoother in FAS) and the upper lip (thinner in FAS). The presence of two or more of these features is regarded as evidence of a characteristic pattern of facial anomalies in the diagnosis of FAS and partial FAS (Hoyme et al. 2005). Figure 1(a) shows the landmarks used to define these features.

Fig 1.

Landmarks used in (a) the first study and (b) the second study: 1, left outer canthion; 2, left pupil centre; 3, left inner canthus; 4, right inner canthus; 5, right pupil centre; 6, right outer canthus; 7, glabella; 8, nasion; 9, sellion; 10, left cheilion; 11, right cheilion; 12, left crista philtre; 13, labiale superius; 14, right crista philtre; 15, stomion; 16, subnasale; 17, midpoint of philtrum furrow; 18, left alare; 19, right alare; 20, pronasale.

Midface hypoplasia is characterized by a flat nasal bridge, seemingly widely spaced eyes, an upturned nose, long philtrum and a generally concave-looking face, and has been documented as being among the minor facial anomalies associated with the FAS facial phenotype (Clarren et al. 1987; Astley & Clarren, 1995; Huang et al. 2005). The second study included landmarks in the mid-facial region that may be affected by midface hypoplasia in FAS subjects (Fig. 1b). The study population for both studies was identical.

Methods and materials

Study population

Study data were obtained during the screening of first-grade children from disadvantaged communities in the Gauteng and Northern Cape Provinces of South Africa for FAS. Only those children presenting signs of growth retardation based on height, weight and head circumference were evaluated for FAS. Each child was appraised by three independent dysmorphologists. The photographs of 56 normal subjects (no growth retardation) and 24 FAS subjects obtained using the stereo-photogrammetric tool described by Meintjes et al. (2002) were considered for use in the study. Of these, 20 normal and 14 FAS image pairs were clear enough for photogrammetric measurement. The rest were discarded due to bad lighting. The age range of the subjects is given in Table 1. The use of young children in the study supports the belief that the facial features of children with FAS become less specifically anomalous after puberty (Streissguth et al. 1991). The relationship between different physical measurements at specific ages, for each sex and for specific ethnicities is expected to be constant (Hall et al. 1989). The study population was balanced on these three demographs. The data were pair matched so that the ratio of FAS to normal subjects was approximately 1 : 2. All the subjects were of mixed ancestry.

Table 1.

Statistical description of the study population

Diagnosis (no.)	Sex (no.)	Mean age (years) (SD)
FAS (14)	Male (8), Female (6)	7.11 (0.40)
Normal (20)	Male (7), Female (13)	6.56 (0.37)

Image capture and feature extraction

Landmark points were obtained using a stereo-photogrammetric method reported on previously (Meintjes et al. 2002; Douglas et al. 2003a,b). Stereo photographs are captured of a child's face within a calibration frame containing markers with known 3D coordinates. The child is asked to look straight at the camera with a neutral facial expression. Images are stored in a database for later analysis. Software developed in Matlab v6.50 (Matworks Inc. 2004) determines a mapping between the stereo image pair using the Direct Linear Transformation (DLT) (Abdel-Aziz & Karara, 1971), and the 2D image coordinates of any point occurring in both images may be transformed into 3D object-space coordinates. The user manually selects, using a mouse, relevant points on both images displayed on a computer monitor. Calibration accuracies are reported to be better than 0.5 mm in each direction (Meintjes et al. 2002). Point selection was done twice for each subject to assess reliability. Guidelines developed by Farkas (1994) were used to estimate the position of those landmarks that do not lie on extremes of curvature and contours.

Morphometric analysis

Shape may be described by locating a finite number of points on the shape outline, or through landmarks. An n-point/landmark shape in k-dimensions can be mathematically represented by concatenating each dimension into a (kxn) vector. By establishing a coordinate reference with respect to position, scale and rotation, true shape representation can thus be obtained. The coordinate reference aligns or superimposes all the shape objects in question and can be obtained using Generalized Procrustes analysis (Rohlf & Slice, 1990; Bookstein, 1997), which optimally superimposes all n landmark points for N objects. Optimum superposition of shape objects is achieved when translation and rotation effects are adjusted so as to minimize the distances between landmarks. Various minimization criteria exist but the most popular is that which minimizes the sum of the squared distances between corresponding points (Halazonetis, 2004). After this establishment of a common coordinate reference for all the shape objects, estimates of shape variability are obtained using statistical procedures. This methodology has been criticised by Richtsmeier et al. (2002) for producing a ‘flawed estimate of variability’ in landmark location if the shape variation is not isotropic (Klingenberg & Monteiro, 2005). Proponents of the methodology, however, have shown it to have the best statistical power and minimal constraints on the variance patterns that can be detected (Adams et al. 2004).

A set of biological objects having the same general shape and belonging to the same biological entity will always have some degree of interpoint correlation (Halazonetis, 2004). The number of shape variables analysed statistically may be reduced by principal component analysis, which derives statistically independent principle components that account for part of the variation in the sample. The components are arranged in decreasing order of significance and those that make little contribution to sample variability are excluded from further analysis.

Shape is considered to be a continuous variable of smoothly varying patterns. The collection of all possible shape patterns may be regarded as shape space (Stegmann & Gomez, 2002; Halazonetis, 2004). Each shape object or pattern will thus be a particular point in this space. Methods using this shape space and its tangent approximations are considered the preferred standard in landmark morphometric analysis. Of importance is that there is a straightforward relationship between objects in shape tangent space and the original 3D space from which the landmarks were extracted, hence the results of statistical analysis performed in shape tangent space can be visualized directly (Klingenberg & Monteiro, 2005).

It is useful to consider the principal components as representative of coordinates that uniquely point to any shape pattern from the collection in shape space. In the present study, principal components were derived from the shapes aligned by Generalized Procrustes analysis. Those principal components accounting for the greatest amount of variation in the sample were retained and subjected to discriminant analysis to determine which provided the largest separation between FAS and normal subjects. A discussion on the use of discriminant analysis in morphometrics may be found in Klingenberg & Monteiro (2005). The shape difference between the FAS and normal groups was assessed through visual inspection of scatter plots of the principal component scores with the greatest separation between the two groups.

The Procrustes superposition was implemented using the program developed by Sheets (2004) which is part of the Integrated Morphometrics Package (IMP) series of geometric morphometrics software and the PAST (PAlaeontologicalSTatistics, v1.35) program by Hammer et al. (2005). Principal component analysis was performed using software developed by Sheets (2003). Discriminant analysis was performed in Statistica v7.0 (Statsoft Inc., 2004). The Procrustes superposition was performed for the FAS and normal datasets separately and the mean configurations were found for the datasets, and superimposed. The FAS and normal datasets were then aligned with their respective mean configurations.

Assessment of measurement error

Reliability was assessed using the landmarks described for the second study. Two separate sets of measurements were used to assess the intraclass coefficient of reliability (R). R reflects the proportion of the variance of an observation attributable to subject-to-subject variability in the absence of measurement error, and increases with increasing reliability (Ward & Jamison, 1991). Both sets of measurements were performed by one operator at different times. For each set of Procrustes fits, a principal component analysis was performed and the component scores were used to quantify reliability in shape variation. Details of the methodology have been reported in Robinson et al. (2002): for each principal component the component score for each subject can be separated into the ‘true’ score, which is the mean of the two scores from the two sets of measurements, and an error score, which is the residual. The reliability R is then a ratio of the variance in the ‘true score’ and the variance of the ‘true score’ plus variance of the residual error term.

Results

First study

Table 2 shows the results of Goodall's F-test to compare the mean shape configurations of the FAS and normal groups. There is no statistically significant difference between the two shape means. No further analysis was done on these sets of landmarks.

Table 2.

Goodall's F-test for comparison of mean shape configurations (FAS vs. normal)

	Goodall's F-test
	F-score	P-value
First study	0.3339	0.99968161
Second study	2.2295	0.00000141

Second study

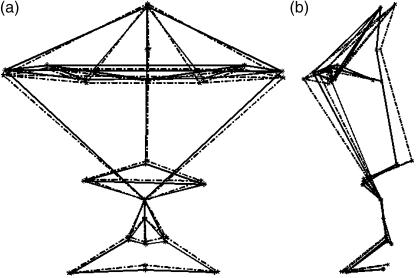
Superimposing the mean configurations for the two groups for both the coronal view and the sagittal view allows a visual comparison (Fig. 2). Goodall's F-test was used to examine differences in mean shape between the two groups. The results are presented in Table 2. The P-value reported is significant, indicating that there is a clear shape difference between two mean shapes for FAS and normal subjects, justifying further analysis.

Fig 2.

The FAS (solid) and normal (dotted) mean configurations superimposed. (a) Coronal view, (b) sagittal view. The lines correspond to those between the landmarks in Fig. 1(b).

The craniofacial shape of males has been shown to be markedly different to that of females in humans (Hennessy et al. 2002). The effects of sexual dimorphism on the analysis were explored by using a sex-matched study sample for the facial shape analysis. Differences in facial shape between FAS and normal subjects remained significant when the analysis was repeated within sexes (P < 0.000001 for Goodall's F-test for both males and females). Further analysis was done on the sex-pooled data.

Principal component analysis

The Procrustes residuals for all subjects were obtained using the IMP software. These were used in principal component analysis to assess shape variability. The Jolliffe cut-off value for eigenvalues, used in the PAST software, is a method to show informally how many principal components (PCs) should be considered significant (Jolliffe, 1986); it retains the PCs associated with the covariance matrix that have eigenvalues greater in magnitude than the average of all the eigenvalues. The Jolliffe cut-off was 0.0001312 for the study sample and the first 15 PCs with eigenvalues greater than this cut-off value were considered for further analysis. The cumulative variance proportion of these components is 93.7%, as shown in Table 3. The reliability R for the first 15 PCs is also presented in Table 3.

Table 3.

Principal components showing percentage variation, and eigenvalues. These first 15 PCs account for 93.7% of the total shape variation. PC1, PC3 and PC14 were identified by discriminant analysis as the most discriminating between FAS and normal subjects. The intraclass correlation of reliability R is presented for the first 15 PCs.

				Discriminant analysis results
Principal component	Eigenvalue	Percentage individual variance	Partial lambda	P-value	Percentage cumulative variance	Reliability R
1	0.00249	24.3	24.3	0.776302	0.000016	0.62
2	0.00113	11.1	35.4	–		0.18
3	0.00105	10.3	45.7	0.818956	0.017016	0.29
4	0.00097	9.4	55.1	–		0.21
5	0.00066	6.4	61.5	–		0.32
6	0.00058	5.7	67.2	–		0.23
7	0.00056	5.5	72.7	–		0.18
8	0.00048	4.7	77.5	–		0.31
9	0.00037	3.6	81.1	–		0.19
10	0.00034	3.3	84.4	–		0.23
11	0.00025	2.4	86.8	–		0.22
12	0.00023	2.3	89.0	–		0.32
13	0.00018	1.8	90.8	–		0.22
14	0.00015	1.5	92.3	0.835767	0.023717	0.15
15	0.00014	1.4	93.7	–		0.22

Discriminant analysis of principal component scores

Some of the shape variation represented by the PCs is expected to be responsible for the difference in facial shape between FAS subjects and normal subjects. A discriminant analysis of the principal component scores for the 15 selected PCs was done to determine which PCs had the greatest discriminating power between FAS and normal subjects. The results are presented in Table 3.

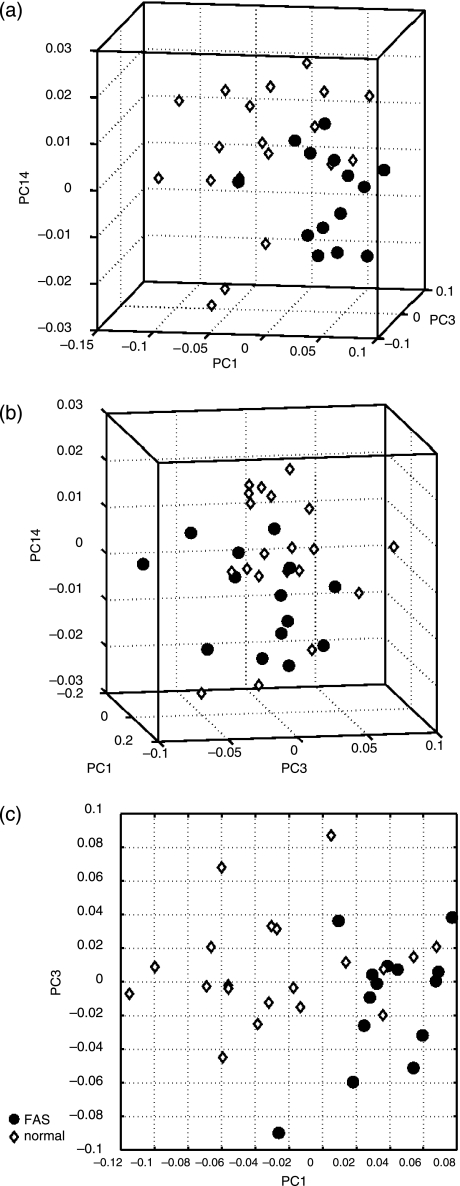
Only PC1, PC3 and PC14 had significant discriminating power as reported by their significant P-values. Scatter plots of PC1, PC3 and PC14 scores against each other for all subjects are shown in Fig. 3. Each subject is located at a particular point in the scatter plot, which here represents shape space. Biological entities with similar shape should generally be located near each other in these scatter plots. PC1 seems to contain the most discriminating power from the scatter plots, i.e. there is greater separation between the groups in the direction of PC1.

Fig 3.

Scatter plots of subjects’ principal scores along PC1, PC3 and PC14. The orientation of the two groups along PC3 and PC14 is ambiguous. FAS subjects, however, generally lie in the positive direction and the normal subjects in the negative direction along PC1.

The FAS subjects generally lie in the positive direction and the normal subjects in the negative direction along PC1. From the great separation between groups along PC1 and the fact that PC1 contributes the most to shape variability (Table 3) it can be deduced that the shape variability along PC1 mostly accounts for the broad differences in shape between the two groups. PC3 and PC14 account for finer details in shape difference.

Visual assessment of shape variability

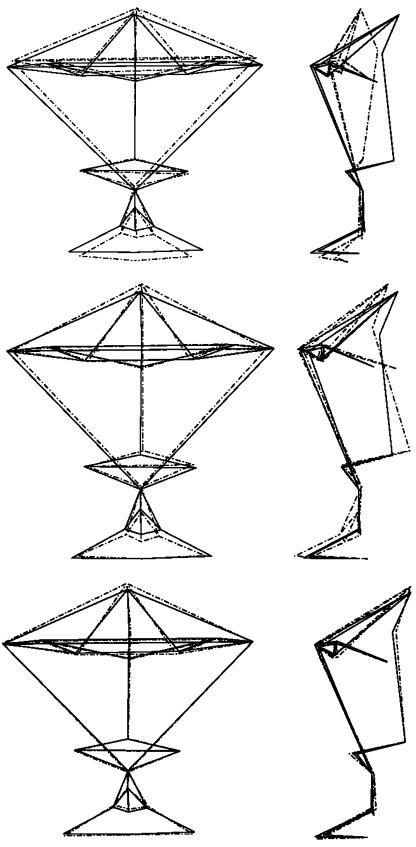
The principal component loadings of each landmark point along the direction of each PC can be used to assess shape variability. The mean shape has by definition all PCs equal to zero. To illustrate the pattern of shape variability represented by each PC, the average or mean shape can be warped by moving the landmark points according to their loadings in the positive and negative direction of the PC by units of standard deviation (Hennessy & Moss, 2001; Robinson et al. 2001; Stegmann & Gomez, 2002; Halazonetis, 2004), as shown in Fig. 4 for PC1 (top images). The standard deviation range of values chosen in the warping is representative of the range of values in principle scores, as shown in the scatter plots above. Visualization is presented only in the positive direction (direction in shape space where the FAS subjects lie), as visualization in the negative direction, where the normal subjects lie, shows the exact opposite shape variability.

Fig 4.

Top: warped shapes depict the variation in shape of PC1, in the coronal (left) and sagittal (right) views corresponding to mean shape +0.15 standard deviation. Middle: warped shapes depict the variation in shape of PC3 in the coronal (left) and sagittal (right) views corresponding to mean shape +0.10 standard deviation. The solid line is the average and the dashed line is the superimposed warped shape. Bottom: warped shapes depict the variation in shape of PC14, in the coronal (left) and sagittal (right) views corresponding to mean shape +0.03 standard deviation. The solid line is the average and the dashed line is the superimposed warped shape.

For completeness the warping of PC3 is presented in Fig. 4 (middle images) and of PC14 in Fig. 4 (bottom images). However, as the scatter plots in Fig. 3 illustrate, it is difficult to pick out the trend in clustering between the two groups along PC3 and PC14. Thus, it is difficult to interpret these warped shapes in terms of how they discriminate between the two groups.

Broad facial feature distinctions between FAS and normal subjects based on PC1

Only PC1 has a clustering of subjects between the two groups that can easily be visually interpreted, as shown in Fig. 3. PC1 accounts for the most shape variability, namely 24.3%. PC1 also has the greatest discriminating power between the FAS and normal subjects. These two factors combined means that any facial features affected by the mode of shape variation along PC1 are those most affected by FAS. A description of these features is presented below.

As FAS subjects generally lie in the positive direction of PC1 it may be inferred that children with FAS have smaller head circumferences, if the measurement of head circumference is between the glabella and the occipital protuberance (bony bulge on the occipital bone at the back of the skull), because there is retraction of the glabella to a more posterior position relative to the average. Underdevelopment of the midfacial region (midface hypoplasia) in the faces of children with FAS is indicated by: the face being flatter, i.e. having frontal facial features such as nose, forehead and lips approaching the same plane in the coronal view vertically; upturning of the nose; diminished nasal protrusion; and increased nasal bridge length. Faces of children with FAS have longer and slightly smoother philtrums. They have shorter outer canthal distances but little lateral movement of the endocanthi, accounting for the small palpebral fissure lengths that are evident in FAS subjects. They have slightly longer midfacial height; specifically, the upper facial height (described here as the distance from the nasion to the subnasale) is greatly increased. This, however, can also be attributed to the backward slanting of the nasion to a more posterior position. The lips are small in width although there is no marked difference in lip thickness between normal faces and those of children with FAS along PC1.

From the FAS direction of PC1 towards the direction where normal subjects lie, there is an increase in nasal protrusion as the pronasale pushes forward as viewed from the sagittal plane. The nasion and subnasale remain in the same position as the average shape. The midfacial height decreases. This could be also attributed to a more forward orientated nasion and glabella relative to the average. Anteroposterior retraction of eye features also occurs. The corners of the mouth become more retracted. Lips seem to be more visible from the side profile of the face. Inner canthal distance, outer canthal distance, palpebral fissure length and interpupillary distance are slightly larger than the average shape. The lips widen, although the thickness remains the same. Philtrum furrows become more pronounced.

Discussion

Application of the Procrustes approach to facial shape analysis is becoming more widespread in syndrome diagnosis (Hennessy et al. 2002; Hammond et al. 2004). The advantage of using principal component analysis in conjunction with Procrustes analysis is the ability to give a comprehensive description of the overall facial shape with a small number of landmark measurements that are not conflicting because they are statistically unrelated (Halazonetis, 2004).

The mean shape difference between FAS and normal subjects in the first analysis is non-significant, with overlap between the facial shape range of FAS subjects and that of normal subjects. This result is unexpected, as the features used in this study are those indicated in the literature to discriminate best between FAS and normal subjects (Astley & Clarren, 1995, 1996).

Palpebral fissure length (PFL) has been found to be correlated with head circumference in some groups of children (Iosub et al. 1985). Our control group excluded children who had been screened positive for growth retardation, as indicated by reduced height, weight and head circumference, and only those children presenting signs of growth retardation were further evaluated for FAS. A correlation between PFL and head circumference and further correlations between PFL and other features may be present in this study population. Generalized Procrustes analysis removes differences in scale that may be present in the comparison groups. If the features used in the first study are highly correlated in size, this normalization would eliminate most of the variation in the data set, and provide an explanation for the absence of shape variation between groups. A lack of correlation among the additional features introduced in the second study and those used in the first would enable shape differences between groups to be detected. An extension of this work into analysis of differences between groups in form space (including both size and shape) (Dryden & Mardia, 1998) may allow the visualization of differences between group forms based on the landmarks used in the first study.

Little has been published on quantitative assessment of mid-face hypoplasia from the sagittal perspective. Adding additional landmarks allowed for shape analysis of midfacial features in both the frontal and the sagittal plane in the second study, resulting in the detection of shape differences between the FAS and normal subjects. Although traditional FAS diagnosis emphasizes on facial features in the coronal plane, additional landmark information in the sagittal plane may be more descriptive of FAS facial anomalies, especially concerning mid-face hypoplasia.

Microcephaly

Microcephaly is shown here to be important in distinguishing FAS subjects but the FAS subjects were taken from a sample screened on the basis of growth retardation, hence microcephaly in the FAS group is expected.

Midfacial hypoplasia

The flattening of the midface seems to dominate the mode of shape variability described by PC1. This agrees well with the facial dysmorphology associated with FAS in the literature (broad or depressed bridge of nose, short nose). Moore et al. (2002) indicate that although there is a general reduction in all facial depth measurements, midfacial depth seems to be affected more than the upper and lower facial depths. The results presented here suggest that the anteroposterior movement of the nasion reduces the facial depth in the middle facial position of FAS subjects. Moore et al. (2002), however, report frontal bossing (a prominent forehead), as suggested by near normal values of minimal frontal breadth that they obtained for FAS subjects. This finding contrasts with the trend found here where the glabella retracts postero-anteriorly in FAS subjects. The increase in midfacial height associated with FAS, evident in Fig. 4, is not indicated in the literature.

Eye anomalies

The wide spaced appearance of the eyes in FAS subjects is confirmed here (Astley & Clarren, 1995, 1996; Moore et al. 2002). The endocanthion in children with FAS is slightly more laterally positioned from the facial midline. There is an accompanying large decrease in outer canthal distance. This gives the appearance of widely spaced eyes. The medial movement of the exocanthion is clearly evident as PC1 is warped in the positive direction where the FAS subjects tend to lie. This, together with fact that the endocanthion is slightly more lateral, accounts for the reduction in palpebral fissures generally reported in FAS subjects.

Philtrum smoothness and upper lip thinness

PC3 seems to account for some of the shape variation that affects philtrum smoothness (Fig. 4, middle images). Although it is a significant discriminator according to the discriminant analysis, visual inspection of the scatter plot in Fig. 3 does not provide any insight into how to separate the two groups along this component. The large overlap of principal scores makes it difficult to assess visually how philtrum smoothness differs between the FAS and the normal facial phenotypes based on PC3. Along PC1, however, the philtrum in FAS subjects appears to be slightly smoother (i.e. the philtrum furrow and philtrum ridges become less distinguishable). The approximate shape used (Fig. 1) for the philtrum ridge and furrows produced results consistent with the literature, indicating that FAS subjects generally have smooth, long philtrums compared with normal subjects (Astley & Clarren, 1995, 1996, 2001). Philtrum length increases greatly in the FAS appearance, as indicated by PC1. This has also been reported as being phenotypical of FAS (Moore et al. 2002). The explanation offered by Moore et al. – that the ratio between philtrum length and nose size is so disproportionate that it makes individuals with FAS only seem to have long philtrums – may not be accurate. The position of the subnasale in FAS subjects is slightly more superior than the average position in the frontal view of Fig. 4. The upper vermillion border in FAS subjects is more inferiorly positioned to that of the average mean shape in the same view. This is evidence of the philtrum being longer in FAS subjects than in normal subjects.

Upper lip thinness, which has become a common diagnostic criterion, does not seem to play as significant a role in distinguishing the FAS facial phenotype in our study population; Douglas & Viljoen (2006) have reported that eye distance measurements in South African children do not consistently mirror published population norms from other parts of the world, and the same may hold for lip measurements. The variation in lip thinness seems to be explained by PC3, although it is difficult to say where the face associated with FAS lies compared with the normal face (i.e. does it have thicker or thinner lips compared with the normal face), because of overlap of principal component scores between the two groups along PC3. The low intraclass coefficient of reliability for PC3 further impedes the interpretation of variations found along this principal component.

Study limitations

The intraclass coefficients of reliability for the second study show that the proportion of variance attributable to error increased with decreasing significance of principal components. Robinson et al. (2002) attribute this to the decrease in recovery of non-random structure in principal component analysis as the components decrease in significance. PC1, which describes most of the shape variability and shape difference, has a high reliability figure, however. Possible errors in landmark positioning were introduced by poor photographic quality, and in some cases subjectivity in landmark selection (estimating the position of some landmarks due the nature of their location on the face).

The landmark-based, stereo-photogrammetric approach presented here was limited by the number of biologically homologous landmarks obtainable (Hammond et al. 2004). Points of biological correspondence on soft tissue surfaces such as the cheek, chin and forehead are not easy to find, although some shape information found on these surfaces could be useful in delineating facial phenotypes of some syndromes (Hammond et al. 2004). Three-dimensional surface scans allow the use of traditional landmark-based geometric analysis with the added advantage that surface information of the face is easily obtainable and can be factored into the facial analysis. The dense surface model approach (Hammond et al. 2004, 2005) using 3D surface scans of the whole face or localized patches of the face has yielded accurate inter-syndrome discrimination rates. The increased complexity and therefore cost of surface scanners compared with stereo-photogrammetry may not be justifiable in morphometric diagnoses where stereo-photogrammetry yields satisfactory results, and where large-scale screening of disadvantaged communities, at low cost, is necessary.

Although the facial shape analysis method presented here is robust to small study samples, the work presented here should be regarded as a preliminary study whose findings motivate further work on larger groups. In addition, deviations from the normal facial shape that are associated with FAS should be explored for different ethnic groups.

Concluding remarks

We have demonstrated the use of facial shape analysis in comparing the FAS facial phenotype with normal faces in children, and largely confirmed the characterization of the FAS facial phenotype found in the literature as based on the gestalt approach and on linear measurements of facial features. Some disagreement between FAS facial shape indicated by our results and FAS features indicated in the literature may be due to ethnic variation. A shape discrimination tool based on the work presented here may be valuable in reducing the cost of large-scale screening for FAS in high-risk communities, and also in improving the consistency of diagnosing the facial appearance associated with FAS in children.