A new method for quantifying three-dimensional interactions between biological structures

Abstract

In this paper we examine a new distance-based method for identifying and characterizing possible interactions between biological structures and objects, with respect to the initial developmental stages of Echinococcus granulosus. By adopting the surface of the foramen as the distance reference, several interesting results have been identified, including the fact that the cell nuclei tend to be organized with respect to the foramen surface as well as the stability of the spatial distribution of these nuclei along the development stages.

Introduction

Understanding the intricate sequence of events underlying animal development remains one of the most challenging issues in post-genomics. Indeed, although the genome provides precise rules for assembling specific proteins, the time and place of the corresponding gene expression are defined by external and internally driven factors, especially the anatomical scaffolding, itself the result of co-ordinated gene expression. In other words, it is only by considering the existing (sometimes temporary) anatomical landmarks that body plans can be properly assembled through gene expression. One particularly critical issue required for the better understanding of animal development involves the accurate and objective measurement of dynamic geometrical properties of anatomical structures, from which developmental models can be proposed and validated against additional biological experiments. The present article focuses on the problem of how effectively to quantify and characterize, in terms of distance, the spatial interaction between tissue differentiation and anatomical configurations during animal development.

An important related issue concerns the quantitative and objective inference of spatial interrelationships between elements and structures involved in animal development (cell distribution, tissue structure, gene expression patterns, etc.). Although previous studies have addressed space–time gene expression quantification (e.g. Costa et al. 2004, 2005; Diambra & Costa, 2006), the present work proposes a comprehensive methodology for characterizing spatial interrelationships in three-dimensional (3D) data of developing biological structures. The key concept underlying our approach is the consideration that the pattern formation dynamics involves spatial correlations and signalling among cell differentiation and existing phenotypic anatomical structures. Both these processes are intrinsically related to distance. For instance, if a specific cell is actively expressing a gene, it is likely that neighbouring cells will also be engaged in a similar activity. Furthermore, the signalling emanating from an anatomical landmark to organize (promote or inhibit) development around its neighbourhood tends to decay with distance from that landmark. Indeed, distance is critical for the development of biological structures (i.e. organ formation under a morphogenetic field), as the substructures have to achieve an internal polarity under the influence of some primary pattern-forming system, as exemplified in model systems such as Drosophila, hydra and plants (Koch & Meinhardt, 1994).

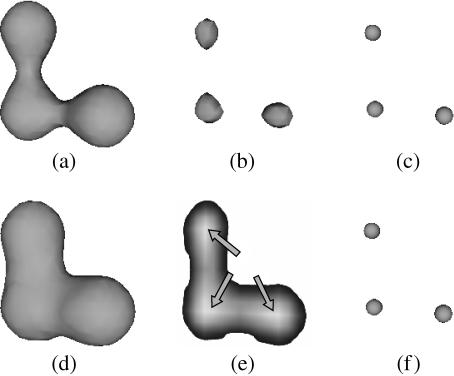
The problem of determining distances in the anatomical structure involves the choice of a suitable reference from which the distances can be obtained. Although the centre of mass of the reference structure, or even its main axes or symmetry planes, could be considered as an origin for calculating the distances, both these alternatives are poor because they do not take into account the possible intricacies of shape (e.g. presence of concavities or convexities such as most organs). Figure 1 shows a simple 2D anatomical structure (in black) surrounded by a myriad of objects (small dots) and the corresponding histograms of distances obtained with the origin at the centre of mass (Fig. 1a,d), main axis (Fig. 1b,e) and the outline of the anatomical structure (Fig. 1c,f). This simple example shows that the surrounding objects can only be properly identified with the reference in Fig. 1(c), implying that there is a sharp peak in the distance distributions (Fig. 1f).

Fig 1.

A simple example of the effects of choosing the centre of mass (a), main axis (b) and border of the anatomical structure (c) as a reference for distance calculation. The distance histograms thus obtained are shown in (d), (e) and (f). That the distribution of surrounding objects is related to the shape of the anatomical structure can only be properly inferred from the sharp peak in (f).

For developing systems, it is important to consider the effect of growth on regional differences. For example, growth may change the distance between sources and sinks of substances, thus changing the overall pattern of their concentrations. Capturing these effects requires methods for incorporating growth into continuous or discrete frameworks (Coen et al. 2004). Furthermore, theoretical studies support the importance of geometrical constraints when surrounding tissues secrete morphogenetic determinants (Diambra & Costa, 2005). It is worth noticing that information on spatial interaction can be inferred from cells or molecules (e.g. proteins, peptides, DNA) related to the transcription activity, which are referred to in this text as objects. For the sake of simplicity, we concentrate on quantifying the interaction between cells and anatomical structures, but the proposed methodology can be extended to other situations.

The key feature of this article is to advocate that more informative, complete references should be considered for defining distances in the analysis of the spatial distribution of cells or molecules. Once such a reference, e.g. the surface of the anatomical landmark, has been chosen, its distance transform (Costa & Cesar, 2001) provides the mathematical subsidy for assigning to each surrounding point the minimal distance between that point and any of the reference points. In addition to describing the methodology, we illustrate its potential with an example involving cell nuclei distribution during the development of the metacestode larval stage (protoscolex) of the parasite Echinococcus granulosus. This cestode is the causative agent of hydatidosis, or hydatid disease, a zoonosis that affects humans and herbivorous domestic animals. The disease is caused by hydatid cysts formed upon ingestion of E. granulosus eggs excreted by definitive hosts (canine) (Thompson & Lymbery, 1995; Cabrera et al. 2003).

Protoscoleces, i.e. the E. granulosus larval stage which is infective to these hosts, develop asynchronously and clonally from the cellular germinal layer of hydatid cysts. This triploblastic cestode is an attractive model for early development studies. The mature protoscolex has a scarce number of visible morphological structures: an apical hook-armoured rostellar pad, a basal stalk, four meso-lateral suckers and conspicuous mesenchimatic calcareous corpuscles. Systematic studies concerning key biological Echinococcus issues, such as germ layer ontogenesis, are still lacking. Recently, Martínez et al. (2005) have shown that early protoscolex morphogenesis is a complex, dynamic process starting from the constitution of a foramen in the early bud, around which cells are distributed mainly at the lateral and apical regions. The number of cells is similar from the early bud stage to the mature protoscolex, strongly suggesting that there is no significant cellular proliferation during final protoscolex differentiation.

In this work, characterization of the cell nuclei distribution is performed with respect to two references: (1) the apical–basal axis and (2) the surface of the hollow portion (foramen) inside the parasite body. The results indicate important cell distribution features along three successive stages of the parasite development, including the conservation of nuclei density profile in terms of distances along the two latter stages, despite the clearly distinct respective foramens. This result was obtained because the methodology proposed here considers the minimal distance between the nuclei and the surface of the reference structure, therefore capturing the spatial congruence between the foramen and nuclei distribution.

Materials and methods

Experimental data

The data used to illustrate the methodology were obtained from confocal images of DNA nuclei distributions at early development stages of Echinococcus granulosus protoscolex. Confocal images are well suited for our purposes, as they cover a good range of depth and provide 3D images without the need for alignment of the slices, as required by traditional histology (microtomy).

Fresh E. granulosus samples (hydatid cysts and associated brood capsules from sheep liver) were obtained in local abattoirs, and fixed in 4% PFA in PBS, treated with RNAse A as described by Martínez et al. (2005). Whole-mount propidium iodide staining for samples A and B, and the acquisition of confocal laser scanning microscopy data sets have also been described by Martínez et al. (2005). Sample C was stained with 5 nm YOYO-1 (Molecular Probes, OR, USA) and washed three times in PBS before mounting (Sotelo-Silveira et al. 2004). The data sets were imaged in an Olympus Fluoview FV300 confocal laser scanning microscope mounted on an Olympus BX61 upright microscope with the following optics: 20× (NA 0.55, dry), 40× (NA 0.75, dry), and 60× (NA 0.9, dry). The voxel sampling resolution at 40× magnification was 0.13 × 0.13 × 2.72 µm. Additionally, and as a morphological control, the same parasites were visualized by differential interference contrast (DIC) using the 40× lens.

The data sets adopted correspond to three successive early developmental stages of the parasite: data set A for early bud stage, B for early elongated bud and C for elongated bud stage. These early developmental stages are suitable to be analysed using whole-mount procedures (for further details see Martínez et al. 2005) and are characterized by a unique morphological structure, namely the foramen, which occupies the central zone of the parasite body along its main developmental axis. Figure 2 shows representative DIC images of two early E. granulosus developmental stages and includes a full mature invaginated protoscolex (PSc, not included in this study). It also includes some of the elongated bud stage inverted confocal slices (dataset C) showing the DNA nuclei in black and the foramen.

Fig 2.

(a) Differential interference contrast of three representative stages during metacestode (protoscolex) development of Echinococcus granulosus. Left to right: early bud stage, full mature invaginated protoscolex and elongated bud stage attached to the germinal layer. f, foramen; PSc, protoscolex; R, prospective rostellar cone; Su, prospective sucker; St, prospective stalk; GL, germinal layer. Scale bar: 50 µm. (b) Confocal laser scanning slices of the elongated bud stage.

Methodology

The methodology suggested for obtaining the distribution/density of objects with respect to the distance to a reference structure involves five main stages: (1) image preprocessing; (2) identification of the spatial coordinates of the objects whose distribution is being analysed; (3) identification of the spatial coordinates of the reference structure; (4) calculation of the distance transform of that structure (e.g. Costa & Cesar, 2001); and (5) calculation of the number of objects in terms of distance and respective density. Each of these steps is described and illustrated in the remainder of this section with respect to the characterization of the distribution of E. granulosus cell nuclei in terms of the distance from the foramen anatomical structure.

Image preprocessing

Before the application of the techniques for identifying objects and reference structure, the slice images have to be preprocessed to reduce noise and other artefacts introduced during image acquisition. We have applied Gaussian smoothing to remove low-level noise (Gonzalez & Woods, 1992).

Object identification

At this stage, the position of each object is determined and labelled. Two image processing techniques have been used: segmentation and connected components labelling. The former technique partitions the volume into two sets of voxels (each point in a 3D volume is known as a voxel – volume element): those corresponding to the nuclei and to background. This is performed by assigning a predefined value (such as ‘1’) to the voxels belonging to the object, and another value (e.g. ‘0’) to the background voxels. Such an operation is traditionally called thresholding (Gonzalez & Woods, 1992; Costa & Cesar, 2001). Figure 3(b) shows the result of thresholding applied to one of the slices in Fig. 3(a). The black points in the segmented image correspond to the cell nuclei. The connected components techniques (Costa & Cesar, 2001) can be used to obtain the voxels corresponding to each individual nucleus. The centre of each connected component is calculated and used to represent the position of the respective nucleus. Figure 3(c) shows the identified nuclei as spheres located at the original nuclei positions. However, by comparing the position and number of detected nuclei with those in the original images, we found that the latter tended to be smaller than expected. This is because nuclei typically appear in large quantities, have a small volume and are close to each other. In some cases, the segmentation algorithm produces a large block of merged nuclei detected (labelled) as a single connected component. The separation of these merged nuclei has been achieved by using two techniques, as follows. For separating nuclei merged through a thin connection, erosion (Costa & Cesar, 2001) has been applied using a six-neighbour 3D structuring element (Dougherty & Lotufo, 2003). By shrinking the merged block, the original nuclei are properly separated and then represented in terms of their centres of mass (see Fig. 4a–c for an example). In case the nuclei are more intensely connected, the distance transform of the border of the objects is obtained, so that the peaks in this transform indicate the original nuclei, as illustrated in Fig. 4(d–f). Each merged block was analysed to verify which of the two techniques allowed the most accurate nuclei separation, so as to allow accurate counting of the number of nuclei in the parasite. In addition to all these checks in testing the methods, further validation was performed through comparisons with previously available results obtained by manual counting (Martínez et al. 2005).

Fig 3.

Nuclei identification and definition of the reference structure. (a) Original confocal slices obtained for the elongated bud. (b) Nuclei segmentation by thresholding the confocal slices. (c) Representation of the nuclei by small spheres obtained by using connected components and other procedures. (d) Segmentation, by thresholding, of the foramen of the cestode used as reference in the proposed methodology. (e) Three-dimensional reconstruction of the reference structure. (f) Joint visualization of the nuclei in (c) and the reference structure in (e).

Fig 4.

The two methods adopted for separation of merged nuclei. Nuclei connected through thin links such as those in (a) can be separated by erosion (b), being further represented in terms of the respective centre of mass (c). Nuclei more densely merged, such as that in (d), have their distance transform calculated (e), so that the location of the peaks obtained in this transform (indicated by the three arrows) are used as the coordinates of the segregated nuclei (f).

Reference structure identification

An essential step in the methodology is the choice of the structure considered as reference for calculating the distances. As in the Objects Identification stage, thresholding can be used to segment such a structure. For the E. granulosus data, the reference chosen was the foramen inside the parasite body. In this case, the choice of a suitable threshold was performed by taking the value which implied the surface of the foramen to be as close as possible to the nucleus closest to the foramen. Note that a small bias in the choice of the threshold would imply a shift along the distance reference which would otherwise have no effect on the overall shape of the density (e.g. width of peaks or slopes). Figure 3(a,d,e) illustrates the procedure adopted for identifying the reference structure. The method starts with the sequence of imaged slices (Fig. 3a). Thresholding is applied to all slices to obtain the segmented objects (Fig. 3b) and reference regions (Fig. 3d). Note that different thresholds are normally used to obtain these two segmentations. The frames containing the segmented objects are then re- constructed in three dimensions to obtain the 3D nuclei (Fig. 3c). Similarly, the frames with the slices of the segmented reference structure are reconstructed in three dimensions to obtain the 3D reference structure (Fig. 3e). The 3D reconstructed nuclei and reference structure are finally brought together (Fig. 3f) by adding the data in Fig. 3(c,e).

The result obtained with this methodology for the early bud stage is shown in Fig. 5(a). A nuclei concentration can be observed along the apical region of the cestode. By contrast, the nuclei were concentrated on the apical and intermediate region of the early elongated bud stage, as illustrated in Fig. 5(b). A similar pattern of nuclei distribution was obtained for the elongated bud, as shown in Fig. 3(f). Note the distinct reference structures obtained in each of the three stages.

Fig 5.

Nuclei and reference structure for the early bud (a) and early elongated bud stages (b). Note that these two stages precede that in Fig. 3(f) along development.

Distance transform

The fourth step of our method involves the calculation of the distance transform (Costa & Cesar, 2001) of the reference structure. This transform assigns to each point outside the reference structure the minimal value of distance between that point and any of the points of the structure. The Euclidean distance metric was adopted, and the distance transform was calculated by using Saito's algorithm (Saito & Toriwaki, 1994), available from the Visualization Toolkit Library (Schroeder et al. 2002).

Object distribution

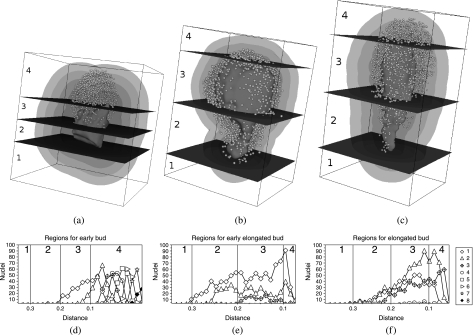
In order to determine the object distribution, the volume surrounding the reference structure was partitioned into regions with the same width, Δd. The number of regions therefore varies according to Δd, with more regions being obtained for small values of this parameter. Such a partitioning into distance regions is necessary to obtain graphs of the population of objects in terms of the distance. Figure 6(a–c) shows a set of regions delimitated by surfaces, assuming large Δd. In addition to organizing the surrounding volume into layers according to the distances, we also considered the apical–basal axis of the parasite as an additional reference, taking advantage of the spatial anisotropy of the overall anatomy. Therefore, it is possible to assign to each object not only its minimal distance to the reference structure, but also the position of its projection onto the apical–basal axis.

Fig 6.

(a–c) Three-dimensional visualization of the reference structure, the nuclei and some distance regions obtained for three different developmental stages of the cestodes. (d–f) The number of nuclei as a function of the distance. (g–i) Volumes of each distance region. (j–l) The density of nuclei in terms of distance. All curves refer to the developmental stages shown in the corresponding column.

Two properties of the objects can be analysed in the two spatial references adopted: the number of objects inside each region and the corresponding densities. For example, the curves in Fig. 6(d–f) quantify the number of nuclei as a function of the distance with respect to each of the three development stages. A total of 25 regions have been considered. Figure 6(g–i) shows the volume of each region in terms of distance (the volume of a region is estimated as the number of voxels whose distance falls inside that region). Figure 6(j–l) presents nuclei density, i.e. the number of nuclei divided by the volume of the region, as a function of distance. The distribution of objects with respect to the apical–basal axis is shown in Fig. 7 for the same developmental stages. This analysis considered the division of the overall structure (foramen and nuclei) into four sections defined by cutting the overall structure by three planes (see Fig. 7a–c) crossing the reference structure at its most basal and apical points as well as at the intermediate point. The distributions of objects within eight distance regions are shown in Fig. 7(d–f) for the three developmental stages, which also identify the sections (i.e. 1–4) defined by the three cutting planes. It can be inferred from Fig. 7(a,d) that the nuclei are concentrated in the apical tip of the growing early bud, reflecting a major cell migration towards the direction of growth. Also, it follows from Fig. 7(b,e) that, in the early elongated bud, cells are more evenly distributed and surround the foramen. Lastly, in Fig. 7(c,f), cells are concentrated in prospective rostellar cone (apical) and sucker (meso-apical, three in Fig. 7c) zones in the elongated bud, although no morphological structure is apparent yet. In conclusion, this analysis highlights the major cellular redistribution leading to the appearance of mature protoscolex morphological structures, and could constitute, together with genetic expression studies, a major tool in addressing the unresolved issue of cestode germinal layer ontogenesis.

Fig 7.

Distribution of distances and nuclei according to four regions defined along the apical–caudal main axis of the foramen for the early bud (a), early elongated bud (b) and elongated bud (c) developmental stages. The respective distributions of nuclei are shown in (d)–(f). The legend identifies each of the distance regions.

Discussion

The study of E. granulosus has motivated important biochemical, molecular and immunological investigations during the last two decades. Nevertheless, fundamental questions of the biology of this parasite, which are relevant to the control and treatment of hydatid disease, remain unanswered, especially those related to the mechanisms controlling the development and growth of the parasite (Thompson & Lymbery, 1995; Fernández et al. 2002; Galindo et al. 2002; Chemale et al. 2003). Several steps have been systematically described during protoscolex development (Galindo et al. 2002; Chemale et al. 2003; Martínez et al. 2005), the first being the appearance of a cell cluster in the germinal layer, which gives rise to the emergence of a semispherical cellular bud towards the cyst cavity or lumen. The undifferentiated buds elongate, generating a new basal–apical axis, and present a typical hollow morphological structure, the foramen, with most of the cells being concentrated at the apical and lateral regions of the nascent larva.

By inspecting the density distributions in Fig. 6(j–l), it becomes clear that the early bud stage presents a spatial arrangement of nuclei which is markedly different from that obtained for the early elongated bud and elongated bud stages. More specifically, the distribution of nuclei at this stage falls monotonically with distance from the foramen. By contrast, the other two stages present a peak of density at an intermediate distance, indicating a clear depletion of nuclei at this distance region. In addition, in analogy to the situation depicted in Fig. 1, the peaks in Fig. 6(k,l) indicate that the nuclei are spatially organized with respect to the surface of the foramen in those cases. The object distribution profiles obtained for the second and third stages are remarkably similar despite the large difference in shape of their foramens and that the cells are displaced toward the apices of the structure in the third stage. The identification of such a conserved density profile, which may reflect requirements implied by gene expression and animal development, has only been possible because of the methodology proposed herein. It would remain completely unnoticed if the reference adopted were the centre of mass or the main axes of the reference structure. In order to compare the proposed approach with these alternative references, we obtained subsidiary results shown in Fig. 8. The two columns represent the distances to the centre of mass (left) and to the apical–basal axis (right). The most straightforward finding is that the three sets of nuclei distribution, i.e. Figs 6(d–f) and 8(a–c,d–f), are intrinsically different. Therefore, if one of these sets is the most appropriate (arguably the distance taken with respect to the foramen surface), the other methods would be inherently biased. The main problem implied by taking as reference the centre of mass or the apical–basal axis is a substantial loss of resolution, as is clearly perceived by comparing, for instance, the curves for the early elongated bud stage (i.e. Figs 6e and 8b,e). In other words, the fact that a considerably narrower curve was obtained for Fig. 6(e) corroborates the enhanced ability of the method proposed here for identifying narrow distributions of objects with overall geometry, not restricted to spheres or cylinders. It is also clear from Fig. 8 that the adoption of these alternative references for the distance transform did not allow the identification of the conserved density profile between the second and third stages. The unsuitability of the centre of mass and main axis as distance references is also clearly illustrated in Fig. 1.

Fig 8.

Distribution of distances with reference to the centre of mass (a–c) and the main axis (d–f) of the reference structure (i.e. foramen).

The distinct density profile obtained for the first stage is possibly a consequence of the initial organization of the nuclei at this developmental period, during which the nuclei are distributed along the foramen until the more stable organization, reflected in the two later stages, is achieved. The relative depletion of nuclei near the foramen at the second and third stages suggests that the tissues near that reference structure mature first along the developmental stages, so that the concentration of nuclei tends to be shifted to greater distances as the individual is formed.

Concluding remarks

The present study introduced a distance-based approach to characterize the spatial distribution of biologically relevant elements during animal development. By taking into account the specific features of the chosen reference structure, the methodology provides a means for quantifying the spatial distribution of objects of interest, which is much more precise than considering the centre of mass or main axes of the reference structure.

The potential of the proposed approach has been illustrated briefly for the nuclei distribution in the developmental stages of early E. granulosus larvae. A series of hypotheses have been inferred from the density profiles, including clues about the timing of tissue differentiation and the possible identification of a stable stage of nuclei distribution, observed between the early elongated bud and elongated bud stages. In order to demonstrate the superior performance of the approach proposed, we also considered simpler alternative choices of references, namely the centre of mass and the apical–basal axis. The comparison pointed to a poor resolution with the use of the latter references, making it impossible to reflect the conserved density profiles between the second and third stages, which were revealed when the foramen was taken as the reference for the distances.

The example considered illustrates that accurate quantitative information on the distribution of objects (in this case nuclei) with respect to anatomical references can provide several insights about putative developmental mechanisms, including tissue differentiation. In the case of biological data including specific information about differentiated gene expression, the range of possibilities extends further than those covered in this work. For instance, it is possible to monitor the density of expression of a set of related genes in terms of the distance to relevant references during development, so as to identify spatial overlaps and exclusions between the different genes. By taking various morphological areas as reference structures, one at a time, it is possible to search for relationships between those references and the gene expression patterns. For the example considered in this work, the surface of the parasite (a membrane) could have been used instead as the reference structure from which to calculate the distances, therefore providing insights about the interplay between the nuclei/gene expression distribution and the boundary of the individual parasites.