Abstract
Semi-aquatic frogs are faced with an unusual locomotory challenge. They have to swim and jump using the same apparatus, i.e. the hind limbs. Optimization of two tasks that require mutually incompatible morphologies or physiologies cannot occur simultaneously. In such cases, natural selection will result in some compromise, i.e. an intermediate phenotype that can perform both tasks reasonably well, but its performance will never match that of a specialized phenotype. We found no direct evidence for a trade-off between jumping and swimming performance nor for a coupled optimization. This could be due to the importance of overall quality, as suggested by the fact that some frogs possess greater overall muscularity than others, irrespective of their body size. Another explanation could be that some morphological characteristics have a positive effect on both locomotor modes and others show a trade-off effect. The net effect of these characteristics could result in an overall absence of correlation between the two locomotor performances. Size has a great influence on the morphological data and on jumping performance, but not if performance is expressed as velocity. The body shape of an anuran is conservative and scales mostly isometrically.
Keywords: ecomorphology, inter-individual variation, locomotor performance, scaling, trade-off
Introduction
Relationships between morphology on the one hand and behaviour and ecology on the other have been widely documented in eco-morphological studies. Such relationships provide evidence that most organisms are to some extent adapted to their environment (Garland & Losos, 1994). One of the central paradigms in eco-morphology is the role of whole-animal performance as a crucial link between the organism's phenotype and its ecology (Arnold, 1983). Performance in this context is defined as an animal's ability to perform an ecologically relevant task when pushed to its morphological, physiological and biochemical limits (Garland & Losos, 1994). Natural selection works as the driving force behind form–function relationships. However, adaptation only occurs when specific conditions are fulfilled. First, phenotypic variation must have a (partly) genetic foundation, and second, this variation must be correlated with variation in fitness. Even when these conditions are fulfilled, evolution is often slowed or even stopped by developmental and historical constraints. To determine the functional basis of differences in performance, inter-individual or inter-species variation in morphology is correlated with variation in ecology. The strength of causal interpretations depends on a sound understanding of the biomechanical mechanisms that underlie the inferred relationship between morphology and ecology (Wainwright, 1994; Aerts et al. 2000).
Locomotion in frogs is an ideal model system for addressing the existence of trade-offs in locomotion, because of the unusual locomotor circumstances. Frogs, and particularly ranids, are not only jumping animals but are also frequent swimmers. Both behaviours are accomplished by the hind limbs but do not necessarily have the same demands. The external force balance is entirely different for the two media (Nauwelaerts & Aerts, 2003). Jumping is considered a short burst event where high power generation is necessary while swimming implies cyclical movements (Navas et al. 1999). In addition, inter-species studies show a shift in morphology according to locomotor mode (Emerson, 1985).
The biomechanical predictions for jumping are fairly straightforward. During jumping, performance is entirely determined by take-off angle and take-off velocity (Marsh, 1994). The take-off velocity is not only determined by how fast, and over what distance, the legs can extend, but is also dependent upon how fast the muscles can contract and how much force they can exert. In addition, it has been suggested that jumping may be more highly and consistently correlated with morphology and physiology than other performance variables (Harris & Steudel, 2002).
Even when the biomechanics are fairly simple, there are still numerous morphological variables that potentially determine an animal's jumping ability, and, as a complicating factor, they are usually dependent on each other because of developmental reasons. The unique combinations of structural and functional properties of each individual will determine locomotor properties, which may emerge in non-obvious ways from their component parts (Vanhooydonck et al. 2001). Locomotor performance capacities are therefore difficult to predict a priori (Bennett, 1989). The unpredictability of the optimal design of an animal's trait for a specific function not only results from the fact that optimization through natural selection does not work on an isolated character, but is also strongly enhanced by the realization that most characteristics serve multiple functions (Vanhooydonck et al. 2001). To simultaneously optimize performance in two tasks that require mutually incompatible morphologies or physiologies is by definition impossible. Under such circumstances, natural selection is expected to result in some intermediate phenotype that provides reasonable performance at both tasks but optimal performance in neither (Shine et al. 2003).
Biomechanical models predict that body size has a direct influence on locomotor ability. This prediction has been tested thoroughly in jumping frogs (Emerson, 1978, 1991; John-Alder & Morin, 1990; Miller et al. 1993; Wilson et al. 2000; Alvarez & Nicieza, 2002), but has also been suggested for swimming animals (fish: Videler, 1993; Wardle, 1975; salamander: Marvin, 2003). Both aquatic and terrestrial burst speed increased with size in a tiger salamander (Bennett, 1989), another amphibian, but increased with size at a different rate in a different species, Pseudotriton ruber(Marvin, 2003). Scaling of locomotor performance seems to be highly species dependent and is therefore a first variable to consider when analysing how morphology explains individual variation in performance. However, not only is size of major importance; shape variability is also known to affect anuran locomotor ability (Zug, 1972; Emerson, 1991).
First, the lengths of the segments could be of importance as they influence not only the extension distance of the hind limbs, but also the moment arms of the muscles. Larger frogs should jump further and if the effect of size is removed, animals with longer hind limb segments and shorter fore limb segments should jump further (Emerson, 1985). Shorter fore limbs will ensure that the centre of mass of the frog will lie backwards, avoiding a pitch forward caused by the acceleration forces generated by the hind limbs. However, the prediction for the fore limbs is only valid when thinking in terms of propulsion. A jumping cycle also contains a landing phase, where fore limbs are used to damp the impact forces and longer fore limbs should be beneficial (Nauwelaerts & Aerts, 2006). A positive correlation between jumping performance and fore limb length was for instance found in a study looking at evolutionary change in morphological variables in Anolis lizards (Losos, 1990). During swimming, where fore limbs provide little propulsion (personal observations) and a landing phase is absent, Emerson's predictions will hold.
Furthermore, the masses of the body segments determine how much force is needed for linear accelerations. Load-carrying experiments, for instance, have shown that adding mass to the feet during running causes an increase in the metabolic rate (Myers & Steudel, 1985). We therefore predict that frogs will benefit from having lighter hind limb segments. During jumping, this will be particularly important for the distal segments (flexible and light foot), as the joints extend in a proximo-distal sequence (Nauwelaerts & Aerts, 2003). During swimming, light segment masses are expected to be important for all segments except for the foot: because it is important to keep the foot perpendicular to the flow (Nauwelaerts et al. 2005), the foot should be rigid and resistant against translation to avoid slip.
However, during push-off, the segments not only translate, but they also rotate about each other. Similar to the relationship between mass and translation, the moments of inertia of the segments are measures of a segment's resistance to rotation. The rotational inertia of a segment is dependent upon the distribution of mass in relation to the axis of rotation. The smaller the mass, and the closer the mass is located to the joint, then the smaller the rotational inertia, and therefore the smaller the force needed to rotate the segment, or the faster the segment will rotate given a specific force input. Moreover, a link between inertia and performance has already been demonstrated in other studies. The current Kenyan dominance in distance running, for instance, has been explained by a smaller circumference of the lower leg (Larsen, 2003). For swimming, the same argument holds true, although it is harder to predict how the added mass (i.e. the mass of water that is accelerated by the movements of the segment) will alter the moment of inertia of the segments. The foot, however, does not rotate during the main part of the propulsion. As the foot needs to resist rotation, a larger moment of inertia would be beneficial.
Finally, the muscle's cross-sectional area, as a measure for maximal force a muscle can exert (Josephson, 1975), and the muscle mass, as a measure for maximal work (force × shortening length, proportional to muscle length) and power (force × contraction velocity) a muscle can generate, are likely to be of importance. Moreover, two studies on frog jumping have already shown a correlation between hind limb muscle mass and maximum distance (Emerson, 1978), and between muscle mass and take-off velocity (Choi & Park, 1996). Based upon the kinematics of movement (Nauwelaerts & Aerts, 2003), we predict that all major extensors and adductors will be important during jumping, while the extensor and abductor muscles will be important in aquatic locomotion. In addition, the flexor muscles will contribute (indirectly) to propulsion during swimming, because during the recovery phase, a mass of water is accelerated forward. This accelerated mass of water is slowed down by the webbed feet. This deceleration of the flow contributes to propulsion (Nauwelaerts et al. 2005).
The present study
This study analyses whether morphology explains anuran individual variation in locomotor performance and to what extent the variables that relate to swimming performance are those that enhance jumping in adult semi-aquatic frogs, Rana esculenta. These semi-aquatic animals occupy an unusual evolutionary position, having to perform in both aquatic and terrestrial environments (Fish & Baudinette, 1999), which inevitably confronts them with a possible conflict in optimization. The possible trade-off will be sought directly by testing whether swimming performance is negatively correlated with jumping performance. We will also investigate possible conflicts in design assuming that jump forces and swimming speed are variables to be optimized. The morphological characteristics that will be studied are the lengths of the long bones, the muscle masses of 17 hind limb muscles, the cross-sectional area of six extensor muscles, and the masses and moments of inertia of all body segments.
Materials and methods
Animals
Forty-six male individuals of Rana esculenta were obtained either from a commercial supplier (Bray-et-Lû, France) or collected at Kalmthout, Belgium. The mean (± SEM) body mass and snout–vent length were 51 ± 13 g (range 27–84 g) and 78 ± 7 mm (range 67–92 mm), respectively. The animals were maintained in five moist terrariums (1.5 × 1 × 1 m) in a climate-controlled room at approximately 15 °C. They were fed crickets ad libitum.
Jumping performance
Jumping ability is regarded as an appropriate performance measurement in amphibian anurans because of its ecological relevance (Tejedo et al. 2000a,b). Predation is an important selection pressure and the origin of saltatory locomotion has been suggested to be an adaptation to escape predators (Gans & Parsons 1966; Wasserzug & Sperry, 1977). We decided on the maximal ground reaction force as a measure for jumping ability as it expressed the ability of the hind limbs to generate enough force to move the animal. Locomotor performance of each frog was tested 10 times over 1 month in the laboratory at 20–22 °C. Each frog was placed upon a small force plate (AMTI, size 20 × 20 cm). This strain gauge platform measured the three orthogonal components of ground reaction forces along the XYZ axes at 1000 Hz. The signal was amplified using an AMTI MC3A amplifier. To reduce noise, the platform was stabilized in a container filled with moist sand. Forces were registered with a resolution of ±0.05 N using an A/D converter (DT2801 Series Board, Data Translation Inc.) and the software package Global Laboratory (Data Translation). For each jump, the resultant force of the XYZ components was calculated and the maximal resultant force was then used in further analysis. Repeatability of maximal resultant force was calculated (Lessells & Boag, 1987). The maximal jumping force of each frog, a measure for escape ability (Heinen & Hammond, 1997), was used for the scaling analysis.
Swimming performance
Each frog was transferred to a swimming tank consisting of two open tanks (0.5 × 0.5 × 0.4 m) connected by a 1-m-long glass tunnel (0.15 × 0.10 × 1 m). The tanks were filled above the level of the tunnel, which compelled the frogs to swim completely submerged when crossing from one tank to the other. Next to the tunnel, eight pairs of photocells were placed at 25-cm intervals. These photocells registered when the frogs swam past them. The elapsed time between passing two subsequent cells was stored in the computer and the velocity over each 25 cm was calculated. The frogs were chased through the tunnel five times to induce maximal performance. The fastest speed over 25 cm was selected as an individual performance measure.
Morphometrics
Length measures of femur, tibiofibula, tarsus, urostyle, humerus, radio-ulna, cranial length and width and snout–vent length of 46 frogs from which maximal performance was measured were taken from X-rays (Siemens Tridoros Optomatic 880 equipped with a Sirecon-2 image intensifier) using electronic callipers (Mitotuyo CD-15DC, UK).
Centres of mass and moments of inertia
Thirty-six animals from which maximal performance was measured, were anaesthetized for 20 min in a 0.5 g L−1 solution of MS-222, and were then killed by pithing. The right hind limb was divided into four segments (foot, mid foot, lower leg and upper leg) by transecting the joint capsules and ligaments. The left leg and both arms were removed from the trunk. This resulted in five body segments, which were all weighed on an FX-3200 electronic balance (precision of 0.01 g).
Each segment was suspended by a string from at least two different points. For each configuration, a photographic slide was taken using a Nikon camera with a 55-mm macro lens. The slide was projected onto a piece of paper, to enable us to draw the segment by tracing its outline. The position of the string was indicated on the same drawing. By overlaying the different slides and ensuring that each drawing was correctly aligned with the previous one, we obtained different intersecting lines by extrapolating the drawings of the strings. The position of the centre of mass lies at the intersection of these lines. The relative position of the centre of mass was calculated afterwards by measuring the lengths on the drawings. As we also have measurements of the segments themselves, we then obtained the absolute positions of the centre of mass, which were expressed in relation to the proximal joint.
A measure for the moment of inertia was obtained by combining the data on the position of the centres of mass with the masses of the segments. Each segment was divided into two parts with equal masses, using the position of the centre of mass along the length axis as the dividing point. The volume of each part was calculated, based on the assumption that the parts were of a homogeneous density. Each part was further modelled as a cylinder with the corresponding length of the segment part and a radius calculated from the general equation of the volume of a cylinder (π × radius2 × length). The moment of inertia of a cylinder is given by 0.25 × mass × radius2 + 0.33 × mass × length2. This was calculated separately for each part, and the total moment of inertia about a transverse axis through the centre of mass was the sum of the moments of inertia of the two parts. Finally, the total moment of inertia in the proximal joint was calculated as the sum of the moment of inertia in the centre of mass and the mass multiplied by the squared distance from the centre of mass to the proximal joint.
Rotational inertia can also be expressed as a radius of gyration, which takes mass into consideration. This radius was calculated as the square root of the moment of inertia divided by the segment mass. The relative radius of gyration was then calculated by dividing this result by the total segment length.
Myology
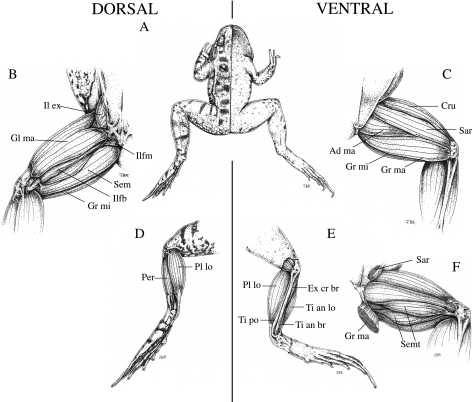
The left hind limb was dissected and 17 muscles (sartorius, gracilis minor, gracilis major, semitendinosus, adductor magnus, glutaeus magnus, cruralis, iliofibularis, semimembranosus, iliacus externus, iliofemoralis, plantaris longus, tibialis posticus, tibialis anticus brevis, tibialis anticus longus, peroneus, extensor cruris brevis – see Fig. 1) were removed intact and weighed. These muscle masses can be considered measures for the potential muscle work and power output.
Fig. 1.
Drawings of the muscular anatomy of Rana esculenta. (A) Ventral and dorsal external anatomy of the frog. (B) Superficial muscles on the dorsal side of the upper leg. Il ex = m. iliacus externus, Gl ma = m. glutaeus magnus, Ilfm = m. iliofemoralis, Sem = m. semimembranosus, Ilfb = m. iliofibularis, Gr mi = m. gracilis minor. (C) Superficial muscles on the ventral side of the upper leg. Cru = m. cruralis, Sar = m. sartorius, Ad ma = adductor magnus, Gr mi = m. gracilis minor, Gr ma = m. gracilis major. (D) Deep muscles on the ventral side of the upper leg with m. sartorius and m. gracilis major removed. Semit = m. semitendinosus. (E) Superficial muscles on the dorsal side of the lower leg. Pl lo = m. plantaris longus, Per = m. peroneus. (F) Superficial muscles on the ventral side of the lower leg. Ti po = m. tibialis posticus, Ex cr br = m. extensor cruris brevis, Ti ant lo = m. tibialis anticus longus, Ti an br = m. tibialis anticus brevis.
Fibre lengths
The six major extensor muscles were, after weighing, put into a 30% hydrous nitric acid solution in order to dissolve the collagenous tissue surrounding the muscle fibres. After 24 h, the fibres were transferred to a 50% hydrous solution of glycerine. Ten fibres from each muscle were chosen at random and drawn using an M32 microscope and a drawing mirror. The resultant drawings were digitized using a Baush & Lomb Hipad Digitizer, linked to a PC. The repeatability was calculated for the measurements within one muscle, within the same muscle for each of the individual frogs and over all the different muscles. The cross-sectional area was defined as the ratio of the muscle volume divided by the average fibre length, where the volume is determined from the muscle mass divided by muscle density 1.05 kg m−3 (Taylor, 1994).
Statistical analysis
Scaling
Scaling exponents were obtained by performing a reduced major axis regression of the variables against size (Riggs et al. 1978; Webb et al. 1981).
Performance
The performance measure of jumping (the maximal ground reaction force) and of swimming (mean velocity over 25 cm) were regressed against the size vector PC1 of all morphometric variables in order to test for possible size effects. The correlation of the resulting residuals was calculated to test for a positive or negative relationship between swimming and jumping performance.
Size-free morphometrics and performance
All morphometric data were log10-transformed and analysed using a principal component analysis (PCA) in STATISTICA v.5.1 for Windows. The first axis of this PCA (PC1) yields the size vector and represents the major source of variation in the data. Scaling factors of the variables with size can be calculated by dividing the factor loadings of the variables on this PC1 by the average factor loading. This gives multivariate scaling factors, but unfortunately does not provide any information regarding the strength of these relationships with size.
As most anatomical features co-vary strongly with body size, size becomes a complicating factor in the analyses. Removing the confounding effects of body size by calculating residuals from regressions of the morphological variable on some body size variable has become routine (e.g. Garland, 1984). To obtain the residuals, all morphometric variables were regressed against the size vector, PC1 of a PCA of all variables without the variable in question, using a model I least squares (LS) method. The residuals of all LS regressions were used to analyse possible correlations with locomotor performance. Because a correlation matrix showed relationships between the residuals of the different variables, two PCAs were performed with all the residuals, the first also included the residuals of the maximal force of jumping, and the second included the log-transformed velocity of swimming.
Moments of inertia and performance
The position of the centre of mass (both absolute and relative), the moment of inertia and radius of gyration (also both absolute and relative) were regressed against segment length using an LS regression in STATISTICA (v.5.1 for Windows).
The residuals of the moments of inertia of each segment (trunk, upper leg, lower leg and foot) against PC1 of the morphometric data were entered into a PCA and the resulting factor scores were used in a multiple regression analysis with the residuals of the maximal force of jumping and the swimming velocities.
Myology and performance
Muscle mass is a measure for potential muscle power output. The muscle masses of the 17 muscles were log-transformed and regressed against the total (log) mass of the animals. The residuals of these regressions were used in multiple regression with maximal force of jumping and swimming velocity. The residuals were also entered in a PCA to check for independence.
To facilitate interpretation of the results, a PCA was performed on all muscle masses. The resulting factor scores were again used in multiple regression with performance.
Cross-sectional area and performance
The repeatabilities of the fibre length measurements were calculated based upon the output of an anova design (Lessells & Boag, 1987).
All cross-sectional areas were log-transformed and regressed against the log-transformed total mass of the frog. The intercepts of these regressions allow ranking of muscles according to size of the cross-sectional area, and hence their potential force output. The residuals of these regressions were used in two multiple regressions, one against the residuals of maximal force and a second against the swimming velocity.
To facilitate interpretation of the results, a PCA was performed on all physiological cross-sections. The resulting factor scores were again used in multiple regression with performance.
Results
Performance
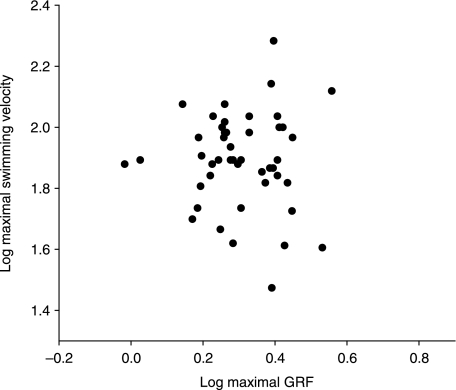
Repeatabilities of maximal performance are high. Based on five swimming sequences and ten jumps, repeatability of performance was 0.77 for swimming and 0.84 for jumping. A strong size effect was found on jumping performance (P << 0.05). Swimming velocity, however, was independent of size (P = 0.42). No significant correlation between jumping and swimming performance (P = 0.18, two-tailed) was found (Fig. 2).
Fig. 2.
Swimming performance (maximal swimming velocity over 25 cm) plotted against jumping perfomance (maximal peak ground reaction force).
Scaling
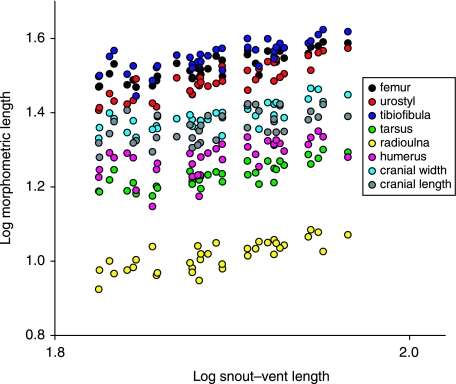
Most linear morphometric variables scale slightly positively with size, but very close to isometry, except for cranial length, the loadings of which are small and the scaling factor of which is smaller than one (Table 1). The raw measurements were log-transformed and plotted against log-transformed snout–vent length to illustrate the relatively small variation irrespective of size (Fig. 3).
Table 1.
PCA loadings on PC1 for the different bone lengths, measured on X-ray images for 56 animals
| Variable | Loading | Scaling factor | Allometry |
|---|---|---|---|
| Tarsus | 0.984 | 1.15 | 1 |
| Tibiofibula | 0.982 | 1.14 | 1 |
| Femur | 0.988 | 1.15 | 1 |
| Urostyle | 0.973 | 1.13 | 1 |
| Radioulna | 0.870 | 1.01 | 1 |
| Cranial width | 0.954 | 1.11 | 1 |
| Cranial length | 0.334 | 0.39 | < 1 |
| Humerus | 0.965 | 1.12 | 1 |
| Snout–vent | 0.978 | 1.14 | 1 |
From these loadings, a multivariate scaling factor could be calculated for each length. ‘1’ indicates a mathematical positive scaling exponent that is not significantly different from one, and ‘< 1’ indicates a positive scaling exponent significantly smaller than one.
Fig. 3.
Log-transformed morphometric variables plotted against log-transformed snout–vent length.
Total muscle mass (the sum of all individual muscle masses) and the individual muscle masses scale mathematically slightly positively with size but not significantly different from isometry, except for m. gracilis major, the mass of which increases more than twice as fast as expected from isometry. Also m. tibialis anticus longus and m. extensor cruris brevis scale with size with a scaling factor of greater than one, although not as dramatically (Table 2).
Table 2.
The scaling exponents of the individual muscle masses with body mass, determined from reduced major axis regressions with PC1 of the length measurements and corrected for its dimension difference (n = 54)
| Muscle | Scaling factor | Allometry |
|---|---|---|
| Sartorius | 1.51 ± 0.25 | 1 |
| Gracilis minor | 1.49 ± 0.21 | 1 |
| Gracilis major | 2.36 ± 0.41 | 1 |
| Semitendinosus | 1.33 ± 0.20 | 1 |
| Adductor magnus | 1.31 ± 0.18 | 1 |
| Glutaeus magnus | 1.34 ± 0.19 | 1 |
| Cruralis | 1.36 ± 0.20 | 1 |
| Iliofibularis | 1.29 ± 0.17 | 1 |
| Semimembranosus | 1.37 ± 0.20 | 1 |
| Iliacus externus | 1.22 ± 0.19 | 1 |
| Iliofemoralis | 1.41 ± 0.23 | 1 |
| Plantaris longus | 1.48 ± 0.23 | 1 |
| Tibialis posticus | 1.41 ± 0.21 | 1 |
| Tibialis anticus longus | 1.73 ± 0.28 | 1 |
| Tibialis anticus brevis | 1.50 ± 0.25 | 1 |
| Peroneus | 1.46 ± 0.23 | 1 |
| Extensor cruris brevis | 1.61 ± 0.23 | 1 |
| Total | 1.36 ± 0.20 | 1 |
‘1’ indicates a mathematical positive scaling exponent that is not significantly different from one, and ‘>1’ a positive scaling exponent significantly greater than one.
Morphometrics and performance
The residuals of the regression against size show a degree of dependence (Table 3). A PCA with the residuals of jumping force, the second axis of which accounting for 28% of the total variance, resulted in factor loadings of +0.76 for jumping force, +0.77 for urostyle length and −0.73 for snout–vent length. A second PCA included swimming velocity and resulted in three axes of which the third axis, accounting for 18% of the total variance, showed factor loadings of 0.97 for swimming velocity and 0.30 for femur length.
Table 3.
Correlation matrix of the residuals of all length measurements against the size vector of a PCA containing all variables except the one under study
| Tarsus | Tibio-fibula | Femur | Urostyle | Humerus | Radio-ulna | Cranial width | Cranial l ength | Snout– vent | |
|---|---|---|---|---|---|---|---|---|---|
| Tarsus | 1.00 | 0.76 | 0.61 | −0.01 | −0.11 | −0.31 | −0.25 | 0.07 | −0.32 |
| Tibiofiula | 1 | 0.80 | −0.01 | −0.15 | −0.34 | −0.08 | −0.06 | −0.35 | |
| Femur | 1 | −0.07 | −0.07 | −0.39 | −0.11 | 0.02 | −0.35 | ||
| Urostyle | 1 | −0.35 | 0.19 | −0.27 | 0.03 | −0.41 | |||
| Humerus | 1 | −0.30 | 0.15 | −0.19 | 0.19 | ||||
| Radioulna | 1 | −0.26 | −0.00 | −0.43 | |||||
| Cranial width | 1 | −0.50 | 0.30 | ||||||
| Cranial length | 1 | −0.25 | |||||||
| Snout–vent | 1 |
Correlation coefficients in bold type have a significant P-value (< 0.05).
Segment masses and performance
Because mass is a measure for the inertial resistance against translation, we tested whether lighter segment masses were important in determining locomotor performance, especially on land. None of the segment masses came out significantly in the size-free multiple regression model for maximal ground reaction force and for maximal swimming velocity.
Moments of inertia and performance
If the mass distribution and shape of the segment remain constant, it is expected that the mass of the segment and the position of the centre of mass should increase with increasing segment length, but that the relative position, expressed as the ratio of the distance from the proximal joint to the centre of mass and the total segment length, is a constant. Similarly, the moment of inertia of the segment and the radius of gyration will increase with increasing segment length, but the relative radius of gyration will remain constant. Regression of the absolute and relative position of the centre of mass, the moment of inertia, and the absolute and relative radius of gyration of all segments (trunk, upper leg, lower leg and foot) against segment length revealed that the trunk and the foot follow these theoretical considerations. The mass of the upper leg, however, does not increase with increasing segment length and the relative radius of gyration of the lower leg does increase with increasing segment length.
A multiple regression of the residuals of the moments of inertia of all segments against PC1 of the morphometric data with the residuals of the maximal jumping force resulted in a larger moment of inertia and therefore a negative effect on performance, except for the foot (Table 4). Only the moment of inertia, however, had a significant relationship between the residuals of the moment of inertia of the foot and the residuals of the jumping performance (P = 0.02). None of the variables was kept in multiple regression with swimming velocity (Table 4).
Table 4.
Overview of the variables determining locomotor performance for each of the separate data sets and for both locomotor modes using two different types of multiple regression
| Jumping | Swimming | |||
|---|---|---|---|---|
| Expected | Observed | Expected | Observed | |
| Size | Yes | Yes | No | No |
| Morphometrics | + hind limb bones | + urostyle | + hind limb bones | + femur |
| +/– fore limb bones (propulsion/landing) | – snout–vent | – fore limb bones | ||
| Moment of Inertia | – hind limb segments, especially distal | + foot | – hind limb segments except foot | |
| + foot | ||||
| Muscle mass | + hind limb extensors | + iliacus externus | + hind limb extensors | + iliofemoralis |
| + adductors | – tibialis posticus | + hind limb flexors | ||
| + gracilis minor | + abductors | |||
| Cross-sectional area | + hind limb extensors | + gracilis major | + hind limb extensors | + glutaeus magnus |
| + adductors | + hind limb flexors | – cruralis | ||
| + abductors | ||||
A ‘+’ indicates a positive effect of this variable on performance, ‘–’ a negative effect.
Myology and performance
If we rank the muscle masses in ascending contribution to total muscle mass, we obtain the following sequence: m. extensor cruris brevis (1%), m. tibialias anticus brevis (1%), m. iliacus externus (2%), m. tibialis posticus (2%), m. gracilis minor (2%), m. tibialis anticus longus (2%), m. iliofibularis (2%), m. sartorius (3%), m. iliofemoralis (3%), m. semitendinosus (4%), m. peroneus (4%), m. glutaeus magnus (6%), m. gracilis major (11%), m. adductor magnus (12%), m. semimembranosus (12%), m. plantaris longus (15%) and m. cruralis (21%). All the muscle masses correlate significantly with each other, as a PCA yielded factor loadings of more than 0.70 for all log-transformed variables. The total explained variance on this PC1 was 82%. The residuals of the muscle masses regressed against PC1 of the morphometric data are all significantly correlated with each other, suggesting some frogs possess greater overall muscularity than others, irrespective of body size. Nevertheless, this overall muscularity does not affect performance: there is no correlation between the PC1 result from a PCA with all muscle masses and maximal jumping force (P = 0.75) nor with maximal swimming velocity (P = 0.58). However, a multiple regression (Table 3) with the residuals of all muscle masses and maximal jumping force resulted in a model in which two muscles contribute significantly: m. iliacus externus (B = 0.55, P = 0.020) and m. tibialis posticus (B = −0.63, P = 0.018). The contribution of a third muscle mass is close to significant: m. gracilis minor (B = 0.45, P = 0.052). Swimming performance, on the other hand, was affected by the muscle mass of m. iliofemoralis (B = 2.16, P = 0.020).
Cross-sectional area and performance
The cross-sectional area of a muscle is a measure of its potential force output. This area is determined by the muscle mass and the average fibre length. This fibre length can vary considerably within a muscle, between muscles and between animals. This is not due to measurement error given that the repeatability of measuring the same fibre length is high (0.82). This variability within a muscle means it is extremely difficult to demonstrate inter-individual differences in fibre length. A repeated-measures anova with all measurements tests if the variation associated with an explained source (muscle, frog and muscle × frog) is large, relative to the unexplained variation (e.g. measurement error). The explained variation in our data is of similar magnitude to the unexplained variation, which results in low repeatabilities: 0.0019 when the individual frog is taken as a source, 0.0014 with muscle and 0.0001 with the interaction of frog and muscle. In further analysis, the average fibre length was used to calculate the cross-sectional areas.
If we rank the cross-sectional areas from small to large, we obtain the following sequence: m. glutaeus magnus, m. peroneus, m. gracilis major, m. semimembranosus, m. plantaris longus and m. cruralis. All cross-sectional areas and their residuals against PC1 of the morphometric variables were strongly correlated with each other. Again, this suggests that there are muscular frogs and less muscular frogs, irrespective of body size.
A multiple regression of all residuals with jumping force (Table 3) resulted in a significant model with m. gracilis major as a significant factor (P << 0.01). A similar analysis with swimming velocity yielded m. glutaeus magnus (P = 0.017) and m. cruralis (P = 0.037) as a significant factor.
A PCA on all cross-sectional areas gave four different axes with eigenvalues greater than one: on axis one, the physiological cross-section of m. peroneus and m. plantaris longus, both muscles of the lower leg, contributed significantly, while axis two consisted of m. gracilis major, axis three of m. semimembranosus and axis four of m. glutaeus magnus.
Discussion
Trade-off swimming vs. jumping
Our data show that swimming and jumping performance are uncoupled, regardless of whether jumping performance is measured as maximal ground reaction force or velocity. Frogs that are good swimmers are not necessarily good (or bad) jumpers. Optimizing morphology or physiology for jumping will not compromise or enhance swimming ability within the variation range of this species. It is possible that this limited variation is a result of natural selection. Theoretically, extending this range to a more terrestrial or more aquatic animal may result in selection on only one of the locomotor abilities, ultimately resulting in a better jumper or swimmer. Within the range of this species, individual quality (Van Damme et al. 2002) or some other unmeasured variable may weaken the negative correlation between jumping and swimming. For instance, a well-fed animal may perform better in an aquatic environment than a poorly fed individual, even though its morphology would theoretically be better equipped for jumping. We aimed for a standardized population by acclimatizing the animals for a few weeks before doing the experiments and put them on the same diet and light–dark regime, but because the animals were obtained from commercial suppliers, it is difficult to rule out all factors.
Size
Size is an important factor in this jumping data set. All morphological characteristics are influenced by size, as is jumping performance. The fact that in the standard multiple regression the femur is retained as the one significant factor that defines jumping performance is essentially an additional effect of size, as it is the femur length that contributes most to the size vector in the PCA. By contrast, the size effect is absent during swimming. Body size as the most important variable affecting the evolution of jumping was also found in a study of Anolis lizards (Losos, 1990).
Scaling factors, the exponents in the allometric power law are a tool to quantify the effect of size. Most linear morphometric variables have a scaling factor of one in relation to size, which is expressed as a linear combination of other linear variables. The morphometric variables therefore follow the assumptions of isometry and a frog's body changes with size according to geometric similarity laws. This is unusual in the animal world, but it has been stated before that anuran shape is very conservative (Emerson, 1978; Marsh, 1994). Hill (1950) stated that similar animals of different size should attain the same velocity. This is indeed the case during swimming. Jumping performance was expressed by the maximal ground reaction force and scaled isometrically with body mass. When we use the ground reaction force profiles to calculate maximal velocity during jumping, no correlation was found with body mass (r = –0.18, n = 46). Hill's predictions therefore seem applicable to frog locomotion. However, Emerson (1978) interpreted Hill's suggestion to mean that animals that are geometrically similar would jump the same absolute distance regardless of size. This is certainly not true (Emerson, 1978; Wilson et al. 2000; our personal observations). At first glance, these findings appear to be contradictory. Distance is a function of velocity and increases with size, while velocity does not. However, we used maximal velocity throughout push-off as a measure for performance. It is possible that there is a size effect on the velocity profile. It is not maximal velocity, but take-off velocity and take-off angle that are of importance. If the co-ordination of larger animals improves and they are more capable of timing the maximal velocity at take-off, then this would account for the differences in absolute distance. However, the small difference between maximal and take-off velocity, which we measured for a small subsample (n = 8) could not account for this difference as it amounted to only 1% of the take-off velocity. Jumping distance can be divided into three components: the distance travelled during take-off, flight and landing (Marsh, 1994). Jumping distance during take-off is essentially the length of the hind limbs projected on the horizontal plane. The absolute value of this distance will be larger with increasing size. The distance travelled during flight is entirely a function of take-off velocity and angle. There is no obvious reason why small animals should succeed in attaining the optimal take-off angle; therefore, it is doubtful that the size effect on jumping distance would originate during this phase. The distance that the centre of mass will move forward during landing is dependent upon the arm length and landing angle (Nauwelaerts & Aerts, 2006). The absolute value of this distance will be larger for larger animals. Hill's predictions therefore seem applicable to adult jumping frogs.
Lengths
For a frog of a given size, it is beneficial to have a small snout–vent length and a larger urostyle for jumping, and a larger femur for swimming. A smaller snout–vent length probably refers to a smaller trunk mass. This would be beneficial for jumping because of the decreased inertia. The underlying biomechanical reasons for a longer urostyle during jumping are more difficult to explain. During swimming, the urostyle is assumed to slide over the pelvic girdle, thereby increasing the distance over which the hind limbs can extend (Videler & Jorna, 1985). By contrast, during jumping the pelvis undergoes vertical rotation (O’Reilly et al. 2000). This makes a longer urostyle for jumping counterintuitive, but can possibly be explained by larger pelvis muscles that are important at the start of the jump to raise the trunk and to align the body with the ground reaction forces (Emerson & DeJongh, 1980). A larger femur during swimming could cause an increase in drag when the legs are fully flexed, but the longer extension distance apparently compensates for this drag effect. A larger moment of inertia for the foot seems at first sight counterintuitive as well, but can possibly be explained by a better grip on the surface. A foot with a higher moment of inertia will be more difficult to rotate and could possibly allow it to stay on the ground longer, thereby making full use of the extension distance.
Masses and moments of inertia
Our predictions were that performance would be enhanced (1) by having relatively lighter segments, especially distal segments in jumping, and (2) by having lower moments of inertia with the exception of the foot during swimming. The foot would have to withstand rotation at the beginning of the extension phase in order to stay perpendicular to the flow (Nauwelaerts et al. 2005). In a multiple regression none of the masses was retained for both locomotor modes. As for the moments of inertia, only the moment of inertia of the foot was found to be positively correlated with jumping performance. Avoiding slip by having a larger moment of inertia for the foot might be an explanation for this correlation. It is, however, surprising that masses and moments of inertia do not show up in the analysis, unless the correlations are concealed due to a lack of variation in these variables. If selection works strongly on having the ‘right’ masses, then perhaps this results in undetectable individual variation.
Muscles
We expected that the extensor and adductor muscles would be important for enhanced jumping ability, because it is during jumping that the legs are brought inwards and under the body; by contrast, during swimming extensor and abductor muscles would be more important, because during swimming the knees are kept apart. During jumping, the cross-sectional area of m. gracilis major and the muscle mass of m. gracilis minor seem to be of great importance. Both muscles have similar origin and insertions, and thus functions, but differ in size. M. gracilis major serves multiple functions (Kargo & Rome, 2002): it is a hip extensor with the longest extensor moment arm among all hip extensors, its contraction causes the femur to rotate internally and it is bifunctional in its abduction/adduction function. The latter means that it is an abductor when the legs are in an abducted position, but it is an adductor when in adducted position. This finding seems to confirm our theoretical predictions.
A smaller cross-sectional area of m. cruralis has a positive effect on swimming performance. M. cruralis is a hip flexor, and in the theory of symmorphosis (see below) would only be costly to have. However, m. iliacus externus and m. iliofemoralis are both hip flexors and their masses determine, respectively, jumping and swimming ability. Because swimming is a cyclical movement and performance was assessed over 25-cm intervals, the recovery phase could have an impact on swimming speed. Flexors could decrease the recovery duration, creating the potential to initiate a new power stroke and therefore ultimately increase swimming speed. The same argument goes for a series of jumps, but this was not how jumping performance was measured in this study. The cross-sectional area of another hip flexor, m. glutaeus magnus, also has a positive effect on swimming performance, but this is possibly due to its second function as a knee extensor. An increase in the mass of m. tibialis posticus, an ankle stabilizer (Peters, 1994), is found to have a negative effect on jumping performance.
Performance measures
In this study, we approached performance as a measure of the ability of an animal to escape from a predator, assuming that a better performance will result in higher escape probability and hence survival. For swimming, velocity was taken as a performance measure, with the idea that faster is better. To find the optimum design for a moving animal, we must realize that there is no preset level of performance that is ‘enough’ (Alexander, 2000). We might intuitively think that as fast as possible is always best, but having hyper-effective legs without an ecological need can produce unnecessary costs. This is the principle of symmorphosis, which predicts that the size of parts in a system match exactly the functional demands (Taylor & Weibel, 1981; Weibel, 2000), satisfying but not exceeding the requirements. Developmental and historical constraints can limit this optimization of structural design (Bennett, 1989), thereby weakening the match between structure and demand. Moreover, if large and small animals escape from the same predator, you would expect that larger animals should have to swim at the same velocity as smaller ones. However, speed corrected for body size has been stated as a better predictor of the vulnerability to predation than absolute speed (Van Damme & Van Dooren, 1999), as a small prey animal moving at the same speed as a larger one is more difficult to detect and catch. In our data, velocity during both locomotor modes was not affected by size.
A frog that could produce the highest ground reaction forces during jumping was regarded as the best jumper in the group. Using ground reaction forces as a individual jumping performance measure has been used before on frogs (Wilson et al. 2000) and in lizard studies (Toro et al. 2003, 2004; Lailvaux et al. 2004; Irschick et al. 2005). The underlying assumption is that jumping is the best solution when facing a predator. We did not test for behavioural compensations for a lack of acceleration capacity. In a comparative study of eight species of skinks, for instance, species were found to have significant behavioural preferences for particular escape modes in the field, which reflected the performance capabilities of an animal in the laboratory (Melville & Swain, 2003). We did not quantify any behavioural responses and animals that were unwilling to jump or swim in our set-up were not used in the study. We were mainly interested in the jumping and swimming capacities of each individual and took a fairly mechanistic approach by taking the highest resultant ground reaction force during jumping and maximal velocity over 25 cm during swimming as performance measures. A higher ground reaction force results in a higher take-off speed, which in turn will positively affect jumping distance. This distance, however, is subject not only to take-off speed. Take-off angle has a strong influence on jumping distance as well. However, escaping is realizing a distance as large as possible between the predator and the prey, as fast as possible. It is possible that achieving a high horizontal velocity is more relevant for escaping in frogs than realizing the longest possible jump. In addition, during the phase spent in the air, the trajectory of the frog is highly predictable, making it easy for the predator to intercept the frog. Performing a series of small jumps would increase the possibility of changing direction and velocity, and therefore increase its manoeuvrability. It is hard to predict whether performing a series of small jumps, as opposed to one long jump, will result in a better chance of escape. A long jump inevitably coincides with a high take-off speed, and thus high acceleration during push-off. For an animal such as R. esculenta, which sits alongside waterbodies and waits until a predator is relatively close before jumping into the water, swimming to the bottom and hiding in the mud, a high acceleration (force) during jumping and a high swimming velocity do appear to be relevant performance measures.
Acknowledgments
We would like to thank Sofie Vande Velde for her help with the dissections and Joe Carragher and Louis Flynn for proofreading the manuscript. This work was supported by an IWT-grant to S.N. and a GOA-BOF grant to P.A.
References
- Aerts P, Van Damme R, Vanhooydonck B, Zaaf A, Herrel A. Lizard locomotion: how morphology meets ecology. Neth J Zool. 2000;50:261–277. [Google Scholar]
- Alexander RMcN. Hovering and jumping: contrasting problems in scaling. In: Brown JH, West GB, editors. Scaling in Biology. Oxford: Oxford University Press; 2000. pp. 37–50. [Google Scholar]
- Alvarez D, Nicieza AG. Effects of induced variation in anuran larval development on postmetamorphic energy reserves and locomotion. Oecologia. 2002;131:186–195. doi: 10.1007/s00442-002-0876-x. [DOI] [PubMed] [Google Scholar]
- Arnold SJ. Morphology, performance and fitness. Am Zool. 1983;23:347–361. [Google Scholar]
- Bennett AF. Integrated studies of locomotor performance. In: Wake DB, Roth G, editors. Complex Organismal Functions: Integration, Evolution in Vertebrates. Chichester: John Wiley & Sons Ltd; 1989. pp. 191–202. [Google Scholar]
- Choi IH, Park K. Variations in take-off velocity of anuran amphibians: relation to morphology, muscle contractile function and enzyme activity. Comp Biochem Physiol A. 1996;113:393–400. [Google Scholar]
- Emerson SB. Allometry and jumping in frogs: helping the twain to meet. Evolution. 1978;32:551–564. doi: 10.1111/j.1558-5646.1978.tb04598.x. [DOI] [PubMed] [Google Scholar]
- Emerson SB, DeJongh HJ. Muscle-activity at the iliosacral articulation of frogs. J Morph. 1980;166:129–144. doi: 10.1002/jmor.1051660202. [DOI] [PubMed] [Google Scholar]
- Emerson SB. Jumping and leaping. In: Hildebrand M, Bramble DM, Liem KF, Wake DB, editors. Functional Vertebrate Morphology. Cambridge, MA: Harvard University Press; 1985. pp. 58–72. [Google Scholar]
- Emerson SB. The ecomorphology of Bornean tree frogs (family Rhacophoridae) Zool J Linn Soc. 1991;101:337–357. [Google Scholar]
- Fish FE, Baudinette RV. Energetics of locomotion by the Australian water rat (Hydromys chrysogaster): a comparison of swimming and running in a semi-aquatic mammal. J Exp Biol. 1999;202:353–363. doi: 10.1242/jeb.202.4.353. [DOI] [PubMed] [Google Scholar]
- Gans C, Parsons TS. On the origin of jumping mechanism in frogs. Evolution. 1966;20:92–99. doi: 10.1111/j.1558-5646.1966.tb03345.x. [DOI] [PubMed] [Google Scholar]
- Garland T. Physiological correlates of locomotory performance in a lizard – an allometric approach. Am J Physiol. 1984;247:R806–R815. doi: 10.1152/ajpregu.1984.247.5.R806. [DOI] [PubMed] [Google Scholar]
- Garland T, Losos JB. Ecological morphology of locomotor performance in squamate reptiles. In: Wainwright PC, Reilly SM, editors. Ecological Morphology – Integrative Organismal Biology. Chicago & London: University of Chicago Press; 1994. pp. 240–302. [Google Scholar]
- Harris MA, Steudel K. The relationship between maximum jumping performance and hind limb morphology/physiology in domestic cats (Felis silvestris catus) J Exp Biol. 2002;205:3877–3889. doi: 10.1242/jeb.205.24.3877. [DOI] [PubMed] [Google Scholar]
- Heinen JT, Hammond G. Antipredator behaviors of newly metamorphosed green frogs (Rana clamitans) and leopard frogs (R-pipiens) in encounters with eastern garter snakes (Thamnophis s-sirtalis) Am Midl Nat. 1997;137:136–144. [Google Scholar]
- Hill AV. The dimensions of animals and their muscular dynamics. Sci Prog. 1950;38:209–230. [Google Scholar]
- Irschick DJ, Vanhooydonck B, Herrel A, Meyers JJ. Intraspecific correlations among morphology, performance and habitat use within a green anole lizard (Anolis carolinensis) population. Biol J Linn Soc. 2005;85:211–221. [Google Scholar]
- John-Alder HP, Morin PJ. Effects of larval density on jumping ability and stamina in newly metamorphosed Bufo woodhousei. Copeia. 1990;1990:856–860. [Google Scholar]
- Josephson RK. Extensive and intensive factors determining performance of striated muscle. J Zool. 1975;194:135–154. doi: 10.1002/jez.1401940109. [DOI] [PubMed] [Google Scholar]
- Kargo WJ, Rome LC. Functional morphology of proximal hindlimb muscles in the frog Rana pipiens. J Exp Biol. 2002;205:1987–2004. doi: 10.1242/jeb.205.14.1987. [DOI] [PubMed] [Google Scholar]
- Lailvaux SP, Herrel A, VanHooydonck B, Meyers JJ, Irschick DJ. Performance capacity, fighting tactics and the evolution of life-stage male morphs in the green anole lizard (Anolis carolinensis) Proc R Soc Lond B. 2004;271:2501–2508. doi: 10.1098/rspb.2004.2891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen HB. Kenyan dominance in distance running. Comp Biochem Physiol. 2003;136:161–170. doi: 10.1016/s1095-6433(03)00227-7. [DOI] [PubMed] [Google Scholar]
- Lessells CM, Boag PT. Unrepeatable repeatabilities: a common mistake. The Auk. 1987;104:116–121. [Google Scholar]
- Losos JB. The evolution of form and function: morphology and locomotor performance in West Indian Anolis lizards. Evolution. 1990;44:1189–1203. doi: 10.1111/j.1558-5646.1990.tb05225.x. [DOI] [PubMed] [Google Scholar]
- Marsh RL. Jumping ability of anuran amphibians. In: Jones JH, editor. Advances in Veterinary Science and Comparative Medicine. 38B. New York: Academic Press; 1994. pp. 51–111. [PubMed] [Google Scholar]
- Marvin GA. Aquatic and terrestrial locomotor performance in a semiaquatic Plethodontic Salamander (Pseudotriton ruber): influence of acute temperature. Thermal acclimation and body size. Copeia. 2003;2003:704–713. [Google Scholar]
- Melville J, Swain R. Evolutionary correlations between escape behaviour and performance ability in eight species of snow skinks (Niveoscincus: Lygosominae) from Tasmania. J Zool Lond. 2003;261:79–89. [Google Scholar]
- Miller K, Monteforte PB, Landis LF. Scaling of locomotor performance and enzyme activity in the leopard frog, Rana pipiens. Herpetologica. 1993;49:383–392. [Google Scholar]
- Myers MJ, Steudel K. Effect of limb mass and its distribution on the energetic cost of running. J Exp Biol. 1985;116:363–373. doi: 10.1242/jeb.116.1.363. [DOI] [PubMed] [Google Scholar]
- Nauwelaerts S, Aerts P. Propulsive impulse as a covarying performance measure in the comparison of the kinematics of swimming and jumping in frogs. J Exp Biol. 2003;206:4341–4351. doi: 10.1242/jeb.00690. [DOI] [PubMed] [Google Scholar]
- Nauwelaerts S, Aerts P. Take-off and landing forces in jumping frogs. J Exp Biol. 2006;209:66–77. doi: 10.1242/jeb.01969. [DOI] [PubMed] [Google Scholar]
- Nauwelaerts S, Stamhuis EJ, Aerts P. Propulsive force calculations in swimming frogs I. A momentum-impulse approach. J Exp Biol. 2005;208:1435–1443. doi: 10.1242/jeb.01509. [DOI] [PubMed] [Google Scholar]
- Navas CA, James RS, Wakeling JM, Kemp KM, Johnston IA. An integrative study of the temperature dependence of whole animal and muscle performance during jumping and swimming in the frog Rana temporaria. J Comp Physiol B. 1999;169:588–596. doi: 10.1007/s003600050259. [DOI] [PubMed] [Google Scholar]
- O’Reilly JC, Summers AP, Ritter DA. The evolution of the functional role of trunk muscles during locomotion in adult amphibians. Am Zool. 2000;40:123–135. [Google Scholar]
- Peters SE. Properties of twitch motor units of the ankle extensor muscles in the bullfrog Rana catesbeiana. J Morphol. 1994;221:121–131. doi: 10.1002/jmor.1052210202. [DOI] [PubMed] [Google Scholar]
- Riggs DS, Guarnieri JA, Addelman S. Fitting straight lines when both variables are subject to error. Life Sci. 1978;22:1305–1360. doi: 10.1016/0024-3205(78)90098-x. [DOI] [PubMed] [Google Scholar]
- Shine R, Cogger HG, Reed RR, Shetty S, Bonnet X. Aquatic and terrestrial locomotor speeds of amphibious sea-snakes (Serpentes, Laticaudidae) J Zool. 2003;259:261–268. [Google Scholar]
- Taylor CR, Weibel ER. Design of the mammalian respiratory system 1. Problem and strategy. Respir Physiol. 1981;44:1–10. [PubMed] [Google Scholar]
- Taylor CR. Relating mechanics and energetics during exercise. Adv Vet Sci Comp Med. 1994;38:181–215. [PubMed] [Google Scholar]
- Tejedo M, Semlitsch RD, Hotz H. Covariation of morphology and Jumping performance in newly methamorphosed water frogs: effects of larval growth history. Copeia. 2000a;2000:448–458. [Google Scholar]
- Tejedo M, Semlitsch RD, Hotz H. Differential morphology and jumping performance of newly metamorphosed frogs of the hybridogenetic Rana esculenta complex. J Herpetol. 2000b;34:201–210. [Google Scholar]
- Toro E, Herrel A, Vanhooydonck B, Irschick DJ. A biomechanical analysis of intra-and interspecific scaling of jumping and morphology in Caribbean Anolis lizards. J Exp Biol. 2003;206:2641–2652. doi: 10.1242/jeb.00473. [DOI] [PubMed] [Google Scholar]
- Toro E, Herrel A, Irschick DJ. The evolution of jumping performance in caribbean Anolis lizards: solutions to biomechanical trade-offs. Am Nat. 2004;163:844–856. doi: 10.1086/386347. [DOI] [PubMed] [Google Scholar]
- Van Damme R, Van Dooren TJM. Absolute versus per unit body length speed of prey as an estimator of vulnerability to predation. Anim Behav. 1999;57:347–352. doi: 10.1006/anbe.1998.0980. [DOI] [PubMed] [Google Scholar]
- Van Damme R, Wilson R, Vanhooydonck B, Aerts P. Performance constraints in decathlon athletes. Nature. 2002;415:755–756. doi: 10.1038/415755b. [DOI] [PubMed] [Google Scholar]
- Vanhooydonck B, Van Damme R, Van Dooren TJM, Bauwens D. Proximate causes of intraspecific variation in locomotor performance in the lizard Gallotia galloti. Physiol Biochem Zool. 2001;74:937–945. doi: 10.1086/324749. [DOI] [PubMed] [Google Scholar]
- Videler JJ, Jorna JT. Functions of the sliding pelvis in Xenopus laevis. Copeia. 1985;1:254–257. [Google Scholar]
- Videler JJ. Fish Swimming. London: Chapman & Hall; 1993. [Google Scholar]
- Wainwright PC. Functional morphology as a tool in ecological research. In: Wainwright PC, Reilly SM, editors. Ecological Morphology: Integrative Organismal Biology. Chicago: University of Chicago Press; 1994. pp. 42–59. [Google Scholar]
- Wardle CS. Limit of fish swimming speed. Nature. 1975;255:725–727. doi: 10.1038/255725a0. [DOI] [PubMed] [Google Scholar]
- Wasserzug RJ, Sperry DG. The relationship of locomotion to differential predation on Pseudacris triseriata (Anura: Hylidae) Ecology. 1977;58:830–839. [Google Scholar]
- Webb T, Howe SE, Bradshaw RHW, Heide KM. Estimating plant abundances from pollen percentages – the use of regression analysis. Rev Palaeobot Palynol. 1981;34:269–300. [Google Scholar]
- Weibel ER. Symmorphosis – on Form and Function in Shaping Life. Cambridge, MA: Harvard University Press; 2000. [Google Scholar]
- Wilson RS, Franklin CE, James RS. Allometric scaling relationships of jumping performance in the striped marsh frog Limnodynastes peronii. Exp Biol. 2000;203:1937–1946. doi: 10.1242/jeb.203.12.1937. [DOI] [PubMed] [Google Scholar]
- Zug GR. Anuran locomotion: structure and function. I. Preliminary observations on relation between jumping and osteometrics of appendicular and postaxial skeleton. Copeia. 1972;1972:613–624. [Google Scholar]