Functional specialisation of the pelvic limb of the hare (Lepus europeus)

Abstract

We provide quantitative anatomical data on the muscle–tendon architecture of the hare pelvic limb (specifically muscle mass, fascicle length, pennation angle, tendon mass and length). In addition, moment arms of major pelvic limb muscles were measured. Maximum isometric force and power of muscles, the moment of force about a joint, and tendon stress and strain were estimated. Data are compared with published data for other cursorial mammals such as the horse and dog, and a non-specialised Lagamorph, the rabbit. The pelvic limb of the hare was found to contain substantial amounts of hip extensor and adductor/abductor muscle volume, which is likely to be required for power production and stability during rapid turning. A proximal to distal reduction in muscle volume and fascicle length was also observed, as is the case in other cursorial quadrupeds, along with a reduction in distal limb mass via the replacement of muscle volume by long distal limb tendons, capable of storing large amounts of elastic energy. The majority of hare pelvic limb muscle moment arms varied with joint position, giving the hare the capacity to vary muscle function with limb posture and presumably different locomotor activities.

Introduction

The hare (Lepus europeus) is arguably the most highly specialised of the Lagomorphs for cursorial locomotion. At high speeds, hares have been observed using a galloping gait similar to that of other cursors (Hildebrand & Hurley, 1985) and with a top speed of 20 m s⁻¹ are claimed to be the fastest land mammals in Britain (Garland, 1983). Hares, however, rarely perform steady-state locomotion, particularly at maximum speeds; they are highly manoeuvrable, and escape from predators involves numerous, rapid changes in direction and maximum acceleration. They can also jump as an evasion strategy and are able to locomote bipedally at times (Grange, 1932). We might therefore expect the musculoskeletal anatomy of the hare to reflect this requirement for a diverse and adaptable locomotor repertoire. Visual inspection of the topographical anatomy of the hare suggests that there is a relatively large amount of musculature situated proximally within the pelvic limb, which indicates a specialisation for power production (and hence accelerative ability), and may also contribute to jumping performance.

Despite the hare's reputation for excellence in both running and jumping, little information is available regarding either its gross musculoskeletal anatomy or its more detailed muscle–tendon architecture. Muscle architecture is a primary determinant of muscle function (Burkholder et al. 1994; Lieber & Friden, 2000). Information regarding muscle fascicle length can be combined with muscle volume data to produce estimates of physiological cross-sectional area (PCSA) and hence the muscle's capacity for maximum isometric force generation, F_max. If maximum contraction velocity (V_max) can also be measured/estimated, then this can be combined with muscle mass to give muscle power. In addition, information on tendon resting dimensions and mass, and muscle isometric strength, can allow estimation of tendon elongation and hence energy storing capacity. In spite of the above, the ratio of the force produced by a muscle to the torque it generates about its joint is actually described by the moment arm of that muscle. Moment arms transform the linear forces developed by muscles into rotational moments that result in movements. Sometimes moment arms vary with joint angle (Brown et al. 2003b), and so a muscle may perform differently at different stages of the stride cycle, as indeed may the effective mechanical advantage (EMA) of the limb. Limb EMA is defined as the ratio of muscle moment arm vs. ground reaction force moment arm, which during stance equals the ratio of ground force vs. muscle force. Increases in EMA hence decrease the mass-specific muscle force required to maintain stability during postural and locomotor behaviours. Limb EMA can be altered by changes in limb posture (for example crouched postures can increase the size of the Ground Reaction Force (GRF) moment arm, and hence limb EMA is reduced in comparison to in more erect postures), but also by changes in the muscle moment arm. Therefore, quantitative descriptions of moment arms are essential to complete our understanding of dynamic muscle function.

Detailed information on muscle–tendon architecture is necessary to understand fully the specific locomotor capacity of individual and groups of muscles within the limbs. During steady-state locomotion, the limbs must support the centre of mass. This role is most effectively fulfilled by short-fibred pennate muscles with long tendons (Biewener & Roberts, 2000). These tendons can function as ‘springs’, storing elastic strain energy. This capacity to store elastic energy allows exchange between kinetic and potential energy forms (Alexander & Bennet-Clark, 1977; Alexander, 2002), thus reducing the amount of mechanical work that muscles must perform. For steady-state locomotion, this mechanism allows substantial energy savings – elastic recoil of tendons has been shown to contribute up to 40% of the positive work required for galloping in horses (Biewener, 1998). However, during non-steady-state activities, such as turning, non-cyclical jumping and accelerating, the requirement for muscle work increases (Biewener & Roberts, 2000). These powerful muscles that are capable of ‘doing’ work tend to be large in volume and have long fibres arranged in a parallel with limited ‘in series’ elastic tissue.

The pelvic limb of a fast quadrupedal runner, the horse (Equus caballus), shows a proximal to distal reduction in muscle volume and fascicle length, with numerous long distal limb tendons (Biewener, 1998; Brown et al. 2003a). Proximal muscles of the horse appear to be specialised for performing work, whilst distally, economical force generation and elastic energy storage are more important. This functional specialisation, within the pelvic limb, allows for high-speed yet efficient locomotion. Similar trends have also been seen in the pelvic limb of fast running bipeds such as the ostrich (Struthio camelus; Smith et al. 2006). This study aims to provide detailed information on muscle–tendon architectural properties and moment arms of the major muscles of the pelvic limb of the hare. We will compare these data with similar data for a more generalised Lagomorph, the rabbit (Oryctolagus cuniculus), and other cursors (the horse and greyhound) in order to increase current understanding of the functional design of muscles in a small, quadrupedal cursor and saltator (hopper). These data will also allow future musculoskeletal modelling, and inverse dynamics calculations to be undertaken.

Materials and methods

Eight hares [mass 3454 ± 500 g (mean ± SD)] were obtained from a game supplier (Freemantle Farm, North Oakley, UK) less than 24 h post-mortem. Hares were obtained in early autumn, and therefore it is probable that most of those obtained were juveniles. Hares were immediately frozen (−20 °C), and stored for 24 h at 4 °C prior to dissection. All hares were free from any obvious musculoskeletal pathology.

Muscle architecture

Eight pelvic limbs were skinned, and individual muscles were identified, exposed and cleared of fascia. They were then removed systematically. An incision was made longitudinally, through each muscle belly at 90° to the internal tendon, or (if no internal tendon), from tendon of origin to tendon of insertion. This revealed muscle fascicles (bundles of individual muscle fibres, visible to the naked eye), and the lengths of a random selection of these, from different areas of the belly, were measured with digital callipers. The measurement of muscle fascicles thus allows an estimate, rather than microscopic measurement of muscle fibre length. Where possible, ten lengths were taken; however, for some smaller muscles it was not possible to distinguish ten clear muscle fascicles and instead as many measurements as possible were taken. The tendon of origin and insertion (if present) were removed, and tendon and muscle belly resting length and mass were measured [using a plastic-coated flexible tape measure and set of electronic scales (EKS), respectively]. Resting pennation angle (to the nearest degree) was also obtained by measuring the angle between the internal tendon (or aponeurisis) and the fascicles using a clear plastic protractor. In addition, back muscles of all hares were removed and spinal muscle mass measured as above.

Tendon cross-sectional area (CSA) was determined by dividing tendon volume (tendon mass divided by a published value for tendon density of 1.12 g cm⁻³; Ker et al. 1988) by tendon length. Muscle volume was determined by dividing muscle mass by muscle density (1.06 g cm⁻³; Mendez & Keys, 1960). PCSA was calculated as muscle volume/fascicle length, and isometric F_max was estimated by multiplying 0.3 MPa – the maximum isometric stress of vertebrate skeletal muscle (Wells, 1965; Medler, 2002) – by PCSA. Muscle power was estimated as one-tenth of the product of F_max and V_max (Hill, 1938) to enable grouping and comparison of muscles with a high force-generating capacity vs. those with a high power output. V_max was estimated as 8L s⁻¹ (L = fibre resting length). As no information regarding contraction velocity is available for hares, this value is based on the assumptions that V_max in hare skeletal muscle is similar to that of rabbit muscle (1.74L s⁻¹ for type IIA fibres at 15 °C (Schiaffino & Reggiani, 1994), that the predominant fibre type in hare skeletal muscle will be type IIA as in horses (Snow, 1983; van den Hoven et al. 1985) and that a 10 °C rise in temperature will result in an approximate doubling of contraction velocity (Gasser & Hill, 1924). Of course this is only an estimate, and implications of this selected contraction velocity will be addressed in the discussion. It is, however, important to stress here that these calculations of F_max and V_max can only provide us with patterns of muscle functional capacity rather than discrete, accurate values.

Muscle moment arms

Four pelvic limbs were skinned (the contralateral limb to those used for muscle architecture), and in a systematic order, moment arms (flexion–extension only) of the major muscles at the hip, knee and tarsus were obtained using the tendon travel method (Spoor & van Leeuwen, 1992). The tendon travel method works on the principle that the distance a tendon moves while the limb moves through an angle in radians is equal to the perpendicular distance between the tendon and joint axis (the moment arm). In simple terms, tendon displacement is determined with respect to the angle of the joint, enabling calculation of the ‘effective moment arm’. Muscle bellies were transected and nylon suture sewn into the stump of the muscle at its insertion. Millimetre scales were super-glued (Loctite, USA) onto the longitudinal axis of the long bones to allow calibration and measurement of the tendon excursion from photographs. Brass eyelets (0.5 mm diameter) were screwed into the long bones at the origin of each muscle (or as close as possible), through which the suture nylon was passed. A 50-g weight was tied to the end of the suture nylon and allowed to hang over the edge of the dissection table to ensure the nylon remained taught throughout testing. A small marker was fixed to the nylon between the muscle stump and the eyelet. A digital camera (Nikon D70) was positioned perpendicular to the plane of joint motion, and digital images were acquired at 10° intervals, as the joint was moved from maximum joint extension to maximum joint flexion, and vice versa. The marker, eyelet and millimetre scales were visible on each image. Tendon travel was defined as the change in length between the marker and eyelet through joint motion. Joint angle was determined using the millimetre scales. Moment arms from muscles with wide origins or insertions were measured by inserting coloured pins at the origin and insertion of the muscle. In this case, tendon travel was defined as the change in distance between the pins through joint motion. Photographs were again taken at different limb positions as for the tendon travel method.

Pictures were manually digitised using freeware software (Image J, National Institute of Mental Health, Bethesda, MD, USA), and graphs of tendon excursion vs. joint angle in radians were plotted. Only joint angles within a realistic range in terms of possible limb postures during locomotion were considered (30–180°). These arbitrary values were chosen as no published values exist for joint angles used in locomotion in the hare. Linear or second-/third-order polynomial lines of best fit were plotted, as appropriate. These were determined by selecting the polynomial regression line with the highest possible R² value. Linear regression equations were used if the equation had an R² of greater than 0.95. If the R² for the linear equation fell below this value, a second-order polynomial was fitted, and so on. If all polynomial equations gave very low R² values, that which appeared visually to mirror the trend of the data best was chosen. Resulting polynomial regression equations were differentiated to give the value for the moment arm (Hughes et al. 1998). For example a regression equation of y = aθ² + bθ + c differentiates to give dy/dθ = 2aθ + b, which is the relationship between joint angle (θ) and instantaneous moment arm (y), given that moment arms change with joint angle. The maximum moment of force of a muscle about its joint, M, was calculated using additional information from dissections (see before) as $M=\sigma Ar$ where σ is the maximum isometric stress of muscle (estimated at 0.3 MPa for vertebrate muscle; Wells, 1965), A is the cross-sectional area of the muscle and r the maximum muscle moment arm.

Results

Muscle mass

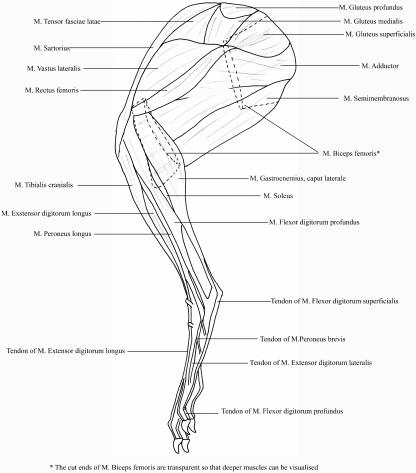
Mean pelvic (single) limb muscle mass accounted for 8.2 ± 0.4% (mean ± SD) of total body mass, which corresponded to a mean pelvic limb muscle mass of 280.0 ± 32.3 g. Total mass of the spinal musculature was 309 ± 70 g, accounting for 8.9 ± 1.4% of body mass. In total, 35 pelvic limb muscles were identified. Their origins, insertions and actions (estimated from anatomical position and dissections) are given in Table 1. Figure 1 shows the anatomical positions of the superficial and deep muscles of the hare pelvic limb. All raw muscle data are provided in Table 2.

Table 1.

Origin, insertion and suggested actions of the major muscles of the hare pelvic limb

Muscle	Abbreviation	Origin	Insertion	Action
Psoas Minor	PMN	Bodies of four posterior lumbar vertebrae	Ilium	Flexor of lumbosacral spine
Psoas Major	PMJ	Base of last 3 ribs and bodies of corresponding vertebrae; lumbar vertebrae	Lesser trochanter of femur	Flexion of hip
Iliacus	IL	Bodies of last lumbar and first sacral vertebrae; body of ilium to ventral boarder of acetabulum	With psoas major on lesser trochanter of femur	Flexion of hip
Gluteus superficialis	GSP	In two portions joined by an aponeurosis: the first from fascia covering sacrum; second, as first but also from anteroventral boarder of iliac wing; fused with TFL	Greater trochanter of femur	Flexion, extension (2nd portion) and abduction of hip
Gluteus medius	GMD	Anterior boarder of wing of ilium; iliac crest; fascia of sacral vertebrae	Greater trochanter of femur	Extension and abduction of hip
Gluteus profundus	GPF	Entire lateral surface of body and wing of ilium	Greater trochanter of femur	Extension and abduction of hip
Tensor fascia lata	TFL	Anterior portion of ventral boarder of wing of ilium	Broad fascia of lateral surface of thigh	Flexion of hip; extension of stifle
Piriformis	PFM	Lateral portions of second and third sacral vertebrae	Tip of greater trochanter of femur	Extension of hip
Biceps femoris Vertebral head	BFV	Spinous processes of last 3 sacral and 3 anterior caudal vertebrae	Flat tendon onto patella; blends with fascia on thigh and onto patella ligament	Extension and abduction of hip; flexion of stifle
Pelvic head	BFP	Isciadic tuber and iscium	Broad fascia onto tibial musculature; fuses distally with vertebral head	As above
Semitendinosis	ST	Ischial tuberosity	Fascia on medial surface of thigh; Tendon onto cacaneal tuber, in common with calcaneal tendon	Extension of hip during stance; adduction of hip; flexion of stifle and extension of hock during swing
Semimembranosis	SM	Lateral process of isciadic tuberosity	Fascia onto medial surface of tibial musculature	Extension of hip during stance, adduction of hip; stifle flexion
Sartorius	SRT	Anterior portion of ventral boarder of wing of ilium	Tibial tuberosity via middle patella ligament; fascia on cranial aspect of thigh and stifle joint	Hip flexion; stifle extension
Gracilis	GRC	Pubic symphysis	Fascia on medial surface of tibia	Hip adduction; stifle flexion
Pectineus	PCT	Pubis	Medial shaft of femur	Adduction of hip
Adductor	AD	Isciadic tuber; iscium; pelvic symphysis	Entire posterior surface of femoral shaft to distal end; medial condyle of tibia	Adduction and extension of hip
Quadriceps femoris	QF
Rectus femoris	RF	Ventral boarder of iliac wing; anterior spine immediately in front of acetabulum	Tibial tuberosity via middle patella ligament; fascia around stifle joint	Flexion of hip; extension of stifle
Vastus lateralis	VL	Anterior surface of greater trochanter	As above	Extension of stifle
Vastus intermedius	VI1/2	Greater trochanter below origin of Vastus lateralis; Anterior surface of femur	As above	As above
Vastus medialis	VM	Medially at base of neck of femur; adjacent portion of femoral shaft	As above	As above
Popliteus	PP	Lateral condyle of femur	Proximal portion of tibia	Flexion and pronation of stifle
Gastrocnemius	G
lateralis	GL	Lateral condyles of tibia and femur	Via calcaneal tendon onto tuber calcanei	Extension of hock; flexion of stifle
medialis	GM	Medial condyle of femur and its sesamoid	As above	As above
Soleus	SL	Head of fibula	As above	Extension of hock
Flexor digitorum superficialis	FDS	Lateral condyle of femur and associated sesamoid	Plantar surface of second phalanges of the four developed digits	Flexion of digits; flexion of stifle
Flexor digitorum profundus	FDP
Flexor digitorum lateralis	FDL	Head of fibula	Via deep flexor tendon onto phalanges of four developed digits	Flexion of digits; extension of hock
Tibialis caudalis	TCD	Lateral condyle of tibia; lateral posterior surface of fibula; closely fused with FDL	As above	As above
Flexor digitorum medialis	FDM	Posterior surface of tibia and fibula; closely fused with TCD	As above	As above
Tibialis cranialis	TCN	Lateral condyle of tibia; corresponding suface of tibial tuberosity	Base of second metatarsal	Flexion of hock
Peroneus longus	PL	Lateral condyle of tibia and head of fibula	End of reduced first metatarsal	Flexion of digit; fine motor control
Peroneus brevis	PB	Lateral condyle of tibia; tibial shaft	Tuberosity at base of fifth metatarsal	As above
Peroneus tertius	PT	Head of fibula	Head of fifth metatarsal; phalanges of fifth digit	Extension of digit; fine motor control
Peroneus quartus	PQ	Fibula with peroneus Brevis	Head of fourth metatarsal	Flexion of digit; fine motor control
Extensor digitorum longus	EDLO	Lateral portion of patellar surface of femur	Phalanges of four main digits	Extension of digits; flexion of hock
Extensor digitorum lateralis	EDLA	Medial condyle and anteriomedial surface from tuberosity to middle of tibia	Unites with tendon of EDLO on dorsal surface of basal phalanx of second digit	Extension of digit; flexion of hock

Fig. 1.

Schematic line drawing showing superficial and underlying musculature of the lateral aspect of the hare pelvic limb.

Table 2.

Muscle data: muscle mass, volume, belly length, fascicle length, physiological cross-sectional area (PCSA), pennation angle, and estimated maximum isometric force and power. Values obtained for muscle force and power were obtained as per Methods described in the text. Values indicate means and range (this is given only for variables that were measured directly) (n = 8)

Muscle	Muscle mass (g)	Volume (cm3)	Belly length (mm)	Fascicle length (mm)	PCSA (mm2)	Pennation angle (°)	Force (N)	Powe (W)
Adductor (combined)	53.0 (39.3–68.0)	50.0	119 (80–131)	82 (64–100)	61.4	0	184	11.9
Biceps femoris (pelvic head)	22.7 (18.3–26.9)	21.4	121 (93–142)	80 (58–103)	26.7	0	80	5.0
Biceps femoris (vertebral head)	36.1 (26.1–48.0)	34.0	113 (100–118)	67 (50–88)	50.6	25 (20–47)	152	8.1
Extensor digitorum longus	3.8 (1.7–4.6)	3.6	85 (69–101)	20 (14–45)	17.9	31 (10–46)	54	0.8
Extensor digitorum lateralis	1.0 (0.4–2.7)	0.9	58 (37–78)	11 (6–14)	8.3	28 (18–31)	25	0.2
Flexor digitorum longus	1.7 (0.7–2.8)	1.6	70 (55–84)	12 (4–23)	13.0	21 (7–26)	39	0.3
Flexor digitorum medialis	0.7 (0.5–0.9)	0.7	56 (37–80)	10 (8–12)	6.8	42 (40–45)	20	0.1
Flexor digitorum superficialis	7.3 (4.9–9.3)	6.9	81 (65–98)	7 (5–12)	97.1	42 (25–51)	291	1.6
Gastrocnemius lateralis	6.4 (5.2–7.3)	6.0	71 (64–80)	11 (7–14)	54.5	31 (25–40)	164	1.5
Gastrocnemius medialis	7.2 (5.6–9.2)	6.8	72 (62–80)	11 (6–16)	63.5	36 (29–47)	191	1.5
Gluteus medius	8.8 (7.1–13.8)	8.3	55 (44–71)	34 (11–45)	24.8	0	75	1.9
Gluteus profundus	7.2 (1.4–11.3)	6.8	43 (28–52)	22 (6–30)	31.6	15 (0–42)	95	1.5
Gluteus superficialis	8.1 (5.0–18.4)	7.6	56 (33–80)	21 (13–31)	37.3	8 (0–31)	112	1.8
Gracilis	8.8 (6.7–11.3)	8.3	81 (67–113)	46 (37–65)	18.1	0	54	1.9
Iliacus	1.9 (1.0–4.2)	1.8	50 (39–65)	18 (14–23)	9.6	0	29	0.5
Peroneus brevis	0.7 (0.3–1.0)	0.6	54 (38–64)	12 (9–17)	5.3	29 (20–39)	16	0.1
Peroneus tertius	0.4 (0.1–0.8)	0.4	57 (52–67)	12 (9–16)	3.3	30 (18–38)	10	0.1
Peroneus longus	0.8 (0.6–1.0)	0.7	58 (48–68)	13 (9–17)	5.9	25 (10–36)	18	0.2
Peroneus quartus	0.3 (0.1–0.5)	0.3	49 (27–73)	9 (4–12)	3.2	32 (28–41)	10	0.1
Psoas major	7.0 (2.3–9.2)	6.6	58 (40–110)	53 (40–77)	12.6	0	38	1.5
Psoas minor	4.3 (0.3–0.9)	4.1	33 (17–36)	35 (13–34)	18.1	0	35	0.9
Rectus femoris	12.7 (9.6–16.3)	12.0	107 (85–115)	22 (16–29)	55.0	31 (25–38)	165	2.9
Sartorius	6.1 (3.9–7.8)	5.8	116 (105–131)	90 (70–108)	6.4	0	19	1.4
Semimembranosis	19.0 (15.9–21.6)	17.9	107 (85–134)	66 (55–73)	27.4	0	82	4.2
Semitendinosis	2.6 (2.0–3.3)	2.4	82 (72–93)	19 (13–25)	12.5	26 (13–37)	38	0.6
Soleus	1.7 (1.3–2.0)	1.6	75 (64–83)	13 (9–17)	12.5	27 (19–40)	37	0.3
Tensor fascia lata	11.1 (8.8–14.1)	10.5	73 (66–86)	30 (22–39)	35.0	0	10.5	24.7
Tibialis caudalis	3.6 (2.6–5.4)	3.4	75 (59–82)	10 (7–12)	35.2	32 (21–36)	10.6	0.8
Tibialis cranialis	3.6 (2.8–5.1)	3.4	83 (75–92)	59 (48–67)	5.7	0	17	0.8
Vastus lateralis	20.1 (17.5–23.8)	19.0	98 (87–107)	36 (29–47)	52.2	24 (20–37)	157	4.5
Vastus medialis	9.1 (6.6–11.0)	8.6	97 (85–109)	29 (26–34)	29.0	31 (20–40)	87	2.1
Vastus intermedius (1)	11.9 (6.8–13.4)	11.3	91 (85–98)	32 (24–44)	35.4	25 (10–38)	106	2.6
Vastus intermedius (2)	2.68 (1.7–5.5)	2.5	72 (61–82)	16.1 (6–35)	15.7	20 (10–33)	47	0.6

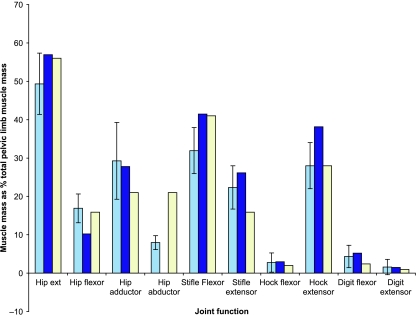
The largest muscle in the pelvic limb was the adductor (AD) muscle, accounting for 18.9 ± 3.2% of total limb muscle mass. This was closely followed by the vertebral and pelvic heads of the biceps femoris muscle (BFV and BFP) at 12.9 ± 1.0 and 8.1 ± 1.1% of limb mass, respectively. The semimembranosus (SM) muscle also accounted for a large amount of the muscle mass. In fact, hip extensor musculature formed the major proportion of the mass of the pelvic limb (49%; Fig. 2), with 81% of the pelvic limb muscle mass functioning at the hip or knee. Note that in Fig. 2 percentage values add to greater than 100%, as some muscles perform functions at more than one joint, and thus some will have been included in more than one group. More distally, the largest muscles positioned below the knee were the flexor digitorum superficialis (FDS), and lateral and medial gastrocnemius (GL and GM) muscles. However, their masses corresponded to only 2.6, 2.3 and 2.6% of total pelvic limb mass, respectively.

Fig. 2.

Functional distribution of muscle mass within the pelvic limb for hares (pale blue bars), rabbits (dark) and horses (white). Rabbit data are from Lieber & Blevins (1989). Note that gluteal, psoas, IL and SRT muscles are missing from this study; see text. Horse data are from Payne et al. (2005). Hare data are means ± SD (n = 8).

Tendon

All tendon data are provided in Table 3. Tendon accounted for only 1.7 ± 0.1% of the total pelvic limb mass. There were no discernible tendons of origin. Tendons of insertion were mainly long and very thin, with the exception of the tendon of rectus femoris (RF), which was short and thick, with a large (though variable) mass and CSA (0.6 ± 0.3 g and 0.2 ± 0.1 cm², respectively). Of the distal tendons, the tendons of the flexor digitorum profundus (FDP) and FDS were the heaviest (1.4 ± 0.2 and 0.8 ± 0.2 g, respectively), and had the largest CSAs (0.07 ± 0.02 and 0.05 ± 0.01 cm², respectively). They were also the longest tendons in the pelvic limb with mean lengths of 16.8 ± 3.6 and 15.9 ± 1.2 cm, respectively. Of the more proximal muscles, the gastrocnemius and vasti muscles and the BFV also had tendons with reasonably high CSAs. The tendon of SM was the longest of the proximal limb muscles at 8.9 ± 2.1 cm; however, although this muscle originates proximally, it inserts onto the medial aspect of the tibia and functions not only as a hip extensor but also as a flexor of the knee joint.

Table 3.

Tendon data: mass, volume, and resting length, and estimated cross-sectional area (CSA), stress, strain, and length change of selected pelvic limb tendons. Estimated parameters calculated using methods described in the text. Data are means (n = 8). Values in parentheses are ranges

Muscle–tendon unit	Mass (g)	Volume (mm3)	Rest length (mm)	CSA (mm2)	Stress (MPa)	Strain (%)	Length change (mm)
Biceps femoris	0.35 (0.17–0.70)	29.0	40 (24–54)	0.8	29	1.9	0.8
Flexor digitorum profundus (combined)	1.35 (1.03–1.66)	112.8	168 (139–253)	0.7	22	1.5	2.5
Extensor digitorum lateralis	0.04 (0.01–0.10)	3.6	93 (52–139)	0.1	63	4.2	3.9
Extensor digitorum longus	0.36 (0.10–0.60)	29.5	107 (90–152)	0.8	20	1.3	1.4
Gastrocnemius	0.38 (0.20–0.73)	128.6	67 (23–85)	0.3	119	7.9	5.3
Gracilis	0.12 (0.10–0.22)	9.6	37 (10–69)	0.2	21	1.4	0.5
Gluteus superficialis	0.05 (0.02–0.07)	4.2	14 (10–17)	0.3	39	2.6	0.4
Rectus femoris	0.52 (0.27–0.96)	43.0	23 (15–30)	2.2	9	0.6	0.1
Flexor digitorum superficialis	0.83 (0.30–1.04)	69.4	159 (132–173)	0.4	67	4.5	7.1
Semimembranosis	0.31 (0.20–0.53)	26.0	89 (64–110)	0.3	28	1.9	1.7
Semitendinosis	0.08 (0.04–0.14)	6.9	34 (20–48)	0.2	18	1.2	0.4
Tibialis cranialis	0.07 (0.04–0.11)	6.2	70 (58–74)	0.1	19	1.3	0.9
Vastus	0.19 (0.13–0.34)	16.0	9 (8–12)	0.6	9	0.4	0.1

Muscle architecture

Distribution of fascicle lengths (Table 2) showed a general trend, with proximal muscles having longer fascicles and the distal muscles relatively short fascicles. Fascicle lengths varied both between hares and within a muscle (hence ten measurements were taken from a variety of regions within the muscle belly; see Methods). However, differences between regions within a muscle have not been quantified as it was often difficult to obtain more than six measures for fascicle length due to the small size of hare muscles in comparison with larger species which have been studied (Gans et al. 1989; Hermanson, 1997; Brown et al. 2003a; Payne et al. 2005; Smith et al. 2006), and therefore it was not feasible to divide muscles into distinct regions. It was not possible to obtain fascicle lengths and pennation angles for all muscles in all hares, particularly in the smaller muscles where it was often difficult to locate the correct plane of incision by which to do this.

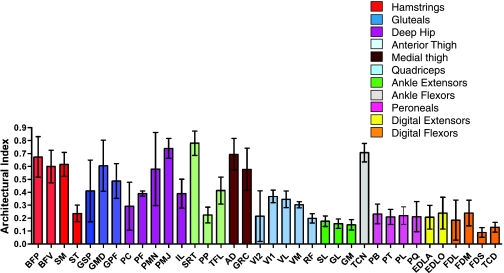
The longest fascicles were seen in sartorius (SRT) (9.0 ± 1.3 cm), AD (8.2 ± 1.4 cm) and BFP (8.0 ± 1.5 cm). The shortest were seen in the pronator teres (PT) (0.2 ± 0.2 cm) and FDS (0.7 ± 0.2 cm) muscles. Tibialis cranialis (TC) had considerably longer fascicles then the other distal limb muscles (5.9 ± 0.6 cm). Long fascicles may simply reflect a long muscle belly length. A parameter known as the architectural index (AI) was therefore calculated (fascicle length divided by muscle length) in order to allow comparison of fascicle length between muscles of different lengths. This can be seen in Fig. 3. With the exception of semitendinosis (ST) (0.23 ± 0.06) and RF (0.20 ± 0.03) muscles, the majority of proximal muscles have an AI above 0.3, the highest being the parallel fascicled SRT (0.78 ± 0.09). Distal muscles tended to have smaller AIs, mostly below 0.3, with the exception of TC, which had one of the highest AIs in the entire limb (0.70 ± 0.07). The smallest AIs in the distal limb were seen in PT, FDS and tibialis caudalis (TCD), which suggests a highly pennate structure (see below).

Fig. 3.

Architectural index (AI) for hare pelvic limb muscles. Abbreviations are given in Table 1. Values are means ± SD (n = 8).

Fascicle pennation angles (Table 2) ranged from parallel (0°) to 50°. The most pennate muscles were the flexors of the digits, in particular flexor digitorum medialis (FDM) (42 ± 4°) and FDS (42 ± 8°). In contrast, much of the proximal musculature within the limb, for example the hip extensors – AD, BFP and SM – and also hip flexors [psoas (PMJ and PMN), iliacus (IL), SRT, tensor fascia lata (TFL)] all had near-parallel orientated fascicles. In the distal limb, only the TC muscle had fascicles orientated in parallel. The remainder of the muscles in the limb had varying degrees of pennation, mostly between 20 and 40°.

Moment arms

Moment arms were only measured for muscles that, as a consequence of their position within the limb, acted in flexion or extension. In addition, moment arms for digital flexors and extensors at the digits were neglected, as the tendon travel method is only suitable for measuring moment arms in a single plane. Muscle–tendon units (MTUs) that were positioned very closely to one another, with the muscles appearing to follow the same line of action, were measured as one. Moment arms were scaled by limb segment length (to the femur length for muscles acting at the hip and knee joints, and to the tibia length for those at the ankle; Payne et al. 2006). Segment lengths are given in Table 4. Equations for the relationships of tendon travel against joint angle are provided in Table 5. Moment arm curves are provided in Fig. 4, and are presented so that muscles acting to flex a joint have positive values whereas those that act to extend the joint in question have a negative value. The sign is irrelevant, however, and absolute values will be referred to here. Maximum mean moment arms and joint moments of force, with the joint angles (within a physiologically realistic range) at which these occur, and muscle fascicle length/moment arm (MFL:MA) ratios are given in Table 6.

Table 4.

Pelvic limb segment lengths used to scale muscle moment arm measurements

Hare no.	Femur length (mm)	Tibia length (mm)
1	100	136
2	112	132
3	124	137
4	125	142

Table 5.

Equations of the trend lines fitted to the plots of tendon excursion against joint angle of flexion in the hare. Equations and R² values are means, N = 4

Muscle–tendon unit	Joint of action	Equation	R2
Tensor fascia lata	Hip	y = 0.16x3 − 1.11x2 +2.73x − 1.06	0.97
	Knee	y = −0.17x + 14.74	0.51
Gluteus superficialis	Hip	y = 8.49x + 41.04	0.71
Gluteus medius	Hip	y = 4.57x2 − 14.64x + 32.37	0.85
Psoas	Hip	y = 2.30x2 + 3.50 + 27.16	0.96
Iliacus	Hip	y = 0.52x2 − 0.32x + 26.28	0.94
Rectus femoris	Hip	y = 11.62x + 6.46	0.99
Sartorius	Hip	y = −0.025x2 + 3.18x − 1.81	0.96
Semimembranosis	Hip	y = −3.46x + 10.58	0.97
	Knee	y = 1.82x2 − 2.71x + 40.80	0.75
Semitendinosis	Hip	y = −3.03x + 10.50	0.98
	Knee	y = −0.91x2 + 17.8x + 8.25	0.97
Gracilis	Hip	y = 0.77x2 − 5.01x + 11.70	0.97
Biceps femoris	Hip	y = −1.05x2 + 2.38x + 12.16	0.87
	Knee	y = −0.36x2 + 1.15x + 12.93	0.65
Adductor	Hip	y = 1.44x3 − 4.63x2 + 0.81x + 5.76	0.99
Vastus and rectus femoris	Knee	y = −11.26x + 38.72	0.98
Gastrocnemius lateralis	Knee	y = 8.50x + 18.0	0.97
Gastrocnemius medialis	Knee	y = 1.65x2 + 6.09x + 1.74	0.95
Flexor digitorum profundus and flexor digitorum superficialis	Ankle	y = 1.09x2 − 10.0x + 55.27	0.77
Extensor digitorum longus	Ankle	y = 2.83x2 − 4.07x + 15.93	0.98

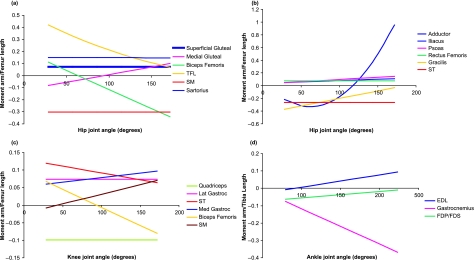
Fig. 4.

Mean moment arms (scaled to femur or tibia length, see Methods described in text; mean femur length 115 mm, mean tibia length 137 mm). Lengths for individual hares are given in Table 4 for selected pelvic limb muscles across the full range of physiologically relevant joint positions. (a) Superficial muscles acting at the hip joint; (b) deep muscles acting at the hip joint; (c) muscles acting at the knee joint; (d) muscles acting at the ankle joint.

Table 6.

Mean maximum moment arms (range given in parentheses), maximum joint moments (calculated as described in the text), and muscle fascicle length/moment arm ratios for hare pelvic limb muscles. Fascicle lengths for grouped muscles were calculated as weighted harmonic means (Alexander et al. 1981). Moment arms used for calculations are the mean of the maxima (n = 4)

Muscle–tendon unit	Joint of action	Joint angle of maximum moment arm (i.e. max flexion/extension)	Mean maximum muscle moment arm (mm)	Maximum joint moment of force (N.cm)	Muscle fascicle length/moment arm ratio
Tensor fascia lata	Hip	Max flexion	56 (37–78)	59.1	0.53
	Knee	All	3 (1–6)	2.6	12.2
Gluteus superficialis	Hip	All	8 (1–13)	95.1	2.47
Gluteus medius	Hip	Max extension	9 (9–12)	68.6	3.71
Psoas	Hip	Max extension	17 (13–25)	65.7	3.07
Iliacus	Hip	Max extension	13 (8–16)	38.0	1.37
Rectus Femoris	Hip	All	12 (10–13)	191.4	1.90
Sartorius	Hip	Max flexion	32 (25–36)	60.4	2.83
Semimembranosis	Hip	All	35 (31–39)	283.7	1.91
	Knee	Max extension	8 (4–14)	67.2	8.05
Semitendinosis	Hip	All	30 (27–34)	115.1	0.63
	Knee	Max flexion	18 (14–22)	68.8	1.05
Gracilis	Hip	Max flexion	42 (26–50)	228.4	1.10
Biceps femoris	Hip	Max extension	39 (28–59)	909.4	1.88
	Knee	Max extension	11 (8–16)	257.5	6.62
Adductor	Hip	Max extension	119	2187.8	0.69
Vastus and rectus femoris	Knee	All	11 (10–13)	635.1	2.39
Gastrocnemius lateralis	Knee	All	9 (10–6)	151.4	1.19
Gastrocnemius medialis	Knee	Max extension	11 (9–13)	212.0	0.99
Gastrocnemius	Ankle	Max extension	50 (19–94)	1778.6	0.22
Flexor digitorum profundus and flexor digitorum superficialis	Ankle	Max flexion	5 (3–10)	191.5	1.84
Extensor digitorum longus	Ankle	Max extension	13 (9–16)	69.66	1.55

The moment arms at the hip (Fig. 4a,b) of RF, SM, ST and gluteus superficialis (GSP) all remained constant with changing joint angle. The moment arm at the hip of TFL (moment arm curve is parabolic) decreased with joint extension, with the maximum moment arm occurring at, or near, full joint flexion. SRT (linear) moment arm was similar to this in pattern, although the absolute change in moment arm length was relatively small. Moment arms at the hip of psoas (PMN and PMJ) and iliacus (IL) (both linear) increased with joint extension, with maximum moment arms occurring at full joint extension. The moment arms of biceps femoris and gluteus medialis (GMD) at the hip were linear in shape with the maximum (absolute) moment arm occurring at full joint extension.

At the knee joint (Fig. 4c), moment arms of TFL, GL and quadriceps femoris all remained constant with joint extension. Moment arms of biceps femoris, SM and GM increased linearly with joint extension and were at their maximum at full joint extension. Conversely, the moment arm of ST decreased with joint extension and was at its maximum in full joint flexion.

At the ankle joint (Fig. 4d), the moment arm of extensor digitorum longus (EDL) increased linearly from flexion to full joint extension, where it reached its maximum. FDP and FDS decreased linearly; maximum moment arm was at full joint flexion. The moment arm of gastrocnemius increased with joint extension, reaching its maximum at full joint extension.

Discussion

Gross anatomy

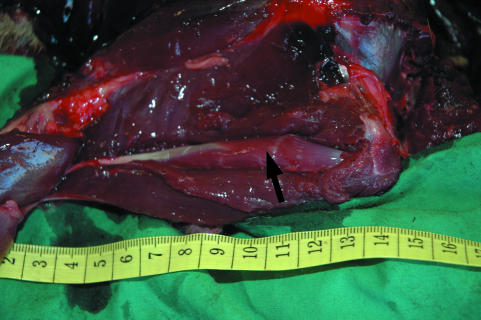
The anatomy of the hare pelvic limb showed large similarities to that of the rabbit pelvic limb. One particularly interesting feature of the hare pelvic limb was that the ST muscle was completely encased within the adductor muscle (see Fig. 5). This feature has also been reported in rabbits (Bensley, 1948). The main difference between hare and rabbit gross muscular anatomy was that whilst the rabbit has only one head to the FDP muscle (flexor digitorum longus), the hare has three clearly distinguishable heads (FDL, TCD, FDM) to this muscle, as is the case in other quadrupeds such as the horse (Nickel et al. 1986). These, however, are closely fused.

Fig. 5.

Semitendinosis muscle (indicated by arrow) within bisected adductor muscle belly. Values on scale are in cm.

Functional distribution of muscle mass within the pelvic limb

Muscle mass predicts capacity for muscle work (introduction), and an animal's capacity for acceleration and jumping, and it is interesting to consider where this muscle is located within the body. Total pelvic limb muscle mass for both limbs (calculated by doubling the value for the dissected limb and thus assuming both limbs are symmetrical) accounted for 16.3 ± 0.9% (mean ± SD) of total body mass. The combined forelimb muscle mass accounts for only 9.3 ± 0.3% of the total body mass of the hare (Williams et al. 2007), suggesting the hare has a substantial bias towards hindlimb propulsion. In addition, the total mass of the spinal musculature accounted for 8.9 ± 1.4% of body mass – a substantial portion of the total locomotor muscle mass (∼26%). Much of the back musculature extends the lumbar spine. As such its contraction will increase the distance from the hind foot to the centre of mass. It could therefore be functionally grouped as part of the pelvic limb musculature. This gives a total pelvic limb muscle mass of 869 ± 45 g (25% of total body mass). We did not collect architectural data for these muscles and equivalent data for other quadrupeds are sparse; however, when normalised for body mass, the back muscles of the hare are much larger than those of the dog and horse. The large longissimus dorsi muscle in particular, when expressed as a percentage of total body mass, weighs almost four times that of the dog, and is able to create more than double the estimated extensor moment about a mid-lumber intervertebral joint (Alexander et al. 1985). In the horse the spinal musculature also accounts for less than 5% of total body mass (C. von Scheven, personal communication). Smaller animals appear to have a large degree of spinal flexibility. Elastic structures are also present, which suggests an important role for the back, and hence spinal musculature in small animals in fast locomotion (Alexander et al. 1985). It therefore seems likely that the large spinal extensors perform substantial work on the centre of mass in the hare.

Within the pelvic limb, the hip extensor muscles accounted for 49% of the total muscle mass. Locating a large proportion of muscle mass as hip extensors points to the functional importance of hip extension in hares and is probably related to the hare's ability to accelerate quickly and jump. In the horse, 56% of the total muscle mass of the pelvic limb has the capacity to extend the hip (Payne et al. 2005), a slightly higher proportion of functional volume than was observed in the hare. An interesting difference between the hare and horse can be seen in the hip adductor muscles, with only 21% of total pelvic limb muscle volume being capable of this function in the horse, but 29% in the hare. The AD muscle was by far the largest muscle within the hare pelvic limb (19% of total pelvic limb muscle mass). This abundance of adductor muscle volume would be beneficial for balance and dealing with the forces associated with rapid changes in direction, in addition to the AD muscle's secondary function as a hip extensor (see above). Hares also appear to have a lesser proportion of their pelvic limb mass capable of knee (stifle) flexion when compared with the horse; instead, the emphasis is on muscles capable of extending this joint (Fig. 2). Knee extension is another feature likely to be important in high-speed running but also in jumping, an activity at which the hare appears to excel.

More distally, interesting similarities with the ostrich and the horse (Payne et al. 2005; Smith et al. 2006) arise in the proportions of limb muscle volume available at the ankle. In the hare, 28% of the functional volume of muscle within the pelvic limb (also 28% in the horse, and 29% in the ostrich) accounts for tarsus extension, another mechanism for accelerating the centre of mass upwards and forwards during stance. Very similar proportions of functional volume are also available in all three species for tarsus flexion (3% hare; 3% ostrich; 2% horse), and for digital flexion and extension (although slightly less digital flexor musculature is present in the horse, presumably due to the reduced number of digits, and therefore number of tendons, and also the fact that most superficial digital flexor muscle volume has been replaced by tendon).

It is interesting to compare the pelvic limb anatomy of the hare to that of a non-specialised Lagamorph, the rabbit, given that the two are similarly sized yet show differences in locomotor ability. The hare is almost identical to the rabbit in the proportions of muscle acting at each joint (Fig. 2). Rabbit data were taken from Lieber & Blevins (1989), but note that in their study, GSP, GMD, gluteus profundus (GPF), PMN, PMJ, IL and SRT muscles were not accounted for. Therefore, the proportion of hip extensor and flexor musculature in rabbits would be somewhat larger than that shown in Fig. 2 had these muscles been included. It is likely therefore that the proportions of musculature at the hip in the rabbit exceed those in the hare. This may indicate an adaptation towards saltatory rather than cursorial locomotion in the rabbit, whereas the hare uses more of a running gait. In addition, the hare appears to have a similar proportion of pelvic limb muscle mass (per total body mass) to the rabbit (16.3% as opposed to 13.3%, respectively), although some muscles (see above) are missing in the rabbit data set. To be comparable with the pelvic limb muscle mass of the hare, these muscles would need to have a combined mass of 37 g (1.5% of body mass). In the hare these seven muscles amount to 1.4% of total body mass, and therefore unless there are very large differences in the proportional size of the gluteal, psoas, IL and SRT muscles between these two species, both animals will have very similar amounts of total body mass located in the pelvic limb. Hence, clearly the muscle mass in the pelvic limb and at each joint of the rabbit and hare are very similar, except at the hip joint where, surprisingly, the rabbit has a greater proportion of pelvic limb mass. This is interesting given the differences in the capacity of each animal for high-speed locomotion. This may reflect the fact that both animals need to accelerate quickly but hares also undertake longer distance steady-speed running. It would, of course, be interesting to combine these data with biomechanical assessment of muscle power and measures during running.

Proximal-to-distal specialisation of muscle architecture

A clear proximal-to-distal specialisation in muscle architecture was seen in the hare, as in other species that are fast runners. BFP, BFV and AD, for example, were by far the largest muscles in the pelvic limb. SM and GMD also had large volumes and these five formed a group of muscles that are all characterised by large volumes, but also long fascicles/high AIs. Proximal pelvic limb muscles in general exhibited this trend (Fig. 3), typical of muscles that are specialised for doing work and achieving high power output (Payne et al. 2005). These muscles are all classified as extensors of the hip, and because quadrupedal runners have been described as ‘rear-wheel drive’, relying on torque generation at the hip in order to propel the centre of mass forwards (Usherwood & Wilson, 2005), it is not surprising that these muscles appear to be adapted in this way. AI decreased distally; muscles acting at the carpus had lower AIs than hip muscles, as well as tending to be smaller, whilst those about the tarsus and digits, particularly GM, GL, SDF, FDL, FDM and TCD, were lower still. The low AI of these muscles reflects their fairly short fascicle lengths (and high pennation angles) and therefore increased PCSA.

Force-generating capacity

The force-generating capacity of a muscle relates directly to its PCSA, which in turn relates to its muscle volume and fascicle length. Therefore, the muscles able to generate the most force are not necessarily those with the largest volume. This is reflected within the hare pelvic limb, as the muscle with the largest PCSA, and therefore highest force-generating capacity, was FDS (PCSA 9.7 cm², F_max 290 N). FDS was only the 14th heaviest muscle within the pelvic limb (although the largest of the distal limb muscles), and hence its highly pennate nature increases its PCSA and F_max sufficiently to exceed even that of the massive AD muscle. The two heads of the gastrocnemius muscle combined were also capable of generating large forces (350 N, due to relatively short fascicles), whilst some of the larger muscles in the proximal limb also had high force-generating capacities (Table 2). In general, distal muscles are therefore more specialised for producing high force than those in the proximal limb, and the high force-generating capacities of the digital flexor FDS, and ankle extensors – GL and GM – estimated here suggest that these muscles in particular are well suited to this role. It should be noted that the actual moment produced at a joint by a muscle depends also on the effective moment arm of the muscle at the joint, as moment arms transform the forces developed by muscles into rotational moments that generate movements. This will be discussed in more detail later.

Power production

Our assumption of homogeneity of fibre type and contraction velocity mean that capacity for power production directly reflects the muscle volume/mass. The muscle capable of the greatest estimated power production was the AD (11.9 W). BFP, BFV, and the lateral head of vastus (VL) were other proximal limb muscles also capable of generating high power. Some muscles that showed limited force-generating potential (due to long fascicles) were capable of high power production, for example SM (82 N, but 4.2 W). By contrast, distal muscles tended to show the ability to develop high force, but not power, such as SDF, DDF, GL and GM. None of the distal limb muscles was capable of producing more than 1.6 W of power (FDS).

Of course, any estimations of power we have made in this study depend on the maximum contraction velocity of skeletal muscle. We have estimated this to be 8L s⁻¹, given that in rabbit muscle a contraction velocity of 1.74L s⁻¹ has been measured for type IIA fibres at 15 °C (Schiaffino & Reggiani, 1994). This value of 8 takes into account the fact that a 10 °C rise in temperature will result in an approximate doubling of contraction velocity (Gasser & Hill, 1924) and hence that a higher velocity is seen in vivo. This estimation has two potential sources of error: first, it assumes that the contraction velocity of hare muscle fibres will be the same as that of rabbit muscle. This is reasonable, given their similar mass and that it is known that contraction velocity scales with mass (Medler, 2002). This may not be entirely accurate given the somewhat different locomotor repertoire of these two animals (for example they may have differing endurance/acceleration capabilities). It is also limited, given that the value for rabbits presumes that the predominant fibre type skeletal muscle will be type IIA as in horses (Snow, 1983; van den Hoven et al. 1985), which may not be the case in rabbits, or hares (indeed the exact distribution of fibre types is likely to vary between animals and within and between muscles). However, it must be stressed that our aim is not to gain accurate power estimates, rather to enable a broad understanding of comparative muscle function.

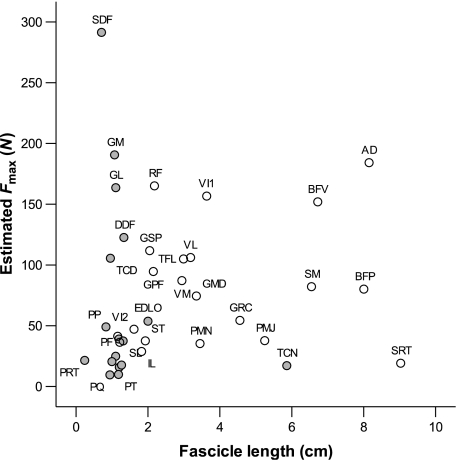
Figure 6 shows F_max plotted against fascicle length for the pelvic limb muscles of the hare. The plot illustrates trends in the specialisation of muscles towards force generation or power production, and can be roughly divided into four quadrants. The top left region of the graph shows those muscles with high PCSAs and short fascicles, indicating a high degree of pennation. These muscles (FDS, GM, GL) are hence specialised towards generating force economically. The upper right area represents those muscles with high PCSAs and long fascicles, i.e. their large area is due to a large muscle volume rather than high degree of pennation. These muscles (specifically, AD and BFV) are hence capable of powerful contraction. The bottom right of the plot shows muscles with long fascicles but a small PCSA. These muscles (SRT, TCN) are specialised for fast contraction and moving joints through a large range of motion. Finally, those muscles in the bottom left quadrant are not capable of generating high force or a significant change in length, and carry out more generalised functions and supporting roles within the limb.

Fig. 6.

Estimated muscle F_max against fascicle length for hare pelvic limb muscles. Values are means (n = 8). Solid points represent distal limb muscles, whilst proximal muscles are represented by open circles. Abbreviations are given in Table 1.

Interestingly, as in the horse (Payne et al. 2005a), it is the hip extensor musculature that is capable of generating the highest power, although the hare's knee extensors such as VL and VI are also relatively powerful. This affirms the idea that quadrupeds power locomotion through torque generation at the hip (Usherwood & Wilson, 2005). The ostrich, a fast bipedal runner, however, has very powerful ankle extensors, particularly the gastrocnemius (Smith et al. 2006). This is not the case in the hare, where the gastrocnemius appears specialised towards generating force economically. This high force generation allows optimisation of the elastic performance of the structure in terms of stretching collagenous components and storing elastic energy (see below). The hare may, for some reason, need to be able to resist high forces at the ankle joint, either for joint rotation or for elastic energy storage. A possible explanation for this requirement is that the hare belongs to a group of animals that are essentially saltators (although the hare appears to use more of a galloping gait at high speed), which might require increased elastic energy storage and an increased need for ankle extension. The major ankle extensor of the hare, the gastrocnemius, is bi-articular, crossing both the ankle and the knee joints. Studies in wallabies suggest that the ankle extensor MTUs appear restricted to spring-like behaviour, rather than contributing to generating work (Biewener et al. 2004). However, it has now been shown in several species, including wallabies, that a substantial amount of the power generated by proximal muscles is likely to be transferred to distal joints via the bi-articular ankle extensors (Jacobs et al. 1996; Aerts, 1998; Dutto et al. 2004; McGowan et al. 2005). Power transfer from the large stifle extensors to the ankle joint may also occur via the gastrocnemius in the hare and this could assist in modulating power output during unsteady-state activities. The elastic gastrocnemius tendon may also aid in modulating the time course of power output of these muscles (power amplification; Galantis & Woledge, 2003). Power transfer is, however, considered to be minimal in the pelvic limb of a running biped, the turkey (Roberts & Scales, 2004), and thus this may explain the apparent lower values seen in ankle extensor estimated power output in horses and hares when compared with those of the ostrich.

Tendons

Data for discernible (mass > 0.01 g) pelvic limb tendons is provided in Table 3. Mass of the tendon of RF (patella tendon) was quite variable. This tendon contains the patella, which is difficult to remove.

We estimated the maximum tendon stress for each tendon from isometric muscle F_max and tendon CSA, as we have no information regarding the velocity of muscle contraction and muscle activity in vivo. Most significant tendons were situated within the distal limb and were relatively long with small CSAs. Estimates of in vivo stress were highest in the gastrocnemius tendon (119 MPa). This value is extremely high and assuming a maximum tendon strength of 100 MPa (Pollock & Shadwick, 1994) means that the estimated safety factor for the hare gastrocnemius tendon is 0.84; this suggests that hares could operate extremely close to their gastrocnemius tendon breaking stress, that gastrocnemius force is controlled via co-ordinated stifle movement or that the gastrocnemius muscle is not fully activated. This maximum stress value is four times greater than that estimated in the horse for the equivalent structure (Payne et al. 2005), and 2–4 times greater than estimated stresses in other mammalian gastrocnemius tendons (Pollock & Shadwick, 1994). However, similar stresses to those estimated in this study (90–112 MPa) are found in the jackrabbit (Lepus townsendii) gastrocnemius (Pollock & Shadwick, 1994) and in human gastrocnemius (Lichtwark & Wilson, 2005a). Although it is uncommon for ankle extensors in large mammals to have low safety factors, it is not surprising. The digitigrade postures of animals such as the horse may mean a greater reliance on the digital flexor tendons for elastic energy storage, and less on the ankle extensor tendons. The relatively more flexed posture of the hare and other smaller mammals could lead to lower digital tendon stresses, but higher stresses in the gastrocnemius tendon. Operating stresses in the gastrocnemius tendon of wallabies and kangaroos during steady hopping are also high, reaching 84 MPa (Alexander & Vernon, 1975). The gastrocnemius muscle in the hare has high F_max estimates, as already discussed, and so the hare may have a greater reliance on the gastrocnemius muscle tendon unit in locomotion, compared with other larger cursors. Of course, we have, by necessity, posed various assumptions in the calculations of stress values for the maximum isometric stress of vertebrate muscle, tendon density and ultimate tendon strength, and these values may be under- or overestimates (it is possible that these parameters vary between and even within individuals); however, the values would need to be significantly different to give a much increased value for the safety factor of the gastrocnemius tendon.

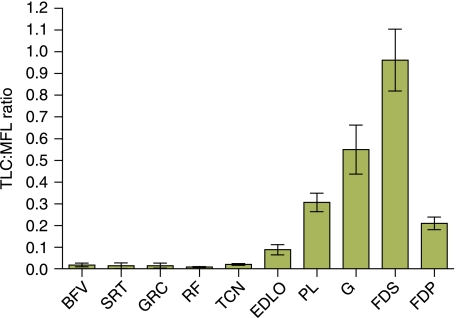
Tendon elongation under maximum isometric force from the muscle was calculated and its ratio to muscle fascicle length considered (Fig. 7). The TLC:MFL ratio gives an index of the relative capacity for/importance of muscle length change vs. tendon length change in locomotion and strain energy storage capabilities at maximum load. In other words, it gives an indication of how ‘stiff’ or how ‘compliant’ an MTU is (note that these definitions are different to those used as mechanical terms). High TLC:MFL ratio values are characteristic of compliant MTUs (those functioning with a high component of passive length change) with tendons that are relatively long and thin, and have relatively short-fibred muscles (able to impose high forces). Such MTUs, e.g. FDS, can function as anatomical ‘springs’, storing and returning elastic energy during locomotion. Those with a low TLC:MFL ratio are stiffer, optimised for actively undergoing maximum length change. Hares appear to have a TLC:MFL ratio in the FDS of near 1, suggesting a considerably stiffer FDS MTU to the horse (9.2). This may indicate a lesser degree of musculoskeletal specialisation in the hare for energy saving during steady-state locomotion than the horse. Nevertheless, all major distal limb tendons are likely to store energy during the stance phase as they are stretched over flexing joints by the loading of body mass through the limb. All had TLC:MFL ratios of greater than 0.4 [above which the tendon can be said to be acting as an elastic energy store (Pollock & Shadwick, 1994)] to support this suggestion.

Fig. 7.

Ratio of tendon elongation (estimated length change elicited at muscle maximum isometric force) to muscle fascicle length (TLC:MFL) for selected pelvic limb tendons in the hare. Data are means ± SD (n = 8).

It has been suggested that it may not be feasible for animals to undertake rapid acceleration if their tendons are evolved to achieve effective energy storage and return at preferred speeds of movement (Biewener, 1998; Biewener & Roberts, 2000). Most mammalian tendons appear to have safety factors higher than expected, evidently to maintain enough stiffness to enable muscles to control length change, posture and limb stiffness. During non-steady activities such as jumping, tendon stress increases to above that seen at preferred speeds and hence a decrease in safety factor occurs (Biewener & Blickhan, 1988). Thicker tendons allow these activities whilst retaining a reasonable degree of ‘safety’. Those animals which possess thinner, more compliant, distal limb tendons, with lower safety factors, are capable of elastic energy storage at preferred speeds of movement, although it is thought that scope for increased muscle forces and hence accelerative ability may then be limited if tendon rupture is to be avoided. It has been shown that adding series elasticity to an MTU will increase the capacity of a muscle to do work, especially on an inertial load (Galantis & Woledge, 2003). Series elasticity also increases versatility (Lichtwark & Wilson, 2005a,b) as the muscle fibres can shorten at a lower speed than the muscle tendon unit, increasing power output at high MTU velocities. In addition, an optimum MTU stiffness exists for optimum function (Lichtwark & Wilson, 2006). Not only therefore may the hare compromise a high gastrocnemius tendon safety factor for increased elastic energy savings, but in addition, this additional benefit of improved versatility may be essential to an animal which often undergoes unsteady-state activities.

Moment arms

The longest maximum moment arms (Table 6) were observed in the gastrocnemius muscle at the ankle joint and the TFL and AD muscles at the hip joint. The AD muscle is extremely large, surrounding the entire posterior and medial aspects of the femur in the hare, and hence it was difficult to measure tendon travel accurately in this large muscle. Therefore, this very large value may not be accurate given the size of the muscle, or it may just reflect the moment arm of the outermost fibres of the AD muscle that are furthest from the joint centre. In addition, although the adductor may play an important role in hip extension, its main action is likely to be in the medio-lateral plane, but due to the configuration and size of the muscle it is difficult to separate or measure the moment arm for each of these functions.

The majority of distal limb muscles had small moment arms with the exception of the gastrocnemius, which surprisingly was especially large in full joint extension. High-force muscles can often have small moment arms to allow a large range of joint motion for a given length change (Lieber & Friden, 2000; Payne et al. 2006). The moment arm of the ankle extensors in bipedal hoppers tends to be large in comparison with quadrupedal animals to create high tendon forces (Alexander et al. 1981). This shows that it is not important for the hare gastrocnemius muscle to create a large range of motion at the ankle (perhaps ground reaction force and tendon elongation are enough to cause this).

In most muscles, moment arms changed with joint angle (Fig. 4) illustrating the importance of measuring and considering moment arms throughout joint motion and not just using a single static measure/estimate. Gastrocnemius at the ankle joint, biceps femoris at both the hip and the knee joints, and TFL and AD at the hip all showed particularly large changes in moment arm from full joint flexion to full joint extension. This may be indicative of the role of the muscle within the limb. A muscle may generate a larger moment of force at a joint at a particular instant of the stride cycle if it has a larger moment arm at this point. For example, the gastrocnemius muscle here can produce a greater moment about the ankle joint when the ankle joint is extended (presuming there is no change in how much force the muscle is producing). The joint is most likely to be fully extended during running (when forces are highest) and especially in late stance, when the MTU is shortening in order to produce the ‘push’ needed to move the centre of mass of the animal up and forwards. This could be an additional adaptation for achieving high power outputs and fast running speeds. Similarly, at the knee joint, biceps femoris has a greater moment arm when the knee is extended. Thus, biceps femoris may have an important role in initiating knee flexion, or supporting the knee joint during flexed postures (such as in stance).

MFL:MA ratios were calculated from mean maximum moment arms (Table 6). A high ratio indicated the ability to move a joint through large ranges (Alexander et al. 1981; Payne et al. 2006). TFL, biceps femoris and SM at the knee joint all had large ratios (long fascicles and small moment arms), suggesting all have capacity to generate force at this joint over a wide range of motion. This may indicate that the hare uses a wide range of knee joint postures during locomotion, which is not surprising given the wide range of locomotor activities a hare might undergo, or that these muscles are important in other activities. Muscles at the hip and ankle joints had much lower MFL:MA ratios, due to larger moment arms/smaller fascicle lengths, respectively, suggesting that their habitual range of motion (during locomotion) may be less than that of the knee joint.

Some researchers have previously discussed the concept of ‘dynamic gearing’ (Carrier et al. 1994, 1998; Gregersen & Carrier, 2004) during locomotion. Muscle force decreases as shortening velocity increases, and so an optimum shortening velocity exists for high muscle power or efficiency. By changing the ‘gear-ratio’ (the ratio between ground reaction force moment arm and muscle moment arm), this may allow the optimum shortening velocity to be maintained throughout different activities, depending on whether power or efficiency is important. Thus, variable muscle moment arms such as described here in the hare (in unison with a changing ground reaction force moment arm) may allow a reduced degree of musculoskeletal specialisation towards one sole function (for example efficient high-speed running, fast acceleration or jumping). In steady-state locomotion, this dynamic gearing is not likely to be beneficial [two-dimesnional spring mass models with constant spring properties explain running dynamics across a wide speed range (McMahon & Cheng, 1990; Robilliard & Wilson, 2005)]; however, to an animal that is likely to undergo unsteady-state activities requiring active shortening of muscles to produce work, the concept of changeable gears might allow muscles in series with elastic elements (for example the gastrocnemius muscle) to continue to produce work effectively across a range of running speeds and thus maximise the animal's accelerative/jumping ability and/or versatility (Carrier et al. 1998). Hence, the apparent variations seen in moment arm with joint angle in the hare, particularly in muscles where large changes are seen, may be essential for maintaining the ability to alter ‘gear-ratio’.

Conclusions

The architecture and moment arms of the pelvic limb muscles of the hare have been quantified. In addition, functional distribution of muscle mass within the pelvic limb has been established. The pelvic limb of the hare consists of relatively large-volume hip extensor muscle, capable of high power, which is essential for activities such as jumping and accelerating quickly. In addition, substantial abduction/adduction musculature may contribute to stability during rapid turning. A proximal-to-distal specialisation in muscle architecture exists in the pelvic limb of the hare, as in other cursorial quadrupeds. Proximal muscles have long fascicles, capable of high power output and performing work. Distal muscles such as the flexor digitorum superficialis and gastrocnemius possess shorter, more pennate fascicles, and are able to produce large amounts of force. In addition, these distal limb muscles possess long tendons, allowing a reduction in distal limb mass and storage of elastic strain energy. Many pelvic limb muscles have moment arms that vary with joint position, allowing change of muscle function at different limb postures and during different locomotor activities.