Prediction of volumetric strain in the human temporomandibular joint cartilage during jaw movement

Abstract

Human temporomandibular joint loading causes pressurization and flow of interstitial fluid in its cartilaginous structures. This largely determines its load-bearing and maintenance capacity. It was hypothesized that during cyclical jaw movements normal pressure distribution dynamics would enable fluid to reach all necessary cartilage regions. This was tested qualitatively by analysis of local volumetric strain dynamics during jaw open–close movements predicted by a dynamic model of the human masticatory system. Finite-element analysis was performed in separate regions of the articular cartilage layers and articular disc. Heterogeneous patterns of dilatation and compression were predicted. Compression was found to be more dominant during jaw closing than opening. The pressure gradient in the superior layer of the articular disc was more mediolaterally orientated than in its inferior layer. The findings suggest that, where necessary, regionally the cartilage can imbibe fluid to protect the subchondral bone from impact loads effectively. In the disc itself presumably all areas receive regular refreshment of interstitial fluid.

Introduction

During jaw movements the human temporomandibular joint is loaded. These loads lead to local deformations in its cartilaginous structures. As both articular cartilage (Mow et al. 1984) and the cartilaginous articular disc (Tanaka & van Eijden, 2003) are not completely incompressible, this causes local volumetric changes.

Cartilage can be considered to be a mixture of solid and fluid constituents (Shrive & Frank, 1998; Wong & Carter, 2003). Local differences in compression or dilatation can cause pressure gradients of the fluid, both within the cartilage, and between the cartilage and the joint cavity. These pressure gradients cause the incompressible fluid to flow through the cartilage matrix and between the cartilage and the joint cavity. This flow supports the exchange of nutrients and waste products within the tissue and their transport into and out of it (Mow et al. 1984). Furthermore, it has been suggested to be a major determinant for chondrocyte biosynthesis (Kim et al. 1995). Consequently, fluid flow is suggested to play a role in the maintenance of the cartilaginous structures of the temporomandibular joint.

Fluid is also a determinant for the mechanical properties of cartilage. Upon loading it pressurizes, making the tissue relatively incompressible. A part of the pressurized fluid moves away with prolonged loading, thereby transferring load to the compressible cartilage matrix. At high strain rates (beyond 0.15% s⁻¹) more than 80% of the load is carried by fluid pressurization, whereas at low strain rates (below 0.005% s⁻¹) the matrix bears more than 80% of it (Li & Herzog, 2004). The cartilage matrix can be treated as hyperelastic, and its stiffness increases with compression (Hasler et al. 1999). Consequently, there is a delicate balance between the relative amount of present fluid and the apparent stiffness of the cartilage.

The synovial fluid also serves as a lubricant between the cartilaginous structures (Tanaka & van Eijden, 2003). When it is pressurized in contacting layers, it carries most of the force down to the subchondral bone through hydrostatic pressure. Roughness of the cartilaginous surfaces will thus hardly contribute to friction between the two (Shrive & Frank, 1998).

For proper maintenance of cartilage it is necessary that nutrients reach every part of it regularly. If nutrients are supplied through fluid flow, the distribution of hydrostatic pressure must change accordingly. The fluid that has been squeezed out of temporarily pressurized locations may return (with fresh nutrients) if the pressure is then released. In structures such as the intervertebral disc a diurnal loading pattern allows for fluid exudation during the day and reimbibition during the night (Li & Herzog, 2004). As the masticatory system remains active during the night (Gallo et al. 1999), the applicability of such a diurnal mechanism for adequate fluid exchange in the cartilaginous structures in the temporomandibular joint is questionable. By contrast, the dynamics of hydrostatic pressure during jaw movement may serve as a mechanism to perform and maintain this function. Furthermore, the loaded region in the temporomandibular joint has been demonstrated to shift continuously during jaw movement (Gallo et al. 2000). This could serve as a mechanism to redistribute the imbibed fluid within the cartilaginous structures.

Pressure and flow of fluid in the cartilaginous structures of the temporomandibular joint during jaw movements cannot be measured. However, they can be predicted by mathematical modelling. To that end a dynamic model of the human masticatory system was developed that included the cartilaginous structures of the temporomandibular joint as finite-element (FE) models (Koolstra & van Eijden, 2005). The transient distribution of dilatation and compression in these cartilaginous structures was analysed during jaw open–close movements. The results were expected to give an indication as to whether this relatively simple movement pattern could contribute to maintain these structures. It was hypothesized that, in particular in the disc, the pressure distribution would be subject to such alterations that it could give rise to flow of fluid throughout the whole disc.

Materials and methods

The model

A biomechanical model of the human masticatory system (Fig. 1A) was constructed using MADYMO 6.1 (TNO Automotive, The Netherlands), a simulation program that combines the capabilities of multibody motion and FE modelling. It contained the skull and the mandible, which were modelled as rigid bodies. They articulated at two six-degrees-of-freedom temporomandibular joints. Twelve pairs of Hill-type muscles were able to move the mandible with respect to the skull (Koolstra & van Eijden, 2005). Their attachments, maximum forces, fibre lengths and sarcomere lengths (Table 1) had been obtained from eight human cadavers (van Eijden et al. 1995, 1996, 1997). The contractile characteristics had been shaped according to van Ruijven & Weijs (1990).

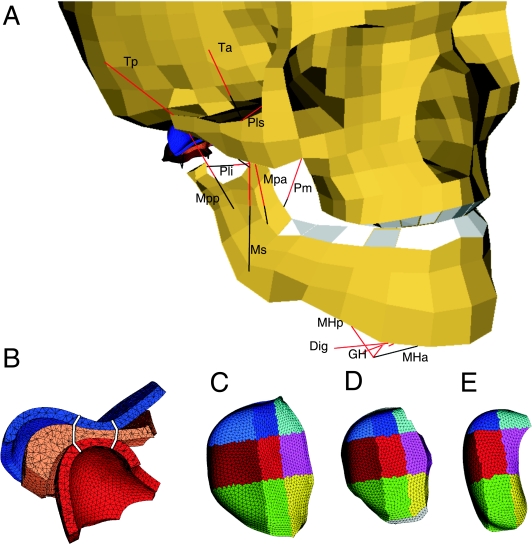
Fig 1.

The model. (A) Anterolateral view. Red lines: muscle contractile element. Black lines: muscle serial elastic element. Ta, anterior temporalis; Tp, posterior temporalis; Ms, superficial masseter; Mpa, anterior deep masseter; Mpp, posterior deep masseter; Pm, medial pterygoid; Pls, superior lateral pterygoid; Pli, inferior lateral pterygoid; Dig, digastric; GH, geniohyoid; MHa, anterior mylohyoid; MHp, posterior mylohyoid. Thin black lines, part of articular capsule. Dig, GH, and Mhp are connected to the hyoid bone (not shown), MHa to the mylohyoid raphe (black line). (B) Sagittal cross-section of the cartilaginous structures of the jaw joint: blue, temporal cartilage layer; orange, articular disc; red, condylar cartilage layer. White lines: separation between anterior, intermediate and posterior regions. (C) Selected regions in the temporal cartilage layer, superior view. Cyan, light blue and blue: medial regions; magenta, light red and red: central regions; yellow, light green and green: lateral regions. Anterior, intermediate and posterior, respectively. (D) Selected regions in the articular disc. (E) Selected regions in the condylar cartilage layer.

Table 1.

Model parameters

Moments of inertia	Mass (kg)	Ixx (kg m2)	Iyy (kg m2)	Izz (kg m2)
Lower jaw	0.44	0.00086	0.00029	0.00061

Muscle	Muscle length (mm)	Max. force (N)	CE, optimum length (mm)	SE, length (mm)
Superficial masseter	48.0	272.8	22.6	25.8
Deep anterior masseter	29.5	73.8	21.8	17.1
Deep posterior masseter	30.9	65.8	15.0	13.3
Anterior temporalis	57.4	308.0	30.7	24.2
Posterior temporalis	62.9	222.0	31.3	28.8
Medial pterygoid	43.3	240.0	14.1	27.6
Superior lateral pterygoid	29.1	38.0	21.5	9.4
Inferior lateral pterygoid	27.2	112.8	22.3	9.0
Anterior digastric	51.9	46.4	42.6	3.0
Geniohyoid	48.5	38.8	35.3	5.4
Anterior mylohyoid	21.8	63.6	24.0	0.0
Posterior mylohyoid	44.8	21.2	39.7	0.0

CE, contractile element; SE, series elastic element.

No. of finite elements	Temporal cartilage	Articular disc	Condylar cartilage
right joint	14 878	12 516	12 123
left joint	14 166	12 660	12 233

Mooney-Rivlin constants	C1	C2
articular disc	9.0 × 105	9.0 × 102
temporal and condylar cartilage	4.5 × 105	4.5 × 102

Both temporomandibular joints contained two deformable articular cartilage layers of 0.5 mm (Hansson et al. 1977) connected to the temporal bone and the mandibular condyle, respectively. As the influence of the stiffness of the bony articular surfaces on the tension and deformation of the overlying articular cartilage layers can be considered to be negligible (Dar & Aspden, 2003) they were assumed to be rigid. Between the cartilaginous articular layers was a freely movable deformable cartilaginous articular disc (Fig. 1B). This was medially and laterally connected to the condylar neck with pairs of inextensible wires representing the lower part of the articular capsule and anteriorly to the attachment of the superior lateral pterygoid muscle to the condylar neck. In the present model the temporomandibular ligaments were not included as they have been demonstrated to be of negligible influence in symmetric jaw movements (Koolstra & van Eijden, 1997; Koolstra et al. 2001). Contact between the deformable cartilaginous structures was assumed to be frictionless. The joint reaction force was computed with a penalty-based contact algorithm. The geometry of the deformable structures had been obtained from the right temporomandibular joint of one cadaver (Beek et al. 2000,2001a). The left side joint was constructed as a mirror image. The volumes of the deformable structures were divided into tetrahedral finite elements with edges of maximally 0.25 mm (HyperMesh 6.0, Altair Engineering GmbH, Böblingen, Germany) as specified in Table 1.

In order to quantify the distribution of hydrostatic pressure in the temporal cartilage, the condylar cartilage and the articular disc, these structures were divided into, respectively, 18, 18 and 27 portions. In the articular disc an anterior, intermediate and posterior region were defined concomitant with its anterior band, intermediate zone and posterior band, respectively. They were subdivided into equally wide lateral, central and medial regions, excluding the lateralmost and medialmost 5% of the discs (Fig. 1D). Each region was subdivided into an upper, middle and lower layer of equal thickness. The temporal cartilage and the condylar cartilage were similarly subdivided (Fig. 1C, E). The regional boundaries coincided with those of the articular disc when the mouth was opened (Fig. 1B). Each region was subdivided in a superficial and deep layer of equal thickness, the latter layer being connected to the subchondral bone.

As the present analysis focused on the response within the relatively short time of an open–close cycle, the material properties of the cartilaginous structures were approximated according to the Mooney–Rivlin material model (Chen et al. 1998; Koolstra & van Eijden, 2005). Its constants (Table 1) were approximated from experiments on human temporomandibular joint discs according to Beek et al. (2003).

Simulations

The jaw was closed at the start of all simulations. From this position symmetrical jaw-open movements were simulated by a 100% activation of the digastric, geniohyoid, mylohyoid and lateral pterygoid muscles simultaneously. Thereafter, the jaw was closed by a 25% simultaneous activation of the masseter, medial pterygoid and temporalis muscles. Finally, a second jaw-open movement was performed. Activation of each muscle was defined as a function of time. These functions included activation and deactivation ramps of 45 and 75 ms, respectively, to incorporate activation dynamics (Winters & Stark, 1987). During jaw closing a force of 50 N was applied between the central incisors to simulate food resistance. This force is about 10 times the yield force of cheese (Gavião et al. 2004).

The results were analysed and visualized using HyperView 7.0 (Altair Engineering GmbH, Böblingen, Germany). Changes in volume in each of the elements in the cartilaginous structures on the right side were monitored as an indication of hydrostatic pressure. The total change in volume of each region served as a measure for volumetric strain.

Results

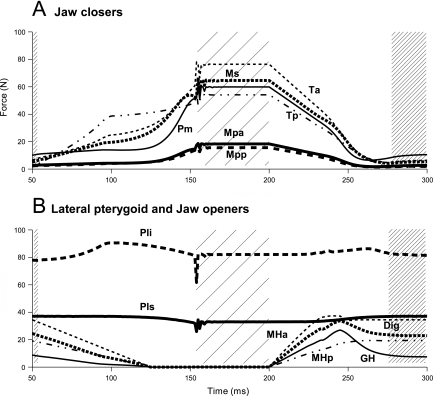
The muscle forces as a result of the applied muscle activation pattern, the force–length and force–velocity relationships, and the passive tensions are depicted in Fig. 2. These forces generated relatively fast jaw movements, but in a pathway similar to that of natural movements. The mandibular condyles moved forward along the articular eminence when the jaw opened to about 3 cm interincisal distance, and moved backward when the jaw closed. The articular disc followed the condylar displacements.

Fig 2.

Muscle forces during jaw close–open movement. Force (N) of masticatory muscles as a function of time (ms). (A) Jaw closers. (B) Lateral pterygoids and jaw openers. Forces of left and right muscles were identical. Start closing movement: t = 50, jaw closed: t = 150, start opening movement: t = 200. Wide and narrow hatchings: jaw closed and open, respectively. Muscle notations as in Fig. 1.

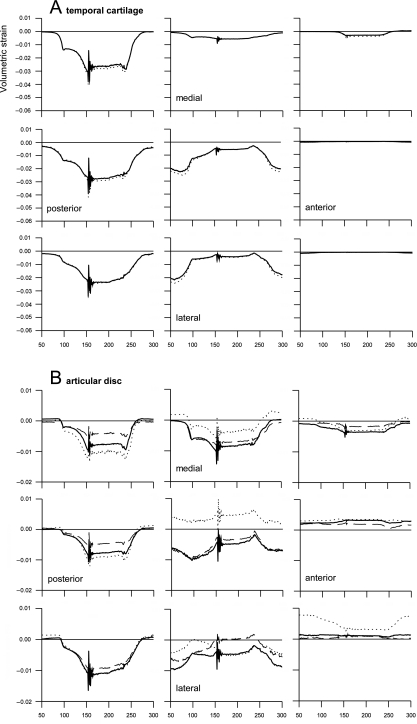
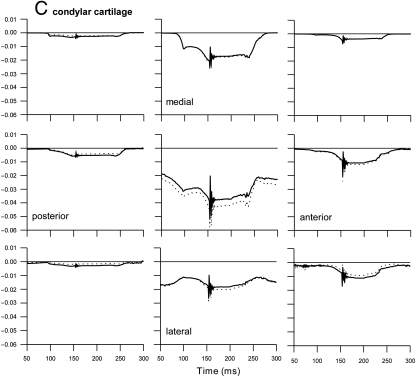
The predicted compressive volumetric strain in the temporal and condylar cartilage reached about 4 and 5.5%, respectively. In the articular disc it remained below 1.5% (Fig. 3). The largest compression was predicted when the teeth contacted each other after the jaw had been closed. In the temporal cartilage the compressed areas alternated between the posterior region (mandibular fossa) and the intermediate region (articular eminence) when the jaw was closed and opened, respectively. In the condylar cartilage compression was concentrated in the central area and was greater as the jaw was closed than when it was open. In both the temporal and the condylar cartilage compression in the surface layer was slightly less than in the deep layer. The medial regions of the temporal and condylar cartilage were relaxed when the jaw was open. They became compressed in the later phase of jaw closing. Their central and lateral regions remained compressed at all times. Consequently, the pressurized area shifted from lateral when the jaw was open to more medial during jaw closing (Fig. 3A, C).

Fig 3.

Volumetric strain during jaw close–open movement. Volumetric strain as a function of time (ms). Positive strain: dilatation, negative strain: compression. Start closing movement: t = 50, jaw closed: t = 150, start opening movement: t = 200. Each panel represents a different region from posterior (first column) to anterior (last column) and from medial (first rows) to lateral (third rows). (A) Temporal cartilage layer; solid lines: surface layer, dotted lines: deep layer. (B) Articular disc; dotted lines: upper layer, solid lines: middle layer, dashed lines: lower layer. (C) Condylar cartilage layer; solid lines: surface layer, dotted lines: deep layer.

Dilatation was predicted only in the articular disc (Fig. 3B). This occurred predominantly in the superior layer of its central part, where simultaneously the middle and inferior layers were compressed. The changes in volumetric strain were relatively small in the anterior band of the disc. In the posterior band, which was compressed during jaw closing and relaxed during jaw opening, they were far more variable. In the lateral portion of the intermediate zone compression decreased upon jaw closing in contrast to its medial portion.

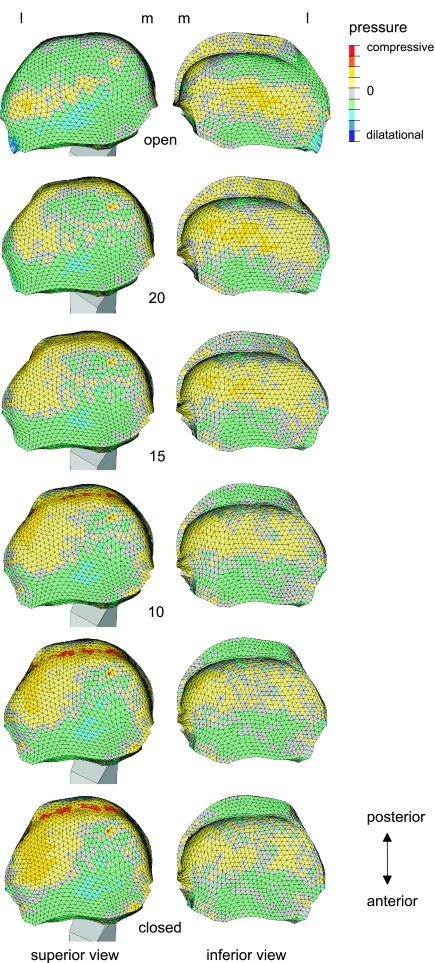
The differences in volumetric strain of the temporal cartilage and the condylar cartilage are reflected in the difference in the predicted distribution of hydrostatic pressure between the upper and lower side of the articular disc (Fig. 4). Superiorly, large portions were under a considerable dilatational pressure. Inferiorly, these areas were more sparse. Superiorly, the pressurization had a strong mediolateral heterogeneity as dilatation on the medial side was accompanied by compression on the lateral side. This mediolateral heterogeneity was not present inferiorly where the heterogeneity had a more antero-posterior orientation.

Fig 4.

Pressure in the articular disc during jaw closing movement. Distribution of pressure as a function of jaw gape (in degrees). Left: superior view, right: inferior view. L, lateral; m, medial. The patterns during jaw opening were similar.

Discussion

The present results suggest that during jaw movement there is a considerable heterogeneity in volumetric strain within and between the cartilaginous structures of the temporomandibular joint. Volumetric strain causes hydrostatic pressure of the interstitial fluid and pressure gradients lead to fluid flow. Although the direct relationship between volumetric strain and hydrostatic pressure is temporary as pressure equilibrates with time as a consequence of fluid flow, the predicted volumetric strain can be considered to be indicative for hydrostatic pressure and thereby for mechanical properties such as stiffness and friction (Shrive & Frank, 1998; Soltz & Ateshian, 1998; Tanaka & van Eijden, 2003; Wong & Carter, 2003). The strain gradients can be considered to be indicative for fluid flow potential and thus for the maintenance capacity of the cartilage (Maroudas, 1976; Mow et al. 1984; Kim et al. 1995).

Although the present model has some limitations, to our knowledge it is the first to enable dynamic analysis of volumetric strain in the temporomandibular joint during jaw movements controlled by muscle activation. The large deformations of the cartilaginous structures of the joint (Beek et al. 2001b) were successfully modelled with the Mooney–Rivlin material model. This material model treats the cartilage as nearly incompressible. This assumption is considered to be acceptable for the relatively fast movements in normal activity (Kim et al. 1995; Shrive & Frank, 1998). It has the consequence, however, that the predicted volumetric strains were relatively small. For loads of longer duration cartilage displays creep. This viscoelastic property is caused by exudation and imbibition of interstitial fluid. Therefore, for slowly changing loads, for instance during clenching, the material does no longer behaves as nearly incompressible, and the applied Mooney–Rivlin material model would be invalid. The modelled resistance to tension is not very different from the resistance to compression while experimentally obtained tensile and compressive material properties can differ by orders of magnitude, for instance as a result of fibre reinforcement (Tanaka & van Eijden, 2003). The predicted strain in the dilated regions is therefore presumably overestimated with respect to the regions under compression. The applied material models disregarded the viscoelastic properties of cartilage. Although various material models have been proposed to implement these characteristics for the articular disc of the temporomandibular joint (Beek et al. 2003; Donzelli et al. 2004; Allen & Athanasiou, 2006; Pérez del Palomar & Doblaré, 2006), each has different characteristics. Furthermore, none of them was applicable in the present dynamic model. The consequences of disregarding viscoelastic behaviour in the present analysis are discussed in the Appendix. They can be considered to be limited. For instance, the viscoelastic creep in the disc is performed with a much longer (up to 45 s) time constant (Tanaka & van Eijden, 2003) than the cycle time of jaw movements, and is presumably limited by surface consolidation (Wong & Carter, 2003). In a qualitative analysis, it has been demonstrated that the applied simplifications do not produce unrealistic results (Koolstra & van Eijden, 2005). Yet, for a quantitative analysis they have to be interpreted with caution. Although fluid flow, one of the major determinants for viscoelastic behaviour, itself was not predicted, its prerequisites are indicated by the predicted strains. The consequence of actual fluid flow is that the hydrostatic pressure gradients generated as a consequence of volumetric strain differences equilibrate with time.

As the cartilaginous structures in the temporomandibular joint have a complex shape and undergo large deformations during functioning, they have been modelled using tetrahedral finite elements. The accuracy of these elements is less sensitive to element shape distortion than, for instance, so-called brick-elements. If such distortions should occur this would lead to numerical instabilities, and the simulation would have to be aborted. Convergence tests have demonstrated that an element size of 0.5 mm was adequate for this model (Koolstra & van Eijden, 2005). The present resolution was 0.25 mm to accommodate a better definition in the predicted stress and strain distributions.

In the articular cartilage layers the predicted volumetric strains were almost exclusively compressive. In the articular disc both compression and dilatation were predicted. Dilatation occurred in its anterior region, and more posteriorly only in the superior layer while the middle and inferior layers remained compressed (Fig. 3B). In the anterior portions the strain is most probably caused by pull of the superior lateral pterygoid. The difference between the superior and the other layers can be attributed to the incongruent joint contact. The articular tubercle makes a smaller and deeper impression in the superior layer of the disc than the mandibular condyle makes in its inferior layer, thereby leaving more room for dilatation. Furthermore, the disc bends as it is pulled taut over the mandibular condyle. These predictions, however, do not indicate necessarily that the articular disc exudes less fluid in the upper joint cavity than in the lower one. Owing to the viscoelastic character of the disc (Donzelli et al. 2004; Allen & Athanasiou, 2006) the hydrostatic pressure equilibrates over time. As viscoelasticity was not implemented in the present model, the effects of fluid exudation and imbibition could not be estimated quantitatively. The predicted volumetric strain differences (Fig. 3) also affect the situation in the solid matrix. This matrix is fibre-reinforced (Tanaka & van Eijden, 2003), which improves its resistance to stretch. As stretch was predicted predominantly in the upper layer of the disc, the present results suggest that this part primarily benefits from fibre-reinforcement. Consequently, the predicted stretch may be overestimated.

Generally, there is more compression during jaw closing than during jaw opening. This implies that the cartilaginous structures in the joint imbibe and exude fluid during, respectively, jaw opening and closing. By contrast, the central and lateral regions of the intermediate zone of the articular disc and temporal cartilage are more compressed during jaw opening as they are primarily load bearing during this movement (Koolstra & van Eijden, 2005).

The predicted heterogeneity in volumetric strain can be related to a relatively rapid distribution of solutes through the different cartilaginous structures (Mow et al. 1984). Although low-molecular-weight nutrients and waste products may be distributed easily by diffusion, for large molecules diffusion is extremely limited (Maroudas, 1976). Therefore, a continuously changing pattern of pressure gradients is particularly beneficial for the distribution of high-molecular-weight solutes (Ferguson et al. 2004).

The differences in predicted strains between the articular cartilage layers and the articular disc are in agreement with the difference in stiffness between these structures. The articular disc of the temporomandibular joint may deform up to 30% when the joint is loaded (Beek et al. 2001b, 2003). The presently predicted volumetric strain was much less. This difference is in agreement with the finding that shear deformation in the disc predominates over compressive deformation (Koolstra & van Eijden, 2005), indicating that changes in shape are much larger than volumetric changes. If the jaw is moved with more muscle force, causing a more heavily loaded joint, compression and relaxation will also be greater.

At the inferior side of the articular disc compression is predicted in and around the intermediate zone while anteriorly and posteriorly of this area some dilatation can be observed (Fig. 4). The differences between compression and dilatation are the largest when the jaw is open. At the superior side of the disc, however, the alternation between compression and dilatation is more medio-laterally orientated. In the open position the intermediate zone was compressed laterally and in the closed position its central part was also compressed. This mediolateral shift is similar to the observations of Gallo et al. (2000). The predicted patterns suggest that pressure gradients in the superior and inferior layer of the disc are more or less cross-wise. Although a quantitative relationship between pressure gradients and the amount of internal fluid flow has not been assessed, these patterns suggest that no area of the disc is a priori excluded from a regular refreshment of interstitial fluid.

The presence of interstitial fluid allows cartilage to protect the subchondral bone from impact loading. This occurs in the jaw joint when the teeth strike each other, or when they meet something hard between them as they close. In Fig. 3 this is indicated by sudden volumetric strain changes about 100 ms after the jaw had started closing. In the regions where the largest effects of impact were observed during jaw opening a relaxation was predicted. Consequently, these regions have had the opportunity to imbibe fluid, suggesting that thereafter they are ready to deal with a possible impact effectively.

In conclusion, the present results indicate that the construction of the human temporomandibular joint permits its cartilaginous structures to regulate their mechanical properties effectively by imbibition, exudation and redistribution of fluid. Furthermore, they suggest that refreshment of this fluid can be performed during normal function, such that for proper maintenance the cartilaginous structures do not have to rely only on an alternation of average baseline loading and relaxation during the day and night, respectively.

Appendix

The applicability of the Mooney–Rivlin material model was tested by analysing the volumetric strain in a cylindrical disc subjected to a large strain indentation. The geometry of the disc (radius = 3.49 mm, thickness = 2.5 mm) and the indenter (radius = 1.97 mm) was similar to that of Beek et al. (2003). The applied material model was either a Mooney–Rivlin model as presently applied or a linear viscoelastic model as described by Allen & Athanasiou (2006). In the latter the relaxation modulus (E_r), the instantaneous modulus (E_i) and the coefficient of viscosity (µ) had been obtained from various regions of porcine temporomandibular joint discs. For the present test their averages, E_r = 133 kPa, E_i = 829 kPa, µ = 5.7 MPa s, were used. The indenter applied a 1-Hz sinusoidal compression cycle to the disc with a maximum strain of 20%. The volumetric strain was assessed in three areas: the centre of the disc, halfway between the centre and the outer rim, and adjacent to the outer rim. They occupied a layer with a thickness of about 1 mm between the upper and lower surfaces.

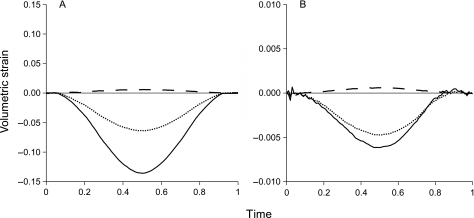
Qualitatively the volumetric strain in these areas was marginally dependent on the applied material model (Fig. A1). The largest compressive strain was predicted in the central area whereas in the outer area dilatation was predicted, irrespective of the applied material model. By contrast, quantitatively there were large differences as the volumetric strains in the linear viscoelastic model were up to 20 times larger than when the Mooney–Rivlin model was applied. Because the interstitial fluid is barely compressible, this difference has to be attributed to flow of this fluid. In areas under compressive volumetric strain fluid has to be squeezed out whereas in areas with dilatational strain it must be imbibed. Consequently, the magnitude of the volumetric strain can be considered to be indicative for the hydrostatic pressure and thus for the dynamics of fluid flow. In the Mooney–Rivlin model the changes in volumetric strain in the central area were less than in the other areas than predicted by the linear viscoelastic model. This suggests that the consequences of high volumetric strain are underestimated in the Mooney–Rivlin model. However, it must be noted that the influence of the non-linear behaviour of cartilage when subjected to large deformations (Hasler et al. 1999) has not been taken into account.

Fig A1.

Influence of the material model on predicted volumetric strain. Predicted volumetric strain in a cartilaginous disc under a 1-Hz, 20% sinusoidal compression cycle. (A) Linear viscoelastic material model. (B) Mooney–Rivlin material model. Continuous lines: area in centre. Dotted lines: area halfway between centre and outer rim. Dashed lines: area adjacent to outer rim.