Abstract
Saccades executed with the head stationary have kinematics conforming to Listing's law (LL), confining the ocular rotational axis to Listing's plane (LP). In unilateral vestibular deafferentation (UVD), the vestibuloocular reflex (VOR), which does not obey LL, has at high head acceleration a slow phase that has severely reduced velocity during ipsilesional rotation, and mildly reduced velocity during contralesional rotation. Studying four subjects with chronic UVD using 3D magnetic search coils, we investigated kinematics of stereotypic rapid eye movements that supplement the impaired VOR. We defined LP with the head immobile, and expressed eye and head movements as quaternions in LP coordinates. Subjects underwent transient whole body yaw at peak acceleration 2,800°/s2 while fixating targets centered, or 20° up or down prior to rotation. The VOR shifted ocular torsion out of LP. Vestibular catch-up saccades (VCUS) occurred with mean latency 90 ± 44 ms (SD) from ipsilesional rotation onset, maintained initial non-LL torsion so that their quaternion trajectories paralleled LP, and had velocity axes changing by half of eye position. During contralesional rotation, rapid eye movements occurred at mean latency 135 ± 36 ms that were associated with abrupt decelerations (ADs) of the horizontal slow phase correcting 3D deviations in its velocity axis, with quaternion trajectories not paralleling LP. Rapid eye movements compensating for UVD have two distinct kinematics. VCUS have velocity axis dependence on eye position consistent with LL, so are probably programmed in 2D by neural circuits subserving visual saccades. ADs have kinematics that neither conform to LL nor match the VOR axis, but appear instead programmed in 3D to correct VOR axis errors.
Keywords: Abrupt decelerations, Listing's law, Saccades, Vestibular catch-up saccades, Vestibulo-ocular reflex
Introduction
Long regarded an organizing principle of ocular motility, constraint on torsion by Listing's law (LL) effectively reduces the rotational freedom of the eye from three to only two degrees (horizontal and vertical) during visually guided eye movements with the head upright and stationary (Tweed and Vilis 1990). Conformity with LL can be demonstrated by expressing ocular rotational axes as mathematical “quaternions”, that, when plotted, lie in Listing's plane (LP) (Haslwanter 1995). Unlike 1D velocity that is simply the time derivative of position, 3D eye velocity is a function both of eye position and its derivative. While it is possible to consider the time derivative of each component of 3D eye position, this set of derivatives differs from 3D velocity in a way critical to neural programming of saccades (Raphan 1997, 1998; Quaia and Optican 1998, 2003). The ocular position axis will be constrained to LP if, in the velocity domain, the ocular velocity axis changes by half the amount of eye position change (Tweed and Vilis 1990). Since with the head upright and stationary the eye begins in LP, half angle behavior constrains the eye to remain in the plane, and so this kinematic velocity constraint can usually be considered equivalent to LL. However, if eye position begins outside LP at onset of an eye movement subsequently conforming to half angle kinematics, eye position remains in a plane parallel to but displaced torsionally from LP. This is the case when saccades are initiated from non-LL torsion: subsequent vertical saccades have velocity axes that change by one half of eye position, but maintain initial non-LL torsion so that their quaternion trajectories parallel LP (Crane et al. 2005b). Therefore, half angle kinematics limit visually guided saccades to 2D.
The VOR violates LL since the reflex must compensate for head rotation about arbitrary axes irrespective of eye position (Misslisch et al. 1994; Thurtell et al. 1999, 2000; Crane et al. 2005a). However, the VOR does not violate LL with the ideal zero-angle dependency, but changes by approximately one quarter the change in eye position in most (Misslisch et al. 1994; Thurtell et al. 1999, 2000; Crane et al. 2005a) but not all situations (Crawford and Vilis 1991; Tweed et al. 1994; Misslisch and Hess 2000). Since the slow phase eye movements generated by the VOR depart LP, the normal VOR may be considered to have kinematics programmed in 3D.
The normal angular VOR is driven in push–pull by sensory inputs from the right and left labyrinths. After unilateral vestibular deafferentation (UVD), the VOR slow phase becomes undercompensatory under many conditions. The deficient VOR slow phase is often supplemented by rapid eye movements. Vestibular catch-up saccades (VCUS) are observed in normal subjects supplementing the heave (Tian et al. 2002a) and surge linear VORs (Tian et al. 2006), and during high acceleration, ipsilesional rotation in chronic but not acute UVD (Tian et al. 2000, 2007; Peng et al. 2005). During both rotation and translation, VCUS significantly increase overall compensatory eye movement gain, and have amplitudes strongly correlated with vestibular gaze position error (Tian et al. 2000).
The VOR slow phase during high acceleration transient yaw also exhibits abnormalities during contralesional rotation: gain is moderately reduced, and the velocity axis is tilted anteriorly to the earth-vertical yaw axis imposed on the head (Aw et al. 1996a; Crane et al. 2005c, 2007; Tian et al. 2007). Rapid eye movements occur that have been termed abrupt decelerations (ADs), because they are associated with horizontal eye velocity slowing, or occasionally even a direction reversal. Normal older humans have modestly reduced slow phase VOR gain during high acceleration yaw, and exhibit ADs (Tian et al. 2001a). This suggests that ADs are associated with a VOR slow phase deficit. However, the kinematics of ADs have not been previously studied using 3D methods. If ADs have kinematics similar to visually guided saccades, then they would maintain any non-Listing's torsion introduced by the preceding VOR slow phase. Alternatively, ADs might also include a slowing or even reversal of non-Listing's slow phase VOR torsion. In that event, ADs might increase or decrease non-Listing's torsion.
Both VCUSs and ADs are evoked by vestibular stimulation, and would not necessarily be expected to conform to LL that is strictly applicable only with the head immobile. The present study examined the complete rotational kinematics of VCUS and ADs in humans with chronic UVD, and compared these with LL. We asked the question whether these two types of rapid eye movements have kinematics restricted to 2D as is the case for visually guided saccades, or whether the kinematics of VCUSs or ADs might be 3D as is typical of the slow phase VOR. Possible differences in the dimensionality of the kinematics of these two types of rapid eye movements might reflect fundamental differences in their neural programming.
Methods
Subjects
Four unilaterally vestibulopathic subjects were studied after giving written informed consent according to a protocol approved by the UCLA Institutional Review Board in conformity with the tenets of the Declaration of Helsinki. Subjects were selected from a larger longitudinal study of 15 subjects with chronic UVD, two-thirds of whom had been noted using 2D methods eventually to exhibit at least some VCUS during high acceleration ipsilesional yaw (Tian et al. 2007), and roughly half to exhibit at least some ADs during contralesional yaw. We studied here using 3D methods subjects with UVD from the larger study who had developed consistent VCUSs, ADs or both during transient whole body yaw rotation. Among the four such subjects, three had both consistent VCUSs on ipsilesional rotation and ADs on contralesional rotation; one subject exhibited consistent ADs on contralesional rotation and had exhibited VCUS on ipsilesional rotation during the first year following acute UVD, but no longer exhibit VCUSs when tested for these experiments 5 years later. Mean age of the current subjects (2 females, 2 males) was 65 ± 13 (standard deviation, SD, range 53–77) years. Subjects had undergone either vestibular nerve section or labyrinthectomy an average of 10 ± 4 (range 5–13) years previously. Both types of surgeries led to functionally similar UVD. Three subjects with UVD had facial palsy after surgery but none had evidence of cerebellar dysfunction or other neurological deficit, and no difficulty in viewing targets binocularly. Subjects underwent ophthalmological examination to verify that they had normal corrected vision in each eye. Subjects were instructed to omit medication on the day of the experiment. Subjects were monitored during experiments via infrared closed circuit television and an intercom.
Magnetic search coil measurements
Angular eye and head positions were measured with dual winding scleral magnetic search coils (Skalar Medical, Delft, The Netherlands) (Collewijn et al. 1975), as described for the current laboratory (Crane and Demer 1998). Reference magnetic fields were generated by three pairs of solenoid coils, each 2 m in diameter, and arranged to form the sides of a cube (C-N-C Engineering, Seattle, WA). This configuration placed the center of the cube near eye level. The two vertically oriented coil pairs were driven by 60 kHz sinusoidal currents in phase quadrature (Collewijn et al. 1975). The horizontally oriented coil pair was driven by a 120 kHz sinusoidal current (Robinson 1963). One subject who had normal facial nerve function and corneal sensation wore binocular search coils. Surgery creating UVD frequently sacrifices the facial nerve, resulting in ipsilesional facial weakness including the orbicularis oculi muscle necessary for normal blinking and corneal protection. Three subjects had poor blinking function and mild exposure keratopathy of the ipsilesional eye due to facial nerve paresis; these three subjects wore a search coil annulus on contralesional eye only to avoid the possibility of ipsilesional corneal injury due to corneal drying. Coils were placed under topical anesthesia with proparacaine 0.5%. Angular head position was measured via dual search coils mounted on a bite bar, custom molded to the upper teeth of each subject so that they were rigidly coupled to skull motion. Search coils were connected to external detectors (C-N-C Engineering, Seattle, WA).
Horizontal, vertical, and torsional components of eye and head positions were displayed on a digital polygraph, passed through precision-matched, programmable low-pass filters with bandwidth (4-pole Butterworth) set to 300 Hz, and digitally sampled at a rate of 1,200 Hz at 16 bit resolution by a Macintosh compatible computer running the MacEyeball software package (©Regents of the University of California) under LabView (National Instruments, Austin, TX).
Stimuli
Subjects were rotated by a 500 N-m stepper motor (Compumotor, Rohnert Park, CA) configured as a position servo described previously (Crane and Demer 1998). The motor resolved 425,984 steps per revolution, below the noise level of the search coil system and thus indistinguishable from continuous rotation. The presence of the motor did not have a detectable effect on search coil measurements. Subjects sat with their heads comfortably upright in non-metallic chair mounted on the servomotor as previously described (Crane and Demer 1998). Subjects were secured via multiple belts to the densely padded chair. In order to faithfully couple rotator motion to the head, the forehead, temples, malar regions, and chin of each subject were firmly secured to a chair-mounted head holder by pads and adjustable clamps cushioned with stiff conforming foam (Confor-foam, Aearo Specialty, Indianapolis, IN).
Every rotational trial was preceded by a 2-s calibration recording in which the stationary subject looked directly at centered target on a tangent screen 175 cm distant. In 60 s recordings, LP was defined for each eye as subjects tracked the quasi-random horizontal and vertical movements of a projected laser target moving over a broad range widely sampling secondary and tertiary positions up to 20° eccentricity. The angular VOR was tested during 50 s trials which included 20 directionally unpredictable transient yaw rotations (10 in each direction). During each trial subjects were asked to fixate a target located at eye level, approximately 20° up, or approximately 20° down. The target consisted of a laser projected dot against a dark background in an otherwise dark room. Onset of rotations varied randomly from periodic by ≤ 250 ms to avoid predictive effects.
Head position was adjusted so that the rotational axis was midway between the external auditory canals, which were about 7 cm posterior to the eyes. This axis was chosen to minimize the translational stimulus to the otoliths. Rotations had a peak acceleration of 2,800° per s2 to a velocity of 190° per s, moving the head 40° in 250 ms, which was the time at which peak velocity occurred. At 300 ms the velocity averaged 150° per s. The head moved to its maximal offset of 55° after 550 ms.
Data analysis
Data were analyzed automatically using custom software written under LabView 7.1 (National Instruments, Austin, TX) on Macintosh G5 computers (Apple Computer, Cupertino, CA). For each subject, rotational transients were grouped based on direction of rotation, and initial eye position. Processing of all data channels was identical to avoid introduction of temporal artifacts. Transient rotations in which eye position varied by >0.2° in the 80 ms prior to rotation were discarded as failures of fixation and not considered for further analysis.
Sampled search coil voltages were corrected for misalignment of the sine non-linearity in the pitch axis of the search coil system, and the resulting Fick angles were converted to rotation matrices as previously described (Haslwanter 1995; Crane and Demer 1997). Some of the data are represented here in Fick angles since this format is intuitively familiar for many readers. Data from LP definition and VOR trials were first corrected for possible imperfect alignment of the coils on the eye in central gaze during the immediately preceding reference trial using quaternions as previously described (Crane et al. 2006a, b, 2007). Position data for each eye and the head were then rotated into and expressed in a Listing's coordinate system defined by the most recent determination of LP for that individual eye. For analysis purposes, this means that if the LPs of the two eyes of the same subject were nonparallel, the same physical head motion would be represented differently relative to the left and right eyes during the same trial.
Artifact due to torsional scleral coil slippage was identified by comparing measured ocular torsion with that predicted by LL during the period of visual target fixation immediately prior to each head rotation. Ideal LL coil torsion (Ψideal) was calculated from the yaw (θ) and pitch (ϕ) eye positions in a Fick coordinate system as given below:
| (1) |
During visual fixations between rotational transients, at roughly 3 s intervals, ideal and measured torsion were compared to detect coil slippage. Since LL prevails during these visual fixations, discrepancies between ideal and actual coil torsion were considered to reflect slippage of the search coil annulus around the limbus, which was corrected using a new reference matrix prior to analysis of the next VOR response to the transient yaw stimulus. Correction was performed during each fixation prior to rotation even though eye position typically did not vary by more than the noise of the system among rotations. After any such corrections, data from each rotational transient was temporally aligned and averaged as previously described (Crane and Demer 1998). Eye-in-head position was then calculated.
For kinematic analysis, eye and head positions relative to LP were determined as quaternions in Listing's coordinates. Velocity vectors (ω) for the eyes and head were computed from the corrected quaternion position (q) and derivative (q̇) as previously described (Haslwanter 1995; Walker et al. 2004; Crane et al. 2005a, b): ω = 2q̇/q. The quaternion derivative (q̇) was calculated from position (q) by taking the derivative of each component of the quaternion and filtering with a third order Butterworth filter with 50 Hz cutoff frequency. The tilt angle of the velocity vector relative to LP, α (in the vertical direction), is determined using the horizontal and torsional components of velocity (Walker et al. 2004; Crane et al. 2005a, b): α = tan−1(t/h). The tilt angle of the velocity vector relative to LP in the horizontal direction (β) was calculated using the vertical and torsional components of the eye velocity vector: β = tan−1 (t/v). Linear regression was used to calculate the ratio of the tilt of the VOR velocity axis in the vertical direction, α, relative to vertical eye position. This value is reported as the tilt angle ratio (TAR) for the VOR. Regression was performed separately for each sampled time point after onset of head motion. After the initial fit, data points lying more than 2SD from the fit were removed. This process was then repeated once to determine the final slope and correlation coefficient (R).
Subjects were chosen so that they all exhibited VCUSs, ADs, or both beginning 40–200 ms after rotation onset. Saccadic eye movements in the same direction as the VOR slow phase were considered to be VCUS (Tian et al. 2000). ADs or reversals in horizontal slow phase eye velocity were considered to be ADs (Tian et al. 2001a). Both VCUSs and ADs were identified by their abrupt change in the derivative of horizontal Fick angle, familiar to readers as “horizontal eye velocity.” The VCUSs and ADs were then analyzed kinematically in 3D in quaternion coordinates. We here present time series data as Fick angle degrees of rotation, as this visualization is more intuitive than attempting to plot quaternions as functions of time. When evaluating Fick angle time series data in relationship to LL, we also plotted for comparison the ideal value of Listing's torsion given by Eq. 1.
When plotted as the full time series of quaternions for each rotation in the horizontal-torsional plane, the head velocity stimulus had a linear trajectory indicating that orientation of the head's rotational axis remained approximately constant throughout the trial. The angle formed by the head axis quaternion trajectory was then measured relative to LP. When similarly plotted in the quaternion plane, segments of the VOR response also had linear trajectories, although these changed at transitions between slow phases, and ADs or VCUSs. To measure relative orientations of the eye and head rotation axes to LP, trajectory angles were calculated in the horizontal-torsional quaternion plane. Initial head and eye trajectory angles were taken to be those formed by the head and VOR slow phase before rapid eye movements. The trajectory angles of VCUSs and ADs were represented in the horizontal-torsional quaternion plane by lines connecting the start and end of each rapid eye movement, relative to LP. Final head and eye trajectory angles were those formed by the terminal positions of the head and eye after VCUSs or ADs.
Results
Listing's plane
Orientation of Listing' plane (LP) varied among subjects. Mean pitch orientation of LP was 15 ± 4° (mean ± SD) up relative to earth vertical, with a range of 13–21°. Mean horizontal LP orientation was 17 ± 4° (mean ± SD) nasally, with a range of 11–20°. Mean LP thickness, characterized as its SD, was 1.5 ± 0.2° with a range of 1.4–1.8 .
VOR slow phase
Horizontal VOR gain (eye velocity/head velocity) was determined using the time derivatives of horizontal Fick angles 50 ms following head rotation onset. This is the familiar manner of computing 1D gain. As expected, ipsilesional VOR gain was markedly reduced, averaging 0.41 ± 0.04 (range 0.36–0.43). Contralesional VOR gain was significantly higher, averaging 0.73 ± 0.09 (range 0.64–0.83) and similar to the normal value of 0.77 ± 0.04 in age matched controls (P > 0.05) (Tian et al. 2001a). However, during contralesional rotation the initial 3D VOR velocity axis, computed using quaternion methods, was shifted forward 9.0 ± 4.0° (range 3–12°) relative to that during ipsilesional rotation.
Vestibular catch-up saccades
Three subjects consistently exhibited horizontal VCUS during ipsilesional rotation. These rapid eye movements were evident for both vertically centered and vertically eccentric initial eye positions.
Central eye position
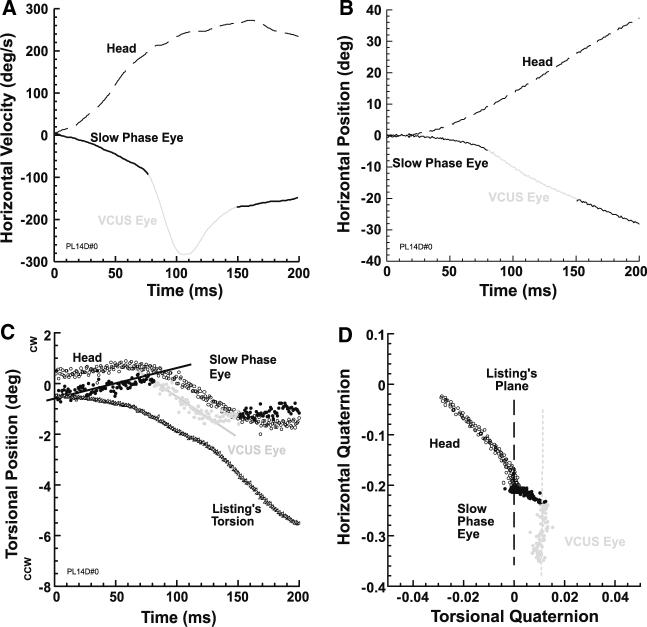
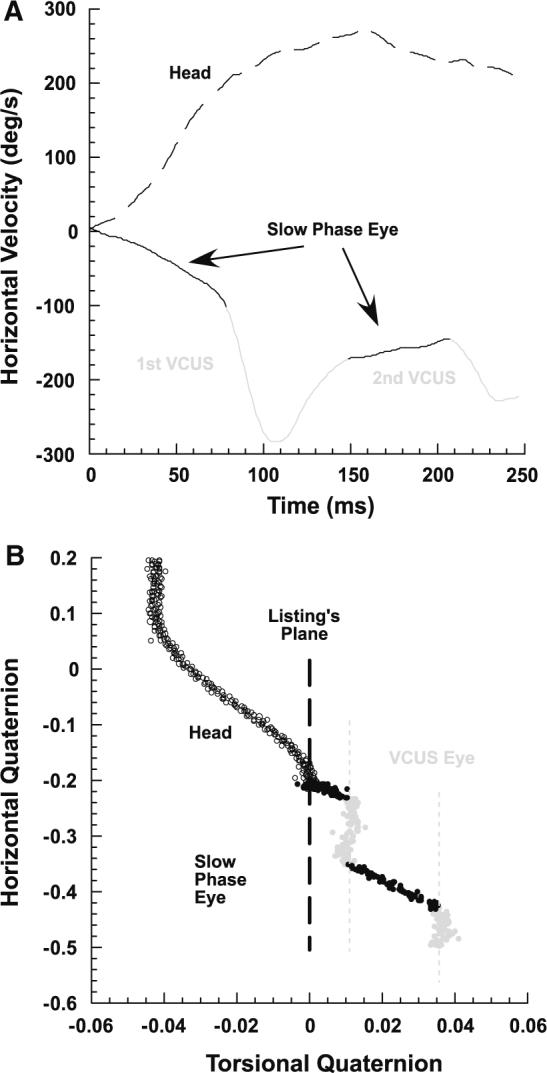
In the three subjects who exhibited them, stereotypic VCUSs occurred during nearly all ipsilesional rotations when the target remained vertically centered. This is illustrated in a representative trial from a subject with right UVD, where we first illustrate the data using Fick angles and their time derivatives (Fig. 1a–c). The VCUS is obvious from its prominent peak in horizontal eye velocity compared with slow phase velocity (Fig. 1a), corresponding to an abrupt increase in the slope of horizontal eye position (Fig. 1b). While the horizontal position and velocity characteristics of the VCUS are distinct from the slow phase, a further difference is evident in torsion (Fig. 1c). Note that from the onset of the slow phase VOR, eye torsion deviated from the value specified by LL, and also deviated from head torsion. Abruptly at VCUS onset, the trajectory of eye torsion changed and subsequently paralleled that of ideal LL torsion (Fig. 1c). The distinct kinematics of VCUS are most clear when eye and head position axes are plotted as horizontal and torsional quaternions in Fig. 1d. The location and orientation of LP is plotted for reference. Note that in the quaternion plane, the head rotational axis included considerable torsion, since this subject's LP was tilted away from the earth vertical axis of rotation. The initial VOR slow phase axis was misaligned with the head axis, and so showed a different trajectory slope, but also contained significant torsion so that the eye left LP (Fig. 1d). Onset of the VCUS is evident in the quaternion plane as a discontinuity of VOR slow phase eye trajectory slope, differing from the slow phase in that the VCUS trajectory roughly paralleled LP. Note that at the end of the VCUS, eye torsion neither matched head torsion, nor returned to LP (Fig. 1d). This behavior was typical of all VCUS observed in all three subjects with consistent VCUS.
Fig. 1.
Typical VCUS initiated with a centered target in subject with right UVD who was rotated ipsilesionally. a VCUS was identified by marked change in horizontal eye velocity from the VOR slow phase. b VCUS was identified by discontinuity in horizontal eye position from the VOR slow phase. c VOR slow phase torsion matched neither the LL value, nor head torsion. However, during the VCUS eye torsion paralleled calculated ideal Listing's torsion. d Data in horizontal-torsional quaternion plane shows that the VOR slow phase (black solid dots) deviated from LP, but that the VCUS (grey) roughly paralleled LP, maintaining the non-Listing torsion generated by the VOR slow phase
Vertically eccentric initial eye positions
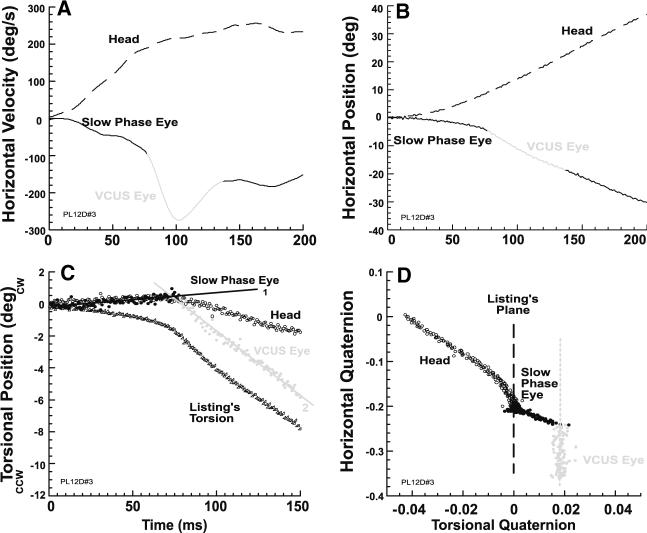
Vestibular catch-up saccades also occurred during nearly all ipsilesional rotations when the three subjects who exhibited them were fixating a vertically eccentric target before motion onset, or made vertical visual saccades during the VOR slow phase. Figure 2 shows representative data from the subject illustrated in Fig. 1, and demonstrates that a typical VCUS with vertically eccentric initial eye position was similar to VCUSs with central initial eye position. In this example, Fig. 2c shows that head torsion was outside LP, reflecting a tilt in LP orientation relative to the earth-vertical rotational axis. The initial VOR slow phase axis did not mirror the head axis, so that their two trajectory slopes differed. Non-LL torsion was evoked by the slow phase VOR so that the eye departed from LP. However, the VCUS again roughly paralleled LP in the horizontal-torsional quaternion plane (Fig. 2d). This behavior was typical of all VCUS initiated from vertically eccentric initial eye positions.
Fig. 2.
Typical VCUS initiated with a target 20° up in subject with right UVD who was rotated ipsilesionally. a VCUS was identified by marked change in horizontal eye velocity from the VOR slow phase. b VCUS was identified by discontinuity in horizontal eye position from the VOR slow phase. c Slow phase VOR torsion matched neither the ideal Listing's torsion, nor head torsion. However, during the VCUS, eye torsion maintained a constant difference from, and thus paralleled, Listing's torsion. d Data in horizontal-torsional quaternion plane shows that the VOR slow phase deviated from LP, but that the VCUS roughly paralleled LP
Tilt angle ratio of VCUS
Compliance of VCUS with LL in the velocity domain was assessed by calculating the TAR of the VCUS velocity axis relative to starting vertical eye position. A representative record from the representative subject of Figs. 1 and 2 is shown in Fig. 3. The VCUS exhibited by this subject had a TAR of 0.51 with respect to vertical eye position, a value consistent with the ideal LL value of 0.5, and typical of all three subjects who consistently displayed VCUS.
Fig 3.
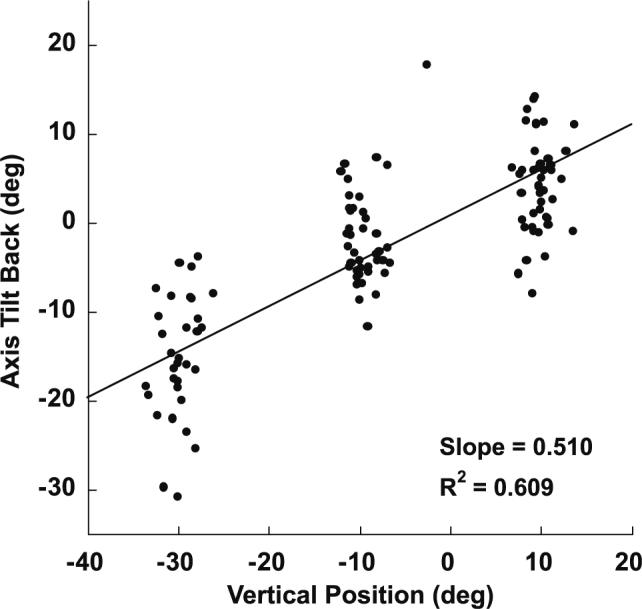
Effect of starting vertical eye position on velocity axis tilt of horizontal VCUS in the subject demonstrated in Figs. 1 and 2. The tilt angle ratio measured during the middle of the VCUS is plotted against its corresponding vertical eye position (relative to Listing's primary position, which differs from straight ahead because Listing's plane is tilted vertically). The slope of 0.51 is consistent with the ideal Listing's law value of 0.5
Secondary VCUS
Subjects occasionally made more than one VCUS during the same rotation. Any VCUSs after resumption of the VOR slow phase following a primary VCUS were termed “secondary.” Secondary VCUS were also easily distinguishable from the VOR slow phase on the basis of high velocity profiles, discontinuous position profiles, and distinctive quaternion plane trajectories. A typical secondary VCUS is illustrated in Fig. 4 for the representative subject with right UVD whose primary VCUS is shown in Fig. 1. Secondary VCUSs maintained the non-LL torsion present at their onset, and had trajectories generally paralleling LP. Secondary VCUS usually occurred 200–300 ms after head motion onset, and 50–80 ms after completion of the primary VCUS. Secondary VCUS were observed after about one third of primary VCUS, especially when the primary VCUS had relatively short latency. Secondary VCUS were seldom observed when primary VCUS latency exceeded 200 ms.
Fig. 4.
A typical secondary VCUS in the same subject of Fig. 1, who had right UVD. The subject was rotated ipsilesionally while fixing a central target. a Primary and secondary VCUSs were identified by corresponding peaks in horizontal eye velocity. b In the horizontal-torsional quaternion plane, trajectories of both primary and secondary VCUS paralleled LP, while the VOR slow phase added non-LL torsion
Abrupt decelerations
Four subjects exhibited stereotypic ADs during contralesional rotations, when viewing either central or vertically eccentric targets.
ADs with central fixation
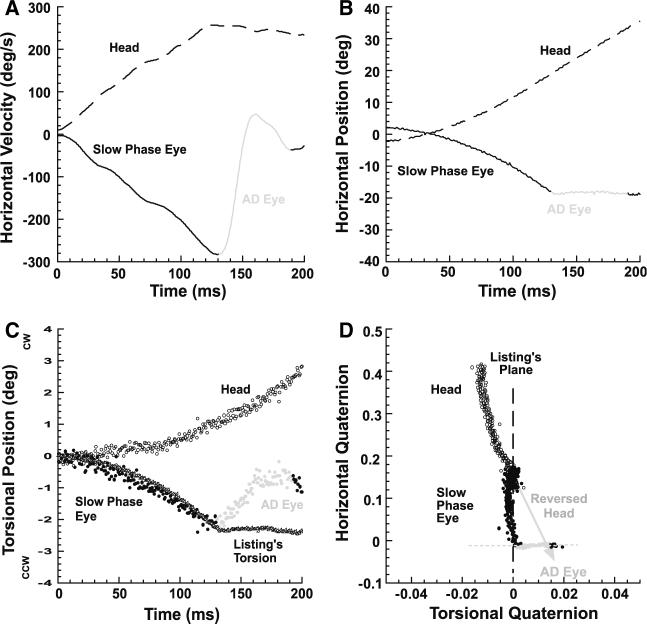
Unlike VCUS, the horizontal components of ADs were in the anti-compensatory direction opposite the VOR slow phase. A typical AD is illustrated in a representative subject with left UVD who was fixating a central target when rotated toward the normal right side (Fig. 5). The AD is obvious from the plot of horizontal eye position as an abrupt reduction of its slope as a function of time (Fig. 5b), and from horizontal eye velocity as reduction to zero in eye velocity (Fig. 5a). In this example, Fig. 5c shows that head torsion was outside LP, reflecting a tilt in LP orientation relative to the earth-vertical rotational axis. While slow phase eye torsion was misaligned with head torsion, eye torsion remained in LP until the AD; the VOR slow phase quaternion plot formed a line having a different slope than the line formed by the head quaternion plot (Fig. 5d). While horizontal eye velocity declined during the AD, non-LL torsion developed, driving torsional eye position perpendicular to LP (Fig. 5d). The horizontal-torsional plane quaternion trajectory of the AD was perpendicular to that of a VCUS (Fig. 1 or 2), which parallels LP. At the end of the AD, however, the ocular position axis nearly matched the inversion (relative to LP) of the head position axis indicated by the gray arrow in Fig. 5d. The ocular axis at the end of the AD was more compensatory than before the AD due to the torsional correction. This behavior was typical of all ADs.
Fig. 5.
Abrupt deceleration (AD) of the VOR slow phase during viewing of central target by representative subject with left chronic UVD rotated contralesionally. a AD was identified by marked change in horizontal eye velocity from the VOR slow phase. b AD was identified by discontinuity in horizontal eye position from the VOR slow phase. c Slow phase VOR torsion did not match head torsion. Torsion during the AD deviated from ideal Listing's torsion. d Failing to match the head, slow phase eye torsion remained in Listing's plane (LP). During the AD, eye torsion trajectory was perpendicular to LP, and brought the eye close to the inverse of head torsion indicated by the grey arrow
ADs with vertically eccentric initial eye position
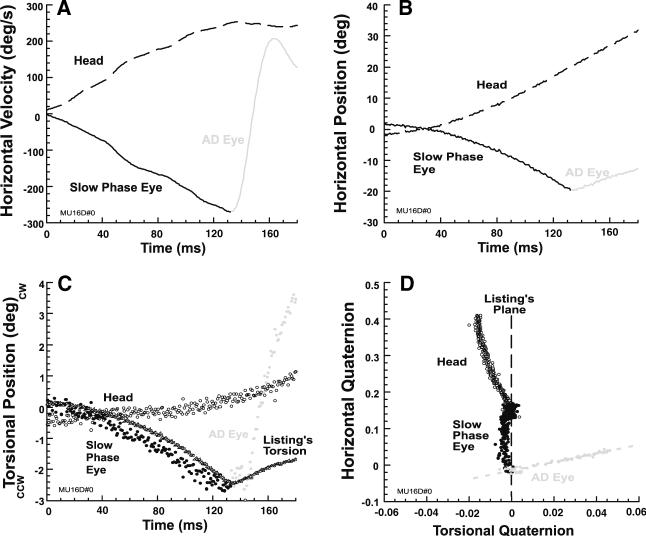
Stereotypic ADs also occurred during contralesional rotation when vertically eccentric targets were initially fixated. Figure 6 shows representative data from the subject illustrated in Fig. 5, and demonstrates a typical AD associated with a 20° upward initial eye position. The AD in Fig. 6 is similar to the VCUS in Figs. 1 and 2 in its prominent velocity change, except that horizontal eye velocity reversed to become anti-compensatory, as typical of a quick phase (Fig. 6a, b). In this example, Fig. 6c, d show that head torsion was outside LP, reflecting a tilt in LP orientation relative to the earth-vertical rotational axis. However, slow phase eye torsion was misaligned with head torsion as indicated by the different slopes of the two trajectories, and remained in LP until the AD (Fig. 6d). Eye torsion during the AD departed markedly from LL torsion (Fig. 6c), so that the quaternion plane trajectory of the AD was nearly perpendicular to LP. In the quaternion plane, eye torsion at the end of the AD exceeded the negative of head torsion (Fig. 6d).
Fig. 6.
Abrupt deceleration (AD) of the VOR slow phase during initial fixation of a target 20° upward by representative subject with left chronic UVD who was rotated contralesionally. Positive values indicate upward, rightward, and clockwise rotations. a The AD rapidly reversed horizontal velocity. b AD corresponded to a discontinuity in horizontal eye position from the VOR slow phase. c VOR slow phase eye torsion did not match head torsion. Torsion during the AD deviated from ideal Listing's torsion. d Failing to match the head, slow phase eye torsion remained close to LP. During the AD, eye torsion trajectory was approximately perpendicular to LP, and caused eye torsion to exceed the negative of head torsion (gray dots)
Velocity axes of ADs
We sought by linear regression evidence of a possible dependence of the AD velocity axis on initial vertical eye position, as was strongly evident in the half angle behavior of VCUSs. However, there was no systematic influence of initial vertical eye position on AD axes.
Trajectory angles from LP in horizontal-torsional quaternion plane
The rotational axes of head rotation, and discrete types of eye motion such as slow phases, VCUSs, and ADs, remained relatively constant so as to inscribe straight lines when plotted as quaternions in the horizontal-torsional plane. The orientations of these straight lines were computed as counterclockwise positive angles relative to LP, for each rotational trajectory of interest. The orientation of LP was always taken to be zero degrees.
VCUS trajectory angles from LP in horizontal-torsional quaternion plane
Direction of the head axis remained stable throughout rotation, and was slightly deviated from LP. The angle formed by a plot of the initial head position quaternion in the horizontal-torsional plane was −3.31° ± 0.70° relative to LP (initial head trajectory angle), not significantly different from the angle defined by a plot of the final head position quaternion of −4.00° ± 0.69° (final head trajectory angle, Fig. 7a). Note that these trajectory angles, formed by quaternions in the position domain, are not expected to have any simple relationship to the orientation of LP relative to the 3D head velocity axis. Mean initial slow phase eye axis trajectory angle was significantly more deviated from LP than the head at 18.48° ± 1.53°, indicating the initial slow phase axis was misaligned with the initial head axis. In general, VCUS paralleled LP and had a trajectory angle near zero. Mean VCUS trajectory angle for the central starting position was only 0.20° ± 0.65° (±SEM), not statistically different from the orientation of LP. Since the VCUS paralleled LP, the final eye trajectory angle at the end of the VCUS was substantially less, but still significantly, deviated from LP at 9.47° ± 1.14° (Fig. 7a). Similar behavior was observed with eccentric vertical starting positions. Eccentric vertical initial eye position did not significantly influence the mean VCUS trajectory angles and final eye trajectory angles. As expected, initial slow phase eye trajectory angle did depend on vertical initial eye position eccentricity (P < 0.005, Fig. 7a).
Fig. 7.
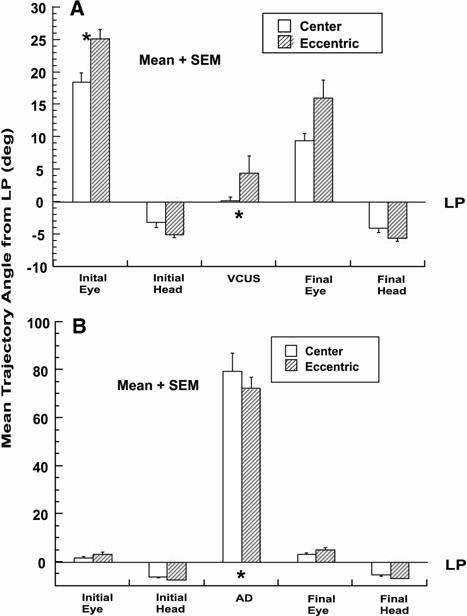
Mean trajectory angles relative to Listing's plane (LP, 0°) in horizontal-torsional quaternion plane for central (open bar) and vertically eccentric (striped bar) initial eye positions. Data for 20° up and down initial eye positions were pooled as they did not differ statistically. * P < 0.005 for comparison of initial and final eye angle to either vestibular catch-up saccade (VCUS) or abrupt deceleration (AD) trajectory angles. a During ipsilesional rotation, where VCUSs frequently occurred. b During contralesional rotation, where ADs frequently occurred
The final VCUS eye trajectory angle was significantly different from the negative of the final head angle (Fig. 7a). This implies that the VCUS did not accurately correct the entire error in the slow phase VOR axis.
AD trajectory angles in the horizontal-torsional quaternion plane
Trajectory angles were computed relative to LP, so that angles close to 90° are approximately perpendicular to LP. The mean of all initial AD trajectory angles for central initial eye position was 79.6° ± 7.5° (±SEM), markedly different from the VCUS trajectory angle and different from LP. Mean AD trajectory angle was also significantly different from mean initial slow phase eye trajectory angle of 2.0° ± 0.5°, and the mean final eye trajectory angle of 3.4° ± 0.5° (Fig. 7b). Mean trajectory angles were similar for vertically eccentric starting eye positions (Fig. 7b). None of the five trajectory angles in AD trials was significantly influenced by eccentric vertical initial eye position (Fig. 7b).
Final AD eye trajectory angle was not significantly different from the negative of the head trajectory angle (Fig. 7b). While this analysis cannot rule out any difference for ADs, it stands in contrast to the large difference evident in Fig. 7a for VCUSs. The similarity to the inverted head angle of the final AD trajectory angle suggests that the ocular axis at the end of the AD had been corrected for the error in the torsion component of the VOR slow phase.
Latency and duration of rapid eye movements
While primary (initial) rapid eye movements were occasionally followed by secondary ones of the same type, only primary VCUSs and ADs were analyzed quantitatively for duration and latency from rotation onset. Analysis was performed in 20 ms bins. The peak of the latency distribution was 40–60 ms for VCUS, but much longer at 142 ms for ADs (Fig. 8a). However, the latency distribution of VCUSs was bimodal with the second peak 120–140 ms, similar to the peak for ADs. Mean VCUS latency was 87 ± 40 (±SD) ms for central initial eye position, and was 93 ± 47 ms for vertical eccentric initial eye positions. Latency was significantly longer for ADs at 140 ± 36 ms and 132 ± 35 ms, for central and vertically eccentric initial eye positions, respectively (Fig. 8b). Although VCUSs had roughly 50 ms shorter mean latency, they had similar mean duration of 32 ± 7 to 32 ± 12 ms for ADs from central initial eye position (Fig. 8c). From vertically eccentric initial eye positions, VCUS had significantly longer mean duration of 33 ± 8 ms than the mean of 27 ± 8 ms for ADs (Fig. 8c). There was no significant influence of vertically eccentric initial eye position on mean VCUS duration (Fig. 8c).
Fig. 8.
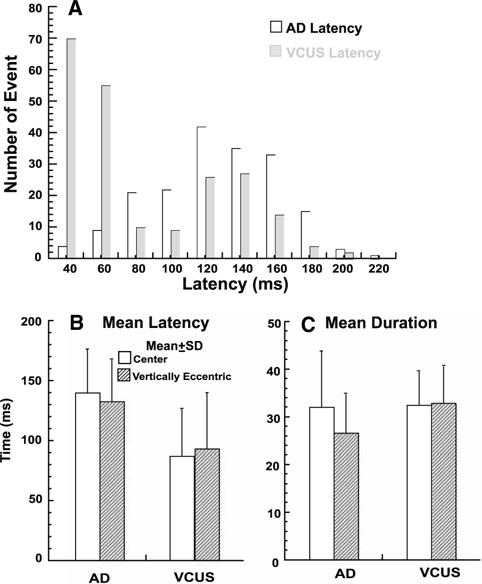
Mean latency and duration of vestibular catch-up saccades (VCUSs) and abrupt decelerations (ADs). a Latency distribution of all primary VCUSs and ADs. The mode was 40–60 ms for VCUSs, but 120–160 ms for ADs. b Mean latency of VCUSs and ADs for central and vertical eccentric starting positions. Mean VCUS latency was significantly shorter than AD latency (P < 0.005), but neither latency was significantly influenced by vertically eccentric starting position. c Mean duration of VCUSs and ADs in central and vertically eccentric starting positions. Mean VCUS duration was significantly longer than AD duration for vertically eccentric initial eye positions, but there was no significant difference for the central initial eye position. Mean duration was significantly influenced by vertically eccentric starting position for ADs but not VCUSs
Discussion
Rapid eye movements with the velocity and acceleration characteristics of saccades may be regarded as intrinsic to the VOR. VCUS supplement deficient VOR slow phases, and are observed in normal subjects during the heave (Tian et al. 2002a) and surge linear VORs (Tian et al. 2006), and during ipsilesional rotation in chronic but not acute UVD (Tian et al. 2000, 2007). Nevertheless, VCUS are not visually evoked, and have distinctively vestibular properties. During ipsilesional yaw rotation, the mode of the latency distribution for VCUS in chronic UVD was 40–60 ms, much shorter than that of visual saccades (Tian et al. 2000). During both rotation and translation, VCUS significantly increase overall compensatory eye movement gain, and have amplitudes strongly correlated with vestibular gaze position error (Tian et al. 2000). These observations argue that VCUS are driven by vestibular input, and constitute compensatory eye movements fundamental to gaze stability during head motion. Furthermore, the occurrence and latency of VCUS during linear acceleration are impaired by both normal aging (Tian et al. 2002a), and by UVD (Tian et al. 2000).
The present study evaluated the 3D kinematics of rapid eye movements during the angular VOR of selected subjects with chronic UVD in response to high acceleration, transient, whole-body yaw. Results confirmed the widely-accepted finding that during ipsilesional rotation, the VOR slow phase in UVD has reduced gain (Halmagyi et al. 1990; Aw et al. 1996a; Crane and Demer 1998; Lasker et al. 1999, 2000; Tian et al. 2001b, 2002b, 2007), and confirm and extend reports that the VOR slow phase rotational axis is tilted anteriorly to the earth-vertical yaw axis imposed on the head during both ipsi- and contralesional rotation (Fig. 7) (Aw et al. 1996a, b; Crane et al. 2005c, 2007). The present findings confirm a small gain reduction of the VOR slow phase during high acceleration, contralesional rotation (Crane et al. 2005c, 2007; Tian et al. 2007).
The subjects with longstanding UVD who were studied here had evolved two distinct types of rapid eye movements compensating for their slow phase VOR deficits: short latency VCUSs evident during ipsilesional yaw, and ADs of horizontal velocity during contralesional yaw. The 3D kinematics of these two types of rapid eye movements were distinct both from the VOR slow phase, and from one another. The mode of VCUS latency during ipsilesional rotation was 40 ms, comparable to that of the otolith mediated VOR (Crane and Demer 1998), and much shorter than the latency of visual saccades (Tian et al. 2000). While in the current experiment we did not examine VCUS in total darkness, other studies have demonstrated that they occur without visual input and remain calibrated to vestibular error (Tian et al. 2000).
Since LP is generally tilted relative to earth vertical, the VOR slow phase during whole body yaw introduced torsion that violated LL. Crane et al. (2005b) demonstrated that visually evoked vertical saccades initiated from non-LL torsion introduced by the VOR nevertheless exhibit a velocity axis dependence satisfying LL. Such visual saccades maintain the initial non-LL torsion, and have trajectories in the quaternion plane that parallel LP rather than returning to it. The present study extends this result to VCUSs, which exhibited kinematics identical to visual saccades initiated from non-LL torsional positions. While the VCUS were compensatory in that they reduced horizontal gaze error arising from reduced magnitude of the VOR slow phase, VCUS did not correct for torsional slow phase errors. Furthermore, VCUS initiated from a range of vertical eccentricities exhibited velocity axes that tilted by half the angle of vertical eye position, conforming to LL in a manner identical to visual saccades. For this reason, VCUS can be considered to be programmed in 2D, in the same sense that visual saccades are programmed. This 2D constraint is consistent with the afferent visual and visuo-motor systems, which in many respects is 2D from the level of the retina down to the level of the superior colliculus, and even to the level of the abducens motor neurons.
During contralesional rotation, subjects with UVD exhibited a lesser degree of VOR slow phase magnitude reduction horizontally, but relatively large directional misalignments of the VOR velocity axis relative to the head velocity axis, reflecting torsional and vertical velocity errors. These predominantly directional errors in the slow phase VOR were corrected by rapid eye movements that we interpreted in 2D studies to be abrupt decelerations (ADs) of horizontal slow phase velocity. The current 3D study indicates that reduction or even anticompensatory reversal in horizontal slow phase velocity during ADs is accompanied by vertical and torsional eye velocities that correct for errors in the VORs slow phase velocity axis (Fig. 5). At the end of the average AD, the torsional component of eye velocity approximated the mirror image of head velocity as is geometrically ideal (Fig. 7b). Since VOR slow phase directional errors ranged widely, the velocity axes of ADs were not parallel to LP, and on average were nearly perpendicular to it (Fig. 7b). This behavior is in conspicuous violation of LL. When ADs were initiated from a range of initial vertical eye positions, the velocity axes of ADs were highly variable and not systematically influenced by initial eye position as is the case for the robust, half-angle dependency of visual saccades and VCUS. These kinematic features are inconsistent with LL, and indicate that ADs are programmed in 3D as is the VOR slow phase, distinct from the 2D programming of visual saccades and VCUS. This implies that motor neuron drive to the extraocular muscles mediating the torsional component of both the slow phase VOR and ADs, is neurally programmed through explicit neural commands to the cyclovertical extraocular muscles, unlike visually guided eye movements for which the torsional component is suggested to arise not by explicit innervation, but instead from mechanical properties of the orbital tissues (Ghasia and Angelaki 2005; Demer 2006). The torsional component of VCUSs presumably also has mechanical rather than explicit neural origins, since VCUS have 3D that have kinematics identical to visual saccades.
The distinctive kinematics of ADs versus VCUSs are evident only when analyzed in 3D. Further examinations of the 3D properties of reflexive eye movements may provide further insight into presumably distinct neural networks that underlie visually guided versus vestibular eye movements. Differences in the programming of 2D versus 3D eye movements evoked by vestibular stimulation are presumably reflected at multiple premotor levels in the brain.
Acknowledgments
United States Public Health Service grants DC-005224. Joseph L. Demer is Leonard Apt Professor of Ophthalmology. Benjamin T. Crane was supported by a grant from the Giannini Family Foundation.
Abbreviations
- LL
Listing's law
- LP
Listing's plane
- SD
Standard deviation
- TAR
Tilt angle ratio
- VOR
Vestibulo-ocular reflex
- 1D
One-dimensional
- 2D
Two-dimensional
- 3D
Three-dimensional
- UVD
Unilateral vestibular deafferentation
- VCUS
Vestibular catch-up saccades
- AD
Abrupt deceleration
Contributor Information
Jun-Ru Tian, Department of Ophthalmology, University of California, Los Angeles, CA 90095−7002, USA.
Benjamin T. Crane, Department of Ophthalmology, University of California, Los Angeles, CA 90095−7002, USA Department of Head and Neck Surgery, University of California, Los Angeles, CA 90095−7002, USA; Jules Stein Eye Institute, University of California, 100 Stein Plaza, UCLA, Los Angeles, CA 90095−7002, USA.
Akira Ishiyama, Department of Head and Neck Surgery, University of California, Los Angeles, CA 90095−7002, USA.
Joseph L. Demer, Department of Ophthalmology, University of California, Los Angeles, CA 90095−7002, USA Department of Neurology, University of California, Los Angeles, CA 90095−7002, USA; Jules Stein Eye Institute, University of California, 100 Stein Plaza, UCLA, Los Angeles, CA 90095−7002, USA; Neuroscience Interdepartmental Program, University of California, Los Angeles, CA 90095−7002, USA; Bioengineering Interdepartmental Program, University of California, Los Angeles, CA 90095−7002, USA.
References
- Aw ST, Halmagyi GM, Haslwanter T, Curthoys IS, Yavor RA, Todd MJ. Three-dimensional vector analysis of the human vestibuloocular reflex in response to high-acceleration head rotations. II. Responses in subjects with unilateral vestibular loss and selective semicircular canal occlusion. J Neurophysiol. 1996a;76:4021–4030. doi: 10.1152/jn.1996.76.6.4021. [DOI] [PubMed] [Google Scholar]
- Aw ST, Haslwanter T, Halmagyi GM, Curthoys IS, Yavor RA, Todd MJ. Three-dimensional vector analysis of the human vestibuloocular reflex in response to high-acceleration head rotations. I. Responses in normal subjects. J Neurophysiol. 1996b;76:4009–4020. doi: 10.1152/jn.1996.76.6.4009. [DOI] [PubMed] [Google Scholar]
- Collewijn H, van der Mark F, Jansen TC. Precise recording of human eye movements. Vision Res. 1975;15:447–450. doi: 10.1016/0042-6989(75)90098-x. [DOI] [PubMed] [Google Scholar]
- Crane BT, Demer JL. Human gaze stabilization during natural activities: translation, rotation, magnification, and target distance effects. J Neurophysiol. 1997;78:2129–2144. doi: 10.1152/jn.1997.78.4.2129. [DOI] [PubMed] [Google Scholar]
- Crane BT, Demer JL. Human horizontal vestibulo-ocular reflex initiation: effects of angular acceleration, linear acceleration, stimulus intensity, target distance, and unilateral lesions. J Neurophysiol. 1998;80:1151–1166. doi: 10.1152/jn.1998.80.3.1151. [DOI] [PubMed] [Google Scholar]
- Crane BT, Tian J, Demer JL. Human angular vestibulo-ocular reflex initiation: relationship to Listing's Law. Ann NY Acad Sci. 2005a;1039:1–10. doi: 10.1196/annals.1325.004. [DOI] [PubMed] [Google Scholar]
- Crane BT, Tian J, Demer JL. Kinematics of vertical saccades during the yaw vestibulo-ocular reflex in humans. Invest Ophthalmol Vis Sci. 2005b;46:2800–2809. doi: 10.1167/iovs.05-0147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crane BT, Tian JR, Demer JL. Temporal dynamics of transient human vestibulo-ocular reflex (VOR) axis after unilateral vestibular deafferentation (UVD). Soc Neurosci Abstr. 2005c electronic publication. [Google Scholar]
- Crane BT, Tian J, Demer JL. Temporal dynamics of ocular position dependence of the initial human vestibulo-ocular reflex. Invest Ophthalmol Vis Sci. 2006a;47:1426–1438. doi: 10.1167/iovs.05-0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crane BT, Tian JR, Demer JL. Temporal dynamics of ocular position dependence of the initial human vestibulo-ocular reflex. Invest Ophthalmol Vis Sci. 2006b;47:1426–1438. doi: 10.1167/iovs.05-0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crane BT, Tian J-R, Ishiyama A, Demer JL. Initial axis of the human vestibulo-ocular reflex after unilateral vestibular deafferentation. JARO. 2007 in press. [Google Scholar]
- Crawford JD, Vilis T. Axes of eye rotation and Listing's law during rotations of the head. J Neurophysiol. 1991;65:407–423. doi: 10.1152/jn.1991.65.3.407. [DOI] [PubMed] [Google Scholar]
- Demer JL. Current concepts of mechanical and neural factors in ocular motility. Cur Opin Neurol. 2006;19:4–13. doi: 10.1097/01.wco.0000198100.87670.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghasia FF, Angelaki DE. Do motoneurons encode the noncommutativity of ocular rotations? Neuron. 2005;47:281–293. doi: 10.1016/j.neuron.2005.05.031. [DOI] [PubMed] [Google Scholar]
- Halmagyi GM, Curthoys IS, Cremer PD, Henderson CJ, Todd MJ, Staples MJ, D'Cruz DM. The human horizontal vestibuloocular reflex in response to high-acceleration stimulation before and after unilateral vestibular neurectomy. Exp Brain Res. 1990;81:479–490. doi: 10.1007/BF02423496. [DOI] [PubMed] [Google Scholar]
- Haslwanter T. Mathematics of three-dimensional eye rotations. Vision Res. 1995;35:1727–1739. doi: 10.1016/0042-6989(94)00257-m. [DOI] [PubMed] [Google Scholar]
- Lasker DM, Backhous DD, Lysakowski A, Davis GL, Minor LB. Horizontal vestibulo-ocular reflex evoked by high-acceleration rotations in the squirrel monkey. II. Responses after canal plugging. J Neurophysiol. 1999;82:1271–1285. doi: 10.1152/jn.1999.82.3.1271. [DOI] [PubMed] [Google Scholar]
- Lasker DM, Hullar TE, Minor LB. Horizontal vestibuloocular reflex evoked by high-acceleration rotations in the squirrel monkey. III. Responses after labyrinthectomy. J Neurophysiol. 2000;83:2482–2496. doi: 10.1152/jn.2000.83.5.2482. [DOI] [PubMed] [Google Scholar]
- Misslisch H, Hess BJ. Three-dimensional vestibuloocular reflex of the monkey: optimal retinal image stabilization versus Listing's law. J Neurophysiol. 2000;83:3264–3276. doi: 10.1152/jn.2000.83.6.3264. [DOI] [PubMed] [Google Scholar]
- Misslisch H, Tweed D, Fetter M, Sievering D, Koenig E. Rotational kinematics of the human vestibuloocular reflex. III. Listing's law. J Neurophysiol. 1994;72:2490–2502. doi: 10.1152/jn.1994.72.5.2490. [DOI] [PubMed] [Google Scholar]
- Peng GC, Minor LB, Zee DS. Gaze position corrective eye movements in normal subjects and in patients with vestibular deficits. Ann NY Acad Sci. 2005;1039:337–348. doi: 10.1196/annals.1325.032. [DOI] [PubMed] [Google Scholar]
- Quaia C, Optican LM. Commutative saccadic generator is sufficient to control a 3D ocular plant with pulleys. J Neurophysiol. 1998;79:3197–3215. doi: 10.1152/jn.1998.79.6.3197. [DOI] [PubMed] [Google Scholar]
- Quaia C, Optican LM. Dynamic eye plant models and the control of eye movements. Strabismus. 2003;11:17–31. doi: 10.1076/stra.11.1.17.14088. [DOI] [PubMed] [Google Scholar]
- Raphan T. Modeling control of eye orientation in three dimensions. In: Fetter M, Haslwanter T, Misslisch H, Tweed D, editors. Three-dimensional kinematics of eye, head, and limb movements. Harwood; Amsterdam: 1997. pp. 359–374. [Google Scholar]
- Raphan T. Modeling control of eye orientation in three dimensions. I. Role of muscle pulleys in determining saccadic trajectory. J Neurophysiol. 1998;79:2653–2667. doi: 10.1152/jn.1998.79.5.2653. [DOI] [PubMed] [Google Scholar]
- Robinson DA. A method of measuring eye movement using a scleral search coil in a magnetic field. IEEE Trans Bio-Med Electron. 1963;10:137–145. doi: 10.1109/tbmel.1963.4322822. [DOI] [PubMed] [Google Scholar]
- Thurtell MJ, Black RA, Halmagyi GM, Curthoys IA, Aw ST. Vertical eye position-dependence of the human vestibuloocular reflex during passive and active yaw head rotations. J Neurophysiol. 1999;81:2415–2428. doi: 10.1152/jn.1999.81.5.2415. [DOI] [PubMed] [Google Scholar]
- Thurtell MJ, Kunin M, Raphan T. Role of muscle pulleys in producing eye position-dependence in the angular vestibuloocular reflex: a model-based study. J Neurophysiol. 2000;84:639–650. doi: 10.1152/jn.2000.84.2.639. [DOI] [PubMed] [Google Scholar]
- Tian J-R, Crane BT, Demer JL. Vestibular catch-up saccades in labyrinthine deficiency. Exp Brain Res. 2000;131:448–457. doi: 10.1007/s002219900320. [DOI] [PubMed] [Google Scholar]
- Tian J-R, Shubayev I, Baloh RW, Demer JL. Impairments in the initial horizontal vestibulo-ocular reflex of older humans. Exp Brain Res. 2001a;137:309–322. doi: 10.1007/s002210000671. [DOI] [PubMed] [Google Scholar]
- Tian J-R, Shubayev I, Demer JL. Dynamic visual acuity during transient and sinusoidal yaw rotation in normal and unilaterally vestibulopathic humans. Exp Brain Res. 2001b;137:12–25. doi: 10.1007/s002210000640. [DOI] [PubMed] [Google Scholar]
- Tian J-R, Crane BT, Wiest G, Demer JL. Effect of aging on the human initial interaural linear vestibulo-ocular reflex. Exp Brain Res. 2002a;145:142–149. doi: 10.1007/s00221-002-1111-z. [DOI] [PubMed] [Google Scholar]
- Tian J-R, Shubayev I, Demer JL. Dynamic visual acuity during passive and self-generated transient head rotation in normal and unilaterally vestibulopathic humans. Exp Brain Res. 2002b;142:486–495. doi: 10.1007/s00221-001-0959-7. [DOI] [PubMed] [Google Scholar]
- Tian J-R, Mokuno E, Demer JL. Vestibulo-ocular reflex to transient surge translation: complex geometric response ablated by normal aging. J Neurophysiol. 2006;95:2042–2054. doi: 10.1152/jn.00635.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian J-R, Ishiyama A, Demer JL. Temporal dynamics of semicircular canal and otolith function following acute unilateral vestibular deafferentation in humans. Exp Brain Res. 2007;178:529–541. doi: 10.1007/s00221-006-0761-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tweed D, Vilis T. Geometric relations of eye position and velocity vectors during saccades. Vis Res. 1990;30:111–127. doi: 10.1016/0042-6989(90)90131-4. [DOI] [PubMed] [Google Scholar]
- Tweed D, Sievering D, Misslisch H, Fetter M, Zee D, Koenig E. Rotational kinematics of the human vestibuloocular reflex. I. Gain matrices. J Neurophysiol. 1994;72:2467–2479. doi: 10.1152/jn.1994.72.5.2467. [DOI] [PubMed] [Google Scholar]
- Walker MD, Shelhamer M, Zee DS. Eye-position dependence of torsional velocity during interaural translation, horizontal pursuit, and yaw-axis rotation in humans. Vision Res. 2004;44:613–620. doi: 10.1016/j.visres.2003.10.009. [DOI] [PubMed] [Google Scholar]