A model for MRI contrast enhancement using T₁ agents

Abstract

Contrast in MRI relies on differences in the local environment of water and is often enhanced by using contrast agents. We present a simple model for evaluating the minimal contrast agent concentration required to produce “satisfactory” contrast enhancement in magnetic resonance images. Previous strategies have been based largely on empirical results for specific systems. The present tissue contrast model (TCM) can be applied to “conventional,” targeted, or biochemically responsive agents. The model results are formulated so that only a small number of parameters are required to analyze a given scenario. The TCM is a particularly useful tool in the development of new classes of magnetic resonance contrast media. These agents will have the ability to target specific cells or tissue, and perhaps be able to report on their physiological status. As an example of the applicability of the TCM, we test it against in vivo magnetic resonance microscopy results in frog embryos that have focal cell populations labeled with contrast agent by using calibrated single-cell microinjection techniques.

One of the powers of magnetic resonance imaging (MRI) is its ability to extract image contrast, or a difference in image intensity between tissues, on the basis of variations in the local environment of mobile water. Differences in the longitudinal relaxation time, or T₁, between tissues is a commonly exploited contrast mechanism. T₁ is the characteristic time constant for a population of nuclear (proton) magnetic moments placed in a magnetic field to equilibrate along the field direction. Because intrinsic differences in T₁ between tissues can be small, a frequent method of contrast enhancement is through the use of exogenous contrast media (1). These agents typically consist of a lanthanide metal ion, usually Gd³⁺, that is chelated to a low molecular weight complex. Water molecules in proximity to the complex experience a reduction in T₁; consequently, contrast enhancement can result from differences in agent concentration. “Conventional” T₁ contrast media, such as gadolinium chelated by diethylenetriaminepentaacetic acid (Gd-DTPA), are routinely used clinically to enhance lesions or fluid compartments (1); such agents are used because they have a nonselective extracellular distribution and are physiologically inert (2).

An emerging field of contrast enhancement, which is still in its infancy, is the development and utilization of several different classes of MRI contrast agents that are designed to highlight specific tissues or organs. These classes can be characterized as having targeted or functional properties. Targeted agents exhibit a preferential increase in agent concentration in specific tissues. This increase can occur due to selective uptake, selective clearance, or direct injection into specific cells or tissues. Functional agents, on the other hand, are designed to be chemically responsive to the physiological state or function of cells or organs. These agents offer the potential of reporting on the local physiological environment by modification of their effectiveness in relaxing nuclear spins, or relaxivity. Certain classes of agents can exhibit both targeting and functional properties in vivo (3–5).

Applications of targeted and functional agents are beginning to emerge. Microinjected contrast agents have allowed microscopic magnetic resonance imaging (μMRI) to visualize cell lineages and track neural development in vivo in developing embryos (6). Other examples of targeted/functional agents include lipophilic agents, which target the liver (4, 5, 7, 8); macromolecular complexes, which function as blood pool markers (9); lymphotropic agents (10); magnetoimmuno agents, which target specific cell surface receptors (11, 12); and, recently, manganese ions, which enter through calcium channels of neurons, have been used to highlight regions of brain activation (13).

In addition to agent concentration differences, in situ modification of the agent’s relaxivity by a number of mechanisms can result in functional contrast enhancement. In complexes such a Gd-DTPA, at high magnetic field strengths, the relaxivity can be modulated by altering the rotational degrees of freedom [parameterized by the correlation time τ_R (14–16)]. Reduction of τ_R through reversible macromolecular binding, for example, is effective in increasing relaxivity (3–5). Modulating other degrees of freedom affecting relaxivity has also been suggested, such as biochemically controlling water exchange to the inner coordination sphere of the chelate-bound metal ion in response to enzymatic activity (17).

The development of novel contrast agents by any of these schemes requires a rational strategy for predicting their effectiveness in producing contrast enhancement. Previous strategies have been based largely on empirical results for specific systems (for example, see ref. 18). Toward this aim, we present a simple theoretical framework for evaluating the minimal agent concentration required to produce “satisfactory” contrast in magnetic resonance images. This tissue contrast model (TCM) can be applied to conventional, targeted, or functional contrast agents. The results of the TCM are a set of equations that approximate the minimal agent concentration: (i) in a targeted area when a finite concentration exists in both regions, (ii) for a local microinjection into one of the regions, and (iii) for a functional agent that is turned “on” in one of the regions by some chemical process. We formulate the results so that only a small number of experimentally accessible parameters are required to analyze a given scenario.

As an example of the applicability of the TCM, we discuss in vivo μMRI results in Xenopus laevis (African clawed frog) embryos that have focal cell populations labeled with gadolinium 10-(2-hydroxypropyl)-1,4,7,10-tetraazacyclododecane-1,4,7-triacetic acid (GdHP-DO3A; ProHance, Bracco Diagnostics, Princeton, NJ) by using calibrated single-cell microinjection techniques. Through the application of the TCM to this specific system, we demonstrate the predictive capabilities of the model and show how the relevant system-specific parameters can be evaluated.

Theory

We consider contrast between two homogeneous tissue regions, labeled a and b. Both regions contain volumes much larger than the voxel size. Intravoxel partial volume effects are not considered. For example, the two regions might correspond to a subset of cells labeled by microinjection within an ensemble of otherwise identical cells. In the absence of any agents, both tissues are assumed to have the same “background” longitudinal relaxation time, T₀₁, and inherent proton environment. The presence of the agent in regions a and b results in T_1a < T_1b. In these regions, T₁ is modulated by changes in either the concentration or the relaxivity of the agent. We assume that within a or b water is in “fast exchange” with the ligand and that the relaxation is described by a monoexponential. Modifications to this model can be made on a case-by-case basis if characteristics, such as T₀₁, T₂, or the relative spin density, differ between regions a and b.

We consider two imaging pulse sequences: the spin-echo (SE) sequence (90° − T_E/2 − 180° − T_E/2 − acquisition − t), and the inversion-recovery spin-echo (IR) sequence (180° − T_I − 90° − T_E/2 − 180° − T_E/2 − acquisition − t). The total sequence repetition time is given by T_R = t + T_E and T_R = t + T_I + T_E for the SE and IR sequences, respectively. We assume that selective pulse excitation profiles are rectangular, and all pulses are short compared with the above times. For real images, the signal per voxel is given by (19–23)

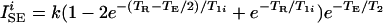1

for the SE sequence and

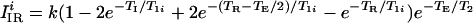2

for the IR sequence, where i = a, b index the two regions. Eqs. 1 and 2 assume that the transverse magnetization is completely dephased before the onset of the next pulse cycle. The value of k depends on many parameters that are specific for a given imaging system, such as details of the radio frequency detection system (coil quality factor, filling factor, etc.). k scales linearly with voxel volume, which is assumed to be equal for the two regions, and is independent of both the interpulse delay times and the relaxation times.

The contrast-to-noise ratio, β, between regions a and b for real images is defined as the difference in the image signal-to-noise ratios (Iⁱ/N) between the two regions, or

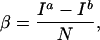3

where N is the statistical image noise and I^a > I^b.

Note that in the limits of T_E → 0, and T_R, T_I → ∞, Eqs. 1 and 2 reduce to Iⁱ = k. The quantity k/N is an important parameter in the model and can be interpreted as the upper limit to the signal-to-noise ratio achievable for a given imaging system and subject. The ratio k/N is independent of imaging protocol (SE or IR) and can readily be estimated from acquired image data (see Experiment).

The contrast-to-noise ratio between regions a and b is experimentally controlled by choosing the parameters T_E, T_R, and T_I. Several authors analyze the choice of these parameters to optimize the T₁-weighted contrast-to-noise ratio (19–23). We assume that T₁-weighted images of regions a and b are acquired by using optimal imaging parameters. When either the SE or the IR sequence is used, T_E should be set as short as possible (often less than, or of order of, 10 ms) and is typically limited by the finite sampling time and other instrumental limitations. T_R and T_I, normally used to adjust T₁ contrast for SE and IR, yield optimal contrast when set to the value T′ given by

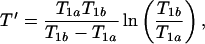4

where Eq. 4 assumes T_E ≪ T_R, T_I, T₂, and a fixed number of averages. In addition, for the IR sequence, one sets T_R ≫ T_I. Eq. 4 is obtained by maximizing β with respect to T_R or T_I for SE or IR, respectively, and has been previously reported [for example, see Hendrick and co-workers (23)].

The ratio T_1a/T_1b can be expressed in terms a set of transcendental equations that describe the amount that T_1a and T_1b must differ to provide a contrast-to-noise ratio of β. For SE, combining Eqs. 1 and 3, we obtain

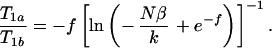5

Similarly for IR, Eqs. 2 and 3 yield

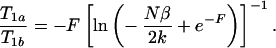6

In Eqs. 5 and 6, f = T_R/T_1b and F = T_I/T_1b. Note that T_1a/T_1b < 1. Our goal is to evaluate the minimal agent concentrations in regions a and b that result in visible image differences. In the following analysis, we will use the value β = 5 as the lower limit to the contrast-to-noise ratio that is visually obvious (see Fig. 1).

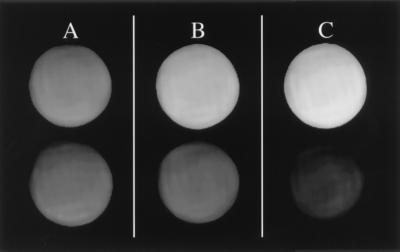
Figure 1.

Estimation of the lower limit to the contrast-to-noise-ratio (β) that is visually obvious. Six capillary tubes containing various aqueous GdHP-DO3A concentrations were imaged simultaneously. The measured β, defined by Eq. 3, for the labeled pairs are 1.0, 4.8, and 9.0, for A, B, and C, respectively. Average intensity differences are easily discerned within pairs B and C, but not within A. We use a value of β = 5, or the approximate value for pair B, as the lower limit to β. This image was acquired by using a two-dimensional Fourier transform (2DFT) SE protocol with T_E/T_R = 10/300 ms. The mean intensity for each tube was measured over a region of interest (ROI) covering approximately 2/3 the central area of a tube. The noise was obtained from the mean voxel intensity (suppressed in this figure) over a similarly sized ROI in a region outside the tubes.

Next, we construct approximate expressions for Eqs. 5 and 6 so that, under optimal imaging conditions, the functional dependence on T_R and T_I is removed from the right-hand side of the equations. We start by examining the behavior of Eq. 5 shown in Fig. 2, where T_1a/T_1b is plotted as a function of T_1b for β = 5 and several values of T_R and k/N. Similar behavior is observed for the case of IR (Eq. 6). Note that for a given k/N, T_1a/T_1b passes through a maximum, which we label

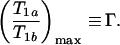7

This maximum corresponds to optimal imaging conditions (Eq. 4) and occurs at a value T_1b = (T_1b)_m. From Fig. 2, an important observation is that Γ is independent of T_R for a given value of k/N. This observation is quite general and applies for all values of k/N and T_R of experimental interest. By using this observation it can be readily shown that the ratio T′/(T_1b)_m is also a function of k/N only. The goal then becomes to find approximate functional forms of T′/(T_1b)_m that depend only on k/N. These are substituted into Eqs. 5 and 6 to eliminate the functional dependence on T_R and T_1b on the right-hand side of these equations. We label the approximate functions for T′/(T_1b)_m as f′(k/N) and F′(k/N) for SE and IR, respectively. The functions f′ and F′ are found by numerically generating a series of curves of T_1a/T_1b versus T_1b for a large number of k/N values and for arbitrarily fixed T′. Maxima for each of these curves are found, and the corresponding (T_1b)_m are tabulated. The resulting array of values for T′/(T_1b)_m, which is equal to f′ or F′, is calculated and parametrically fit as a function of k/N. The results are:

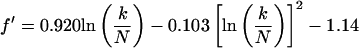8

for SE, and

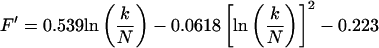9

for IR. We note that the above form of the fitting function is not unique. The relations between Eqs. 5–9 are given by

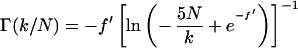10

for SE, and

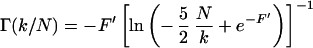11

for IR.

Figure 2.

The behavior of Eq. 5, where T_1a/T_1b is plotted as a function of T_1b for β = 5 and several values of T_R and k/N. Note that for a given k/N, T_1a/T_1b passes through a maximum value, which we label Γ. This maximum occurs at a value T_1b = (T_1b)_m. An important observation is that Γ is independent of T_R for a given value of k/N. Using this property, we obtain an approximate function for T_R/(T_1b)_m that depends only on k/N. This is substituted into Eq. 5 to eliminate the functional dependence on T_R and T_1b on the right-hand side of this equation. A similar procedure was used to obtain the relevant expressions for IR.

The modification of T₁ due to the presence of contrast agent is described by

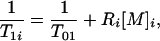12

where R_i and [M]_i are the relaxivity and concentration of the agent in region i = a, b. The ratio T_1a/T_1b is given by

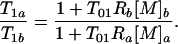13

We substitute Γ for T_1a/T_1b in Eq. 13 and consider two limiting cases in the TCM:

(i) [M]_a ≠ [M]_b, R_a = R_b = R.

This is the case of targeted delivery. This includes, for example, agent delivery by strategic uptake of the paramagnetic complex to cell surface receptors or by microinjection techniques. From Eq. 13, the concentration in region a required to provide satisfactory contrast is given by

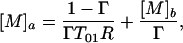14

where Γ is evaluated by using Eqs. 8 and 10 (SE) or 9 and 11 (IR). Normally [M]_b = 0 for the case of microinjection.

(ii) [M]_a = [M]_b = [M], R_a ≠ R_b.

This is the case where the concentration of the agent is the same in both regions, but the relaxivity differs in one of the regions due to biochemical modification of the paramagnetic complex. From Eq. 13, we obtain

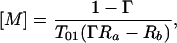15

where the physically relevant concentrations are for ΓR_a > R_b.

Experiment

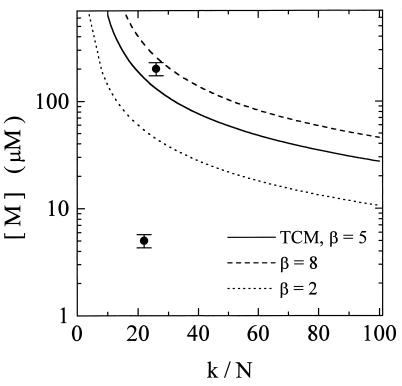
To demonstrate the applicability of the TCM in a real experimental system, we have performed a series of high-resolution three-dimensional (3D) in vivo μMRI experiments on cleavage and blastula stage Xenopus laevis embryos. Various concentrations of GdHP-DO3A were introduced into single blastomeres by using calibrated microinjection techniques. The TCM was used to predict the minimal agent concentration in the labeled cells that would provide satisfactory image contrast between labeled and unlabeled cells. Fig. 3 shows the calculated results from Eq. 14 with [M]_a = [M], [M]_b = 0, and R_a = R_b = R. For a given value of k/N, images of cell populations labeled with concentrations falling on or above the curve should be easily distinguished from unlabeled cells, whereas cells with concentrations significantly below the curve should be indistinguishable.

Figure 3.

Predictions using the TCM (solid line) for the minimal agent concentration needed to give satisfactory image contrast for the Xenopus microinjection imaging experiments. In this situation Eq. 14 applies, with [M]_a = [M], [M]_b = 0, and R_a = R_b = R. For a given k/N, cells labeled with concentrations falling on or above the curve are easily distinguished from unlabeled cells; concentrations well below the curve should not be detected. The TCM assumes a contrast-to-noise ratio, β, equal to 5 (Fig. 1). Other values of β are also shown (β = 2, dotted line; β = 8, dashed line). The points at 5 and 200 μM correspond to the agent concentrations in the labeled cells used in the imaging experiments. These results are displayed in Fig. 4. In Fig. 3, we emphasize that the data points only map the experimental conditions onto the theoretical curve and are not used for fitting the model. In calculating Fig. 3, we have used R = 4.1 ± 0.1 mM⁻¹⋅s⁻¹, which is the relaxivity of GdHP-DO3A measured at 500 MHz, and T₀₁ = 1.3 ± 0.2 s, which is the T₁ of unlabeled cells in the blastocoel roof. All measurements were performed at 15°C.

Materials and Methods

To test the model predictions, we prepared a series of stage 4 (8-cell) Xenopus embryos, each with a single blastomere injected with a known concentration and volume of GdHP-DO3A. Two concentrations were used, and four embryos were injected per concentration. Ascertaining the final concentration in the cell required an estimate of the dilution factor obtained from knowledge of the agent volume delivered and the volume of the targeted cell. The injection volume was controlled by using a pulsed constant-pressure picoinjector (PLI-100, Medical Systems, Greenvale, NY) that delivers a reproducible volume of agent by means of a quartz micropipette that impales the cell. The pressure and pulse duration of the picoinjector were adjusted so that a 4-nanoliter (nl) bolus was always delivered. The volume of the target blastomere was estimated by measuring the diameter of the stage 4 animal cap and assuming that a single blastomere represents 1/8 the volume of a sphere whose diameter is equal to that of the animal cap; typical values were about 125 nl. For the frogs used in the imaging experiments, the final blastomere concentrations were 5 and 200 μM, which differ by a factor of 40. The uncertainty in these concentrations is estimated to be of order of ±14%; the primary source of uncertainty is in the estimation of the blastomere volume, which varies between different batches of eggs and is slightly overestimated when the measurement procedure outlined above is used.

The agent concentrations do not change appreciably over the time course of the imaging experiments (2–3 hr). At early stages in frog development the total embryo volume remains constant, and cell cleavage is not accompanied by cell growth. As a result, the agent concentration within cells and their progeny remains relatively constant throughout early development. Furthermore, we observed no significant diffusion of the agent across the cell membrane out of the injected cell and its descendants.

After injection, the embryos were left at room temperature in Ringer solution (1×) for approximately an hour before imaging to permit healing from the pipette wounding and to allow the agent to uniformly diffuse throughout the blastomere volume. After this period, four embryos of the same concentration and one control (uninjected) embryo were placed in a 2.5-mm-diameter quartz tube in diluted Ringer solution (0.1×). The tube was placed in a laboratory-built radio frequency solenoid microimaging probe, which was maintained at a temperature of 15°C. At this temperature embryonic development is normal but slowed. The embryos were imaged while they developed through approximately stages 7 to 10. Images were acquired by using a Bruker AMX500 (Bruker Instruments, Billerica, MA) microimaging system with a wide-bore (89-mm) 11.7-T magnet. A 3D SE pulse sequence was used to acquire images with 256 × 64 × 64 image points, 1.28 × 0.32 × 0.32 cm field of view, and 50 μm isotropic resolution. The data were zero-filled before Fourier transformation, yielding a final isotropic resolution of 25 μm.

The acquisition parameters T_E and T_R were set to optimize T₁-weighted contrast between labeled and unlabeled cells (regions a and b) for a fixed number of averages. T_E was set to the minimum value of 10.2 ms, which is limited by our imaging system instrumentation. T_R varied for each of the three injection concentrations and was calculated by using Eq. 4. In these calculations we set T_1b = T₀₁ = 1.3 ± 0.2 s, which is the measured T₁ of unlabeled cells in the blastocoel roof; T_1a was calculated from Eq. 12 by using R = 4.1 ± 0.1 mM⁻¹⋅s⁻¹, which is the relaxivity of GdHP-DO3A measured at 500 MHz and 15°C.

Results

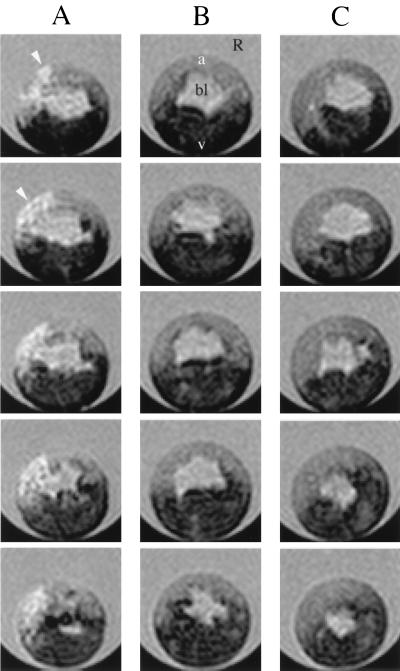
Fig. 4 shows the in vivo images of representative Xenopus embryos. The sets of contiguous panels labeled A and B are 25-μm-thick slices through separate embryos with blastomere agent concentrations of 200 μM and 5 μM, respectively. A control or uninjected embryo is shown in C. In A, labeled cells (arrowheads) are clearly visible in the animal cap region and appear hyperintense. In the lower concentration embryos (B), no detectable contrast enhancement is observed compared with the control.

Figure 4.

Slices through 3D in vivo μMR images of Xenopus embryos labeled with calibrated microinjections of various concentrations of GdHP-DO3A into single blastomeres. A single blastomeres in the animal cap at stage 4 (8 cells) was injected, and the final agent concentration in blastomere after dilution was estimated to be 200 μM in A and 5 μM in B. A control or uninjected embryo is shown in C. The embryos were imaged while they developed through approximately stages 7 to 10. Regions common to all these embryos have been indicated in the top panel of B: the blastocoel (bl), animal region (a), vegetal region (v), and regions (R) containing the Ringer solution, which is surrounding the embryos in the quartz tube. In A, the labeled cells are clearly visible in the animal cap region (arrows) and appear hyperintense. In B, no detectable contrast enhancement is observed compared with the control (C) (matching the predictions of Fig. 3). The vegetal region, which contains yolk, is darker in the image presumably because of a small amount of T₂-weighting. A 3D SE pulse sequence was used to acquire images at 50-μm isotropic resolution. The data were zero-filled before Fourier transformation, yielding a final isotropic resolution of 25 μm. Single 25-μm slices are displayed in each panel, and slices in contiguous panels are separated by 100 μm. For all images, two scans per phase encoding step were averaged, and T_E = 10.2 ms. The T_R values were calculated by using Eq. 4 for each concentration; T_R values equal to 1.28 and 0.885 s were used for the 5 and 200 μM embryos, respectively. The images were acquired at 15°C.

From the results shown in Fig. 4, we calculated the parameter k/N for each image. First, the signal-to-noise ratio (I_SE^b/N) was measured for each image by standard methods (24). The signal, I_SE^b, was obtained from the mean intensity over a ROI in unlabeled cells in the blastocoel roof. The statistical noise, N, was measured from the mean image intensity over a ROI containing no protons. In these experiments, ROIs contained approximately 90 voxels. The measured I_SE^b/N values for all images ranged from 13 to 15. The k/N value for each image was calculated by using Eq. 1 in the form of k/N = (I_SE^b/N)/[1 − exp(−T_R/T_1b)] in the limit of T_E ≪ T_R, T₂. Note that if the images were acquired by using an IR pulse sequence, the relevant equation would be k/N = (I_IR^b/N)/[1 − 2exp(−T_I/T_1b)]. In calculating k/N, we used the parameters I_SE^b and T_1b for the uninjected cells, instead of the parameters for region a (injected cells), although in principle either set should give similar results. Normally, T_1b is obtained by a direct T₁ measurement using IR, for example. On the other hand, T_1a is calculated indirectly by using Eq. 12. Thus, under most circumstances, T_1b is known to a higher accuracy than T_1a.

For the Xenopus experiments, the relevant [M] and k/N values are mapped onto Fig. 3. The image results are consistent with the predictions of the TCM. The embryos with the largest concentration, [M] = 200 μM, are in a range where the labeled blastomeres should easily be detected; this is observed in Fig. 4A. The embryos with [M] = 5 μM fall below the curve, and should be indistinguishable from unlabeled blastomeres; this is also observed (Fig. 4B).

Discussion

We present a simple two-region model that can be used to estimate the minimal MRI contrast agent concentration that results in satisfactory contrast enhancement. Unlike previous results, the model is designed to be applicable to a range of imaging subjects and classes of contrast agents. The results of the TCM are a set of equations that approximate the minimal agent concentration when a finite concentration exists in one or both regions, or when a functional agent is turned “on” in one of the regions due to a modification in the agent’s relaxivity. The TCM contains only a small number of parameters, which can realistically be estimated for a given system and agent. These parameters include intrinsic properties of the subject and agent, such as the “background” T₁ of the subject, the agent relaxivity, and the parameter k/N, which is closely related to the image signal-to-noise ratio and is independent of imaging protocol (SE or IR). The model is most useful in the design of novel classes of contrast media, such as targeted and functional agents.

Using an assay from developmental biology, we demonstrate how the TCM can be applied to a real system of current interest. In our assay, single blastomeres within Xenopus embryos were labeled with known concentrations of GdHP-DO3A, the model-specific parameters were evaluated, and it was shown that the in vivo μMR images obtained were consistent with predictions of the TCM.

In addition to contrast considerations, the model’s ability to estimate the minimal agent concentration can also be important for in vivo physiological characterizations, such as the determination of agent toxicity, excretion pathways, and stability. Also, the model can be used to estimate the minimal image signal-to-noise ratio required to obtain satisfactory results for a given agent concentration; this ratio can influence the choice of animal model or imaging parameters used for testing the agent.

For realistic in vivo situations, the TCM is intended only to provide reasonable expectations as to the minimal concentrations. The accuracy of the TCM’s predictions are limited by the extent to which model assumptions are valid and by uncertainties in parameter values. The most stringent of the model’s assumptions are the existence of equal spin densities in regions a and b, and that T₀₁^a = T₀₁^b. (T₂ variations between a and b can also affect the model’s accuracy; however, this source of error can be made small by minimizing T_E.) In the Xenopus experiments, the model’s assumptions are strictly met; however, this is not always the case, especially when the two regions correspond to different tissue types (25). If variation in spin density and T₀₁ⁱ are small between the regions, the model can still provide reasonable estimates. If higher-accuracy estimates are desired in specific systems, extension of the TCM is straightforward. Starting with knowledge of the relative spin densities and/or T₀₁ⁱ in a and b, and more general forms of Eqs. 1 and 2 (19–24), one can derive expressions analogous to Eqs. 5 and 6. Then, using the same numerical procedures outlined above, one can obtain expressions similar to Eqs. 8–11.

The model parameters that require quantitative estimation include [M]_i, R_i, T₀₁ⁱ, and (Iⁱ/N). Measurement of the image signal-to-noise ratio, Iⁱ/N, and the background longitudinal relaxation, T₀₁ⁱ, is straightforward and is not discussed further. On the other hand, estimating [M]_i and R_i requires careful experimental design. In most systems, [M]_i is the most challenging to determine accurately. This was relatively simple in the Xenopus experiments: [M]_b = 0 and [M]_a was controlled by calibrated microinjection. However, in systems where the mechanism of agent delivery is more passive, such as through selective uptake, determining [M]_i may be more involved. For example, [M]_i could be determined by using a radioactive analog of the agent. For low molecular weight hydrophilic compounds, such as GdHP-DO3A, the values of R_i measured in aqueous solutions are often good approximations to the relaxivity in vivo (2). This situation has been demonstrated in Gd-DTPA (26). For biochemically active agents, or agents with binding interactions to proteins or membranes, R_i ideally should be determined in vivo. This determination requires a measurement of T₁ⁱ and an independent determination of [M]_i; R_i can then be calculated by using Eq. 12. Several reviews (2, 27, 28) discuss additional issues concerning accurate quantitation of [M]_i and R_i in vivo.

As an example of the applicability of the TCM to functional agents, consider the class of compounds described by Moats et al. (17). In this family of agents, the relaxivity is increased in response to local enzymatic activity. The mechanism for this increase stems from a steric blocking of water access to the inner coordination sphere of the Gd³⁺ by using a galactopyranose unit attached to the tetraazamacrocycle chelate. When the agent is exposed to the enzyme β-galactosidase, the galactopyranose ring is cleaved from the macrocycle, making an inner coordination site of the Gd³⁺ available for water exchange; this availability effectively turns “on” the agent. For the analysis of this agent, Eq. 15 is applicable. To estimate the minimal agent concentration, we have used the in vitro relaxivities for the uncleaved and cleaved agent equal to 1.8 mM⁻¹⋅s⁻¹ and 2.4 mM⁻¹⋅s⁻¹, respectively (at 500 MHz),† and we assume T₀₁ equals the value for the unlabeled Xenopus embryo (1.3 s). From Eq. 15 we see that the minimal concentration is strongly dependent on the parameter k/N and diverges at low k/N. For example, for a specific imaging system and subject with a k/N value equal to 60, the minimal agent concentration would be on the order of 1.4 mM.

Conclusions

Although MRI is a powerful tool for noninvasively mapping biological structure and function, it is important to keep in mind that the method has ubiquitous limitations in the available signal-to-noise ratio. This limitation is especially true as the method is pushed to increasingly higher resolutions. A consequence is that the ability to discriminate between tissues on the basis of differences in T₁ can be limited. Thus, when exogenous contrast agents are utilized to enhance T₁ differences, relatively large agent concentration or relaxivity differences must be delivered. Typically, for conventional agents, concentrations in excess of ≈50 μM are required. When developing new classes of contrast agents, it is important to have an understanding of these concentration and relaxivity requirements as a component of an overall design strategy. The goal of this work is to provide this component.

ABBREVIATIONS

DTPA

diethylenetriaminepentaacetic acid

GdHP-DO3A

gadolinium 10-(2-hydroxypropyl)-1,4,7,10-tetraazacyclododecane-1,4,7-triacetic acid

μMRI

microscopic magnetic resonance imaging

TCM

tissue contrast model

SE

spin-echo

IR

inversion-recovery SE

ROI

region of interest

3D

three-dimensional