THE EVOLUTION OF BET-HEDGING ADAPTATIONS TO RARE SCENARIOS

Abstract

When faced with a variable environment, organisms may switch between different strategies according to some probabilistic rule. In an infinite population, evolution is expected to favor the rule that maximizes geometric mean fitness. If some environments are encountered only rarely, selection may not be strong enough for optimal switching probabilities to evolve. Here we calculate the evolution of switching probabilities in a finite population by analyzing fixation probabilities of alleles specifying switching rules. We calculate the conditions required for the evolution of phenotypic switching as a form of bet-hedging as a function of the population size N, the rateθ at which a rare environment is encountered, and the selective advantage s associated with switching in the rare environment. We consider a simplified model in which environmental switching and phenotypic switching are one-way processes, and mutation is symmetric and rare with respect to the timescale of fixation events. In this case, the approximate requirements for bet-hedging to be favored by a ratio of at least R are that sN > log(R) and $\theta N>\sqrt{R}$.

Bet-hedging organisms decrease their risk in an unpredictable environment by producing offspring of different phenotypes according to some probabilistic rule (Seger and Brockman, 1987). Bet-hedging theory was originally developed to describe an annual plant’s tradeoff between germinating seeds immediately versus germinating them over a larger number of years (Cohen, 1966). When only two different environments are encountered, one good and one bad, and the number of seeds produced is large, the predicted optimal strategy is to germinate a proportion of seeds each year approximately equal to the probability that a seed will encounter a good environment that year (Cohen, 1966).

Bet-hedging theory has been applied in many traditional ecological settings, including the resistance of weeds to eradication (Roberts and Feast, 1972; Swanton and Weise, 1991), invertebrate silk ballooning dispersal (Bell et al., 2005), the perennial life cycle of plants (Tuljapurkar, 1990), variable diapause in such diverse animals as crustaceans (Hairston and Munns, 1984), mosquitoes (Andreadis, 1990), sponges (Fell, 1995) and fish (Martin, 1999), and variable offspring size in frogs (Crump, 1981). There has also been much interest recently in phenotypic switching behaviors in microbes as a form of bet-hedging against novel and hostile environments (Avery, 2006; Kussell et al., 2005; Kussell and Leibler, 2005; Stumpf et al., 2002; Thattai and van Oudenaarden, 2004; Wolf et al., 2005). Examples of bet-hedging in the form of phenotypic switching or phase variation include pili expression in bacteria (Abraham et al., 1985), phage growth limitation machinery (Sumby and Smith, 2003), bacterial persistence (Balaban et al., 2004; Kussell et al., 2005; Kussell and Leibler, 2005), the yeast prion [PSI⁺] (Masel, 2005; Masel and Bergman, 2003; True and Lindquist, 2000), viral latency (Stumpf et al., 2002), as well as many other examples (Avery, 2006; Hallet, 2001; Henderson et al., 1999).

In the study of bet-hedging strategies, optimality is usually defined according to the maximization of expected geometric mean fitness over time, even at the expense of a decrease in arithmetic mean fitness (Seger and Brockman, 1987). If one phenotype is very strongly adaptive, but only on very rare occasions whose frequency isθ, then geometric mean fitness calculations predict that the phenotype will be optimally expressed with probabilityθ. This geometric mean fitness approach to bet-hedging has recently been exploited to explain phenotypic switching phenomena in microbes (Kussell et al., 2005; Kussell and Leibler, 2005; Stumpf et al., 2002; Thattai and van Oudenaarden, 2004; Wolf et al., 2005).

Unfortunately, geometric mean fitness calculations invoke infinitely large populations, and hence cannot capture the dynamics of weak selection. It has been suggested that selection for optimal bet-hedging in real populations may be weak, and that true optimality is not always achieved (Philippi, 1993). There are two scenarios of weak selection. First, selection for bet-hedging may be of recent origin, with insufficient time for optimal strategies to evolve. Second, selection for bet-hedging may be infrequent. In this case, even if an allele that hedges against rare catastrophic events has maximal geometric mean fitness, short-term selection against this allele may drive it extinct before the next catastrophic event occurs. This second limitation relating to the “myopic” nature of natural selection has largely been considered with regards to the evolution of evolvability (e.g, Sniegowski and Murphy (2006)), but also applies to the evolution of all bet-hedging strategies against rare events.

One way to study the limitations posed by weak selection of this kind is to focus on fixation probabilities rather than geometric mean fitness, thus explicitly capturing extinction dynamics (Masel, 2005; Masel and Bergman, 2003; Nowak et al., 2004; Proulx and Day, 2001). Here the fixation probability of a bet-hedging strategy is the probability that it replaces the resident strategy in a population, when it is originally held by a single individual. In this setting, optimality, rather than maximizing some explicit fitness function, becomes a game-theoretic notion. For example, in the formulation of Masel (2005), a strategy S is called optimal if, for every strategy T, the fixation probability of S in a resident population of T is at least as large as the fixation probability of T in a resident population of S.

The optimal strategy was computed according to this definition by Masel (2005), using a simplified model of a fluctuating environment and various approximations for computing fixation probabilities. Counterintuitively, as the population size increased, the optimal strategy diverged from the expected result of phenotype expression with probability equal to that of the environment making the phenotype useful. This discrepancy at large population sizes is puzzling in the light of the fact that the expected result was derived for an infinite population (Kussell et al., 2005). Here we revisit the Masel (2005) model, and describe improved analytical and computational methods for estimating fixation probabilities, which we validate using Monte Carlo simulations. This leads to qualitatively and quantitatively different results to those of the earlier study (Masel, 2005), including the elimination of this puzzling discrepancy.

2. MATHEMATICAL MODEL

We consider individuals having two phenotypes, A and B. These phenotypes are heritable, but subject to random switching: with probability m an offspring of a type A individual will be of type B, and with probability m′ an offspring of a type B individual will be of type A. Here the probabilities m and m′, which completely characterize the bet-hedging strategy, are assumed to be governed by some heritable modifier allele M.

We also consider two environments, E and F, with stochastic switching between the environments. The waiting times until environmental changes are modeled as being exponentially distributed, with rateθ from E to F and rateθ ′ from F to E. Here the units of time are generations, so for example when starting in environment E, the probability that a change to F happens within t generations is given by 1 − e ^−θt. In environment E, type A individuals have fitness f_AE and type B individuals have fitness f_BE. In environment F, type A individuals have fitness f_AF and type B individuals have fitness f_BF.

Note that our assumption of discrete and heritable phenotypes has been most frequently studied in microbial contexts, but also applies to any epigenetically inherited state. Similarly, the highly autocorrelated environments that we model are most frequently assumed in microbial contexts in which environmental change is rare relative to generation time, but our model also applies to exceptionally rare events in the context of organisms with longer generation times. Note that our model describes bet-hedging against aggregate rather than idiosyncratic risk (Robson et al., 1999).

We are concerned with the following two main problems:

1. Given two genotypes that differ only in modifiers controlling their phenotypic switching probabilities m and m′, what is the probability that a single individual with one genotype replaces a resident population with the other genotype?

2. What are the “optimal” switching probabilities m and m′, for some suitable definition of optimality? (For this question to be interesting, A individuals should be more fit than B individuals in one of the two environments, and less fit in the other.)

2.1 Full model

To address these questions we consider a haploid population of constant size N consisting of four types of individuals, A₁, A₂, B₁, B₂, where A and B indicate the phenotypes, and the subscript indexes the modifier allele --- subscript 1 for modifier allele M₁, which has switching probabilities (m₁, m₁′ ), and subscript 2 for modifier allele M₂, which has switching probabilities (m₂, m₂′ ).

We use a Moran model for the evolutionary process: at each step one individual is chosen uniformly at random to die, and one individual (possibly the same) is chosen to reproduce with probability proportional to its fitness in the current environment. The newly-born individual immediately switches phenotype with probability m₁, m₂, m₁′, or m₂′, according to its type. Before taking each step, the environment has an opportunity to change: if the environment is currently E, it switches to F with probability T_1,2, and if the environment is currently F, it switches to E with probability T_2,1, where T = exp(R) is the rate matrix $R=\left(\begin{array}{cc}-\theta /N& \theta /N\\ {\theta }^{\prime }/N& -{\theta }^{\prime }/N\end{array}\right)$. Note that N birth-death rounds in the Moral model correspond to one generation for the population, and that when θ′ = 0 we have $T=\left(\begin{array}{cc}{e}^{-\theta /N}& 1-e^{-\theta /N}\\ 0& 1\end{array}\right)$.

Eventually one of the two modifier alleles will be lost, and the population will consist entirely of type A₁ and B₁ individuals, or entirely of type A₂ and B₂ individuals. Under this model, the evolution of the population and environment are jointly Markovian, so by standard Markov chain theory it is in principle possible to compute the probabilities of each of these two outcomes by solving a particular system of linear equations --- see, for example, section 1.3 of Norris (1998).

The number of equations in this system is equal to the size of the state space (≈ N ³/3; see Appendix A). The system of equations is quite sparse, as each state can move in one step to at most 13 other states. By ordering the states appropriately, one can structure the system of equations to be band-diagonal with upper- and lower- bandwidth of order N ², but no smaller (even for a single environment), as described in Appendix A. Solving this system directly with a band-diagonal solver would then have space requirements of order N⁵ and time requirements of order N ⁷ (see e.g. section 4.3 of Golub and Van Loan, (1996)), making it currently impractical for N above 100 or so. It may be possible to bring the time and space requirements closer to order N ³ by using a direct method that exploits the sparseness via a different strategy, or by using an iterative method such as conjugate gradients, but we do not pursue these direction here. Rather, we make several simplifying assumptions, and use several approximations, to arrive at an algorithm for computing approximate fixation probabilities in order N time and space. This is suitable for population sizes up to at least 10 million.

2.2 Simplifications and approximations

To simplify the problem, we assume that different evolutionary processes occur on sufficiently different time scales such that they can be separated (Gillespie, 1983). In particular, we assume that environmental change events are rare relative to the time scales of phenotypic switching and of fixation at the modifier locus. Rare environmental change events mean that we can study switching from environment E to F and associated adaptive phenotypic switching from A to B separately from switching in the reverse direction. Without loss of generality, we consider environmental switching in a single direction only, and set θ ′ to zero.

The next simplifying assumption is that phenotype B has fitness 0 in environment E, i.e., that f_BE = 0. This is a conservative assumption, simplifying the mathematics while increasing the cost of phenotypic switching and hence making it harder for bet-hedging to evolve. As only the relative fitnesses within each environment matter, we may assume without loss of generality that f_AE = 1 and f_AF = 1, and we will write f_BF = 1 + s.

Since we are studying evolutionary processes associated only with switching from E to F, we begin in environment E as our initial condition. Since phenotype B has fitness 0 in environment E, we initialize the population with phenotype A only. Phenotypic switching from B to A now has no opportunity to occur in environment E, and in F it is both rare and disadvantageous, so we approximate m′ as zero.

Again employing the “weak mutation” separation of timescales approximation (Gillespie, 1983), we assume that mutations at the switching modifier locus are rare relative to other processes. We therefore consider events occurring after each such mutation, and begin with N – 1 individuals of type A₁ and a single individual of type A₂. We define p_fix(m₁, m₂) to be the probability that modifier allele M₂ with switching probability m₂ ultimately fixes, i.e. that the population eventually consists entirely of type A₂ and B₂ individuals. We will sometimes write p_fix (m₁, m₂) as p_fix(m₁, m₂, N, θ, s) to emphasize its dependence on N, θ, and s.

These same simplifying assumptions were used in Masel (2005), and in what follows we mostly use the same notation as in that study, except that here we denote fixation probabilities by p_fix rather than p_invasion, and we use hats to denote approximate values e.g., p̂_fix

With these simplifications, we can approximate the population in environment E as consisting of two types of individuals, A₁ and A₂, having fitnesses 1 – m₁ and 1 – m₂, respectively. This approximation becomes exact if we change the rules of the Moran model in environment E slightly, so that new-born individuals of type B, which have fitness 0, are replaced immediately. This effectively reduces the state space of the Markov chain to size N + 1, and allows us to compute the probability q(1, i) that there are exactly i individuals of type A₂ at the time of the first environmental change to F, given that there was initially just one. Details are given in section 2.4.

In environment F, we again explicitly track only the numbers of types A₁ and A₂ individuals, but here we introduce “jump” moves --- each time a new type B individual appears by phenotypic switching, we estimate the probability that it and its descendents eventually take over the population, treating this as a single step in the Markov chain. Using this chain we compute the approximate probability p(i) of a modifier allele with switching probability m₂ fixing, given that there are exactly i individuals of type A₂ at the time of the environmental change. Details are given in section 2.5.

Our approximation p̂_fix(m₁, m₂) to p_fix(m₁, m₂) is then computed as

$${\widehat{p}}_{\text{fix}}(m_1,m_2)=\sum _{i=0}^{N}q(1,i)p(i)$$ (1.)

The values q(1, i) for i = 0, …, N can be computed numerically by solving a single system of N + 1 linear equations, as can the values of p(i) for i = 0, …, N. In both cases the systems of equations are tridiagonal, so can be solved in time and space of order N ---see, e.g., Golub and van Loan (1996). These systems can be solved in memory for N up to about 10 million on a computer with 1GB of RAM.

2.3 Optimality

To address problem (2) above, we need a definition of optimality. As in Masel (2005), we will say that the switching probability m₁ is optimal (for given N, θ, and s) if p_fix(m₁, m₂, N, θ, s) ≥ p_fix(m₂, m₁, N, θ, s) for all switching probabilities m₂. (Here we are still assuming that θ ′ = 0 and m′ =0, although the above definition of optimality readily extends to the more general case.) The two-way comparisons used to define optimality are equivalent to asking which of two possible alleles will be more prevalent if mutation rates are symmetric and mutations are rare relative to fixation time --- see section 4.1.

With this definition, for any given parameters N, θ, and s we can ask whether an optimal switching probability exists and whether it is unique. While we do not presently have a formal answer to either of these questions for this model, both appear to hold numerically for all of the parameter values we have tried. Moreover, for this particular model it appears, from Fig. 3A and other numerics, to be sufficient to check optimality locally, i.e., that if p_fix (m₂, m₁) ≥ p_fix (m₁, m₂) holds for all m₂ in a small interval [m₁ −ε, m₁ +ε] around m₁ (with ε> 0), then it also holds for all m₂ in the entire interval [0, 1]. This makes numerical search algorithms for m_opt straightforward, while allowing all values of m_opt returned by the algorithm to be subsequently checked for global optimality.

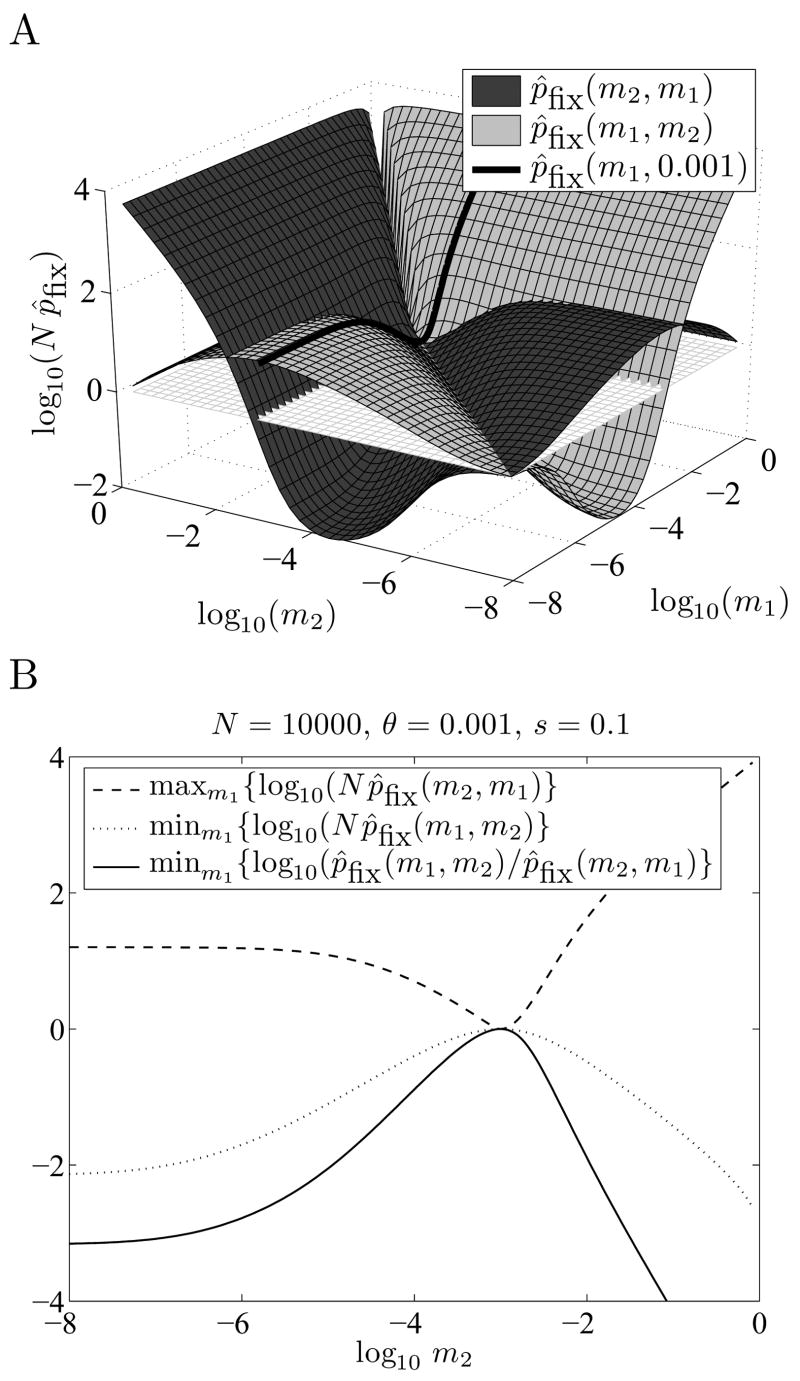
Figure 3.

The optimal switching probability is unique. Part A shows the surfaces of estimated fixation probabilities p̂_fix(m₁,m₂) and p̂_fix(m₂, m₁). Here m̂_opt ≈ θ = 0.001 --- note that p̂_fix (m₁,0.001) ≥ p̂_fix (0.001,m₁) for all m₁ in the interval [0, 1]. Part B shows that there is a unique optimal value: m̂_opt ≈ = 0.001 is the only m₂ for which p̂_fix(m₁, m₂) ≥ p̂_fix(m₂, m₁) for all m₁ (solid line). It is also the only m₂ for which p̂_fix(m₁, m₂) ≥ 1/N for all m₁ (dotted line), and the only m₂ for which p̂_fix (m₂, m₁) ≤ 1/ N for all m₁ (dashed line).

2.4 Model preceding environmental change

Suppose we are in environment E, and that a population currently consists of i individuals of type A₌ and N – i individuals of type A₁. The number of type A₂ individuals increases to i + 1 after one step of the Moran model if a type A₂ individual is chosen to reproduce and a type A₁ individual is chosen to die. The probability that both these events happen is given by

$${\lambda }_i=\frac{(1-m_2)i}{((1-m_1)(N-i)+(1-m_2)i)}\times \frac{N-i}{N}.$$

The probability that the number of type A₂ individuals decreases from i to i – 1 is given by the probability that a type A₁ individual is chosen to reproduce and a type A₂ individual is chosen to die:

$${\mu }_i=\frac{(1-m_1)(N-i)}{((1-m_1)(N-i)+(1-m_2)i)}\times \frac{i}{N}.$$

Let q(i, j) be the probability that there are exactly j individuals of type A₂ at the time of the next environmental change event, given there are initially i individuals of type A₂. To evaluate Equation 1, only the values q(1, j) for j = 1, …, N are needed. (The value q(1,0) is not needed since p(0) = 0.) The values q(1, j) for j = 1, …, N –1 can be found by solving the single tridiagonal system of linear equations

$$\begin{array}{l}q(1,j)=1-e^{-\theta /N}+e^{-\theta /N}\left({\mu }_{j+1}q(1,j+1)+(1-{\lambda }_j-{\mu }_j)q(1,j)\right)\hspace{0.17em}\text{for\hspace{0.17em}}j=1\\ q(1,j)=e^{-\theta /N}\left({\lambda }_{j-1}q(1,j-1)+{\mu }_{j+1}q(1,j+1)+(1-{\lambda }_j-{\mu }_j)q(1,j)\right)\hspace{0.17em}\text{for\hspace{0.17em}}j=2,\dots ,N-2\\ q(1,j)=e^{-\theta /N}\left({\lambda }_{j-1}q(1,j-1)+(1-{\lambda }_j-{\mu }_j)q(1,j)\right)\hspace{0.17em}\text{for\hspace{0.17em}}j=N-1\end{array}$$

and q(1,N) --- the probability that a single m₂ individual fixes by drift before an environmental change --- is given by $q(1,N)=q(1,N-1)\frac{e^{-\theta /N}}{1-e^{-\theta /N}}{\lambda }_{N-1}$. The derivation of the single tridiagonal system of linear equations is given in Appendix B: this is the key mathematical observation of the current work, as it reduces a calculation that appears to be of order N² to a far more tractable order N. This allows us to compute the values q(1, j) directly, avoiding several of the approximations used in Masel (2005).

2.5 Model after environmental change

Suppose now we are in environment F. If the population consists of i individuals of type B (which have fitness 1 + s) and N – i individuals of type A (which have fitness 1), and if we neglect further phenotypic switching, then following Ewens (2004) Eq. 2.158, the probability π(i) that type B fixes is given by

$$\pi (i)=\frac{1-{(1+s)}^{-i}}{1-{(1+s)}^{-N}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for\hspace{0.17em}}s\ne 0;\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\pi (i)=i/N\hspace{0.17em}\text{for\hspace{0.17em}}s=0.$$ (2.)

In what follows we set y = π (1) --- the probability that a single B replaces a resident population of type A. Suppose that at the time of the change to environment F, there are i individuals of type A₂ and N – i individuals of type A₁. We wish to compute p(i), the probability that the m₂ allele fixes --- this includes both the possibility of adaptive B₂ individuals sweeping the population, and the possibility of A₂ individuals taking over by drift.

To avoid explicitly tracking four types of individuals, we instead consider a population consisting only of type A individuals, say i of type A₂ and N – i of type A₁. This is always the case in environment E, since we have assumed that type B individuals have fitness zero there, and are replaced immediately. This population evolves by neutral drift until it reaches an absorbing state i = 0 or i = N, but with the following modification:

Each time an A₂ is born, with probability m₂ it switches to B₂. In this case with probability y we jump immediately to state i = N; this jump corresponds to the new-born B₂ variant being destined for fixation. With probability 1 – y this variant does not become fixed, and is eliminated from future consideration: this reduces the number of A₁ and A₂ individuals to N –1. To keep the size of the population we are tracking constant, we replace the B₂ by an A₁ with probability (N – i)/(N – 1) and by an A₂ with probability (i –1)/(N – 1). (Note that these replacement individuals are not given the opportunity to switch phenotype, but such two-in-a-row switching should happen with probability of order m².)

Similarly, each time an A₁ is born, with probability m₁ it switches to B₁. In this case with probability y we jump immediately to state i = 0; otherwise the B₁ is replaced by an A₁ with probability (N − 1 − i)/(N − 1) and by an A₂ with probability i/(N − 1).

Under this approximation, the values p(i) satisfy the following tridiagonal system of linear equations:

$$\begin{array}{l}p(0)=0\\ p(i)=r_i+a_{i}p(i-1)+b_{i}p(i)+c_{i}p(i+1)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for\hspace{0.17em}}i=1,\dots ,N-1\\ p(N)=1\end{array}$$

where

$$\begin{array}{l}{a}_i=[i(N-i)(1-m_1)+i(N-i)m_1(1-y)(N-i-1)/(N-1)+i^2\hspace{0.17em}{m}_2(1-y)(N-i)/(N-1)]/N^2\\ c_i=[i(N-i)(1-m_2)+i(N-i)m_2(1-y)(i-1)/(N-1)+{(N-i)}^2\hspace{0.17em}{m}_1(1-y)i/(N-1)]/N^2\\ b_i=1-a_i-c_i-i\hspace{0.17em}{m}_2\hspace{0.17em}y/N-(N-i)m_1\hspace{0.17em}y/N\\ r_i=i\hspace{0.17em}{m}_{2}y/N\end{array}$$

This formulation differs from that in Masel (2005) in several regards, and has the advantages that it becomes exact when y = 1, and gives p(i) = i/N when m₁ = m₂.

Note that, for s > 0, if there is more than one type B variant, then y overestimates the probability that any particular one of these type B variants eventually takes over the population. (For example, when s = 0.2 and N is large, y is roughly 1/6; if there are ten type B variants they certainly cannot each have probability more than 1/10 of taking over the population.) In some cases the population may become pure B while it is still comprised of a mixture of B variants with independent origins. This is known as a “soft sweep”, as opposed to the traditional scenario considered by population genetics of a “hard sweep” in which a single adaptive variants is selected to the point of fixation (Hermisson and Pennings, 2005). In practice, however, our approximation works well for a wide range of parameters, as analyzed in Appendix C and assessed with Monte Carlo simulations in Appendix D.

2.6 The accuracy and biological significance of m̂_opt

For fixed N, θ, and s, if the curves for p_fix(m_opt, m, N, θ, s) and p_fix(m, m_opt, N, θ, s), as functions of m, are flat for m close to m_opt, then even if our approximate fixation probabilities are accurate, our approximation m̂_opt may be less accurate. In such cases the accuracy of m̂_opt can be difficult to assess with Monte Carlo simulations, because small differences in probabilities require many simulation runs to resolve. In addition, when these curves are flat then the theoretical superiority of m̂_opt relative to close values of m does not reflect a significant biological advantage.

To give a sense of the flatness of the curves, after computing m̂_opt, we found the range of m surrounding m̂_opt for which p̂_fix (m,m̂_opt)/p̂_fix (m̂_opt ,m)< R , for several thresholds R > 1. (By the definition of m̂_opt, this ratio is at least 1.) For mild inaccuracies in computing fixation probabilities, these intervals should contain the true value of m_opt. Under certain assumptions the ratio p_fix (m, m_opt )/p_fix (m_opt ,m) is also approximately equal to the ratio of times for which a population is homogeneous for m_opt versus m alleles (Proulx and Day, 2001) --- see section 4.1. For this reason, the magnitude of R can be interpreted as a measure of the extent to which m_opt is superior.

3. RESULTS

In Figure 1A we show the estimated optimal probability of phenotypic switching, m̂_opt, as a function of the three parameters of the model, N, θ and s. For N larger than some critical cutoff, we get m̂_opt ≈ θ. (Note that since θ can be arbitrarily large but m can be at most 1, this relationship breaks down for largeθ; it is more accurately given by m̂_opt ≈ 1−e^−θ = θ− θ²/2! + θ³/3!-..., where 1−e^−θ is the probability that the environment changes within one generation. The difference between θ and 1 − e^−θis barely noticeable in the curve for θ = 0.1 in Figure 1A (where 1 − e^−θ= 0.095), and is negligible for smaller θ.) This result agrees with the classical result (Cohen, 1966) confirmed for phenotypic switching through geometric mean fitness calculations (Kussell et al., 2005), namely that the optimum probability of expressing a trait is approximately equal to the probability that the trait is adaptive.

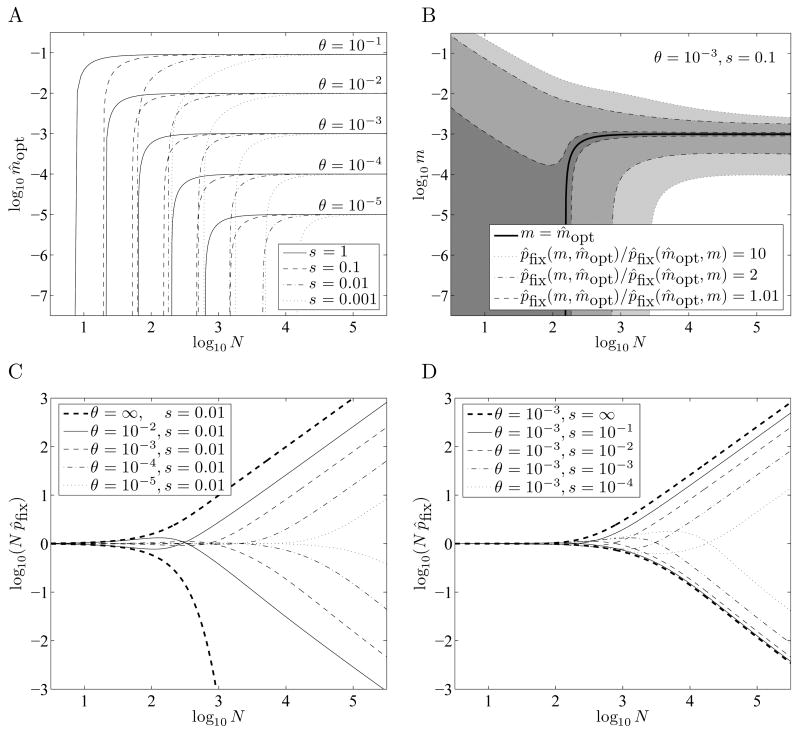
Figure 1.

Optimal switching probabilities and the extent to which they are favored. A: The estimated optimal switching probability m̂_opt is approximately θ for N larger than a threshold that increases as s decreases. Note that on the curves for θ = 0.1, m̂_opt is slightly less than 0.1 even for large N, but is approximately equal to 1 − e^−0.1 = 0.095. B: A broad range of switching probabilities m are only slightly disfavored relative to m̂_opt when N is less than the threshold for which m̂_opt ≈ θ. C and D: These graphs compare p̂_fix (0, θ, N, θ, s) and p̂_fix (θ, 0, N, θ, s) for a variety of s, N, and θ. For small N the switching probability m = 0 has an advantage over the switching probability m = θ, but the latter dominates for large N. (In C, the fixation probabilities for θ = ∞ were computed as π(1) and 1 – π(N – 1): the fixation probabilities of type B and type A alleles in environment F, in which they have fitness 1 + s and 1, respectively.)

With smaller population sizes, bet-hedging alleles are not favored by natural selection. The minimum cutoff value of N depends on the parameters s andθ; the cutoff increases as s decreases and as θ decreases. Below this cutoff value of N, bet-hedging alleles are only mildly disfavored, however. In Figure 1B we show envelopes around m̂_opt consisting of those m for which p̂_fix (m, m̂_opt) / p̂_fix (m̂_opt ,m)<R , for R = 1.01, 2, and 10, where R is a good measure of the extent to which one allele is favored over another, as described in Sections 2.6 and 4.1. These envelopes are rather broad for small N, and narrow as N increases. When m = 0, we refer to the ratio R =p̂_fix (0,m_opt ) / p_fix (m_opt ,0) as the “advantage of bet-hedging.”

In Figures 1C and 1D we compare the fixation probabilities for m = 0 and m =θ alleles, for a variety of parameters N, s, and θ. For small N, m = 0 is favored over m =θ, although only slightly. As N increases, m = θ becomes favored over m = 0 (provided s > 0 and θ> 0). Note in Figure 1C that for small sN, the switching probability m =θ can be disfavored relative to no switching. This approximate result is confirmed in Figures 4F and 4I. When sN is very small, switching phenotypes gives only a negligible advantage in environment F. But it gives a disadvantage in environment E that depends on mN, which can be larger. So the switching probability m =θ can be worse than m = 0 when sN is small. Of course, in such cases sufficiently small positive switching probabilities m < θ will be approximately neutral.

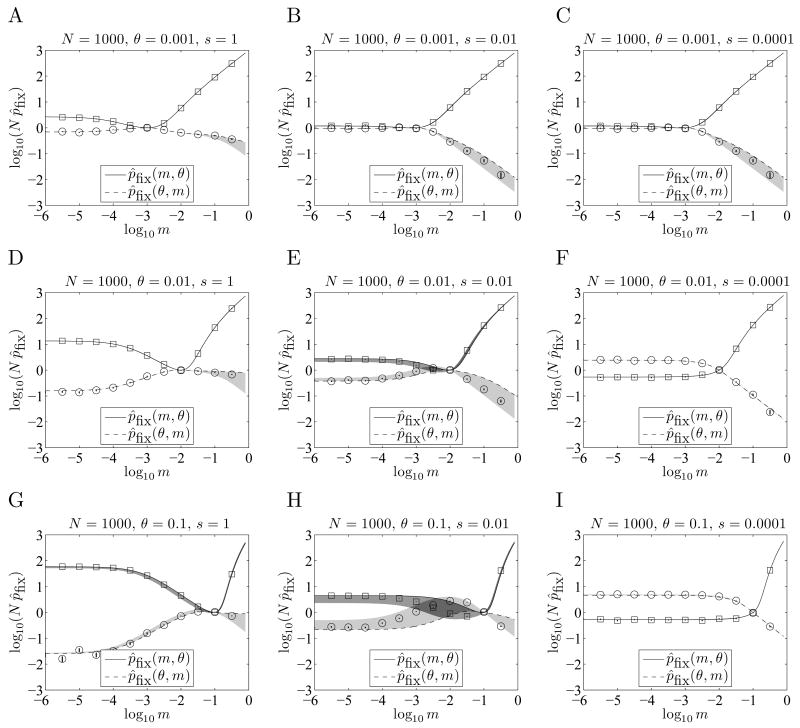
Figure 4.

Accuracy of fixation probability formula. Here we compare the approximate fixation probabilities computed with Equation 1 to Monte Carlo (MC) simulations for N = 1000. In parts A - I, θ varies by row, and s by column. The MC estimates for p_fix (m, θ) and p_fix (θ, m) are indicated by squares and circles respectively, and the vertical bars through these symbols indicate the standard error based on 10⁶ trials. Equation 1 sometimes becomes inaccurate when θ and m are large, particularly for intermediate values of sN ≈ 10, for which selection is important but fairly slow. This is most noticeable in part H. Note that m̂_opt ≈ θ for s = 1, but switching probabilities smaller than θ are favored for s = 0.0001. The gray shaded areas indicate the regions between p̂_fix from Equation 1 and the heuristic bound for p_fix described in Appendix C. The heuristic bound for p_fix (m₁, m₂) is typically a lower-bound when m₁ < m₂ and an upper-bound when m₂ < m₁. (The shaded areas are often too narrow to be seen.)

In Appendix E we look at the minimum value of N more carefully as a function of θ and s, showing that the smallest value of N for which m̂_opt > 0 is around

$$N_{min}\approx \sqrt{\frac{2(s+1)}{s\theta }}.$$ (3.)

But we are more interested in knowing for which parameters bet-hedging is strongly favored, say p̂_fix (0,m̂_opt, N,θ, s) / p̂_fix (m̂_opt,0, N,θ, s)>R for R = 10 or R = 100. We first consider the case of large θ, then the case of large s.

For fixed N and s > 0,p̂_fix (0, m̂_opt , N, θ, s) / p̂_fix(m̂_opt ,0, N, θ, s) increases as θ increases; it is bounded above by the ratio of the fixation probabilities of type B to type A alleles in environment F, which is given by π(1)/(1 – π (N – 1)), with π (i) as defined in Equation 2. This ratio simplifies to (1 + s) ^{N – 1}, providing the bound R≤(1 + s) ^{N – 1} < (1 + s) ^N. Rearranging this inequality gives the bound N > log(R)/log(1 + s), and the bound

$$\text{s}>R^{1/N}-1$$ (4.)

The approximation (1 + s)^N≈e^sN is good for large N when sN is not too large. It is accurate to within about two percent when N > 10⁴ and sN < 20, so for N >10⁴ and R up to about 10⁹ we can use the simpler approximate bound

$$s>log(R)/N.$$ (5.)

Next we consider the case of large s. Let θ_min (R, N, s) denote the minimum θ required for bet-hedging to have advantage R, as a function of N and s. We can numerically compute a lower-bound θ_min (R, N, s) by setting y = 1 in our formula for p(i), corresponding toθ_min (R, N,∞). It appears that

$$\theta =3\frac{\sqrt{(R-1)log(R)}}{Nlog(N)},$$ (6.)

gives a good approximation to θ_min (N, R, ∞) for R between roughly 1 + 10 log(N)²/N and N ² /100. Figures 2A and 2B show target ratios R plotted against the computed ratios p̂_fix (0,m, N, θ, s) /p̂_fix (m,0, N, θ, s), where, θ is given by Equation 6, s = ∞, and m = 1 – e^−θ≈ m_opt. Note that θ in Equation 6 is roughly proportional to R^1/2 in Figure 2A, and to (R–1)^1/2 in Figure 2B (using the approximation log(1 + x) ≈ x for small x), and that the advantage of bet-hedging is sensitive to θ in the ranges shown --- θ has not saturated, so no significantly smaller θ would allow as large an advantage. This range of R shown in Figures 2A and 2B corresponds to a range of θ from ~30log(N)/N ² to ~0.1. Note also that although the condition y = 1 corresponds strictly to s = ∞, the computed ratios change very little for s down to about 10.

Figure 2.

Minimum conditions for bet-hedging to evolve in a finite population. R = p̂_fix (0, m̂_opt, N, θ, s) / p̂_fix (m̂,0, N, θ, s) denotes the estimated advantage provided by using the optimal bet-hedging strategy over using no bet-hedging. A and B: When $\theta =3\sqrt{(R-1)logR}/(N\text{log}N)$ (from Equation 6), s = ∞, and m−1−e^−θ ≈ m̂_opt, the ratio p̂_fix (0, m̂_opt, N, θ, s) / p̂_fix(m̂_opt, 0, N, θ, s) , shown on the vertical axis, is approximately R. Curves in A are shown for R < N²/100, and in B for R > 1 + 10 log(N)²/N, roughly the range for which the approximation is accurate. (Note that B covers the range from R = 1.001 to R = 2.) C: Rectangular regions in which s and θ must fall to allow for a given advantage R; these are necessary but not sufficient conditions. For smaller R these rectangles are encroached on by the approximate equation for N_min Computed estimates are shown for θ ≤ s. D: Estimated parameters θ and s for which R = 100, given as hyperbolas in log (s) and log(θ). Our computed estimates become less accurate for small sN and large θ, and are shown only for sN > 10. The curve for N = 10⁸ is extrapolated using Equation 7.

Thus for bet-hedging to have an advantage of at least R, the parameters s and θ should satisfy Inequality 4 (or s > log(R)/N, for appropriate R and N) and θ>θ _min (N, R, ∞), which can be approximated by Equation 6 when R is between 1 + 10 log(N)²/N and N²/100. They should also satisfy the inequality sθ> 2/N ², although this provides no additional restriction when R is greater than about log(N)². Figure 2C shows the regions of parameter space defined by these inequalities for various R, with N = 10⁶. In Figure 2D we attempt to make these regions more precise for R = 100 and various N, by numerically computing estimates of θ_min (N, R, s) for finite s.

The minimum rate of environmental change θ increases gradually as s decreases down to about 100/N, and increases sharply for smaller s. Our computed values p̂_fix (m₁, m₂ , N, θ, s) can become noticeably inaccurate for sN < 10 when θ is large (see Fig. 4H). Because of this, we have limited these curves to s > 10/N and approximated the entire range for s > log(R)/N by a hyperbola in log(s) and log(θ) having asymptotes at s = log(R)/N and at θ given by Equation 6. Such a hyperbola is given generically by

$$log(\theta )=\frac{g(N,R)}{log(s)-log(log(R)/N)}+log\left(3\frac{\sqrt{(R-1)log(R)}}{Nlog(N)}\right)$$ (7.)

where the adjustable parameter g(N,R) was fit by eye as 0.12 log(N) for R = 100; we did not explore the dependence of g(N,R) on N or R in detail, but this simple estimate allows us to roughly extrapolate a curve for N = 10⁸. This covers the range of the estimated effective population size N_e ≈ 10⁷–10⁸ for Saccharomyces, and is at the lower-end of the estimated effective population sizes for prokaryotes (Lynch and Conery, 2003; Wagner, 2005).

For bet-hedging to provide an organism with a 100-fold advantage in a population of effective size N_e = 10⁸, necessary conditions are s > 4.6×10⁻⁸ (from Inequality 5) and θ> 3.5×10⁻⁸ (from Equation 6). From the approximations in Figure 2D it appears that a conservative sufficient condition is for both s > 10⁻⁶ and θ> 10⁻⁶ to hold, as the rectangle described by these two inequalities lies completely above the curve for N = 10⁸.

Note that the persistent nature of both the environment and heritable phenotypes are important to our results. Consider the case of non-persistent switching in environment F: If each individual chooses phenotype B with probability θ, independently in each round of the Moran model, then the selective advantage of switching would scale as s θ The value of sθN required for switching to be favored by a ratio R would then scale as log(R) in environment F --- a much more stringent requirement than given above. This condition is relaxed somewhat if phenotype B persists for the duration of an individual’s life, and is further relaxed if phenotype B is heritable, which is the framework we consider. The example above corresponds to the case where a persistent change to environment F has been made. The results would again be different if environmental changes were nonpersistent, so that F occurred independently with probability θ each generation.

Note also that we do not claim that m₂ = m_opt is the optimal response to all switching probabilities m₁, in the sense of maximizing p_fix (m₁,m₂ ) / p_fix (m₂ ,m₁ ) simultaneously for all m₁ in the interval [0, 1]; In particular, we do not claim that m₂ = m_opt maximizes this ratio when m₁ = 0. Based on computations using Equation 1, and Monte Carlo simulations, it appears that when m₁ = 0 this ratio can be maximized for m₂ much smaller than m_opt --- decreasing m₂ can lead to a modest decrease in p_fix(0,m₂) that is more than compensated for by a large decrease in p_fix(m_2,0). It should therefore be emphasized that the minimality of θ in Equation 6, and the curves in Figure 2C and 2D --- apply to the case of m₂ = m_opt and m₁ = 0. An advantage R over no switching (m₁ = 0) may be attainable for θ< θ _min (R, N, s) by a suboptimal switching probability m₂ < m_opt. But such a switching probability m₂ would be disfavored relative to m_opt.

In Figure 2D, for the points calculated along the curves for N =10⁵–10⁷ we have m̂_opt≈0.9θ when sN = 10, and θ > m̂_opt>0.99θ when sN > 100. In Figure 1A, we see that for fixed s and N,m̂_opt approaches θ sooner for larger θ. Thus we expect that m_opt is very nearly θ (or 1 – e^−θ when θ> 0.1) within the entire region satisfying s > 10⁻⁶ and θ> 10⁻⁶ described above for N = 10⁸.

In Figure 3A, we show the surfaces defined by p̂_fix (m₁,m₂) and p̂_fix(m₁,m₂) for all m₁ and m₂, for N = 10000, θ = 0.001, and s = 0.1. In Figure 3B we show that for these parameters there is a unique m̂_opt for which p̂_fix (m,m̂_opt )/ p̂_fix (m̂_opt ,m)≥1 for all m. Note that Figure 3A and other numerical computations suggest that for this particular model it may be sufficient to check optimality locally, i.e., if p_fix (m₂, m₁)≥p_fix (m₁, m₂) holds for all m₂ in a small interval [m₁ –ε, m₁ + ε] around m₁ (with ε > 0), then it also holds for all m₂ in the entire interval [0, 1].

In Appendix D and Figure 4 we assess the accuracy of our approximations for p_fix (m₁, m₂) , and the tightness of our heuristic bounds, using Monte Carlo simulations of the Moran model, and find good agreement for a wide range of parameters.

4. DISCUSSION

Using a finite population, we have confirmed the classical bet-hedging prediction that the optimum probability for employing a strategy is approximately equal to the probability that the strategy will be useful, provided the population size N is sufficiently large.

When $N<\sqrt{2(s+1)/(s\theta )}$ bet-hedging appears not to be favored, or to be favored so weakly that it can barely be detected numerically. The approximate requirements for bet-hedging to be favored by a ratio of at least R (where R is between 2 and N ²/100), are that N > log(R)/ log(1+s) and $N>\sqrt{R}/\theta$. (Note that the former condition is roughly equivalent to N > log(R)/s when s < 0.1, and that the latter condition is obtained by rearranging Equation 6 and ignoring lower-order terms.) A general pattern in population genetics is that the balance between selection and drift is determined by the product sN, with values close to 1 being critical. For bet-hedging in finite populations, we have obtained two conditions relating to two such products, θN and sN, corresponding to the frequency of selection as well as its intensity when it does occur.

Our results differ both quantitatively and qualitatively from earlier work (Masel, 2005) that addressed the same problem using different approximations. In Masel (2005) the expectations of functions of certain random variables were approximated by functions of the expectations of the random variables (e.g., Equation A4 of Masel (2005)). Also, given that an environmental change occurs before fixation or loss of a B allele, the probability of having exactly i type B individuals at the time of the environmental change was assumed to be proportional to τ̄_1i--- the expected time spent in state i before loss or fixation in a static environment. These approximations introduced several artifacts, such as p̂_fix (m ₁, m ₂, N, θ, s) sometimes differing markedly from 1/N when m₁ = m₂ (e.g., in Fig 3C of Masel (2005)), and m̂_opt decreasing from θ to 1/N as N increases (e.g., in Fig 2A of Masel (2005)). Our present formulation avoids these artifacts. Moreover we have confirmed the accuracy of our approximations for a broad range of parameters using Monte Carlo simulations.

Note that we have described a switch from environment E to environment F in the short term. Over the long term, the model could switch back-and-forth between these two environments, and so the scenario we analyze could arise repeatedly. Alternatively, it could be interpreted as a continued progression to novel environments: i.e., after the dynamics of the switch are complete, environment F can be renamed environment E, and some totally novel environment G plays the role of environment F. In this context, switching can be between suppressing and revealing variation (evolutionary capacitance), rather than between two distinct phenotypes, each of which has been honed by natural selection in an environment that the population has encountered many times before.

An ideal model for bet-hedging scenarios other than evolutionary capacitance would allow the environment to switch in both directions. We have considered an approximation in which environmental change events are sufficiently rare to be treated according to a separation of timescales, and hence switching in each of the two directions can be treated separately. Our conditions on θ, N and s indicate the likely parameter range under which bet-hedging can evolve, and provide a finite-population complement to infinite-population approximations of other bet-hedging scenarios. Our approach relies on several approximations, most critically that both the appearance of new alleles and changes in the environment are rare relative to all other processes. The sensitivity of our conclusions to these assumptions remains to be explored.

4.1 Fixation probabilities and evolutionary dynamics

The overall evolutionary dynamics are governed not just by fixation probabilities, but also by the rates with which different alleles appear by mutation or migration, and the speed with which different alleles replace the resident population. Suppose there are just two alleles, with switching probabilities m₁ and m₂, that the rates at which these appear are equal, and that the rates at which they appear and fix are small relative to the fixation time. Then the proportion of the time for which m₂ alleles are fixed is approximately p_fix(m₁, m₂)/( p_fix(m₁, m₂) + p_fix(m₂, m₁)) (see, e.g., Proulx and Day (2001)). But if m₁ alleles appear much more often than m₂ alleles, this can give m₁ alleles an advantage over m₂ alleles even when p_fix (m₂, m₁) < p_fix (m₁, m₂) --- the proportion of the time for which m₂ alleles are fixed is given more generally by approximately

$$\frac{r(m_2,m_1)p_{\text{fix}}(m_1,m_2)}{r(m_2,m_1)p_{\text{fix}}(m_1,m_2)+r(m_1,m_2)p_{\text{fix}}(m_2,m_1)},$$

where r(m_i, m_j) is the rate of mutation from m_j to m_i. One might expect, for example, that alleles with m₁ = 0, corresponding to loss of function of the modifier allele, could appear by mutation more often than alleles with m₂ = m_opt. The extreme scenario of unidirectional mutational degradation is examined in Masel et al. (2007), although under a somewhat different framework that includes environmental-dependent fitness but does not explicitly model stochastic switching.

In the more general case, if there is a discrete number K of known allele types and the probabilities associated with all mutational transitions can be estimated, then we can find the equilibrium solution of the corresponding system of K equations derived from the values of r(m_j ,m_i ) p_fix (m_i, m_j ) . The solution yields the long-term behavior according to the stationary probability distribution of the system (Claussen and Traulsen, 2005; Fudenberg and Imhof, 2006; Fudenberg et al., 2006), including the long-term mean value of m. Note that this approach depends on the assumption that fixation events are rare relative to fixation times.

4.2 Evolutionary optimality in finite populations

Evolutionary theory includes many metrics that attempt to predict what will and will not evolve. The oldest is reproductive fitness (Haldane, 1932), normally defined as the expected number of offspring. The concept of inclusive fitness expands this to include the reproductive fitness of other individuals with similar genotypes (Hamilton, 1964). Bet-hedging theory shows that in a variable environment, geometric mean fitness is a better metric than arithmetic mean fitness (Seger and Brockman, 1987).

Both arithmetic and geometric mean fitnesses may vary according to allele frequency, for example when individuals interact, and hence break down as a clear metric. The concept of an evolutionary stable strategy addresses the problem of frequency-dependence by focusing only on the fitness of rare mutants. An ESS was originally defined as a strategy that once established, has higher fitness than any rare mutant (Maynard Smith and Price, 1973). To avoid reference to a particular definition of fitness, an ESS is often defined instead as a strategy that, once established, cannot be invaded by a rare mutant, where “invasion” means that the mutant will increase in frequency (Maynard Smith, 1982). The ESS approach has also been applied to variable environments, where invasion is predicted using a Lyapunov exponent as a refinement of geometric mean fitness when rare (Benton and Grant, 2000; Kussell et al., 2005; Metz et al., 1992; Rand et al., 1994; Tuljapurkar, 1982).

Unfortunately, the invasion-based definition of an ESS breaks down for finite populations, which can always be invaded at some (possibly very low) stochastic rate. This problem is not just theoretical: ESSs have been shown to fail to predict the behavior of finite populations (Fogel et al., 1998; Imhof et al., 2005). Attempts have been made to broaden metrics of environment-dependent (Masel, 2005) and frequency-dependent (Nowak et al., 2004) selection to finite populations. The approach we have followed (Masel, 2005) focuses strictly on fixation probabilities. This captures the long-term evolutionary dynamics of the system under the simplifying assumptions that mutation is both symmetric and rare relative to the timescale of fixation. The alternative ESS_N formulation attempts to follow more closely the spirit of an ESS by using both local stability (invasion) and global stability (fixation) criteria (Nowak et al., 2004) (see Lessard (2005) for the relationship between these criteria and a regular ESS). This represents a compromise between strategies that represent the dynamics in the very long-term and strategies that are difficult to disrupt once present.

But while resistance to the invasion of rare mutants may be a well-defined measure for frequency-dependent selection in a fixed environment as in Nowak et al. (2004), it is not obvious what its analogue should be in the case of fluctuating environments. Even with constant selection within each environment, the initial spread of a mutant depends on the environment at the time. Requiring resistance to the initial spread of a mutant in each environment would be one possible analogue, but this condition will not be satisfied by any strategies in settings for which different phenotypes are favored in different environments. (For an infinite population in an ergodic environment, the expected long term growth rate does not depend on the initial environment, but for a finite population the initial environment can be critical.) Our definition of optimality in a stochastic system, with its focus exclusively on replacement probabilities, is more broadly applicable than a definition that also considers invasion when rare. These definitions are not equivalent: for example we expect the existence of multiple ESS_Ns to be more common.

The approach to optimality we use is appropriate if the rules and frequencies specifying the range of environments stay constant and known over a long period of time. To apply it in its entirety by calculating the stationary probability distribution of states, it is necessary to have an estimate of the relative frequencies of mutations of different types, as discussed above. If all mutation rates are equal, then they can be neglected, and the state of the system that is more frequent than any other can be calculated as described in Section 4.1.

Our algebraic approximations to fixation probabilities complement prior work in which the risk of extinction is estimated by considering the variance of the growth-rate in an infinite population (Wolf et al., 2005), or in which stochastic simulations are used to estimate extinction probabilities of finite populations (Kussell et al., 2005; Menu et al., 2000; Wolf et al., 2005).

4.3 Autocorrelated environments

Both frequency-dependent and environment-dependent selection can provide an advantage for stochastic (mixed) strategies over fixed (pure) strategies. The phenotypic switching we consider is akin to a mixed strategy, where the pure strategies are phenotypes A and B. But here, in a fluctuating environment, we consider first-order Markov strategies, in which the probabilities of an offspring adopting a particular strategy depends on the strategy held by its parent, as opposed to the zeroth-order switching in which each individual makes an independent decision as to its strategy. This matches the first-order Markov dynamics of our model of environmental change, which produces what is sometimes referred to as an autocorrelated (Menu et al., 2000) or temporally patchy environment (Jablonka et al., 1995), as opposed to the completely random (zeroth-order) environment in, e.g., Cohen (1966).

The ability to sense the environment, even imperfectly, can allow for higher growth-rates (Jablonka et al., 1995; Kussell and Leibler, 2005; Wolf et al., 2005). But stochastic strategies may be preferred to sensing when to the environment changes very infrequently, due to the metabolic cost of sensing (Avery, 2006; Kussell et al., 2005; Kussell and Leibler, 2005; Stumpf et al., 2002; Thattai and van Oudenaarden, 2004; Wolf et al., 2005). Sensing may also offer little advantage when the environment changes very frequently and there is a lag between sensing and phenotypic switching (Jablonka et al., 1995). Note that an organism’s awareness of its own current phenotype provides it with indirect information about an autocorrelated environment, since selection in the current environment has sculpted the frequencies of the phenotypes. First-order phenotypic switching exploits this introspection implicitly, since the probability of an offspring adopting a particular phenotype depends on the phenotype of its parent.

4.4 Variable population size

The mathematical approach used here works only with constant population sizes, whereas changes in population size and resulting density-dependent dynamics may be critical in real populations. More realistic ecological scenarios such as this can be addressed using simulations (Benton and Grant, 2000; Menu et al., 2000). In such cases, our optimality criteria can still be applied by numerical estimation of fixation and counterfixation probabilities as an alternative to numerical estimation of the Lyapunov exponent (Benton and Grant, 2000) or short-term persistence (Menu et al., 2000).

APPENDIX A: BAND DIAGONAL STRUCTURE OF FULL MARKOVIAN SYSTEM

The state space consists of all pentuples of nonnegative integers (e, i, j, k, l) with e = 1 or 2 and i + j + k + l = N --- e indexes the environment, and i, j, k, and l represent the number of individuals of type B₁, A₁, B₂, and A₂ respectively. There are two choices for e, and there are $\left(\begin{array}{c}N+3\\ 3\end{array}\right)\approx N^3/6$ choices for (i, j, k, l) by the “stars and bars” trick for counting compositions --- see, e.g., Stanley (1997). The state space therefore has size ≈N³ / 3. The equations corresponding to states with i + k = 0 or j + l = 0 can be eliminated, since in these cases one modifier allele is already lost, but there are only 4(N + 1) such states.

In a fixed environment there are $\left(\begin{array}{c}N-1\\ 3\end{array}\right)$ states for which i, j, k, l > 0. Each of these states can move to any of the others in fewer than N steps of the Moran model, in either direction. If the upper (resp. lower) bandwidth of the transition matrix of the Moran model were b, then at most bN states would be accessible within N forward (resp backwards) steps from each of these states. Thus we have bN ≥ $\left(\begin{array}{c}N-1\\ 3\end{array}\right)$ ≈ N³/6, so b is of order at least N ², even for a single environment. This bound is attainable: the state ordering defined by (i, j, k, l) > (i′, j′, k′, l′) if i(N+1)² + j(N + 1) + k > i′(N + 1)² + j′(N + 1) + k′ gives bandwidth of (N + 1)² for a single environment. Interleaving states ordered this way for two environments doubles this bandwidth, so is still of order N².

APPENDIX B: REDUCTION TO A SINGLE TRIDIAGONAL SYSTEM IN ENVIRONMENT E

Let q(i, j) be the probability that there are exactly j individuals of type A₂ at the time of the next environmental change event, given there are initially i individuals of type A₂. For fixed j, the N + 1 values q(i, j) are the solution to the following tridiagonal system of linear equations:

$$\begin{array}{l}q(0,j)=0\\ q(i,j)=r(i,j)+e^{-\theta /N}({\lambda }_i\hspace{0.17em}q(i+1,j)+{\mu }_i\hspace{0.17em}q(i-1,j)+(1-{\lambda }_i-{\mu }_i)q(i,j)),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,N-1\\ q(N,j)=0\end{array}$$

where r(i, j)=1−e^−θ/N for i=j and 0 otherwise, and λ_i and μ_i are as defined in Section 2.4.

The only values of q(i, j) required for our purposes are q(1, j) for j = 1, …, N. As formulated above, we recover only one value q(1, j) from each tridiagonal system; this leads to a total computational time of order N², which is potentially problematic for realistically large population sizes. Fortunately, the total computational cost can be reduced to order N, as described below.

The (N−1) × (N−1) matrix Q with i,j-th entry q(i, j) satisfies the matrix equation AQ=R, where A is the (N−1) × (N−1) tridiagonal matrix with a(i,i+1)= e^−θ/N λ_i for i=1,..., N−2, a(i,i) = e^−θ/N (1−λ_i−μ_i)−1 for i=1,..., N−1, and a(i−1,i) = e^−θ/N μ_i for i = 2,..., N−1; and R is the (N−1) × (N−1) diagonal matrix with diagonal entries r(i,i) = 1− e^−θ/N for i=1,..., N−1. The j-th tridiagonal system above solves for the j-th column of the matrix Q. But to compute p_fix (m₁ ,m₂ , N, θ, s) we require only the N−1 entries q(1, j), i.e. the first row of Q. Note that R is just e^−θ/N −1 times the identity matrix I, so Q=A⁻¹ /( e^−θ/N −1) . Since matrix inverses are two sided, Q and A commute and we have QA=R . Transposing both sides gives A^tQ^t = (QA)_t = R_t = R . Thus we can solve for the i-th row q of Q, which is the (transpose of the) i-th column of Q^t, by solving the single tridiagonal system A^tq^t = r , where r is the i-th column of the matrix R. For i =1 this amounts to solving the following tridiagonal system:

$$\begin{array}{l}q(1,j)=1-e^{-\theta /N}+e^{-\theta /N}\left({\mu }_{j+1}q(1,j+1)+(1-{\lambda }_j-{\mu }_j)q(1,j)\right)\hspace{0.17em}\text{for\hspace{0.17em}}j=1\\ q(1,j)=e^{-\theta /N}\left({\lambda }_{j-1}q(1,j-1)+{\mu }_{j+1}q(1,j+1)+(1-{\lambda }_j-{\mu }_j)q(1,j)\right)\hspace{0.17em}\text{for\hspace{0.17em}}j=2,\dots ,N-2\\ q(1,j)=e^{-\theta /N}\left({\lambda }_{j-1}q(1,j-1)+(1-{\lambda }_j-{\mu }_j)q(1,j)\right)\hspace{0.17em}\text{for\hspace{0.17em}}j=N-1\end{array}$$

We also require q(1, N) --- the probability that a single m₂ fixes by drift before an environmental change. Consider the last time the system has N − 1 individuals of type A₂, conditioned on either fixation of A₂ or an environmental change while in state N − 1 taking place. The relative probabilities of these two outcomes are e^−θ/N λ_N−1 (for fixation) to 1 − e^−θ/N (for environmental change). Thus we have $q(1,N)=q(1,N-1)\frac{e^{-\theta /N}}{1-e^{-\theta /N}}{\lambda }_{N-1}$.

We can similarly compute the probability q(1,0) that a single A₂ is lost by drift before an environmental change by $q(1,0)=q(1,1)\frac{e^{-\theta /N}}{1-e^{-\theta /N}}{\mu }_1$, or by $q(1,0)=1-\sum _{i=1}^{N}q(1,i)$, but this is not needed for computing ${\widehat{p}}_{\text{fix}}(m_1,m_2)=\sum _{i=0}^{N}q(1,i)p(i)$, since p(0) = 0.

APPENDIX C: APPROXIMATION THAT SUCCESSFUL SELECTIVE SWEEPS OCCUR INSTANTANEOUSLY

If at some initial time there are i type B individuals, with i > 1, y overestimates the probability that the entire population is ultimately descended from any particular one of these individuals. But in practice, the approximation 1−π(i)≈(1−y)ⁱ is quite good for small i (see, e.g., Orr and Betancourt (2001)) --- even though the probability that any given type B variant takes over is overestimated, by treating the failure of each type B variant to take over as independent, one arrives at approximately the correct probability that none of them takes over.

Our use of this approximation differs somewhat in that we are considering type B variants that appear by phenotypic switching, and not just from standing variation. The idea here is that the probability that the chain jumps directly to an absorbing state at some step before reaching an absorbing state by drift should be approximately correct, although the probability that this happens at any given point may be an overestimate. We would also like the relative probabilities of jumping to the absorbing states N and 0 to be accurate.

If the Markov chain is currently in state i, the probability of jumping directly to state N is m₂yi/N, and the probability of jumping directly to state 0 is m₁y(N−i) /N. The ratio of these probabilities, m₂ i / (m₁(N − i)) does not depend on y. But overestimating the probability of a jump from state i can introduce a bias if, during the sojourn that is being collapsed into the single jump step, the expected relative rates of appearance of new B₂ and B₁ variants changes from m₂i/(m₁(N−i)). As we do not consider back-switching from type B to type A, this can be an issue if the switching from A₁ to B₁ or from A₂ to B₂ begins to saturate. But this should have only a mild effect when the sojourn time τ is such that (1− (1− m₂)^τ)/(1 − (1 − m₁)^τ) ≈ m₂ / m₁ (or when m₁ = 0); this is the case when (1− m₂)^τ and (1 − m₁)^τ are still approximately linear as functions of τ, say for τm₁< 0.1 and τm₂ < 0.1.

Ignoring subsequent phenotypic switching, when s = 0 the expected sojourn time τ̄ of a type B variant destined for fixation is N generations; this decreases for s > 0, and for sN > 2 or so it is approximately 2 log(sN + 0.577) / s generations (Hermisson and Pennings, 2005). But the conditions τ̄m₁ < 0.1 and τ̄m₂ < 0.1 are by themselves much too conservative, since the bias enters mainly through the jump moves, which happen rarely for small θ since then the probability of environment F being reached is small. (The probability of the chain being absorbed by a jump move to state N can be computed by changing the initial condition p(N) = 1 to p(N) = 0 in the triadiagonal system above.) Also, regardless of θ, when Ns is small enough so that y ≈1/N, the bias is again small, since y no longer overestimates the absolute probability that any particular type B variant eventually takes over the population.

Note that our values p(i) are exact in the case of y = 1; this corresponds to the limit as s approaches infinity, since y ≈ s/(s + 1) for large N. By setting y = 1 when evaluating Equation 1, we can compute bounds on fixation probabilities for finite s.

Because such bounds can be weak for smaller s, we also computed heuristic (i.e., not rigorously proven) bounds by modifying the algorithm for computing p̂_fix (m₁, m₂) as follows. In environment F (but not E), we decrease the larger of m₁ and m₂: when m₂ > m₁ we replace m₂ by m₁ × (1 − (1 − m₂)^T)/(1 − (1 − m₁)^T), and when m₁ > m₂ we replace m₁ by m₂ × (1 − (1 − m₁)^T)/(1 − (1 − m₂)^T). Here T is half of the mean sojourn time τ̄. We computed τ̄ exactly, as in Eq. 2.159 of Ewens (2004) --- this amounts to solving two tridiagonal systems, and can be done in order N time --- but similar bounds are obtained using the approximations for τ̄ given above. The factor of one half in T = τ̄/2 is a conservative way to boost type B variants that appear earlier in the sojourn, since these should have an advantage over those that appear later.

APPENDIX D: ASSESSING ACCURACY WITH MONTE CARLO SIMULATIONS

We assessed the accuracy of our approximations for p_fix(m₁, m₂ ), and the tightness of our heuristic bounds, using Monte Carlo simulations of the Moran model. In each run of the simulation, all four types A₁, A₂, B_1, and B₂ were tracked until either both A₁ and B₁ were lost, or both A₂ and B₂ were lost. The population began with a single individual of type A₂ and with N − 1 individuals of type A_1, and was in environment E. We also did Monte Carlo simulations using the alternate model for environment E, in which there are only two types, A₁ and B₁, with fitnesses 1 − m₁ and 1 − m₂ respectively; in environment F all four types were again explicitly tracked.

In Figure 4 we assess the accuracy of the values we compute for p̂(m₁, m₂, N, θ, s). Here we fix N = 1000 (small enough to allow for accurate Monte Carlo estimates), and compare p̂_fix(m, θ, N, θ, s)to p̂_fix(θ, m, N, θ, s) for various values of θ and s to see how the accuracy of depends on m, θ, s. Each Monte Carlo estimate used 10⁶ trials, with the standard error estimated as $\sqrt{f(1-f)/{10}^6}$, where f is the fraction of trials that ended in fixation of type B variants. Note that the discrepancy between p̂_fix(m₁, m₂, N, θ, s) and the Monte Carlo estimate is usually very small, and is most noticeable when m is close to 1. Note also that when there is a noticeable discrepancy, to within the standard error the Monte Carlo estimates appear to be bracketed between p̂_fix (m₁, m₂, N, θ, s) and our heuristic bound from section 2.5, which is a lower bound when m₂ > m₁ and an upper bound when m₂ < m₁.

We performed the Monte Carlo simulations using two models for environment E, as described in section 2.2. The results shown are for the model in which type B variants are replaced immediately in environment E, but aside from a slight difference when m > 0.1, the results were not noticeably different. This suggests that when type B variants in environment E are not immediately replaced, but have fitness 0, it is not critical to explicitly account for type B variants that preexist at the time of the environmental change. This is because they tend to reappear in approximately the right proportions in the first generation following the environmental change.

APPENDIX E: MINIMUM POPULATION SIZE FOR BET-HEDGING

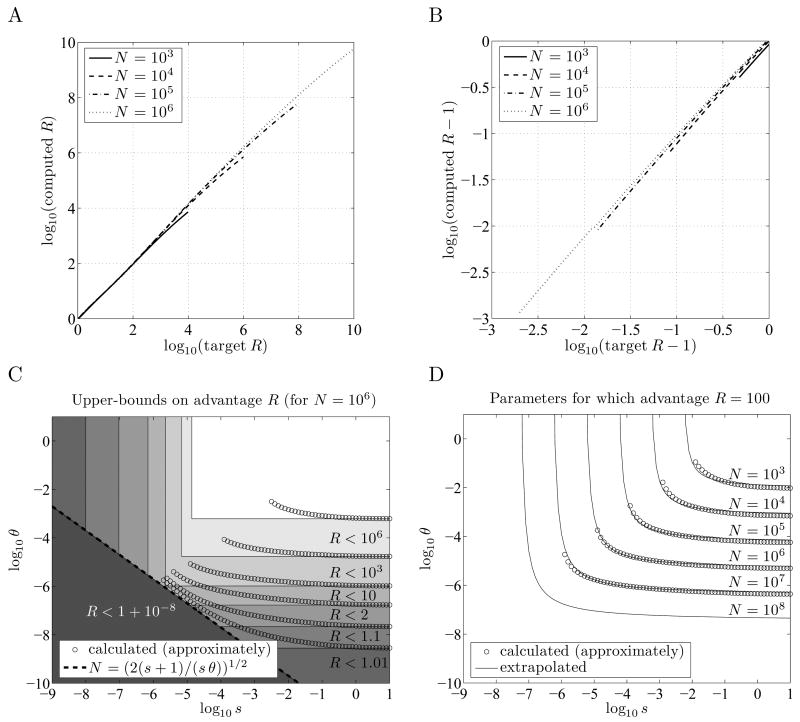
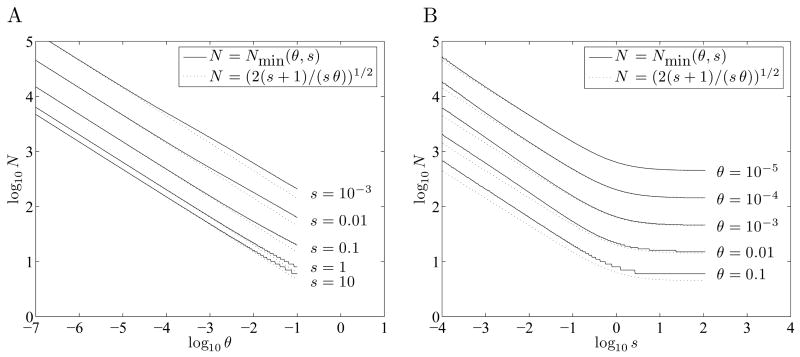
In Figures 5A and 5B we look at the minimum value of N as a function of θ and s, showing the smallest value of N for which m̄_opt > 0. Since we are computing fixation probabilities numerically, we cannot distinguish between m̄_opt being exactly zero, or just being very nearly zero. But clearly m_opt is exactly zero when θ = 0 or when s ≤ 0, so by the continuity of fixation probabilities, for fixed N, m = 0 will be nearly optimal for sufficiently small positive θ and s. Figures 5A and 5B show the smallest value of N for which p̄_fix(0, m̄_opt, N, θ, s) / p̄_fix (m̄_opt, 0, N, θ, s) > 1 + 10⁻⁸; we refer to this value of N as N_min.

Figure 5. Minimum population sizes for bet-hedging.

R = p̂_fix (0, m̂_opt, N, θ, s) / p̂_fix(m̂_opt, 0, N, θ, s) denotes the estimated advantage provided by using the optimal bet-hedging strategy over using no bet-hedging. A and B: N_min the smallest N for which R > 1 + 10⁻⁸, is approximately $\sqrt{2(s+1)/(s\theta )}$.

Judging from Figures 5A and 5B, we have

$$N_{min}\approx \sqrt{\frac{2(s+1)}{s\theta }},$$ (8.)

with this approximation underestimating N_min somewhat for smaller s and θ. Note that Equation 8 is roughly the same as $N_{min}\approx \sqrt{2/(s\theta )}$ when s < 0.1, but stabilizes at $N_{min}\approx \sqrt{2/\theta }$ as s goes to infinity. As our computations were limited to N ≤ 10⁷, the precise choice of 1 + 10⁻⁸ in defining N_min may mask some effects of order 1/N here.

Note that to have R > 1 + 10⁻⁸ we should have s > 10⁻⁸/N, and that this condition is not implied by Equation 8, which saturates for large s but not for largeθ. Thus Equation 8 may underestimate N_min when s is extremely small, but the critical value s ≈ 10⁻⁸/N falls well below the range of parameters we are most interested in.