Spatiotemporal imaging of human brain activity using functional MRI constrained magnetoencephalography data: Monte Carlo simulations

Abstract

The goal of our research is to develop an experimental and analytical framework for spatiotemporal imaging of human brain function. Preliminary studies suggest that noninvasive spatiotemporal maps of cerebral activity can be produced by combining the high spatial resolution (millimeters) of functional MRI (fMRI) with the high temporal resolution (milliseconds) of electroencephalography (EEG) and magnetoencephalography (MEG). Although MEG and EEG are sensitive to millisecond changes in mental activity, the ability to resolve source localization and timing is limited by the ill-posed “inverse” problem. We conducted Monte Carlo simulations to evaluate the use of MRI constraints in a linear estimation inverse procedure, where fMRI weighting, cortical location and orientation, and sensor noise statistics were realistically incorporated. An error metric was computed to quantify the effects of fMRI invisible (“missing”) sources, “extra” fMRI sources, and cortical orientation errors. Our simulation results demonstrate that prior anatomical and functional information from MRI can be used to regularize the EEG/MEG inverse problem, giving an improved solution with high spatial and temporal resolution. An fMRI weighting of approximately 90% was determined to provide the best compromise between separation of activity from correctly localized sources and minimization of error caused by missing sources. The accuracy of the estimate was relatively independent of the number and extent of the sources, allowing for incorporation of physiologically realistic multiple distributed sources. This linear estimation method provides an operator-independent approach for combining information from fMRI, MEG, and EEG and represents a significant advance over traditional dipole modeling.

The ultimate goal of our research is to characterize in both space and time areas of the brain participating in a given task or behavior. The integration of the spatial and temporal domains represents a unique challenge because of the existence of anatomically distinct processing regions that communicate across several time scales. Within the last decade, a number of different techniques have been described for noninvasively measuring human brain activity (1–8). These can be broadly classified into either hemodynamic/metabolic or electromagnetic measurements. Current hemodynamic measurements, particularly functional MRI (fMRI), provide excellent spatial resolution (millimeters) but are temporally limited by the latency of the hemodynamic response (seconds) (9, 10). Conversely, electroencephalography (EEG) and magnetoencephalography (MEG) provide excellent temporal resolution (milliseconds) but uncertain spatial localization, as discussed below (11, 12). Our hypothesis is that improved spatiotemporal maps can be obtained by combining information from both types of measurements (13–18). We previously have described a general mathematical framework for combining EEG/MEG with anatomical MRI and fMRI data (15). Here, Monte Carlo simulation studies were used to evaluate the accuracy of this method, under a variety of realistic conditions.

Localization of neuronal activity within the brain, based on external measurement of the electric potential (EEG) and/or the magnetic field (MEG), requires the solution of two separate, but related, problems. The “forward problem” of calculating the electric potential and magnetic field outside the head, given the conductive current source distribution within the head and the individual conductive properties of the tissues, is a well-defined problem, governed by the quasi-static limit of Maxwell’s equations (11, 19, 20). In contrast, the “inverse problem” of determining the spatial distribution of current sources inside the head, based solely on external electric and/or magnetic measurements, is fundamentally ill-posed (21). That is, for any set of instantaneous EEG and/or MEG measurements, there are infinitely many current source distributions within the head that are consistent with those recordings. Thus, to solve the electromagnetic inverse problem one must place some constraints on the otherwise infinite solution space.

Historically, the most common approach to the inverse problem has been to assume that the electric and magnetic measurements are generated by a given (small) number of focal sources, each of which can be modeled as a single fixed or moving dipole. The locations, orientations, and strengths of these “equivalent current dipoles” (ECDs) then can be estimated by fitting these parameters using the electric and/or magnetic measurements (22). This fitting involves a multidimensional, nonlinear optimization. A disadvantage of this approach is that the time required to solve this optimization problem grows exponentially with the number of ECDs, and thus the global optimum can be found only for models involving a small number of ECDs. For models involving larger numbers of ECDs, approximate techniques have to be used, where the solution found depends on the initial estimate of the locations and orientations of the dipoles. A potential problem with all ECD-based methods is that the solution depends strongly on the number of assumed dipoles. Although techniques have been proposed for estimating the model order (23–25), the actual number of dipoles generally cannot be determined a priori.

A number of other approaches have been proposed to overcome the assumption of focal sources inherent in the ECD-based methods. These take advantage of the fact that if the locations of all possible sources are known a priori, the problem of determining the strength of each dipole (or dipole component) is a linear one. Because the number of possible source locations is, in general, much larger than the number of sensors, this is an underdetermined problem. One common method for solving such underdetermined linear problems is to choose the solution with the least power, also known as the minimum-norm (Moore-Penrose pseudoinverse) solution (26). These linear approaches have certain advantages, including statistical properties that are well-known and easily characterized. Importantly, the continuous current source model readily allows for the incorporation of fMRI data and is more biologically plausible than the discrete current dipole model.

Although mathematically convenient, the constraints imposed on the inverse solution by the above procedures are not based on the actual underlying brain physiology and anatomy. Fortunately, today a great deal is known about the anatomy and functional properties of the brain. For example, empirical and theoretical evidence suggests that the majority of the observed electromagnetic signals arise from the cortical gray matter, specifically the apical dendrites of the cortical pyramidal cells. These neurons have a columnar organization, oriented perpendicular to the cortical sheet (11, 20). Thus, if the shape of the cortical sheet is known, this information can be used to constrain the locations and orientations of the cortical sources. Furthermore, there is considerable evidence, including optical experiments in monkeys (27) and direct cortical grid mapping comparisons with fMRI in patients (28–32), for a close coupling between local hemodynamic response and the underlying neuronal activity. These findings suggest the use of both anatomical information and functional information from MRI as constraints on the bioelectromagnetic inverse problem.

Modeling studies described herein provide a rational basis for the proper inclusion of these MRI constraints. Our simulations use an anatomically constrained linear estimation approach that explicitly incorporates fMRI information as an a priori spatial estimate of activity (15). An optimal linear inverse operator is computed, which maps the external electromagnetic field measurements into an estimated distribution of dipole strength across the cortical surface.

Although the MRI constraints have a sound physiological basis, one can foresee situations in which the anatomic, hemodynamic, and electromagnetic measurements might differ. These “mis-specifications” between EEG/MEG and MRI measurements can be divided into two broad categories, which we refer to as fundamental and experimental. Fundamental mis-specifications can arise because EEG/MEG and fMRI measure physically different aspects of brain function. Therefore, it is possible that areas deemed active by fMRI produce no observable electromagnetic signal (extra sources); conversely, some electromagnetically active sources might not be detected by fMRI (missing sources). Additionally, the precise location and extent of the observed fMRI areas might differ from those of the corresponding electromagnetic sources. Experimental mis-specifications refer to measurement or estimation errors that can be corrected, at least in theory. Such errors might include misregistration between the EEG/MEG and fMRI coordinate systems, incorrect estimates of the physical parameters of the realistic head model used in the forward solution, and errors in the reconstructed cortical surface.

Through the use of Monte Carlo simulations we have investigated the effects of some of these potential mis-specifications on our linear estimation inverse calculation. Errors caused by possible fundamental mis-specifications are of particular interest, because they cannot be corrected by better measurement methods.

METHODS

Forward Solution.

In the typical frequency range of neural activity, the electric and magnetic fields of the brain can be accounted for by the quasistatic limit (negligible inductive and capacitive effects) of Maxwell’s equations (19, 20). This results in a linear relationship between the electromagnetic recordings and the sources at any location in the brain. We can express the forward solution in simple vector notation:

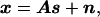1

where x is the vector of instantaneous electric and/or magnetic recordings, A is the so-called gain matrix (with each column specifying the electric and/or magnetic forward solution for a given dipole component), s is a vector of dipole component strengths, and n is a vector specifying the noise at each electrode/sensor. The elements of A are complicated nonlinear functions of the sensor locations and the geometry and conductive properties of the head. Historically, the gain matrix has been calculated by assuming an idealized head shape, typically multiple concentric spheres of different conductivities. However, recent advances in numerical techniques, computer technology, and high-resolution MRI have made it practical to compute the forward solution for a more realistic nonspherical head that is customized to each individual subject’s anatomy.

In these model studies, we used conductivity boundaries and cortical surfaces determined from the MRI anatomy of a normal volunteer using the technique described by Dale and Sereno (15). For calculation of the forward solution, the cortical surface is tiled with approximately 5,600 vertices. The standard sensor geometry of the 122-channel Neuromag (Helsinki, Finland) MEG system (33) was used. We have adapted a realistic boundary element method for calculating the forward solutions (34, 35).

The EEG forward solution computation requires the specification of boundaries between brain cerebro spinal fluid and skull, skull and scalp, and scalp and air, and the relative conductivities of each of those regions. The MEG forward solution, on the other hand, has been shown to require only the inner skull boundary to achieve an accurate solution (12, 36).

In these model studies we evaluated the results only for the MEG case. The biomagnetic sources were constrained to be within the cortical gray matter. Each possible source location was represented either by three orthogonal current dipoles placed at that location (i.e., no cortical orientation constraint) or by a single current dipole oriented normal to the cortical surface.

Inverse Solution.

There are various derivations for the linear inverse operator used here. Minimization of expected error (37), Bayesian estimation (38), Tichonov regularization (39), and the generalized Wiener filter (40) all result in an equivalent inverse operator (W):

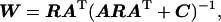2

where C is the covariance matrix of n, and R is the a priori covariance matrix estimate for s from Eq. 1 (15). W is a linear operator that maps a recording vector x into an estimated solution vector ŝ. Note that if both C and R are set to a scalar multiple of the identity matrix then this approach reduces to the well-known minimum-norm solution (11, 26). This approach provides a convenient framework for incorporating information from fMRI into the inverse problem.

Our working hypothesis is that there is a positive correlation between local electric/magnetic activity and local hemodynamic response over time. Because the diagonal elements of the matrix R encode the prior estimates of dipole strength variance (power) over time at each location i, that is, R_ii = σ_i², we can incorporate this assumption by making each diagonal element R_ii a monotonically increasing function of the corresponding fMRI activation. Large values indicate those locations that are more likely to be active and small values indicate locations that are less likely to be active. Setting R_ii to zero effectively precludes any activity at location i.

If one had knowledge of the correlation of activity between different sources, say locations i and j, such information could be incorporated through the off-diagonal elements of the R matrix, by setting R_ij = 〈s_is_j〉 = σ_iσ_jcorr(i,j).. Although not considered in the present study, this would allow the imposition of a smoothness constraint on the inverse solution, as suggested by the LORETA approach (41).

Once the optimal linear inverse estimator W is calculated the estimated spatiotemporal pattern of electric/magnetic activity (dipole strength) is calculated by using the simple expression:

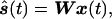3

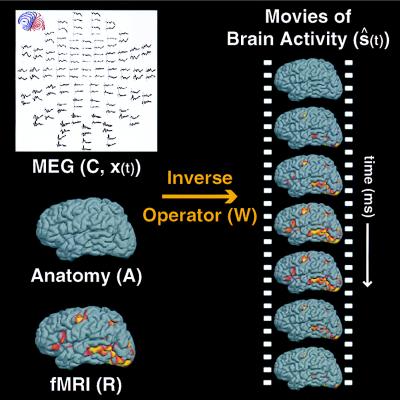
where ŝ(t) and x(t) are the estimated dipole strength and recording vectors as a function of time, respectively. The general approach used is shown in Fig. 1.

Figure 1.

Spatiotemporal imaging of brain activity. The linear estimation approach for combining electromagnetic measurements with anatomical MRI and fMRI information is illustrated schematically. The inverse operator (W) is computed from anatomical information in the forward solution (A), fMRI information in the estimated source covariance matrix (R), and the sensor noise covariance matrix (C) from the MEG measurements. Applying the inverse operator to the MEG measurements [x(t)] yields movies of estimated cortical source activation over time [ŝ(t)]. The movies depict spatiotemporal estimates of the orchestration of cortical activation during a given task or behavior.

Monte Carlo Simulations.

To simulate fMRI areas of activation, either 5, 10, or 20 sources were randomly located on the folded cortical surface, each with varying volumetric extent (point source, 1-cm or 2-cm diameter). The random selection ensures no systemic location bias in these model studies. The numbers and extents of sources chosen represent experimentally realistic fMRI data. Although point sources are not physiologically realistic, they were included in our simulations to allow comparison with standard ECD models. The diagonal elements of R corresponding to fMRI visible areas of activation were set to 1. The a priori variance estimates, or weighting, at other locations not visible by fMRI (missing locations) were varied between σ_i² = 0, 0.01, 0.1, or 1. This corresponds to 100, 99, 90, and 0% relative fMRI weighting, respectively. The classical minimum norm solution is equivalent to a relative fMRI weighting of 0%. We made no a priori assumptions about source correlation. Therefore, the off-diagonal elements of R were set to zero. It should be noted that this does not force the sources to be uncorrelated or orthogonal in time. Noise was assumed to be additive, Gaussian, uniform, and spatially uncorrelated. Here, we assumed a conservative signal-to-noise ratio (SNR) of 10, which is consistent with typical MEG experiments. In actual experiments, the noise is usually spatially correlated, and thus the off-diagonal elements of C are typically nonzero. In practice, the entire C matrix can be estimated from the experimental MEG/EEG data (see, e.g. ref. 11).

The estimated source strength (ŝ_i) at each location i can be written as a weighted sum of the actual source strengths at all locations, plus a noise contribution. More formally,

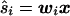4

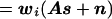5

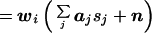6

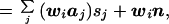7

where w_i is the ith row of W, and a_j is the jth column of A. Note that the first term in Eq. 7 is the sum of the activity (s_j) at every location j, weighted by the scalar w_ia_j. The second term reflects the noise contribution to the estimated activity at location i.

Our primary goal is to obtain accurate estimates of the temporal activity within/between fMRI visible regions. Therefore, we would like an explicit expression for the relative sensitivity of our estimate at a given location to activity coming from other locations. We define a “crosstalk” metric (ξ_ij), similar to the averaging kernel of the Backus–Gilbert method (42, 43) as follows:

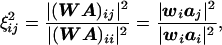8

where WA is the resolution matrix (44, 45) or resolution field (46).

By comparing Eqs. 7 and 8, we see that the crosstalk metric ξ_ij describes the sensitivity (or weighting) of the estimate at location i to activity at location j, relative to activity at location i, and provides a measurement of the distortion caused by location j.

A crosstalk value of 0% means that the estimated activity at location i is completely insensitive to activity at location j. A crosstalk value of 100% means that the estimated activity at location i is equally sensitive to activity at locations i and j. For each location, the crosstalk from all other locations can be calculated. This computation shows the spatial spread of the estimate at each location. Thus, those locations with small spatial spread will have more accurate localizations than those locations with large spatial spread. We note that such a crosstalk map depends on the individual brain anatomy and recording geometry of the MEG sensor array.

Two different types of crosstalk were calculated: (i) fMRI visible crosstalk between two fMRI sources, and (ii) fMRI invisible crosstalk from a missing fMRI source (fMRI invisible or fMRI missing location) onto an fMRI source. The random fMRI source placement was repeated 10 times, and the crosstalk metrics were averaged, depending on the conditions being examined. For each random source placement, 100 fMRI missing locations were randomly selected.

RESULTS

Several studies have used fMRI or positron emission tomography (PET) activation data as a prior constraint on the inverse solution. In one such approach, single ECDs are placed at the center-of-mass of fMRI (47) or PET (17, 18) defined regions of cortical activation. A refinement of this approach uses a continuous source model (16). In the linear estimation framework presented here, these cases correspond to setting the fMRI weighting to 100%, assuming an infinite SNR, and either point or extended source models. Here, cortical areas of fMRI activation are tiled uniformly with dipoles. By either fixing the dipole orientation (e.g., using anatomical information), or allowing the ECDs to freely rotate over time, the estimated time courses of these fMRI-defined sources then can be determined by using a standard pseudoinverse technique.

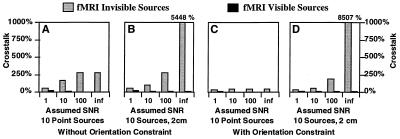
In our first simulation study, we examined the sensitivity of these proposed methods to the potential presence of fMRI invisible (missing) sources as a function of assumed sensor SNR in the noise covariance matrix C. The potential benefits of including an orientation constraint (in addition to the fMRI weighting) also were evaluated in these simulations. Using 100% fMRI weighting, Fig. 2 shows that the crosstalk from fMRI visible sources is quite small (<21%), but the crosstalk from fMRI invisible sources is potentially quite large, particularly for the extended source model. It should be noted that assuming infinite signal-to-noise is equivalent to using the Moore–Penrose pseudoinverse as the inverse operator. Importantly, the data further indicate that allowing for finite signal-to-noise greatly reduces the predicted distortion from fMRI invisible sources. However, the crosstalk remains high, and thus the presence of fMRI invisible sources could still be quite problematic.

Figure 2.

Crosstalk versus assumed SNR. Crosstalk is shown for 10 sources (point and 2 cm in diameter), with and without orientation constraint. The assumed SNR was either 1, 10, 100, or infinite. A relative fMRI weighting of 100% was used. The results indicate that allowing for finite SNR greatly reduces the predicted distortion from fMRI invisible sources. The extremely large amount of distortion from fMRI invisible sources, observed when assuming infinite SNR, demonstrates a potential problem with an fMRI-constrained pseudoinverse solution (which implicitly assumes infinite SNR).

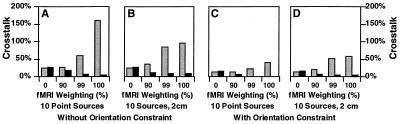
Based on the above results, we explored the effect of varying the degree of fMRI weighting. We calculated the crosstalk from both fMRI visible and fMRI invisible locations, of varying source extents. Fig. 3 shows the results for two different source sizes: point sources and extended sources of 2-cm diameter. The point source (although physiologically unrealistic) typically is used in ECD modeling, whereas the 2-cm extended source is representative of the extent of contiguous activation typically observed with fMRI.

Figure 3.

Crosstalk versus relative fMRI weighting. Crosstalk is shown for 10 sources (point and 2 cm in diameter), with and without orientation constraint. The relative fMRI weighting was either 0%, 90%, 99%, or 100%. The optimal fMRI weighting requires a compromise between resolving fMRI visible sources (i.e., higher fMRI weighting) and minimizing distortion from fMRI invisible sources (i.e., lower fMRI weighting). The results indicate that a 90% fMRI weighting greatly reduces the crosstalk from fMRI visible sources, while only slightly increasing the crosstalk from fMRI invisible sources.

For a given fMRI visible source, Fig. 3 shows that with increasing relative fMRI weighting, the crosstalk from other fMRI visible locations decreases, whereas the crosstalk from fMRI invisible locations increases. The use of the cortical orientation constraint reduces crosstalk from both fMRI visible and invisible sources. With no fMRI weighting (0%), crosstalk from both fMRI visible and invisible sources is identical, as would be expected. This corresponds to the well-known minimum norm solution. At this limit, a substantial crosstalk of 28% and 15% is predicted for the anatomically unconstrained and anatomically constrained cases, respectively. At the other limit of 100% fMRI weighting, the crosstalk from fMRI visible sources is minimized (<8%); however, the crosstalk from invisible sources is greatly increased (>40%). Thus, unless the coupling between neuronal and hemodynamic activity is perfect, and unless fMRI and MEG were both entirely accurate in detecting each form of activity, the use of 100% fMRI weighting is not optimal.

One would like to select a weighting that results in acceptably low distortion between fMRI visible locations while achieving reasonable levels of distortion from the fMRI invisible locations. Inspection of the results in Fig. 3 B and D (for the realistic extended source case) indicates that most of the benefit of fMRI weighting is achieved at a level of 90%. Although this weighting does not minimize the crosstalk from other visible sources, the improvement of going to 99% or even 100% fMRI weighting is small. More importantly, the data indicate that 90% fMRI weighting does not significantly increase crosstalk from invisible sources. In other words, 90% fMRI weighting is a reasonable compromise for typically sized extended source distributions. Therefore, we report here only the results from 90% fMRI weighting in our remaining simulation data. We note that the general pattern of results is similar for other fMRI weightings.

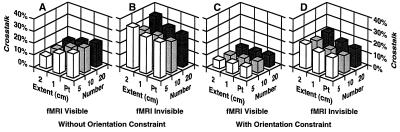
In a typical fMRI experiment, a number of discrete regions of activation are observed. Any inverse procedure that is applied to this type of data will have to handle multiple, extended sources. Fig. 4 shows that the crosstalk from both fMRI visible and invisible sources is relatively independent of the number and the spatial extent of the sources, within the realistic range plotted. Importantly, using the orientation constraint consistently results in very small crosstalk (<10%) from the fMRI visible sources, whereas the crosstalk from potential fMRI invisible sources remains moderate (<21%). This demonstrates the ability of this linear approach to cope with physiologically realistic source distributions, even in the presence of fMRI invisible (missing) sources. Obviously, because the crosstalk is substantially higher for fMRI invisible sources than for fMRI visible sources, the accuracy of the source activity estimates deteriorates with increasing neuronal activity from fMRI invisible locations.

Figure 4.

Crosstalk versus extent and number of sources. Crosstalk is shown for a variety of extents and numbers of sources. The extent of sources was either point, 1 cm or 2 cm in diameter, and the number of sources was 5, 10, or 20 (indicated by different gray scale). A partial fMRI weighting of 90% was used in these simulations. The results indicate that the crosstalk is relatively independent of source extent and number. This demonstrates that the proposed linear estimation method is appropriate for modeling multiple, extended areas of activation, as typically encountered in functional neuroimaging studies.

The above simulation results demonstrate that constraining activity to the cortical surface greatly reduces the predicted crosstalk from both fMRI visible and invisible sources. Obviously, the usefulness of this anatomic constraint depends on the accuracy of the anatomic information. In general, both errors in the cortical location and orientation will affect the solution, with orientation errors the more problematic of the two. We therefore examined the effect of cortical orientation errors on the accuracy of the inverse solutions. Orientation errors were simulated by randomly perturbing the assumed cortical orientation by ± 30° about the correct orientation, a range presumably exceeding our true measurement error. Angle errors were drawn from a uniform distribution. The crosstalk metric was computed to provide a quantitative measure of sensitivity to orientation error. Comparison of these crosstalk values to those in Fig. 4 revealed very little difference, with only a slight increase in distortion averaging 2%. We conclude that orientation errors within this range would not significantly affect the accuracy of our localization.

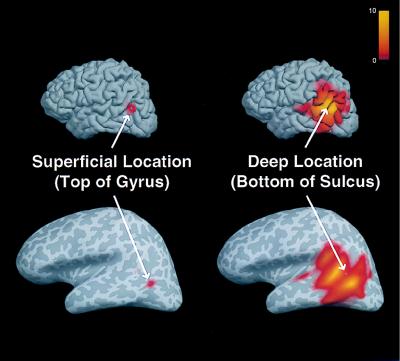
All cortical locations may potentially contribute to the estimated activity at any given location (see Eq. 7). The computed crosstalk for two locations is shown in Fig. 5 on the normal and inflated cortical surfaces. The cortical inflation process allows for visualization of the entire cortical surface, including areas buried within deep sulci (15, 48, 49). The maps indicate the relative weighting of activity at each and every location (j) contributing to the estimated activity at the indicated locations (i, white arrow). These crosstalk maps were calculated by using the cortical location constraint and no fMRI constraint (equivalent to 0% relative fMRI weighting). The superficial location on top of the gyrus (Fig. 5, Left) clearly shows much less sensitivity to activity at other locations, and consequently intrinsically higher spatial resolution, than the deeper location at the bottom of the nearby sulcus (Fig. 5, Right). The example further suggests that deep sources potentially benefit most from the additional inclusion of the fMRI constraint.

Figure 5.

Crosstalk maps of a superficial and a deep source location. Maps of the crosstalk metric (ξ_ij) for two different locations i (see arrows) were computed for all locations j, shown in folded (Upper) and inflated (Lower) cortical surface views. Surface curvature is represented in gray scale (light and dark gray corresponding to gyri and sulci, respectively). The crosstalk represents the relative sensitivity of the dipole strength estimate at a given location to activity at other locations [shown in color, ranging from 0 (gray) to 10 (yellow)]. Note the greater spread of the crosstalk for the deep location (Right) relative to the superficial location (Left), reflecting different intrinsic spatial resolution for these locations, when only anatomical constraints are used.

This type of spatial crosstalk information can show which regions of the brain are intrinsically less sensitive to localization error. In addition, such crosstalk maps can directly address the issue of mislocalized activity between two or more areas of fMRI activation. If there is little overlap between the crosstalk maps of those areas, one can be confident that the localization at one area is unaffected by activity at the other area. Conversely, if the spatial crosstalk map of one region of fMRI activity encompasses another region of fMRI activity, this particular method would not be able to accurately separate the activity from those two areas. Individual crosstalk maps potentially can be used to place some confidence limits on the interpretation of the estimated time courses.

DISCUSSION

Our simulation results demonstrate that the use of anatomical MRI and fMRI information can significantly improve the accuracy of spatiotemporal estimates of dynamic human brain activity. In the ideal case, where all neuronal source activity is accurately detected by fMRI (no missing or fMRI invisible sources), the properly fMRI weighted and noise regularized linear inverse produces source time-course estimates that should accurately reflect the true neuronal activity within the cortex. Happily, this holds true even for multiple and extended sources, as are typically encountered in human fMRI data. Additionally, the simulations demonstrate that the use of an orientation constraint consistently improves the accuracy of source estimates. Perhaps surprisingly, we found that errors in the specified cortical orientation, over a rather large range (encompassing any realistic error), produce very little distortion in the estimates.

Our data indicate that a fMRI weighting of approximately 90% is a reasonable compromise between sensitivity to crosstalk from fMRI visible and invisible sources. The optimal fMRI weighting, which depends on the confidence in the hypothesis that neuronal and hemodynamic activity are tightly coupled, currently cannot be determined a priori. However, even if this hypothesis is strictly correct, the hemodynamic response caused by a given neuronal source may be too small to be detected, given finite fMRI SNR. Therefore, some intermediate level of fMRI weighting is required to properly account for potential fMRI invisible sources.

In addition, EEG/MEG-averaged data always contain some finite residual noise caused by spontaneous brain activity (i.e., activity not time-locked to the stimulus). It is therefore essential to allow for a finite amount of additive noise. Sensitivity to such noise can be minimized by its proper estimation and inclusion within the noise covariance matrix C in the linear inverse operator. As shown in Fig. 2, decreasing the assumed EEG/MEG SNR (in the C matrix) also has the effect of reducing the effect of missing sources. However, such modeling errors are more properly accounted for by judicious fMRI weighting (in the R matrix). Experimentally, the C matrix can and should be computed from the actual EEG/MEG measurement data. We note that our studies also made assumptions about noise (Gaussian, uncorrelated) that possibly will not be strictly valid. Although the general conclusions reached here are likely to remain true, more realistic noise assumptions will be examined in future studies.

The distortion between fMRI visible locations is quite small and is further reduced by incorporating an orientation constraint. We note that extra sources do not result in additional crosstalk at other fMRI visible locations, because the crosstalk from fMRI visible sources has little dependence on the number of sources. In comparison, fMRI invisible sources (electromagnetic generators that are not detected by fMRI) are still problematic.

The crosstalk metric also has uses beyond these modeling studies. For a given experimental setup, the crosstalk metric can be calculated over the entire cortical surface. This spatial crosstalk map provides one measurement of the spatial resolution of the linear estimation method. Using the spatial crosstalk map potentially provides a principled argument for determining which brain regions can be well localized with this technique.

In conclusion, we have simulated the use of structural MRI and fMRI data to constrain the biomagnetic inverse problem. We have examined the expected accuracy of our estimations given several possible types of model mis-specification, including missing (fMRI invisible) sources, and orientation constraint errors. Future studies will investigate other possible types of mis-specification, including errors in the forward solution caused by incorrect head model parameters, and misregistration between fMRI/EEG/MEG coordinate systems. Overall, we find that with proper fMRI weighting and noise regularization, the MRI constraints improve the accuracy of the computed source time courses. This represents a major advance over simple dipole modeling of complicated brain activation data. This linear estimation approach provides an operator-independent method for combining information from fMRI, MEG, and EEG, to produce high-resolution spatiotemporal estimates of human brain activity.

ABBREVIATIONS

fMRI

functional MRI

MEG

magnetoencephalography

EEG

electroencephalography

ECD

equivalent current dipole

SNR

signal-to-noise ratio