Mortality invariants and their genetic implications

Abstract

Old noninbred fly mortality decreases according to the inverse linear law and reduces to a single suborder-specific age. Relative child mortality (the mortality at a given age related to the mortality at 10 years) from 1 mo to 11 years is the same with 8% mean accuracy for all humans, independent of race, country, sex, and birth year (from 1780 to 1995), in contrast to birth mortality, which in developed countries changed fiftyfold during the last century. The concept of invariants, which is very powerful in physics, is applied to mortality of species as remote as humans and flies. It provides quantitative estimates for the selection of hereditary Methuselahs, who live, e.g., over six-mean lifespans and who may be relatively young biologically. It also demonstrates that old fly and relative child mortality are determined genetically and that the former is related to genetic heterogeneity.

1. Mortality Invariants.

The evidence that genes influence aging and longevity is abundant (1–4). It includes identification of longevity genes and lifespan extension mutants (3, 5–10), as well as artificial selection for postponed senescence. Yet, it is still uncertain to what extent mortality is genetic (11–14). Natural selection seems inconsistent with genetically programmed mortality because few wild animals live to senescence; it might be consistent with genetically determined mortality (1, 15–20), which is linked to some other vital character, such as, e.g., stress resistance (12). Large fly populations (13, 16, 17) demonstrated mortality leveling off and decreasing at older ages. To explain it, demographic heterogeneity models (18–20), density effects (21, 22), changes at the individual-level physiology (23), and extension (24) of the “disposable soma” model (25), a model of both the pleiotropy (trade-off) and mutation accumulation (26) in age-structured populations (27) was considered (28) according to the Hamilton–Charlesworth theory. Yet, it still remains a challenge (29, 17, 22), and numerical studies (ref. 30 and refs. therein) of a model of mutation accumulation yielded only mortality increase in old age. Fly mortality (13, 16) presents an even greater surprise (31). Eighteen (of 500,000) male medflies in cages, who survived to 4.3-mean lifespans, all lived almost another lifespan; three (of 24,000) medflies in cells, who lived to 4.4-mean lifespans, all survived to almost 8 lifespans. Does this finding suggest there is no genetically determined mortality and thus no lifespan limit? Why, then, do all humans rapidly die out in the vicinity of 100 years (i.e., 1.25-mean lifespans now and 3-mean lifespans two centuries ago (32–36) and, e.g., in 1780 Sweden) and none of billions of humans lived beyond 122 years? Clearly, a comprehensive study is called for, which allows for quantitatively verifiable predictions. Phenomenological theory (31, 38) predicts that old age mortality of certain species is inversely linear with age and reduces to the only species-specific age. The next section verifies this prediction† (see section 3 for specifics) with all available noninbred fly data (13, 16, 17) and determines their species-specific age, which equals 68 days independent of conditions (overcrowded cages, individual cells, and cups), sexes, and even different families. These data establish a new empirical law of old fly mortality, which reduces to the species- (possibly suborder) specific age. If a quantity (an invariant) is the same for a given class of objects (“universality class”), then it depends on what is common to all representatives of this class. So, this age, which is the same for all representatives of a given species (mortality invariant), must be genetically determined together with the old age mortality, which reduces to it.‡ Therefore, extremely old flies, which yield it (e.g., 85 medflies that survived in cups to 4-mean lifespans), also must be genetic Methuselahs. The established law of their mortality provides an estimate of the initial fly population, which is predicted to produce a desired number of Methuselahs of a given age. Their preserved eggs and the following successive selection in several generations may yield the fly population, whose hereditary mean lifespan is, e.g., six times longer than the lifespan of the initial population. Mortality study of large populations of insects like aphids might be of special interest. If they yield universally decreasing old age mortality, then parthenogenetic eggs of their Methuselahs may provide hereditary Methuselah clones. Populations of hereditary Methuselahs might determine explicit characters linked to longevity. Such characters may allow for an estimate of the lifespan of an individual and an easier selection of the populations with increasing mean lifespans.

Mortality is used to quantify senescence in a population (1). If lower mortality implies younger biological age (for a given species), then the decreasing old age mortality implies that biologically older animals die out very rapidly, only biologically very young (and correspondingly rare) genotypes survive, and the average biological age of the surviving Methuselah subpopulation decreases with age. Thus, hereditary Methuselahs may be biologically relatively young (at least in some physiological aspects, which are to be specified).

Infant mortality is determined largely by environment. Indeed, improvements in social and medical conditions decreased it fiftyfold within the last century (32–36). However, life tables (32–36) prove that mortality always reaches a minimum§ at the age x_m = 10.5 years, which is a species-specific mortality invariant and is therefore genetic. The next section verifies† with 272 life tables (32–36) that, (although mortality changes fiftyfold) in agreement with the prediction of phenomenological theory (39), the relative mortality (i.e., the mortality at a given age related to the mortality at 10 years) from 1 mo to 11 years is inversely linear with age and is the same (with 8% mean square deviation) for all humans, independent of race, country, sex, and birth year. So, relative mortality is (90%) species-specific and thus genetically determined.

Empirical, species- (possibly suborder) specific mortality laws are a challenge to any theory. Their biological origin, implications, and problems are discussed in section 3.

2. Universal Laws.

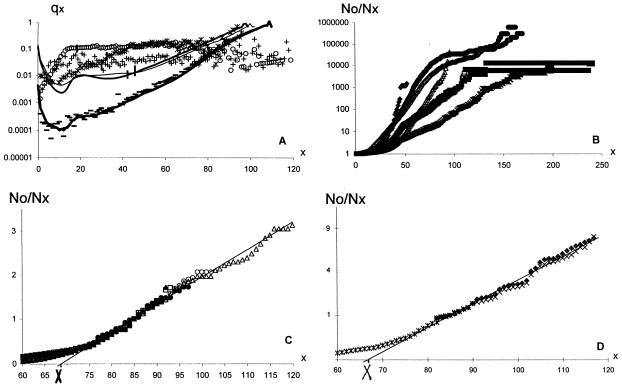
Large noninbred fly populations were studied for male and female medflies (13, 16) in different conditions (1,203,646 in 167 cages, 27,181 in individual cells, and 21,204 in individual cups), and 121,894 male Drosophilas were reared in mixed-sex cages (17). Even the largest number of medflies (60% of 1780 and 25% of 1891 Swedish population) exhibited large fluctuations in mortality rate (cf. flies and humans in Fig. 1A). Semilogarithmic curves in Fig. 1B are more explicit. The slope presents a mortality rate and demonstrates its course-grained change with age.¶ Phenomenological theory predicts (31) that, depending on old population heterogeneity (see the next section for quantitative details), the inverse relative number of old survivors is linear or quadratic with age and that the level age is species-specific. This prediction is verified in Fig. 1 C and D with all noninbred fly data. Fig. 1C demonstrates the linear dependence of N₈₅/N_x, which proceeds for medflies from 74 days until the number of survivors drops down to very low statistics (18 male at 97 days, 26 females at 120 days in cages, and 30 males and 46 females at 88 days in cells), i.e., up to 2.5-mean lifespans (and during a more limited interval for all flies). Fig. 1D demonstrates the linear dependence of 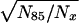on x for medflies in cups and Drosophilas in cages (from 80 to 117 days with 38 male and 59 female medfly survivors and from 70 to 88 days with 39 Drosophila survivors). The level age of X of linear interpolations in Fig. 1C and D is 69 and 67 days respectively. With 1.5% accuracy, X is the same (68 days) for different conditions, sexes, and even families (med- and fruitflies), i.e., it is a (suborder-specific) mortality invariant. Within the age limits stated above, the figures verify the theoretical predictions and make them empirical laws: with 7% accuracy, the inverse relative number of old fly survivors (correspondingly for Fig. 1 C and D) is

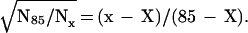1

The 7% accuracy in old age (with significantly higher fluctuations due to low statistics) is remarkable: before the universality region, N₈₅/N_x changes thousandfold, from 0.00005 (male medflies in cages) to 0.05 (female medflies in cups). The validity interval of the interpolation is very long, significantly longer (compared with the mean lifespan) than the well-known Gompertz law (40, 31) (which corresponds to linear regions in Fig. 2A). According to Eq. 1, mortality rate q_x = −dℓnN_x/dx is correspondingly‖

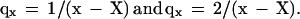2

By Eq. 1 and refs. 13 and 16, five million medflies in cages and 150,000 in cups are expected to provide 50 survivors to 10-mean lifespans, i.e., to 200 days in cages and to 300 days in cups. The validity of Eq. 1 with a species-specific X for insects like aphids is a litmus test for the possibility to use parthenogenetic clones to select hereditary Methuselahs.

Figure 1.

(A) Mortality rate for Japanese females (1891/98, thin line; 1935–36, medium line, 1990, thick line), Swedish males, 1990 (dashes), 605,528 female medflies in cages (circles), 10,741 in individual cups (crosses), and 121,894 male Drosophilas in cages (stars). Twenty-six medflies in cages and 53 in cups lived beyond 120 days, to 171 and 241 days respectively (see Fig. 1B); cf. the ratio of the maximal and the mean (thick vertical lines) lifespans for humans and medflies. Mortality rate is calculated according to q_x = ℓn(N_x/N_x+1), where N_x is the number of survivors to the age x (years for humans and days for flies). (B–D) Inverse relative number of survivors (N₈₅/N_x) to a given age (x) in days for medfly females (+, □, O), males (X, □, O), and all medflies (⋄, Δ, Δ) in cups, cells, and cages respectively; for male Drosophilas in cages (∗) and 5,751 (inbred ones in Fig. 1B only) in vials (♦) on semilogarithmic (B), linear (C), and quadratic (D) scales. For clarity, data beyond the age with reliable statistics in C and D, and before the linear region for medflies in cups in D, are dropped out. Solid lines are linear interpolations. Note that many data points overlap.

Figure 2.

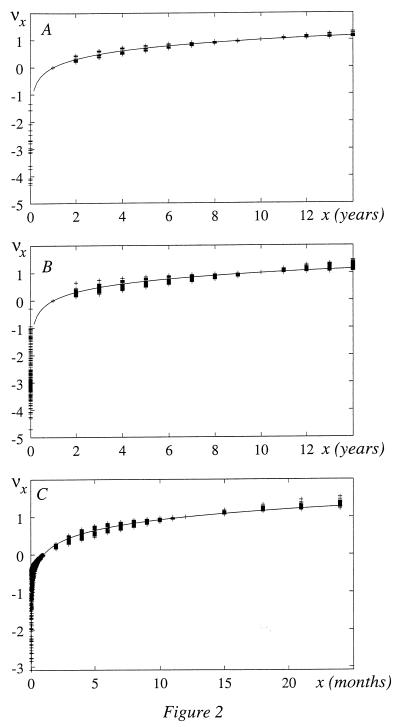
Relative number ν_x of deceased male and female children between 1 and x years according to 1871–1994 German (A), 202 combined 1871–1994 German, 1891–1990 Japanese, and 1780–1995 Swedish lifetables (B) and between 1 and x mo according to 210 infant male and female 1891–1995 Swedish lifetables (C). In A and B, ν_x = [ℓn(N₁/N₁₀)]⁻¹ ℓn(N₁/N_x); in C, ν_x = (N₁ − N_x)/(N₁ − N₁₂). Solid lines are ℓn x/ℓn 10 in A and B and ℓn x/ℓn 12 in C. Each data point (a cross) corresponds to a lifetable.

Consider child mortality. Its statistics in modern, developed countries is rather low. For instance, 50,208 girls were born in 1995 Sweden. Fifty-one died the first day; 54 the next week; 24 the next month; 50 more until the end of the first year; and 15, 9, and 6 in their second, fourth, and ninth year, respectively. This yields large mortality fluctuations (see Fig. 1A). So, let us study the relative number of deceased children. Phenomenological theory predicts (39) that it is a universal function of age with no fitting parameters. Specifically, if the number of survivors to x years is N_x, and** n_x = ℓn(N₁/N_x), then beyond a few weeks

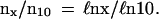3

The function n_x/n₁₀ is presented in Fig. 2A according to 1871–1994 German (35) and in Fig. 2B according to 1871–1994 German, 1891–1990 Japanese (36), and 1780–1995 Swedish male and female lifetables (32, 34). From 1 to 11 years the mean quadratic deviation from the average values is 5% in both figures. (Characteristically, the mean quadratic deviation at birth is 30 times larger and is presumably nongenetic.) The mean deviation of the average values from ℓnx/ℓn10 is 2% in Fig. 2A and 5% in Fig. 2B. The 210 Swedish infant lifetables (32) (which present raw data daily until 1 mo and monthly until 1 year for every year from 1891 to 1995) yield ΔN_x/ΔN₁₂ (x is in months) as shown in Fig. 2C. From 1 to 24 mo, the mean deviation from the averages and of the averages from ℓnx/ℓn12 is 8%. Thus, from 1 mo to 11 years the relative number of deceased children is indeed a universal species specific (with 8% mean accuracy) function of age, independent of race, country, sex and birth year, whereas the birth and the first week mortality is predominantly nongenetic (premature) and crucially depends on social and medical conditions.

Eq. 3 implies that child mortality q_x is inversely linear with age:

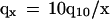4

(x is in years). This is similar to old fly mortality (2), but the factor q₁₀ in Eq. 4 is not universal (see, e.g., Fig. 1A). However, relative mortality q_x/q₁₀, by Eq. 4, is species-specific, ≅ 10/x and is therefore genetically determined.

An important comment is in order. Although Eqs. 1 and 3 present (with 7% and 8% accuracy, respectively) empirical survival data, Eqs. 2 and 4 provide mortality rates according to their interpolations. If q_x is calculated according to q_x = ℓn(N_x/N_x+1), then the nonuniversality of q₁₀/q_x is significantly higher.

3. Phenomenological Theory and Human-Fly Universality.

The previous section empirically demonstrates a fly mortality invariant X (which is independent of conditions, sex, and the degree of population heterogeneity of a given suborder) and thus the predominantly genetic nature of old fly mortality,‡‡ which, by Eq. 2, reduces to X. Because an old individual does not get younger with age, presumably the chances to die do not decrease either. So, genetic mortality decrease must be related to genetic heterogeneity of the fly population. To survive to very old age, individuals must have very low genetic mortality, significantly lower than the mortality of the population at large. Therefore, populations become more and more selected as they age, and subpopulations with low death rates constitute the majority of individuals in the oldest age classes. And, indeed, by Eq. 2 mortality of medfly survivors to 120 days is 10 times lower than mortality of the (much larger number of) survivors to 80 days. In fact, by Eq. 2, at 120 days it is the same as the mortality of the population in Fig. 1A at 10 days (with 90% of survivors). Thus, with respect to mortality, flies are genetically very heterogeneous, and old age mortality crucially depends on the heterogeneity of the initial population and on the subpopulations that survive to old age under given conditions.†† At very old age, the number of survivors is so low that the population mortality becomes stochastic, strongly depending on individual mortalities, and is highly nonuniversal. Usually beyond a certain (nonuniversal) age, it rapidly increases, in agreement with phenomenological theory (31) (see Fig. 1B). However, the last survivors may accidentally have anomalously low genetic mortality and yield long “survival plateaus” as shown in Fig. 1B, in which flies do not die (presumably, their genetic mortality is extremely low). Eighteen male medflies in cages (0.003% of the initial population) survive to 4.3-mean lifespans η. They all live another 0.9 η. Two female medflies in cups survive to 5.5 η and live until 6.6 η. Three medflies in cells (0.03% of the initial population) who survive to 4.4 η, all three live another 3.5 η, to 7.9 η. (Such genetic “quasi-immortals” may be of special interest.) Smaller old age plateaus in Fig. 1 B and C are multiple. Corresponding quasi-steps in Fig. 1 B–D may manifest successive extinction of certain subpopulations.

The previous section demonstrated that, although the child mortality rate (especially at birth) crucially depends on conditions and strongly fluctuates, its decrease with age is predominantly species-specific and thus genetic. One may speculate that mortality decreases because genotypes with anomalously high mortality die out anomalously early and determine the law of mortality decrease (39) (i.e., relative child mortality is related to genetic heterogeneity). Remarkably, Drosophila mortality at early age also decreases to a minimum at the age ≅ X/10 and yields the same law (39) with the mean quadratic deviation of 16%. Mortality minimum in human louse (16) is reached in pupal stage. Possibly, in medflies and in some other insects mortality also decreases before an adult stage.

Universally for flies and humans, advanced age yields (31, 38, 39) plateaus in mortality curves. Because mortality strongly fluctuates, plateaus are more explicit as linear regions in the curves in Fig. 1B. (For other mortality regions and invariants, see refs. 31, 38, and 39.)

Similarities in mortality of species as remote as humans and flies suggest a general mortality pattern. This suggestion is verified with a general invariant, which unites metabolism and lifespan (41). All animals (from invertebrates to mammals) consume 20 oxygen molecules per body atom per lifespan. For many animals an experimental error may be by a factor of 3; some animals have anomalous (also by a factor of 3) oxygen consumption (41, 42). Yet, the relative accuracy of this invariance is remarkably high because 3 should be compared with 10¹⁰ (which represents the change in the number of body atoms). A general invariant suggests a general origin of genetically determined mortality, which did not change at any stage in evolution. Indeed, analysis of human and fly data presents (31) a general mortality law†† applicable to individual species. In contrast to the Gompertz–Strehler–Mildvan-type law (see it in refs. 31 and 40 and refs. therein), its mortality may vanish at any age for certain genotypes.††

A few comments. Small terriers and large Irish wolf hounds, which belong to the same species of domestic dogs; workers and much larger queens of ants, social bees, and termites (43), have significantly different average lifespans. A universal allometric relation between the average lifespan and the body mass (refs. 41 and 44 and refs. therein) implies that this is not accidental. Possibly, some species have several mortality invariants (39), but a comprehensive study is called for.

The suggested phenomenological approach yields universal mortality laws and universal (across all animal species) oxygen consumption, demonstrates species- and suborder-specific mortality invariants, establishes predominantly genetic nature of old fly and relative child mortality, and provides quantitative estimates for the selection of hereditary Methuselah populations. Once verified, quantitative universal laws, which generalize empirical data, may serve as a basis for a theory of their biological origin. The latter was, e.g., suggested for allometric relations (44) (but a specific universal value of oxygen consumption remains to be explained). If a population of hereditary Methuselahs (which may be relatively young physiologically) is selected, it might elucidate the biology of mortality invariants and genetic mortality, which is beyond phenomenological approach.