Are mortality rates for different operations related? Implications for measuring the quality of non-cardiac surgery

Structured Abstract

Background

Except in cardiac surgery, measuring quality with procedure-specific mortality rates is unreliable due to small sample sizes at individual hospitals. Statistical power can be improved by combining mortality data from multiple operations. We sought to determine whether this approach would still be useful in understanding performance with individual procedures.

Methods

We studied eleven high-risk operations performed in the national Medicare population (1996–1999). For each operation, we calculated 1) the risk-adjusted mortality rate for the procedure and 2) the mortality rate with up to ten other operations combined (“other” mortality). To test for an association between these mortality rates, we calculated the correlation coefficient adjusting for random variation. We then collapsed hospitals into quintiles of other mortality and calculated procedure-specific mortality rates within each of these quintiles.

Results

Mortality with specific operations was modestly correlated with other mortality: coefficients ranged from 0.14 for pneumonectomy to 0.35 for esophagectomy. Despite small to moderate correlations, other mortality was a good predictor of procedure-specific mortality for 10 of the 11 operations. Pancreatic resection had the strongest relationship, with procedure-specific mortality rates at hospitals in the worst quintile of other mortality 3-fold higher than those in the best quintile (15.2% vs. 6.3%, p<.001). Pneumonectomy had the weakest relationship, with no significant relationship between other mortality and procedure-specific mortality.

Conclusions

Hospitals with low mortality rates for one operation tend to have lower mortality rates for other operations. These relationships suggest that different operations share important structures and processes of care related to performance. Future efforts aimed at predicting procedure-specific performance should consider incorporating data from other operations at that hospital.

Introduction

Because of widespread recognition that surgical quality varies widely, there is growing demand from patients, providers, and payers for better measures of surgical outcomes (1,2). Risk-adjusted mortality rates are a simple and reliable measure of surgical quality and have been used to good effect in cardiac surgery (3,4). Unfortunately, most operations are not performed frequently enough to reliably discriminate quality among individual hospitals using this approach (5,6).

One way to improve outcomes measurement in non-cardiac surgery is to combine several operations together when assessing hospital mortality rates (7). However, this approach will only be useful to the extent that hospital performance with different operations is correlated—i.e., that hospitals good at one operation are also good at others. While previous studies show relatively weak relationships between outcomes for different medical diagnoses, there is some reason to believe these relationships may be stronger in surgery (8,9). Many high-risk operations are dependent on the same hospital-level resources, staffing, and processes of care (10). We conducted this study to examine relationships between mortality rates with different non-cardiac procedures in the national Medicare population.

Methods

Study overview

We studied 11 high-risk operations in the national Medicare population over a four-year period, 1996–1999 (Table 1). We identified all patients aged 65 to 99 undergoing these operations using appropriate combination of International Classification of Diseases, version 9 (ICD-9) codes. The definition of these patient cohorts are described in detail in our previous work (11).

Table 1.

Number of Medicare cases, number of hospitals performing operation, and baseline mortality rates for the 11 high-risk operations (1996-1999).

Operation	Medicare Cases (1996–1999)	Hospitals Performing Operation	Baseline Mortality Rate
Colon resection	97,560	4,002	6.6%
Pancreatic resection	3,634	1,090	10.3%
Gastric resection	9,574	2,449	11.5%
Esophageal resection	1,988	832	15.%
Nephrectomy	19,738	2,686	3.0%
Cystectomy	7,430	1,729	5.3%
Abdominal aneurysm repair	45,282	2,344	5.7%
Carotid endarterectomy	156,635	2,629	1.8%
Lower extremity bypass	78,947	2,717	5.5%
Pneumonectomy	3,066	1,133	14.3%
Pulmonary lobe resection	24,921	2,221	5.5%

The analysis was comprised of two main parts. First, we explored correlations between procedure-specific mortality rates and mortality rates for up to 10 other operations combined (“other” mortality). Second, we created five groups of hospitals (quintiles) based on their risk-adjusted mortality with other operations and calculated procedure-specific mortality within each of these groups. Although some hospitals did not perform all 10 procedures, we determined other mortality based on those they did perform. We combined multiple operations to increase sample size and create a more precise mortality measure for both of these analyses. For this study, we defined operative mortality as a composite of in-hospital and 30-day mortality.

Risk-adjustment

To calculate risk-adjusted mortality rates, we used logistic regression to predict the probability of death for each patient based on demographics (age, gender, and race), type of operation, urgency of admission, and comorbid diseases. We used the Charlson score to assess comorbid diseases using secondary ICD-9 diagnostic codes (12,13). Our previous work based on these datasets has shown no difference between this and other approaches to adjusting for coexisting diseases (11). Predicted mortality probabilities were then summed for patients at each hospital to estimate expected mortality rates. The ratio of observed to expected mortality was then multiplied by the overall mortality rate to obtain the risk-adjusted mortality rate.

Correlation analysis

We assessed the relationship between each operation’s mortality rate and the mortality rate with other operations using a Pearson’s correlation coefficient adjusted for random variation. This adjustment was necessary because of the large amount of noise accompanying rates of mortality with small numbers of cases. This adjustment resulted in slightly larger correlation coefficients for all 11 operations compared to the correlations estimated without such an adjustment. To perform this adjustment, we estimated the amount of random variation for each of the mortality rates (procedure-specific mortality and other mortality) and rescaled the correlation coefficient to provide an estimate of the underlying true correlation. See the technical appendix for a full description of the methods used to adjust for random variation in this analysis.

Quintile analysis

We calculated a t-statistic for each hospital’s “other” mortality rate (observed minus expected mortality with other operations divided by the standard error). We then divided patients into 5 equal sized groups (at the patient-level) based on their hospital’s t-statistics. Because all of the patients at an individual hospital fall into the same quintile, this method effectively divides hospitals into 5 groups but ensures equal patient sample sizes in each group. The use of t-statistics, rather than raw mortality rates, statistically weights the hospital rankings to account for the size of individual hospital caseloads and to further reduce the impact of random variation. For example, a small hospital with a large difference between observed and expected mortality will have a lower t-statistic (and appear closer to average) than a large hospital with the same difference between observed and expected mortality. This type of analysis is desirable when measuring mortality rates because the large differences between observed and expected mortality rates seen in small hospitals are more likely to be due to chance than those at large hospitals. After creating these quintiles of other mortality, we estimated risk-adjusted, procedure-specific mortality within each quintile. This analysis was repeated 11 times, once for each operation included in the study. We tested the statistical significance across quintiles using a test of trend with logistic regression.

Results

During the years 1996 through 1999, 448,775 patients underwent one of the 11 high-risk operations included in our study. Table 1 shows the number of each type of case performed, the number of hospitals performing them, and the baseline mortality rate for each operation. Correlations between procedure-specific mortality and the mortality rate for other operations were small to moderate, even when adjusted for random variation (Table 2). The adjusted correlation coefficients ranged from a low of 0.14 for pneumonectomy to a high of 0.35 for esophagectomy.

Table 2.

Correlation between procedure-specific mortality and the mortality rate for other high-risk operations combined.

Operation	Correlation Coefficient
Colon resection	0.22
Pancreatic resection	0.31
Gastric resection	0.34
Esophageal resection	0.35
Nephrectomy	0.32
Cystectomy	0.17
Abdominal aneurysm repair	0.32
Carotid endarterectomy	0.20
Lower extremity bypass	0.12
Pneumonectomy	0.14
Pulmonary lobe resection	0.19

Despite small to moderate correlations, other mortality was a strong predictor of procedure-specific mortality for 10 of the 11 operations (Figure 1). Pancreatic resection demonstrated the strongest relationship: hospitals in the worst quintile of other mortality had procedure-specific mortality rates more than double than those in the best quintile (15.2% vs. 6.3%, p<.001). Pneumonectomy had the weakest relationship, with no significant relationship between other mortality and procedure-specific mortality. For all other operations other mortality was a statistically significant predictor of procedure-specific mortality (Figure 1).

Figure 1.

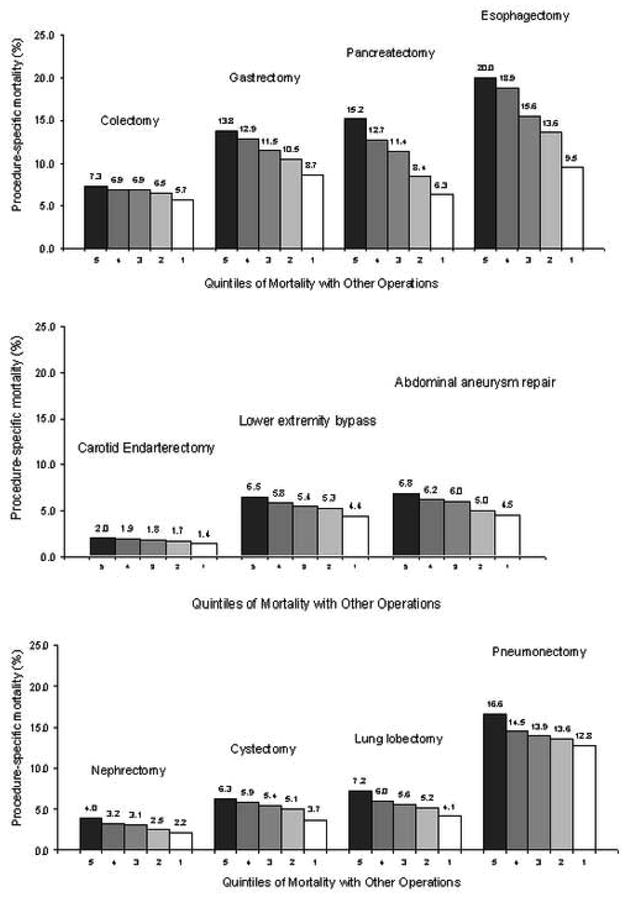
Procedure-specific mortality rates within quintiles of mortality for all other operations combined. P<.001 for the comparison of the best (quintile 1) to the worst (quintile 5) for all operations except pneumonectomy.

Discussion

We systematically evaluated the relationship between mortality rates for different non-cardiac operations performed at the same hospital. Our findings suggest that procedure-specific mortality is strongly related to a hospital’s mortality with other operations. In some cases, mortality with other operations is a better predictor than other proxy measures of quality, including hospital volume (11). The main result, that hospitals good at one operation tend to be good at others, has important implications for measuring the quality of non-cardiac surgery.

Although our study is the first to examine non-cardiac surgery, previous studies have evaluated correlations in hospital mortality rates between other populations. Most studies assessed the relationship for different medical diagnoses (e.g., pneumonia and acute myocardial infarction), and found weak correlations in mortality rates (8,9). There are two alternative explanations for the lack of correlations found in these studies. First, they may be due to problems with methodology. In particular, the small sample sizes at each hospital may have prevented the true relationships from being unmasked. Evidence from a prior simulation by Rosenthal et al. supports this assertion. If the “true” correlations were perfect (r=1.0), it would require several thousand cases in each hospital to identify them (8). Second, the relationships between mortality with different medical conditions may truly be weak. Patients with different medical diagnoses receive care in different parts of the hospital and are generally treated by different groups of physicians with few shared processes of care.

There is reason to believe that correlations should be stronger in surgery. Different operations share many elements of staffing and infrastructure. Structural characteristics important to all high-risk operations include intensivist staffing of critical care units, high nurse to patient ratios, and the presence of high-volume, specialty trained surgeons. They also depend on many of the same processes of care. Shared processes of care related to patient outcomes include preoperative cardiac evaluation, appropriate use of perioperative antibiotics, beta blockers, and venous thromboembolism prophylaxis, and postoperative pain management. Indeed, a recent study on different cardiac surgery operations by Goodney et al. found strong correlations between mortality rates for coronary artery bypass grafting and mortality rates for both mitral valve surgery (r = 0.54) and aortic valve surgery (r = 0.59) (10). Our current study extends these findings to other non-cardiac surgical procedures.

We should consider our findings in the context of certain limitations. First, we used the Medicare population, which includes only one-half of the cases for each operation. As a result, our estimates of mortality may be less precise than those calculated from an all-payer sample. Unfortunately, there are currently no all-payer databases inclusive of all US hospitals. If such a dataset were used, the more precise hospital-level estimates of mortality would likely increase the strength of the observed correlations. Our analysis is also limited by case-mix adjustment with administrative data. However, imperfect case-mix adjustment would only threaten the validity of our findings if patient severity was systematically correlated across operations. If this were true, unmeasured case-mix differences would lead to an overestimate of the correlations observed. Most likely, patient severity varies randomly within hospitals by year and procedure type. If so, limitations in risk-adjustment would tend to bias our findings towards the null hypothesis.

Our findings suggest mortality data for multiple operations can be combined to create more precise measures of hospital-level quality. One such approach would be to rely on the overall hospital mortality rate as a proxy for procedure-specific performance. This approach is already used in one of the most high profile quality improvement programs in non-cardiac surgery, the National Surgical Quality Improvement Program (NSQIP) (7). The NSQIP, present in Veterans Affairs and a growing number of private-sector hospitals, uses an aggregate mortality (and morbidity) rate as a hospital-level quality measure. However, our results should not be considered a direct validation of this approach. The NSQIP combines a more heterogeneous group of operations (both low-risk and high-risk) in their measure, whereas we considered only high-risk operations. Correlations between overall mortality rates and procedure-specific mortality rates are likely weaker when more heterogeneous procedures are aggregated.

Another approach would be to use the information from multiple operations to create so-called integrative measures of procedure-specific performance. By this method, all information available about quality for a given operation (e.g., mortality rates, morbidity rates, procedure volume, and mortality rates with other operations) would be used to make a prediction about each hospital’s “true” mortality rate (19). Explicit consideration is given to the degree of relatedness between procedures, and the exact contribution of each operation to another operation’s prediction is estimated using sophisticated weighting techniques. Methods that integrate multiple domains of quality have yielded promising results for measuring quality of care after acute myocardial infarction (19) and neonatal intensive care (15), but could be readily extended to surgery.

These integrative measures are a generalization of the standard empirical Bayes (or shrinkage) estimator that places more weight on a hospital’s own mortality rate when the ratio of signal to noise in the mortality estimate is high, but shrinks back toward the population mean when the ratio of signal to noise is low (14). But where the usual shrinkage estimator is a weighted average of a single outcome measure and its mean, the shrinkage estimator of an integrative measure would be weighted average of all outcome measures and their means. This approach would yield a generalized empirical Bayes estimator for the mortality rate of each procedure that is a linear combination of the mortality and complications measures for all procedures in each hospital. In principal, the key advantage of such estimates is that they would optimally combine all available quality measures to form the best prediction of each hospital’s true mortality rate.

Although creating more precise hospital quality rankings using these techniques may help identify the best hospitals, our findings also have important implications for improving care where it already occurs. The relationships between other mortality and procedure-specific mortality imply shared structures and processes of care across high-risk surgery. Identifying and promoting wide implementation of these shared characteristics and best practices could improve care at all hospitals. Because an aggregate measure of mortality allows precise identification of the “best” and “worst” hospitals, these hospitals can be targeted further research in evaluating which characteristics are most important. But we should note that the correlations between different operations are not perfect. There no doubt remain other important structures and processes of care specific to each type of operation. Subsequent efforts at improving the quality of surgical care at all hospitals also depend on isolating and disseminating these procedure-specific factors.

Technical Appendix

Our adjustment of correlation coefficients for random variation is motivated by a hierarchical model in which data at the first (patient) level provides noisy estimates of an underlying true mortality observed at the second (hospital) level. The adjusted covariance matrix captures the (true) underlying correlations between procedure-specific mortality rates and mortality rates with other procedures, net of the estimation error. At the first level, the distribution of the estimates conditional on the underlying true mortality is:

$$\text{E}({\text{Y}}_{\text{i}}\mid {\mu }_{\text{i}})={\mu }_{\text{i}},\hspace{0.17em}\text{and\hspace{0.17em}Var}({\text{Y}}_{\text{i}}\mid {\mu }_{\text{i}})={\text{V}}_{\text{i}},$$ (1)

where Y_i is a 2×1 vector of the mortality rate for the procedure under consideration and the mortality rate for patients with all other procedures for hospital i; μ_i is the corresponding 2×1 vector of (true) underlying mortality that represents the average mortality that a typical patient could expect at this hospital; and V_i is the 2×2 sampling variance-covariance matrix for the estimates in Y_i. Note that the hierarchical nature of the data allows us to estimate V_i for each hospital (i) in a straightforward manner, since this is simply the sampling variance of a vector of estimates derived from a sample of patients at hospital i. In particular, the diagonal (variance) terms of V_i are the square of the standard errors for the two mortality rates at hospital i (Y_i), while the off-diagonal (covariance) term is zero because the two mortality rates are estimated from different samples of patients and therefore independent (conditional on μ_i).

At the second level, the distribution of the underlying true mortality rates across hospitals is:

$$\text{E}({\mu }_{\text{i}})=\mu \hspace{0.17em}\text{and\hspace{0.17em}Var}({\mu }_{\text{i}})=\mathrm{\sum },$$ (2)

where μ is a 2×1 vector of mean mortality rates in the entire population and Σ is the 2×2 variance-covariance matrix in mortality rates summarizing the relationship between the mortality rate for the procedure under consideration and the mortality rate for other procedures.

To estimate of the variance-covariance matrix of mortality rates (Σ), we calculate the covariance matrix of the risk-adjusted mortality rates (Y_i), and adjust for sampling variability by subtracting the average sampling-error covariance matrix (V_i), so that:

$$\widehat{\mathrm{\sum }}=\mathit{Var}(Y_i)-\mathit{Mean}(V_i),$$ (3)

where $\mathit{Var}(Y_i)=\frac{1}{N-1}\sum _{i=1}^N(Y_i-\overline{Y})(Y_i-\overline{Y}{)}^{\prime }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{Mean}(V_i)=\frac{1}{N}\sum _{i=1}^N{V}_i$

The correlation coefficients that we report were derived from this estimate of the variance-covariance matrix of the risk-adjusted mortality rates (Σ̂), and in this way were adjusted for random variation. These estimators are those proposed by Morris in his 1983 review article on parametric empirical Bayes (14), and have been used to estimate the correlation across quality measures in a number of prior applications (15–18).