On NUFFT-based gridding for non-Cartesian MRI

Abstract

For MRI with non-Cartesian sampling, the conventional approach to reconstructing images is to use the gridding method with a Kaiser-Bessel (KB) interpolation kernel. Recently, Sha et al. [1] proposed an alternative method based on a nonuniform FFT (NUFFT) with least-squares (LS) design of the interpolation coefficients. They described this LS_NUFFT method as shift variant and reported that it yielded smaller reconstruction approximation errors than the conventional shift-invariant KB approach. This paper analyzes the LS_NUFFT approach in detail. We show that when one accounts for a certain linear phase factor, the core of the LS_NUFFT interpolator is in fact real and shift invariant. Furthermore, we find that the KB approach yields smaller errors than the original LS_NUFFT approach. We show that optimizing certain scaling factors can lead to a somewhat improved LS_NUFFT approach, but the high computation cost seems to outweigh the modest reduction in reconstruction error. We conclude that the standard KB approach, with appropriate parameters as described in the literature, remains the practical method of choice for gridding reconstruction in MRI.

1 Introduction

For notational simplicity, we describe a 1D version of MR reconstruction by gridding. The generalization to 2D and 3D is straightforward using separable interpolators as described previously, e.g., [2–4]. Given samples {F(ν_m)}, m = 1, …, M of the Fourier transform of an object f(x), one can estimate f by an approximate inverse Fourier transform as follows:

$$\widehat{f}(x)=\sum _{m=1}^M{d}_{m}F({\nu }_m)e^{i2\pi {\nu }_{m}x},$$

where {d_m} are sample density compensation factors that one can determine with a variety of methods, e.g., [5]. For practical purposes, it suffices to evaluate f̂(x) at a finite set of N samples:

$$f_n\triangleq \widehat{f}((n-\tau ){\mathrm{\Delta }}_{\text{x}}),\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }n=0,\dots ,N-1,$$ (1)

$$=\sum _{m=1}^M(d_{m}F({\nu }_m){\text{e}}^{-i2\pi {\nu }_m{\mathrm{\Delta }}_{\text{x}}\tau }){\text{e}}^{i2\pi {\nu }_m{\mathrm{\Delta }}_{x}n},$$ (2)

The parameter τ indicates the center of the field of view relative to the image sampling, where typically τ = N/2 or (N − 1)/2. Defining ω_m ≜ 2πν_mΔ_x and the phase modulated spectrum

$$F_m\triangleq d_{m}F({\nu }_m){\text{e}}^{-i{\omega }_m\tau },$$ (3)

the essence of the gridding reconstruction method is to evaluate summations of the following form:

$$f_n=\sum _{m=1}^M{F}_m{\text{e}}^{i{\omega }_{m}n},\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }n=0,\dots ,N-1.$$ (4)

This is a “type 1” NUFFT as defined for example in [6].

The central approximation underlying gridding methods is:

$${\text{e}}^{i\omega n}\approx e_n(\omega )\triangleq s_n\sum _{k=0}^{K-1}{\psi }_k(\omega /\gamma ){\text{e}}^{i\gamma kn},$$ (5)

for some K ≥ N, where γ ≜ 2π/K and ${\{{\psi }_k(\omega /\gamma )\}}_{k=0}^{K-1}$ denotes interpolation coefficients associated with frequency ω. The (positive) s_n values are called scaling factors [7]. The design problem is to choose the scaling factors s = (s₀, …, s_N−1) and the interpolator φ_k(·) to minimize the approximation error in (5).

If one imposed no constraints on φ_k, then (5) could be made to be exact by choosing uniform scaling factors s_n = 1, and by using the following ideal interpolator:

$$\begin{array}{rl}{\psi }_k(\kappa )& =\frac{1}{K}\sum _{n=0}^{N-1}{\text{e}}^{i\gamma \kappa n}{\text{e}}^{-i\gamma kn}\\ & =\frac{N}{K}\frac{1}{N}\sum _{n=0}^{N-1}{\text{e}}^{i\gamma (\kappa -k)n}={\psi }_0(\kappa -k),\end{array}$$ (6)

for k = 0, …, K − 1, where

$${\psi }_0(\kappa )\triangleq \frac{N}{K}{\text{e}}^{-i\gamma \kappa {\eta }_0}{\delta }_N(\kappa ),$$ (7)

where η₀ ≜ (N − 1)/2 and δ_N denotes the following K-periodic Dirichlet kernel:

$${\delta }_N(\kappa )\triangleq \frac{1}{N}\sum _{n=0}^{N-1}{\text{e}}^{i\gamma \kappa (n-{\eta }_0)}=\frac{sin(\pi \kappa N/K)}{Nsin(\pi \kappa /K)}.$$ (8)

Note that δ_N(κ), the “core” of the ideal interpolator, is real; the only complex aspect of (7) is the linear phase term. Furthermore, the κ − k argument in (6) indicates an (integer) shift invariance. It is logical therefore to expect that other useful interpolators will have such integer shift invariance and will have the same form as (7), namely, the product of a linear phase term with a real interpolation kernel.

Substituting (7) into (5) and (4) and simplifying yields the following expression for the ideal interpolation process:

$$f_n=\frac{N}{K}\sum _{k=0}^{K-1}\left[\sum _{m=1}^M(F_m{\text{e}}^{i{\omega }_m{\eta }_0}){\delta }_N\left(\frac{{\omega }_m}{\gamma }-k\right)\right]{\text{e}}^{i\gamma k(n-{\eta }_0)}.$$ (9)

In this form, if τ = η₀, then we use the real, symmetric interpolator δ_N (·), followed by an inverse FFT centered at η₀.

The ideal interpolator (7) would be computationally impractical, so in practice one allows φ_k(κ) to have at most J ≪ K nonzero values for each ω. In particular, for simplicity one uses the J neighbors that are nearest to ω (in a modulo-2π sense). Define the integer offset as follows:

$$k_0(\omega )\triangleq \{\begin{array}{ll}\left[(\omega /\gamma )modK\right]-\frac{J+1}{2},\hfill & J\hspace{0.17em}\text{odd}\hfill \\ \lfloor \text{(}\omega /\gamma \text{)}modK\rfloor -\frac{J}{2},\hfill & J\hspace{0.17em}\text{even},\hfill \end{array}$$ (10)

where ⌊·⌋ denotes the integer floor function, and [·] denotes rounding to the nearest integer. This offset satisfies the following (integer) shift invariance property:

$$k_0(\omega +l\gamma )=l+k_0(\omega ),\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\forall l\in \mathbb{Z}.$$ (11)

Then we replace (5) by the equivalent expression

$${\text{e}}^{i\omega n}\approx {\widehat{e}}_n(\omega ;\mathit{u})=s_n\sum _{j=1}^J{u}_j(\omega ){\text{e}}^{i\gamma (k_0(\omega )+j)n},$$ (12)

where u(ω) = (u₁(ω), …, u_J (ω)) denotes the vector of length J of interpolation coefficients associated with frequency ω.

In principle the interpolation coefficients u(ω) could be shift variant, but we will show shortly that good choices for u(ω) satisfy a shift-invariance property equivalent to that of (6), contrary to the implication of [1, Fig. 1]. Having made the approximation (12) we can evaluate the NUFFT (approximately) as follows:

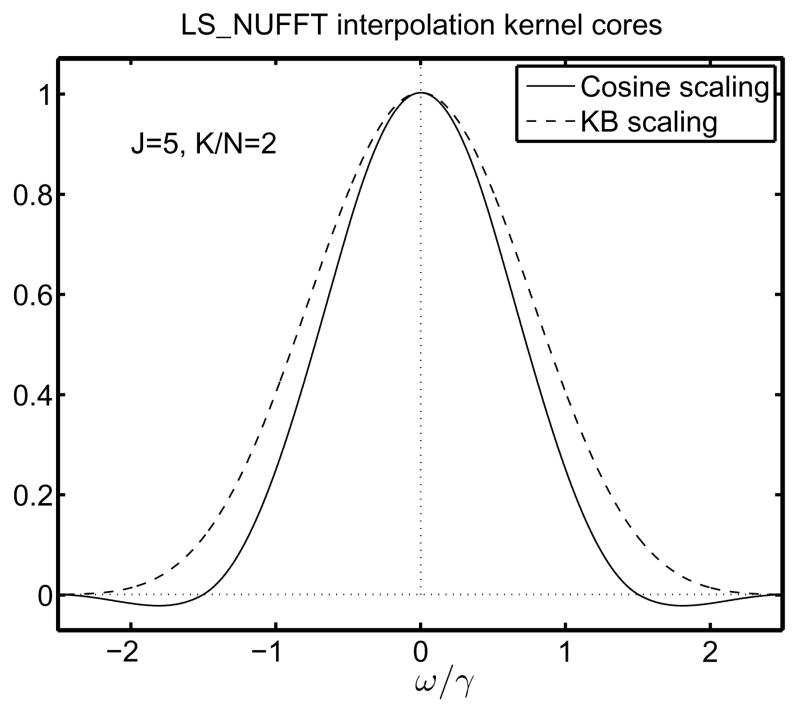
Figure 1.

Interpolator cores for the LS_NUFFT interpolator with cosine scaling factors, and for the conventional Kaiser-Bessel interpolator, normalized to unity maximum.

$$\begin{array}{rl}{f}_n\approx {\widehat{f}}_n& \triangleq \sum _{m=1}^M{F}_m\left[s_n\sum _{j=1}^J{u}_j({\omega }_m){\text{e}}^{i\gamma (k_0({\omega }_m)+j)n}\right]\\ & =s_n\sum _{j=1}^J\sum _{m=1}^M{F}_m{u}_j({\omega }_m){\text{e}}^{i\gamma (k_0({\omega }_m)+j)n}.\end{array}$$ (13)

This double summation can be implemented using an O(MJ) interpolation (gridding) from the nonuniform frequency space sample locations {ω_m} onto the nearby Cartesian samples {γk}, followed by an O(K log₂ K) inverse FFT.

The approximation (5) leads to the following bounds on the average weighted squared error:

$$\begin{array}{l}\frac{1}{N}\sum _{n=0}^{N-1}{w}_n{\mid f_n-{\widehat{f}}_n\mid }^2\\ \le \frac{1}{N}\sum _{n=0}^{N-1}{w}_n\sum _{m=1}^M{\mid F_m\mid }^2{\mid {\text{e}}^{i{\omega }_{m}n}-{\widehat{e}}_n({\omega }_m;\mathit{u})\mid }^2\\ \le \left(\sum _{m=1}^M{\mid F_m\mid }^2\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\underset{\omega }{max}{E}^2(\omega ;\mathit{s};\mathit{u}),\end{array}$$ (14)

where

$$E^2(\omega ;\mathit{s};\mathit{u})\triangleq \frac{1}{N}\sum _{n=0}^{N-1}{w}_n{\mid {\text{e}}^{i\omega n}-{\widehat{e}}_n(\omega ;\mathit{u})\mid }^2.$$ (15)

This upper bound is tight because it would be achieved for a spectrum F_m that is concentrated entirely on the worst-case frequency. In light of this tight bound, it is desirable to design the scaling factors s and the interpolation coefficients u(ω) to minimize the worst-case error by the following min-max criterion (cf. [4, eqn. (10)]):

$$\underset{\mathit{s}\in {ℂ}^N}{min}\underset{\omega }{max}\underset{\mathit{u}\in {ℂ}^J}{min}E(\omega ;\mathit{s};\mathit{u}).$$ (16)

In particular, for a given choice of s, we design u(ω) for each ω as follows:

$$\mathit{u}(\omega )\triangleq \underset{\mathit{u}\in {ℂ}^J}{argmin}E(\omega ;\mathit{s};\mathit{u}).$$

Having optimized u(ω), the worst-case error is the following function of the scaling factors:

$$E_{max}(\mathit{s})\triangleq \underset{\omega }{max}E(\omega ;\mathit{s};\mathit{u}(\omega )).$$ (17)

Finding u(ω) by minimizing (15) is simply a weighted least-squares problem that is linear in u. Solving that minimization directly leads to complex expressions, e.g., [1, eqn. (7)] that perhaps shroud the nature of the interpolator. For more insight, we rewrite the error as follows (cf. [4, eqn. (14)]):

$$\begin{array}{rl}{E}^2(\omega ;\mathit{s};\mathit{u})& =\sum _{n=0}^{N-1}{w}_n{\mid {\text{e}}^{i\omega n}-s_n\sum _{j=1}^J{u}_j(\omega ){\text{e}}^{i\gamma (k_0(\omega )+j)n}\mid }^2\\ & ={\parallel \mathit{b}-\mathit{S}\mathit{C}\hspace{0.17em}\mathbf{\Lambda }(\omega )\mathit{u}(\omega )\parallel }_{{\mathit{W}}^{1/2}}^2,\end{array}$$ (18)

where ${\parallel \mathit{b}\parallel }_{{\mathit{W}}^{1/2}}^2={\mathit{b}}^{\prime }\mathit{W}\mathit{b}$ and

$$\begin{array}{rl}\mathit{W}& \triangleq \frac{1}{N}\text{diag}\{w_n\}\\ b_n(\omega )& \triangleq {\text{e}}^{i(\omega -\gamma \hspace{0.17em}{k}_0(\omega ))(n-{\eta }_0)}\\ \mathit{S}& \triangleq \text{diag}\{s_n\}\\ C_{nj}& \triangleq {\text{e}}^{i\gamma j(n-{\eta }_0)}\end{array}$$ (19)

$${\mathrm{\Lambda }}_{jj}(\omega )\triangleq {\text{e}}^{-i(\omega -\gamma (k_0(\omega )+j)){\eta }_0}.$$ (20)

Clearly the (weighted) LS minimizer is

$$\mathit{u}(\omega )={\mathbf{\Lambda }}^{\ast }(\omega ){\mathit{T}}^{-1}\mathit{r}(\omega ),$$ (21)

because Λ⁻¹ = Λ*, where

$$\begin{array}{rl}\mathit{T}& \triangleq {\mathit{C}}^{\prime }{\mathit{S}}^{\prime }\mathit{W}\hspace{0.17em}\mathit{S}\mathit{C}\\ \mathit{r}(\omega )& \triangleq {\mathit{C}}^{\prime }{\mathit{S}}^{\prime }\mathit{W}\mathit{b}(\omega ).\end{array}$$

The elements of the J × J Toeplitz matrix T and the N-vector r(ω) are given by

$$\begin{array}{rl}{T}_{lj}& =\frac{1}{N}\sum _{n=0}^{N-1}{w}_n{s}_n^2{\text{e}}^{i\gamma (l-j)(n-{\eta }_0)}\\ r_j(\omega )& =\frac{1}{N}\sum _{n=0}^{N-1}{w}_n{s}_n{\text{e}}^{i(\omega -\gamma (k_0(\omega )+j))(n-{\eta }_0)}.\end{array}$$

The key to this representation is the following fact: in the usual case where w_n and s_n are chosen to be symmetric about η₀ (see (22) below), then T is a real matrix, and r(ω) is a real vector. In particular, the elements simplify to

$$\begin{array}{rl}{T}_{lj}& =\frac{1}{N}\sum _{n=0}^{N-1}{w}_n{s}_n^2\text{cos(}\gamma (l-j)(n-{\eta }_0)\text{)}\\ r_j(\omega )& =\frac{1}{N}\sum _{n=0}^{N-1}{w}_n{s}_n\text{cos(}(\omega -\gamma (k_0(\omega )+j))(n-{\eta }_0)\text{)}.\end{array}$$

Thus the term T⁻¹ r(ω) in (21), which is the core of this LS optimal interpolator, is real; the only complex aspect of the LS_NUFFT interpolator (21) is the linear phase term in (20). This linear phase term corresponds directly to the phase of the ideal interpolator in (7). Furthermore, the frequency ω enters the expressions above only in the form ω − γ k₀(ω). So due to (11), the LS_NUFFT optimal interpolator satisfies exactly the same type of shift invariance seen in the ideal interpolator (7).

Note that the LS optimal interpolator in (21) depends only on each frequency location ω individually, rather than depending on the entire collection of samples {ω_m}.

1.1 Choosing the scaling factors s_n

Having optimized the interpolator coefficients u(ω), the next step is to design the scaling factors s to minimize the worst-case error in (17). Unfortunately there is no apparent analytical optimizer for s. Therefore, one must use numerical methods to optimize s. In the literature, several choices for s have been proposed, all of which have the form

$$s_n=1/\mathrm{\Psi }((n-{\eta }_0)/K),$$ (22)

for various choices for the function Ψ(t), such as uniform factors, i.e., Ψ(t) = 1, cosine factors [7]: Ψ(t) = cos(πt), and Gaussian factors [7, 8]: $\mathrm{\Psi }(t)=\sigma \sqrt{2\pi }{\text{e}}^{-\pi {(t\sigma \sqrt{2\pi })}^2}$ with σ chosen to minimize E_max. For the “type 2” NUFFT we have recommended Kaiser-Bessel factors previously [4].

1.2 Choosing the weights w_n

The results shown in Section 2 below are all for the un-weighted error criterion where w_n = 1. This weighting seems the most natural from a practical MR perspective because usually we lack prior information that would favor weighting the error in some parts of the field of view more or less than other parts. However, from a computational perspective, note that by choosing $w_n=1/s_n^2$ the matrix T becomes independent of s [9], and has a simple closed-form solution [4, eqn. (29)]:

$$T_{lj}={\delta }_N(j-l),$$

where δ_N was defined in (8). Furthermore, if we expand 1/s_n using a suitable truncated Fourier series, then a closed-form solution for r(ω) is also available [4, eqn. (30)]. However, because u(ω) can be tabulated easily for a finely sampled grid of ω values, closed-form expressions for T and r(ω) seem unessential. The convenience of such expressions may be offset by the subjectivity in choosing s-dependent w_n values.

2 Results

Following [1], we considered the case J = 5, N = 2⁸, and K/N = 2. Fig. 1 Shows the “core” of the LS_NUFFT interpolator, i.e., T⁻¹ r(ω), for the case of cosine scaling factors recommended in [1]. The actual LS_NUFFT interpolator consists of this core multiplied by the linear phase factor (20). The nature of this interpolator is more clearly understood by isolating its real core, compared to the results described in [1, Fig. 1c]. Fig. 1 also shows the core of the conventional KB interpolator. We chose the shape parameter α for the KB kernel using the empirical formula proposed by Beatty et al. [10]:

$$\alpha =\pi \sqrt{\frac{J^2}{{(K/N)}^2}{\left(\frac{K}{N}-\frac{1}{2}\right)}^2-0.8}.$$ (23)

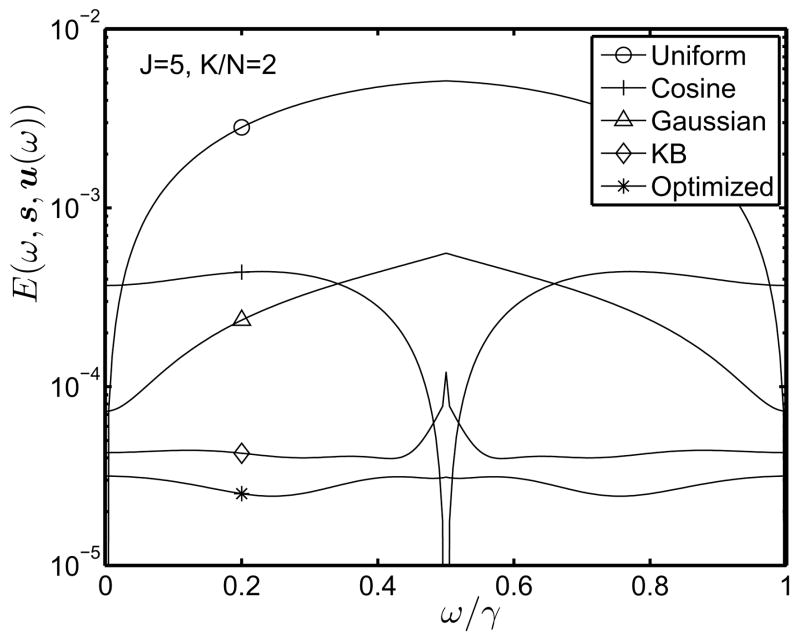
Fig. 2 shows the error E(ω, s, u(ω)) for three versions of the LS_NUFFT interpolator (with uniform, cosine, and Gaussian scaling factors) as well as for the standard KB interpolator. Our implementation of the “standard” KB interpolator includes the linear phase factors that appear in both the ideal interpolator (6) and in the LS_NUFFT interpolator (21). The implementation is analogous to (9). For most frequencies, the LS_NUFFT interpolator with any of the above scaling factors yields about an order of magnitude higher errors than the standard KB interpolator. The LS_NUFFT with cosine scaling factors is more accurate only for frequencies ω that are very close to γ/2. This is a narrow portion of the spectrum, so for most practical signals the standard KB interpolator will yield lower overall error than the LS_NUFFT approach with uniform, cosine, or Gaussian scaling factors.

Figure 2.

Plots of the error E(ω, s, u(ω)) of the LS_NUFFT approach vs ω/γ for three conventional choices of the scaling factors s, for the conventional Kaiser-Bessel interpolator, and for the LS_NUFFT approach with numerically optimized scaling factors.

To illustrate, we generated M = 200 random ω_m values uniformly distributed over [−π, π], and complex F_m values where the real and imaginary parts were each uniformly distributed over [0, 1]. We computed the exact direct summation (4) and then the NUFFT approximations (13) for various interpolators. We evaluated the normalized RMS error ||f̂ − f||/||f||, yielding the following results.

Method	NRMSE (%)
LS_NUFFT Uniform	0.36117
LS_NUFFT Cosine	0.04853
LS_NUFFT Gaussian	0.02574
Conventional KB	0.00361

Again, the conventional KB interpolator yields about an order-of-magnitude lower error than the LS_NUFFT method with cosine scaling factors. These empirical results corroborate the worst-case predictions shown in Fig. 2.

To try to further optimize the LS_NUFFT method, we used the Nelder-Mead simplex method [11] to minimize E_max(s) in (17) over s numerically. We then recomputed the LS_NUFFT interpolator using the resulting “optimal” scaling factors s. Fig. 2 shows that the resulting approximations errors are slightly lower than those of the conventional KB approach. This small improvement would seem to be outweighed by the long computation required for optimizing s. Such optimization would need to be repeated for new values of J, N, and K/N. In contrast, the scalar formula for α given in (23) works well for all practical cases of interest, so no further optimization is needed.

3 Discussion

By rearranging the factors in the derivation of the LS_NUFFT method, we have shown that the LS_NUFFT interpolator has a real-valued core with a linear phase term that matches that of the ideal interpolator. We have also shown that the LS_NUFFT interpolator is shift invariant, contrary to [1]. Our results show that the standard KB interpolator, when implemented with the shape parameter α optimized as described in (23), yields lower overall errors than the LS_NUFFT method with uniform, cosine, or Gaussian scaling factors. in [1],

Although [1] states that the LS_NUFFT method is “free from the procedure of parameter optimization,” the LS_NUFFT method does require choices for both the scaling factors s and the weighting values w_n. These choices strongly affect the resulting accuracy as seen in Fig. 2, and finding the globally optimal s remains a vexing open problem. The shape parameter α described in (23) for the conventional KB approach works very well.

If one must perform gridding repeatedly for the same values of J, N and K/N, then optimizing the scaling factors s of the LS_NUFFT method numerically may be beneficial. But in the absence of such optimization, the conventional KB approach for gridding is preferable to the LS_NUFFT approach with conventional scaling factors including cosine scaling factors [1, 7].