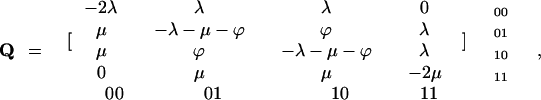Exon/intron structure of aldehyde dehydrogenase genes supports the “introns-late” theory

Abstract

Whether or not nuclear introns predate the divergence of bacteria and eukaryotes is the central argument between the proponents of the “introns-early” and “introns-late” theories. In this study we compared the goodness-of-fit of each theory with a probabilistic model of exon/intron evolution and multiple nonallelic genes encoding human aldehyde dehydrogenases (ALDHs). Using a reconstructed phylogenetic tree of ALDH genes, we computed the likelihood of obtaining the present-day ALDH sequences under the assumptions of each competing theory. Although on the grounds of its own assumptions each theory accounted for the ALDH data significantly better than its rival, the introns-early model required frequent intron slippage, and the estimated slippage rates were too high to be consistent with reported correlations between the boundaries of ancient protein modules and the ends of ancient exons. Because the molecular mechanisms proposed to explain intron slippage are incapable of providing such high rates and are incompatible with the observed distribution of introns in higher eukaryotes, the ALDH data support the introns-late theory.

The “introns-early” theory suggests that the “genes-in-pieces” structure of eukaryotic genes emerged long before the Eubacteria, Archaebacteria, and Eukaryota diverged as separate groups (1–3). According to this theory (i) the present-day exon/intron structures originated through the aggregation of short primordial mini-genes (encoding 15–20 amino acids) that were critically important for generating protein diversity through exon shuffling; (ii) the apparent absence of spliceosomal introns in bacterial and organelle genomes reflects secondary loss; and (iii) the nuclear splicing machinery is as old as the nuclear introns themselves. The theory further presumes that introns can easily be lost and postulates an intron slippage mechanism that can displace introns for short distances (1–12 nucleotides; see ref. 4), while leaving the coding sequence intact.

The alternative “introns-late” theory (5–7) maintains that (i) gene segmentation arose by random insertion of introns into primordial continuous protein-coding regions; (ii) the genes of cellular organelles and those of bacteria never had spliceosomal introns; and (iii) the spliceosomal machinery emerged through coevolution of group II self-splicing introns with eukaryotic proteins (6, 8, 9). Although the introns-late theory rejects the notion of shuffling of primordial exons, it denies neither the possibility of recent exon shuffling within eukaryotic lineages nor early protein evolution by fusion, duplication, and permutation of primordial protein modules. However, the introns-late theory does not permit intron slippage and thus regards all introns occupying different sites within related proteins as nonhomologous.

Several lines of argument have been advanced to either support or reject one of the two theories. (i) A few introns were found in homologous positions in genes duplicated before the separation of eukaryotes and bacteria (supporting introns-early) (10), although the distribution of most introns in such genes seems to be better explained by intron insertion (9). (ii) Introns-early supporters correctly predicted the position of a new intron in a gene of the mosquito Culex tarsalis (11), although this was later interpreted as a lucky coincidence (12–14). (iii) Introns-early supporters have claimed that exon/intron boundaries statistically correlate with the ends of units of protein three-dimensional structure (ancient modules, e.g., see ref. 15), but this conclusion was also vigorously challenged (14, 16). (iv) Multigene analyses of the distribution of intron phase (the codon positions interrupted by introns) indicated a significant excess of exons and exon groups with the same phase at both ends (presented as evidence for the introns-early theory; refs. 17 and 18), but this could have resulted from recent exon shuffling events and is thus compatible with both theories (13). (v) Parsimonious reconstructions of the evolution of the exon/intron structure in eukaryotes supported the introns-late view (9, 14), although the possibility of intron slippage was neglected in these analyses.

We present here a new method aimed at qualitatively analyzing homologous gene sequences under the respective assumptions of the two competing theories (compare to ref. 19), scrutinizing the internal consistency of the results of each analysis, and evaluating factual support for the assumptions underlying each theory. The application of this new method is illustrated by an analysis of aldehyde dehydrogenase (ALDH) genes.

Human ALDH Genes

Human ALDH Genes Are Ancient.

Aldehyde dehydrogenases catalyze the conversion of aldehydes into acid metabolites (20, 21). Humans have at least 10 homologous ALDH genes that evolved by a series of duplications of a single ancestral gene (22–29), and which have diverse exon/intron structures (Fig. 1). Although all known human ALDHs are nuclearly encoded, at least three of them [ALDH2, ALDH5, and methylmalonate-semialdehyde dehydrogenase (MMSDH)] have leader peptides and are transported to the mitochondria after synthesis.

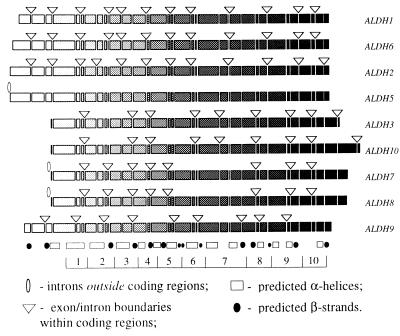
Figure 1.

Exon/intron structures of human ALDH genes mapped to the alignment of their amino acid sequences. The sequences themselves are shown as shaded rectangles, where the shading intensity increases in direction from the N to C terminus of the protein; deletions and insertions are not shown. Each discontinuity in rectangles corresponds to an exon/intron boundary observed in at least one of the genes; triangles and ellipses indicate only those introns that are actually found in the corresponding gene. Also shown is the predicted secondary structure that is assumed to be similar for all compared proteins: the hatched boxes indicate α-helices and the solid circles correspond to β-strands. The secondary structure was predicted with a neural network algorithm implemented by the PHD program (30, 31). The bottom of the figure shows an artificial segmentation of the protein into the 10 domains that were used in the computation of likelihood values.

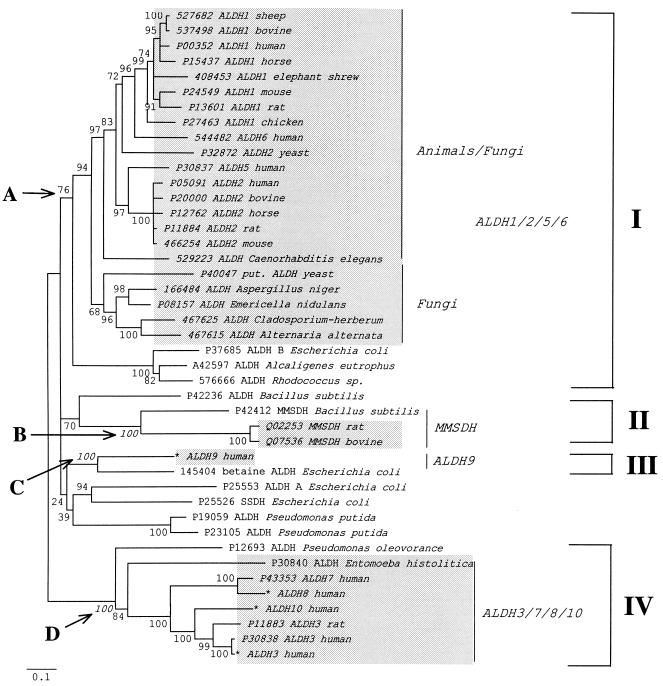
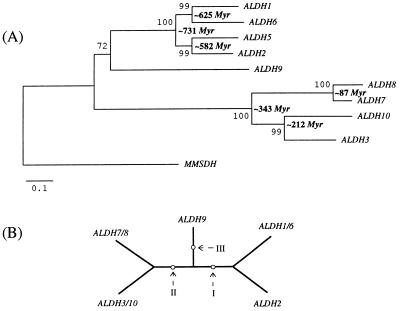
A neighbor-joining tree of ALDH-like sequences from several eukaryotic and prokaryotic species yielded four well-defined clusters of eukaryotic genes (Fig. 2; refs. 30–35). Although the average substitution rate in the group IV cluster (ALDH3/7/8/10) was twice as large as the rate in the group I cluster (ALDH1/2/5/6), each group individually conformed to a molecular clock (Figs. 2 and 3A), thus permitting an estimation of the divergence times of the genes (see refs. 36 and 37). These estimates (Fig. 3A) indicated that duplications in group I were likely to have occurred much earlier than those in group IV. In our reconstruction, diversification within group I happened in the Neoproterozoic period (38), whereas duplications in group IV arose much later, in the Phanerozoic period, when diverse vertebrate and invertebrate animals were already abundant. The latest two duplications in group IV occurred approximately 212 and 87 million years ago, respectively (Fig. 3A), dates that roughly correspond to the appearance and then subsequent radiation of mammals. Finally, the apparent existence of at least four ancient ALDH genes suggests that the divergence times of the four clusters are greater than 2,110 million years, which is the estimated age of the oldest known eukaryote (39).

Figure 2.

Neighbor-joining tree (32) generated by mega (33) from 43 ALDH-like protein sequences using the Poisson correction for multiple hits (ref. 34; for ALDH data virtually all currently available corrections for multiple hits give essentially the same tree); the branch lengths are proportional to the number of amino acid substitutions per site. Deletions and insertions were excluded from the analysis. Shaded areas indicate sequences from eukaryotic organisms. We excluded plant ALDHs from the analysis to facilitate interpretation of the resulting phylogeny. Bootstrap P values are shown next to the corresponding interior branches; interior branches that were supported by 20% or less of 500 bootstrap replications (35) were set to zero. The description of each protein sequence includes either the SwissProt or the GenBank accession number (asterisks indicate new sequences) and the protein and species name. A, B, C, and D indicate the interior branches defining four stable clusters of proteins from both eukaryotes and eubacteria. The tree may indicate that at least four ALDH-like genes (ALDH1/2/5/6-like, ALDH3/7/8/10-like, ALDH9-like, and MMSDH-like genes) predated the divergence of eukaryotes and eubacteria. SSDH, succinate-semialdehyde dehydrogenase.

Figure 3.

(A) Neighbor-joining tree (32) generated by mega (33) from 11 human protein sequences using the Poisson correction for multiple hits (34). The percentage of bootstrap (35) resamplings (out of 500) supporting each sequence partition is shown next to the corresponding interior branch; the divergence times between human genes were estimated with the “linearized tree” algorithm (36). In this estimation we used known ALDH protein sequences from Rodents, Primates, and Artyodactyls and the divergence time 104 million years (37) for the Rodentia/Artiodactyla bifurcation. (B) Unrooted tree topology that was used in the maximum likelihood analysis of exon/intron organization of ALDH genes. There are three pairs of ALDH genes that have identical exon/intron patterns within each pair: ALDH1 and ALDH6, ALDH3 and ALDH10, and ALDH7 and ALDH8. The unrooted tree topology is the same as the neighbor-joining tree in A. Arrows show three alternative positions of the tree root (in the maximum likelihood computation we refer to these rooted trees as tree I, tree II, and tree III, see Table 1).

Our phylogenetic reconstruction thus indicated that the “progenote”—the common ancestor of bacteria and eukaryotes—was likely to have had at least four ALDH genes, since eubacterial and animal genes were grouped together with high bootstrap (35) support. An alternative explanation of the same tree would require three or more lateral gene transfers between bacteria and animals after the time of the bacteria/eukaryotes divergence. Either explanation is compatible with the maximum likelihood analysis presented here.

Intron Evolution in ALDH Genes: Comparison of Competing Theories.

We developed a model that was flexible enough to accommodate each rival theory. Our model incorporates the following assumptions. (i) There are three events causing changes in exon/intron pattern: intron insertion, intron deletion, and intron slippage, which is a short-range movement of an intron within the same gene. (ii) The actual number of such events occurring along a tree branch follows a Poisson distribution. (iii) Given a fixed exon/intron arrangement, the probability of each new evolutionary event does not depend on either the order or the number of past events in the evolutionary history of the gene. (iv) Rates of intron insertion, deletion and slippage are fixed along each branch of the tree, but can vary among branches. We also assumed that the correct unrooted tree topology for human ALDH genes is known and can be rooted in three alternative ways (Fig. 3B).

Starting with the above assumptions, we applied a standard set of matrix manipulations (40) used in the theory of Markov chains for deriving transition probabilities between different exon/intron patterns. These probabilities were then used to compute the conditional probability of observing the present-day gene structures given a specified tree and a fixed set of the model parameter values (41). First, we defined instantaneous transition rate matrices corresponding to a first-order Markov chain description of intron evolution. The entries of each matrix were assigned rate parameters λ, μ, or ϕ, whenever the corresponding pair of intron arrangements was separated by a single intron insertion, deletion, or slippage, respectively; the matrix entries were set to zero whenever the distance between corresponding intron arrangements exceeded one elementary event. The diagonal elements of each rate matrix were chosen to ensure that the sum of the elements in each row is equal to zero. For example, for a hypothetical gene with only two sites potentially hosting introns, there are four possible intron/exon configurations: 00, 01, 10, and 11, where zero and one stand for intron absence and presence, respectively. Thus, the transition from configuration 00 to configuration 01 corresponds to an intron insertion; the transition from 01 to 00 indicates intron loss; and a transition from 10 to 01 denotes an intron slippage. The resulting instantaneous transition rate matrix, Q, is then written as follows

where λ, μ, and ϕ stand for the instantaneous rates of intron insertion, deletion, and slippage, respectively.

Second, the matrices of transition probabilities between exon/intron arrangements were computed numerically as matrix exponentials of the corresponding instantaneous transition rate matrices. This operation produces a matrix of transition probabilities between gene arrangement states during time t (expressed in terms of the expected number of events of each type) and is symbolically expressed as e^Qt. Third, the likelihood value was calculated as described by Felsenstein (41), with the number of ancestral introns at the root of the tree and the mean rate of intron rearrangement along each tree branch treated as model parameters. All numerical computations were performed with the matlab 4.0 package produced by Mathworks (Natick, MA). To make the required computations feasible, we divided the ALDH genes into 10 domains (see Fig. 1) and prohibited intron slippage between domains. We defined the boundaries between domains to minimize the number of the ancestral introns required to explain the present-day genes, as is commonly done in introns-early analyses. Without this segmentation, the computation of likelihood functions would be effectively impossible because of the large number of intermediate sequence states at each node of the tree. Indeed, each sequence with n potentially intron-bearing sites can be observed in 2ⁿ different binary states, where 0 stands for an intron absence and 1 for an intron presence. This is a very large number even for a moderate n (e.g., more than 10⁹ for n = 30), and the likelihood values have to be computed by evaluating transition probabilities through each of 2ⁿ states for each interior node of the tree. Fortunately, it was possible to compute an approximate likelihood value by assuming that intron slippages can move introns only within each of the 10 defined domains, such that within each domain n ≤ 5, and 2ⁿ ≤ 32. Only the present-day intron positions were used for the computation. Finally, we used multidimensional simplex numerical optimization to find a set of parameter values maximizing the likelihood value. In the analyses, ALDH5 was omitted because it apparently resulted from a single processed mRNA reverse transcription event.

With this model we were able to directly compare the fit of each alternative theory to the actual ALDH data. The fits of any two models to the data set can be objectively compared with the Akaike Information Criterion (AIC; ref. 42). The AIC value is computed for each model according to the formula, AIC_i = 2 N_i − 2 log L_i, where N_i is the number of parameters used in the ith model and log L_i is the logarithm of the maximum likelihood value obtained under the model. The criterion is designed in such a way that the model with the better fit has the smaller AIC value.

The results of each analysis depended on the assumptions incorporated by the model. Comparison of AIC values (Table 1, scenarios A, B, and C) showed that the probability of generating the actual ALDH data under the no-slippage assumption and the insertions only model (= introns-late) was almost 10⁶ times as large as the corresponding probability under the deletions only (= introns-early) model. To our surprise, re-analysis of the same data with allowance for intron slippages (introns-early assumption, see Table 1, D, E, and F) resulted in a complete reversal of the conclusion. That is, the model deletions plus slippages (= introns-early) became the best one with a large advantage in AIC values.

Table 1.

Comparison of alternative scenarios of exon/intron evolution in the maximum likelihood analysis

Scenario	N*	lnL†	AIC	Ancestral intron no.	Maximum branch
					Slip‡	Ins§	Del¶
A. Only deletion
Tree I/II/III	8	−176.75	369.51	31‖	0	0	1.68
B. Only insertion
Tree I	8 + 1	−166.75	349.50	0**	0	0.02	0
Tree II/III		−167.16	352.32		0	0.02	0
C. Insertion + Deletion
Tree I	8 + 8 + 1	−165.75	365.50	0**	0	0.02	0
Tree II/III		−167.16	368.32		0	0.02	0
D. Deletion + Slippage
Tree I		−92.68	219.35		11.6	0	0.23
Tree II	8 + 8 + 1	−92.67	219.34	10**	7.9	0	0.23
Tree III		−92.69	219.38		11.7	0	0.23
E. Insertion + Slippage
Tree I		−165.320	364.64		0	0.02	0
Tree II	8 + 8 + 1	−163.882	361.76	0**	0	0.02	0
Tree III		−165.992	365.98		0	0.02	0
F. Deletion + Insertion + Slippage
Tree I	8 + 8 + 8 + 1	−92.66	235.33	10**	19.7	0	0.22
Tree II/III		−92.67	235.34		22.4	0	0.22

^*Number of model parameters. 

^†Natural logarithm of the likelihood value. 

^‡§¶Maximum likelihood estimates of the rates of intron slippage, intron insertion, and intron deletion, respectively, expressed as per site per branch of the tree. 

^‖Number of ancestral introns was preset rather than estimated. 

Thus, the intron slippage assumption is critical for discriminating between the two theories. Below we examine the consistency of the available experimental data with the parameter estimates obtained in our maximum likelihood analysis. We demonstrate that although the model with the smallest (most likely) AIC value corresponds to the introns-early theory (see Table 1 D), the parameter estimates obtained under this model appear to be incompatible with both available experimental data and previous arguments in favor of the introns-early theory.

Mechanism of Intron Slippage and Distribution of Introns in Human Genes.

There presently is no plausible molecular mechanism to account for both frequent intron slippage and the actual patterns of intron distribution in eukaryotes. The simplest explanation for intron slippage is deletion of several nucleotides at the end of one exon and insertion of the same number of nucleotides at the end of an adjacent exon, thus leaving the coding region undamaged. Since each of the two rearrangements by itself must be highly deleterious, this mechanism would seem to be inadequate to account for frequent slippage. Martinez et al. (43) suggested a more plausible mechanism based on the “single-intron-deletion” scenario of Fink (44). Fink’s mechanism includes a normal excision of an intron from pre-mRNA, reverse transcription of the modified pre-mRNA, and homologous recombination of the resulting cDNA with the original gene. Martinez et al. (43) hypothesized an additional event that involves imprecise re-insertion of an excised intron back into the pre-mRNA (see ref. 45 for experimental evidence of reverse splicing). The advantage of the Fink–Martinez model is that it accounts for a clean displacement of an intron within a coding region, although leaving the supposed 12 bp limit for intron slippage (4) unexplained. Because reverse transcription in retroviruses occurs only within the viral particle isolating cellular RNAs from the virus enzyme, the Fink–Martinez mechanism requires the presence of a defective retrovirus with a mutation in the packaging signal (44). [The simultaneous loss of several introns, as in the human ALDH5 gene, can be explained by re-integration of the reverse-transcribed mRNA into the genome (44, 46).]

Unless there is strong selection preserving the number and/or spatial distribution of introns, evolution under the Fink–Martinez model should result in very characteristic exon/intron structures (44): Intron deletion should be more frequent than intron slippage, leading to a progressive loss of introns. The retained introns should be concentrated near the 5′ end of each gene because reverse transcription begins at the 3′ poly(A) tract of mRNA but rarely extends completely to the 5′ end, and recombination between genes and cDNAs affects the ends of genes less frequently than the middle. As a consequence, intron slippage should be rarely observed at the ends of genes, especially at the 5′ end. These predictions are in good accord with the exon/intron structures observed in yeast (44), but are clearly inconsistent with human ALDH genes: Human genes have numerous introns evenly distributed over the entire length of the coding regions (see Fig. 1), and to fit the introns-early theory intron slippages have to be invoked at both ends of genes.

Unlike intron slippage intron deletion can result from a one-step mutation event, and in the absence of counteracting selection it should be observed more frequently than intron slippage.

There are at least two hypothetical mechanisms explaining intron insertion. One is reverse splicing of an excised intron into a nonhomologous pre-mRNA, followed by reverse transcription and homologous recombination (44). Another possible mechanism involves invasion of a group II intron (from organelles) into the nuclear genome, followed by a one-mutation transformation of the intron into a regular nucleosomal intron (6, 47–50): only a single nucleotide substitution is required to convert “(U/C)A … GU” dinucleotides flanking group II introns into canonical “GA … GT” dinucleotides flanking nuclear introns, and it was recently discovered (51) that group II introns from yeast mitochondria can integrate directly into double-stranded genomic DNA. Therefore, the integration of group II introns into the genome is a one-step event where all molecular machinery is provided by the intron itself.

Thus, according to the available experimental evidence and plausible evolutionary scenarios, intron slippage should be considerably less likely than intron deletion. In contrast, our maximum likelihood analysis under the introns-early assumptions (see Table 1 D, E, and F) suggested that to explain real data under this theory intron slippage has to be two orders of magnitude more frequent than intron deletion.

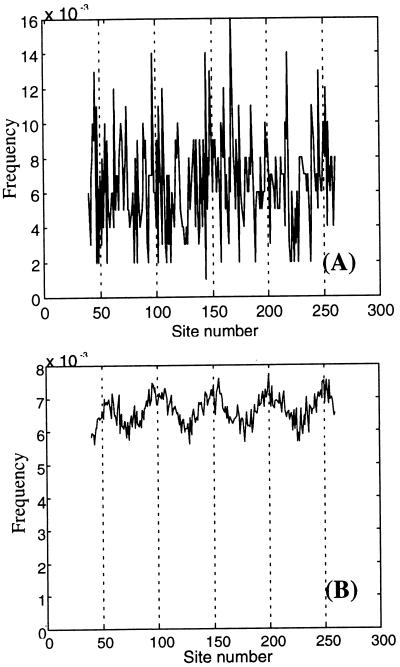
To demonstrate that the estimated rates of intron slippage contradict any support for the introns-early theory that is based on a putative correlation between the ends of ancestral protein “modules” and the boundaries of proto-exons (e.g., see ref. 52), we performed a computer simulation built on the assumptions of the introns-early theory. This simulation (Fig. 4) demonstrated that the reported correlation cannot be detected from any reasonable number of present-day genes (say, < 10,000) if intron slippage rates are as high as estimated in our analysis (Fig. 4). In our simulation, present-day genes independently evolved from a hypothetical ancestral gene with multiple introns separated by 50-nucleotide exons (broken lines indicate positions of the ancestral introns). Approximately two-thirds of the ancestral introns were then randomly deleted, and the remaining introns were subjected to slippage at a rate of nine events per site. The direction of each slippage (either 5′ or 3′) was chosen randomly; the length of each movement was sampled from a uniform distribution defined by the interval from 1 to 12. The figure shows the resulting distribution of introns from a sample of 1,000 (Fig. 4A) and 100,000 genes (Fig. 4B). In our simulation the present-day genes were assumed to evolve independently; the phylogenetic nonindependence of actual present-day genes should increase the variance of intron distribution.

Figure 4.

(A) The nonrandomness of intron distribution along the gene is effectively undetectable when slippage rates are as high as was estimated in our maximum likelihood analysis and the number of independent present-day genes under analysis is not unrealistically large (<10,000). The figure shows a frequency distribution of introns that was computed through averaging 1,000 “present-day” genes obtained in computer simulation (broken lines indicate positions of the “ancestral” introns). (B) To significantly prove the nonrandomness of intron distribution for the same model and parameter values one needs a very large sample of present-day genes. This frequency distribution of intron positions was obtained by “averaging” over 100,000 present-day genes from the computer simulation.

Assuming that introns were inserted into coding sequences relatively recently, how can one explain the nonrandomness of intron distribution? Recent experimental data (e.g., ref. 53) indicate that nuclear DNA of eukaryotes is nonuniformly protected by proteins maintaining chromosome structure. For example, during transcription of the Dam gene in yeast, each nucleosome associated with Dam selectively shielded approximately 80 bp of yeast DNA, while allowing methylation enzymes free access to DNA in internucleosome “linkers” (53). Therefore, we hypothesize that the nonuniform distribution of introns in eukaryotic genes reflects preferential intron insertion into stretches of DNA that were temporarily liberated from nucleosome protection.

Conclusion

The intron slippage assumption is the cornerstone of the introns-early theory yet, according to our analysis of ALDH genes, it is precisely this assumption that leads to an internal contradiction between the arguments supporting the theory. First, the estimated intron slippage rates are much higher than the estimated intron deletion rates. Second, high intron slippage rates question the reported correlation between the boundaries of the ancient protein “modules” and the ends of “proto-exons” (15). Indeed, if intron slippage is allowed, each putative ancestral intron would have had to move at least once to arrive at the present-day exon/intron arrangement in human ALDH genes. This is because all intron positions between groups ALDH1/2/6 and ALDH3/7/8/10, and ALDH3/7/8/10 and ALDH9 are different (see Fig. 1) and only one of nine intron positions is conserved between ALDH9 and ALDH3/7/10.

In summary, the assumption of frequent intron slippage leads to inconsistencies with both the available body of experimental evidence and the data analyses provided by proponents of the introns-early theory. Without this assumption, the human ALDH data support the introns-late theory. The methods illustrated here can be readily applied to other data sets to test the generality of the conclusions drawn from the ALDH data.

Figure.

ABBREVIATIONS

ALDH

aldehyde dehydrogenase

MMSDH

methylmalonate-semialdehyde dehydrogenase

AIC

Akaike Information Criterion