Abstract
Vibratory communication in arthropods is a widespread phenomenon. Arthropods living on plants have been reported to use only dispersive bending waves in the context of prey–predator, competition, social and sexual interactions. Differences in signal structure have also been postulated to work as species recognition mechanisms and speciation agents. Using two identical laser Doppler vibrometers and a wavelet analysis, we quantified the wave propagation modes in rush stems (Juncus effusus) over the whole range of frequencies used by arthropods. A non-dimensionalized analysis shows that mechanical waves propagate not only as dispersive bending waves, but also as non-dispersive waves. Our analysis implies that an arthropod can communicate through non-dispersive bending waves by either producing signals of high frequencies or by choosing large stems, two widely different options tapping into the physiological and the behavioural repertoires, respectively. Non-dispersive waves, unreported so far in insect vibratory communication in plants, present serious advantages over dispersive bending waves in terms of signal integrity and may well be much more widely used than anticipated, in particular for species recognition.
Keywords: plants, substrate-borne vibrations, bending waves, wave dispersion, animal communication
1. Introduction
Vibratory communication is widespread among insects and arachnids (Gogala 1985; Barth 2002; Greenfield 2002; Čokl & Virant-Doberlet 2003; Virant-Doberlet & Čokl 2004; Drosopoulos & Claridge 2006). Its role has been established in a great variety of contexts, such as prey–predator interactions, competition, brood care, social interactions and sexual communication (Cocroft 2001; Cocroft & Rodrìguez 2005; Casas & Magal 2006). Several temporal and frequency parameters of the vibratory songs are species-specific and have potentially a great impact on the mate choice of species, in particular, cryptic species (Henry 1994; Sueur 2006). The analysis of female preference for male vibratory signals also strongly supports the hypothesis that such sexual communication systems might act as speciation agents in sympatric conditions (Rodriguez et al. 2006).
Despite repeated calls for a better understanding of the physics of signal propagation, vibratory responses of plant structures have been rarely studied (Bell 1980; Michelsen et al. 1982; Keuper & Kühne 1983; Markl 1983). The pioneer study of Michelsen et al. (1982) reported mainly low-frequency bending, or flexural, waves used by plant-dwelling insects. This has been supported by all recent studies (e.g. Cocroft 2000; Miles et al. 2001; McNett et al. 2006) and is now standard in textbooks on animal communication (e.g. Greenfield 2002). Such bending waves are known to be dispersive, i.e. each frequency travels at its own speed, leading to substantial spreading of wave packets along the transmitting path. This dispersive property may greatly alter signal shape and consequently its efficiency for information transfer. This is an obvious challenge for arthropods as signal integrity is a sine qua non condition for proper identification, discrimination among otherwise quite similar signals and adequate behavioural response. Solutions to this problem might be to produce signals at low repetition rate, to communicate at very short distance or to use waves the least dispersive as possible. The characterization of propagation modes and velocities of waves propagating in a solid can be done using at least two distant measurement points, being two accelerometers or two contact free laser vibrometers (McDevitt et al. 1993). Unfortunately, very few studies used such a set-up (Magal et al. 2000; Cocroft et al. 2006; McNett et al. 2006) and most of these studies were limited to a frequency range below 2 kHz. Although the majority of vibrating insects produce low-frequency signals, some of them produce vibrations extending above 5 kHz (Keuper & Kühne 1983; Gogala 1984; Devries 1991). Arthropod drummers like jumping spiders, stoneflies, beetles and termites also generate signals covering a broad frequency spectrum with high-frequency content when hammering a part of their body against the substrate (White et al. 1993; Elias et al. 2003; Evans et al. 2005). Similarly, many stridulating or tymballing insects also transmit wide-band signals through the substrate (Keuper & Kühne 1983; Gogala 1984; Stölting et al. 2002). Receivers among these species could be tuned only to these high frequencies.
The aim of this work was, therefore, to quantify bending wave propagation in plants over the complete range of frequencies covered by insects and to better characterize the mode of wave propagation. We used a plant structure as simple as possible, a stem, and a two-channel laser Doppler vibrometer system enabling simultaneous measurements at two distant points. To assess dispersion overall frequency range, we used a century old technique (Kolsky 1963; Graff 1975) by producing sharp impact like transients and computing the frequency dependent wave velocity using wavelet transform. We discuss the implication of the observed propagation for arthropod vibratory communication.
2. Material and methods
The propagation speed of substrate-borne waves was measured in five rush stems (Juncus effusus, Juncaceae) ranging in radius from 0.85 to 2.1 mm (other values: 1.25, 1.55 and 1.65 mm, mean=1.48 mm). Such stems were selected for their simple structure: they are not ramified and have no leaves. They are selected as a natural host by numerous vibrating insects, such as planthoppers and leafhoppers (Nickel & Remane 2002). Stems were collected from a site close to the laboratory just prior to testing. The set-up was composed of two laser Doppler vibrometers (Ometron VS 100, Harpenden, UK) with a sensitivity of 1 μm s−1 placed on a vibration isolation table (Newport, Irvine, USA), a rush stem fixed on both ends, a small metal ball weighting 2.5 mg and a multi-channel SigLab data recorder working at a sampling rate of 51.3 kHz (Spectral Dynamics, San José, USA). An electrical magnet was used to drop the metal ball on the stem 6 cm from the closest attachment point and from a height of 2 cm. The energy transmitted to the stem by the falling ball was 5×10−7 Nm (E= mgh, with m=2.5 mg, g=9.81 m s−2, h=2 cm). Previously used with success for the mechanical study of natural material (Casas et al. 1998; Magal et al. 2000), such signal generator is highly repeatable and produces high frequencies difficult to stimulate with conventional electromagnetic shakers. The impact generated a sharp Dirac-like transient in the stem (Kolsky 1963; Graff 1975). This reference signal was recorded by the first laser placed between 9 and 24 mm from the ball impact point. This distance was required in order to avoid any interference between the impacting device and the laser beam. The second laser was used to record the wave after its propagation through the stem. The distance between the reference point (first laser) and the measurement point (second laser) was 35 cm for one stem and 45 cm for four stems. Larger distances would have led to excessive tapering of the tip of the stems. Each stem was impacted five times, and the cleanest signal was kept for further analysis.
Transients such as those generated through the stems by the falling ball cannot be analysed using conventional Fourier analysis (Qian & Dapang 1996). We then opted for a Continuous Wavelet Transform using the Daubechies wavelet of order 2. This type of wavelet is particularly well adapted for the analysis of sharp discontinuities (Jensen & La Cour Harbo 2001). Wavelet analyses were computed using the Matlab wavelet toolbox (Misiti et al. 1996) and plotted with R (R Development Core Team 2004). We extracted the dispersion relation of the group velocity following the works of Wahl & Bolton (1993). The sharp discontinuity at the measurement point near the impact point sets time at zero. For a given scale, the first peak in the wavelet intensity appearing at the further measurement point gives the arrival time of a wave at that scale. We first analysed signals using a wavelet scale a ranging from 2 to 20 with steps of one (corresponding frequency range: 25.6–2.5 kHz). Then we used steps of 10 for changing scale between 21 and 91 (2.4–0.526 kHz) and steps of 100 for changing scale between 101 and 2001 (0.506–0.025 kHz). Dividing the travelled distance by the amount of time gives the frequency dependent velocity.
Since bending wave velocity is a function of the square root of frequency, we looked for any correlation between these two variables. In order to compare the mechanical behaviour of all stems in an integrated fashion, all data were non-dimensionalized by replacing the frequency f (Hz) by r/λ (r=stem radius (m), λ=wavelength (m)) and the velocity c (m s−1) by c/cmax (cmax=maximal velocity). Such a non-dimensionalization allows the investigation of not only the effect of frequency, but also the effect of stem radius on wave velocity. The data were compared with Bernoulli–Euler and Timoshenko beam theories. Bernoulli–Euler's theory is known to establish a positive linear relationship between frequency and velocity for r/λ<0.1. Timoshenko's theory states that the wave velocity levels off at high frequencies and predicts a maximal speed unrelated to radius (Kolsky 1963; Graff 1975). Bernouilli–Euler's theory is a special case of Timoshenko's in which shear and rotary inertia are neglected and both assume that the deformations are small. These theories respectively follow the equations (Sayir 1983; see Graff (1975) and Cremer et al. (2005) for alternative formulations):
| (2.1) |
| (2.2) |
| (2.3) |
where E is the Young's modulus (N m−2), ρ is the mass density (kg m−3), G is the shear modulus (N m−2) and ν is the Poisson's coefficient.
A plant stem is a highly heterogeneous and anisotropic structure, in contrast to the materials used in the conventional engineering models. Thus, we did not try to implement parameter values reflecting approximate behaviour (see Lange (1963) for an early failure with wood bars and the explanation thereof) but concentrated on the overall shape and qualitative behaviour of the dispersion curves. We, therefore, fitted our values to the general formulae derived from the equations (2.1) and (2.2) with nonlinear regression method using SYSTAT:
| (2.4) |
| (2.5) |
3. Results
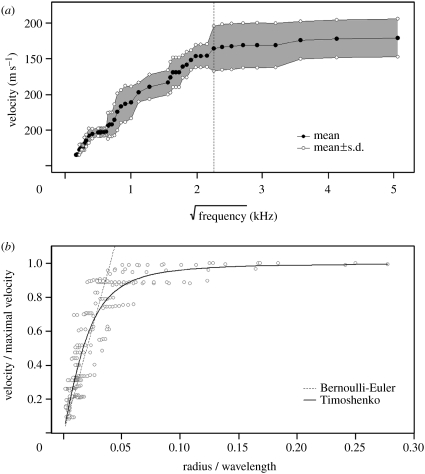
Wavelet analysis of the signal after propagation typically showed dispersive patterns for frequency below 5 kHz (figure 1). The propagation speed was indeed an increasing function of the square root of wave frequency below 5 kHz but was uncorrelated to it above 5 kHz (figure 2a). The data agreed with the Bernoulli–Euler's theory for r/λ<0.03 and to the Timoshenko's theory for r/λ>0.03 (figure 2b). The propagation speed was an increasing function of stem radius for low values of r/λ>0.03 and then became independent of radius. Thus, waves propagated in a non-dispersive way for large stem radius and at high frequencies.
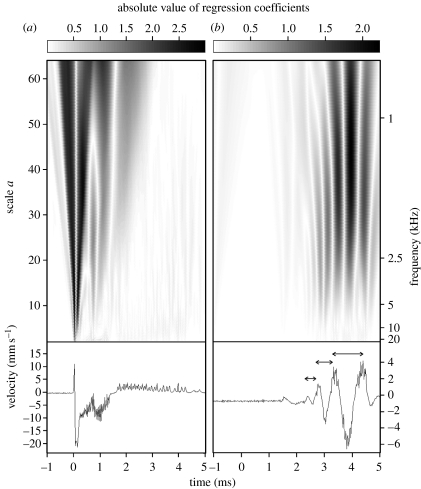
Figure 1.
Scalograms (two-dimensional plots of continuous wavelet transform) and oscillograms of signals recorded by the two distant lasers focusing on a rush stem. (a) The first laser recorded a typical transient signal generated by the falling ball. The scalogram indicates a wide-band spectrum. The second laser recorded the signal after its propagation through the plant at 45 cm from the impact point. Because of dispersion phenomenon, the signal recorded (b) after propagation shows high frequencies arriving first, leading lower frequencies (see arrows). This phenomenon is, however, true only for frequencies lower than 5 kHz. Y-axis of oscillograms refers to signal velocity but not to wave velocity. Note the change of range between the oscillograms. For convenience, wavelet scale a has been converted into frequency scale (kHz). Horizontal grey level bar indicates the range for the absolutes values of regression coefficients.
Figure 2.
Dispersion of substrate-borne waves in a rush stem. (a) Relation between the square root of the frequency f (kHz) and velocity c (m s−1) for five stems: velocity first increases with the square root of frequency and then remains stationary whatever the frequency. The vertical dashed line is at f=5 kHz (i.e. √f=2.23 kHz). (b) Non-dimensionalized analysis investigating the combined effects of frequency and stem radius on wave velocity. Observations are compared with Bernouilli–Euler (dashed line) and Timoshenko (continuous line) beam theories.
4. Discussion
Dispersive bending waves are invariably reported in the literature regarding insect vibratory communication in plants, even though a comprehensive analysis over a wide frequency range was never carried out due to the lack of appropriate technology. Our study clearly shows that a plant stem, as simple as a rush stem, can transmit dispersive and non-dispersive bending waves. Wave velocity was indeed proportional here to the square root of the frequency at low frequencies, a signature of bending waves that can be modelled using the Bernoulli–Euler's theory, but also shows a levelling off at high frequencies following Timoshenko's theory. In addition, propagation speed on stems with large diameter was independent of the diameter size, as it was independent of frequencies at high frequencies. The stem then became equivalent to a semi-infinite solid. The propagation speed is known, in the limit, to approach the propagation speed of the Rayleigh wave speed, typical of surface waves (Graff 1975). In other words, the larger the stem, the more difficult is the distinction between surface waves and bending waves. Despite being roughly characterized by a hard skin and a soft internal core, a rush stem is mechanically not equivalent to a hollow cylinder, as energy can leak through the internal ‘foam’ material. Wave propagation in sandwich stem and leaf structures is a virgin field of research (refer to Gibson et al. (1988) for a pioneer static study on a leaf and Spatz et al. (1997) for a similar study on a stem). Thus, a rigorous distinction between wave types produced by insects has still to be carried out despite the fact that insects have been proved so far to produce only bending waves (Michelsen et al. 1982). New technology, such as the use of multiple laser vibrometers applied here and very recently (Cocroft et al. 2006; McNett et al. 2006), is a major step towards fulfilling this task.
Given the influence of small differences in the signals of arthropods, like for hemipteran (Claridge & Vrijer De 1994) or neuropteran insects (Henry 2006), smearing and merging of signals should be strongly avoided to ensure species recognition. One way to mitigate the dispersive nature of bending waves is to communicate at short distance only, before signal degradation becomes significant. This implies, however, other delicate communication mechanisms, such as long-distance chemical and/or optic communication, for meeting at precise sites. Dispersive bending waves have then a set of intrinsic characteristics conflicting with the need of high signal integrity in vibratory communication over large distances. By contrast, the shape of a non-dispersive wave is maintained as it will travel over long distances. The sender can emit signals of complex nature and the receiver does not need to filter out the possible effects of the transmission channel. Our analysis suggests that arthropods might also produce non-dispersive bending waves through plants. In fact, we expect the production of non-dispersive bending waves to be much more frequent than anticipated, for example for plectopteran drumming on large plants, or for dead-watch beetles drumming on large wood beams. Studies on the forces applied by insects to their substrates are needed to compare with our set-up, to estimate the muscular power needed and to fix the range of signals that can be produced.
As revealed by our non-dimensionalized analysis, an arthropod could produce non-dispersive waves either by producing signals of high frequencies or by choosing large stems, two widely different options tapping into the physiological and the behavioural repertoires, respectively. Our results may provide an adaptive explanation for the occurrence of high frequency vibratory signals produced by some insects despite their high attenuation. Even if insects can produce high frequency signals, they remain constrained in the frequency range they can produce, either due to the power output of their muscles, to the mechanisms of vibration production, or to the filtering of specific frequency bands by the environment. The later influence has been postulated as a driving force explaining the wide-band signals produced by insects (Forrest 1994; Miklas et al. 2001).
Choosing a location well suited for producing non-dispersive waves without having to generate high frequencies, such as a large stem, seems to be an easier and energy sparse task. For instance, producing a signal above around 4–5 kHz on the larger stem we studied (radius=2.1 mm) is enough to produce non-dispersive waves. Some singing insects are known to communicate in a particular micro-habitat and/or during a specific temporal window that maximize transmission (Bennet-Clark 1998; Römer 1998). Similar studies regarding the adaptation of vibrational signals for transmission through plants are quite rare and gave inconsistent results (Cocroft & Rodrìguez 2005; Čokl et al. 2005). We do know, however, that choosing an exact location on the plant substrate can be of major importance for signal transmission. The energy contained in a signal could decrease by 80% within an apple leaf, depending on the type and number of veins between sender and receiver. Major veins are effective low pass filters, implying that animals sitting on either sides of a leaf will experience different signals (Magal et al. 2000).
The identification of different modes of wave propagation available for communication in plants implies that we need to increase our efforts on understanding not only the biophysics of vibration production and reception, but also the microhabitat choices of the animals, as well as the costs and benefits of the different options available to them. This is an ambitious but timely programme given the increasing role ascribed to the details of communication in sexual selection and speciation processes for the numerous and very large groups of arthropods using vibratory communication.
Acknowledgments
We thank Thomas Steinmann, Michael Greenfield and two anonymous reviewers for their comments on the manuscript. The manuscript was completed while the first author held the 2006 distinguished invited professorship at the Centre of Insect Science, Tucson. Its director, Nicholas Strausfeld and the centre staff are thanked for the wonderful hosting facilities.
References
- Barth F.G. Springer; Heidelberg, Germany; New York, NY: 2002. A spider's world: senses and behavior. [Google Scholar]
- Bell P.D. Transmission of vibrations along plant stems: implications for insect communication. N. Y. Entomol. Soc. 1980;88:210–216. [Google Scholar]
- Bennet-Clark H.C. Size and scale effects as constraints in insect sound communication. Phil. Trans. R. Soc. B. 1998;353:407–419. doi:10.1098/rstb.1998.0219 [Google Scholar]
- Casas J, Magal C. Mutual eavesdropping through vibrations in a host–parasitoid interaction: from plant biomechanics to behavioural ecology. In: Drosopoulos S, Claridge M.F, editors. Insect sounds and communication: physiology, behaviour, ecology and evolution. CRC Press; Boca Raton, FL: 2006. pp. 263–271. [Google Scholar]
- Casas J, Bacher S, Tautz J, Meyhöfer R, Pierre D. Leaf vibrations and air movements in a leafminer–parasitoid system. Biol. Control. 1998;11:147–153. doi:10.1006/bcon.1997.0593 [Google Scholar]
- Claridge M.F, Vrijer De P.W.F. Reproductive behavior: the role of acoustic signals in species recognition and speciation. In: Denno R.F, Perfect T.J, editors. Planthoppers: their ecology and management. Chapman & Hall; London, UK: 1994. pp. 216–233. [Google Scholar]
- Cocroft R.B. Directionality in the mechanical response to substrate vibration in a treehopper (Hemiptera: Membracidae: Umbonia crassicornis) J. Comp. Physiol. A. 2000;186:695–705. doi: 10.1007/s003590000123. doi:10.1007/s003590000123 [DOI] [PubMed] [Google Scholar]
- Cocroft R.B. Vibrational communication and the ecology of group-living, herbivorous insects. Am. Zool. 2001;41:1215–1221. doi:10.1668/0003-1569(2001)041[1215:VCATEO]2.0.CO;2 [Google Scholar]
- Cocroft R.B, Rodrìguez J.G. The behavioral ecology of insect vibrational communication. Bioscience. 2005;55:323–334. doi:10.1641/0006-3568(2005)055[0323:TBEOIV]2.0.CO;2 [Google Scholar]
- Cocroft R.B, Shugart H.J, Konrad K.T, Tibbs K. Variation in plant substrates and its consequences for insect vibrational communication. Ethology. 2006;112:779–789. doi:10.1111/j.1439-0310.2006.01226.x [Google Scholar]
- Čokl A, Virant-Doberlet M. Communication with substrate-borne signals in small plant-dwelling insects. Annu. Rev. Entomol. 2003;48:29–50. doi: 10.1146/annurev.ento.48.091801.112605. doi:10.1146/annurev.ento.48.091801.112605 [DOI] [PubMed] [Google Scholar]
- Čokl A, Zorovič M, Žunič A, Virant-Doberlet M. Tuning of host plants with vibratory songs of Nezara viridula L. (Heteroptera: Pentatomidae) J. Exp. Biol. 2005;208:1481–1488. doi: 10.1242/jeb.01557. doi:10.1242/jeb.01557 [DOI] [PubMed] [Google Scholar]
- Cremer L, Heckl M, Petersson B.A.T. Springer; Berlin, Germany: 2005. Structure-borne sound: structural vibrations and sound radiation at audio frequencies. [Google Scholar]
- Devries P.J. Call production by myrmecophilous riodinid and lycaenid butterfly caterpillars (Lepidoptera): morphological, acoustical, functional, and evolutionary patterns. Am. Mus. Novit. 1991;3025:1–23. [Google Scholar]
- Drosopoulos S, Claridge M.F. CRC Press; Boca Raton, FL: 2006. Insect sounds and communication: physiology, behaviour, ecology, and evolution. [Google Scholar]
- Elias D.O, Mason A.C, Maddison W.P, Hoy R.R. Seismic signals in a courting male jumping spider (Araneae: Salticidae) J. Exp. Biol. 2003;206:4029–4039. doi: 10.1242/jeb.00634. doi:10.1242/jeb.00634 [DOI] [PubMed] [Google Scholar]
- Evans T.A, Lai J.C.S, Toledano E, McDowall L, Rakotonarivo S, Lenz M. Termites assess wood size by using vibration signals. Proc. Natl Acad. Sci. USA. 2005;102:3732–3737. doi: 10.1073/pnas.0408649102. doi:10.1073/pnas.0408649102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forrest T.G. From sender to receiver: propagation and environmental effects on acoustic signals. Am. Zool. 1994;34:644–654. [Google Scholar]
- Gibson L.J, Ashby M.F, Easterling K.E. Structure and mechanics of the iris leaf. J. Mater. Sci. 1988;23:3041–3048. doi:10.1007/BF00551271 [Google Scholar]
- Gogala M. Vibration producing structures and songs of terrestrial heteroptera as systematic character. Biološki Vestnik. 1984;32:19–36. [Google Scholar]
- Gogala M. Vibrational communication in insects (biophysical and behavioural aspects) In: Kalmring K, Elsner N, editors. Acoustic and vibrational in insects. Paul Varey; Leeds, UK: 1985. pp. 117–126. [Google Scholar]
- Graff K.F. Dover; New York, NY: 1975. Wave motion in elastic solids. [Google Scholar]
- Greenfield M.D. Oxford University Press; Oxford, UK: 2002. Signalers and receivers: mechanisms and evolution of arthropod communication. [Google Scholar]
- Henry C.S. Singing and cryptic speciation in insects. Trends Ecol. Evol. 1994;9:388–393. doi: 10.1016/0169-5347(94)90061-2. doi:10.1016/0169-5347(94)90061-2 [DOI] [PubMed] [Google Scholar]
- Henry C.S. Acoustic communication in Neuropterid insects. In: Drosopoulos S, Claridge M.F, editors. Insect sounds and communication: physiology, behaviour, ecology and evolution. CRC Press; Boca Raton, FL: 2006. pp. 153–166. [Google Scholar]
- Jensen A, La Cour Harbo A. Springer; Heidelberg, Germany; New York, NY: 2001. Ripples in mathematics: the discret wavelet transform. [Google Scholar]
- Keuper A, Kühne R. The acoustic behaviour of the bushcricket Tettigonia cantans. II. Transmission of airborne-sound and vibration signals in the biotope. Behav. Processes. 1983;8:125–145. doi: 10.1016/0376-6357(83)90002-5. doi:10.1016/0376-6357(83)90002-5 [DOI] [PubMed] [Google Scholar]
- Kolsky H. Dover; New York, NY: 1963. Stress waves in solids. [Google Scholar]
- Lange J.N. Bending wave propagation in rods and plates. J. Acoust. Soc. Am. 1963;35:378–388. doi:10.1121/1.1918475 [Google Scholar]
- Magal C, Schöller M, Tautz J, Casas J. The role of leaf structure in vibration propagation. J. Acoust. Soc. Am. 2000;108:2412–2418. doi: 10.1121/1.1286098. doi:10.1121/1.1286098 [DOI] [PubMed] [Google Scholar]
- Markl H. Vibrational communication. In: Markl H, Huber F, editors. Neuroethology and behavioral physiology. Springer; Heidelberg, Germany; New York, NY: 1983. pp. 332–353. [Google Scholar]
- McDevitt T.E, Koopmann G.H, Burroughs C.B. Two-channel vibrometer techniques for vibrational intensity measurements, part 1: flexural intensity. J. Vib. Acoust. 1993;115:436–440. [Google Scholar]
- McNett G.D, Miles R.N, Homentcovschi D, Cocroft R.B. A method for two-dimensional chracterization of animal vibrationl signals transmitted along plant stems. J. Comp. Physiol. A. 2006;192:1245–1251. doi: 10.1007/s00359-006-0153-2. doi:10.1007/s00359-006-0153-2 [DOI] [PubMed] [Google Scholar]
- Michelsen A, Fink F, Gogala A, Traue D. Plants as transmission channels for insect vibrational songs. Behav. Ecol. Sociobiol. 1982;11:269–281. doi:10.1007/BF00299304 [Google Scholar]
- Miklas N, Stritih N, Čokl A, Virant-Doberlet M, Renou M. The influence of substrate on male responsiveness to the female calling song in Nezara viridula. J. Insect Behav. 2001;14:313–332. doi:10.1023/A:1011115111592 [Google Scholar]
- Miles R.N, Cocroft R.B, Gibbons C, Batt D. A bending wave simulator for investigating directional vibration sensing in insects. J. Acoust. Soc. Am. 2001;110:579–587. doi: 10.1121/1.1369106. doi:10.1121/1.1369106 [DOI] [PubMed] [Google Scholar]
- Misiti M, Misiti Y, Poppenheim Y, Poggi J.-M. The Math Works Inc.; Cambridge, UK: 1996. Wavelet toolbox for use with Matlab. [Google Scholar]
- Nickel H, Remane R. Artenliste der Zikaden Deutschlands, mit Angabe von Nährpflanzen, Nahrungsbreite, Lebenszyklus, Areal und Gefährdung (Hemiptera, Fulgoromorpha et Cicadomorpha) Beiträge zur Zikadenkunde. 2002;5:27–64. [Google Scholar]
- Qian S, Dapang C. Prentice Hall; Upper Saddle River, NJ: 1996. Joint time-frequency analysis. [Google Scholar]
- R Development Core Team. R Foundation for Statistical Computing; Vienna, Austria: 2004. R: A language and environment for statistical computing. [Google Scholar]
- Rodriguez J.G, Ramaswamy K, Cocroft R.B. Evidence that female preferences have shaped male signal evolution in a clade of specialized plant-feeding insects. Proc. R. Soc. B. 2006;273:285–293. doi: 10.1098/rspb.2006.3635. doi:10.1098/rspb.2006.3635 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Römer H. The sensory ecology of acoustic communication in insects. In: Hoy R.R, Popper A.N, Fay R.R, editors. Comparative hearing: insects. Springer; New York, NY: 1998. pp. 63–96. [Google Scholar]
- Sayir M. Biegewellen in Sandwich-Strukturen. Schweizer Ingenieur und Architekt. 1983;101:215–219. [Google Scholar]
- Spatz H.-C, Beismann H, Bruechert F, Emanns A, Speck T. Biomechanics of the giant reed Arundo donax. Phil. Trans. R. Soc. B. 1997;352:1–10. doi:10.1098/rstb.1997.0001 [Google Scholar]
- Stölting H, Moore T.E, Lakes-Harlan R. Substrate vibrations during acoustic signalling in the cicada Okanagana rimosa. J. Insect Sci. 2002;2:1–7. doi: 10.1093/jis/2.1.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sueur J. Insect species and their songs. In: Drosopoulos S, Claridge M.F, editors. Insect sounds and communication: physiology, behaviour, ecology and evolution. CRC Press; Boca Raton, FL: 2006. pp. 207–217. [Google Scholar]
- Virant-Doberlet M, Čokl A. Vibrational communication in insects. Neotrop. Entomol. 2004;33:121–134. doi:10.1590/S1519-566X2004000200001 [Google Scholar]
- Wahl T.J, Bolton J.S. The application of the Wigner distribution to the identification of structure-borne noise components. J. Sound Vib. 1993;163:101–122. doi:10.1006/jsvi.1993.1151 [Google Scholar]
- White P.R, Birch M.C, Church S, Jay S, Rowe E, Keenlyside J.J. Intraspecific variability in the tapping behavior of the deathwatch beetle, Xestobium rufovillosum (Coleoptera, Anobiidae) J. Insect Behav. 1993;6:549–562. doi:10.1007/BF01048122 [Google Scholar]