Skip to main content
PMC home page
BMC Evolutionary Biology logoLink to BMC Evolutionary Biology
. 2003 Aug 28;3:19. doi: 10.1186/1471-2148-3-19

Position specific variation in the rate of evolution in transcription factor binding sites

Alan M Moses 1, Derek Y Chiang 2, Manolis Kellis 3,5, Eric S Lander 4,5, Michael B Eisen 1,2,6,✉
PMCID: PMC212491  PMID: 12946282

Abstract

Background

The binding sites of sequence specific transcription factors are an important and relatively well-understood class of functional non-coding DNAs. Although a wide variety of experimental and computational methods have been developed to characterize transcription factor binding sites, they remain difficult to identify. Comparison of non-coding DNA from related species has shown considerable promise in identifying these functional non-coding sequences, even though relatively little is known about their evolution.

Results

Here we analyse the genome sequences of the budding yeasts Saccharomyces cerevisiae, S. bayanus, S. paradoxus and S. mikatae to study the evolution of transcription factor binding sites. As expected, we find that both experimentally characterized and computationally predicted binding sites evolve slower than surrounding sequence, consistent with the hypothesis that they are under purifying selection. We also observe position-specific variation in the rate of evolution within binding sites. We find that the position-specific rate of evolution is positively correlated with degeneracy among binding sites within S. cerevisiae. We test theoretical predictions for the rate of evolution at positions where the base frequencies deviate from background due to purifying selection and find reasonable agreement with the observed rates of evolution. Finally, we show how the evolutionary characteristics of real binding motifs can be used to distinguish them from artefacts of computational motif finding algorithms.

Conclusion

As has been observed for protein sequences, the rate of evolution in transcription factor binding sites varies with position, suggesting that some regions are under stronger functional constraint than others. This variation likely reflects the varying importance of different positions in the formation of the protein-DNA complex. The characterization of the pattern of evolution in known binding sites will likely contribute to the effective use of comparative sequence data in the identification of transcription factor binding sites and is an important step toward understanding the evolution of functional non-coding DNA.

Background

Although non-coding DNA makes up the majority of most eukaryotic genomes, relatively little is known about its function or the nature of the constraints on its evolution. Here we focus on the evolution of an important and relatively well-understood class of functional non-coding sequences, the binding sites of sequence-specific transcription factors.

Transcription factors recognize degenerate families of short sequences (5–25 base pairs). The binding specifities of transcription factors are typically represented as consensus sequences or position weight matrices [1] that summarize their position-specific sequence preferences. In some cases, such 'motif' models of transcription factor binding sites can be inferred from genome sequences using computational methods [2-7].

Despite the absence of a detailed understanding of the evolution of transcription factor binding sites, the comparison of sequences from related species has been used to identify transcription factor binding sites en masse, with the guiding hypothesis that functional regulatory sequences will be more conserved than the surrounding DNA. Several methods [8-12] have been developed to identify conserved non-coding sequences that, when tested, often function as regulatory sequences in vivo (reviewed in [13]).

Here we characterize the evolution of known transcription factor binding sites using the complete genome sequences of the closely related budding yeasts Saccharomyces mikatae, S. bayanus, S. paradoxus [12] and S. cerevisiae [14]. We limit our focus to the conservation of binding sites due to purifying selection [15-18], though binding site turnover [15,16] (the loss and reappearance of binding sites) and other processes also occur. Preferential conservation of transcription factor binding sites has been observed previously in the genomes of organisms from bacteria [10,11] to mammals [16-18], and we expect the same to be true of yeast. In addition to the availability of complete genome sequences, the budding yeasts are a particularly appealing system in which to test these hypotheses because of the relative wealth and easy accessibility of biochemical and genetic information [e.g., [20]].

Characterizing the pattern of evolution within transcription factor binding sites allows us to explore the nature of functional constraints on these sequences. As is well known for protein sequences [21-23], we expect the pattern of evolution in transcription factor binding sites to reflect the particular patterns of constraint under which they function; important regions or residues should be constrained, while unimportant positions may show fixed changes. Unlike protein sequences, where the relationship of the amino acid sequence to the functional constraint is often difficult to discern, in the case of transcription factor binding sites, we suggest that the evolutionary constraints can be interpreted directly with respect to the physical constraints imposed by the DNA-binding protein.

Protein-DNA interactions are of much interest (e.g., [24-27]) and an understanding of the evolution of the binding motifs may provide insight into these interactions. In particular, it has recently been shown that there is a relationship between the pattern of degeneracy in certain binding motifs and regions of contact between the DNA and the binding protein: positions with fewer points of contact in the structures of protein-DNA complexes show greater variability among binding sites within a single genome [28]. If these degenerate positions are less important for the formation of the protein-DNA complex, they might be expected to show less constrained evolution, as changes at these positions have a smaller effect on the relative fitness of the organism, and therefore may become fixed in the population by drift with greater probability. Conversely, changes at positions in the motif that disrupt the recognition of the binding site by the binding-protein are likely to be deleterious, and therefore removed from the population by purifying selection. This intuition leads to a theoretical prediction that the rate of evolution at each position is a function of the frequencies in the position weight matrix (analogous to the predictions for protein sequences found in [29]).

Results

Characterized binding sites show fewer substitutions than background DNA

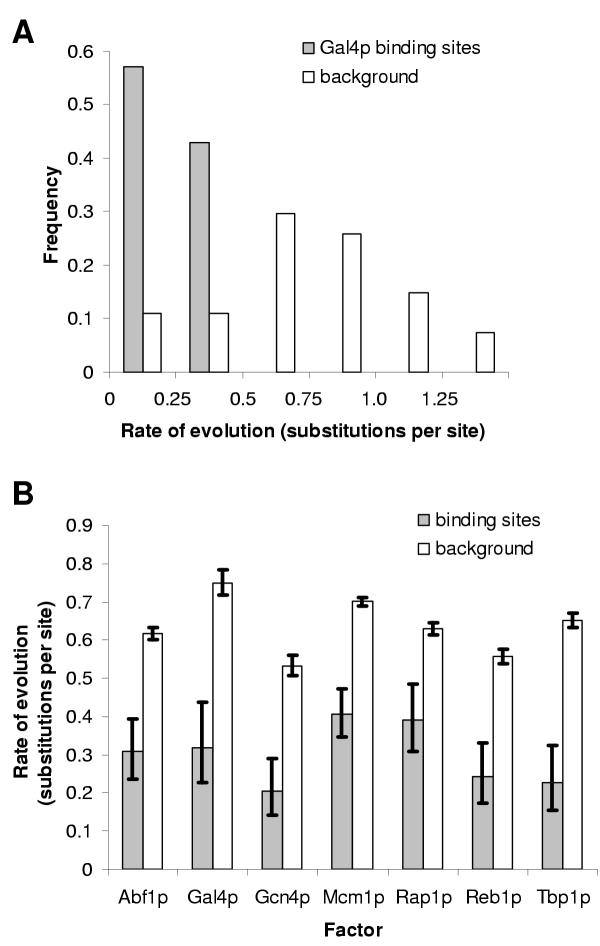
We first sought to verify that functional non-coding regions evolve more slowly than 'background sequences.' To do so, we selected several transcription factors for which there were multiple experimentally validated binding sites in the S. cerevisiae genome listed in the Promoter database of Saccharomyces cerevisiae (SCPD[20]), and compared the rate of evolution within these binding sites to that of the promoter regions in which they were found. We measured the rate of evolution in substitutions (i.e., inferred nucleotide changes) per site, where 'site' refers to a single nucleotide position, not the multi-basepair 'binding sites' of transcription factors. We first looked at Gal4p, a very well studied Zn[2]Cys[6] binuclear cluster domain transcriptional activator [30]. The average rate of evolution within known Gal4p binding sites is 0.32 (+0.12, -0.09, n = 119) substitutions per site, substantially slower than the 0.75 (± 0.03, n = 2760) substitutions per site observed in the promoters in which these Gal4p binding sites are found (fig. 1A, 1B compare Gal4 'motif' and 'background.')

Figure 1.

Figure 1

Open in a new tab

Characterized binding sites evolve more slowly than the promoters in which they are found. A. Histogram of the rate of evolution (estimated by maximum parsimony) in characterized Gal4p binding sites and randomly chosen sequences of the same length (17 basepairs) from the same promoters. B. Differences in the mean rate of evolution in motifs and the mean rate in the promoters in which they are found. Grey boxes represent the average in binding sites; unfilled boxes represent the average over the promoters in which the motifs are found (see methods). Error bars represent exact 95 % confidence intervals for a Poisson distribution.

To test the generality of this observation, we chose six other transcription factors representing different types of DNA-binding domains (see table 1) with relatively many characterized binding sites in the SCPD database. In each case there are significantly fewer substitutions (p < 0.05, 1000 bootstraps) in the characterized binding sites than in the promoters in which they lie (figure 1B), suggesting that, in general, characterized transcription factor binding sites evolve more slowly than the surrounding intergenic sequences. This is consistent with the hypothesis that these sequences are under functional constraint and their evolution reflects purifying selection.

Table 1.

Correlation between information content and substitutions per site for the experimentally characterized binding sites in the SCPD database.

Factor Type of DNA-binding domain (YPD) Number of binding sites (SCPD) Width of motif Spearman's rank correlation p-value
Gcn4p BZIP 15 12 -0.84 <0.001 **
Gal4p Zn[2]Cys[6] zinc finger 10 17 -0.83 <0.001 **
Abf1p Atypical CHC2-type zinc finger 16 12 -0.70 0.005 *
Mcm1p MADS box 35 14 -0.70 0.002 *
Rap1p Myb-like 17 15 -0.72 <0.001 **
Reb1p Myb-like 18 10 -0.81 0.002 *
Tbp1p TATA-binding 15 9 -0.46 0.106
Open in a new tab

P-values refer to the significance of the Spearman Rank correlation coefficient. * Indicates significance at a per-factor error rate < 0.05. ** Indicates significance after Bonferoni correction to keep the global error rate < 0.05, assuming 50 tests were done in total.

Functionally important positions are preferentially conserved

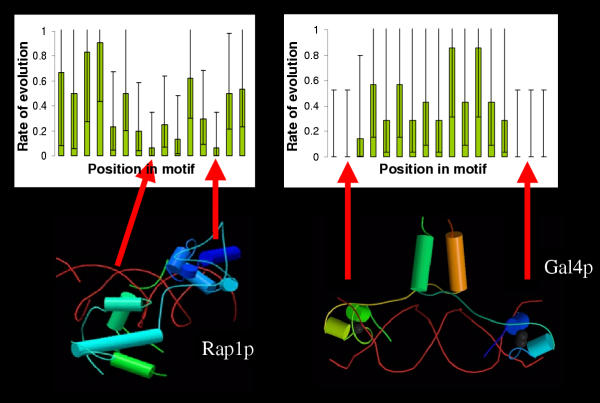
In order to further explore the functional constraints on transcription factor binding site evolution, we computed the rate of evolution at each position within the motif and observed that the rate of evolution is not constant over the binding sites. Some positions in the motif show fewer substitutions than background, while others do not. For example, in the Gal4p binding sites positions 1, 2, 3, 15, 16, and 17 show fewer substitutions than do positions 4–14 (fig. 2, right panel).

Figure 2.

Figure 2

Open in a new tab

Comparison of rates of evolution to structures of protein-DNA complexes implies a model for the variation in the rate of evolution across binding motifs. The DNA backbone appears as a red helix; proteins appear as linked coloured cylinders. We propose that the formation of the protein-DNA complex is the functional constraint that leads to purifying selection, and therefore fewer substitutions at certain positions in the binding motif. Images of protein-DNA complex structures are from the Protein Data Bank [47]. Rate of evolution is in substitutions per site (estimated by maximum parsimony) and error bars represent exact 95 % confidence intervals for a Poisson distribution.

Functionally important positions are expected to be under stronger purifying selection and therefore show stronger conservation. Indeed, the conserved positions in the Gal4p binding sites correspond to the points of contact in the crystal structure of the protein-DNA complex (fig. 2, right panel) that are required for the recognition of the target sequence [30].

Another particularly interesting example is the case of Mcm1p. Although there is no specific base in the consensus at positions 8, 9 and 10, there is a strong A/T bias in the matrix at these positions and mutagenesis studies [31] of the binding site have suggested that this is needed to allow the high degree of bending known to be necessary for the formation of Mcm1p-DNA complex [32-34]. The relative paucity of substitutions at positions 8, 9 and 10 (0.37, 0.22 and 0.5 respectively, compared to 0.70 over the entire promoters) further supports the notion that the constraint on functionally important positions slows their evolution.

Positional variation within one genome is correlated to variation between genomes

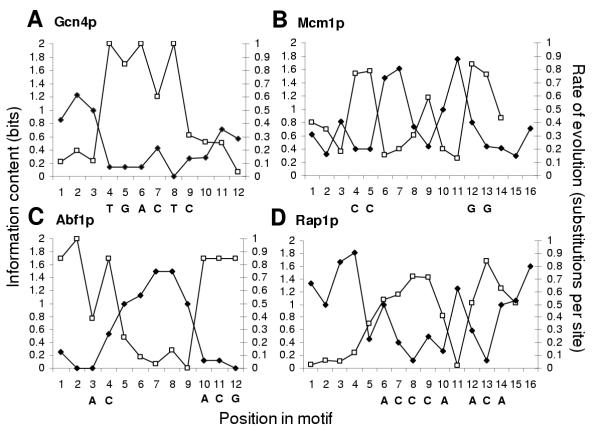
Noting that positions with fewer substitutions seem to coincide with the positions that are non-degenerate in the consensus, we constructed position weight matrices using the characterized binding sites from S. cerevisiae and, in order to quantify the degeneracy, computed the information content at each position. The information content of a position within a binding site has been shown to correlate with the importance of that position in the formation of the protein-DNA complex [28]. For the transcription factors used above (fig. 1B), we observe that positions of high information correspond to positions with fewer substitutions (e.g., Fig. 3). In 6 of 7 cases we found this correlation (Spearman's rank of -0.70 to -0.84) statistically significant (p < 0.01), the lone exception being Tbp1p, where a negative correlation was observed (-0.46), but was not significant (p = 0.11). (Table 1 & see discussion.) Thus the sequence variation in characterized transcription factor binding sites within one genome is directly related to the sequence variation at individual sites between genomes.

Figure 3.

Figure 3

Open in a new tab

Association between information profile and rate of evolution in characterized binding sites from SCPD. A–D. Representative plots of information content and substitutions per site reveal a correspondence between positions of high information content and slower rates of evolution. Open symbols represent information content and filled symbols the number of substitutions per site (estimated by maximum parsimony). Consensus letters are included below the appropriate positions in the motif.

Site-specific substitution rates are consistent with the proportionality of Halpern and Bruno

If the nucleotide frequencies at each position of a position weight matrix accurately reflect the allowed sequence specificity for the formation of a functional protein-DNA complex, it is possible, under several assumptions, to predict the rates of evolution based on these frequencies, as has been done using the frequencies of residues in protein sequences [29]. The underlying intuition is that if, for example, at a given position in the motif, a transcription factor recognizes only guanine, i.e., (fA,fC,fG,fT) = (0,0,1,0), a mutation to any other nucleotide should prohibit formation of the protein-DNA complex, and therefore be deleterious. Such mutations should be removed from the population and therefore the number of observed substitutions at such a position is expected to be very small. Similarly, if the binding protein requires, say, A or T at a given position with no preference, i.e., (fA,fC,fG,fT) = (1/2,0,0,1/2), we expect changes between A and T to persist in the population, but changes to C or G to be removed; we should therefore observe somewhat more substitutions, but still fewer than at positions where there is no preference at all, i.e., (fA,fC,fG,fT) = (1/4,1/4,1/4,1/4), and all types of substitutions are permitted. Under several assumptions, it is possible to write the following proportionality for the rates of substitution between various residues and a function of their frequencies ([29] equation 10 & see methods).

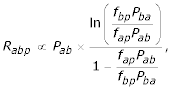
graphic file with name 1471-2148-3-19-i1.gif

where Rabp is the observed rate of substitution from residue a to residue b at position p, Pab and Pba are the (position independent) underlying rates of mutation from residue a to residue b and b to a, respectively, and fap and fbp are the frequencies of residue a and b at position p in the position weight matrix. The predicted rate of evolution at each position, Kp, is just the sum of the Rabp times the probability that that base was observed, i.e.,

graphic file with name 1471-2148-3-19-i2.gif

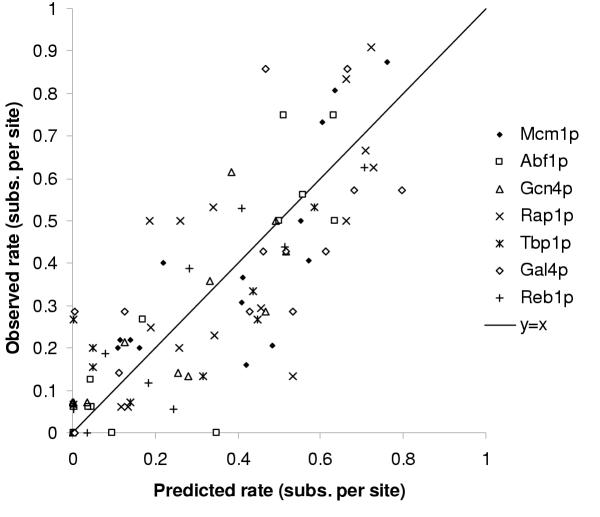
In order to test these predictions, we estimated a background mutation model (Pab) by fitting the HKY85 model [34] to entire promoter sequences using the PAML package [35], treating all positions independently (see methods). Using the seven position weight matrices (fap) trained on the characterized binding sites (all from S. cerevisiae,) and scaling the proportionality by the total number of changes observed in the motif, we compared the predicted rates to the observed rates and the results are shown in figure 4. Although there is quite a bit of variability, the observed rates of evolution seem to agree with the predictions (R2 = 0.67).

Figure 4.

Figure 4

Open in a new tab

Test of the Halpern-Bruno proportionality. Observed rate of evolution versus the predictions based on the nucleotide frequencies in the binding motif in S. cerevisiae. Each point represents the predicted and observed rates at a given position in a motif. For each factor the proportionality has been normalized by the total number of substitutions observed in the corresponding binding sites. See text for details.

Computationally predicted binding sites show similar evolutionary properties

There are relatively few transcription factors for which the number of experimentally characterized binding sites was sufficient to reliably estimate the information profile and rate of evolution at each position. To further establish the generality of these observations we extended the analysis to include additional factors where some information regarding the consensus or target genes was available. We ran the MEME motif-finding program [3] on the promoter regions of groups of genes that showed similar expression patterns to the known targets of these factors in microarray experiments to derive models of their binding specificity and identify putative binding sites. As in the experimentally characterized cases, the rate of evolution in these binding sites was slower than that of the promoters in which the sequences were found (table 2.) Furthermore, most of the motifs showed the characteristic correlation between the information content at each position and the number of substitutions per site (table 2).

Table 2.

Evolution of motifs with known consensus, but binding sites identified by MEME

Cluster Factor Consensus identified by MEME Motif subs. Bg subs. Corr. p-value
Protein folding + Hsf1p TTTTCTAGAAAGTTC 0.14 0.68 -0.42 0.060
Glycolysis + Gcr1p AAATAGAGGAAGCCCA 0.23 0.63 -0.80 <0.001 **
Nitrogen + Gln3p/ Dal80p TCTTATCA 0.39 0.74 -0.78 0.010 *
Gluco-neogenesis + Sip4p (?) CSRE CCGTTTGTCCG 0.33 0.57 -0.84 <0.001 **
G1 phase + Mbp1p Swi6 TTACGCGTTTT 0.22 0.64 -0.67 0.011 *
Respiration + Hap2/3/4p TGATTGGTCCA 0.20 0.67 -0.53 0.048 *
Methionine + Cbf1p ATGTCACGTG 0.13 0.75 -0.49 0.078
Proteasome + Rpn4p ATTTTGCCACCG 0.20 0.73 -0.75 0.002 *
M/G1 transition + Swi5p/ Ace2p AACCAGCA 0.26 0.61 -0.57 0.074
Repressed in Stress ++ (?) PAC ATGCGATGAGCTGAG 0.24 0.71 -0.69 0.006 *
leu/ilv bio-synthesis++ Leu3p GCCGTTTCCGG 0.31 0.70 -0.54 0.044 *
Phosphate +++ Pho4p CCCACGTGCG 0.29 0.65 -0.74 0.005 *
119 positions in all computationally identified motifs -0.60 4e-14 **
Open in a new tab

Here binding sites are identified by running the MEME program [3] on genes that clustered with targets in micro-array gene expression data. Expected consensus sequences (from [20,40] or [7]) are underlined. 'Motif subs.' and 'bg subs.' are the substitutions per site in the binding sites and the promoters in which they are found respectively. 'Corr.' and 'p-value' are the Spearman's rank correlation coefficient and the associated p-value between the rate of evolution at each position and the information content at each position. * Indicates significance at a per factor error rate of < 0.05. ** Indicates significance after Bonferoni correction for a global error rate < 0.05, assuming 50 tests were done in total. (?) indicates uncertainty as to the identity of the binding protein. + indicates clusters taken from hierarchical clustering [40] of yeast data from the Stanford Microarray database [42], ++ indicates clusters taken from hierarchical clustering of 300 genetic perturbations [43] and +++ indicates clusters taken from hierarchical clustering of 64 control experiments [43]

The pattern of evolution may be useful in distinguishing real motifs from computational artifacts

A challenge in computational motif detection is that algorithms often identify sequence motifs that do not represent real transcription factor binding sites. For example, in addition to the cases described above (table 2), there were several cases where the motif identified by MEME was not the binding motif for the factor known to regulate these genes. We computed the number of substitutions per site as well as the correlation between the number of substitutions and the information content for these motifs as well, and found no significant correlations (Table 3), suggesting that the reported motifs in these cases may be computational artefacts. It is possible that a reduction in the average number of substitutions per site, and a correlation between the information profile and the substitutions across the motif will prove to be useful heuristics in assessing the support from comparative sequence data for computationally identified motifs.

Table 3.

Motifs identified by MEME that do not correspond to the expected consensus sequences for the transcription factors thought to be regulating the cluster.

Cluster Factor (expected) Consensus identified by MEME Motif subs. Bg. subs. Corr. p-val
TRX2 + Yap1p AAAAAGAGGAAAAAA 0.80 0.78 -0.21 0.23
CTT1 + Msn2/4p GAAAAAAAAAAAAAA 0.51 0.67 0.13 0.67
Transport ++ Pdr1/3p AAAGAGAGAAAAAAA 0.57 0.69 0.20 0.76
Ergosterol bio-synthesis++ Upc2p/ Ecm22p ATCTTTTTTTTTTTT 0.81 0.55 0.06 0.58
60 positions in background sequence 0.08 0.73
Open in a new tab

These motifs do not show the characteristic correlation with rate of substitution or the substantial decrease in substitution rate observed for the computationally identified motifs with the expected consensus. + indicates clusters taken from hierarchical clustering of yeast data from the Stanford Microarray database [42], ++ indicates clusters taken from hierarchical clustering of 300 genetic perturbations [43].

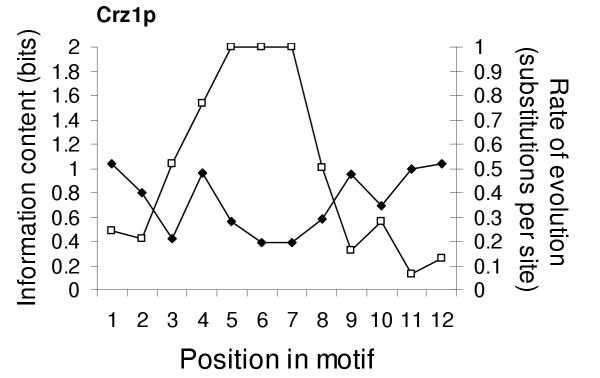
In order to further test this idea we ran MEME on the promoters of a group of proposed Crz1p target genes identified in a recent microarray study [36]. We found that the resulting motif (figure 5) was on average more conserved (0.38 subs. per site, n = 297) than the promoters of the genes in the group (0.65 subs. per site, n = 11832). In addition, it showed the characteristic correlation between the information profile and rate of evolution across the motif (Spearman's rank = -0.78, p = 0.001). Thus, in this case, the comparative sequence data support the hypothesis that this is a functional binding motif in these genes.

Figure 5.

Figure 5

Open in a new tab

Information and rate of evolution for the recently reported Crz1p motif. This motif shows the characteristic pattern of evolution observed for real motifs. Open symbols represent information content and filled symbols, the number of substitutions per site (estimated by maximum parsimony.) Consensus letters are included below the appropriate positions in the motif.

Discussion

Motifs are conserved on average, but individual binding sites are not perfectly conserved

We confirm an important motivating assumption of comparative sequencing projects: the rate of evolution within functional non-coding sequences elements is slower than the surrounding intergenic DNA (fig. 1). While this means that on average binding sites are conserved, it is important to note, however, that in no case was the average number of substitutions over the motif reduced to zero. Since substitutions do occur in characterized binding sites, simply searching through alignments for perfectly conserved segments would not have revealed all the real binding sites used in this study. Nevertheless, binding sites do show characteristic patterns of evolution, and it should be possible to take these into account in attempting to distinguish the functional instances of the motif.

Position specific variation in the rate of evolution is consistent with models of functional constraint

The observation that the rate of evolution is not constant over functional non-coding DNA sequences mirrors similar observations of regional variation in the number of substitutions per site in peptide sequences; residues that are more important to the function or structure of the protein change much less rapidly, presumably because mutations at these positions are likely to be deleterious, and therefore do not drift to fixation [21-23]. By analogy to peptide sequences, the observation that the positions in functional non-coding DNA with high information content evolve more slowly is consistent with these positions being more important for the formation of the protein-DNA complex, and therefore under more functional constraint. Unlike peptide sequences, however, the purifying selection and accompanying reduction in the rate of substitution in transcription-factor binding sites seems to be a relatively straightforward mapping from the physical interaction of the DNA with the binding protein (as in fig. 2). Since the information content has been shown to correlate with the physical constraints imposed by transcription factors on their motifs [28] it is consistent that we observe significant correlations between the information profiles and the rate of evolution as well.

The binding sites of sequence specific transcription factors afford a rare opportunity to test theoretical predictions of the effects of purifying selection on site-specific rates of evolution. By assuming the nucleotide frequencies from position specific weight matrices are the equilibrium frequencies under the purifying selection imposed on these sequences, we could make seemingly reasonable predictions for the rate of evolution at each position (figure 4). Although we do not have sufficient data to reliably estimate the rates for each type of substitution (e.g., A→T vs. A→G,) the results presented here are promising. The same intuition that allows us to construct position weight matrices (i.e., that we may average over all the binding sites to learn the average sequence specificity) allows us to compute the rate of evolution across the motif by averaging the changes observed in the individual binding sites.

Improved understanding of binding site evolution can guide the use of comparative data

An accurate understanding of the evolution of functional regulatory sequences is critical to the optimal use of comparative sequence data in the analysis of transcriptional regulation. Without such an understanding, it remains difficult to distinguish sequences under functional constraint from sequences that are similar because of shared descent, or to differentiate among the various classes of conserved non-coding sequences. We believe our observations linking position-specific variation in the rate of evolution within transcription factor binding sites to position-specific sequence variation within genomes (and to structural features of the protein-DNA complex) will be useful in comparative sequence analysis.

For example, comparative sequence data can be used to verify the predictions of de novo motif finding algorithms that have been applied to single genomes, by allowing us to ascribe increased confidence to predicted motifs that are also conserved. However, simply assessing whether motifs are 'present' in other species can be ineffective as similar sequences are expected to be present in closely related species because they have had insufficient time to diverge or as the result of other functional constraints. We propose that the patterns of evolution we observe for known motifs – their conservation relative to flanking sequences and the correlation between position-specific rate of evolution and intragenomic degeneracy – can more accurately distinguish motif models that correspond to bona fide transcription factor binding sites from computational artefacts (compare tables 2 and 3). As a demonstration we show that comparative sequence supports the motif reported in [36] (fig. 5). Verification of computationally predicted motifs may be an immediate practical application of our observations and computational methods that incorporate models of binding site evolution should take more effective advantage of comparative sequence data.

More generally, just as faster evolution at synonymous sites is an evolutionary signature of protein coding regions [21-23], the pattern of position-specific variation in evolutionary rates within binding sites can be thought of as an evolutionary signature of transcription factors. We have shown here how these evolutionary signatures might be used to identify sequences or motifs that collectively have the properties of transcription factor binding sites. With sufficient sequence data, it should ultimately be possible to estimate the rate of evolution at every base in a genome, and to identify individual short sequences with the evolutionary characteristics of functional transcription factor binding sites.

Conclusions

We show that the rate of evolution in characterized and predicted transcription factor binding sites is slower than that of the intergenic regions in which they are found. In addition we show that there is position specific variation in the rate of evolution across these binding sites. We show that this variation is correlated to the variability in the sequence specificity for that factor and can be modelled by assuming that purifying selection acts to maintain these specificities. Together this suggests that the variation in the rate of evolution is a direct reflection of differences in the strength of purifying selection due to differing physical constraints on the DNA imposed by the interaction with the binding protein.

The characterization of the pattern of conservation over known binding sites is an important step in understanding the evolution of functional non-coding DNA, and perhaps also towards the general understanding of protein-DNA interactions. Our observations should contribute to the effectiveness of comparative non-coding sequence analysis.

Methods

Rates of binding-site and intergenic evolution

Global alignments of intergenic regions from S. mikatae, S. paradoxus and S. bayanus were computed using clustalw (as described in [12]). Using the accepted species tree (Sbay, Smik,(Spar, Scer)) [8,12], we computed the minimal number of changes needed for each column of the alignment (the so called cost) using the classical parsimony algorithm (as described in [37]). We included only alignments where sequence from all four species was available; regions of ambiguity or missing sequence in the alignment, were treated as gaps. The average rate of evolution within a binding site (in fig. 1A) is the sum of the cost at each position in the binding site divided by its length. The average rate of evolution for a motif (in fig. 1B) is the sum of the cost in the binding sites divided by the total number of ungapped positions in the binding sites. Although gaps are not expected in alignments of functional binding sites, we allow for them so that we can apply the same metrics to binding sites as the surrounding sequences. The background histogram in figure 1A was made by calculating the average rate of evolution in randomly drawn 17-mers from the promoters of the genes containing the binding sites. The rate of background evolution (in fig. 1B) is the sum of the cost over the entire alignment divided by the total number of ungapped positions. The average rate of evolution at each position is the sum (over all the binding sites) of the cost at that position divided by the total number of binding sites that have no gap at that position. Although a maximum likelihood estimator for the number of substitutions per site in DNA sequences has been constructed [38] its performance is expected to be similar to parsimony methods for short evolutionary distances as are considered here.

We note that the rate of background evolution differed significantly among the groups of genes examined (characterized targets, expressions clusters.) We address this variation, and examine possible explanations in another manuscript (Hunter B Fraser, AMM and MBE in preparation).

Statistics

A Poisson distribution for the number of substitutions was used when reporting confidence intervals, and for error bars in figures 1 and 2, because this is thought to be a reasonable model for the underlying distribution for neutral substitution events.

The significance of difference of means between motifs and background was estimated by bootstrapping. We randomly selected sequences the same length as the motif (with replacement) from the upstream regions in which they were found, until we had the same number as we had characterized binding sites. We then calculated for these samples the mean number of substitutions exactly as for the characterized binding sites. Finally, we repeated this process 1000 times, and asked how often we observed an evolutionary rate smaller than for the characterized sites. Both the rate of evolution in promoter sequences and the locations of yeast transcription factor binding sites are known to show positional preferences ([39], AMM and MBE, unpublished data). To control for possible effects of these biases, we also calculated the number of substitutions in sequences of the same size as the motif 5 basepairs away on either side of the binding sites, for each of the factors shown in fig. 1B. To be as conservative as possible, we simply computed the probability of observing the number of changes in the binding sites out of the total number of changes in the binding sites and the flanking regions with no assumptions about the underlying distribution of the changes (using the hypergeometric distribution) and found that there were fewer substitutions in the binding sites than in the flanking regions (data not shown).

Identification of binding sites and construction of position weight matrices

Characterized binding sites were taken from SCPD [20] for Gal4p (n = 10), Mcm1p (n = 35), Abf1p (n = 16), and Rap1p (n = 17). For some of the short Gcn4p (n = 15), Reb1p (n = 18) and Tbp1p (n = 15) sites up to 5 flanking base pairs were included. Although SCPD lists additional binding sites for many of these factors, we excluded many of these because they were redundant listings of binding sites that have been characterized multiple times (e.g., STE6 has 4 Mcm1p binding sites listed, but these are actually the same two listed twice) or they were found in divergently transcribed genes, and were listed independently for both genes (e.g., GAL1 and GAL10 both have 4 Gal4p binding sites listed, but in fact they share these sites). For each factor, the sequences were aligned using the MEME program [3] and the 'letter-probability-matrix' from its output was used as the position weight matrix.

SCPD lists binding sites for many other regulatory elements and transcription factors, most of which have few sites, or have sites from a small number of target genes. For each transcription factor, we attempted to identify groups of genes with similar expression patterns as the known target genes, as well as known target genes of other transcription factors (from [40]). These groups were then chosen by hand from hierarchical clustering [41] of expression data from various experimental treatments and over the cell-cycle, downloaded from the Stanford Microarray Database [42] or from 300 publicly available deletion and drug treatment experiments or 64 control experiments [43]. We ran MEME on the putative promoter regions of genes in expression clusters with the following parameters: motif width was allowed to range between 8 and 16, 'zoops' and 'tcm' models were both tried for each case, and both strands of the promoter were searched. When the 'tcm' model was used, we specified between 0.5 n and 2 n for the number of occurrences where n is the number of genes in the cluster. For MEME runs, promoter regions were taken to be the 600 basepairs upstream of the translation start (basepairs in other coding regions were excluded), except in the case of the proteasome and the repressed stress genes where 300 basepairs were used because of a positional bias in the location of those binding sites (AMM and MBE unpublished results.) For computationally predicted binding-sites, occurrences were taken to be those listed in the MEME output, and the 'letter-probability-matrix' was used as position weight matrix. In the case of Crz1p we used the starting consensus NNNNGGCNCNN, which was reported in [36].

Correlation with information profiles

Information at each position was calculated as

graphic file with name 1471-2148-3-19-i3.gif

where fbp is the frequency of base b at position p in the motif, with b ∈ {A, C, G, T}, and p ∈ [1, W] where W is the width of the motif. Spearman's rank-order correlation (the linear correlation of the ranks) was computed and the significance of the correlation coefficient was assigned as described in [44].

Predictions of the rate of evolution

We follow exactly the derivation for protein sequences found in [29]. Briefly, if we assume that sites are independent, evolution is reversible, and underlying probabilities of mutation are invariant across sites, we can write the rate of evolution at each position as

Rabp ∝ Pab × Fabp,

where Rabp is the rate of substitution from residue a to residue b at position p, Pab is the rate of mutation from residue a to residue b and Fabp is the probability of fixation of a mutation from residue a to residue b at position p. If we assume that the time of fixation is small relative to the time between fixations, a so-called weak-mutation model [45], we can use Kimura's equations [46] and write the following.

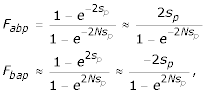
graphic file with name 1471-2148-3-19-i4.gif

where N is the effective population size and sp is the coefficient of selection at position p. As was noted in [29], if equilibrium has been reached, i.e., there has been sufficient time for all the possible mutations at that position to occur and either be fixed or removed, then

graphic file with name 1471-2148-3-19-i5.gif

where fap is the equilibrium frequency of residue a at position p, in our case the frequency in the position weight matrix. This implies

graphic file with name 1471-2148-3-19-i6.gif

and therefore

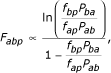
graphic file with name 1471-2148-3-19-i7.gif

which can be substituted to give the proportionality used in results.

To fit a background mutation model, we used PAML [35] to fit the HKY model [34] to the promoters that contain the characterized binding sites for each factor. We fixed the alpha parameter at 0 to use a constant rate across sites. The HKY model accounts for equilibrium frequencies of nucleotides as well as transition-transversion mutation bias. The equilibrium frequencies differed from (1/4,1/4,1/4,1/4), and transitions were more probable than transversions (kappa between 3 and 4.) We also tested the site-specific predictions for the rate of evolution assuming that all types of substitutions were equally likely and qualitatively the results were very similar (data not shown).

Authors' contributions

MK and ESL generously provided sequence alignments. DYC provided assistance with the organization, calculations, statistics and writing of the manuscript. MBE oversaw the project and provided much of the conceptual framework. AMM performed the computations and prepared the manuscript.

Acknowledgments

Acknowledgements

We thank Dr. Justin Fay, Dr. Audrey Gasch, Dr. Paul Spellman and Dr. Casey Bergman for comments on the manuscript. In addition, we thank Dr. Audrey Gasch for suggesting the extension to computationally predicted motifs, as well as Dr. Justin Fay for stimulating discussions. Thanks to Dr. William Bruno for pointing us to his work. MBE is a Pew Scholar in the Biomedical Sciences. This work was conducted under the US Department of Energy contract No. ED-AC03-76SF00098.

Contributor Information

Alan M Moses, Email: amoses@lbl.gov.

Derek Y Chiang, Email: dchiang@ocf.berkeley.edu.

Manolis Kellis, Email: manoli@mit.edu.

Eric S Lander, Email: lander@genome.wi.mit.edu.

Michael B Eisen, Email: mbeisen@lbl.gov.

References

  1. Stormo GD. DNA binding sites: representation and discovery. Bioinformatics. 2000;16:16–23. doi: 10.1093/bioinformatics/16.1.16. [DOI] [PubMed] [Google Scholar]
  2. Lawrence CE, Altschul SF, Boguski MS, Liu JS, Neuwald AF, Wootton JC. Detecting subtle sequence signals: a Gibbs sampling strategy for multiple alignment. Science. 1993;262:208–214. doi: 10.1126/science.8211139. [DOI] [PubMed] [Google Scholar]
  3. Bailey TL, Elkan C. Proceedings of the Second International Conference on Intelligent Systems for Molecular Biology. AAAI Press, Menlo Park, California; 1994. Fitting a mixture model by expectation maximization to discover motifs in biopolymers; pp. 28–36. [PubMed] [Google Scholar]
  4. Eskin E, Pevzner PA. Finding composite regulatory patterns in DNA sequences. Bioinformatics. 2002;18:S354–363. doi: 10.1093/bioinformatics/18.suppl_1.s354. [DOI] [PubMed] [Google Scholar]
  5. Liu XS, Brutlag DL, Liu JS. An algorithm for finding protein-DNA binding sites with applications to chromatin-immunoprecipitation microarray experiments. Nat Biotechnol. 2002;20:835–839. doi: 10.1038/nbt717. [DOI] [PubMed] [Google Scholar]
  6. Marsan L, Sagot MF. Algorithms for extracting structured motifs using a suffix tree with an application to promoter and regulatory site consensus identification. J Comput Biol. 2000;7:345–362. doi: 10.1089/106652700750050826. [DOI] [PubMed] [Google Scholar]
  7. Tavazoie S, Hughes JD, Campbell MJ, Cho RJ, Church GM. Systematic determination of genetic network architecture. Nat Genet. 1999;22:281–285. doi: 10.1038/10343. [DOI] [PubMed] [Google Scholar]
  8. Cliften PF, Hillier LW, Fulton L, Graves T, Miner T, Gish WR, Waterston RH, Johnston M. Surveying Saccharomyces genomes to identify functional elements by comparative DNA sequence analysis. Genome Res. 2001;11:1175–1186. doi: 10.1101/gr.182901. [DOI] [PubMed] [Google Scholar]
  9. Blanchette M, Schwikowski B, Tompa Algorithms for phylogenetic footprinting. J Comput Biol. 2002;9:211–223. doi: 10.1089/10665270252935421. [DOI] [PubMed] [Google Scholar]
  10. McCue L, Thompson W, Carmack C, Ryan MP, Liu JS, Derbyshire V, Lawrence CE. Phylogenetic footprinting of transcription factor binding sites in proteobacterial genomes. Nucleic Acids Res. 2001;29:774–782. doi: 10.1093/nar/29.3.774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Rajewsky N, Socci ND, Zapotocky M, Siggia ED. The evolution of DNA regulatory regions for proteo-gamma bacteria by interspecies comparisons. Genome Res. 2002;12:298–308. doi: 10.1101/gr.207502. 10.1101/gr.207502. Article published online before print in January 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kellis M., Patterson N, Endrizzi M, Birren B, Lander ES. Sequencing and Comparison of Yeast Species to Identify Genes and Regulatory Elements. Nature. 2003;423:241–254. doi: 10.1038/nature01644. [DOI] [PubMed] [Google Scholar]
  13. Hardison RC. Conserved noncoding sequences are reliable guides to regulatory elements. Trends in Genetics. 2000;16:369–372. doi: 10.1016/S0168-9525(00)02081-3. [DOI] [PubMed] [Google Scholar]
  14. Goffeau A, Barrell BG, Bussey H, Davis RW, Dujon B, Feldmann H, Galibert F, Hoheisel JD, Jacq C, Johnston M, Louis EJ, Mewes HW, Murakami Y, Philippsen P, Tettelin H, Oliver SG. Life with 6000 genes. Science. 1996;274:563–567. doi: 10.1126/science.274.5287.546. [DOI] [PubMed] [Google Scholar]
  15. Ludwig MZ, Patel NH, Kreitman M. Functional analysis of eve stripe 2 enhancer evolution in Drosophila: rules governing conservation and change. Development. 1998;125:949–958. doi: 10.1242/dev.125.5.949. [DOI] [PubMed] [Google Scholar]
  16. Dermitzakis ET, Clark AG. Evolution of Transcription Factor Binding Sites in Mammalian Gene Regulatory Regions: Conservation and Turnover. Mol Biol Evol. 2002;19:1114–1121. doi: 10.1093/oxfordjournals.molbev.a004169. [DOI] [PubMed] [Google Scholar]
  17. Elnitski L, Hardison RC, Li J, Yang S, Kolbe D, Eswara P, O'Connor MJ, Schwartz S, Miller W, Chiaromonte F. Distinguishing regulatory DNA from neutral sites. Genome Res. 2003;13:64–72. doi: 10.1101/gr.817703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Wasserman WW, Palumbo M, Thompson W, Fickett JW, Lawrence CE. Related Human-mouse genome comparisons to locate regulatory sites. Nat Genet. 2000;26:225–228. doi: 10.1038/79965. [DOI] [PubMed] [Google Scholar]
  19. Levy S, Hannenhalli S, Workman C. Enrichment of regulatory signals in conserved non-coding genomic sequence. Bioinformatics. 2001;17:871–877. doi: 10.1093/bioinformatics/17.10.871. [DOI] [PubMed] [Google Scholar]
  20. Zhu J, Zhang MQ. SCPD: a promoter database of the yeast Saccharomyces cerevisiae. Bioinformatics. 1999;15:871–877. doi: 10.1093/bioinformatics/15.7.607. [DOI] [PubMed] [Google Scholar]
  21. Kimura M. The Neutral Theory of Molecular Evolution. Cambridge University Press, Cambridge; 1983. [Google Scholar]
  22. Li WH. Molecular Evolution. Sinauer Associates, Sunderland MA; 1997. [Google Scholar]
  23. Nei M. Molecular Evolutionary Genetics. Columbia University Press, New York; 1987. [Google Scholar]
  24. Matthews BW. Protein-DNA interaction. No code for recognition. Nature. 1988;335:294–295. doi: 10.1038/335294a0. [DOI] [PubMed] [Google Scholar]
  25. Suzuki M, Brenner SE, Gerstein M, Yagi N. DNA recognition code of transcription factors. Protein Eng. 1995;8:319–328. doi: 10.1093/protein/8.4.319. [DOI] [PubMed] [Google Scholar]
  26. Kono H, Sarai A. Structure-based prediction of DNA target sites by regulatory proteins. Proteins. 1999;35:114–131. doi: 10.1002/(SICI)1097-0134(19990401)35:1&#x0003c;114::AID-PROT11&#x0003e;3.3.CO;2-K. [DOI] [PubMed] [Google Scholar]
  27. Benos PV, Lapedes AS, Stormo GD. Is there a code for protein-DNA recognition? Probab(ilistical)ly. Bioessays. 2002;24:466–475. doi: 10.1002/bies.10073. [DOI] [PubMed] [Google Scholar]
  28. Mirny LA, Gelfand MS. Structural analysis of conserved base pairs in protein-DNA complexes. Nucleic Acids Res. 2002;30:1704–1711. doi: 10.1093/nar/30.7.1704. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Halpern AL, Bruno WJ. Evolutionary distances for protein-coding sequences: modelling site-specific residue frequencies. Mol Biol Evol. 1998;15:910–917. doi: 10.1093/oxfordjournals.molbev.a025995. [DOI] [PubMed] [Google Scholar]
  30. Marmorstein R, Carey M, Ptashne M, Harrison SC. DNA recognition by GAL4: structure of a protein-DNA complex. Nature. 1992;356:408–414. doi: 10.1038/356408a0. [DOI] [PubMed] [Google Scholar]
  31. Acton TB, Zhong H, Vershon AK. DNA-binding specificity of Mcm1: operator mutations that alter DNA-bending and transcriptional activities by a MADS box protein. Mol Cell Biol. 1997;17:1881–1889. doi: 10.1128/mcb.17.4.1881. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kerppola TK. Transcriptional cooperativity: bending over backwards and doing the flip. Structure. 1998;6:549–554. doi: 10.1016/s0969-2126(98)00057-4. [DOI] [PubMed] [Google Scholar]
  33. Tan S, Richmond TJ. Crystal structure of the yeast MATalpha2/MCM1/DNA ternary complex. Nature. 1998;391:660–666. doi: 10.1038/35563. [DOI] [PubMed] [Google Scholar]
  34. Yang Z, Goldman N, Friday AE. Comparison of models for nucleotide substitution used in maximum likelihood phylogenetic estimation. Mol Biol Evol. 1994;11:316–324. doi: 10.1093/oxfordjournals.molbev.a040112. [DOI] [PubMed] [Google Scholar]
  35. Yang Z. PAML: a program package for phylogenetic analysis by maximum likelihood. Comput Appl Biosci. 1997;13:555–556. doi: 10.1093/bioinformatics/13.5.555. [DOI] [PubMed] [Google Scholar]
  36. Yoshimoto H, Saltsman K, Gasch AP, Li HX, Ogawa N, Botstein D, Brown PO, Cyert MS. Genome-wide Analysis of Gene Expression Regulated by the Calcineurin/Crz1p Signalling Pathway in Saccharomyces cerevisiae. J Biol Chem. 2002;277:31079–31088. doi: 10.1074/jbc.M202718200. [DOI] [PubMed] [Google Scholar]
  37. Durbin R, Eddy S, Krogh A, Mitchison G. Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press, Cambridge, UK; 1998. [Google Scholar]
  38. Nielsen R. Site-by-site estimation of the rate of substitution and the correlation of rates in mitochondrial DNA. Syst Biol. 1997;46:346–353. doi: 10.1093/sysbio/46.2.346. [DOI] [PubMed] [Google Scholar]
  39. Hampson S, Kibler D, Baldi P. Distribution patterns of over-represented k-mers in non-coding yeast DNA. Bioinformatics. 2002;18:513–528. doi: 10.1093/bioinformatics/18.4.513. [DOI] [PubMed] [Google Scholar]
  40. Hodges PE, Payne WE, Garrels JI. The Yeast Protein Database (YPD): a curated proteome database for Saccharomyces cerevisiae. Nucleic Acids Res. 1998;26:68–72. doi: 10.1093/nar/26.1.68. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci U S A. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Gollub J, Ball CA, Binkley G, Demeter J, Finkelstein DB, Hebert JM, Hernandez-Boussard T, Jin H, Kaloper M, Matese JC, Schroeder M, Brown PO, Botstein D, Sherlock G. The Stanford Microarray Database: data access and quality assessment tools. Nucleic Acids Res. 2003;31:94–96. doi: 10.1093/nar/gkg078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Hughes TR, Marton MJ, Jones AR, Roberts CJ, Stoughton R, Armour CD, Bennett HA, Coffey E, Dai H, He YD, Kidd MJ, King AM, Meyer MR, Slade D, Lum PY, Stepaniants SB, Shoemaker DD, Gachotte D, Chakraburtty K, Simon J, Bard M, Friend SH. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
  44. Press WH, Teukolsky ST, Vetterling WT, Flannery BP. Numerical Recipes in C. 2. Cambridge University Press, Cambridge, UK; 1992. [Google Scholar]
  45. Golding B, Felsenstein J. A maximum likelihood approach to the detection of selection from a phylogeny. J Mol Evol. 1990;31:511–523. doi: 10.1007/BF02102078. [DOI] [PubMed] [Google Scholar]
  46. Kimura M. On the probability of fixation of mutant genes in a population. Genetics. 1962;4:713–719. doi: 10.1093/genetics/47.6.713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from BMC Evolutionary Biology are provided here courtesy of BMC

RESOURCES