Solution measurement of DNA curvature in papillomavirus E2 binding sites

Abstract

‘Indirect readout’ refers to the proposal that proteins can recognize the intrinsic three-dimensional shape or flexibility of a DNA binding sequence apart from direct protein contact with DNA base pairs. The differing affinities of human papillomavirus (HPV) E2 proteins for different E2 binding sites have been proposed to reflect indirect readout. DNA bending has been observed in X-ray structures of E2 protein–DNA complexes. X-ray structures of three different E2 DNA binding sites revealed differences in intrinsic curvature. DNA sites with intrinsic curvature in the direction of protein-induced bending were bound more tightly by E2 proteins, supporting the indirect readout model. We now report solution measurements of intrinsic DNA curvature for three E2 binding sites using a sensitive electrophoretic phasing assay. Measured E2 site curvature agrees well the predictions of a dinucleotide model and supports an indirect readout hypothesis for DNA recognition by HPV E2.

INTRODUCTION

Sequence-specific DNA recognition by proteins is a fundamental feature of DNA packaging, recombination and gene expression. DNA site discrimination by proteins reflects free energy release due to the combination of: (i) enthalpically favorable protein–DNA contacts; (ii) entropically favorable release of bound water and cations; and (iii) favorable or unfavorable energetics of conformational changes in the two partners. Direct recognition of base-specific hydrogen bond donor and acceptor arrays is often fundamental to site discrimination. Hydrogen bonding at specific sites minimizes energy penalties associated with hydrogen bond donor–donor and acceptor–acceptor clashes. Because of the frequent requirement for conformational changes upon binding, there is evidence that the local shape or flexibility of the DNA sugar–phosphate backbone contributes to the energetics of binding site selection. Such sequence-dependent DNA recognition without base contacts has been termed ‘indirect readout’.

Indirect readout was initially proposed to explain DNA site discrimination by the bacterial trp repressor where base-specific contacts within the cognate binding site are conspicuously absent (1). An analysis of thermodynamic and structural correlations relevant to indirect readout has been presented for a set of protein–DNA complexes (2). The human papillomavirus (HPV) E2 proteins have recently been proposed to exemplify indirect readout in their discrimination among E2 binding sites in the viral genome (3). Papillomaviruses are DNA tumor viruses, many of which infect humans and other mammals. While HPV strains 6 and 11 are associated with common warts, other strains including HPV-16 and HPV-18 appear to be causative factors in cervical carcinoma (3). Among viral gene products, the regulatory E2 proteins are important dimeric DNA binding proteins involved in the regulation of viral gene transcription and genome replication (3). HPV E2 proteins recognize DNA via a unique dimeric β-barrel motif within the DNA binding domain, linked to activation domains by poorly conserved linker domains of 40–200 amino acids.

E2 binding sites occur as variations of the sequence 5′-ACCGNNNNCGGT in duplex DNA. Multiple E2 binding sites exist in all papillomavirus genomes. These sequences conserve the N₄ spacing in the recognition sequence, but the N₄ sequence itself is variable. In a detailed initial study, it was shown that (i) the nature of the N₄ sequence determines HPV-16 E2 protein binding affinity and (ii) protein binding is accompanied by DNA bending (4). In particular, HPV-16 E2 binding affinity is relatively low for the N₄ spacer 5′-ACGT, is 8-fold higher for the N₄ spacer 5′-TTAA and is 33-fold higher for the N₄ spacer 5′-AATT (5).

Because the N₄ spacer sequence influences HPV E2 binding affinity, it was logical to presume that critical protein–DNA contacts involve these bases. It was therefore puzzling when X-ray structures of E2 protein–DNA complexes (6) revealed that no base-specific contacts are made with the central N₄ sequence (Fig. 1A) (reviewed in 3). E2 binding site DNA is bent by 40–50° in the various co-crystals and the general features of the complexes do not depend on the particular N₄ sequence present. Base-specific recognition occurs in two consecutive major grooves, with bending into the intervening minor groove (Fig. 1A). It has, therefore, been proposed that the intrinsic shape or flexibility of the N₄ non-contacted spacer within the E2 binding site plays an indirect role in determining E2 binding affinity. In this model, the intrinsic DNA shape and/or flexibility of each N₄ spacer creates a distinct energy cost for converting the intrinsic DNA conformation to the protein-bound conformation.

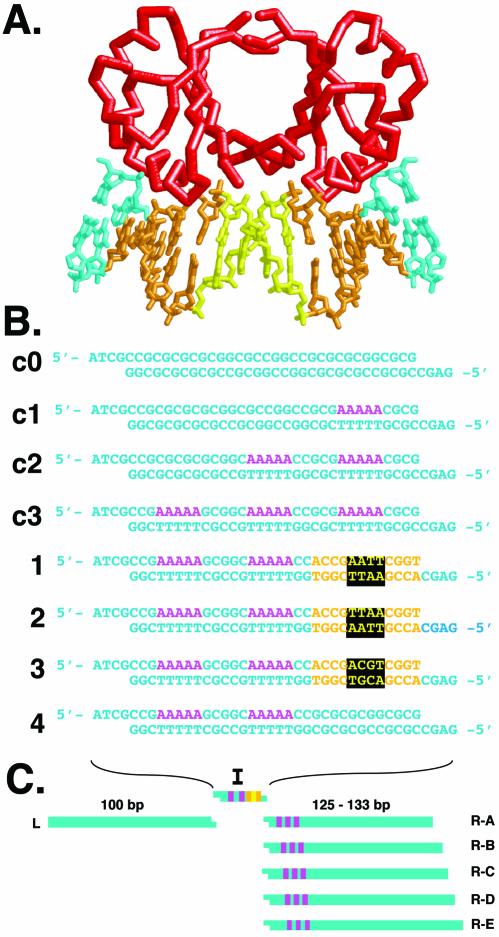
Figure 1.

E2/DNA interaction and DNA curvature analysis. (A) Schematic representation of HPV-18 E2 binding protein (red) in complex with E2 binding site DNA. DNA recognition sequences are shown in gold, the spacer sequence in yellow, and flanking sequences in cyan. The model is based on Kim et al. (6) (PDB code 1JJ4). (B) DNA sequences analyzed in this study. Inserts c0–c3 are curvature standards containing zero to three phased A₅ tracts (magenta). Inserts 1–3 contain two phased A₅ tracts and a single E2 binding site with a different spacer sequence in each case [color coding as in (A)]. Insert 4 contains two phased A5 tracts and no E2 binding site. (C) Semi-synthetic phasing assay for electrophoretic measurement of intrinsic DNA curvature within inserts 1–4. A single left arm (L) participates in trimolecular ligations with the insert (I) of choice, and each of five possible right arms (R-A through R-E). Each ligation product creates a different spacing between the insert sequences and the three phased A₅ tracts of the right arm.

The concept that variant E2 binding sites might display different intrinsic shapes has been supported by detailed experimental data from X-ray crystal structure analysis of DNA sequences in the absence of protein (7,8). These data suggest that the N₄ spacer 5′-AATT is intrinsically curved toward the center of the narrowed minor groove (8). Additional intrinsic curvature in the flanking major grooves gives rise to an overall helix axis deflection of ∼10°. In contrast, the N₄ spacers 5′-ACGT and 5′-GTAC are straight (7).

We considered it important to determine the intrinsic shape of several relevant E2 binding sites in solution. Given the availability of relatively simple and sensitive electrophoretic assays of DNA apparent curvature, we wished to explore the intrinsic shapes of three E2 binding site variants (N₄ spacers in bold): 5′-ACCGAATTCGGT (high affinity), 5′-ACCGTT AACGGT (medium affinity) and 5′-ACCGACGTCGGT (low affinity). We report the application of a semi-synthetic electrophoretic phasing assay (9) to estimate the intrinsic curvature of each of these three test sequences. Our DNA curvature estimates correlate directly with the published order of E2 binding site affinities for HPV-16 E2 protein (5).

Our results support the hypothesis that E2 binding affinity reflects the intrinsic shape or flexibility of variant E2 binding sites. Specifically, the degree of intrinsic DNA curvature (or predisposition to curvature) into the minor groove at the center of the uncontacted N₄ spacer determines E2 binding affinity.

MATERIALS AND METHODS

DNA curvature prediction and molecular modeling

Predicted DNA structures in Protein Data Bank format were generated according to Liu–Beveridge parameters (10), implemented at http://ludwig.chem.wesleyan.edu/dna/.

Molecular structures from PDB files were depicted using RasMol version 2.6 for Macintosh (11).

Design of duplex inserts

Oligonucleotides (36 nt) were purified by electrophoresis through 10% polyacrylamide (1:19, bisacrylamide:acrylamide) gels containing 7.5 M urea. Oligonucleotides were end-labeled with [γ-³²P]ATP and T4 polynucleotide kinase, annealed to the appropriate complementary strand and diluted to a concentration of ∼10 nM.

Trimolecular ligations

Semi-synthetic phasing assays were performed as described (9). Equimolar amounts (∼1 nM final concentration) of the left DNA arm, right DNA arm and duplex DNA inserts with proper termini (Fig. 1B) were ligated at room temperature for 2 h, using 400 U of T4 DNA ligase (New England Biolabs), in 10 µl reactions. Ligations were terminated by the addition of gel loading buffer and EDTA (50 mM final concentration).

Quantitative analyses of phasing probe mobilities

Ligation products (∼240 bp) were analyzed by electrophoresis through 8% native polyacrylamide (1:29, bisacrylamide:acrylamide) gels in 0.5× TBE buffer, at 10 V/cm at 22°C for 5 h. After imaging by storage phosphor technology, mobilities of trimolecular products were measured (mm) and normalized to the average mobility of each group of five ligation products sharing the same duplex insert, but containing the five different right arms, according to:

µ_rel = µ/µ_avg       1

where µ_rel is the relative mobility, µ is the mobility of each ligation product (in mm) and µ_avg is the average mobility of a group of probes sharing the same duplex insert.

The value of µ_rel was plotted against the spacing (in bp) between the center of the E2 site (inserts 1–3) or proximal A₅ tract (inserts c0–c3) and the center of the 5′ A₅ tract in R-A to R-E. Data were then fit using KaleidaGraph™ software to the phasing function (12):

µ_rel = (A_PH / 2){cos[2π(S – S_T) / P_PH]} + 1       2

where A_PH is the amplitude of the phasing function, S is the normalized spacer length, S_T is the trans spacer length and P_PH is the phasing period (set at 10.5 bp/turn). The value of A_PH estimated from curve fitting is related to the magnitude of curvature in the synthetic insert. The value of S_T estimated from curve fitting allows evaluation of the direction of insert duplex curvature relative to the phased A₅ tract array intrinsic to the right arm.

DNA curvature estimates

The empirical relationship between DNA curvature and phasing amplitude is established using duplex insert standards containing zero to three phased A₅ tracts. This relationship is linear, providing a standard curve for extracting DNA curvature estimates (in degrees of helix axis deflection). This standard curve is based on an assumption of 18° of static helix axis deflection per A₅ tract, with curvature toward the minor groove viewed in a reference frame set one half of a base pair 3′ from the center of the A₅ tract.

RESULTS AND DISCUSSION

Experimental design

The structural details of an HPV E2 protein–DNA complex are shown in Figure 1A. Key recognition base pairs (gold) flank the central non-contacted N₄ sequence (yellow). Our approach to measuring the intrinsic shape of various E2 binding sites involves calibration of an electrophoretic phasing assay with standard DNAs whose curvature is due to zero to three phased A₅ tracts (Fig. 1B, duplexes c0, c1, c2, c3). These duplexes are individually tested by ligation between ∼100 bp DNA arms ‘L’ and ‘R-A’ through ‘R-E’ (Fig. 1C) in an in vitro trimolecular ligation facilitated by appropriate unique DNA cohesive termini (9). The resulting DNA probes systematically alter the spacing between an array of three phased A₅ tracts in the right arms ‘R-A’ through ‘R-E’ and elements of curvature in the inserted synthetic duplex, I (Fig. 1C). To assess E2 binding site shape, DNA duplexes 1–4 were synthesized (Fig. 1B). Duplex 1 contains a high-affinity E2 binding site whose minor groove at the center of the N₄ spacer is in phase with two adjacent A₅ tracts. Duplexes 2 and 3 (Fig. 1B) contain similar arrangements including a medium-affinity (duplex 2) or low-affinity (duplex 3) E2 binding site. Control duplex 4 (Fig. 1B) contains two phased A₅ tracts and no E2 binding site.

Electrophoretic phasing assays exploit the observation that intrinsic DNA curvature (or anisotropic flexibility) reduces gel mobility. Systematic alteration of helical phasing between two elements of curvature in DNA will alter the global DNA shape from a fast-migating ‘S-shaped’ conformation to a slow-migrating ‘C-shaped’ conformation. Analysis of gel mobility as a function of helical phasing for standards of known intrinsic curvature (typically provided by A_5–6 tracts) provides an empirical relationship between phasing amplitude and DNA curvature. This relationship can be used to assign curvature estimates to new DNA sequences (9).

Prediction of E2 site intrinsic shape

Prior X-ray crystallography studies have suggested intrinsic curvature for certain E2 binding sites (7,8). Before analysis in solution, we implemented the optimized dinucleotide bending model of Liu and Beveridge (10) to visualize calculated trajectories of the three 12 bp E2 sequences in duplexes 1–4 (Fig. 1B), flanked by intrinsically straight DNA sequences (tandem direct repeats of arbitrary 5 bp segments). For each input sequence, a single DNA structural representation is produced by this algorithm. It is important to note that this ‘structure’ is a representation of both DNA curvature and flexibility.

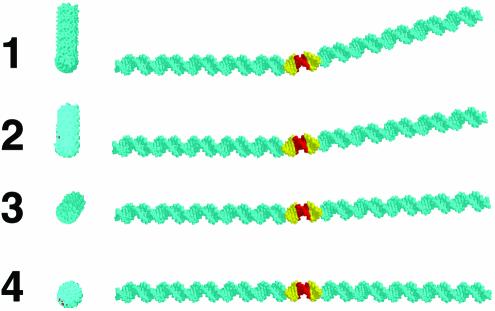
This dinucleotide model algorithm predicts significant differences in the shapes of the various E2 binding sites. The results are shown in Figure 2. The high-affinity E2 binding site in duplex 1 is predicted to be curved by ∼17° toward the minor groove at the center of the N₄ sequence (Fig. 2). In the medium-affinity sequence in duplex 2, the curvature angle is predicted to be 8° in the same direction. The low-affinity E2 binding site in duplex 3 is predicted to be curved by only 3° toward the minor groove, and the corresponding 12 bp non-E2 sequence in duplex 4 is predicted to be straight (Fig. 2). It is striking that these curvature predictions correspond well to expectations for affinity rankings based on the extent to which pre-existing DNA curvature simulates the bent DNA conformation in the E2–protein complex.

Figure 2.

Predicted DNA curvature. Molecular models depict end views (left) and side views (right) of the 12 bp E2 recognition sites of inserts 1–4, positioned between 56 bp segments of intrinsically straight DNA. Structures were predicted by the Liu–Beveridge model (10) (see Materials and Methods). Atoms corresponding to the E2 recognition sites and N₄ spacers sequence are shown in gold and red, respectively.

Solution detection of DNA curvature

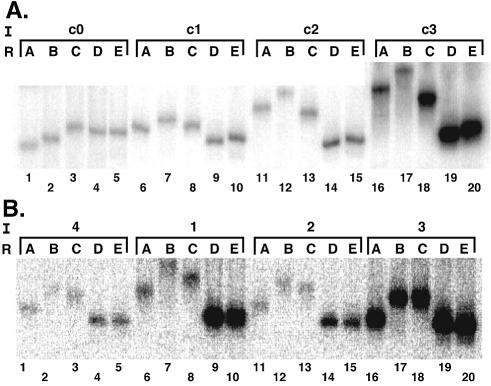
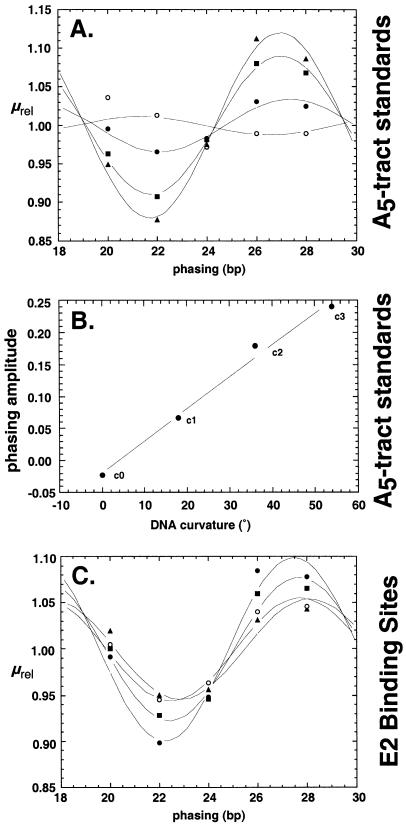
Trimolecular ligations and phasing assays were performed using native polyacrylamide gels to monitor DNA shape by mobility changes. The results of an initial calibration experiment are shown in Figure 3A. Each group of five lanes shows ligation products derived from the indicated duplex insert (see Fig. 1B) and different right arms. Inspection of the data reveals that increasing the number of phased A₅ tracts increases the amplitude of the electrophoretic migration anomaly. Relative mobility was plotted as a function of phasing distance and fit to a conventional phasing function as described in Materials and Methods. The result is shown in Figure 4A. When the phasing amplitudes derived from these data fits were plotted against the total expected DNA curvature for these standards (assuming the conventional value of 18° of curvature per A₅ tract), a linear relationship was obtained (Fig. 4B). Similar results have been obtained previously (9). This simple function allows the sensitive estimation of DNA curvature for an unknown sequence when it is substituted in the position of the proximal A₅ tract of the test array.

Figure 3.

Semi-synthetic phasing analysis of intrinsic DNA curvature. (A) DNA curvature analysis with the indicated standard inserts (I) containing zero to three phased A₅ tracts ligated to the left DNA arm and the indicated right arm (R). (B) Phasing analysis for inserts 1–4 (see Fig. 1) containing E2 binding sites with different spacer sequences.

Figure 4.

Quantitative analysis of phasing data. (A) Plot of µ_rel (defined in Materials and Methods) as a function of phasing between zero (c0; open circles), one (c1; closed circles), two (c2; closed squares) or three (c3; closed triangles) phased A₅ tracts in the insert and the array of three phased A₅ tracts in the right arm. Fitting to equation 2 is as described in Materials and Methods. (B) Calibration of the linear relationship between intrinsic DNA curvature and phasing amplitude for inserts c1–c3. (C) Phasing data for analysis of E2 binding site inserts 1 (closed circles), 2 (closed squares), 3 (closed triangles) and 4 (open circles).

Electrophoretic experiments were repeated for duplexes 1–4 (Fig. 1B) and the raw data are shown in Figure 3B. Fitting of the data to the phasing function is shown in Figure 4C, and the resulting DNA shape estimates are shown in Table 1. Duplex 4 contains two phased A₅ tracts and no E2 binding site. Its estimated absolute curvature was 28° (reflecting the presence of two phased A₅ tracts), so this value was subtracted in all cases to produce net curvature estimates. As shown in Table 1, the estimated E2 site curvatures are significantly different for the three E2 sites with different N₄ spacers. The most curved is the E2 site containing the 5′-AATT spacer (duplex 1). The curvature estimate for this duplex is 17.8°, which compares favorably with the curvature of 17° predicted by the Liu–Beveridge dinucleotide model (Fig. 2). Table 1 shows that duplex 2 has a lower curvature, 11.2°, similar to the 8° prediction (Fig. 2). Neither duplex 3 (E2 site with 5′-ACGT spacer) nor 4 (no E2 site) displayed significant curvature (Table 1). These results again are similar to predictions of the Liu–Beveridge model.

Table 1. E2 site DNA curvature in solution.

Insert (N4)	E2 site net curvaturea (°)	Curvature directionb (bp)
1(AATT)	17.8 ± 1.2	22.26 ± 0.10
2(TTAA)	11.2 ± 2.5	22.42 ± 0.01
3 (ACGT)	1.2 ± 3.0	22.88 ± 0.06
4	0	22.45 ± 0.03

^aDNA curvature relative to insert 4. Curvature estimates were obtained as described in Materials and Methods. Curve fitting of phasing data to equation 2 allowed extraction of a phasing amplitude for each construct. Using phasing amplitudes for phased A₅ tract reference standards and an assumption of 18° curvature per A₅ tract, amplitudes were converted to degrees of DNA curvature. The reported E2 site curvature was obtained by subtracting the absolute curvature of insert 4 (∼28°) from curvature estimates for inserts 1–4. Data are averages ± standard deviations based on two experiments.

^bThe curvature direction is defined as the base pair spacing (arbitrary reference frame) separating the E2 test sequence in the insert duplex from the phased A₅ tract array in the right phasing arms, that gives rise to the minimum mobility (maximum curvature, hence maximal alignment of loci of curvature). For A₅ tract standards, this parameter has a value of 21.85 bp. The observation that this reference frame remains within ∼1 bp from the center of the E2 site indicates curvature in the expected direction. Deviation from the value of 21.85 bp observed for A₅ tracts can also reflect a subtle difference in the helical repeat parameter for the E2 binding sequence relative to the corresponding sequence in insert 4.

Table 1 also lists the curvature direction, a fitting parameter that reflects the horizontal position of the minima and maxima of the cosine function in phasing graphs such as Figure 4C. The curvature direction is similar in all cases (∼22 bp) and is within 1 bp of the standard construct in which two arrays of three A₅ tracts are maximally aligned. This confirms that the measured curvature is in the expected direction, i.e. toward the minor groove at the center of the E2 sequence.

Because the 5′-AATT and 5′-ACGT sequences have previously been examined by X-ray crystallography both alone (7,8) and in complex with E2 proteins (reviewed in 3), it is possible to directly compare our ‘low-resolution’ solution measurements of DNA shape with these prior reports. Both studies agree that the low-affinity site containing the 5′-ACGT sequence is minimally curved. For the high-affinity E2 site containing the 5′-AATT sequence, X-ray crystallography showed three duplex forms with an average curvature of ∼10°. Our solution curvature estimate for this sequence is ∼18°. Possible explanations for the difference include the different experimental conditions and the absence of a crystal environment. Both methods concur that the intrinsic curvature direction for the high-affinity site is as expected, i.e. toward the minor groove at the center of the E2 binding site. Our work goes beyond prior high resolution studies by also providing a shape estimate for the intermediate-affinity E2 binding site with 5′-TTAA spacer. In accord with its intermediate affinity, the site has an apparent intermediate curvature of ∼11°.

It is important to note that we have, by convention, interpreted electrophoretic retardation by both our A₅ tract standards and E2 test sequences in terms of static curvature. This is supported by the X-ray structure of an E2 site containing 5′-AATT spacer (8) where static curvature is observed. Nonetheless, electrophoretic measurements cannot distinguish between static curvature and anisotropic flexibility. Thus, it cannot formally be excluded that the E2 sites containing 5′-AATT and 5′-TTAA sequences are not intrinsically curved, but display variable propensities to deformation toward the minor groove at the center of the non-contacted central spacer. Whether static curvature or anisotropic flexibility, the case remains that an intrinsic physical property of DNA in the non-contacted region of E2 sites correlates with observed binding affinity.

Recently, detailed all-atom molecular dynamics simulations have been undertaken by Byun and Beveridge to examine a series of DNA constructs comparable with those studied here (13). The concordance between these simulations and the results of crystallography and the solutions measurements reported here is compelling.

As both DNA curvature estimates and equilibrium E2 protein binding affinities become available, it may be possible to predict (or rationalize) the E2 protein binding affinity for each variant E2 site by estimating the free energy cost of DNA deformation from its intrinsic (free) state to the bent conformation in the protein complex. This cost would appear as a penalty in estimating equilibrium dissociation constants for the corresponding protein–DNA complexes. It would be predicted that the lowest-affinity spacers would be intrinsically curved toward the major groove at the center of the binding site (i.e. the ‘wrong’ direction with respect to the protein complex), while the highest affinity sites will be, as shown here, most intrinsically curved toward the central minor groove.

Interestingly, bovine papillomavirus (BPV) E2 proteins are similar to HPV E2 proteins and bind the same E2 sites; BPV E2 proteins reportedly show little discrimination between sites on the basis of N₄ sequences (5). This observation shows that subtle features of a DNA–protein complex may influence the importance of indirect readout in binding energetics.

CONCLUSIONS

Our data support a model in which the binding affinity of HPV-16 E2 proteins for variant E2 binding sites reflects an energy balance between the favorable free energy release associated with the protein–DNA interaction and the unfavorable free energy cost of altering the conformation of the E2 binding site DNA to allow protein interaction. In this simple model, E2 binding sites whose intrinsic shapes better approximate the DNA conformation in the E2 protein–DNA complex suffer smaller energy penalties for DNA deformation and enjoy larger residual binding energies. Such sites are therefore observed to be bound with higher affinities by E2 proteins. The electrophoretic measurements reported here tend to corroborate the results of X-ray crystallography (7,8) and support the predictive dinucleotide model of Liu and Beveridge (10,14).