Abstract
The Stokes radius characteristics of reduced and carboxamidated ribonuclease A (RCAM RNase) were determined for transfer of this “random coil” protein from water to 1 M concentrations of the naturally occurring protecting osmolytes trimethylamine N-oxide, sarcosine, sucrose, and proline and the nonprotecting osmolyte urea. The denatured ensemble of RCAM RNase expands in urea and contracts in protecting osmolytes to extents proportional to the transfer Gibbs energy of the protein from water to osmolyte. This proportionality suggests that the sum of the transfer Gibbs energies of individual parts of the protein is responsible for the dimensional changes in the denatured ensemble. The dominant term in the transfer Gibbs energy of RCAM RNase from water to protecting osmolytes is the unfavorable interaction of the osmolyte with the peptide backbone, whereas the favorable interaction of urea with the backbone dominates in RCAM RNase transfer to urea. The side chains collectively favor transfer to the osmolytes, with some protecting osmolytes solubilizing hydrophobic side chains as well as urea does, a result suggesting there is nothing special about the ability of urea to solubilize hydrophobic groups. Protecting osmolytes stabilize proteins by raising the chemical potential of the denatured ensemble, and the uniform thermodynamic force acting on the peptide backbone causes the collateral effect of contracting the denatured ensemble. The contraction decreases the conformational entropy of the denatured state while increasing the density of hydrophobic groups, two effects that also contribute to the ability of protecting osmolytes to force proteins to fold.
The adaptation of certain higher organisms to harsh environments is enabled by the intracellular presence of small organic solutes (osmolytes) that protect proteins and other cell components from the denaturing environmental stresses (1). Arakawa and Timasheff (2) have shown that the osmolytes act by raising the chemical potential of the denatured state relative to the native state, thereby increasing the (positive) Gibbs energy difference (ΔG) between the native and denatured ensembles. A pictorial description of the results of Arakawa and Timasheff is presented in the Gibbs energy diagram below, where ΔG1 is the unfolding Gibbs energy difference between native (Naq) and unfolded (Uaq) protein in aqueous buffer solution, and ΔG3 is the Gibbs energy change for the same reaction in the presence of osmolytes. Transfer of Naq or Uaq from water to osmolyte solution (Nos and Uos respectively) raises the chemical potential of the unfolded ensemble (ΔG2) much more than it does that of the native state ensemble (ΔG4), resulting in a greater stability of the protein in the osmolyte solution than in buffer, i.e., ΔG3>ΔG1. We have determined the transfer Gibbs energy changes of amino acid side chains and peptide backbone from water to solutions of the osmolytes trimethylamine N-oxide (TMAO), sarcosine, and sucrose (3, 4). From knowledge of these transfer Gibbs energy changes and the fractional exposure of the side chains and backbone in the native and unfolded states of proteins, we have estimated the overall transfer Gibbs energy changes for Naq → Nos (ΔG4) and Uaq → Uos (ΔG2) and obtained the same type of Gibbs energy diagram as Arakawa and Timasheff (3, 4). Our approach identified the unfavorable interaction of the peptide backbone with osmolyte as the thermodynamic force responsible for raising the chemical potential of both the native and unfolded states upon their transfer from water to osmolyte solution. The unfavorable interaction causes a preferential exclusion of the osmolyte in the solution-containing volume element in contact with the backbone.
From Chart 1, it is clear that protein stabilization is brought about by the action of osmolyte on the denatured state of the protein. To better understand the primary forces responsible for the increase in chemical potential of the denatured ensemble (ΔG2) and the physical and chemical consequences of these forces, we consider here the effects of particular osmolytes on the dimensional and thermodynamic properties of a representative denatured ensemble, a randomly coiled polypeptide chain. The osmolytes used are representative members of the three chemical classes of osmolytes: (i) polyols, represented by sucrose; (ii) methylamines, represented by sarcosine and TMAO; and (iii) certain amino acids, exemplified by proline. 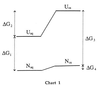
RNase A with disulfide bonds reduced and modified to prevent reoxidation has been described as being a random coil in dilute aqueous salt solution, in which all parts of the molecule spend at least part of their time in contact with solvent components (5–8). Reduced and carboxyamidated ribonuclease A (RCAM RNase) is used here as a model of the unfolded ensemble, and we report the effects of one molar concentrations of various osmolytes on the dimensions of RCAM RNase. Because we found that the unfavorable interaction of osmolyte with the peptide backbone dominates the favorable interaction of osmolytes with side chains (3, 4), we expect the RCAM RNase Stokes radius to be contracted by the osmolytes in proportion to the algebraic sum of the favorable and unfavorable interactions between osmolyte and the side chains and backbone exposed in the random coil. Our aim is to determine the extent of correlation between the dimensional changes in RCAM RNase brought about by the osmolytes and the propensities of the side chains and peptide backbone (shown by the Gibbs energy of transfer) to interact with those osmolytes.
MATERIALS AND METHODS
Diketopiperazine (DKP), L-amino acids, or amino acid salts all with purity >99% were purchased from Sigma. The solubilities of amino acids and DKP at 25°C in 1 M proline were measured according to the procedure of Liu and Bolen (3). In a typical solubility limit determination, increasing amounts of crystalline amino acid were weighed into 8–10 glass vials. To each of these vials, a fixed weight of solvent (1 M proline solution) was added such that the crystalline amino acid in one-half of the vials would dissolve completely, whereas the amino acid solubility would be exceeded in the other one-half of the vials. The sealed vials placed horizontally in the waterbath were kept shaking at 25.00 ± 0.05°C for ≈48 hr to reach solution equilibrium. The vials were left to stand in the waterbath to settle any particulate matter, and the solution in each vial was withdrawn, filtered through a glass-fiber filter, and then injected into a DMA-602 densimeter (Anton Parr, Ashland VA) for density measurement. The density of the solution or supernatant of each vial was plotted as a function of the mass composition of each vial (grams of the amino acid per 100 grams of solvent). For the unsaturated samples, density and solvent composition data were fitted to a two- to five-degree polynomial, whereas data for the saturated samples were fitted to a linear function. The solubility limit was obtained at the intersection of these two lines.
In the determination of tyrosine solubility, the protocol was identical to that for other amino acids except the concentration in the supernatant was evaluated by absorbance measurements at 274 nm, and a plot of the absorbance vs. composition for each vial was used to evaluate the solubility limit.
RCAM RNase was prepared by a modification of the method of Imoto and Yamada (9). Two milliliters of 8 M urea (ICN), 0.575 M tris⋅HCl buffer, and 5.25 mM EDTA at pH 8.6 were added to a small vial, and 50 mg of RNase A (ICN) previously purified by fast protein liquid chromatography on a Source S column (Pharmacia) and lyophilized, was dissolved in the buffered 8 M urea solution. The content of the vial was transferred to a temperature-controlled Metrohm (Brinkmann Instruments, Westbury, NY) titration vessel (40°C) and flushed continuously with nitrogen (at the same vapor pressure as the 8 M urea) to remove oxygen. Then, 25 μl of mercaptoethanol was added, and the nitrogen-flushed solution was mixed at 40°C for 1 hr with magnetic stirring. The temperature was then decreased to 21°C, after which ≈72 mg of iodoacetamide was added with stirring to the RNase A solution, and the solution was kept 15 min in the dark. The reaction was quenched by addition of 38 ml of 4°C 8 M urea stock, and the resulting mixture was dialyzed at 4°C against 3.5 liters of distilled water for 18 hr. Mass spectral analysis of RCAMRNase showed the predicted and experimentally determined mass to be within 2 mass units of one another. The RCAMRNase was used without lyophilization.
Size exclusion chromatography by using a BioCad chromatography system with UV detection at 220 and 280 nm was performed on a (300 mm × 7.8 mm) Phenomenex Biosep SEC-S3000 gel filtration column (Perseptive Biochemical) equilibrated at room temperature with 0.02 M Tris⋅HCl and 0.2 M NaCl, pH 7.0 buffer ± 1 M concentration of one of the following solutes: urea, TMAO, sarcosine, sucrose, or proline. In a typical experiment, the column was equilibrated with one of the buffers, and 100 μl of a stock solution of the buffer containing 0.1–0.2 mg/ml of either RNase A or RCAM RNase was injected onto the column previously equilibrated with the buffer. In addition, using the same buffer, stock solutions of blue dextran (100 μl of 0.5 mg/ml) or 2′-cytidine monophosphate (2′CMP; 100 μl of 0.017 mg/ml) also were injected and eluted in separate runs. The elution volumes of these species were used to determine Kd values for either RNase A or RCAM RNase according to the definition, Kd = (Ve prot − Ve BD)/(Ve 2′-CMP − Ve BD), where Ve prot represents the elution volume of either RNase A or RCAM RNase, and Ve 2′-CMP and Ve BD are the elution volumes of 2′-CMP and blue dextran, respectively.
RESULTS
The transfer Gibbs energies of amino acid side chains and backbone have been determined previously for sarcosine, TMAO, and sucrose (3, 4). These osmolytes represent the methylamine and polyol classes of osmolytes, but to study the effects of the third chemical class of osmolytes (certain amino acids), we have determined the transfer Gibbs energy changes of side chains and backbone from water to 1 M proline, a naturally occurring osmolyte important in organisms that have adapted to osmotic stresses in the environment (1, 10, 11). At the limit of solubility of an amino acid in water or a 1 M proline solution, the chemical potentials of the amino acid in the solution (water or 1 M proline) and in the crystal are equal. Thus, at the points of saturation, the amino acid chemical potentials in water and in 1 M proline can be set equal, and the transfer Gibbs energy change (ΔGtr) for the amino acid from water to 1 M proline can be derived from Eq. 1 (12)
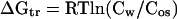 |
1 |
Here, Cos and Cw respectively represent the molar concentrations of the amino acid in osmolyte (1 M proline) and in water at their solubility limits, and R and T are the gas constant and absolute temperature. The concentrations, rather than the activities, of the amino acids are used because activities for three-component systems are very difficult or impossible to obtain with any accuracy (13–15). Following the lead of others, we report the ΔGtr values as apparent transfer Gibbs energy changes (12, 16–21).
Table 1 presents solubility limits and transfer Gibbs energy changes of all amino acids except cysteine and cystine from water to 1 M proline solution. Also provided are the transfer Gibbs energy changes of the amino acid side chains (Δgtr sc), which were determined by subtracting ΔGtr for glycine from that for all other amino acids. The transfer Gibbs energy change of the peptide backbone (Δgtr bb) is taken as one-half of ΔGtr for DKP to account for the fact that two peptide backbone groups of this cyclic glycylglycine peptide are transferred (3).
Table 1.
Amino acid solubilities and apparent transfer Gibbs energies from water to 1 M proline and 2 M urea solutions
| Amino acid | Solubility, g of AA/100 g solvent
|
Density at solubility limit
|
ΔGtr, cal/mol Water to 1 M proline | Δgtrsc Water to 1 M proline | Δgtrsc Water to 2 M urea‡ | ||
|---|---|---|---|---|---|---|---|
| Water† | 1 M Proline | Water† | 1 M Proline | ||||
| Gly | 25.1 | 20.00 | 1.08302 | 1.09603 | 102.63 | 0.00 | 0.00 |
| Ala | 16.6 | 13.29 | 1.04295 | 1.06416 | 104.28 | 1.65 | −7.67 |
| Phe | 2.81 | 2.59 | 1.00528 | 1.03543 | 28.49 | −74.14 | −169.09 |
| Trp | 1.36 | 1.53 | 1.01 | 1.03367 | −82.50 | −185.14 | −269.68 |
| His | 4.30 | 3.77 | 1.01206 | 1.04185 | 57.72 | −44.91 | −100.83 |
| Tyr* | 0.0469 | 0.0484 | 0.99705 | 1.02957 | −33.88 | −136.51 | −89.94§ |
| Met | 5.69 | 4.95 | 1.01340 | 1.04211 | 61.82 | −40.81 | −102.36 |
| Val | 5.73 | 4.59 | 1.00951 | 1.03401 | 110.78 | 8.15 | −43.12 |
| Ile | 3.35 | 2.73 | 1.00345 | 1.03366 | 100.10 | −2.53 | −76.66 |
| Gln | 4.19 | 3.50 | 1.01133 | 1.04071 | 85.69 | −16.94 | −94.29 |
| Thr | 9.74 | 8.11 | 1.02896 | 1.05459 | 85.05 | −17.58 | −43.43 |
| Leu | 2.15 | 1.74 | 1.00090 | 1.03187 | 104.90 | 2.27 | −111.63 |
| Asn | 2.64 | 2.31 | 1.00746 | 1.03806 | 59.47 | −43.16 | −103.02 |
| Ser | 42.9 | 35.96 | 1.12805 | 1.13897 | 70.22 | −32.42 | −40.05 |
| Pro | 181.5 | 152.54 | 1.19418 | 1.19418 | 38.63 | −64.01 | −35.34 |
| NaAsp | 77.9 | 76.61 | 1.28523 | 1.27071 | 12.38 | −90.25 | 7.35 |
| NaGlu | 62.4 | 60.49 | 1.21785 | 1.21323 | 13.66 | −88.97 | 1.69 |
| LysHCl | 71.3 | 62.31 | 1.12780 | 1.13727 | 42.95 | −59.68 | −45.32 |
| ArgHCl | 85.3 | 74.07 | 1.15905 | 1.1668 | 42.64 | −59.99 | −42.14 |
| DKP | 1.68 | 1.43 | 1.00252 | 1.03382 | 75.77 | ||
| DKP/2 | 37.89 | −69.15 | |||||
Solubilities determined spectrally.
Data taken from Liu and Bolen (3).
Data taken from Wang and Bolen (4).
Tyr data in 2 M urea were newly measured and not reported in the previous paper of Wang and Bolen (4). Δgtrsc represents the transfer Gibbs energy of indicated side chains determined from subtraction of the ΔGtr of glycine from ΔGtr of each of the other amino acids.
Because of its low solubility, tyrosine cannot be evaluated by densimetric methods, so the spectral methods described in Methods were used to evaluate its transfer Gibbs energy changes. Table 2 presents solubility limits and transfer Gibbs energy changes for tyrosine from water to 1 M TMAO and 1 M sucrose. It was found that the value for tyrosine transfer from water to 1 M sucrose reported by Liu and Bolen (3) was in error; corrected results are included in Table 2.
Table 2.
Tyrosine solubilities and apparent transfer Gibbs energies from water to 1 M sucrose and 1 M TMAO
| Osmolyte | Solubility, g of amino acid/100 g solvent
|
Density at solubility limit
|
ΔGtr, cal/mol Water to 1 M osmolyte | Δgtrsc Water to 1 M sucrose | Δgtrsc Water to 1 M TMAO | ||
|---|---|---|---|---|---|---|---|
| Water† | 1 M Osmolyte | Water† | 1 M Osmolyte | ||||
| Sucrose | 0.0469 | 0.0371 | 0.99705 | 1.12723 | 66.10 | −78.40 | |
| TMAO | 0.0469 | 0.0417 | 0.99705 | 0.99973 | 67.99 | −114.11 | |
Data taken from Liu and Bolen (3).
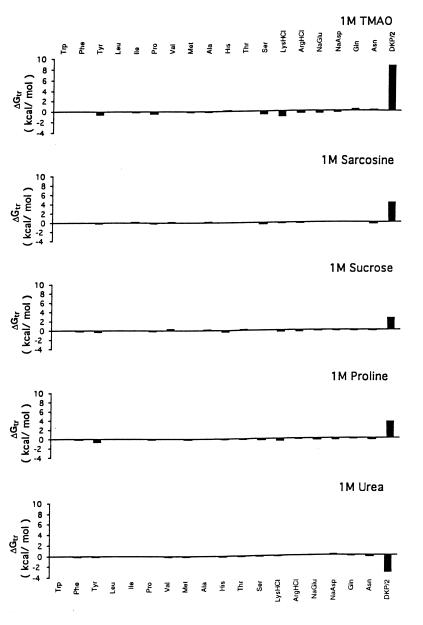
The Gibbs energy contribution for transfer of RCAM RNase from water to 1 M osmolyte- or urea-containing solutions was estimated by summation of the transfer Gibbs energy contributions of individual parts of the protein (3). First, the static accessible surface areas of the side chains and backbone were obtained from the extended form of RCAMRNase by using the Lee and Richards (22) accessible surface area algorithm as modified by Lesser and Rose (23). Creamer et al. (24) have pointed out that there are more realistic representations of a denatured polypeptide chain than an extended conformation and suggested two limiting models that bracket the expected behavior of an unfolded chain. One extreme that sets the upper bound involves a hard sphere model with attending excluded volume effects, that behaves as might a homopolymer in a good solvent. The lower bound is represented by excised fragments of folded proteins that retain intramolecular interactions representative of more compact denatured species. Upper (ΔGtr ub) and lower (ΔGtr lb) bound transfer Gibbs energy values of RCAM RNase were estimated by using the following two equations, where Δgtr is the side chain or backbone transfer free energy, ni is the total number of each type of side chain (i) or the total number of backbone units, αi is the average fractional exposure of side chain i or backbone unit (stand ASA) represents the standard accessible surface area of each type of amino acid side chain or backbone unit calculated using the extended chain, and (low ASA) and (upper ASA) are the lower and upper bound accessible surface areas of each particular side chain and backbone given in Table 1 of Creamer et al. (24). The ΔGtr ub values for transfer of RCAM RNase from water to 1 M solute-containing solutions are presented in Fig. 1, and show the contributions from the various side chains and backbone to the estimated transfer Gibbs energy of RCAM RNase as a whole.
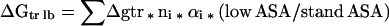 |
2 |
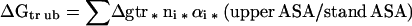 |
3 |
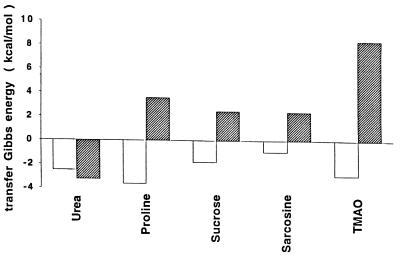
For the sake of comparing what parts of the protein contribute to the RCAM RNase transfer Gibbs energy, Fig. 2 shows the upper bound Gibbs energy of transfer of RCAM RNase from buffer to 1 M solutes (ΔGtr ub) dissected into contributions from side chains and backbone. The algebraic sum of side chain and backbone contributions for each transfer gives the corresponding ΔGtr ub from which it can be shown that transfer of RCAM RNase to urea is favorable, and to osmolytes is unfavorable, with increasing unfavorability in the order: proline, sucrose, sarcosine, and then TMAO.
Figure 1.
Upper bound limits of Gibbs energies for transfer of side chains and peptide backbone of RCAM RNase from water to 1 M concentrations of urea and protecting osmolytes. DKP/2 represents the transfer of the peptide backbone unit summed over the entire chain length of RCAM RNase, and the values for the transfer of specific amino acid side chains represent the sum of all such side chains in the protein. Data for transfer Gibbs energies of side chains and backbone from water to 1 M concentration of urea and TMAO are from Wang and Bolen (3), sucrose and sarcosine are from Liu and Bolen (4), and proline are from the present work.
Figure 2.
Upper bound transfer Gibbs energies of RCAM RNase from water to 1 M concentration of each solute indicated. Filled bars represent the sum total contribution of the peptide backbone, whereas unfilled bars show the sum total contribution of side chains to the transfer.
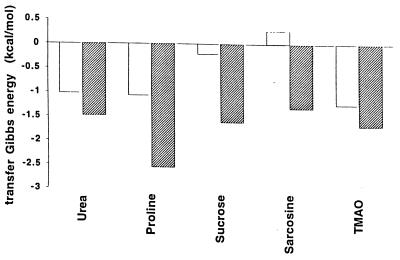
To further clarify the roles of the side chains in protein stabilization or destabilization, they were classified as either hydrophobic or as polar/charged residues; the transfer Gibbs energy contributions of these two classes to RCAM RNase are presented in Fig. 3. Dissecting the side chain contributions roughly into those residues that are generally exposed in the native protein (polar/charged) and those that are generally buried (hydrophobic), demonstrates the relative importance of the transfer of side chains from water to protecting osmolytes (proline, sucrose, sarcosine, and TMAO) compared with transfer to the nonprotecting osmolyte (urea).
Figure 3.
Side chain contributions to the transfer Gibbs energy (upper bound) of RCAM RNase from water to 1 M concentrations of urea, proline, sucrose, sarcosine, and TMAO. The transfer Gibbs energy changes are segregated into two classes of side chains, the hydrophobic class (W, F, Y, L, I, P, V, M, A; unfilled bars) and the polar/charged class (T, S, Q, N, K, R, H, E, D, G; filled bars).
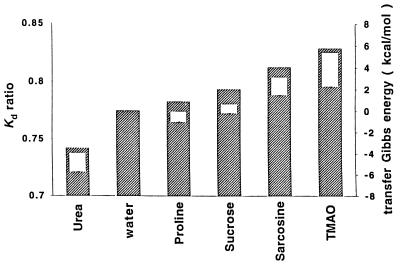
The degree of favorable and unfavorable interactions of various parts of the protein fabric and the solutes shown in Fig. 2 should affect the dimensions of a random coil species like RCAM RNase. Fig. 4 presents the effects of 1 M concentrations of osmolytes and urea on the gel filtration chromatographic characteristics of RCAM RNase and RNase A, the Kd ratio. Measuring the elution behavior of proteins given in terms of Kd (defined in Methods section) permits comparisons of the dimensional characteristics of the random coil RCAM RNase to that of its incompressible counterpart, RNase A. The Stokes radii of proteins were found to be directly proportional to 1/Kd (I. Baskakov and D.W.B., unpublished results), so the ratio of the Kd values for RCAM RNase to those for RNase A reflects the ratio of Stokes radii of RNase A to RCAM RNase. Elutions in all solvents (including “water”) were carried out at room temperature in the presence of 0.2 M NaCl and 20 mM tris⋅HCl buffer at pH 7; in buffered water solution the Stokes radius of RNase A is 0.775 that of RCAM RNase. Fig. 4 shows that RCAM RNase was contracted to differing degrees by the solutes, with 1 M urea causing an expansion of the random coil protein (1 M urea is insufficient to unfold or expand RNase A) while the osmolytes cause the Stokes radius of RCAM RNase to shrink in the order of effectiveness: proline<sucrose<sarcosine<TMAO. Also shown in Fig. 4 for each solute-containing solution is a rectangle representing RCAM RNase transfer Gibbs energy, whose upper and lower bounds (ΔGtr ub and ΔGtr lb) are determined by using the two limiting models of unfolded protein (see Eqs. 2 and 3) (24).
Figure 4.
Kd ratio of elution behavior for RCAM RNase:RNase A, and upper and lower bounds of Gibbs energies of transfer of RCAM RNase from water to 1 M of the solutes indicated. The Kd ratio of RCAM RNase:RNase A is proportional to the Stokes radius ratio of RNase A:RCAM RNase. Filled bars represent the Kd ratio data and unfilled bars are the transfer Gibbs energies of RCAM RNase (see text) representing the upper and lower bounds of transfer Gibbs Energies, ▵Gtr ub and ▵Gtr lb from Eqs. 2 and 3. Errors in Kd ratios estimated from elution volume data are less than 1%.
DISCUSSION
Timasheff and coworkers and others have provided convincing evidence that osmolytes are preferentially excluded from both the native and denatured states of proteins (2, 25–37). On transferring either native or denatured protein from water to osmolyte solution, the resulting preferential exclusion of osmolytes means the interaction between protein and osmolyte is unfavorable and ΔGtr will have a positive value. Because more protein fabric is exposed in the unfolded than in the native state, ΔGtr of the unfolded state is a larger positive quantity than ΔGtr of the native state, i.e., in Chart 1, ΔG2 > ΔG4. The major reason, then, that proteins are thermodynamically more stable in the presence of osmolyte than in water (i.e., in Chart 1, ΔG3 is more positive than ΔG1) is the very large positive Gibbs energy effect that osmolytes have on the unfolded states of proteins.
We recently proposed that the chemical origin of the unfavorable transfer of native and unfolded proteins from water to osmolyte solutions as measured by Timasheff and coworkers (25–32), and the associated preferential hydration of these protein species, is the unfavorable interaction between osmolyte and the peptide backbone (3). Support for this proposal comes from agreement between experimentally measured transfer Gibbs energy data for native and unfolded RNase T1 with that predicted by summing the transfer contributions of solvent-exposed individual parts of the protein by using side chain and backbone transfer Gibbs energy data (4). Because estimation of transfer Gibbs energies of native and unfolded states (ΔG4 and ΔG2) relies on additivity as well as other assumptions and approximations (3), it is prudent to determine what other properties of proteins are influenced by the effects of osmolytes on side chains and backbone and to gauge the correlation between the property and the molecular-level forces. The transfer Gibbs energy changes for RCAM RNase is assumed to reflect the molecular level interactions between solvent components and the protein fabric, and these thermodynamic forces should expand and/or contract the random coil in proportion to the magnitudes of their transfer Gibbs energy contributions. The identical rank order of efficacies between the estimated transfer Gibbs energy change and the dimensional effects of the solutes on RCAM RNase (shown in Fig. 4), provides strong evidence that the molecular level forces that comprise ΔGtr go hand-in-hand with the observed effects on molecular dimensions. At the same time, the data suggest which functional groups on the protein contribute to dimensional changes and ΔGtr and the magnitudes of their respective involvements.
There are several protein folding issues raised by the effect of urea and the osmolytes on Gibbs energy and the dimensions of the random coil protein, RCAM RNase. Among these issues are: (i) How does solvation of the backbone and side chains influence protein folding in urea and in protecting osmolyte solutions? (ii) How does solvation of the backbone influence protein folding in water alone? And (iii) how does contraction of the denatured ensemble by osmolytes affect the folding of proteins in osmolyte-containing cells? Although complete answers to these questions cannot be derived from the data at hand, several interesting possibilities are suggested from the results.
At issue in the first question is the effect on solvation of side chains by solutes. It has been known for some time that urea interacts favorably with the polypeptide backbone as well as nonpolar side chains (12, 38). And it is commonly thought that the favorable interactions of denaturants with nonpolar side chains serve to distinguish denaturants from protectants (39). However, the data in Fig. 3 show that urea is no better at solubilizing hydrophobic side chains than is TMAO, a protecting osmolyte that has an extraordinary ability to force proteins to fold (40). The overall side chain interactions with urea and the protecting osmolytes are favorable, implying that all these solutes should denature proteins. But what determines primarily whether the solute will be a denaturing or a protecting solute and by how much is the magnitude of the favorable vs. unfavorable interactions of the backbone with the solute.
Because the backbone plays such a dominant role in the effects of both urea and the protecting osmolytes (as shown in Figs. 2 and 4), it is certainly possible that the backbone might play a role in protein folding in water, a possibility that is the subject of the second question listed above. Are backbone-water interactions more favorable than backbone-backbone interactions? Or phrased another way, is water a “good,” a “theta,” or a “poor” solvent for the peptide backbone as expressed in the ratings of polymer science (41)? From data on the solubility of glycine-based peptides of increasing chain length, a case may be made that water is a poor solvent for the backbone. The solubility of carbobenzoxyglycineamide in water (9.5 mM) decreases markedly with increasing chain length [Cbz-gly2-NH2, 4.5 mM; Cbz-gly3-NH2, 1.2 mM (38)], and polyglycine peptide solubility becomes extremely low with chain lengths only a small fraction of that of a protein. The high insolubility of glycine peptides suggests that water is a relatively “poor” solvent for the peptide backbone. This possibility raises the intriguing question of whether solvophobicity of the backbone in water has been overlooked as a contributor to the collapse and folding of a protein in aqueous solution. Clearly, its importance in the Gibbs energy of transfer from water to each of the protecting osmolytes and urea shows that the backbone is the major player in denaturation and protein stabilization, so its possible role in protein folding in aqueous solution cannot be ruled out.
The third question provided above involves the contraction of the denatured ensemble by osmolytes. As shown in Chart 1 and Fig. 2, the most important effect in the transfer of native and unfolded protein from water to osmolyte is to raise the Gibbs energy of the denatured ensemble. In addition to raising the chemical potential of the denatured ensemble, the unfavorable interaction of backbone and osmolytes causes a collateral effect that results in the contraction of the denatured ensemble. The contraction decreases the entropy of the denatured ensemble, an effect that will promote its two-state counterpart, the native state ensemble. In addition, contraction increases the density of hydrophobic side chains within the contracted unfolded ensemble relative to that ensemble in buffered water. This encourages intramolecular interactions and again promotes folding. All of these factors contribute to the extraordinary ability of osmolytes like TMAO to force thermodynamically unfolded proteins to fold (40). The degree to which the intramolecular forces for collapse and folding are favored by contraction of the unfolded ensemble will depend on: (i) the efficacy of the osmolyte in contraction of the denatured ensemble, (ii) the osmolyte concentration, and (iii) whether any intracellular denaturing stress (e.g., temperature or urea) is also acting on the system. These dependencies are currently under investigation.
Protein folding/protein stabilization in organisms adapted to environmental stresses is an important part of biology that can teach much about the interaction of solvent and solvent components with native and denatured states of proteins. Through natural selection, nature has used osmolytes to advantage in generically stabilizing proteins against denaturing stresses (1). Forces involving the side chains are emphasized in protein folding taking place in buffered water solution, and those same forces are involved in protein folding in buffered osmolyte solution (4). What distinguishes stabilizing osmolytes is that an additional driving force, the solvophobic effect on the peptide backbone, raises the Gibbs energy of the denatured ensemble. This force causes increases in the chemical potential of the denatured ensemble important in stabilizing proteins and also causes collateral effects on the physical dimensions that encourage side chain interactions within the denatured ensemble. All these effects arising as a consequence of the unfavorable interaction of osmolytes with the peptide backbone contribute an extraordinarily strong driving force for protein folding.
Acknowledgments
We thank Dr. Ilia Baskakov for accessible surface area calculations and helpful comments on this work. Supported by U. S. Public Health Research Grant GM49760, The John Sealy Memorial Endowment Fund for Biomedical Research, and Amgen Inc.
ABBREVIATIONS
- RCAM RNase
reduced and carboxyamidated ribonuclease A
- RNase A
ribonuclease A
- TMAO
trimethylamine N-oxide
- DKP
diketopiperazine
- Naq
native protein in buffered water
- Uaq
unfolded protein in buffered water
- Uos
unfolded protein in osmolyte solution
- 2′CMP
2′-cytidine monophosphate
Footnotes
This paper was submitted directly (Track II) to the Proceedings Office.
References
- 1.Yancey P H, Clark M E, Hand S C, Bowlus R D, Somero G N. Science. 1982;217:1214–1222. doi: 10.1126/science.7112124. [DOI] [PubMed] [Google Scholar]
- 2.Arakawa T, Bhat R, Timasheff S. Biochemistry. 1990;29:1914–1923. doi: 10.1021/bi00459a036. [DOI] [PubMed] [Google Scholar]
- 3.Liu Y, Bolen D W. Biochemistry. 1995;34:12884–12891. doi: 10.1021/bi00039a051. [DOI] [PubMed] [Google Scholar]
- 4.Wang A, Bolen D W. Biochemistry. 1997;36:9101–9108. doi: 10.1021/bi970247h. [DOI] [PubMed] [Google Scholar]
- 5.Harrington W F, Schellman J A. C R Trav Lab Carlsburg, Ser Chim. 1956;30:21–43. [PubMed] [Google Scholar]
- 6.Harrington W F, Sela M. Biochim Biophys Acta. 1959;31:427–434. doi: 10.1016/0006-3002(59)90017-4. [DOI] [PubMed] [Google Scholar]
- 7.Tanford C. Protein Denaturation Part A: Characterization of the Denatured State. Vol. 23. New York: Academic; 1968. pp. 121–217. [Google Scholar]
- 8.White F H. J Biol Chem. 1961;236:1353–1360. [PubMed] [Google Scholar]
- 9.Imoto T, Yamada H. In: Protein Function a Practical Approach. Creighton T E, editor. Oxford, UK: IRL; 1989. pp. 247–277. [Google Scholar]
- 10.Nash D, Paleg L G, Wiskich J T. Aust J Plant Physiol. 1982;9:47–57. [Google Scholar]
- 11.Paleg L G, Douglas T J, van Daal A, Keech D B. Aust J Plant Physiol. 1981;8:107–114. [Google Scholar]
- 12.Nozaki Y, Tanford C. J Biol Chem. 1963;238:4074–4080. [PubMed] [Google Scholar]
- 13.Schönert H, Stroth L. Biopolymers. 1981;20:817–831. [Google Scholar]
- 14.Uedaira H. Bull Chem Soc Jpn. 1972;45:3068–3072. [Google Scholar]
- 15.Uedaira H. Bull Chem Soc Jpn. 1977;50:1298–1304. [Google Scholar]
- 16.Lapanje S, Skerjanc J, Glavnik S, Zibret S. J Chem Thermodyn. 1978;10:425–433. [Google Scholar]
- 17.Nozaki Y, Tanford C. J Biol Chem. 1965;240:3568–3573. [PubMed] [Google Scholar]
- 18.Nozaki Y, Tanford C. J Biol Chem. 1970;245:1648–1652. [PubMed] [Google Scholar]
- 19.Nozaki Y, Tanford C. J Biol Chem. 1971;246:2211–2217. [PubMed] [Google Scholar]
- 20.Pittz E P, Bello J. Arch Biochem Biophys. 1971;146:513–524. doi: 10.1016/0003-9861(71)90156-1. [DOI] [PubMed] [Google Scholar]
- 21.Tanford C. Protein Denaturation Part C: Theoretical Models for the Mechanism of Denaturation. Vol. 24. New York: Academic; 1970. pp. 1–95. [PubMed] [Google Scholar]
- 22.Lee B, Richards F M. J Mol Biol. 1971;55:379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
- 23.Lesser G J, Rose G D. Proteins Struct Funct Genet. 1990;8:6–13. doi: 10.1002/prot.340080104. [DOI] [PubMed] [Google Scholar]
- 24.Creamer T P, Srinivasan R, Rose G D. Biochemistry. 1997;36:2832–2835. doi: 10.1021/bi962819o. [DOI] [PubMed] [Google Scholar]
- 25.Arakawa T, Bhat R, Timasheff S. Biochemistry. 1990;29:1924–1931. doi: 10.1021/bi00459a037. [DOI] [PubMed] [Google Scholar]
- 26.Arakawa T, Timasheff S N. Biochemistry. 1982;21:6545–6552. doi: 10.1021/bi00268a034. [DOI] [PubMed] [Google Scholar]
- 27.Arakawa T, Timasheff S N. Biochemistry. 1982;21:6536–6544. doi: 10.1021/bi00268a033. [DOI] [PubMed] [Google Scholar]
- 28.Arakawa T, Timasheff S N. Arch Biochem Biophys. 1983;224:169–177. doi: 10.1016/0003-9861(83)90201-1. [DOI] [PubMed] [Google Scholar]
- 29.Arakawa T, Timasheff S N. Biochemistry. 1984;23:5912–5923. doi: 10.1021/bi00320a004. [DOI] [PubMed] [Google Scholar]
- 30.Arakawa T, Timasheff S N. Biochemistry. 1984;23:5924–5929. doi: 10.1021/bi00320a005. [DOI] [PubMed] [Google Scholar]
- 31.Arakawa T, Timasheff S N. J Biol Chem. 1984;259:4979–4986. [PubMed] [Google Scholar]
- 32.Arakawa T, Timasheff S N. Biochemistry. 1985;24:6756–6762. doi: 10.1021/bi00345a005. [DOI] [PubMed] [Google Scholar]
- 33.Lee J C, Timasheff S N. J Biol Chem. 1981;256:7193–7201. [PubMed] [Google Scholar]
- 34.Lee J C, Lee L L-Y. J Biol Chem. 1981;256:625–631. [PubMed] [Google Scholar]
- 35.Lee L L-Y, Lee J C. Biochemistry. 1987;26:7813–7819. doi: 10.1021/bi00398a042. [DOI] [PubMed] [Google Scholar]
- 36.Timasheff S N. Annu Rev Biophys Biomol Struct. 1993;22:67–97. doi: 10.1146/annurev.bb.22.060193.000435. [DOI] [PubMed] [Google Scholar]
- 37.Timasheff S N. Biochemistry. 1994;33:12695–12701. doi: 10.1021/bi00208a021. [DOI] [PubMed] [Google Scholar]
- 38.Robinson D R, Jencks W P. J Am Chem Soc. 1965;87:2462–2470. doi: 10.1021/ja01089a028. [DOI] [PubMed] [Google Scholar]
- 39.Creighton T E. Proteins: Structures and Molecular Properties. New York: Freeman; 1993. [Google Scholar]
- 40.Baskakov I, Bolen D W. J Biol Chem. 1998;273:4831–4834. doi: 10.1074/jbc.273.9.4831. [DOI] [PubMed] [Google Scholar]
- 41.Flory P J. Statistical Mechanics of Chain Molecules. New York: Wiley Interscience; 1969. [Google Scholar]