Kinetic Analysis of Secretory Protein Traffic and Characterization of Golgi to Plasma Membrane Transport Intermediates in Living Cells

Abstract

Quantitative time-lapse imaging data of single cells expressing the transmembrane protein, vesicular stomatitis virus ts045 G protein fused to green fluorescent protein (VSVG–GFP), were used for kinetic modeling of protein traffic through the various compartments of the secretory pathway. A series of first order rate laws was sufficient to accurately describe VSVG–GFP transport, and provided compartment residence times and rate constants for transport into and out of the Golgi complex and delivery to the plasma membrane. For ER to Golgi transport the mean rate constant (i.e., the fraction of VSVG–GFP moved per unit of time) was 2.8% per min, for Golgi to plasma membrane transport it was 3.0% per min, and for transport from the plasma membrane to a degradative site it was 0.25% per min. Because these rate constants did not change as the concentration of VSVG–GFP in different compartments went from high (early in the experiment) to low (late in the experiment), secretory transport machinery was never saturated during the experiments.

The processes of budding, translocation, and fusion of post-Golgi transport intermediates carrying VSVG– GFP to the plasma membrane were also analyzed using quantitative imaging techniques. Large pleiomorphic tubular structures, rather than small vesicles, were found to be the primary vehicles for Golgi to plasma membrane transport of VSVG–GFP. These structures budded as entire domains from the Golgi complex and underwent dynamic shape changes as they moved along microtubule tracks to the cell periphery. They carried up to 10,000 VSVG–GFP molecules and had a mean life time in COS cells of 3.8 min. In addition, they fused with the plasma membrane without intersecting other membrane transport pathways in the cell. These properties suggest that the post-Golgi intermediates represent a unique transport organelle for conveying large quantities of protein cargo from the Golgi complex directly to the plasma membrane.

The secretory membrane system synthesizes and secretes highly processed and complex molecules, allowing eukaryotic cells to modify their outer surfaces and surroundings and to control growth and homeostasis. The system is comprised of distinct membrane-bound compartments (including ER, Golgi complex, and plasma membrane) and tubular-vesicular transport intermediates that transfer newly synthesized cargo between compartments. Secretory cargo molecules in this system are synthesized in the ER and transported to the Golgi complex for processing and maturation. Upon reaching the trans-Golgi network (TGN), they are sorted and packaged into post-Golgi transport intermediates that move through the cytoplasm to fuse with the cell surface.

Genetic and biochemical approaches have provided insight into the molecular machinery for the formation, targeting, and fusion of secretory transport intermediates (Schekman and Orci, 1996; Rothman and Wieland, 1996). The morphological and kinetic properties of this membrane transport system are less understood. It is not clear, for example, exactly how cargo-enriched transport intermediates bud off from donor membranes (i.e., as vesicles or tubules), how they translocate through the cytoplasm (i.e., by diffusion or along microtubules), how long cargo resides in a particular compartment, and the rate of cargo influx and efflux out of a given compartment. Answers to these questions are fundamental to understanding how the molecular machinery for secretory protein traffic functions in living cells.

The emergence of green fluorescent protein (GFP)¹ technology (Chalfie, 1994) has made it possible to study protein localization and trafficking in single living cells. Membrane proteins fused to GFP can be visualized easily within cells and are often remarkably photostable to repetitive imaging with low light level illumination (Rizzuto et al., 1995; Sciaky et al., 1997; Shima et al., 1997; Wacker et al., 1997). With high illumination levels, GFP fusion proteins can be photobleached, permitting analysis of the movement of unbleached GFP chimeras into bleached areas of the cell (Cole et al., 1996). Quantification of GFP chimeras using sensitive light detection systems is also possible, enabling the fluorescent signal from a chimera to be converted to the number of corresponding molecules (Lippincott-Schwartz et al., 1998; Piston et al., 1998). These characteristics make such proteins ideal for use in time-lapse imaging studies to analyze dynamic cellular processes quantitatively over extended periods of time.

In this study we use the thermoreversible folding mutant, ts045 vesicular stomatitis virus G protein, fused to GFP at its cytoplasmic tail (VSVG–GFP) as a reporter to address a number of unresolved questions regarding the dynamic properties of secretory membrane transport in living cells. The ts045 VSVG membrane protein has been widely used for studying membrane transport (Wehland et al., 1982; Arnheiter et al., 1984; Kreis et al., 1986; Plutner et al., 1992; Balch et al., 1994). It misfolds and is retained in the ER at 40°C, but upon temperature shift to 32°C moves as a synchronous population to the Golgi complex before being transported to the plasma membrane (Bergmann, 1989). These properties are preserved in the chimeric protein (Presley et al., 1997; Scales et al., 1997). Previous work using VSVG–GFP has focused on ER-to-Golgi transport (Presley et al., 1997; Scales et al., 1997). Here we analyze the overall kinetic properties of secretory transport of VSVG–GFP and characterize the intermediates involved in its delivery from the Golgi complex to the plasma membrane.

The kinetics of VSVG–GFP transport were analyzed from digital time-lapse imaging sequences of chimera-expressing COS cells after they were shifted from 40° to 32°C. Fitting the time course data to trafficking models did not require a changing rate constant (or rate coefficient) as the concentration of VSVG–GFP in different compartments went from high (early in the experiment) to low (late in the experiment). Rather, a series of first order rate laws connecting the ER, Golgi, and plasma membrane was sufficient to accurately account for the data, indicating that secretory transport machinery was never saturated during VSVG–GFP transport. This allowed us to calculate VSVG–GFP flux (i.e., molecules per second) into and out of the Golgi complex and delivery to the plasma membrane in individual cells. We also were able to determine the overall residence time for VSVG–GFP in different subcellular compartments, including the Golgi complex, and examine how various perturbants (i.e., actin and microtubule depolymerization) affected each of the rate-limiting steps in VSVG–GFP transport. The processes of budding, translocation, and fusion of post-Golgi transport intermediates were also investigated using VSVG–GFP. Post-Golgi intermediates containing VSVG–GFP were large, irregularly-shaped structures that budded as a whole from the Golgi complex and moved along microtubules to the cell periphery without intersecting other membrane transport pathways. Quantitative kinetic modeling techniques revealed that these structures have a mean life time of 3.8 min within cells and are the major vehicles for VSVG–GFP delivery to the cell surface.

Materials and Methods

Cells, DNA Construct, Antibodies, and Reagents

COS-7 cells (African Green Monkey; American Type Culture Collection, Rockville, MD) were used in all experiments. They were maintained in DME (Biofluids, Rockville, MD) supplemented with 10% FBS, 2 mM glutamine, 100 U/ml penicillin, and 100 μg/ml streptomycin at 37°C in a 5% CO₂ incubator. The cloning and expression of VSVG–GFP are as previously described (Presley et al., 1997). In brief, pCDM 8.1 vector carrying VSVG-ts045 with EGFP (Clontech, Palo Alto, CA) directly linked to the carboxy terminus was expressed in COS-7 cells using electroporation. VSVG–GFP expressing cells were grown on either 13-mm glass coverslips or in chambered coverglasses (Lab Tek, Naperville, IL). They were imaged in 2–3 ml RPMI without phenol red (Biofluids) which contained 20 mM Hepes buffer, pH 7.4, 150 μg/ml cycloheximide, and 20% fetal calf serum. The concentration of cycloheximide was sufficient to inhibit protein synthesis by 90% (Cole et al., 1998). All drugs were purchased from Sigma Chemical Co (St. Louis, MO). The following antibodies were used: rabbit polyclonal antiserum to AP1 and furin (J. Bonifacino, National Instutite of Child Health and Human Development [NICHD], National Institutes of Health [NIH]); rabbit polyclonal antiserum to GM130 (G. Warren, Imperial Cancer Research Fund, London, UK); rabbit polyclonal antiserum to β-COP; and, mouse monoclonal antibodies to hemagglutinin (HA) (HA.11; Berkeley Antibody, Richmond, CA). Rhodamine-conjugated secondary antibodies were purchased from Southern Biotechnology (Birmingham, AL).

Fluorescence Microscopy and Image Processing

Cells were imaged at 40° or 32°C using a Zeiss LSM 410 (Carl Zeiss Inc., Thornwood, NY) with a 100× Zeiss PlanApochromat oil immersion objective NA 1.4, or a Zeiss upright model 3 photomicroscope with a Nikon Planapo 60× oil immersion objective NA 1.4 equipped with a silicon-intensified target video (SIT) camera VE1000SIT (Dage-MTI, Michigan City, IN) attached to an Argus-10 image processor (Hamamatsu, Hamamatsu City, Japan). Temperature was controlled with a Nevtek air stream stage incubator (Burnsville, VA). On the confocal microscope, GFP molecules were excited with the 488 line of a krypton-argon laser and imaged with a 515–540 bandpass filter. Rhodamine-labeled antibodies were excited with the 568 line and imaged with a long-pass 590 filter. Filter sets for conventional fluorescein imaging and a neutral density filter were used for imaging VSVG–GFP expressing cells on the SIT video microscope system. Images from the SIT camera were digitized and collected directly to RAM (8–15 frames/s) with an Apple Power Macintosh 9600/200 equipped with a PCI-based LG-5 video grabbing card (Scion, Frederick, MD) and 768 Mbytes of RAM space. Image capturing, processing, and automatic and manual data acquisition were performed using NIH Image 1.62 (Wayne Rasband Analytics, Research Services Branch, NIH, Bethesda, MD). Export to analogue video was performed with a Targa 1000 image capturing board (Truevision, Santa Clara, CA).

Confocal Image Acquisition for Kinetic Analysis and Quantitation

Confocal digital images (see Figs. 1–3) were collected using a Zeiss Plan-Neofluor 25× oil immersion objective NA 0.8 with a pinhole of 150 (corresponding to a focal depth of ∼22 μm) in order to maintain the entire cell within the center of the focal depth and thus to minimize changes in fluorescence efficiency due to VSVG–GFP moving away from the plane of focus. Time-lapse images were captured at 30–120 s intervals with 30–50% maximum laser power and 99% attenuation. The combination of low energy, high attenuation, and the less concentrated excitation laser beam caused by the low NA objective resulted in negligible photobleaching during repetitive imaging for over 3 h. Thus, VSVG-GFP–expressing cells incubated for 20 h at 40°C and imaged for 3 h in the presence of brefeldin A (5 μg/ml) and cycloheximide (150 μg/ml) showed no change in total fluorescence intensity. Average intensities for total cellular fluorescence and Golgi-associated fluorescence were measured using NIH Image 1.62 software after subtraction of background outside the cell. The overlap by ER and plasma membrane in Golgi regions of interest (ROI) was accounted for by fitting the measured Golgi fluorescence intensity values against the Golgi compartment plus small contributions from ER plus plasma membrane. The magnitudes of these small contributions were estimated directly by least squares fitting of the experimental data.

Figure 1.

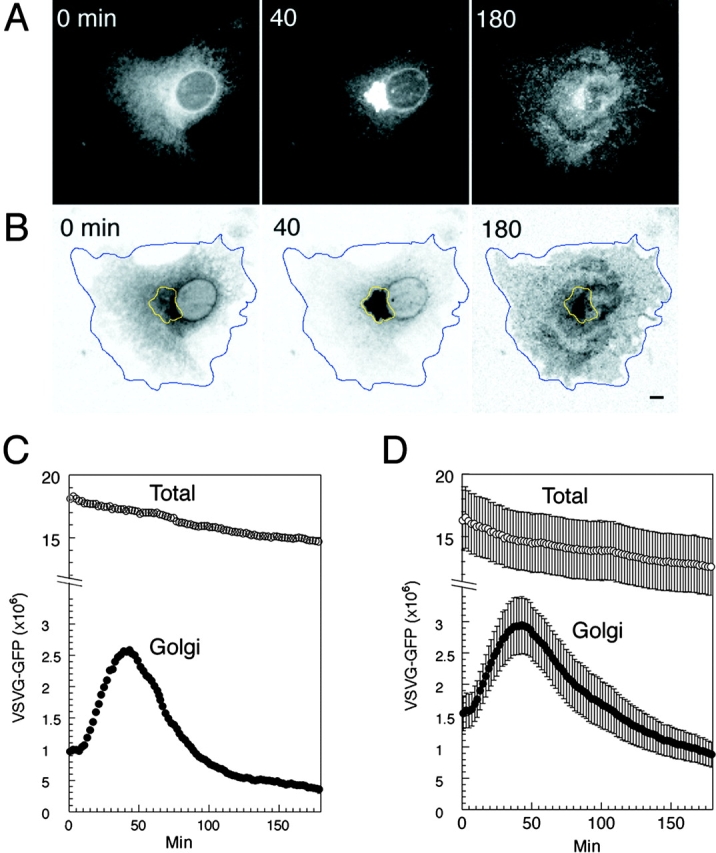
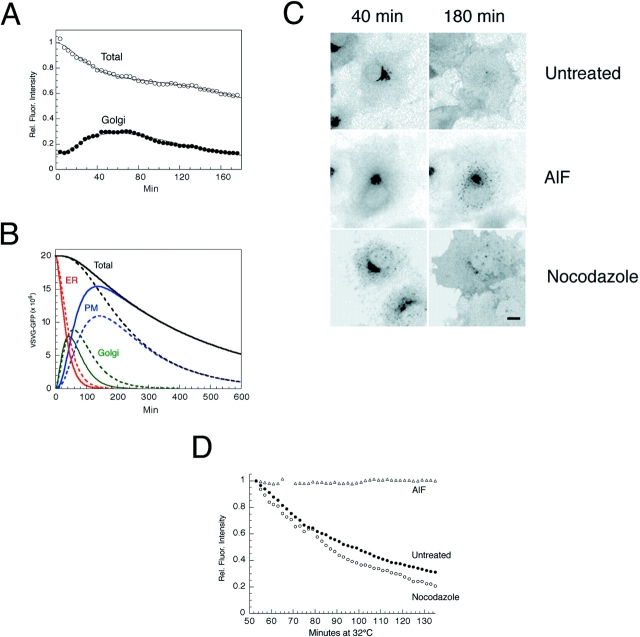
Kinetics of VSVG– GFP transport. (A) VSVG– GFP expressing cells were incubated for 20 h at 40°C, shifted to 32°C, and then imaged every 30 s for 3 h using a confocal microscope. Shown are images at 0, 40, and 180 min after temperature shift. See Quicktime movie sequence at http://dir.nichd. nih.gov/cbmb/pb7labob.html. The waves of VSVG–GFP seen propagating out from the Golgi region 60 min after temperature shift in the movie represent plasma membrane ruffling, possibly in response to the arrival at the cell surface of VSVG–GFP. (B) ROIs used for quantitative analysis of transport. Blue line, total cell fluorescence; yellow line, Golgi fluorescence. The images are inverted to better reveal the ROI. (C) Fluorescent intensities associated with the Golgi ROI (Golgi, solid circles) and entire cell ROI (Total, open circles) for one representative cell after shift to 32°C are plotted at 30 s intervals for 3 h. Fluorescence intensity is expressed as number of molecules based on a comparison of cellular VSVG–GFP fluorescence with known concentrations of GFP as described in Materials and Methods. (D) Distribution of VSVG– GFP molecules associated with the Golgi area and total cell for nine cells after shift to 32°C. Bar, 5 μm.

Figure 3.

Effect of pharmacologic reagents on VSVG– GFP trafficking kinetics. (A) VSVG-GFP–expressing cells were incubated for 20 h at 40°C and shifted to 32°C in the presence of cytochalasin-B (10 μM). Relative fluorescent intensities in the Golgi ROI (solid circles) and total cell ROI (open circles) with time are plotted. The smooth curves represent the optimized fit to the three-compartment model B. Levels of VSVG–GFP in each of the three compartments with time calculated by the model solution to the data shown in A for a cyto B–treated cell (dashed lines) and an untreated cell (solid lines). (C) Cells expressing VSVG–GFP were shifted to 32°C. AlF (AlCl₃, 60 μM and NaF, 20 mM) or nocodazole (33.3 μM) was added after 40 min at 32°C. The images were collected at this time (40 min) or 140 min later (180 min). (D) Fluorescent intensities associated with the Golgi region in the experiment described in C are plotted against time. Bar, 10 μm.

Conversion of Fluorescence Intensity to Number of GFP Molecules

The number of VSVG–GFP molecules expressed in a single cell was estimated by comparing the total cellular pixel intensity value in digitized images to a standard curve generated with solutions of known concentrations of recombinant purified GFP (Clontech) at identical power, attenuation, contrast, and brightness settings on the confocal microscope (Lippincott-Schwartz et al., 1998). The fluorescence in a 100-μm² ROI was then plotted against the number of GFP molecules estimated to be within the volumetric region of interest, determined by the product of the 100 μm² area and the full width half maximum (FWHM). The FWHM is the distance in the z direction between planes where the intensity is 50% that at the plane of focus. It can be calculated as in the equation (obtained from Zeiss confocal microscope manual),

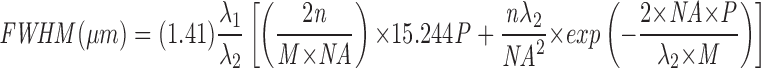where λ₁ = emission wavelength (nm); λ₂ = excitation wavelength (nm); NA = numerical aperture; M = magnification; n = refractive index of immersion medium; P = pinhole setting in digital units. During data aquisition for kinetic analysis the pinhole setting of 9.84 was used yielding a FWHM of 22 μm. Plots of GFP molecules versus total fluorescence (the sum of the pixel values in an area) were fitted precisely with a linear function in the range of GFP concentrations throughout this paper.

In generating the standard curve, it was assumed that the FWHM approximates the z-dimensional thickness of the sample which contributes to the fluorescence signal, and that the efficiency of detection of fluorescence within the volume is constant. The validity of these assumptions was confirmed by imaging spherical droplets of GFP solution in oil with diameters smaller then the FWHM but also within the range of analyzed cells and organelles. In applying the standard curve to living cells, we assumed that the fluorescence parameters (i.e., quantum yield, detection efficiency, and proportion of properly folded and fluorescent GFP molecules) were similar for GFP chimeras in cells and for GFP in aqueous solution (Piston et al., 1998).

Kinetic Modeling of the Secretory Pathway

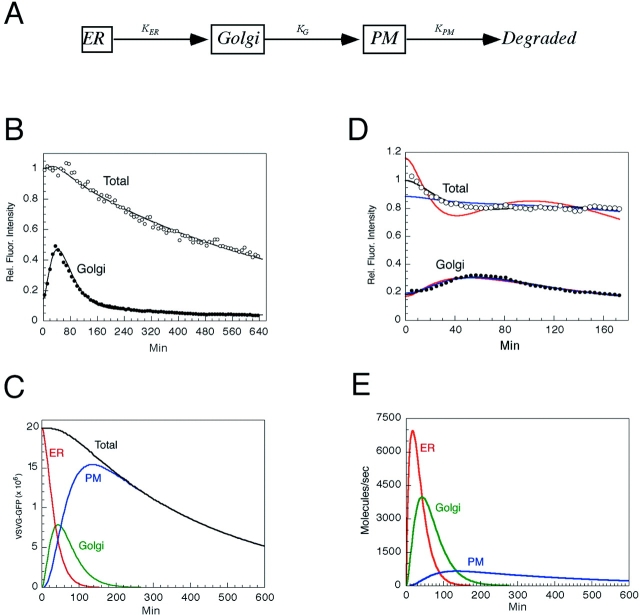
To extract information from the time-lapse digital images, standard techniques of kinetic analysis were adapted to fluorescence microscopy. The model used is shown in Fig. 2 A, and contains seven parameters whose values could be determined from the fluorescence data. There are three independent rate constants: K _ER is the effective overall rate constant for a two-compartment ER which was used to approximate the lag associated with VSVG folding, sorting, and export; K _G characterizes the rate-limiting steps between arrival in the Golgi and arrival in the PM, and K _PM represents the rate-limiting steps between arrival at the PM and lysosomal degradation. There are also three sampling efficiencies, and one initial value for VSVG–GFP in the ER at the switch to permissive temperature. Values for the physiologically important parameters are given in Results (Table I). A small portion of the ER and PM is sampled in the Golgi ROI simply because a portion of these membranes overlays the Golgi region. These contaminating fractions were found to be 16.2 ± 8.8 (SD)% for ER contamination of the Golgi fluorescence and 15.5 ± 9.8 (SD)% for PM contamination of the Golgi fluorescence. These numbers were obtained by least squares fitting and represent the fractions of the ER and the PM that fell within the Golgi ROI outlined in Fig. 1 B. The sampling efficiency for Golgi fluorescence itself was found to be 86.5 ± 24.7 (SD)% and represents the efficiency with which light was collected from the Golgi compartment. We suspect this is less than 100% due to the complex geometry of the Golgi apparatus, the possibility that there is significant Golgi thickness flanking the focal plane, or because the fluorescent molecules are more tightly packed in the Golgi resulting in quenching of the fluorescence signal. In contrast, when the entire cell is taken as the region of interest, all the ER fluorescence was collected (sampling efficiency, 100%) and the resulting sampling efficiency for the plasma membrane was found to be 100% (measured over the entire cell, not just the Golgi) in nearly all cells analyzed (overall average: 97.8 ± 6.2 [SD]%).

Figure 2.

Kinetic modeling of VSVG–GFP transport through the secretory pathway. (A) The three compartment model for trafficking of VSVG–GFP. (B) VSVG-GFP–expressing cells incubated for 20 h at 40°C were shifted to 32°C and imaged every 120 s for 10 h. The fluorescent intensities with time within the Golgi ROI (solid circles) and total cell ROI (open circles) are plotted. The smooth curves show fit by the model solution. (C) VSVG–GFP levels in each of the three model compartments over time as calculated by the fit shown in B. (D) Sensitivity of fits to changes in rate constants. Red curves, the data when K _ER is increased by a factor of 1.8 and other parameters are allowed to readjust. Blue curves, K _G increased by a factor of 1.8 and other parameters are allowed to readjust. Black lines, optimized fit to data. (E) VSVG–GFP fluxes out of each compartment as a function of time after a shift to 32°C.

Table I.

Kinetic Characterization of VSVG Trafficking

		Exit rate constants						Mean residence time
		ER		Golgi		PM min −1		ER		Golgi		PM min
Control		0.0284		0.0303		0.00255		39.4		42.0		709
(n = 32)		± 0.002		± 0.0026		± 0.00034		± 2.3		± 4.0		± 100
Cyto-B		0.0227*		0.0192* ±		0.00612**		46.1*		57.4*		179**
(n = 18)		± 0.0012		0.0015		± 0.00044		± 2.4		± 4.1		± 14

Cells expressing VSVG–GFP were incubated for ∼20 h at 40°C before shift to 32°C. Shown are effective rate constants and corresponding residence times obtained by least squares fitting of the VSVG–GFP time course data to the three compartment model. Numerical values are mean ± SE for the number of cells indicated. Asterisks, statistical significance compared to control:  

^*, P < 0.05;  

^**,  P < 0.001;  

^**,  P < 0.000001.  

These compartments and processes were translated to the corresponding system of mass-balance ordinary differential equations using the SAAM II (v 1.1) software (SAAM Institute, Seattle, WA) (Foster et al., 1994). The two data sets, total cell fluorescence and Golgi fluorescence, were fitted simultaneously using the generalized nonlinear least squares optimization procedure (Bell et al., 1996) in the SAAM II software to quantify the rate constants and sampling efficiencies for each cell. In other words, for each cell, the same rate constants and sampling efficiencies account for both data sets. This simultaneous fitting is essential; it is impossible to estimate K _ER and K _G from the time course of Golgi fluorescence alone. Mean residence times reported in Results are calculated as reciprocals of the effective exit rate constant for the cellular compartment in question. Convergence was achieved for all data sets with only an occasional (10 out of 67 cells analyzed) requirement for inclusion of a Bayesian, a priori, term based on the entire population. All the individual cells' rate constants and sampling efficiencies were readily estimated from the experimental data. Summarizing for all the cells in Table I, the mean coefficients of variation were 2.1% for K _ER, 2.5% for K _G, 5.0% for K _PM, 2.8% for the Golgi sampling efficiency, 4.3% for the contribution of ER to the Golgi ROI, and 3.5% for the contribution of the PM to the Golgi ROI. This means that all of the individual values, which contribute to the mean and standard deviations reported in Results, were determined with precision. Statistical significance of differences among the experimental groups (reported in Table I) was assessed using the standard t test for populations with unequal variance. Model hypothesis testing applying Michaelis– Menten rate laws was preformed using SAMMII (Foster et al., 1994).

Kinetic Modeling of PGCs

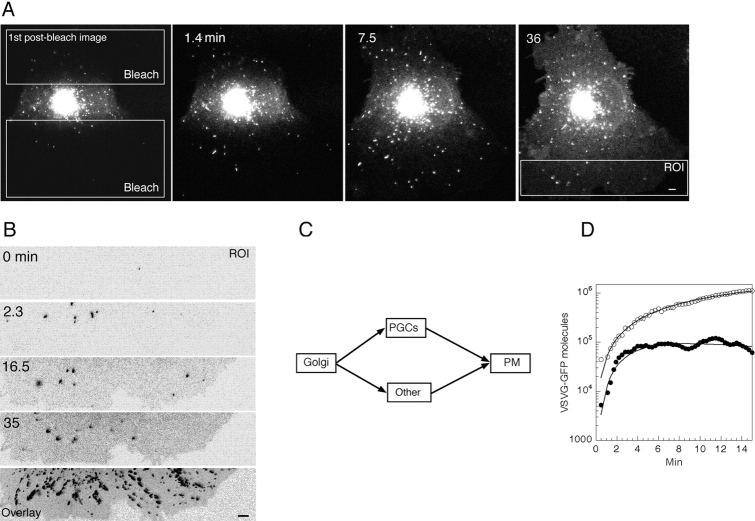
The same techniques and software were applied to the analysis of data on post-Golgi traffic via PGCs, shown in Fig. 7. In this case the model (see Fig. 7 C) contains four parameters whose values could be determined from the simultaneous fitting of PGC fluorescence and total fluorescence in the ROI. These parameters are the initial postbleach fluorescence in the Golgi compartment, the rate constant distributing VSVG–GFP to PGCs, the rate constant distributing VSVG–GFP to the other pathway, and the residence time for VSVG–GFP in PGCs. The least squares optimizer determined these parameters with coefficients of variation of 16.8, 19.6, 21.5, and 7.9%, respectively. Interestingly, the optimizer could not determine the residence time for VSVG–GFP arriving in the ROI by the other pathway, except to require that it be much (at least 17-fold) shorter than the residence time in PGCs. This suggests that the other pathway is not likely to represent post-Golgi intermediates that travel via microtubular tracks (since their residence times would be similar to PGCs), and may instead represent VSVG–GFP that has diffused into the ROI from regions of the PM outside the ROI. Derived parameters such as the fraction of post-Golgi traffic distributed to measured PGCs, the fraction distributed to the other pathway, and the residence time in the PGCs were determined with coefficients of variation of 5.2, 8.2, and 7.9%, respectively. Sampling efficiencies were taken as 100% for all structures in this ROI since they are in the most peripheral and flattened portion of the imaged cell.

Figure 7.

Quantitation of fluorescence intensity in post Golgi intermediates. (A) Upper and lower non-Golgi regions (white rectangles) of a cell expressing VSVG–GFP were repetitively photobleached using high energy illumination 40 min after a shift to 32°C. The entire cell was then imaged with low illumination levels for 36 min at 3.4 images/min. See Quicktime movie sequence at http://dir.nichd.nih.gov/cbmb/pb7labob.html. The ROI that was analyzed is shown in the far right panel. (B) The representative ROI at different times after photobleaching. Bottom panel is an overlay of all the images taken during the 36 min after photobleaching. Note the many paths followed by individual PGCs to the plasma membrane. (C) The compartmental model used to determine the fraction of VSVG–GFP conveyed to the PM in PGCs (Materials and Methods). (D) The fluorescent intensity in PGCs (defined as structures larger than 0.2 μm² or five pixels) (solid circles) and the total fluorescence (i.e., the sum of fluorescence intensity in PGCs, PM, and all other fluorescence; open circles) within the ROIs are plotted against time. The optimal model solution generated by the model in C is shown by solid lines (Materials and Methods). The rate constants obtained by least squares fitting were 1.94 ± 0.47 (SD)% per min for the Golgi-to-PGC pathway and 1.22 ± 0.32 (SD)% per min for the Golgi-to-other pathway. Given this model structure, the data also permitted resolution of the VSVG–GFP residence time in measured PGCs (3.38 ± 0.26 [SD] min), but could not resolve the VSVG–GFP residence time in carriers associated with the “other” pathway. Optimization required that the residence time in the “other” pathway was no more than 0.2 min.

Results

Quantitative Analysis of VSVG–GFP Trafficking

The kinetic properties of VSVG–GFP transport through the secretory pathway were studied using confocal time-lapse imaging techniques in single living cells. COS cells expressing VSVG–GFP at 40°C were shifted to 32°C in the presence of the protein synthesis inhibitor cycloheximide to synchronously release VSVG–GFP from the ER into the secretory pathway. Images were captured every 0.5–2 min for 3–10 h under conditions that minimized both the photobleaching of VSVG–GFP and the differences in its detection efficiency during transport (Materials and Methods).

The changes in subcellular distribution of VSVG–GFP upon shift from 40° to 32°C are shown in Fig. 1 A (obtained at 0, 40, and 180 min after shift to 32°C; see Quicktime movies for full sequence available at http://dir.nichd.nih.gov/cbmb/pb7labob.html). VSVG–GFP molecules which were localized to widely dispersed ER membranes at 40°C redistributed into the juxtanuclear Golgi complex within 40 min of shift to 32°C. By 180 min, nearly all the molecules had been exported out of the Golgi complex and delivered to the plasma membrane. Our imaging conditions had the entire cell depth residing within the center of the focal plane (Materials and Methods), so that all fluorescent VSVG–GFP molecules could be detected throughout the time course of the experiment. This population corresponded to ∼2 × 10⁷ VSVG–GFP molecules for the cell shown in Fig. 1 A, calculated by comparison of cellular VSVG–GFP fluorescence with known concentrations of GFP (Materials and Methods).

To study quantitatively the changes in distribution of VSVG–GFP during its transport to the cell surface, fluorescent intensities within ROI containing the juxtanuclear Golgi compartment and the entire cell (Fig. 1 B, areas enclosed by yellow and blue lines, respectively) were measured and plotted for each digital image acquired during the experiment. As shown for a single cell in the graph in Fig. 1 C, Golgi-associated fluorescence rose sharply within the first 5–30 min after the temperature shift. It peaked at ∼40 min with ∼2.5 × 10⁶ VSVG–GFP molecules in the Golgi complex, and then steadily declined over the next 100 min. The time course of distribution of Golgi fluorescent intensities among nine other cells expressing 1.4– 2.0 × 10⁷ molecules of VSVG–GFP (Fig. 1 D) indicated that different cells exhibit similar VSVG–GFP transport kinetics.

Loss of total cellular fluorescence in these experiments was not the result of photobleaching from repetitive scanning. The total fluorescence over time remained constant when using identical imaging conditions with fixed cells or with cells treated with brefeldin A to retain VSVG–GFP in the ER (data not shown). A potential explanation for the fluorescence loss therefore is cellular degradation of VSVG–GFP after delivery to the plasma membrane.

Modeling of VSVG–GFP Kinetics

We examined whether the kinetic data obtained above could be fit to a simple model for VSVG–GFP transport (Fig. 2 A), consisting of three compartments, ER, Golgi, and plasma membrane, arranged in series. In this model VSVG–GFP is transported out of each compartment into the succeeding one at a rate equal to a rate constant (i.e., K _ER, K _G, and K _PM) multiplied by the amount of VSVG– GFP in the originating compartment. Simple linear first order kinetics through a series of homogeneous compartments with no backflow is assumed. Total VSVG–GFP fluorescence is conserved at each transfer step, until VSVG–GFP is internalized from the plasma membrane and is degraded.

To see whether the model could account for the data, and if so, to extract rate parameters, we used generalized least squares optimization to simultaneously fit to the model Golgi and total fluorescence intensities with time for each of 32 cells (Materials and Methods). Fig. 2 B shows an optimal fit for a typical cell imaged for 10 h after a shift to permissive temperature. Solid and empty circles are the experimental data points for Golgi and total fluorescence, respectively. The two lines represent the corresponding model solution. In fitting the model to the data we assumed that all VSVG–GFP was initially in the ER at the time of temperature shift from 40° to 32°C. The Golgi fluorescent intensity values are nonzero initially because a small fraction of the ER overlaps the Golgi ROI. Similarly, at late times the Golgi fluorescent intensity values are nonzero, because a fraction of the plasma membrane falls within the Golgi ROI. This overlap was accounted for by fitting the measured Golgi fluorescent intensity values against the Golgi compartment plus small contributions from ER and plasma membrane.

The levels of VSVG–GFP in each of the three model compartments is shown in Fig. 2 C as calculated by the fit in Fig. 2 B. Note that arrival of VSVG–GFP molecules on the plasma membrane occurred before all of the VSVG– GFP had left the ER. Indeed, more than 100 min were required to completely empty the ER, whereas the Golgi complex was not completely emptied until 200 min after a shift to the permissive temperature. The final slope of the total and plasma membrane curves represents the loss of VSVG–GFP after its delivery to the plasma membrane.

On a cell by cell basis, the model fits of the data were very good. The average coefficient of variation for the effective ER rate constant, K _ER, was only 2.13% (over all cells). For the Golgi rate constant, K _G, it was 2.46%, whereas for the plasma membrane rate constant, K _PM, it was 5.01%. Coefficients of variation for the fluorescence sampling efficiencies were similarly low; all were less than 5%. This means that for each individual cell, the three rate constants and three sampling efficiencies were readily and accurately determined.

Table I summarizes the mean rate constants (± standard error) from the model solutions obtained from analysis of the 32 cells (in five separate experiments). The mean rate constant for VSVG–GFP export out of the ER (K _ER) was 2.84 ± 0.20% per minute, whereas export out of the Golgi complex (K _G) was 3.03 ± 0.26% per minute. Degradation (K _PM) of VSVG–GFP occurred at a rate of 0.25 ± 0.03% per minute from plasma membrane-derived membranes.

To illustrate the sensitivity of the fit to changes in rate constants, curves of simulated data are shown in Fig. 2 D where we increased either K _ER (red curve) or K _G (blue curve) by a factor of 1.8 and allowed the remaining parameters to readjust. The discrepancies in these fits to the experimental data are substantial. For comparison, the black lines show the optimized fit. The standard error in Table I and Fig. 1 D, therefore, reflects cell-to-cell variability, rather than the error in any one fit.

The average time spent by a single VSVG–GFP molecule in the ER, Golgi, or plasma membrane (i.e., mean residence time) as it moved through the secretory pathway was obtained by inverting the optimized rate constants cell by cell and then averaging (Table I). We found that a VSVG–GFP molecule spends on average about the same time in the Golgi complex as in the ER compartment; mean residence time was ∼40 min for each. In contrast, mean residence time in the plasma membrane and its associated membranes before degradation was ∼700 min.

The data fit also allowed us to estimate the fluxes between compartments. As shown in Fig 2 E, for a cell containing ∼2 × 10⁷ VSVG–GFP molecules, the peak ER-to-Golgi flux was 7,000 molecules/s (15–20 min after shifting to permissive temperature), whereas the peak Golgi-to-plasma membrane flux was 4,000 molecules/s at 40–45 min. The peak flux of degradation from the plasma membrane and its associated membranes was 700 molecule/s at a time of 125–150 min.

The accuracy of the linear kinetic model in fitting the data is a preliminary indication that in our experiments, no rate-limiting transport step is saturated by the expression levels of VSVG–GFP. To ask more quantitatively whether we were saturating any rate-limiting transport step with high expression levels of VSVG–GFP, we enlarged the model to include standard Michaelis–Menten kinetics (Materials and Methods). The Michaelis constants, K _m, obtained from the fits for both the ER and Golgi steps, were 10–100 times the maximum levels of VSVG–GFP expression in our cells. This meant that the processes underlying VSVG–GFP trafficking in our experiments were operating on the linear portion of their Michaelis–Menten curves. Thus, no effects of saturation occurred even though each step of the secretory pathway was confronted with a wide range of VSVG–GFP levels (i.e., from 2 × 10⁷ at the start of imaging to nearly zero by the end of the experiment). We also examined a different population of cells incubated for shorter periods of time at 40°C (4–5 compared with 20 h), resulting in lower levels of VSVG–GFP expression (i.e., 2–5 × 10⁶ VSVG–GFP molecules/cell). The linear model was again sufficient to fit the data. The rate constants increased somewhat (i.e., 1.4-fold) (see Discussion), but the quality of the fits to linear kinetics were comparable to those shown above. Thus, using the currently available data no greater complexity was required than the simple linear model of Fig. 2 A and its first order rate constants, K _ER, K _G, and K _PM to characterize VSVG–GFP trafficking in our cells.

Perturbants of VSVG–GFP Transport

The above methodology was used to analyze the effect on VSVG–GFP transport of different pharmalocogical reagents that have been reported to interfere with secretory protein trafficking. These reagents included: cytochalasin B (cyto B), which disrupts the actin cytoskeleton and thereby blocks membrane transport along actin filaments; aluminum fluoride, which causes persistent activation of heterotrimeric G proteins (Gilman, 1987), and induces binding of peripheral coat proteins to Golgi membranes (Melancon et al., 1987; Barr et al., 1991; Donaldson et al., 1991; Robinson and Kreis, 1991; Bomsel and Mostov, 1992; Ktistakis et al., 1992); and nocodazole, which interferes with microtubule polymerization, blocking microtubule-dependent translocation of membrane transport intermediates (Rogalski et al., 1984; Presley et al., 1997).

In cells treated with cyto B to depolymerize actin, changes in Golgi fluorescence intensities over time after shift to permissive temperature could be effectively fit to the model of Fig. 2 A (see Fig. 3 A). However, the fits required different values of K _ER, K _G, and K _PM compared with untreated cells; K _ER was 1.2-fold lower, K _G was 1.6-fold lower, and K _PM was 2.4-fold higher (Table I). The calculated mean residence time for VSVG–GFP was 46 min in the ER, 57 in the Golgi complex, and 179 on the plasma membrane. For comparison, the times in untreated cells were 39, 42, and 709 min, respectively (Table I).

Changes in VSVG–GFP levels in ER, Golgi, and plasma membranes as a function of time in cyto B and untreated cells calculated from the model fits are shown in Fig. 3 B (dashed curves, cyto B-treated cells; solid curves, untreated cells). Cyto B treatment only slightly slowed export of VSVG–GFP out of the ER compartment system. The effect on Golgi egress, however, was significant with VSVG–GFP requiring 300 instead of 200 min to completely empty out of the Golgi complex. VSVG–GFP also spent a much shorter time in plasma membrane-derived membranes before being degraded. This data suggests that cyto B affects the processes whereby VSVG–GFP is exported out of the Golgi complex, as well as trafficking events at the plasma membrane.

The effects of AlF and nocodazole treatment on Golgi egress of VSVG–GFP were also examined (Fig. 3 C). In these experiments, AlF and nocodazole were added 40 min after a shift to permissive temperature to allow VSVG–GFP to accumulate in the Golgi complex before addition of the drug. VSVG–GFP was not exported out of the Golgi system and remained concentrated in centralized Golgi membranes in AlF-treated cells. By contrast, nocodazole treatment had very little effect on Golgi to plasma membrane trafficking of VSVG–GFP. These results are shown quantitatively in Fig. 3 D, which plots changes in Golgi-associated fluorescence due to export to the plasma membrane in AlF- and nocodazole-treated cells, as well as in untreated cells, as a function of time after addition of the drugs.

Morphological Analysis of Post-Golgi Transport: Budding from the Golgi Complex

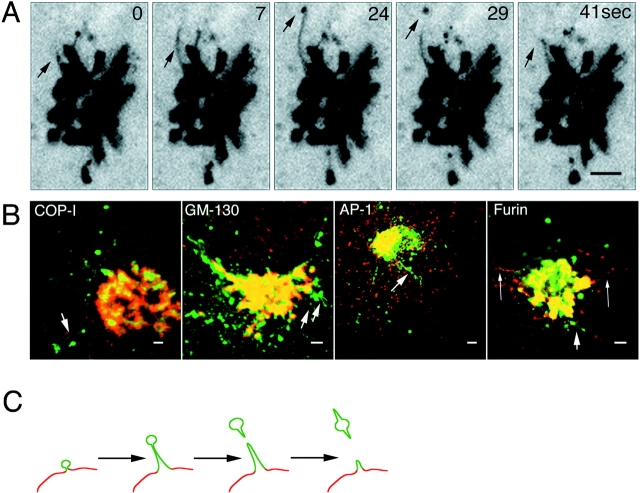
To visualize post-Golgi trafficking of VSVG–GFP, confocal images of cells were collected at short time intervals and at high magnification when VSVG–GFP flux out of the Golgi complex was greatest (i.e., after 50 min of shift from 40° to 32°C as shown in Fig. 2 E). The time-lapse sequences in Fig. 4 A show VSVG-GFP–containing membranes pulling off from the Golgi complex as tubular processes that extended several microns in length. VSVG–GFP was accumulated at the tips of these tubules, appearing as a ball-like mass. After a variable time the enlarged tip regions detached and moved outward as separate post-Golgi elements, whereas the remaining membrane stalk retracted back to the Golgi body (Fig 4 A, arrows). Tubule growth and detachment occurred repeatedly and appeared to be an important mechanism for the Golgi export of VSVG–GFP. The Golgi-derived tubules were seen in cells expressing either high or low levels of VSVG–GFP and were also observed in HeLa, NRK, CHO, primary rat glial astrocytes, and MDCK cells. In all cases, VSVG-GFP– containing tubule membranes pulled off as entire domains from the Golgi complex, detached, and then subsequently moved to the cell periphery.

Figure 4.

Budding of post-Golgi carriers from the Golgi complex. (A) Cells expressing VSVG–GFP at 40°C were shifted to 32°C. The sequence shows the Golgi region after 50 min at 32°C. The images were taken at 2.6-s intervals with a narrow pinhole. Inverted images are displayed at the indicated time intervals. Arrows, tubule budding off from the Golgi body and its tip region detaching. See Quicktime movie sequence at http://dir.nichd.nih.gov/cbmb/pb7labob.html. (B) Comparison of the distribution of VSVG–GFP with Golgi resident proteins. After 50 min at 32°C, VSVG-GFP–expressing cells were fixed (2% formaldehyde), permeabilized, and then stained with antibodies to βCOP, GM-130, or AP-1. The distribution of furin was examined in VSVG-GFP–expressing cells cotransfected with HA-tagged furin (Bosshart et al., 1994) and stained with HA antibodies. Short arrows, tubular structures containing VSVG–GFP that are connected or adjacent to the Golgi complex and are not labeled with antibodies. Long arrows, tubules containing furin but not VSVG– GFP. (C) A schematic model depicting sorting of VSVG–GFP into discrete membrane domains (green) of the TGN (red) that bud and elongate into tubules before detaching from the Golgi complex. Bars: (A) 5 μm; (B) 2.5 μm.

To further characterize the membrane tubules involved in Golgi export of VSVG–GFP, double-labeling experiments were performed with antibodies to resident proteins of the Golgi and TGN (Fig. 4 B). These included: the coat proteins β-COP (COP-I) (Pepperkok et al., 1993) and AP1 (Stamnes and Rothman, 1993), which cycle on and off Golgi membranes and potentially regulate budding and sorting events (Kreis, 1992); GM130, a Golgi matrix protein (Nakamura et al., 1995); and furin, a proteolytic enzyme that cycles between the cell surface, endosomes and TGN (Bosshart et al., 1994). Although significant overlap in the distribution of these proteins and VSVG–GFP occurred in the Golgi body (Fig. 4 B, yellow from overlap in the merged images of red antibody labeling and green VSVG–GFP), no colocalization was detected in VSVG-GFP–containing tubule elements extending out or detached from the Golgi complex (arrows). These findings suggest that VSVG–GFP is actively sorted into discrete domains of the Golgi complex during export, consistent with electron microscopic studies showing a nonuniform distribution of proteins at the TGN (Ladinsky et al., 1994; Geuze et al., 1987; Narula and Stow, 1995; Ikonen et al., 1996). Such domains elongate as tubules before detaching from the Golgi body as diagrammed schematically in Fig. 4 C and do not contain the known coat proteins AP1 or β-COP.

Size and Dynamics of Post-Golgi Carriers

After detaching from the Golgi complex, tubule elements containing VSVG–GFP typically underwent dramatic shape changes as they translocated to the cell periphery. In confocal sections captured at high speed they could be seen to bifurcate (Fig. 5 A, short arrow, a bifurcating element still attached to the Golgi, see also Quicktime movie available at http://dir.nichd.nih.gov/cbmb/pb7labob.html), and they showed elastic properties, including extension and retraction during movement (Fig. 5 A, long arrows). Tubules sometimes broke in half when one region was pulled through the cytoplasm whereas another region was held behind (Fig. 5 A, arrowheads). They also often rounded up into spherical shapes. These dynamic properties yielded a population of post-Golgi carriers (PGCs) with diverse morphologies (Fig. 5 B) that could be observed at both high and low VSVG–GFP expression levels. When tubules extended off the spherical body of a PGC, they usually pointed in the direction of movement as if they were being pulled. Under these conditions, the spherical domain (i.e., varicosity) often changed position along the PGC length (see Quicktime movie sequence at http://dir.nichd.nih.gov/cbmb/pb7labob.html for Fig. 5 C). Similar looking spherical domains have been found associated with fluorescently labeled tubular endosomes imaged in living cells (Hopkins et al., 1990), suggesting they are a common feature of tubule transport intermediates.

Figure 5.

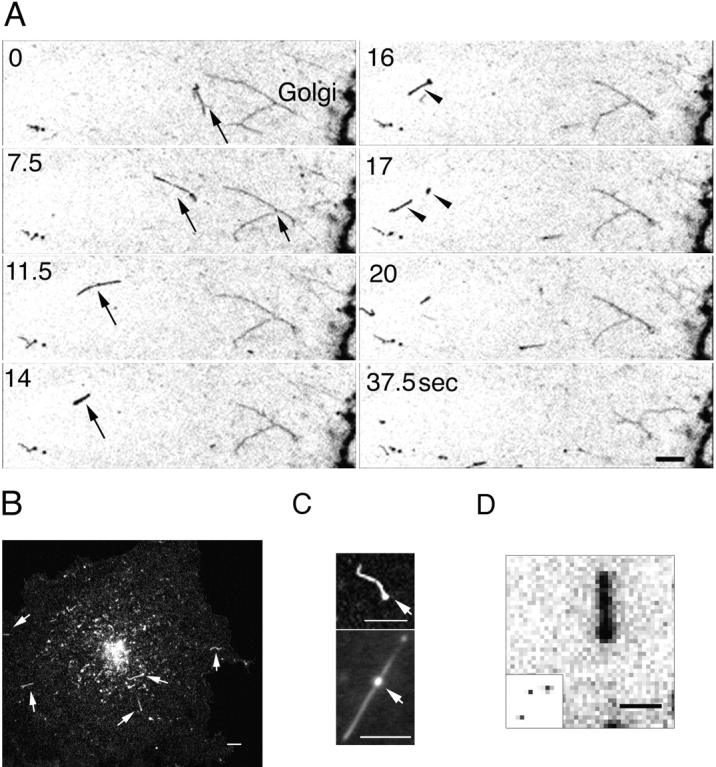
Structure and dynamics of post-Golgi carriers. (A) Inverted images of a VSVG-GFP–expressing cell 50 min after shift from 40° to 32°C. Images were captured every 2 s at high magnification using a confocal microscope. Short arrow, tubule bifurcating. Long arrows, PGC extending and retracting during translocation. Arrowheads, PGC breaking in half. See Quicktime movie sequence at http://dir.nichd. nih.gov/cbmb/pb7labob. html. (B) A digital confocal image of a cell expressing VSVG– GFP ∼70 min after a shift to 32°C. Arrows, PGCs. (C) Images of PGCs taken with a confocal (top) or SIT video (bottom) microscope. Arrows, varicosities within tubules. (D) An enlarged image of a PGC taken with a confocal microscope. Pixels are 0.2 × 0.2 μm. The insert shows 0.1-μm-diam fluorescent beads collected under identical imaging conditions to demonstrate the resolution of the confocal microscope and the size difference of PGCs versus 100-nm structures. Bars: (A and D) 2 μm; (B and C) 5 μm.

PGCs were large and carried significant amounts of VSVG–GFP cargo. An average-sized PGC occupied an area of 1.3 μm² corresponding to 32 pixels (with each pixel 0.2 × 0.2 μm), as shown in Fig. 5 D. For comparison, a 100-nm fluorescent bead shown at the same magnification and imaging conditions occupied a single bright pixel (Fig. 5 D, inset). Based on the measured conversion factor between fluorescence and number of VSVG–GFP molecules (Materials and Methods), ∼10,000 VSVG–GFP molecules were contained within an average-sized PGC at peak VSVG–GFP flux out of the Golgi in a cell expressing in the order of 2 × 10⁷ VSVG–GFP molecules. A 100-nm vesicle at an equal surface density as found in the PGCs, by comparison, would carry no more than 100 VSVG– GFP molecules.

Microtubule-dependent Translocation of PGCs

The path and velocity of PGCs were analyzed from time-lapse sequences captured with a video camera system between 60 and 90 min after temperature shift to 32°C in VSVG-GFP–expressing cells. At this time numerous, fluorescently labeled PGCs were seen moving out from the Golgi region. The movement of two such structures taken from images captured with a high speed SIT camera is plotted in Fig. 6 A, revealing their saltatory motion and velocities of up to 2.7 μm/s. PGCs usually moved along straight or curvilinear tracks toward the cell periphery, although sometimes they reversed directions (Fig. 6 C, red arrows, paths of three PGCs in an untreated cell). The rapid outward movement of PGCs is illustrated in Fig. 6 B where eight images, each 10 s apart, are overlaid. The position of one representative PGC is highlighted over time by boxes. Over 70 s, this PGC moved more than 60 μm from the central Golgi region to the tip of a plasma membrane extension (see Fig. 6 B, see also Quicktime movie at http://dir.nichd.nih.gov/cbmb/pb7labob.html).

Figure 6.

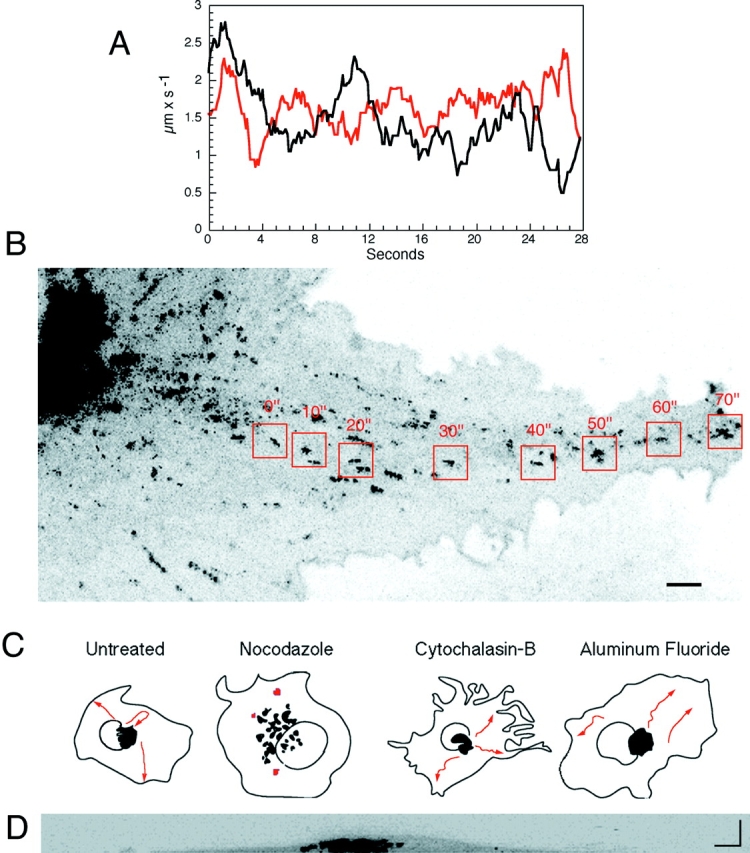
Translocation of PGCs. (A) Velocity of two PGCs (red and black). Images were collected with a SIT camera at a rate of 8 images/s and the velocity measured as the distance between the pixel coordinates in consecutive images. The graph shows a trend line of a rolling average along 2-s steps (every data point is an average of 16 samplings). (B) The route of a single PGC to the cell periphery. Confocal images of a VSVG–GFP expressing cell 60 min after temperature shift from 40° to 32°C. Eight images at 10-s intervals were overlaid. Boxed areas, movement of one PGC. See Quicktime movie sequence at http://dir.nichd. nih.gov/cbmb/pb7labob.html. (C) Camera lucid pictures showing pathway (red arrows) of VSVG-GFP–containing PGCs within an 8-min period imaged with a confocal microscope 60 min after shift to 32°C in untreated cells and cells treated with nocodazole, cyto B, or aluminum fluoride. Cells were treated with nocodazole (33.3 μM) on ice for 10 min to ensure microtubule depolymerization at 60 min after shift to 32°C and then returned to 32°C for imaging. Cyto B (10 μM) was added at the time of temperature shift from 40° to 32°C. AlF (AlCl₃ 60 μM and NaF 20 mM) was added 60 min after a shift to 32°C. (D) A 90° cross-section of a cell 40 min after shift to 32°C. Image was reconstructed from 30 sections 0.2-μm apart using a confocal microscope. Bars, 5 μm.

Microtubules were responsible for the directed transport of PGCs. This was demonstrated in experiments where VSVG-GFP–expressing cells were treated with nocodazole after PGCs had formed and moved out of the Golgi region (i.e., 60 min after a temperature shift to 32°C). Under these conditions PGCs stopped their movement and remained stationary in the cell periphery (Fig. 6 C, nocodazole-treated cell). This contrasted with the effects of cyto B– and AlF treatment. Neither drug blocked translocation of PGCs through the cytoplasm (Fig. 6 C, cyto B– and AlF-treated cells), even though both drugs affected the formation of PGCs from Golgi membranes (Fig. 3). In nocodazole-treated cells, VSVG–GFP was delivered to the plasma membrane over time despite the lack of directed movement of PGCs (Fig. 3). This may occur by random diffusion to and fusion of PGCs to nearby top or bottom cell surfaces, since COS cells viewed in reconstructed cross-section (Fig. 6 D) revealed these surfaces were less than 1 μ apart in many areas. A likely role for microtubule dependent transport of PGCs, therefore, is in delivery of PGCs to specific domains of the plasma membrane.

Quantitation of VSVG–GFP Delivery to the Cell Surface by PGCs

Although a single PGC could carry up to 10,000 VSVG– GFP molecules, we wanted to quantify the overall contribution to post-Golgi trafficking made by these large structures. In particular, we wanted to know what fraction of the total Golgi to plasma membrane transport of VSVG–GFP is by PGCs, rather than by some alternate pathway (for example, by small 100-nm-diam vesicles). We approached this question by applying kinetic analysis of the precursor–product relationship of PGC fluorescence and plasma membrane fluorescence. First we quantified the time course of accumulation of VSVG–GFP fluorescence on the plasma membrane, and then compared it with the rate of appearance of PGCs containing VSVG– GFP and their fusion with the plasma membrane. This made it possible to determine the fraction of the product (plasma membrane fluorescence) that is contributed by the measured precursor (PGC fluorescence).

Using the imaging tools described in Materials and Methods, we designed a protocol in which VSVG–GFP was first allowed to transit through the secretory pathway for 40 min, accumulating substantial fluorescence in the Golgi complex. The entire cell excluding a strip containing the Golgi region was then subjected to repetitive photobleaching to remove fluorescence in all areas outside the Golgi complex (Fig. 7 A, see Quicktime movie at http: //dir.nichd.nih.gov/cbmb/pb7labob.html). High-resolution digital images of the entire cell were then collected every 17 s for ∼30 min to characterize VSVG–GFP transport out of the Golgi complex and into the photobleached area. The aim of this procedure was to measure the time course for appearance in the photobleached region of both total VSVG–GFP and VSVG–GFP contained within PGCs. These two measurements could then be used for precursor–product analysis of VSVG–GFP delivery to the plasma membrane. For data analysis, we used an ROI made up of the most peripheral half of one of the bleached areas (Fig. 7 A, ROI). PGCs were defined operationally as fluorescent structures having a projection area larger then 0.2 μm² (corresponding to a 0.45 × 0.45-μm square box).

A kinetic model of Golgi-to-plasma membrane trafficking was constructed which included two independent pathways of delivery of VSVG–GFP into the bleached ROI (Fig. 7 C). One pathway used PGCs that translocated into the ROI and then fused with the plasma membrane. The other pathway encompassed all other routes, including small vesicles that might translocate into the ROI and fuse, as well as lateral diffusion within the plasma membrane of VSVG–GFP that was delivered to the plasma membrane outside the ROI. Because the experiment provided time-course data on the PGC fluorescence (the precursor), we could determine the minimum contribution made by PGCs to Golgi to plasma membrane trafficking by examining the fraction of total plasma membrane fluorescence that could be accounted for using the measured PGCs as precursor.

The data to be fitted included total VSVG–GFP fluorescence and VSVG–GFP fluorescence associated with PGCs in the ROI as a function of time after the photobleach (Fig. 7 D, open and solid circles, respectively). Total fluorescence continually increased over time, whereas fluorescence associated with PGCs reached a pseudo steady state due to new PGCs arriving in the ROI at approximately the same rate as others fused with the plasma membrane (Fig. 7 B, see Quicktime movie at http://dir.nichd.nih.gov/cbmb/pb7labob.html). The slight decline in PGC fluorescence seen reflected the slow rate of Golgi emptying. Fitting simultaneously total and PGC fluorescence as a function of time using least squares optimization yielded an optimal fit (Fig. 7 D, smooth lines) when 61.5% of the VSVG–GFP was transported via PGCs and 38.5% was transported via the other pathway. The coefficients of variation on these estimates were 5.2% respectively, yielding 95% confidence limits of 57.2–65.8% for the PGC contribution. Thus, the majority of VSVG–GFP trafficking to the plasma membrane occurred via PGCs. Interestingly, the fit also required very rapid transport in the other pathway (i.e., 17 times faster than the rate for PGC translocation and fusion). A possible source of this rapid transport is lateral diffusion of VSVG–GFP into the ROI from plasma membrane outside the ROI where other PGCs might have fused. The fact that VSVG–GFP is highly mobile in the plasma membrane (see Fig. 8) is consistent with this idea. Thus, our results of 61% for the PGC pathway should be viewed as a minimum estimate.

Figure 8.

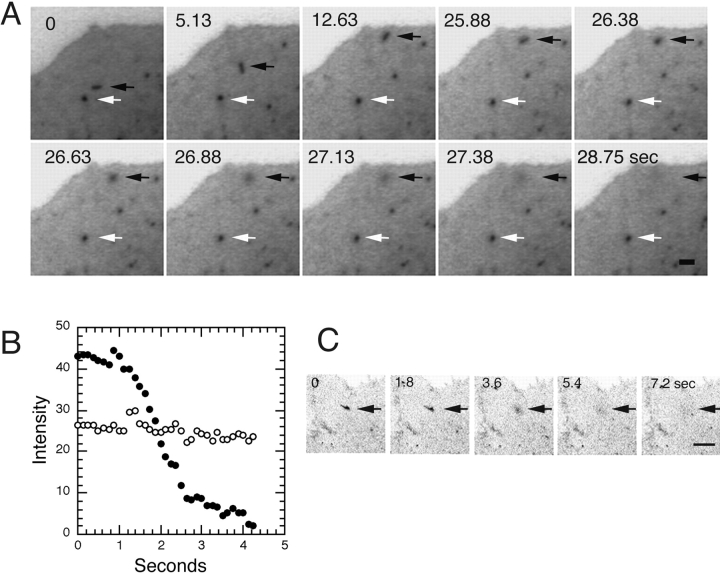
Fusion and dispersion of VSVG–GFP at the plasma membrane. (A) Inverted images of VSVG-GFP–expressing cell collected with a SIT video camera at a rate of 8 images/s ∼50 min after shift from 40° to 32°C. The sequence shows fusion of a PGC (black arrows) with the plasma membrane. A different PGC (white arrows) did not fuse or go out of the plane of focus during this time period. See Quicktime movie sequence at http://dir.nichd.nih.gov/cbmb/pb7labob.html. (B) Change in intensity of PGC during fusion with the plasma membrane reveals rapid dispersion of VSVG–GFP in the plasma membrane. Black and white circles are the intensities of the fusing and reference PGCs that are indicated by the black and white arrows in A. (C) Fusion of PGC with the plasma membrane and dispersion of its VSVG–GFP cargo observed with a confocal microscope. Bars: (A) 1 μm; (B) 5 μm.

Lifetime and Fusion of PGCs with the Plasma Membrane

The average lifetime of a PGC before fusing with the plasma membrane was calculated to be 3.8 min based on the PGC kinetic modeling data above. During this period PGCs showed no overlap with endosomal structures labeled with Texas red-conjugated transferrin, or with structures labeled with antibodies to β-COP, or with the adaptor complexes, AP1, AP2, or AP3 (data not shown). This indicated that the PGCs did not intersect with any other compartments before delivering their cargo to the cell surface.

Fusion of PGCs with the plasma membrane was studied using a SIT camera system to continuously collect images. Fig 8 A shows a video sequence taken at 8 frames/s of a single PGC (black arrows) moving toward the edge of the cell, remaining stationary for 14 s, and then rapidly dispersing its fluorescence in the plasma membrane. The fact that fluorescence could be seen spreading across the plasma membrane as it was lost from the PGC indicated VSVG–GFP was highly mobile in the plasma membrane and that fusion was occurring, rather than movement out of the focal plane. A different PGC (Fig. 8 A, white arrow) that did not fuse with the plasma membrane remained visible over this period. The rate of dispersion of VSVG– GFP fluorescence upon fusion with the plasma membrane is shown quantitatively for this experiment in Fig. 8 B. Dispersal of PGC fluorescence occurred in ∼2 s (Fig. 8 A, solid circles). For comparison, the PGC identified by the white arrow in Fig. 8 A, showed no change in fluorescent intensity (open circles). An example of an irregularly shaped PGC fusing with the plasma membrane is shown in Fig. 8 C. Note that the entire structure rapidly delivered its cargo to the plasma membrane, indicating that a single, continuous structure was involved.

Discussion

Secretory pathway dynamics has been approached historically using a variety of techniques. Indeed, Palade's classic papers (Jamieson and Palade, 1967; Palade, 1975) on the pancreatic exocrine pathway include several time courses based on the appearance of autoradiographic particles over cellular structures identified by electron microscopy. Later, radiolabeled amino acids were used as tracers for studying the synthesis, processing, and transport of secretory and integral membrane proteins (Scheele et al., 1978; Lodish et al., 1983; Fries et al., 1984). This required devising methods of cellular homogenization, marker enzymes, sucrose gradients, and polyacrylamide gels. These and other techniques have contributed and are contributing to our understanding of secretory pathway kinetics, but there have been a number of seemingly insurmountable problems. Even though the ER is denser than cis-Golgi, and cis-Golgi is denser than medial, and so on, in precursor– product order to the plasma membrane, it has remained impossible to prepare pure fractions of particular cellular organelles. Although the marker enzymes are concentrated in certain fractions, upon isolation they are distributed in a more or less Gaussian way across the spectrum of secretory pathway compartments. This has made it difficult to know with certainty where the labeled protein isolated on the gel was located in the cell. Moreover, the biochemistry of these techniques is enormously labor intensive. Consequently, it is extremely rare to find a time course of more than six data points for cell fractions in the protein trafficking literature (Fries et al., 1984; Scheele and Tartakoff, 1985; Green et al., 1987).

In this paper we apply a recently developed technique for studying secretory trafficking dynamics: fluorescence time-lapse imaging of GFP tagged proteins in living cells. The GFP chimeras are easily expressed within cells, are bright, and can be imaged repetitively without significant photobleaching using conventional fluorescence microscopy techniques (Cubitt et al., 1995; Sullivan and Shelby, 1998; Piston et al., 1998). It can also be demonstrated that the GFP tag does not alter protein transport or function (Lippincott-Schwartz et al., 1998). This makes them ideal for tracking proteins through intracellular pathways. The essentially continuous time courses yielded by fluorescence time-lapse imaging of GFP chimeras allow unprecedented detailed measurements of the kinetic characteristics of the secretory pathway. This, in turn, provides the basis for addressing for the first time in single living cells such key questions as how long a typical protein spends in a particular compartment such as the Golgi complex, where the slowest steps in the secretory pathway are, and which steps are subject to pharmacological or physiological control.

Kinetic Modeling of Secretory Protein Transport

Kinetic data for VSVG–GFP transport through the secretory pathway were obtained from time-lapse imaging experiments of individual cells under conditions where all fluorescent VSVG–GFP molecules could be detected at any time. Temporal changes in the number of VSVG–GFP molecules within ROIs encompassing the juxtanuclear Golgi region and entire cell were measured and plotted. We found that a simple model comprised of a series of linear rate laws connecting three compartments (ER, Golgi complex, and plasma membrane) was sufficient to fit the data. More complex, nonlinear rate laws (for example, Michaelis–Menten) involving a changing rate constant (or rate coefficient) as the concentration of VSVG–GFP in different compartments went from high (early in the experiment) to low (late in the experiment) were not required. Rather, at all times, VSVG–GFP moved between compartments at a rate equal to a rate constant (K _ER, K _G, and K _PM) multiplied by the amount of VSVG–GFP in the donor compartment.

The ability to fit the kinetic data to linear rate laws indicated that under our experimental conditions VSVG–GFP did not pass any saturation bounds and that regulatory mechanisms as a whole remained constant. Combining the kinetic analysis with the known relationship between fluorescence intensity and number of molecules, we obtained estimates of peak VSVG–GFP fluxes exiting from each organelle. In a cell expressing 2 × 10⁷ molecules of VSVG– GFP, peak ER exit flux was ∼7,000 molecules of VSVG– GFP/s. Peak exit from the Golgi was 4,000 molecules/s, and internalization/degradation from the plasma membrane peaked at 700 molecules/s. These transport rates are the first to be reported for a specific protein in single living cells.

It is interesting to compare the peak fluxes of VSVG– GFP in the three secretory compartments in our model for the data in Fig. 2, with those required for the cell to double in size every 20 h. Assuming two lipids per 1 nm², a protein to lipid density of 1:50 typical of the plasma membrane (Alberts et al., 1994), and a characteristic plasma membrane area of 2.5 × 10³ μm² (Griffiths et al., 1986), we infer that the cell has to synthesize a minimum of 1,400 plasma membrane proteins per second. If protein turnover is considered this number would be several times higher. Thus, our peak ER to Golgi flux of 7,000 per second or Golgi to plasma membrane flux of 4,000 per second are large, but do not dwarf the basal secretory flux.

Although we fit the time-lapse imaging data to a simple model consisting of three compartments and three rate constants, each of these rate constants summarizes numerous biochemical processes occurring in what are, in fact, heterogeneous organelles. K _ER includes processes involved in the folding and sorting of VSVG–GFP in the ER, as well as those required for delivery of VSVG–GFP to the Golgi complex. K _G represents all steps between entry into the Golgi complex and delivery to the plasma membrane, including intra-Golgi transport (e.g., carbohydrate modification and transport between cisternae), sorting/packaging steps at the TGN, and PGC trafficking. K _PM encompasses trafficking events that occur at the plasma membrane, including internalization and degradation. The fact that linear rate laws could summarize each of these sets of processes as a single rate constant suggests that, within each set, the processes can be effectively characterized by a single rate-limiting step and that neither the identity nor the quantitative features of this rate-limiting step is perturbed by VSVG–GFP trafficking.

Trafficking Models That Fail

Kinetic modeling is a tool for quantitative hypothesis testing. In the preceding section, we have described the simplest model that is consistent with all of our experimental data. Here, we briefly list several hypotheses which were tested and found wanting. The first alternative model did not include internalization and degradation of VSVG– GFP from the plasma membrane. We tested this idea by eliminating K _PM and refitting the experimental data. In all cases, but especially in the 10-h experiments, this model failed to account for the final slope of the total cell fluorescence. We also tested the possibility that the slow decline in total cell fluorescence over 10 h was due to photobleaching or degradation of VSVG–GFP from multiple cellular compartments. This hypothesis was tested quantitatively by permitting loss of fluorescence from every cellular compartment at a single rate. This model failed to account for most of the data sets. Moreover, we have the direct experimental demonstration that total cellular fluorescence does not decrease with time during imaging in either cells treated with BFA to prevent VSVG–GFP export out of the ER or in fixed cells. Models involving a slow Golgi recycling compartment instead of the degradation pathway, or models that place the rate limiting step for internalization/degradation in late endosomes (localized in the Golgi ROI) instead of at the plasma membrane, also could not account for the terminal slope of the Golgi and total cell fluorescence.

A number of other trafficking pathways were tested, and found to be unresolvable. This means they were consistent with the available data, but the data contained insufficient information to estimate the corresponding rate constants. For example, we could not resolve a post-Golgi intermediate compartment except in the experiment (Fig. 7) designed specifically for analysis of PGCs and fusion events. We also could not resolve possible retrograde trafficking of VSVG–GFP from Golgi to ER; experiments in which the ER can be resolved from the plasma membrane will likely be essential to quantify any retrograde trafficking of VSVG–GFP.

To summarize, we have formulated and tested many physiologically reasonable kinetic models of VSVG trafficking. The model presented in Fig. 2 A represents the simplest model that is quantitatively consistent with our experimental data on VSVG–GFP trafficking in COS cells. With additional imaging approaches we anticipate that it will be possible to refine this model to characterize specific pathways in more detail. For example, in Fig. 7 we show how photobleaching combined with high resolution imaging can be used to highlight transport intermediates involved in Golgi to plasma membrane trafficking. By kinetically modeling the data we were able to calculate the fraction of total Golgi to cell surface transport of VSVG– GFP that occurs by PGCs, and to estimate the lifetime of PGCs within cells.

Rate Constants for VSVG–GFP Trafficking

Rate constants represent the fundamental kinetic characteristic for any process because they describe the fraction of the material that moves by way of the process per unit of time. For ER to Golgi transport the mean rate constant for VSVG–GFP was 2.8% per min, for Golgi to the plasma membrane transport it was 3.0% per min, and for transport from the plasma membrane to a degradative site it was 0.25% per min. Rate constants measure the number of cargo molecules moved per time normalized by the number of molecules remaining to be moved. This is why changes in rate constants are informative; changes occur only when nonlinearities such as saturation and physiological regulation are reflected in the data. In Table I, for example, we report a significant decrease in the Golgi exit rate constant caused by treatment with cyto B. Within our model this change cannot have been caused by decreased delivery of VSVG–GFP from the ER, because such changes would have no effect on the Golgi exit rate constant. Instead, the decrease in K _G must be due to a regulatory change in Golgi function or export mechanisms.

The precision of our estimated rate constants for VSVG– GFP trafficking are unprecedented. The coefficients of variation ranged from 2.1 to 5.0% depending on the particular rate constant. In contrast, radiolabeled amino acid pulse–chase kinetics combined with cell fractionation and immunoprecipitation (representing the previous state-of-the-art in secretory trafficking kinetics) typically yield precision in the range of 30–50% and are thus an order of magnitude less precise (Fries et al., 1984; Scheel and Tartakoff, 1985; Green et al., 1987). This precision of our GFP imaging method arises from two principal sources. First, we are collecting hundreds of data points from the same cell, rather than six data points averaged over thousands of different cells as is typical in biochemical kinetic analyses. Second, our Golgi “fraction” (i.e., a spatial site within a single cell) is exceptionally well defined, in contrast to biochemical isolation of Golgi fractions from gradients where contamination with other organelle fractions is unavoidable.

The differences in rate constants at low and high expression levels of VSVG–GFP that we observed when cells were incubated at short or long periods at 40°C are significant. A possible explanation for this is that the different levels of expression lead to physical changes in the size or morphology of compartments resulting in different transport rates. For example, if the ratio of ER surface area to ER exit sites increases with longer incubation times at 40°C, it could take longer for VSVG–GFP to find ER exit sites upon shift to permissive temperature resulting in a lower value of K _ER. This is different from the possibility that higher expressing cells are near saturation for some transport component. If that were true then there would be some point in the high expression experiment when the abundance of VSVG–GFP in ER and Golgi membranes falls to the levels of the low expression experiments. At this point, the rate constant characterizing the transport process in higher expressing cells should change to that of the lower expressing cells. We do not observe this. Distinct rate constants, K _ER, K _G, and K _PM were identified in the high and low expressing cells and did not change as the concentration of VSVG–GFP went from high (early in the experiment) to low (late in the experiment). Because the transport processes were linear throughout the experiment, no step in VSVG–GFP transport was ever saturated in both high and low expressing cells.

On the Nature of the Rate-limiting Steps for VSVG–GFP Trafficking

The fact that linear rate laws can accurately describe the processes underlying each of our rate constants is somewhat surprising given the substantial membrane surface area that is likely to traffic with VSVG–GFP through the secretory pathway. If we assume that a transmembrane protein like VSVG–GFP is surrounded by a shell of 50 lipids (Edidin, 1997) and that two lipids occupy 1 nm², then for the cell analyzed in Fig. 2, with 2 × 10⁷ molecules of VSVG–GFP, ∼500 μm² of lipid is needed to transport VSVG–GFP to the plasma membrane, and a like amount of area is added to the plasma membrane. That this quantity of membrane is significant relative to the total surface area of the plasma membrane in these cells is suggested by our finding that between 60–100 min after shift to permissive temperature, coincident with the arrival of VSVG– GFP to the surface, the plasma membrane began to ruffle and expand in size (see Fig. 1 and Quicktime movie). The area of the ER is many times the area of the plasma membrane (DePierre et al., 1988), so overexpression of VSVG– GFP is probably not a relatively large perturbation for the ER. The surface area of the Golgi complex, on the other hand, is estimated to be less than the plasma membrane (Griffiths et al., 1986), so passage of VSVG–GFP and its accompanying lipid through the Golgi is likely to enlarge the size of this organelle.

Assuming the amount of membrane delivered to the Golgi after VSVG–GFP release is a significant fraction of that normally present, the linearity we discovered in VSVG–GFP kinetics provides an important clue as to the nature of the rate limiting step for Golgi export. If the rate-limiting step for Golgi export involved a simple binary reaction between VSVG–GFP and some Golgi constituent (e.g., a Golgi enzyme or regulatory component), we would expect K _G to vary inversely with the membrane surface area of the Golgi. This is because the effective concentration of the processing/regulatory machinery would be transiently diluted by the incoming VSVG-GFP–associated membrane. Because VSVG–GFP transport does not show such nonlinear dilution effects, the secretory pathway would appear to have evolved mechanisms that insulate protein processing/transport steps from the vagaries of excess membrane traffic.

One way to obtain a rate that would not vary when a processing enzyme or transport component is diluted is via phase separation (Siggia, 1979). This phenomenon can occur uniformly within a compartment, with the time to create a “phase-separated” domain a function of the domain size and not the size of the compartment. Phase separation is likely to be a property of the protein–lipid system together (e.g., proteins with a certain transmembrane length/ composition prefer lipids of a certain class [Mouritsen and Bloom, 1993; Bretscher and Munro, 1996]). It could occur when material is introduced into the Golgi, and ER components are recycled back; internal to the Golgi when, as a result of carbohydrate processing, certain species that were miscible no longer are; or at the TGN level where proteins are sorted for export. Recent ideas regarding microdomains and “rafts” within the Golgi complex are in accord with the idea of phase separation (Harder et al., 1997; Edidin, 1997). Because it represents a category of phenomenon which does not respond to dilution, phase separation would allow Golgi transport processes to accommodate incoming ER material efficiently, whatever the size.

Tubule-mediated Export of VSVG–GFP from the Golgi Complex

Visualization of VSVG–GFP export from the Golgi complex by high resolution imaging of the Golgi region 50 min after shift to permissive temperature revealed long tubule processes containing VSVG–GFP that pulled off and detached from the Golgi complex. Such structures were not an artifact of VSVG–GFP expression since they were observed at both high and low expression levels of VSVG– GFP in diverse cell types, and were also seen in cells expressing other GFP chimeras (including human chromogranin B and soluble VSVG, data not shown). Rather, the tubule processes appeared to serve as vehicles for protein export from the Golgi complex. Golgi tubules have previously been implicated in protein export from the Golgi complex. Time-lapse imaging studies of living cells labeled with NBD-ceramide (which preferentially inserts into TGN membranes, Lipsky and Pagano, 1985) revealed numerous tubule processes extending out from the Golgi complex (Cooper et al., 1990). Moreover, electron microscopy studies have shown that tubules at the trans- face of the Golgi are numerous and appear to “peel off” from closely stacked Golgi cisternae (Rambourg et al., 1979; Roth et al., 1985; Griffiths and Simons, 1986; Ladinsky et al., 1994). Indeed, Ladinsky et al. (1994) found that most vesicular profiles adjacent to the TGN seen in single thin sections were, in fact, tubules connected to the TGN when reconstructed three dimensionally. These observations, combined with the time lapse-imaging data of VSVG– GFP reported here, suggest that Golgi tubule growth and detachment are fundamental mechanisms for membrane protein export out of the Golgi complex.

Given a role of tubules in Golgi export, what can be said about their formation and detachment from Golgi membranes? Our finding that nocodazole does not significantly affect export of VSVG–GFP from the Golgi complex implies that the tubules involved in Golgi export do not require microtubules to form or detach from the Golgi complex. Rather, microtubules seem to play a role only in the peripheral extension and translocation of these structures. The delay of VSVG–GFP egress from the Golgi in cyto B–treated cells, by contrast, implies actin-based cytoskeletal elements facilitate protein export from the Golgi complex (Fath and Burgess, 1993; Musch et al., 1997). Interestingly, Golgi-derived tubules formed in cyto B–treated cells, but they were significantly longer than in untreated cells (data not shown), suggesting actin-based cytoskeletal components could be involved in the detachment of these transport intermediates (Musch et al., 1997). The finding that AlF abolished all export of VSVG–GFP from the Golgi complex suggests that AlF-sensitive components underlie Golgi protein export, and is consistent with work of Melancon et al. (1987) and Yoshimori et al. (1996). Whether AlF blocks protein export from the Golgi by preventing sorting of VSVG–GFP to Golgi exit sites (for example, by vesiculation of Golgi membranes induced by massive binding of peripheral coat proteins) or by some other mechanism remains to be determined.

The fact that the Golgi coat proteins β-COP and AP1 did not localize to VSVG-GFP–containing tubules suggests that these proteins are not directly involved in the formation of the tubules. Whether or not other coat proteins will be identified which localize to the tubules and regulate their function needs to be addressed in future work. However, alternative mechanisms for the budding of these structures to those based simply on coat recruitment and envelopment should be considered. Recent ideas regarding lipid based sorting at the TGN provide one possible model for how VSVG–GFP might sort into the tubule processes (Harder and Simons, 1997).

An important question is whether sorting of VSVG– GFP occurs before or during the formation of tubules and what relationship exists between protein sorting and tubulation at the TGN (Geuze and Morre, 1991; Griffiths and Simons, 1992; Ladinsky et al., 1994). The presence of dynamin (a GTPase) on Golgi membranes raises the possibility that this protein might have some role in the formation and/or detachment of the Golgi tubules (Jones et al., 1998). In vitro studies have demonstrated that dynamin can convert liposomes into tubules which are severed upon addition of GTP (Sweitzer and Hinshaw, 1998; Takei et al., 1998). Because tubule formation and detachment from Golgi membranes are dynamic processes that occur on a rapid time scale, time-lapse imaging studies of different cargo and peripherally attached proteins associated with Golgi tubules which are imaged simultaneously in cells using GFP chimeras that excite/emit at different wavelengths of light (Heim and Tsien, 1996; Rizzuto et al., 1996; Ellenberg et al., 1998; Zimmermann et al., 1998) should be important tools for addressing these questions.

Characterization of PGCs

After detaching from the Golgi complex, tubule elements containing VSVG–GFP typically moved out to the cell periphery and underwent dramatic shape changes (extending out as tubules and then retracting into spherical bodies) during transport. Movement of these PGCs was saltatory and occurred at a maximal speed of 2.7 μm/s. The fact that nocodazole, but not cyto B, blocked movement of the PGCs indicated that these structures moved along microtubule tracks rather than an actin-based cytoskeletal system. These observations are similar to those obtained from other studies that have examined exocytic transport of secretory cargo (Wacker et al., 1997; Nakata et al., 1998; Toomre et al., 1998). In those studies as well as our own, the net movement of post-Golgi structures was outward from the Golgi region to the cell periphery. This suggested that the plus end–directed microtubule motor protein, kinesin, was involved. This movement contrasted with the uniform minus end–directed motion observed for pre-Golgi structures carrying VSVG–GFP (Presley et al., 1997; Scales et al., 1997) which has been proposed to be mediated by cytoplasmic dynein (Presley et al., 1997; Burkhardt, 1998). Insight into the identity of these plus end– and minus end–directed motor proteins (and their associated components) and understanding how they coordinate membrane traffic into and out of the Golgi complex is an important challenge for future work.

Although movement of PGCs was inhibited by microtubule depolymerization, we found that VSVG–GFP was still delivered to the plasma membrane under these conditions. One explanation for this finding is that the cell type used in these experiments (i.e., COS) are very flat, with a distance of only 1–2 μm between the Golgi complex and/ or PGCs to the overlying plasma membrane. Delivery of VSVG–GFP to the plasma membrane after microtubule disruption therefore is likely to occur by random diffusion of PGCs and their fusion with nearby plasma membrane sites.

Our quantitative imaging techniques demonstrated that PGCs enriched in VSVG–GFP were large (occupying an average area of 1.3 μm²) and that they carried a significant amount of VSVG–GFP cargo. During peak flux of VSVG– GFP out of the Golgi complex, for example, individual PGCs carried an average of 10,000 VSVG–GFP molecules. Similarly large exocytic structures have been observed by Nakata et al. (1998) in their imaging studies using GFP-tagged secretory proteins.

We found that PGCs were the major vehicle for delivery of VSVG–GFP to the cell surface. In experiments where the time course for appearance of VSVG–GFP into a photobleached region outside the Golgi complex was measured, more than 60% of the cell fluorescence which reappeared did so via PGCs. Rather than diffusion of small vesicles into the photobleached box, much of the remaining percentage of fluorescence which recovered was likely to have derived from PGCs fusing with the plasma membrane in areas outside the photobleached box, allowing VSVG–GFP to move by lateral diffusion along the cell surface into the photobleached box. Consistent with this possibility, recovery of the remaining pool of VSVG–GFP into the photobleached area was more than 15 times faster than the movement of PGCs (and presumably vesicles) within the cytoplasm. From these experiments we were also able to determine that PGCs have an average lifetime of ∼3.8 min in COS cells. Moreover, we could demonstrate that PGCs carrying VSVG–GFP fuse directly with the plasma membrane without intersecting other membrane pathways in the cell.

The ability to visualize and kinetically model protein trafficking in single cells using GFP technology provides a powerful new approach for addressing numerous questions relevant to the regulation and functioning of the secretory pathway. Do different cargo molecules traverse the Golgi complex at similar rates, as predicted by cisternal progression models? Are there lags for transport between presumed Golgi subcompartments? What trafficking steps are affected by perturbation in trafficking machinery and are they subject to pharmacological control? The dual advantages of quantitation and in vivo experimentation using GFP constructs should permit analysis of these central questions about membrane function and trafficking. For example, photobleaching of GFP chimeras can be combined with kinetic analysis to define a new subpopulation of membranes or highlight an intermediate. The use of two-color GFP variants in double labeling studies, now technically feasible (Rizzuto et al., 1996; Ellenberg et al., 1998; Zimmermann et al., 1998), adds more capabilities. Such approaches are expanding our understanding of secretory pathway dynamics, and promise to shed new light on how molecular machinery functions on a system-wide basis within secretory membranes of living cells.

Abbreviations used in this paper

cyto B

cytochaslin B

FWHM

full width half maximum

GFP

green fluorescent protein

PGC

post-Golgi carrier

ROI

regions(s) of interest

SIT

silicon-intensified target

VSVG– GFP

vesicular stomatitis virus G protein fused to GFP