The Shake-and-Bake structure determination of triclinic lysozyme

Abstract

The crystal structure of triclinic lysozyme, comprised of 1,001 non-H protein atoms and ≈200 bound water molecules, has been determined ab initio (using native data alone) by the “Shake-and-Bake” method by using the computer program SnB. This is the largest structure determined so far by the SnB program. Initial experiments, using default SnB parameters derived from studies of smaller molecules, were unsuccessful. In fact, such experiments produced electron density maps dominated by a single large peak. This problem was overcome by considering the choice of protocol used during the parameter-shift phase refinement. When each phase was subjected to a single shift of ±157.5° during each SnB cycle, an unusually high percentage of random trials (≈22%) yielded correct solutions within 750 cycles. This success rate is higher than that typically observed, even for much smaller structures.

Traditional direct-methods procedures used to determine three-dimensional structures from single-crystal x-ray diffraction data are not suitable for large molecules. These conventional methods depend on accurate estimates of the structure-invariant phase relationships, but estimated invariant values become less reliable with increasing structural complexity (1). Furthermore, existing direct methods require the measurement of atomic resolution data. As a result, protein crystallographers must rely on heavy atom methods, multiple wavelength anomalous diffraction (MAD) phasing, or prior chemical knowledge in conjunction with molecular replacement to determine their structures. Consequently, it often takes several weeks or even months of work to determine a new protein structure. With the use of better sample preparation techniques (affecting both purification and crystallization) and the development of improved data collection facilities at synchrotron radiation sources, a growing number of protein crystals diffract to atomic or near-atomic resolution. These advances, coupled with recently developed direct-methods programs, show promise of offering a fast and automatic route to structure determination for many proteins.

“Shake-and-Bake” is an ab initio multitrial method for crystal structure determination aimed specifically at larger molecules (2–4). This algorithm was first implemented in the computer program SnB (5) and also has been incorporated into the computer program shelxd (6, 7). Shake-and-Bake is an iterative two-step procedure; a reciprocal space phase refinement process automatically and unconditionally is followed by the imposition of real space constraints through peak picking, including a 1.0-Å minimum inter-peak distance criterion. In contrast, conventional direct methods routinely depend on phase refinement alone and, when real space filtering is used at all, it is applied manually during the final few cycles (8). In addition, conventional methods of phase refinement rely primarily on the tangent formula (9), whereas the Shake-and-Bake algorithm permits alternative optimization strategies. In the SnB program, phases typically are refined by using a parameter-shift technique (10) to reduce the value of the minimal function (11–13), which is a measure of the mean-square difference between the values of the structure invariants calculated by using a set of trial phases and their expected values as predicted by their conditional probability distribution.

During the parameter-shift (phase-refinement) procedure that is invoked in every SnB cycle, each phase is shifted, in turn, a maximum number of times (N_shift) by angles of ±δ. The minimal function is evaluated for each such set of phases to select the best value for the current phase under consideration. For practical reasons, the unconstrained minimal function is used for this purpose, although it is actually the constrained minimum calculated after peak picking that yields the correct set of phases (14). The complete phase list is passed through N_iteration times each time the parameter-shift procedure is called. For simplicity, this parameter-shift protocol can be abbreviated by the notation PS (δ, N_shift, N_iteration). A PS (90°, 2, 3) protocol has been shown to perform well in most space groups, but structures in space group P1 have been found to respond best to less phase refinement (15). Thus, in space group P1, PS (90°, 2, 1) is the default PS strategy.

The SnB computer program has been applied successfully to numerous molecules with 200–500 independent non-H atoms (16–19). These structures would have been intractable to conventional direct methods. The largest structure previously solved by SnB was the protein toxin II (Tox II) from the scorpion Androctonus australis (20). This toxin consists of ≈650 non-H protein atoms and bound water molecules in the asymmetric unit. Approximately 1,600 random sets of trial phases were required before the first solution was found, although later the success rate was improved dramatically to ≈1.5% after extensive studies were performed on a variety of structures, resulting in an adjustment in the number of peaks selected during each SnB cycle (21).

The program shelxd implements a version of Shake-and-Bake in which only tangent-formula phase refinement is used, but the real-space filtering process is enhanced by peaklist optimization (22) to improve the set of selected peaks. Successful applications of shelxd (G. M. Sheldrick, personal communication) include the 55-residue protein hirustasin (≈600 total non-H atoms), a mutant of high potential iron protein from Chromatium vinosum (≈1,500 atoms), and octaheme cytochrome C₃ (≈2,000 protein atoms). It should be noted that both the high potential iron protein and cytochrome C₃ structures contain eight iron atoms that might be expected to make them more readily solvable than all-light atom structures of the same size.

The structure of triclinic hen egg white lysozyme (1,001 non-H protein atoms) was first solved and refined by conventional protein methods to 1.5-Å resolution (23), and the refined coordinates are available from the Brookhaven Protein Data Bank (1LZT). In this paper, the successful application of the SnB program to triclinic lysozyme is reported.¶ The focus of this paper is on the choice of parameters used in the phase refinement, which proved to be critical in improving the percentage of random trial structures that result in solutions.

METHODS

Crystals of triclinic hen egg white lysozyme were grown from 1% aqueous lysozyme solution containing 2% NaNO₃ and sodium acetate buffer at pH 4.5 (24). X-ray diffraction data were collected on station A1 at Cornell High Energy Synchrotron Source, using an ADSC Quantum 1 CCD detector. A single crystal (0.2 × 0.2 × 0.1 mm) was transferred from a hanging drop to a solution of mother liquor and 20% glycerol; after a few seconds, the crystal was mounted on the goniometer in a glass fiber loop positioned in a cold gas stream at 100K. Several passes of data collection were required to sample completely the full dynamic range of the diffraction (Table 1). A combination of eventual radiation damage and the 80-mm detector aperture, placed as close as possible (37.5 mm) to the crystal, limited the completeness in the highest resolution bins. The data were reduced by using the hkl program suite (25). As shown in Table 2, the crystal diffracted to 0.85 Å. The data set is 86.4% complete to 0.98 Å, with a completeness of 63.5% in the 1.01–0.98 Å resolution shell. The cell parameters were refined in scalepack to be a = 27.03 Å, b = 31.26 Å, c = 34.03 Å, α = 89.1°, β = 72.4°, γ = 67.9°. Normalized structure factors (E-values) for input into the SnB program (5) were calculated using the programs levy and eval (26).

Table 1.

Data collection from a single crystal of triclinic lysozyme

Images, n	Oscillation range, °	Exposure time, s	Detector distance, mm
600	0.3	4	37.5
80	2.0	4	37.5
60	2.0	2	57.8
60	3.0	3*	57.8

^*The beam was attenuated to prevent overloads at low resolution. 

Table 2.

Data processing statistics for the complete triclinic lysozyme data set

Resolution range	Unique reflections	Completeness	I/Sigma(I)	Rsym
100.00–2.31	4241	98.0	31.6	0.020
2.31–1.83	4208	97.5	38.0	0.032
1.83–1.60	4171	96.3	31.6	0.047
1.60–1.45	4099	94.4	23.5	0.046
1.45–1.35	4001	93.1	21.8	0.048
1.35–1.27	3998	91.8	18.7	0.052
1.27–1.21	3899	90.3	17.8	0.054
1.21–1.15	3834	87.9	16.4	0.058
1.15–1.11	3681	85.5	12.9	0.064
1.11–1.07	3437	80.0	11.9	0.073
1.07–1.04	3238	74.8	10.9	0.084
1.04–1.01	2996	69.5	10.3	0.091
1.01–0.98	2773	63.5	9.0	0.094
0.98–0.96	2507	58.1	8.7	0.00*
0.96–0.94	2305	53.9	8.3	0.00*
0.94–0.92	2206	50.6	7.3	0.00*
0.92–0.90	1992	46.4	7.0	0.00*
0.90–0.88	1793	41.0	6.0	0.00*
0.88–0.86	1046	24.2	5.8	0.00*
0.86–0.85	328	7.6	5.1	0.00*
All hkl	60753	70.2	28.6	0.030

^*There was no redundancy of observation in these resolution shells. 

RESULTS

In this section, the experiments used to determine the triclinic lysozyme structure with SnB are described in detail.

Initial Experiments.

Approximately 2,000 sets of random trial phases were investigated using a combination of SnB v1.1.0 running on the IBM SP2 supercomputer at the Cornell Theory Centre and SnB v1.5.0 running on a network of 10 ≈233-MHz Digital Alphastations. Default SnB parameters were used for these trials. First, the 11,000 reflections with the largest E values were used to generate 110,000 triplet structure invariants. Each set of trial phases was then refined for 600 cycles by using a PS (90°, 2, 1) protocol. As suggested by the improved success rate for toxin II, only 400 peaks were selected each cycle from the resulting electron density map (E-map), which was computed by using a Fourier grid of 0.33 Å. The top 10 of these peaks were weighted as sulfurs during the structure–factor calculation in the following cycle, and all other peaks were weighted as nitrogen atoms.

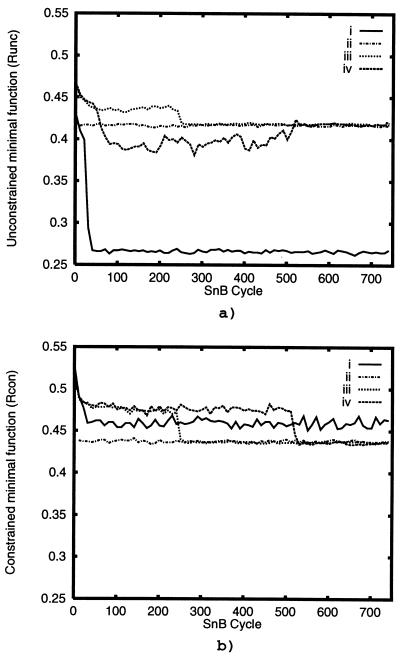
Using the default set of parameters supplied by SnB, no solutions were found. The resulting structures were characterized by a clustering of the top peaks in the resulting E-maps. In fact, these maps were dominated by a single large peak and some surrounding ripples. E-maps of this type will be referred to in this paper as “uranium” maps. Improved diagnostics provided in a prerelease version of SnB v2.0 revealed an unexpected behavior of the unconstrained minimal function R_unc (i.e., the minimal function value computed immediately after phase refinement but before the imposition of real space constraints). The value of R_unc decreased rapidly and irrevocably to a very low value during the first few SnB cycles. This behavior occurred for each of the 2,000 trials, but the fall in R_unc values was accompanied by only a slight decrease in the constrained minimal function R_con computed after peak picking (Fig. 1 a and b, curve I).

Figure 1.

Plots of the unconstrained (R_unc) (a) and the constrained (R_con) (b) minimal function vs. SnB cycle. i, trials with default parameters that resulted in a uranium map; ii, a stability test with the known atomic positions as the starting peaks; iii, a correct solution where R_unc and R_con exhibit similar behavior; and iv, a correct solution where R_unc and R_con exhibit different behavior.

A stability test, which consists of performing the Shake-and-Bake procedure for a trial structure generated by using the known atomic positions, often helps to explain unexpected results. In this case, the stability test gave a higher R_unc and a lower R_con (Fig. 1 a and b, curve ii), compared with the random trials. Changes then were made to SnB v2.0 so that trials could be screened rapidly on the basis of their R_unc values. In this way, trials that were expected to produce a uranium map were detected and aborted as soon as R_unc fell below 0.3. This generally occurred within the first 50 SnB cycles. In this way, another 10,000 trials were tested, and once again no solutions were found. Several SnB input parameters, including the numbers of phases, invariants, and peaks selected, were varied. Changing these parameters had little impact on the progress of R_unc during Shake-and-Bake refinement. Reducing the size of the Fourier grid to 0.28 Å seemed to slow down the progress of R_unc toward its minimum; however none of the 50 trials tested managed to complete a trial without R_unc falling to a low minimum value.

Parameter Optimization.

A search of the Brookhaven Protein Data Bank (27) for other P1 structures yielded a small proteinase inhibitor (PDB code 3OVO; ref. 28) containing 450 non-H atoms including six sulfurs. Calculated (error-free) data from 10.0 Å to 1.0Å were generated for this structure by using the program sfall (29), and E values were computed using the programs levy and eval. Of the 25 random sets of trial phases processed with default SnB parameters, 10 yielded correct solutions, and the remaining 15 trials resulted in uranium maps similar to those of the triclinic lysozyme trials described above.

An attempt then was made to improve the success rate (i.e., percentage of trials going to solution) for this proteinase inhibitor. Its smaller size meant that trials could be screened relatively quickly and, because the default parameters already gave a relatively high success rate, only a few trials were needed to suggest changes in the protocol. It was found that, by using a single 90° shift, it was possible to avoid uranium maps altogether and achieve the desired improvement. Furthermore, changing the phase-shift angle resulted in an additional dramatic increase in success rate. Phase shifts of 67.5° and 135° were tested and, in both cases, all 25 random trials converged to the correct solution within 200 SnB cycles.

Triclinic Lysozyme Structure Solution.

The effect of varying the parameter-shift strategy then was explored for triclinic lysozyme. At first, calculated (error-free) data from 10.0 to 0.9 Å were used to increase the chance of success. Based on a small sample size of 50 trials, shift angles of 90° always resulted in uranium maps, even when the number of shifts per cycle was reduced from two to one as suggested by the study of the proteinase inhibitor. Similarly, when a shift angle of 67.5° was used, uranium maps still seemed to dominate. However, using a shift of 135° yielded a few true solutions. The success rate continued to improve as the phase-shift angle was increased, and a shift of 157.5° was found to give the optimal success rate for all the shift angles tested. Finally, the number of peaks picked during each SnB cycle was reduced to 350. At this point, a SnB run resulted in 11 of 13 random trials converging to the correct solution.

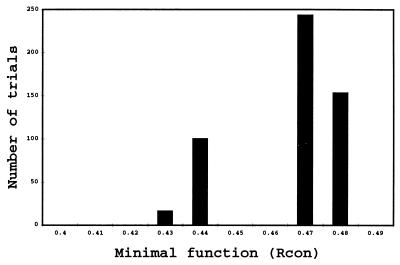
When the same set of parameters was applied to the experimental data, the bimodal nature of the minimal function distribution (Fig. 2) suggested that solutions had been identified. Plots of the minimal function value vs. SnB cycle number for representative trials in the bin with r = 0.44 also showed a characteristic sudden drop indicative of a solution (Fig. 1 a and b, curve iii). The SnB phases then were compared with the known phases to provide unequivocal identification of solutions. In all cases, the minimal function correctly identified the actual solutions. The use of a single 157.5° phase shift clearly allows SnB to escape from local unconstrained minima (Fig. 1a, curve iv).

Figure 2.

A histogram of final constrained minimal function values based on 512 random trials, resulting in a bimodal distribution with 116 correct solutions.

A complete study of the effects of varying the shift angle then was undertaken, and the results are presented in Table 3. In this experiment, a reduced Fourier grid size of 0.28 Å was used, and a total of 750 refinement cycles was performed. It should be noted that, under these conditions, a single solution (1 of 548 trials) finally was obtained using the default two-shift conditions PS (90°, 2, 1), but no solutions were obtained for 565 trials refined using the tangent formula. The range of single parameter-shift angles producing solutions is remarkably narrow, and the success rate varies abruptly over this range. The first solutions occur after ≈150 refinement cycles. The efficiency of the refinement process continues to increase steadily until ≈500 cycles and then decreases slowly. Using the 157.5° shift and 500 cycles of phase refinement, an average of ≈8 h of computation was required to find a solution using a single SGI R10000 workstation. Using a 0.33-Å resolution grid significantly reduces the maximum success rate from 21.9 to 11.7% (60 of 512 trials), although the overall efficiency of the calculation remains approximately constant because of the reduced running time with a coarser grid.

Table 3.

Success rates for single-step parameter-shift phase refinement

Shift size, °	Trials, n	Solutions, n	Success rate, %
22.5	514	0	0.0
45.0	607	3	0.5
67.5	620	0	0.0
90.0	967	0	0.0
112.5	611	0	0.0
135.0	1176	0	0.0
146.0	685	15	2.2
151.9	256	11	4.3
154.7	690	85	12.3
156.1	256	50	19.5
156.8	192	40	20.8
157.5	1263	277	21.9
158.2	256	54	21.1
158.9	256	49	19.1
160.3	256	45	17.6
163.1	256	47	18.4
169.0	577	44	7.6
180.0	645	9	1.4

Other important parameters for these 750-cycle SnB trials were: 11,100 reflections (phases), 111,000 invariants, 350 peaks used in each structure–factor calculation, and a Fourier grid size of 0.28 Å. 

Assessment of Lysozyme Maps.

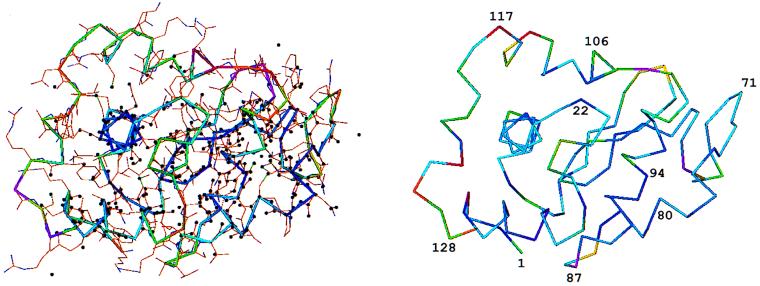
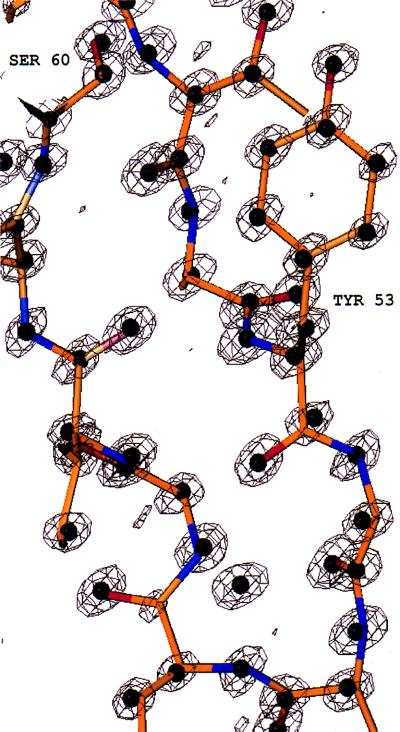
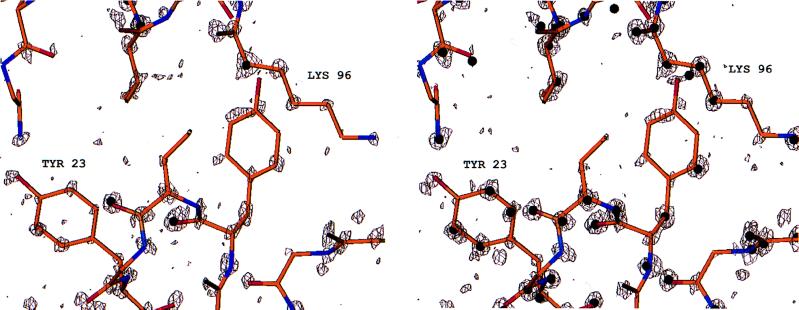
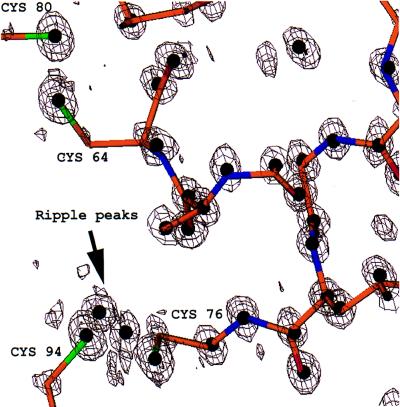
The 350 peaks chosen by SnB as part of a solution matched many of the most ordered atoms found in the superimposed PDB model (Fig. 3). In one typical example, 338 peaks showed an overall rms deviation of 0.19 Å from atoms in the known lysozyme model, and 9 of the top 10 peaks corresponded to sulfur atoms. There was a close correlation between the temperature factor of the atoms in the PDB model and the real-space fit of this model to the electron density maps calculated with phases produced by SnB (Fig. 3). The mean temperature factors and rms deviations for different atom types are shown in Table 4. The electron density was very well defined and complete in regions of the structure where a high proportion of SnB peaks were found (Fig. 4). In the poorer regions of the structure, where the initial SnB solution returned few peaks, there were still strong peaks in the E-maps corresponding to atoms in the known model, even for the side chains of some lysine and tyrosine residues (Fig. 5 Left). When the best 700 peaks from the same trial were examined, 657 of them were found to match atoms in the PDB model with an overall rms deviation of 0.20 Å (Fig. 5 Right). The mean temperature factors and rms deviations for this expanded peak set also are shown in Table 4. Altogether, 77% of the main chain atoms were accounted for in this expanded peak set, and many of the peaks corresponding to less ordered side-chain atoms were now present. It is interesting to note that the top two peaks, corresponding to a disulfide bridge, were surrounded by several ripple peaks (Fig. 6). This does not appear to be the result of disorder. A trace of the locations of the top peaks during successive SnB cycles shows that there was a build-up of peaks in this region before a true solution finally was reached.

Figure 3.

(Left) Peaks obtained from SnB (black) superimposed onto the triclinic lysozyme model from the PDB. The Cα trace is color-coded according to the temperature factor of the main chain of the model, from 3.5 (blue) to 15.0 (red). (Right) Cα traces for the triclinic lysozyme model color-coded according to the real space fit using program O (0.9 blue, 0.15 red) for main chain atoms with the electron density (E-maps) from SnB. Some residue numbers are marked.

Table 4.

Information on atoms found in an initial SnB solution of 350 peaks and also an expansion of this solution where 700 peaks were picked

		Carbon		Nitrogen		Oxygen		H2O	Sulphur
		Main Chain	Side Chain	Main Chain	Side Chain	Main Chain	Side Chain		Side Chain
350-atom solution	Number in solution	104	61	68	5	70	14	6	10
	Temperature factor	5.2	8.3  (6.2)*	5.4	8.3	6.1	6.7	9.9	6.2
	rms deviation, Å	0.18	0.23	0.16	0.26	0.17	0.16	0.18	0.08
700-atom expansion	Number of solution	190	183	106	15	102	29	22	10
	Temperature factor	6.1	7.5  (6.6)*	6.1	12.7  (8.9)*	7.0	9.1	11.7	6.2
	rms deviation, Å	0.18	0.21	0.19	0.29	0.16	0.23	0.29	0.09

The temperature factors are for the corresponding atom in the PDB model, and the rms deviations are between the SnB peaks and these atoms. 

^*The numbers in parentheses correspond to mean temperature factors when the side chain atoms for TRP62 are omitted. This residue is highly disordered in the PDB model but appears to be well ordered in this structure. 

Figure 4.

Electron density E-map calculated with E-values and phases obtained from SnB (contoured at 3σ) for an ordered part of the structure where SnB finds many peaks. Both the SnB peaks (in black) and the PDB model are superimposed.

Figure 5.

Electron density E-maps calculated with E-values and phases obtained from SnB for (Left) a less ordered part of the structure (contoured at 2.25σ) where SnB picks few of the 350 peaks found during a solution and (Right) the same region when SnB has been used to extend the solution in (Left) by picking 700 peaks (contoured at 2.5σ). The SnB peaks are superimposed in black, and the PDB model is also superimposed.

Figure 6.

Electron density E-maps calculated with E-values and phases obtained from snb (contoured at 3σ) for the region around two of the disulfide bridges. The snb peak positions are indicated by the black circles and the PDB model also is superimposed.

DISCUSSION

The results presented here demonstrate that triclinic hen egg-white lysozyme, a protein containing 1,001 independent non-H atoms, can be solved by the Shake-and-Bake method by using the SnB program and experimental data 86.4% complete to 0.98 Å and extending to 0.85 Å resolution. The behavior of this data set, when subjected to SnB refinement, is unusual compared with previous studies of smaller molecules. The probability of successfully obtaining a solution given a particular set of random starting structures varies dramatically with changes in parameters such as (i) the numbers of reflections, invariants, and peaks selected, (ii) the Fourier grid size, and (iii) the conditions of PS refinement. The use of the default PS protocol of two 90° shifts per cycle for each phase rarely led to success. On the other hand, single phase shifts in the range of 150–170° gave reasonable success rates, and the peak success rate of ≈21.9% is unusually high, even for much smaller structures (4, 21).

The precise reason for these choices of parameters remains unclear. The treatment of the electron density around the top peak in the E-maps would appear to be important in avoiding uranium solutions. In the earlier trials, conducted with default snb parameters, electron density ripples around the top peak soon became the next highest peaks selected. These peaks then were weighted as sulfurs in the subsequent structure–factor calculation. This situation resulted in the uranium maps. Changing the grid size to 0.28 Å certainly affected the peak selection in this region. It also can be shown that, given the precise coordinates of just two sulfur atoms, SnB automatically can converge on the correct solution. Therefore, the proximity of sulfur atoms present in disulfide bridges, of which there are four in triclinic lysozyme, may explain the significance of the Fourier grid size and may also be part of the reason for the high success rate achieved. Two of these disulfide bridges are also themselves in close proximity.

It previously has been shown that, during Shake-and-Bake refinement, P1 structures behave differently from structures crystallizing in other space groups (15). For example, P1 success rates are often high relative to similar-sized structures in other space groups, but it is always advisable to do less phase refinement and more real-space refinement in P1. The reasons are unclear, but such phenomena undoubtedly are related to the fact that space group P1 is unique in that the origin can be located anywhere in the unit cell. Consequently, some subset of peaks is always internally consistent. It is uncertain whether the unexpectedly high success rates observed for triclinic lysozyme, when only a single phase-shift of ≈157.5 was applied, are related to the space group. Preliminary tests using P1 data for the 471-atom α-1 peptide indicate that this is not the case.‖ Default parameters for this structure gave a 13.7% success rate whereas the comparable experiment using a single shift of 157.5° had a success rate of only 3.3%. The astonishing success rates of 100% or nearly 100% for the error-free data for proteinase inhibitor 3OVO and triclinic lysozyme, respectively, require further investigation, as does the reason for the results obtained with the nonstandard 157.5° shift. Until a more thorough study can be completed, it is important that snb users consider single phase shifts significantly different from 90° in cases in which default parameters do not readily yield a solution.

ABBREVIATION

PS

parameter-shift