An entropy criterion to detect minimally frustrated intermediates in native proteins

Abstract

The analysis of the information flow in a feed-forward neural network suggests that the output of the network can be used to compute a structural entropy for the sequence-to-secondary structure mapping. On this basis, we formulate a minimum entropy criterion for the identification of minimally frustrated traits with helical conformation that correspond to initiation sites of protein folding. The entropy of protein segments can be viewed as a nucleation propensity that is useful to characterize putative regions where folding is likely to be initiated with the formation of stretches of α-helices under the predominant influence of local interactions. Our procedure is successfully tested in the search for initiation sites of protein folding for which independent experimental and computational evidence exists. Our results lend support to the view that folding is a hierarchical event in which, in harmony with the minimal frustration principle, the final conformation preserves structural modules formed in the early stages of the process.

Quite recently, the advent of powerful experimental and computational approaches (1–13) have led to an upsurge of interest in the pathways of protein folding. Such pathways are usually investigated by direct observation of the forward process leading from the shapeless molecule to the final structural organization. Here, we take a backward approach to the problem and show that the study of native structures of globular proteins sheds light on the chronology of structure formation and ultimately provides a test of the principle of minimal frustration (14, 15). In this context, one of the basic questions that is being posed is whether dissecting the fold of proteins in a hierarchy of structures, besides being an instrumental way to handle with their architectural complexity, reflects some fundamental feature of protein folding. Furthermore, it has been argued that the folding process must be parallelized and must avoid nonproductive pathways that end up in low energy nonnative conformations (10, 12, 16, 17). Such dead ends may be the typical fate of protein folding because of the fact that proteins are frustrated systems, i.e., systems for which the simultaneous minimization of all interaction energies is impossible (15). Frustration entails that proteins are characterized by a rugged energy landscape in which a huge number of relative minima corresponds to misfolded structures. The most remarkable effect on the kinetics of folding is that the random search for the lowest energy structure takes inordinately large times that exceed by several orders of magnitude the folding times of real proteins (Levinthal’s paradox) (18). The paradox can be circumvented by assuming that the inevitable frustration of proteins is reduced by the existence of some local structures, dictated essentially by short range interactions, that are compatible with the overall fold of the protein in the native state (principle of minimal frustration; refs. 14 and 15). Stated in this form the requirement of minimal frustration is consistent with a model of protein folding according to which the early steps of folding occur, before the rate-limiting step that involves the folding nucleus (19, 20), in the initiation sites (10) under the predominant influence of local forces (10, 11, 13, 19, 21–34). Thus in the early stages of folding, local search involves residues close to each other in sequence and results in the formation of stretches of secondary structure that may possibly be stabilized by nonspecific long-range interactions in the form of hydrophobic effects or the formation of a molten globule (10, 12, 20, 23, 26, 35–37). Our interest is mainly focused on the formation of the earliest traits of helical secondary structure that are supposed to be conserved throughout the remainder of the folding process (11, 13, 19, 29, 30, 35, 38) and form the core of the nucleation sites stabilized later. In particular, we pursue the aim of testing the hypothesis that α-helices may function as independent “seeds for folding” (38).

The present work relies on the notion that local interactions are a necessary prerequisite for both the formation of native secondary structure and the foldability of proteins (13, 35, 39, 40). This feature justifies the application of a method that is primarily sensitive to local interactions to detect α-helix fragments that are viable candidates for the role of minimally frustrated initiation sites. To this end, we take advantage of recent progress in the prediction of protein secondary structures from the residue sequence with neural networks (41) to estimate the nucleation propensity of traits of the protein molecule. We use a feed-forward neural network with standard backpropagation learning algorithm. In the present set up, more thoroughly described in refs. 41 and 42, the current input pattern ℐ is generated by a sliding window, 13 residues in length, scanning the whole residue sequence. The output layer contains two real-valued output neurons, with activations o_ℐⁱ ∈ [0, 1], i = 1, 2. Each of them codes for a specific structural class σ_i (α-helix, non-α-helix) to be ascribed to the residue lying in the central position of the current input ℐ (for brevity, the structure will be thought of as being assigned to the pattern ℐ). Between the input and the output layers there is an additional hidden layer comprising two neurons.

The essential premise to our method is that the network reconstructs a mapping from the space of amino acid sequences to the space of the secondary structures that is equivalent, in some average sense detailed below, to the real folding process and can be viewed as an implementation of Anfinsen’s hypothesis (43). It can be stated that the neural network mimics protein folding in that the mapping has been proved to be equivalent to a model of the early stages of protein folding based on the kinetic equations of contact variables (44). From a statistical perspective, one can argue that the network is sensitive to statistical regularities (45), and its application in the search for initiation sites can be justified firstly, by analyzing the flow of information in the neural network and, secondly, by making a conjecture as to the general mechanism of folding. The starting point is a theorem that ensures the convergence of the outputs o_ℐⁱ of backpropagation neural networks to the conditional probabilities P(σ_i | ℐ) that the input ℐ is found in the structure σ_i (46). The statistical meaning of the o_ℐⁱ is to be contrasted with Anfinsen’s thermodynamic hypothesis (43) that can be cast in the form

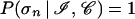1

where 𝒞 indicates the remainder of the protein sequence, or context, and σ_n is the native structure. It is evident that the output of the perceptron captures less information than is needed for the unambiguous assignment of the local structure. As expected, the neglect of relevant pieces of information contained in 𝒞 introduces some degree of uncertainty. In more rigorous terms, the relationship

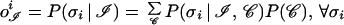2

shows that the structural assignment, carried out by the network on the basis of the bare pattern ℐ, relies on an average over all contexts (more precisely, over the contexts contained in the training set). Even when the network is working at its best, the approximation entailed by the averaging procedure is the main performance limiting factor (45) for those patterns whose essential determinants of the native secondary structure reside in the tertiary structure of the protein (47, 48). Conversely, averaging has little effect on the patterns ℐ_r, henceforth termed reliable, whose secondary structure is largely independent of the context 𝒞. In fact, if we express the defining property of reliable patterns as

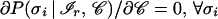3

and make use of Eq. 1, the above average over contexts simplifies to ∑_𝒞 P(σ_n | ℐ_r, 𝒞)P(𝒞) = P(σ_n | ℐ_r, 𝒞) ∑_𝒞 P(𝒞) = 1, which ultimately implies P(σ_n | ℐ_r) = 1. However, under actual working conditions, it is to be expected that only approximate convergence is realized by the perceptron (46), i.e., o_ℐⁱ ≈ P(σ_i | ℐ). In this case, the reliable patterns are more realistically defined by the condition

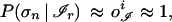4

which, in the following, will be referred to as the local version of the thermodynamic hypothesis. Eq. 4 provides a useful alternative definition of reliable patterns in terms of the output of the network.

A more practical way to implement the criterion of Eq. 4 is to define the entropy of the output vector

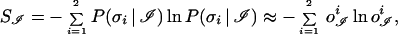5

and turn Eq. 4 into a minimal entropy criterion,

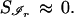6

Some remarks about the physical content of Eq. 3 are in order to elucidate the meaning of the minimal entropy criterion of Eq. 6. Our selection of the reliable helices through Eq. 3 bears on the question about the relative weight of local and long-range (tertiary) contacts in the stabilization of the secondary structure. As far as the reliable traits with helical conformation are concerned, Eq. 3 is compatible with two alternative views but the properties of the reliable patterns thus selected change correspondingly. In the first case, the reliable pattern is context-independent and intrinsically stable so that it can assume its native structure in solution even when it is excised from the protein. The existence of such segments is investigated in (11–13, 23, 28, 31, 33, 40, 49–58). Reliable patterns conforming to the second possibility are weakly context-dependent in that they are expected to be stabilized by long-range generic contributions (10, 12, 20, 23, 26, 28, 35–37) depending on compositional properties of the sequence rather than on specific tertiary interactions. Such properties supposedly are associated with those features shared by most of the sequences of the database (hence Eq. 3 is fulfilled) and correspond to the so-called self-averaging features in the terminology of spin glass theory (15).

Therefore, in agreement with the hierarchical models of folding (13, 22–26, 38), we argue that it is reasonable to equate the reliable patterns with the initiation sites where folding is started in the early stages, because they share the distinguishing feature, formalized in Eq. 3, that the attendant local structure is formed with the minor contribution of tertiary interactions. This conjecture enables us to convert the search of the initiation sites of folding to the problem of assessing, for any input ℐ, the conformity of the o_ℐⁱ with Eq. 4.

Accordingly, a useful test of the minimal entropy criterion can be carried out by comparing our predictions with data from the literature concerning the existence and location of folding intermediates and initiation sites. To select the initiation sites of folding, we draw plots of S_ℐ along the residue sequence of each protein. After the signal is regularized, by averaging S_ℐ over k neighboring residues, we search the entropy profile for the most pronounced minima corresponding to native helices that, supposedly, are correctly identified by the network. Fig. 1 exemplifies the trend of the average entropy 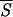_k with k = 5, that is the requisite span compatible with the shortest stretches of α-helices. Fig. 2 confirms that we may be confident that the entropy-driven selection of the helices predicted by the neural network is a reliable procedure to identify native structures of the protein. The diagram makes clear that the lower the values of 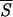_k (up to segments of length k = 5) the more exact is the prediction of the corresponding patterns, indicating that the probability density P(σ | ℐ_r), as approximated by the o_ℐⁱ, peaks on the correct (i.e., native) structure σ_n. This agreement is not surprising because our entropy provides much the same information as the reliability index discussed, for example, in ref. 59. As a crucial benchmark, we have selected the folding nuclei, determined by energy minimization procedures (11, 12, 49), that are expected to be intrinsically stable. We also have taken into consideration a set of proteins for which the participation of some tagged residues in intermediate stages of folding has been proved experimentally (3, 35, 60, 61, 63, 64) or supported by computer simulations (65). The data collected in Fig. 3 demonstrate that there is substantial agreement between our findings and the results obtained with the alternative methods. Notably, a glance at the entropy values listed in the caption of Fig. 3 shows that most of the selected helices of type a have entropies coinciding with or close to the absolute minimum of the 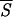₅ profile.

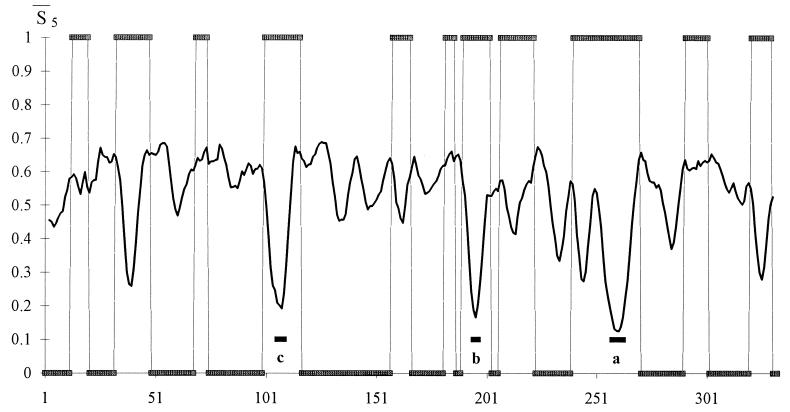
Figure 1.

Profile of the smoothed entropy 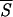₅ (continuous curve) for the protein 1GD1_O. The computation of 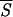₅ involves the prediction of the secondary structure of the pattern ℐ and, subsequently, the evaluation of S_ℐ (Eq. 5) for each of the 334 residues of the protein. We have used a two-output network, designed to discriminate between α-helices and non-α structures. For crossvalidation of the network, we have used a training set comprising 300 nonhomologous globular proteins with <25% of sequence homology. Furthermore, we have normalized the actual output of the network to minimize the effect of small deviations of the o_ℐⁱ from the ideal condition where they sum to unity. Next, a local average of S_ℐ has been performed over a movable window five-residue long and centered on the current residue. The abscissa indicates the running position of the central residue along the protein backbone. We have superimposed a binary step function with nonzero plateaus spanning the regions that the network predicts in a α-helix structure. The zero plateaus of the step function (on the abscissa) indicate the segments that the neural network classifies in nonhelical structure. According to the minimal entropy criterion, the lowest minima of ₅, corresponding to helical conformations, hallmark the residues that are likely to belong in the initiation sites of folding of the protein. The boundaries of each initiation site have been fixed by admitting deviations in 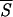₅ of 0.05 around each local minimum. The three sites (c, b, a) are indicated by black bars under the corresponding entropy minimum and have been redrawn in Fig. 3 as boxes of appropriate length along the protein backbone.

Figure 2.

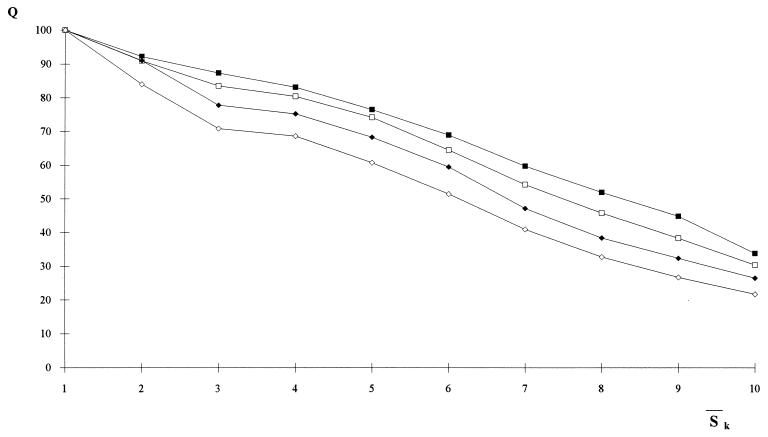
Correlation between entropy measures and the performance Q of the network. The accuracy Q for each entropy interval is the percentage of the correctly predicted patterns normalized to the total number of patterns of the training set whose entropy lies in that same entropy interval. The entropy axis reports the average entropies 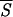_k, with k = 1,3 (open □ and filled ■ square), k = 5,7 (open ⋄ and filled ♦ diamond). Note that S_ℐ of Eq. 5 coincides with 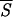₁. The range of entropy values has been discretized for convenience by dividing the allowed range [0, ln 2] into 10 equal intervals. The plot shows that there exists a strong correlation between the correctness of the network’s prediction and low entropy segments up to five residues in length. Accordingly, we have used 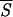₅ in the search for the initiation sites reported in Fig. 3.

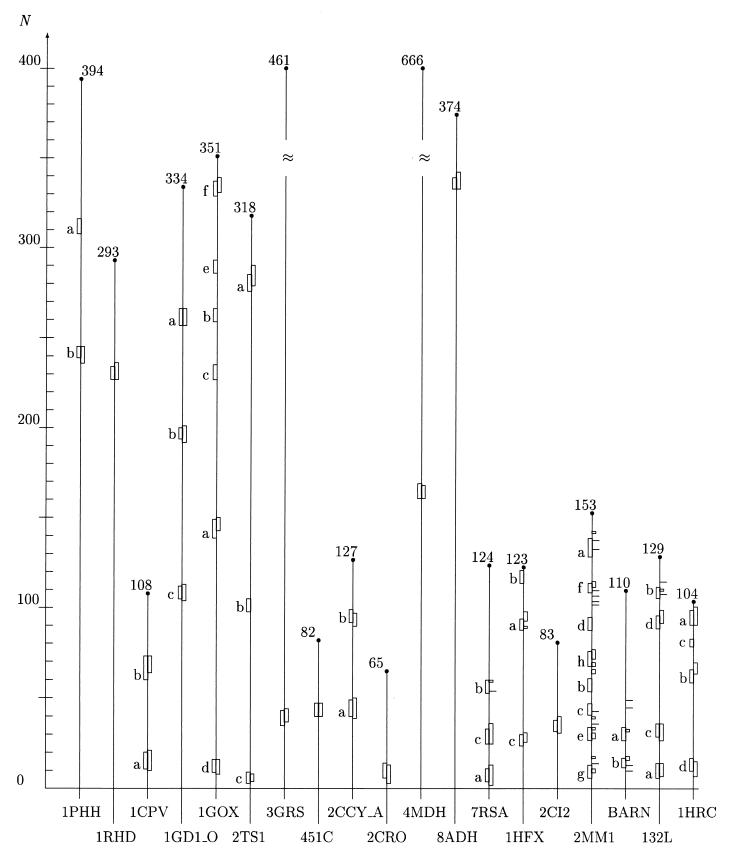
Figure 3.

Initiation sites of folding assuming helical structure determined by means of the minimal entropy criterion and other methods. On the abscissa, we have listed the Brookhaven codes of the proteins examined. The grid on the N-axis marks the position of the amino acids along the protein backbones, which have been skeletonized as vertical filaments of appropriate length. For convenience, the total number of residues of each protein is shown at the upper end of each filament. The boxes attached to each protein backbone highlight the location and extent of the earliest stretches of helical structure being formed during the folding process. The boxes on the left side of each filament have been positioned in the regions around the lowest minima of the average entropy 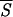₅ according to the criterion described in the caption of Fig. 1. The boxes or tick marks (in the case of single residues) on the right side of each backbone visualize the initiation sites as they result from experimental and computational works. Our segments are labeled with letters indicating ascending values of the entropy minima. The data for the first 12 proteins (1PHH, 1RHD, 1CPV, 1GD1O, 1GOX, 2TS1, 3GRS, 451C, 2CCYA, 2CRO, 4MDH, and 8ADH) are drawn from ref. 49; the experimental results for 7RSA have been drawn from ref. 11 for site a and c and ref. 62 for site b. The site a also has been predicted in ref. 12 in the same position as determined in ref. 11. Helix c (but the last two residues) also has been shown to be present in the early folding intermediate identified in ref. 62. The experimentally detected sites for 1HFX, 2CI2, 2MM1, BARN (barnase), 132L, and 1HRC are drawn, respectively, from refs. 35, 60, 3, 61, 34, and 64. Our initiation site for 2CI2 includes the first two residues that comprise the folding nucleus according to ref. 65. The experimental data reported in ref. 3 for 2MM1 and ref. 34 for 132L essentially confirm the previous analysis in refs. 13 and 63, respectively. In the following, we list the range of variation δS of the entropy in the entropy profile and the site entropy S for each protein examined. 1PHH: δS = 0.224–0.690, S(a) = 0.224, S(b) = 0.253; 1RHD: δS = 0.173–0.687, S=0.173; 1CPV: δS=0.237–0.677, S(a) = 0.237, S(b) = 0.305; 1GD1O: δS = 0.125–0.689, S(a) = 0.125, S(b) = 0.166, S(c) = 0.192; 1GOX: δS = 0.288–0.691, S(a) = 0.288, S(b) = 0.290, S(c) = 0.294, S(d) = 0.307, S(e) = 0.311, S(f) = 0.315; 2TS1: δS = 0.227–0.687, S(a) = 0.256, S(b) = 0.273, S(c) = 0.284; 3GRS: δS = 0.154–0.688, S = 0.245; 451C: δS = 0.142–0.688, S = 0.237; 2CCYA: δS = 0.094–0.672, S(a) = 0.094, S(b) = 0.178; 2CRO: δS = 0.259–0.637, S = 0.259; 4MDH: δS = 0.166–0.690, S = 0.261; 8ADH: δS = 0.153–0.690, S = 0.292; 7RSA: δS = 0.326–0.689, S(a) = 0.350, S(b) = 0.508, S(c) = 0.533; 1HFX: δS = 0.341–0.691, S(a) = 0.435, S(b) = 0.490, S(c) = 0.520; 2CI2: δS = 0.300–0.684, S = 0.428; 2MM1: δS = 0.264–0.686, S(a) = 0.264, S(b) = 0.378, S(c) = 0.451, S(d) = 0.460, S(e) = 0.466, S(f) = 0.524, S(g) = 0.616, S(h) = 0.616; BARN: δS = 0.261–0.689, S(a) = 0.376, S(b) = 0.558; 132L: δS = 0.190–0.688, S(a) = 0.301, S(b) = 0.494, S(c) = 0.556, S(d) = 0.647; 1HRC: δS = 0.244–0.688, S(a) = 0.296, S(b) = 0.374, S(c) = 0.586, S(d) = 0.644. The helices marked a correspond to helical structures with the lowest entropy. They coincide with or are close to the absolute minimum of the entropy profile (see text). We have included as many segments as needed to scan all the α-helices assigned to each protein in the literature. Our numeration for 2CI2 is shifted ahead by 19 residues with respect to the one in ref. 60.

In conclusion, we note that our implementation of the minimal entropy criterion shares the simplicity of all neural approaches in that one needs a minimum amount of a priori information to achieve an effective extraction of statistical features. A more cumbersome analysis relying on an entropy concept can be found in ref. 66. The physical meaning attached to Eq. 3 justifies our contention that the lowest minima of the entropy plot are appropriate markers for minimally frustrated regions, where local cooperativity is the basic determinant of early helical structures that have inherent harmony with other structural features (15). Furthermore, the compatibility of the helical structure of our initiation sites with virtually any context of the training set makes the reliable patterns eligible as building blocks of secondary structure that are formed early and are retained throughout the later stages of folding (12. 23) irrespective of the subsequent adjustments of the tertiary structure.

The remarkable agreement of our data with the results in (49) indicates that self-stabilizing segments are successfully captured by our criterion. Notably, experimental investigations have shown that some of the initiation sites predicted in Fig. 3 settle autonomously in the helical conformation even when they belong to isolated peptides in solution. This is the case of the helices a, b, and c of 7RSA studied in refs. 51–53 and the a helices of 2MM1 and 1HRC tested in refs. 54 and 55. However the 2-fold interpretation of our selection rule for reliable patterns (Eq. 3) does not allow one to infer that isolated reliable patterns are necessarily stable in solution. Examples of such segments for which the local helical propensity must be assisted by a suitable hydrophobic environment are the B and C helices of α-lactalbumin [entirely unfolded in water (35)] that correspond to the d and b traits of 1HFX in Fig. 3.

By contrast, tertiary interactions dictate more stringent and specific constraints to the conformation of unreliable patterns that are characterized by higher values of the entropy than the reliable ones. Turns appear to be good candidates for unreliable patterns in α-helical proteins on account of their role of floppy regions in which local effects are overcome by long-range interactions (67). Notably the existence of a mix of unreliable and reliable patterns has been shown to favor the foldability of proteins (40).