Universal patterns of purifying selection at noncoding positions in bacteria

Abstract

To investigate the dependence of the number of regulatory sites per intergenic region on genome size, we developed a new method for detecting purifying selection at noncoding positions in clades of related bacterial genomes. We comprehensively quantified evidence of purifying selection at noncoding positions across bacteria and found several striking universal patterns. Consistent with selection acting at transcriptional regulatory elements near the transcription start, we find a universal positional profile of selection with respect to gene starts and ends, showing most evidence of selection immediately upstream and least immediately downstream from genes. A further set of universal features indicates that selection for translation initiation efficiency is the major determinant of the sequence composition around translation start in all clades. In addition to a peak in selection at ribosomal binding sites, the region immediately around translation start shows a universal pattern of high adenine frequency, significant selection at silent positions, and avoidance of RNA secondary structure. Surprisingly, although the number of transcription factors (TF) increases quadratically with genome size, we present several lines of evidence that small and large genomes have the same average number of regulatory sites per intergenic region. By comparing the sequence diversity of the most and least conserved DNA words in intergenic regions across clades we provide evidence that the structure of transcription regulatory networks changes dramatically with genome size: Small genomes have a small number of TFs with a large number of target sites, whereas large genomes have a large number of TFs with a small number of target sites each.

What is the global structure of transcription regulatory networks in bacteria of disparate genome size? In this study we address this question through a comprehensive and quantitative analysis of conservation statistics at noncoding positions, both in intergenic regions and within genes, across sequenced bacterial genomes. Our main motivation stems from the observation (Stover et al. 2000; van Nimwegen 2003) that the number of transcription regulators grows approximately quadratically as a function of the total number of genes in the genome. For example, according to the DBD database (Kummerfeld and Teichmann 2006), the number of transcription factors (TFs) per genome in bacteria varies from only three (of a total of 504 genes) in Buchnera aphidicola, to 801 (of a total of 7717 genes) in Burkholderia sp. 383. To put the latter number in perspective, the vastly bigger genomes of Caenorhabditis elegans and Drosophila melanogaster have a lower estimated total number of TFs according to the same database.

The simplest interpretation for the large range in the number of TFs across bacteria is that it reflects a large range in complexity of gene regulation across bacteria. For example, as an endosymbiont of aphids, Buchnera lives in a very stable environment and some evidence suggests it shows little transcriptional regulation (Moran et al. 2005). In contrast, Burkholderia can live under extremely diverse ecological conditions including soil, water, as a plant pathogen, and as a human pathogen, which most likely require complex regulatory mechanisms.

Quantitatively, the approximately quadratic scaling of the number of TFs thus means that the largest bacterial genomes have about a 20 times higher fraction of genes involved in transcriptional regulation than the smallest, i.e., increasing from ∼0.5% in Buchnera to ∼10% in Burkholderia. Put differently, the number of TFs “per gene” increases from one per 200 genes to one per 10 genes. This has important implications for the structure of transcription regulatory networks. One can think of the transcription regulatory network as a graph, with nodes corresponding to genes, and directed edges going from TFs to their target genes. The total number of edges in this network is given by the number of TFs times the average number of outgoing edges per TF, but also by the total number of genes times the average number of incoming edges per gene. That is, if r is the number of TFs, g the number of genes, 〈i〉 the average number of incoming edges per gene, and 〈o〉 the number of outgoing edges per TF we have r〈o〉 = 〈i〉g. Since the number of TFs “per gene” grows linearly with the total number of genes, i.e., r/g ∝ g, we cannot have that both the average number of outgoing edges per TF and the number of incoming edges per gene are the same in bacteria of different genome size. In particular, we must have 〈i〉/〈o〉 ∝ g. That is, either the number of incoming edges per gene must increase with genome size, i.e., genes are regulated by more TFs in larger genomes, or the number of outgoing edges per TF must decrease with genome size, i.e., the regulon size decreases with genome size (or of course a combination of these two). The main aim of this study was to investigate how the number of incoming edges per gene and the number of outgoing edges per TF depends on the genome size across bacteria.

Transcription regulation is generally implemented through the sequence-specific binding of transcription factors (TFs) to transcription factor binding sites (TFBSs) located mostly in intergenic regions upstream of genes (Wagner 2000). Therefore, the average number of incoming regulatory edges per gene is directly related to the average number of TFBSs per intergenic region. Here we will assume that the average numbers of regulatory sites can be estimated by comparing conservation statistics of noncoding positions in alignments of orthologous sequences from clades of related bacterial genomes. For a large number of sequenced bacterial genomes one can find other sequenced genomes that are closely related, meaning that orthologous genes and intergenic regions can be identified for a large number of genes, and the intergenic regions show enough conservation to be aligned, yet are sufficiently diverged such that a substantial fraction of nucleotides has undergone substitution since they diverged from their common ancestor. Under the assumption that much of the regulation of orthologous genes is conserved across closely related species within a clade, we below infer the presence of regulatory sequences from the conservation statistics at noncoding positions in genes and intergenic regions.

In particular, by calculating the likelihood of alignment columns under “foreground” and “background” evolutionary models, we quantify the evidence for purifying selection at different classes of noncoding positions (silent position within genes, positions upstream of genes, and positions downstream from genes) and as a function of position relative to starts and ends of genes across 22 clades of bacteria. Apart from allowing us to investigate the overall density of regulatory sites in intergenic regions, this analysis also reveals several universal characteristics in the patterns of purifying selection at noncoding positions in bacteria.

Results

Operon number and intergenic region sizes

Before turning to the analysis of conservation patterns, one might ask to what extent the large range in the number of TFs is reflected in the overall organization of intergenic regions across bacteria. In prokaryotes, genes are organized in operons which are transcribed together and are under the control of common regulatory elements that occur in the intergenic region upstream of the first gene in the operon. Thus, as TFBSs likely occur predominantly upstream of the first gene in each operon, it is relevant to ask how the total number of operons grows as a function of the total number of genes. Previous studies have shown that the number of operons increases only slightly faster than linear with the total number of genes (Cherry 2003; van Nimwegen 2004). In the Supplemental Material we redo this analysis for 416 currently sequenced bacteria, using operon predictions from a recent Bayesian method (Price et al. 2005), and find that the number of operons grows approximately as the number of genes to the power 1.09. This implies that the number of TFs “per operon” still grows almost quadratically with the total number of genes.

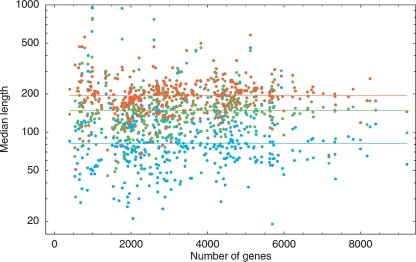
Another relevant question is how the lengths of intergenic regions depend on genome size. In eukaryotes, there is a trend for more complex organisms to possess larger amounts of intergenic DNA per gene, and one might expect that large bacterial genomes, with their much larger number of TFs, may also have longer intergenic regions. This question has been investigated previously (Rogozin et al. 2002; van Nimwegen 2004) and, somewhat surprisingly, no correlation was found between the average size of intergenic regions and overall genome size. Figure 1 shows the median size of intergenic regions across currently sequenced bacteria as a function of the total number of genes in the genome. We classified the intergenic regions into three different types: nonregulatory (NR) regions that are downstream from two convergently transcribed genes (blue dots), single-regulatory (SR) regions upstream of the first gene in an operon and downstream from another gene (green dots), and double-regulatory (DR) that are between two divergently transcribed genes (red dots).

Figure 1.

Average lengths of intergenic regions (vertical axis) as a function of the total number of genes (horizontal axis) for intra-operonic regions (red), NR regions (blue), SR regions (green), and DR regions (red) across all sequenced bacteria. Each dot corresponds to one genome. Both axes are shown on logarithmic scale. The horizontal lines correspond to average region lengths averaged over all genomes.

In none of the three classes have we found evidence of correlation between intergenic region size and the number of genes. What we did find was that NR regions are significantly smaller than SR regions and that SR regions are smaller than DR regions. In Rogozin et al. (2002) it was suggested that intergenic regions in bacteria are under selection pressure to minimize their size while maintaining the necessary regulatory sites. This view is supported by our observation that DR regions, which contain regulatory signals for two genes, are largest, and that the NR regions are the smallest. Interestingly, if intergenic region length indeed reflects the number of regulatory sites that occur in it, then the absence of a correlation between intergenic region length and genome size would imply that the average number of regulatory sites per intergenic region is the same in small and large genomes. We now investigate this in more detail by analyzing the evidence for purifying selection across noncoding positions in 22 clades of closely related bacterial genomes.

Quantifying evidence of purifying selection at noncoding positions

We briefly outline our procedure for quantifying evidence of purifying selection across noncoding positions genome-wide in bacterial genomes. Details are described in the Methods section and additional technical details can be found in the Supplemental Material. Our procedure takes as input a set of related bacterial genomes (a “clade”) as provided by the NCBI Microbial Genome Database (http://www.ncbi.nlm.nih.gov/genomes/lproks.cgi), of which one is denoted as the “reference species.” For each gene and each intergenic region of the reference species we extract orthologous genes and intergenic regions from the other species and produce multiple alignments. We determine cliques of orthologous proteins (sets of genes that are all mutual orthologs between all species in the clade) and infer the topology of the phylogenetic tree from the concatenated alignment of all cliques.

For each alignment column we calculate the likelihood under two evolutionary models: a “foreground” and a “background” model. The background model assumes a simple F81 substitution rate model (Felsenstein 1981) which is parametrized by the branch lengths of the phylogenetic tree and a vector w of nucleotide frequencies, with w_α being the frequency of nucleotide α. In the F81 model the rate of substitution r_αβ from base β to base α is simply proportional to w_α and independent of β. As nucleotide frequencies vary significantly between intergenic positions, coding positions, and third positions of fourfold degenerate codons, we separate positions into 12 different categories and construct a background model for each. The categories we distinguish are first, second, and third codon positions in genes, intergenic positions, and third positions in each of the eight fourfold degenerate codons (silent positions). To estimate the parameters of the background models we determine the overall nucleotide frequencies w_α in each of the 12 categories of positions and fit the branch lengths of the phylogenetic tree from the alignments of silent positions using maximum likelihood. Our background models thus explicitly incorporate the overall nucleotide and codon biases of different classes of sites.

For each of the 12 background evolution models we have a corresponding foreground model. The only difference between the foreground and background model is that, whereas the background model assumes that all positions undergo substitutions from base β to base α at the same rate r_αβ ∝ w_α, in the foreground model we assume that, at a given position i, the substitution rates rⁱ_αβ ∝ 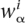are altered due to specific selection preferences for certain bases at this position, which are parametrized by the “target” nucleotide frequencies 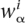. Since the 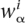at each position are unknown we treat them as nuisance parameters that are integrated out of the likelihood. Such evolutionary models have been used by several groups to model the evolution of positions in regulatory sites (Sinha et al. 2003, 2004; Moses et al. 2004; Siddharthan et al. 2005). The reason we use the simpler F81 substitution rate model rather than the related, but more general, Halpern-Bruno model (Halpern and Bruno 1998) is that the necessary integrals over the unknown position-dependent frequencies 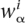can only be performed for the F81 model.

For each alignment column of the reference species, both in genes and in intergenic regions, we calculate the ratio R of likelihoods of foreground and background evolutionary models. This statistic quantifies the evidence that the alignment column evolves under a different set of substitution rates than the background model. In addition, we estimate the effective substitution rate reduction Q relative to the substitution rate of the background model at each alignment column (see Supplemental Material). In practice we find that columns of high R (clear deviation from the background model) correspond to columns of high Q (low substitution rate). We thus interpret R and Q as quantifying the amount of purifying selection at each alignment column relative to the background model.

R values at different types of noncoding positions

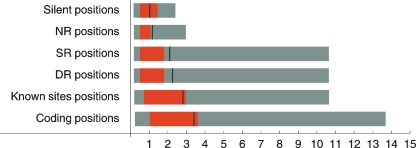
To investigate the ability of our R statistic to detect positions in TFBSs we focused on Escherichia coli for which a large collection of experimentally determined TFBSs is available (Salgado et al. 2006). Figure 2 summarizes the distribution of R values at silent sites, sites in NR regions, SR regions, DR regions, positions in known TFBSs, and sites at coding regions. Silent positions in E. coli have an average R close to 1, which suggests that most silent positions evolve according to their background model (see Supplemental Material). Sites downstream from genes (in NR regions) also typically have small R values. On the contrary, sites upstream of genes (SR and DR regions) show significantly higher R values. The 25 percentile occurs at similarly low values of R for silent, NR, SR, and DR positions, indicating that there is a significant fraction of positions in upstream regions that are not under purifying selection. In contrast, the 75 and 95 percentiles are shifted significantly upward for SR and DR regions, indicating that a substantial number of positions in SR and DR regions are under purifying selection. This is also evident from the fact that the average for SR and DR is above the 75 percentile. Known TFBSs show even larger average R values than upstream positions in general, and both the 25 and 75 percentiles are shifted upward with respect to SR and DR regions. Nonetheless, not all positions in known sites show large R values, which is to be expected, since many TFBSs have internal spacers that are presumably not under purifying selection. Finally, positions in coding regions show the largest R values with ∼75% of all positions having an R < 1. In summary, the results in Figure 2 show that the R statistic clearly detects purifying selection at coding positions, that upstream regions show increased purifying selection compared to downstream and silent positions, and that known binding sites are characterized by elevated R values whose average nears the average R at coding positions.

Figure 2.

Distributions of R values in different classes of positions in E. coli. For each category of positions the black line denotes the average R value, the red bar the 25–75 percentile, and the gray bar the 5–95 percentile.

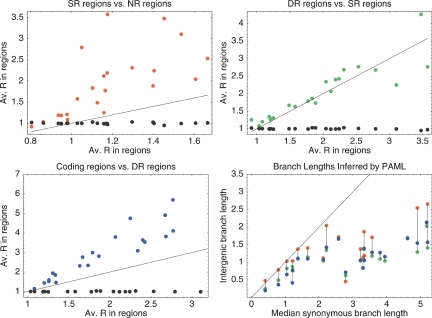
We next turned to comparing R values between silent positions, intergenic positions, and coding positions across all 22 clades. For each clade we averaged the R values of sites at silent positions, at positions in NR regions, in SR regions, in DR regions, and at coding positions (Fig. 3). We see that, in all clades, silent positions appear to evolve according to the background model, i.e., R is close to 1. Note that the fact that R = 1 at silent positions does not necessarily mean that there is no purifying selection at third positions, but it does imply that the selection which may exist at silent positions is accurately captured by the overall codon bias which is incorporated into the background model. In contrast, all intergenic regions show evidence for purifying selection deviating from the background model (which incorporates the overall nucleotide bias in intergenic regions). Even for NR regions downstream from genes there is some evidence for purifying selection deviating from the background model, i.e., most dots in the top-left panel occur to the right of R = 1. The same panel also shows that SR regions always show more evidence of purifying selection than NR regions, i.e., all red dots are above the diagonal. The top-right panel shows that DR regions generally exhibit more evidence of purifying selection than SR regions, i.e., most green dots are above the diagonal. The bottom-left panel demonstrates that, for all clades, the purifying selection at coding positions is still significantly larger than that in DR regions, i.e., all blue dots are above the diagonal. In summary, these three panels show that our observations from E. coli generalize to all clades. This universal order in average R values (largest in DR, followed by SR, then NR, and R = 1 at silent positions) strongly suggests that conserved regulatory elements occur in the upstream regions of all clades and are responsible for the observed increase in average R.

Figure 3.

Comparison of average R values in different regions for 22 clades of bacteria. The red dots in the top-left panel show the average R in SR regions (vertical axis) against the average R in NR regions (horizontal axis). The green dots in the top-right panel show the average R in DR regions (vertical) against the average R in SR regions (horizontal). The blue dots in the bottom-left panel show the average R in coding positions (vertical) against the average R in DR regions (horizontal). The black dots in all panels show the average R in silent positions (vertical). The line y = x is also shown in all panels. The bottom-right panel shows, for each clade, the total branch lengths in the phylogenetic trees as inferred by PAML on alignment columns from NR (red), SR (green), and DR (blue) regions, as a function of the total branch length in the phylogenetic tree inferred from the silent positions (horizontal). Dots corresponding to the same clade are connected by vertical lines.

Our model makes various simplifying assumptions that might affect our results, e.g., it ignores transition-transversion bias. To check the robustness of our results we performed an analogous analysis using a completely different method. For each region type (NR, SR, DR, coding, silent) we extracted all alignment columns. Each set of alignment columns was then concatenated into a pseudoalignment of all positions in regions of that type. These pseudo-alignments were then given as input to the PAML program (Yang 1997), which performed a maximum likelihood inference of the branch lengths of the phylogenetic tree of each pseudoalignment using a HKY85 evolutionary model (Hasegawa et al. 1985). We then compared the branch lengths of the phylogenetic trees that PAML inferred for each region type. The bottom-right panel shows the total branch length of the tree inferred by PAML from the pseudoalignments of positions in NR (red), SR (green), and DR (blue) regions, as a function of the total branch length of the tree inferred from the silent positions, together with the diagonal y = x. The more purifying selection acts to conserve positions in regions of a given type, the shorter the inferred branch lengths will be. The PAML results agree with the results in the three other panels of Figure 3: In essentially all clades the inferred distance in all types of intergenic regions is lower than that in silent positions, i.e., there is evidence of purifying selection acting in all three types of intergenic regions. Also, SR and DR regions have always more evidence of purifying selection than NR regions. In contrast to the results we obtained with our R statistic, the PAML results do not show a consistent ordering of the inferred branch lengths for the DR and SR regions.

R profiles relative to gene starts and ends

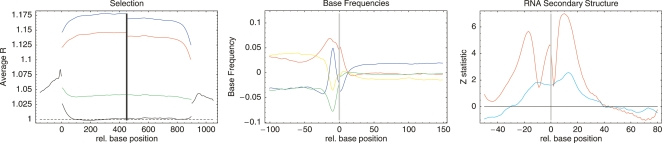
To gain further insight in the selection patterns across bacteria we calculated the average value of R as a function of the relative position of the alignment column with respect to the start and stop codons of genes. The left panel of Figure 4 shows this position-dependent selection profile averaged over all 22 clades.

Figure 4.

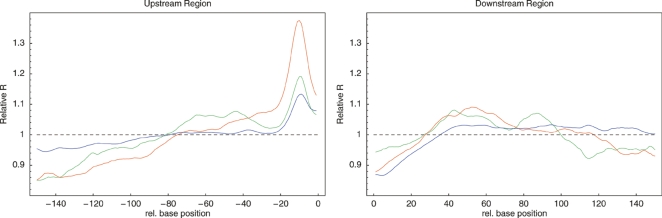
Universal position-dependent profiles in selection, base frequencies, and secondary structure as a function of position relative to translation start (position 0) and, in the left panel, stop (position 900). Statistics are averaged over all 22 clades in each panel. Left panel: R value profile averaged over all clades for first (red), second (blue), and third (green) positions in codons as well as intergenic/silent positions (black). Middle panel: Relative base frequencies, i.e., A (red), C (green), G (blue), and T (yellow) around translation start, averaged over all clades. Right panel: z-statistics for the probability of a given position to be unpaired relative to the average over the regions (−50,−31) and (31,80) (red) and relative to synthetic sequences with the same base composition (blue).

Strikingly, the main characteristics of this profile are shared across all 22 clades (see Supplemental Material): As in Figure 3, the highest R values are observed for those positions that most often affect the amino acid sequence, i.e., in order: second (blue), first (red), and third (green) codon positions. Interestingly, whereas there is a clear drop in R at first and second positions near the starts and ends of the genes, at the third positions there is an increase in R near the starts of genes. Intergenic regions show clear evidence of purifying selection (R > 1) with R significantly higher upstream of genes than downstream, though selection is lower than at coding positions. Consistent with a pattern in which regulatory elements are most common near the starts of genes we find that R values are highest near the translation start and fall off progressively further upstream. In contrast to the coding positions and intergenic regions, the bulk of the silent positions seems to evolve according to the background model, i.e., R = 1.

The R value profiles in addition show a number of universal features that, as we will now argue, relate to efficiency and regulation of translation initiation. First, we find a sharp peak in R just upstream of translation start which is accompanied by a sharp peak in the frequency of guanines (middle panel of Fig. 4). Closer inspection shows that this peak corresponds to highly conserved Shine-Dalgarno sequences (Shine and Dalgarno 1974) to which the ribosome binds. As shown in the Supplemental Material, although varying significantly in strength between clades, this Shine-Dalgarno peak is found in essentially all clades. In addition, 20 of the 22 clades show a sharp peak in G nucleotide frequency at this position matching the known Shine-Dalgarno consensus. Interestingly, this peak in G nucleotides is absent in the two clades of Cyanobacteria, where, instead, a peak in C nucleotides is observed. The R statistic thus detects universally occurring purifying selection at ribosome binding sites.

In addition, in essentially all bacterial clades (see Supplemental Material), R rises sharply at silent positions immediately downstream from the ATG, and this heightened selection is accompanied by an increase in the frequency of adenines, which extends into the upstream region. This rise in R is not caused by an increase of codon bias at gene starts, nor is it caused by misannotation of start codons (Supplemental Material). In fact, an increase in adenine frequency around the start codon, accompanied by elevated conservation at silent positions immediately downstream, has been observed previously, i.e., Eyre-Walker and Bulmer (1993) observed this pattern in E. coli and suggested that it is the result of selection for the avoidance of RNA secondary structure in this area of the mRNA, which in turn is the result of selection for translation initiation efficiency. In Bacillus subtilis the same pattern was observed, accompanied by reduced secondary structure in this area (Rocha et al. 1999). Moreover, experimental studies showed that increasing the frequency of A nucleotides immediately following translation start increases translation efficiency (Sato et al. 2001; Stenstrom et al. 2001; Voges et al. 2004).

Avoidance of RNA secondary structure around start codons

To provide further evidence that both the increased selection immediately downstream from the start codon as well the increased frequency of adenines are the result of selection for avoiding RNA secondary structure at the start of the open reading frame, we extracted for each gene the RNA sequence from 60 bp upstream (which is the typical length of 5′ UTRs in E. coli, see Supplemental Material) to 90 bp downstream and used the Vienna RNA package (Hofacker et al. 1994) to determine the probability, for each nucleotide, to be paired with another nucleotide in the RNA secondary structure. By averaging over all genes in the genome we then obtained an average “openness” profile around the translation starts of genes for each clade (Supplemental Material). The red curve in the right panel of Figure 4 shows a z-statistic profile for the average openness at a given position compared to the average openness in the flanking regions (−50,−31) and (+31,80), averaged over all clades. There is a clear preference for the region immediately upstream of and downstream from translation start to be more free of secondary structure than regions further away. Again this pattern is observed in all clades (Supplemental Material). Second, for each clade we determined the position-dependent nucleotide frequencies in the regions (–60,+90) around translation starts. We then created synthetic sequences that have the exact same position-dependent base composition as the true sequences in that clade, and folded them. The blue curve in the right panel of Figure 4 shows the z-statistic of the openness of the true sequences compared to these synthetic sequences. Again we see a clearly positive z-statistic in the region immediately around translation start. In summary, the right panel of Figure 4 shows that the base composition around translation start significantly reduces the amount of secondary structure in this area (red curve) and that, beyond this, correlations between bases at different positions further reduce the amount of secondary structure compared to sequences with the same base composition (blue curve).

Two further tests indicate that the avoidance of RNA secondary structure around translation start is associated with selection for translation initiation efficiency. If the avoidance of secondary structure around gene starts were related to transcription rather than translation initiation, we would expect to observe this pattern only in genes that are the first in their operon. However, we observe elevated R values immediately downstream from ATGs of both genes with large and genes with small intergenic regions (Supplemental Material). Second, there is an approximate linear correlation between R at the Shine-Dalgarno peak and the average R in the first 20 amino acids downstream from ATG (Supplemental Material), suggesting a link between these two signals. Interestingly, the five firmicutes clades deviate from this pattern: They have very strong Shine-Dalgarno sequences but only moderately increased R immediately downstream from ATG (Supplemental Material). This suggests that in firmicutes translation initiation is dependent mainly on the ribosome binding site. In summary, a pattern of increased conservation and increased frequency of A nucleotides was observed in E. coli (Eyre-Walker and Bulmer 1993) and B. subtilis (Rocha et al. 1999) and was hypothesized to be the result of selection for translation initiation efficiency which leads to avoidance of RNA secondary structure around translation start. Here we provided additional evidence which supports that selection for translation initiation efficiency is indeed the cause of this pattern, and showed that this pattern extends to all bacteria.

Density of regulatory sites as a function of genome size

Having shown that our R statistic accurately describes sites under purifying selection including known regulatory elements such as the TFBSs in E. coli and the Shine-Dalgarno sequences, we now return to the main motivation of our study: investigating how the density of regulatory sites in intergenic regions varies with genome size. Since, as mentioned in the introduction, organisms with large genomes appear to have complex life styles that require much greater regulatory complexity, and the number of TFs per gene is much larger in larger genomes, we a priori expected that either R itself or a suitably normalized version would correlate with genome size. However, no such correlation exists. As shown in the Supplemental Material, we analyzed the absolute values of R, as well as different combinations of relative differences or ratios of R values in different regions, but none showed any correlation with genome size.

To verify the robustness of this result we performed an analogous analysis using two different methods. First, we used the Q statistic which measures the substitution rate reduction at each alignment column relative to the background model. As detailed in the Supplemental Material, the Q statistic recovers all the results we found using the R statistic, e.g., substitution rates are lower upstream of than downstream from genes, the silent positions evolve according to the background model, substitution rates are lowest upstream of ATG and increase with distance from ATG, and the pattern of lower substitution rates at the Shine-Dalgarno sequence and immediately downstream from ATG. However, as with the R statistic, we found that neither the substitution rates themselves, nor differences of substitution rates between different regions show any correlation with genome size. Second, no combination of differences or ratios of the branch lengths inferred by PAML (bottom-right panel of Fig. 3) shows correlation with genome size. In summary, all three methods find clear evidence of regulatory sites under purifying selection upstream of genes, but in spite of considering a large number of statistics, none of them finds any evidence that the density of regulatory sites in upstream regions increases with genome size. Our results thus strongly suggest that the density of regulatory sites in upstream regions is in fact the same for small and large genomes (and, because intergenic region length does not correlate with genome size, so is the total number of regulatory sites per upstream region).

To verify this further we investigated if there are clear differences in the shape of the R statistic profile upstream of and downstream from genes for genomes of different size. Figure 5 shows the shapes of the R profiles upstream of and downstream from genes, i.e., as in the left panel of Figure 4, but now separately for the small, medium-sized, and large genomes. The shapes of the profiles are very similar for the three classes of genome sizes. In medium-sized genomes the Shine-Dalgarno peak is most pronounced and least pronounced in large genomes. Similarly, the R profile appears to drop fastest with distance from ATG for medium-sized genomes and slowest for large genomes. The shape of the small genome profile falls somewhere in between the shapes of the profiles for large and medium-sized genomes. Thus, although there are some small differences in the shapes of the profiles, these differences do not show a consistent trend with genome size. In the Supplemental Material we show that we find essentially the same result with the substitution rate statistic Q. Overall, the similarity of the profile shapes for small, medium, and large genomes supports that there is a common architecture of regulatory sites which is independent of genome size. Note that, as mentioned in the discussion of Figure 1, this result is also supported by the absence of a correlation between intergenic region size and genome size.

Figure 5.

Relative average R values upstream of and downstream from genes as in the left panel of Figure 4 but now averaged separately over genomes with <2000 genes (green), genomes with between 2000 and 4500 genes (red), and genomes with >4500 genes (blue). In order to compare the shapes of the R value profiles the values on the vertical axis are scaled to have a mean of 1 when averaged over the 150 bp upstream and when averaged over the 150 bp downstream.

The combination of results just presented provides compelling evidence that the average number of regulatory sites per upstream region is independent of genome size. This implies that, whereas the number of TFs increases quadratically with genome size, the total number of regulatory sites increases only linearly with genome size. There are now two possibilities. The first possibility is that in small genomes there are significantly more TFBSs per TF than in large genomes, i.e., regulon size decreases with genome size. The second possibility is that TFs in large genomes more often “share” TFBSs, i.e., that each TFBS is bound by multiple TFs. In eukaryotes one often finds families of TFs with highly similar DNA binding domains that have essentially identical sequence specificities, such that a given binding site can be bound by all members of the family (Sandelin and Wasserman 2004). In prokaryotes, however, such potential sharing of binding sites by families of related TFs has so far not been investigated in detail.

Clustering of TFs with similar DNA binding domains

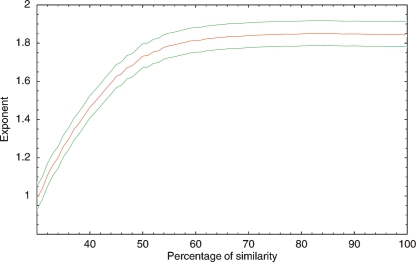
If sharing of TFBSs by multiple TFs is more common in large genomes, we would expect more clusters of TFs with highly similar DNA binding domains in large genomes than in small genomes. In particular, we would expect that, whereas the total number of TFs grows approximately quadratically with genome size, the number of distinct families of TFs would grow more slowly with genome size. Figure 6 shows that this is not the case. We collected the DNA binding domains of all TFs in each genome using Pfam (Bateman et al. 2004). For different similarity cutoffs p we then used single-linkage clustering to cluster all domains with at least p percent identity. We find that, at various cutoffs p, the number of clusters grows roughly as a power-law of the total number of genes (Supplemental Material). Fitting the exponents of the power-laws that are obtained for different cutoffs p (Fig. 6), we found essentially the same exponent when we clustered DNA binding domains, as when we fitted the power-law of the total number of TFs as a function of the total number of genes (1.85). That is, even if we cluster all TFs whose DNA binding domains are 50% identical (at the amino acid level) we still find that the number of clusters grows with almost the same exponent as when each TF is counted independently. For comparison, we compared the DNA binding domains of all E. coli TFs for which the binding specificity is known (Salgado et al. 2006) and found 10 pairs of TFs with at least 50% similarity in their DNA binding domains. Of these 10 pairs only four show similarity in their binding specificity (data not shown). In summary, there is little evidence for families of TFs with high similarity in their DNA binding domains, and no evidence that such families are more common in large than in small genomes.

Figure 6.

Fitted exponent (vertical axis) for the number of DNA binding domain clusters as a function of genome size for different similarity cutoffs (horizontal axis). For a given similarity p we clustered all TFs in each genome whose DNA binding domains had a similarity of at least p percent. We then fitted the number of clusters as a function of the total number of genes in the genome to a power-law. The fitted exponent is shown as the red line, with the green lines indicating the 95% posterior probability interval.

Sequence diversity of DNA 7-mers under most and least purifying selection

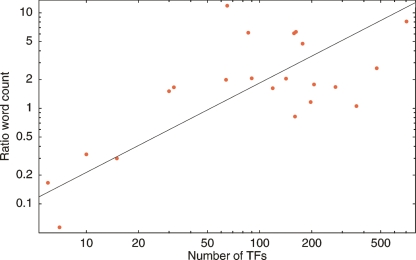
As the “sharing” of TFBSs does not seem to increase with genome size, and the number of regulatory sites per intergenic region appears constant, the necessary consequence is that the number of TFBSs “per TF” must decrease with genome size. That is, our results suggest that small genomes have a small number of large regulons, while large genomes have a large number of small regulons. To test this directly, we compared the sequence diversity of the most conserved sequence segments with the diversity of the least conserved sequence segments in the intergenic regions of each genome. For each clade, we enumerated all 4⁷ 7-mers, counted their number of occurrences in intergenic regions, and ranked them by the amount of evidence they show of being under purifying selection (see Methods). Then, starting from the most significantly selected 7-mer, we counted how many distinct 7-mers are necessary to account for 5% of all intergenic sequence segments of length 7. We denote this number by n_t. Similarly, starting from the bottom of the list, we counted how many distinct “unselected” 7-mers n_b are necessary to account for 5% of all intergenic sequence segments. Figure 7 shows the ratio n_t/n_b for each genome as a function of the number of TFs in the genome. We find that in small genomes one needs only a small number of highly selected 7-mers to account for 5% of all intergenic sequence segments, whereas in large genomes a large number of highly selected 7-mers is needed to account for 5% of all sequence segments (this also holds when taking 10% or 20% instead of 5%, see Supplemental Material). To put it differently, in small genomes the most selected 7-mers are much more frequent than poorly selected 7-mers whereas in large genomes the most selected segments are much less frequent than poorly selected segments. This observation provides a strong piece of independent evidence that, indeed, the regulon sizes of small genomes are significantly bigger than regulon sizes in large genomes. Note that the changes in the ratio n_t/n_b are substantial: The ratio n_t/n_b increases over almost two orders of magnitude, i.e., roughly by the same factor as the number of TFs (straight line fit in Fig. 7).

Figure 7.

Sequence diversity of the most and least conserved 7-mers as a function of the number of TFs in the genome. For each genome we ordered all 7-mers by their evidence for being under purifying selection and collected the most and least conserved unique 7-mers such that each 7-mer of both sets accounts for 5% of all sequence segments in the genome. The vertical axis shows the ratio between the number of most conserved and least conserved 7-mers in the corresponding set as a function of the total number of TFs in the genome (horizontal axis). Both axes are shown on logarithmic scale. The black line shows a linear fit.

Discussion

The intriguing observation that the number of TFs increases almost quadratically with the total number of genes in bacteria implies that there must be important structural differences between the transcription regulatory networks in small and large bacterial genomes. As the number of TFs per gene increases linearly with genome size, either large genomes have on average more regulatory inputs per gene, i.e., more regulatory sites per upstream region, or TFs in large genomes have on average less regulatory outputs per TF, i.e., smaller regulons (or a combination of the two). In order to investigate these possibilities we set to estimate the density of conserved sites in intergenic regions of 22 “clades,” comprising a total of 105 bacterial species.

We produced multiple alignments of orthologous genes and intergenic regions, and estimated the phylogenetic tree of each clade from third positions in fourfold degenerate codons using a “background” evolution model that takes codon bias into account. We defined an R statistic that measures, at each alignment column, the likelihood that the position evolves under substitution rates significantly different from the substitution rates of the background model. We showed that our statistic accurately captures known selection pressures and reveals known regulatory elements. For instance, in all clades we find a sharp peak in R at Shine-Dalgarno sequences a few bases upstream of the start codon. In addition, using the annotation of known regulatory sites in E. coli, we showed that the average R values are almost as high at these known regulatory sites as at coding positions, and significantly higher than the overall average R in upstream regions.

We comprehensively quantified the evidence for purifying selection acting at noncoding positions genome-wide for all 22 clades and found a number of remarkably universal features. First, we found that the bulk of the silent positions within genes evolve according to the estimated background model, whereas essentially all intergenic regions show evidence of purifying selection. Experimental studies suggest (Beletskii and Bhagwat 1996) that transcription itself can increase mutation rates (although comparative genomic studies suggest precisely the opposite; see, e.g., Ochman 2003) and one may wonder if the apparent increase in purifying selection can be explained by a lower mutation rate in intergenic regions. Several of our observations strongly argue against this possibility. An overall lower rate of mutation in intergenic regions would affect all intergenic regions equally, whereas we clearly find most evidence of purifying selection in DR regions, followed by SR regions, and much lower evidence of purifying selection in NR regions. Furthermore, the universal pattern of high R immediately upstream of starts and low R immediately downstream, the universal Shine-Dalgarno peak, and the elevated R at known E. coli regulatory sites all demonstrate that R is capturing conserved regulatory elements and not a decrease in mutation rate.

Another universal pattern that we uncovered is a sharp increase of R values at silent positions immediately downstream from translation start, which is accompanied by a peak in the frequency of adenines around translation start. Previously this pattern has been observed in E. coli (Eyre-Walker and Bulmer 1993; Sato et al. 2001) and B. subtilis (Rocha et al. 1999), and was suggested to result from selection for avoiding secondary structure in the region around translation start. In addition, several experimental studies (Stenstrom et al. 2001; Voges et al. 2004) have shown that increase of adenines immediately downstream from the start codon leads to high translation efficiency. Here we showed that this pattern characterizes all bacterial clades, and we provide evidence that, indeed, the RNA secondary structure around the start codon is one of the main determinants of translation initiation efficiency. We believe that it should be possible to use the biased base composition around gene starts, and the even stronger bias for avoiding RNA secondary structure, to significantly improve ab initio gene finding and gene start annotation in bacterial genomes, especially since the pattern seems to apply universally.

The universal patterns in purifying selection that we observe are confirmed by two independent measures: the Q statistic, which estimates the effective substitution rate at each position relative to the background model, and the branch lengths inferred by PAML from alignments of positions from different regions. We next applied these three measures to evaluate the correlation between genome size and the amount of purifying selection in intergenic regions.

Previous work has shown that operon sizes decrease only slightly with genome size (Cherry 2003; van Nimwegen 2004) and that the sizes of intergenic regions are independent of genome size (Rogozin et al. 2002; van Nimwegen 2004). This implies that, every time the size of a bacterial genome doubles, the total amount of intergenic DNA upstream of operons roughly doubles as well. Yet the number of TFs roughly quadruples, implying that large genomes have a larger number of TFs per gene. One may therefore expect that large genomes have a larger number of regulatory sites per upstream region, especially considering that bacteria with large genomes are generally thought to exhibit much more complex transcription regulation than small parasitic bacteria. In spite of attempts to identify such a correlation using three different methods for measuring purifying selection, and using a large number of different statistics, we found no correlation whatsoever between genome size and the amount of purifying selection in intergenic regions, suggesting that large and small genomes have on average the same density of regulatory sites per gene.

Given that our conservation statistics can only measure the density of “conserved” regulatory sites, an alternative possibility is that large genomes have a higher density of regulatory sites but that these sites tend to be less conserved. Although in principle possible, this scenario would require a general correlation between genome size and the rate of regulatory site turnover and, moreover, it would require that, as the density of sites increases, the turnover rate increase so as to precisely counterbalance the increased site density, leaving no correlation between the number of “conserved” binding sites and genome size. Assuming that site densities simply do not correlate with genome size seems to us a much more parsimonious assumption. In addition, the profiles of R and Q upstream of gene starts have similar shapes for small, medium-sized, and large genomes, which further supports that promoter architectures and regulatory site distributions are similar for large and small genomes. Finally, it is thought that bacteria are generally under selection to minimize the size of their genomes and peudogenes are typically removed from the genomes relatively quickly. It has therefore been argued (Rogozin et al. 2002) that the “sizes” of intergenic regions reflect the amount of regulatory sites within them. Consistent with this hypothesis, we find that DR regions are longer than SR regions and that NR regions are by far the shortest. Yet the sizes of different types of intergenic regions also do not show any correlation with genome size.

All these observations are consistent with the simple conjecture that the number of regulatory sites per intergenic region is constant for small and large genomes, leading us to hypothesize that the basic molecular mechanisms of transcription regulation in bacteria strongly constrain the number of different TFs that can coregulate a given bacterial gene. That is, we hypothesize that bacteria do not have the molecular mechanisms that allow them to place a gene under the control of many different regulatory elements. As a consequence, bacterial genes have on average the same (small) number of regulatory elements per gene, independent of the genome size and the total number of TFs in the genome. This is in stark contrast to what is observed in eukaryotes. Especially in higher eukaryotes genes can receive regulatory inputs from many different regulatory modules that can be located many tens of kilobases from the transcription start site and it is generally assumed that the number of inputs per gene increases with the complexity of the organism. Correspondingly, the sizes of intergenic regions increase dramatically as one moves from simple to more complex eukaryotes. We thus propose that a key difference between the transcription regulatory networks of prokaryotes and eukaryotes is that prokaryotes are constrained to only a small number of regulatory inputs per gene.

The quadratic growth of TFs with genome size together with an on average constant number of regulatory sites per gene now imply that the number of unique regulatory sites per TF decreases significantly with genome size, i.e., by a factor of 20 between the smallest and largest genomes. Given that we find that clusters of TFs with highly similar DNA binding domains are typically small and the size of these clusters does not grow with genome size, we conclude that there is little evidence of “site sharing” in bacteria, which in turn implies that TFs have on average much fewer TFBSs per TF in large compared to small genomes. This conclusion is further supported by our observation that there is a highly significant correlation between genome size and the sequence diversity of the most conserved sequence segments: Whereas in small genomes the most conserved 7-mers tend to also be the most common 7-mers in intergenic regions, in large genomes the most conserved 7-mers are the least common 7-mers. This provides a strong independent piece of evidence that regulon sizes are large in small genomes and small in large genomes.

The main global statistic of genome organization that we have left largely unexplored is the role of base composition and codon bias. There are a number of intriguing observations that suggest that there may be intimate connections between genomic GC content, codon bias, genome size and regulatory complexity, and selection acting at intergenic and silent positions. First, highly expressed genes tend to show more codon bias (Sharp and Li 1987) and, as tRNA abundances generally correlate with codon bias, this is interpreted as a result of selection at silent positions to ensure translation efficiency of highly expressed genes. Second, more recently evidence has been presented that codon bias is largely driven by an underlying bias in GC content of the genome (Knight et al. 2001; Chen et al. 2004). Traditionally it has been assumed that GC contents of genomes simply reflect the underlying mutational biases, and Ochman (2003) and Chen et al. (2004) provide some evidence in support of this hypothesis. If this is indeed the case, then compositional bias, codon bias, the relative abundances of different tRNAs, and the selection at silent sites in highly expressed genes would all derive from an underlying mutational bias. Moreover, our background models would accurately reflect mutational biases, so that the deviations from these background models measure selection directly. There are several observations, however, that suggest that reality may be more complicated. First, experimental studies of mutational biases as well as comparative studies on pseudogenes all suggest a general bias of GC to AT mutations (Ochman 2003). Second, from a metabolic perspective AT nucleotides are energetically less costly than GC nucleotides, and it has been suggested (Rocha and Danchin 2002) that this leads to selection for AT over GC nucleotides in situations where energy resources are limiting. Both of these observations beg the question as to why there are genomes with very high GC content at all. Third, there is a clear correlation between GC content and genome size, with very small genomes being almost all AT rich and large genomes being almost all GC rich (Bentley and Parkhill 2004). It is hard to imagine why genome size and mutational biases would be directly correlated, suggesting again that GC content may be the result of a more complex interplay of effects including selection. Finally, GC content differs in a consistent way between different intergenic regions (Mitchison 2005) and genes, suggesting a link between GC content and the regulatory organization of a genome. In essentially all species NR regions have the lowest GC content, followed by SR regions, followed by DR regions, and it was suggested in Mitchison (2005) that this is a result of the preference of regulatory sites for AT-rich sequences. We, in addition, find that GC content is higher in genes than in intergenic region in all clades. Together, all these observations form pieces of a puzzle that relates GC content, codon bias, genome size, and selection in intergenic and silent positions. Working out how these pieces fit together is one of the main issues regarding bacterial genome evolution that remain to be solved.

Methods

Determination of the median intergenic region lengths

To determine the median intergenic region lengths in 416 currently fully sequenced bacterial genomes we used the predictions of a recent Bayesian operon-prediction algorithm (Price et al. 2005), which we downloaded from http://www.microbesonline.org/operons/. Once the operons are predicted, we calculate the median length of NR regions, SR regions upstream of the first gene in an operon, and DR regions, separately for each genome.

Ortholog mapping and determining phylogenetic topology

Our procedure for mapping orthologs modifies the standard “best-reciprocal hit” procedure to be both conservative and take advantage of the significant amount of gene-order conservation between the closely related species. For each pair of organisms in a clade we estimate the evolutionary distances between each pair of genes using PAML (Yang 1997), i.e., as in Wall et al. (2003). An initial set of “trusted pairs” is constructed by taking only those best-reciprocal hits that align >50% of both proteins and for which the evolutionary distance of the second best hit is at least twice the evolutionary distance of the best hit. We then resolve additional orthology relations by making use of gene-order information. We first construct diagonals of trusted pairs that are consecutive in both genomes and search for additional orthologous pairs that lie within the gaps or at the edges of the diagonals of already identified orthologs. Details of this and all other methods are given in the Supplemental Material.

Our inference of the phylogenetic tree, base composition, and codon bias of each clade is based on cliques of orthologous genes. A “clique of orthologs” is a set of genes, one from each species in the clade, that all are mutually orthologous. We sort cliques by the amount of conservation at silent positions and remove the top and bottom 10% for our further inferences. This is done to avoid that outliers, such as the ribosomal genes that are significantly more conserved at silent positions than other genes, or genes whose orthologs have been misidentified, would skew the parameters of the background models. To determine the topology of the phylogenetic tree of a clade we align all cliques of orthologous proteins using T-Coffee (Notredame et al. 2000) and apply TREE-PUZZLE (Schmidt et al. 2002) to the concatenation of protein alignments.

Evolutionary model

The molecular evolution of natural populations is an extraordinarily complex process, involving so many different confounding influences (e.g., mutational biases, epistatic interactions, heterogeneous recombination rates, population mixing patterns, temporal variations in population size, time-dependent selection, frequency-dependent selection, and so on), that essentially all models of molecular evolution are not more than simple cartoons that focus on a few processes which are judged to be the most relevant. Consequently, there is a large variety of models and approaches to detecting natural selection from sequence data (for review, see Nielsen 2005). Detecting sequence substitutions that are the result of adaptive evolution, i.e., that were positively selected, is especially challenging and typically requires the comparison of polymorphism data within one species with substitution data between closely related species (for review, see Eyre-Walker 2006).

Here we are concerned with using conservation statistics of multiple alignments of orthologous DNA from related species to infer sites that are under purifying selection. A simple and robust approach to this problem is to compare conservation statistics of “pairwise” alignments of presumed “neutral” segments with the statistics of conservation in nearby segments that may contain constrained sites. This approach has, for instance, been applied to estimate the fraction of sites that are under purifying selection in intergenic DNA of Drosophila (Halligan et al. 2004; Halligan and Keightley 2006). In the context of bacterial genomes, a very similar approach has been used to extract putative regulatory sites in E. coli using pairwise alignments of orthologous intergenic regions from related species (Rajewsky et al. 2002). Such approaches can be generalized to the analysis of alignments of multiple species. Here the most commonly used approach is to introduce an explicit model of the substitution rates along the branches of the phylogenetic tree relating the species. Such models assign probabilities to multiple-alignment columns in terms of the substitution rates and lengths of the branches (Felsenstein 1981). Hidden Markov models are then used to segment multiple alignments into two (or a small number of) classes of sites (Yang 1995; Felsenstein and Churchill 1996), i.e., those that evolve at slower overall rates and those that evolve at higher overall rates. Maximum likelihood is used to estimate the substitution rates in the different classes of sites. This approach has for example been used to estimate the fraction of DNA that is evolving slowly, presumably because of purifying selection, in the genomes of a substantial number of eukaryotes (Siepel et al. 2005).

Here we are interested in estimating the density of conserved transcription factor binding sites (TFBSs) from multiple alignments of bacterial orthologous intergenic regions. To do this we introduce two types of evolutionary models, a “background model”, which describes the overall evolution of a category of sites (such as all sites in intergenic regions or all sites at third positions of a particular fourfold degenerate codon), and a “foreground” model, describing the evolution of positions in regulatory sites or, more generally, positions that evolve under a significantly different set of substitution rates. We then use the likelihood-ratio of the “foreground” and “background” models for each alignment column to quantify the evidence that the position is part of a regulatory site.

Binding sites for a given TF are generally represented through position-specific weight matrices w where 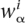denotes the fraction of regulatory sites (for the TF in question) having nucleotide α at position i. Biophysical models of TFs binding to their target sites show (Berg and von Hippel 1987; Bintu et al. 2005; Mustonen and Lässig 2005) that, to a good approximation, the total binding free energy of a TF to a binding site is the sum of independent binding energies from each nucleotide in the site. In addition, the binding energy 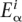of nucleotide α at position i is, to a reasonable approximation, proportional to the logarithm log(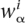) of the frequency 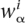of α at position i. Because the binding energies 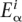vary significantly, with both the identity of the preferred nucleotides and the strength of the preference varying from position to position, one generally cannot assume uniform substitution rates across positions in TFBSs. Indeed, studies of the evolution of known regulatory sites show that substitution rates vary significantly from position to position and in correspondence with the equilibrium frequencies 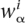(Brown and Callan 2004; Moses et al. 2004; Mustonen and Lässig 2005).

We thus felt it to be essential that our model for the evolution of TFBSs takes into account that both the preferred nucleotides and the strength of the preference vary from position to position. Our model assumes that different positions in regulatory sites evolve independently from each other. Since selection most likely acts on the binding energy of the entire site to the TF, this assumption is only an approximation, as stressed in Mustonen and Lässig (2005). However, the fact that different positions in known TFBSs show only marginal correlation indicates that this approximation is fairly accurate, and indeed this approximation is followed by virtually all currently used models of regulatory site evolution. Second, for each position i in a regulatory site we assume there is a (generally unknown) set of four selection coefficients for the possible nucleotides at this position, which are constant through time and, in the limit of large time, lead to the set of equilibrium frequencies 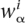. Following Golding and Felsenstein (1990), Halpern and Bruno (1998) have shown that, in the weak mutation limit of the standard Kimura-Ohta theory, one can uniquely determine substitution rates in terms of the mutation rates and the equilibrium frequencies 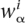. In particular, if 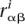is the rate of substitution from β to α at position i, μ_αβ the rate of mutation from β to α, and 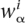the equilibrium frequency of α at this position, we have (Halpern and Bruno 1998)

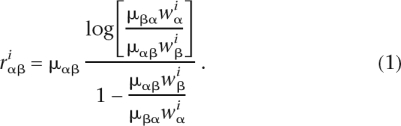Under the Halpern-Bruno (HB) model, the probability to evolve from nucleotide β in the ancestor to nucleotide α in the descendant over the course of a time t is then given by

where μ denotes the matrix of mutation rates, wⁱ denotes the vector of equilibrium frequencies at position i, and rⁱ the matrix of substitution rates at this position. The matrix exponential e^rit is generally calculated by (numerically) diagonalizing the matrix rⁱ.

Given the transition probabilities (Eq. 2) and given a phylogenetic tree T, one can then calculate the likelihood L_HB(C|w, μ, T) for an alignment column C. Formally the likelihood is the product over transition probabilities P_HB(α|β, μ, wⁱ, t) for each branch of the tree, summed over all possible nucleotides for the internal nodes, and can be calculated efficiently using the recursive algorithm introduced by Felsenstein (1981). This calculation requires, however, that we know the mutation matrix μ and the equilibrium frequencies 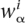. In some situations, these quantities may indeed be known. For example, for a given TF one can determine the equilibrium frequencies 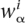from collections of known binding sites and one can then use the model with substitution rates (Eq. 1) to identify conserved binding sites for the TF in multiple alignments of intergenic regions. This approach has been implemented by the MONKEY algorithm (Moses et al. 2004). In our situation, however, the equilibrium frequencies 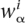are intrinsically unknown. The rigorous Bayesian solution in this situation is to treat the equilibrium frequencies as nuisance parameters that need to be integrated out of the likelihood. That is, given a prior probability distribution P(w) over possible equilibrium frequencies, we would calculate

where the integral is over all vectors w such that w_α ≥ 0 for all α, and ∑_αw_α = 1. Unfortunately, because of the complicated dependence of the rates r_αβ on the equilibrium frequencies w, these integrals are generally intractable. If the likelihood were sharply peaked as a function of w, we could approximate the integral by the value at its peak and a correction factor such as the Bayesian Information Criterion (Schwarz 1978). However, since in our case the “data” consist of only a single-alignment column C with nucleotides from typically a handful of species, the likelihood function is typically not sharply peaked so that such approximations are not suitable.

We thus sought to approximate the Halpern-Bruno model with a simpler model for which the integral (Eq. 3) can be performed and that maintains the feature that selection coefficients (and correspondingly the limit frequencies 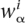) can vary from position to position in regulatory sites. This can be achieved by using the following substitution rate model introduced by Felsenstein (1981)

also known as the F81 model. The F81 model makes the simplification that the substitution rate is dependent only on the identity of the target base. In addition, whereas the HB model explicitly separates the effects of mutation rate biases and selection on the equilibrium frequencies, the F81 model parametrizes the overall mutation rate by a single parameter μ and subsumes the effect of mutational biases and position-dependent selection into the position-dependent equilibrium frequencies 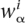. Alternatively, one can think of the F81 model as assuming equal rates of all mutations and assuming that, at position i, the probability of a mutation to base α has a probability 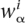to be fixed in the population. Under the F81 model the probability P(α|β, t, w) to evolve from ancestral base β to offspring base α over a time t is

In spite of the conceptual differences between the HB and F81 models, in practice the transition probabilities of the HB and F81 models are typically not very different numerically. The model we use here has been successfully applied in a number of algorithms (Sinha et al. 2003, 2004; Siddharthan et al. 2005) for regulatory motif finding in alignments of orthologous intergenic DNA.

To calculate the likelihood L_F81(C|μ, T) of an alignment column C we now need to calculate the integral

For the prior we use standard Dirichlet priors of the form

with the λ_α being the so-called pseudocounts. Since the likelihood L_F81(C|w, μ, T) is simply a polynomial in the equilibrium frequencies w_α, we can perform the integral term by term using the general identity

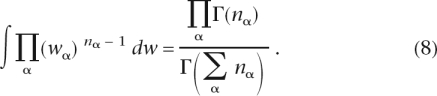In summary, in order to incorporate the fact that in regulatory sites the selection coefficients vary significantly from position to position, we used a simplified version of the general Halpern-Bruno model, i.e., the F81 model, to calculate the likelihood L_F81(C|μ, T) of any alignment column C as a function of the mutation rate μ and phylogenetic tree T.

Background evolution models

Our evolutionary model for regulatory sites thus assumes an F81 substitution rate model with independent equilibrium frequencies w_α at each position, which are treated as unknown nuisance parameters that are integrated out of the likelihood. We contrast this “foreground” model with a “background” model, which is exactly the same, except that the equilibrium frequencies w_α are not assumed unknown and varying from position to position, but rather they are assumed the same at each position and are estimated from the overall nucleotide frequencies. It is clear, however, that using a single background model for all noncoding positions is not appropriate. One generally finds significantly higher AT content in intergenic regions than in genes and, moreover, different fourfold degenerate codons show significantly different frequencies of the nucleotide in their third position. We thus introduce separate background models for intergenic positions and for each of the eight fourfold degenerate codons. To compare the likelihood-ratios between foreground and background models at noncoding positions with those at coding positions we also introduce background models for first, second, and third positions in codons in general. For each of these 12 background models we estimate the equilibrium frequencies w_α by simply determining the base frequencies at all positions in each of the 12 classes genome-wide.

Finally, for each of the 12 classes of sites we set the pseudocounts in the prior (Eq. 7) equal to the estimated nucleotide frequencies in the corresponding class, i.e., λ_α = w_α. As shown in the Supplemental Material, this guarantees that, in the limit of very short branch length t → 0, the foreground and background models will obtain the same likelihood.

Phylogenetic tree estimation

The likelihoods of foreground and background models still depend on the product μt of overall mutation rate μ and branch length t, i.e., Equation 5, for each branch of the tree. Note that, since the likelihood depends only on the product μt, we can set μ = 1 without loss of generality. To estimate the branch lengths t for each branch of the tree we use third positions in fourfold degenerate codons to estimate distances between every pair of species in the clade. For a pair of species, we collect from all aligned clique genes the third positions in fourfold degenerate codons with conserved amino acids and count the number of times 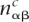that base α occurs in the first species and base β in the other, in codons of type c. We then fit the distance t between the pair of species by maximizing the likelihood of the observed counts 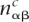under the background evolutionary model using, for each fourfold degenerate codon c, the estimated nucleotide frequencies 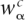at third positions of this codon genome-wide (Supplemental Material). After having determined the distances between all pairs of species in the clade we fit branch lengths t_b for each branch b of the tree using the standard least-squares phylogenetic distance estimation for a fixed tree (Cavalli-Sforza and Edwards 1967; Supplemental Material).

Likelihood ratios R at each alignment column

Using the estimated tree and the nucleotide frequencies in each of the 12 categories of positions we calculate the likelihoods of foreground and background models at each multiple-alignment column. The multiple alignments of positions in genes were obtained as described above. To obtain the multiple alignments of intergenic regions we collect, for each intergenic region, the orthologous regions from the other species in the clade; a region is orthologous if both flanking genes are orthologous and the genes are in the same relative orientation. To avoid boundary effects of the alignment algorithm we align all orthologous intergenic regions plus their flanking genes using T-Coffee (Notredame et al. 2000).

For each alignment column C in the genome of the reference species we determine the class c of the position and determine the likelihoods L_fg(C|c) and L_bg(C|c) of the foreground and background models for a site in this class.

The likelihood ratio

quantifies the amount of evidence that column C is evolving with substitution rates different from the background model. As the Supplemental Material shows, R = 1 on average for positions evolving according to the background model. In practice large values of R occur for columns that are significantly more conserved then expected or, more generally, where the variation of bases is less than expected according to the background model.

We analyze the evidence of purifying selection in different groups of positions by calculating the average value of R(C|c) for different groups of positions. In particular, we determine the average value of R in different types of intergenic regions, the average value of R within different classes of positions within genes, and the average value of R at given locations relative to the start codons and stop codons of genes.

To verify the robustness of our results we also analyze conservation statistics using two separate methods. First, as detailed in the Supplemental Material, we can use the same foreground and background models to estimate the average substitution rate at each position and we quantify the amount of purifying selection by the relative reduction Q of the estimated substitution rate relative to the expected substitution rate under the background model. Second, we also estimate the amount of purifying selection in intergenic regions of different types using PAML with the HKY85 substitution rate model. This gives a completely independent assessment using an evolutionary model that takes into account that transition and transversion mutations occur at different rates. We find that our results are highly robust: All of the main results are confirmed using Q statistics and also by the branch lengths inferred using PAML.

Sequence diversity of most and least conserved 7-mers

The probability that a sequence segment evolves under the foreground rather than the background model is quantified by the sum of the log(R) values of the alignment column in the segments. Moving with a sliding window of length 7 over all intergenic region alignments we assigned a score X, equal to the sum over log(R) values, to each window. For each of the 4⁷ possible 7-mers s we collected all n(s) occurrences of the 7-mer in intergenic regions and calculated the average score 〈X(s)〉 and its variance var(X(s)). We also calculated the overall average 〈X〉 over all n windows of length 7 and the overall variance var(X). Assuming that the scores of the n(s) windows with 7-mer s were drawn from a Gaussian distribution with unknown mean and variance, the probability that the mean differs from the overall mean〈X〉 is quantified by the z-statistic

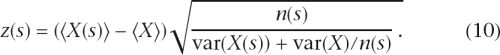For each clade we calculate the z-statistics z(s) for each 7-mer s and produced an ordered list of 7-mers, with the most conserved at the top and least conserved at the bottom. We then collected the top n_t 7-mers such that the sum of the n(s) equals 0.05n, i.e., 5% of all windows. Similarly we collected the bottom n_b 7-mers such that the sum of their occurrences n(s) equals 0.05n. Finally, we calculated the ratio n_t/n_b for each clade.