Buffered Diffusion around a Spherical Proton Pumping Cell: A Theoretical Analysis

Abstract

H⁺ ions are a substrate of many active and passive membrane transporters in all cells. Absolute proton fluxes are often quantified using intracellular pH sensitive microelectrodes or pH sensitive dyes. These measurements, however, rely on a priori estimates of the intracellular buffer capacity and on the assumption of diffusive equilibrium inside the cell. Here, assuming local equilibrium of protons with a single mobile buffer, we model the diffusion of H⁺ in the extracellular medium around an H⁺ pumping cell to estimate the expected pH changes as a function of time, distance from the cell, extracellular buffer capacity, and the absolute proton flux across the membrane. In particular, using accurate numerical simulation, we gauge the range of validity of an explicit, analytical solution of the linearized, nonstationary diffusion equation. Our results provide a framework to quantify the absolute membrane proton flux, if spatiotemporal information about the extracellular pH change is available, e.g., using imaging of pH dependent fluorescent dyes.

INTRODUCTION

The survival of all living organisms depends on the transport of ions and other substrates across biological membranes. In this respect, protons (H⁺) have a special role: an appropriate H⁺ concentration (pH) is critical for many physiological processes and the energy stored in the H⁺ electrochemical gradient can be used for the production of ATP and for the transport of ions and other substances across the membrane. Considering the variety of these functions, it is not surprising that H⁺ are moved across membranes by a huge diversity of proteins, encompassing primary active, secondary active, and passive transporters, either as the sole substrate or being co- or countertransported. These H⁺ transporting proteins include proton channels (gramicidin, M₂ viral proton channel, voltage-gated proton channels), F-type, P-type, V-type ATPases, bacterial reaction center, cytochrome c oxidase, channelrhodopsin (1,2), major facilitator superfamily (MFS) proteins such as LacY, GlpT, and ErmD (3), small multidrug resistance (SMR) proteins (EmrE), resistance-nodulation-division (RND) proteins (AcrB) (4), H⁺-coupled nitrate, tetracycline, amino acid, oligopeptide, and sugar transporters (5), Na⁺/H⁺ antiporters (6), bacteriorhodopsin (7), H⁺-coupled organic cation transporters (hOCTN1) (8), and members of the natural resistance-associated macrophage protein (Nramp) family, implicated in heavy metal ion transport (9).

Several methods have been developed to quantify the absolute proton flux across the membrane. These include, e.g., pH sensitive microelectrodes (10,11) or pH sensitive dyes (12,13). A precise determination of the proton flux is helpful to gain insight into the mechanism of transport. For example, if a single type of H⁺ transporter dominates the overall transport, as, e.g., in overexpressing heterologous systems, and if the number of transport proteins is known, the knowledge of the proton flux allows an absolute measurement of the single transporter turnover rate. Furthermore, if an independent measurement of the flux of a cotransported substrate is available, knowing the proton flux allows a determination of the stoichiometry of transport. This method for estimating the stoichiometry is especially useful if it is impossible to determine the conditions under which the transporter is in equilibrium. For strictly coupled electrogenic transporters, the reversal potential coincides with the voltage at which no net transport occurs. For example, the 2 Cl⁻:1 H⁺ stoichiometry of the bacterial Cl⁻/H⁺ exchanger ClC-ec1 has been determined from the reversal potential of the associated currents (14) and from flux experiments (15). Using pH sensitive microelectrodes or BCECF fluorescence a Cl⁻/H⁺ exchange activity has also been demonstrated for the mammalian ClC-4 and ClC-5 proteins (11,13). However, for these proteins, it is practically impossible to determine a true reversal potential because these transporters are extremely outwardly rectifying (16,17). Consequently, it is impossible to determine the transport stoichiometry based on the reversal potential.

Picollo and Pusch (11) have measured the extracellular pH close to the surface of ClC-5 expressing Xenopus oocytes to demonstrate the transport of H⁺ across the membrane. The biggest advantage of measuring the extracellular pH (and not intracellular pH) is that the composition of the extracellular solution can be precisely controlled. In particular, the buffer capacity can be adjusted at will. In this article we analyze the mathematics of diffusion around a spherical cell that transports protons homogenously and at a constant rate to gauge the possibility of using spatiotemporal information of the pH around the cell to determine the absolute flux across the membrane. We use numerical methods to solve the nonlinear diffusion equation in the presence of a mobile buffer, assuming a fast buffering reaction. Furthermore, we derive an analytical solution of the linearized diffusion equation. We then compare the exact, but slow, numerical integration with the approximate analytical solution to determine the range of experimental conditions for which the approximate solution can be applied.

RESULTS

Theory

We consider a spherical cell of radius a (in meters) that begins to extrude H⁺ at t = 0 at a constant flux, J (in mol/m²/s) (Fig. 1). This flux corresponds to an equivalent current, I, of magnitude

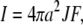where F is the Faraday constant. The free H⁺ concentration, [H⁺] = H, around the cell has initially the value

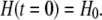FIGURE 1.

Schematical sketch of the topology used for the simulation studies. The radius of the cell is a, the maximal radius is r_max, and the proton flux out of the cell is J. The concentric spheres have a distance of Δr from each other.

Because concentrations are measured in mol/liter (and not mol/m³), attention has to be paid when introducing the flux into the equations. The extracellular solution contains a single mobile buffer at the total concentration

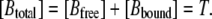The buffer is characterized by the reaction

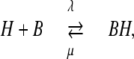with second order association rate constant, λ, first order dissociation rate constant, μ, and the equilibrium dissociation constant

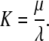If we assume that the free buffer and the H⁺-bound buffer have the same diffusion coefficient, D_B, and if the buffer is initially distributed homogeneously, the local total concentration remains constant (18). We will assume spherical symmetry and homogeneity of the density of the transport proteins on the membrane surface. This is, of course, an oversimplification, because it is known that membrane proteins are often clustered (see, e.g., Gomez-Hernandez et al. (19)). The consequences of this assumption will be considered in more detail in the Discussion. The assumption of spherical symmetry and homogeneity greatly simplifies the mathematical treatment of the problem, which can be expressed by the combined reaction-diffusion equations (18,20)

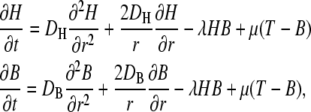(1)

where r is the distance from the center of the cell, B denotes the concentration of free buffer, H the free proton concentration, D_B the diffusion coefficient of the buffer (assumed to have the value of 5 × 10⁻¹⁰ m²/s), D_H the H⁺ diffusion coefficient (assumed to have the value of 9.3 × 10⁻⁹ m²/s), and T the total buffer concentration.

Protons and at least one of the buffer species (either the protonated buffer, the unprotonated buffer, or both) are electrically charged. Thus, a full description of buffered diffusion should incorporate effects of the electric field in an electrodiffusion approach (20). Furthermore, if H⁺ is co- or countertransported with another substrate a gradient will be generated for the other substrate, too, that in turn will influence the proton diffusion. For example Na⁺ ions are countertransported in NHE exchangers (6), Cl⁻ ions are countertransported in CLC proteins (14). Fortunately, in most cases, the co- or countertransported ions are present at much higher concentrations than protons. For example, Cl⁻ ions are usually present in tens of millmolar. Thus the Cl⁻ concentration will change much less in relative terms than the proton concentration. Most importantly, the bulk ion concentration in physiological solutions is generally much higher than the change of the proton and buffer concentration achieved by the transport activity. Thus, any electrical gradient will be quickly compensated by small diffusive adjustments of the bulk ion concentrations (21). Therefore, for moderate H⁺ transport rates, we can safely neglect the effect of electrical gradients caused by transport and diffusion.

Because the chemical reaction of protons with buffer is fast (22), an accurate solution of Eq. 1 is numerically expensive. We shall assume that the buffering reaction, characterized by λ and μ, is very fast, such that protons and buffer are in local equilibrium. Later, we will test the validity of this assumption. With the assumption of fast buffering, B can be expressed in terms of H via the equilibrium condition

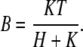Taking the difference of the two reaction diffusion equations (Eq. 1) eliminates the explicit dependence on the rate constants λ and μ:

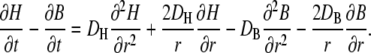For convenience we define

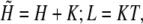with these abbreviations and using

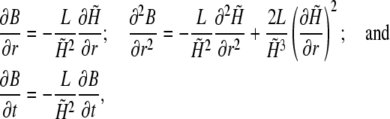the above differential equation can be rewritten as

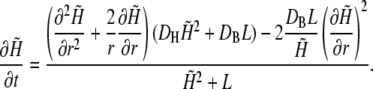(2)

This equation was solved numerically imposing the boundary condition of constant total proton flux, J, for r = a as described below.

Equation 2 provides an accurate description of the diffusion process. However, its evaluation is rather slow to be used in rapid data analysis that necessitates a fit to the experimental conditions. We sought therefore to derive an analytical solution of the linearized equation. To this end we define the variations of H and B around their initial values, as h and b, respectively:

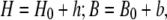where h and b can also assume negative values.

Inserting these into the equilibrium buffering condition, 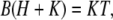yields

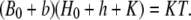Because

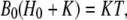it follows

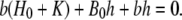The approximation used consists in neglecting the term bh in the above expression. Thus,

For convenience we define

Taking, as above, the difference of the temporal derivatives of H and B cancels out the buffering terms

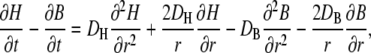and inserting here the above expression for b yields

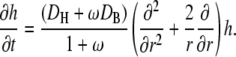We define the effective diffusion coefficient, D, by

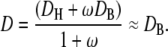The above approximation holds because D_H is only ∼20-fold larger than D_B, whereas ω ≫ 1. With this notation, the linearized version of the diffusion equation is that of a simple, unbuffered diffusion:

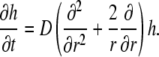(3)

The boundary condition at infinite distance is simply

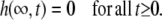On the other hand, for the boundary condition at the border of the cell, we have to consider that the assumed constant flux, J, of protons across the membrane is immediately buffered and increases the proton concentration only according to the buffer capacity. Thus, instead of the simple condition 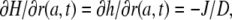for all t ≥0, we have to put

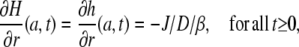where β is defined as the required addition of absolute proton concentration per change in free proton concentration. This depends on the total buffer concentration and is, in principle, not constant, but depends on the saturation of the buffer. For now, we are interested in “small” changes and we regard β as a constant that has to be determined experimentally.

For the simple monovalent buffer described by the above reaction equation, the value of β is approximately given by (18,23)

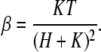This expression is valid within the linear approximation, i.e., for small variations of H around the equilibrium value. For now, we treat β as an experimental parameter that depends on the solution.

The initial condition can be formulated as

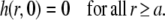Defining

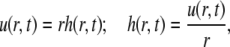from Eq. 3 it follows that

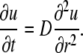The boundary conditions for u are

and the initial condition is

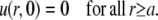We define the Laplace transform of u as

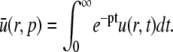Using standard Laplace transform rules (24) it can be concluded that ū satisfies the ordinary differential equation

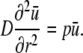This has the unique solution

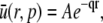where

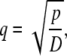and A has to be determined from the boundary conditions.

resulting in

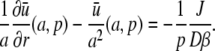Thus

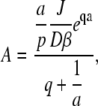and the full solution for the Laplace transform is

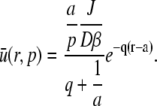From Table 2.2 of Crank (25) the inverse Laplace transform can be found with the result

(4)

with

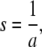and where erfc(.) denotes the complementary error function.

Conditions for numerical simulation

In our simulations we analyzed and compared two standard experimental systems used for the biophysical analysis of heterologously expressed ion transporters: Xenopus oocytes and cultured cell lines. Xenopus oocytes are large (diameter ∼1 mm), almost spherical cells. Cultured cells (e.g., HEK cells) are much smaller (typical diameter 20 μm) and of variable geometry. However, for many cell lines, almost spherical cells are relatively frequent. A spherical geometry is also favored if cells are detached from the culture dish, e.g., after establishing the whole cell configuration of the patch-clamp technique. Thus, the two systems considered in this manuscript are an oocyte of radius 0.5 mm (from now on called “oocyte”) and a spherical cultured cell of radius 10 μm (from now on called “small cell”). Typical expression levels in these systems, in terms of currents evoked in voltage-clamp experiments, are of the order of μA in oocytes and nA in small cells. For example, for the Cl⁻/H⁺ antiporter ClC-5, expression levels in small cells range from 100 pA to 2 nA and in oocytes from 0.5 to 10 μA (G. Zifarelli and M. Pusch, unpublished data). This corresponds to charge fluxes densities of 0.83–16 μmol/s/m² for small cells and from 1.6 to 33 μmol/s/m² for oocytes. Thus, in both systems, the flux density is of the same order of magnitude.

The nonlinear partial differential equations (Eqs. 1 and 2) were solved using the Crank-Nicolson algorithm (26) with Crank-Nicolson parameter 0.5 (semiimplicit discretization). The region around the cell (Fig. 1) was divided into N_R slices, up to a maximum radius, r_max, resulting in a width of each slice of

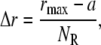where a is the cell radius. The time step of integration is designated as Δt. The discrete values at these mesh points are thus

for i = 0, …, N_R, j = 0, …, N_T, where N_T is the number of time steps, where f stands for H and B (Eq. 1) or for 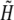(Eq. 2) ( see Table 1).

TABLE 1.

Glossary of symbols

Symbol	Meaning	Units
A	Amplitude coefficient of the Laplace transform	mol/m2/s
a	Radius of cell	m
B	Free buffer concentration	mol/m3
B0	Bulk free buffer concentration	mol/m3
b	B − B0	mol/m3
β	Buffer capacity (ΔHtotal/ΔHfree)	–
D	Effective diffusion coefficient ((DH + ωDB)/(1 + ω))	m2/s
DB	Diffusion constant of buffer (used value, 5 × 10−10 m2 s−1)	m2/s
DH	Diffusion constant of protons (9.3 × 10−9 m2 s−1)	m2/s
F	Faradays constant	C/mol
Δr	Radius step for integration	m
Δt	Time step for integration	s
ΔHfree	Change in free proton concentration	mol/m3
ΔHtotal	Change in total proton concentration	mol/m3
H	Free proton concentration	mol/m3
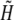	H + K	mol/m3
H0	Bulk free proton concentration	mol/m3
h	H − H0	mol/m3
I	Proton current through the membrane	A
J	Proton flux density through the membrane	mol/m2/s
K	Dissociation constant of the mobile buffer	mol/m3
L	K T	mol2/m6
λ	Association rate constant of mobile buffer	m3 mol/s
μ	Dissociation rate constant of mobile buffer	s−1
NR	Number of slices in the numerical simulation	–
NT	Number of time steps in the numerical simulation	–
p	Variable of the Laplace transform	s−1
pK	Negative decadic logarithm of K (measured in mol/l)	–
q		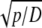m−1
ω	B0/(H0 + K)	–
r	Distance from the cell center	m
rmax	Maximum radius in the numerical simulation	m
s	1/a	m−1
T	Total buffer concentration	mol/m3
u(r,t)	r × h(r,t)	mol/m2
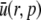	Laplace transform of u	mol s/m2

The second spatial derivative was approximated by

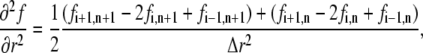being the average of the “future” and the “present” derivative (26).

Second-order difference equations were also used for the spatial first-order derivatives. The final difference equations result in a tridiagonal matrix equation for the “future” values of f (27) that was solved using standard routines (27).

To impose bulk pH at “infinite” distance the boundary values were fixed by 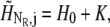where K is the dissociation constant of the buffer. The constant total flux for r = a was imposed as follows: The total amount of protons being transported during time Δt is given by

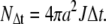This leads to an increase of the total proton concentration in the first volume shell of

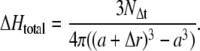For the solution of Eq. 1, this amount was added to the proton concentration of the first volume shell. In contrast, for Eq. 2, according to the fast buffering reaction, this change in total proton concentration leads to the following change in free proton concentration

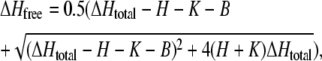where H is the previous free proton concentration and B the associated free buffer concentration in the first volume shell. For each time step, after solving the difference equations, this value for ΔH_free was added to 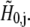All numerical calculations were implemented in Visual C++ using double (8-byte) floating point arithmetic.

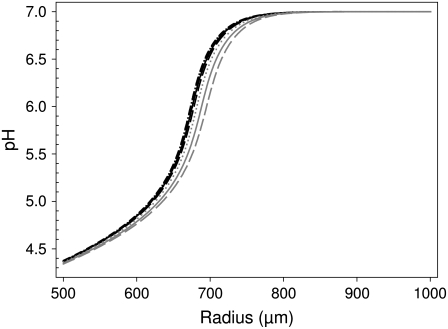
In a first set of simulations we determined the largest time step (Δt) and Δr-values that were acceptable for a precise numerical solution of Eq. 2. The procedure is illustrated in Fig. 2 that shows various solutions of Eq. 2, 10 s after the onset of a proton current of 1 μA and a total buffer concentration of 0.2 mM (initial pH 7, pK of buffer 7). The figure shows the dependence of the pH as a function of the distance from the oocyte center (starting at 500 μm, the radius of the oocyte). The solutions for (Δr, Δt) = (10⁻⁷ m, 10⁻⁶ s) (solid black curve), (Δr, Δt) = (10⁻⁷ m, 10⁻⁵ s) (dotted black curve), and (Δr, Δt) = (2 × 10⁻⁷ m, 2 × 10⁻⁶ s) (dashed black curve) are almost indistinguishable. Even the dash-dotted black curve obtained with the very small values (Δr, Δt) = (10⁻⁸ m, 10⁻⁷ s) is very similar to these approximations. In contrast, solutions for (Δr, Δt) = (5 × 10⁻⁷ m, 10⁻³ s) (solid gray curve), (Δr, Δt) = (2 × 10⁻⁷ m, 10⁻³ s) (dotted gray curve), or (Δr, Δt) = (10⁻⁶ m, 2 × 10⁻⁶ s) (dashed gray curve) are significantly different from the presumably exact solution. Thus, for the particular condition shown in Fig. 2, we can conclude that (Δr, Δt) values of (10⁻⁷ m, 10⁻⁵ s) provide a sufficiently fine grid to guarantee a precise numerical solution. The method of “visual inspection” to judge the quality of the numerical solution may seem arbitrary. However, applying several different standardized rigid criteria led to unsatisfactory solutions in various parameter regimens (data not shown). We therefore preferred the somewhat subjective method described above. Based on a very large data set of simulations under various conditions, we compiled tables with the values of (Δr, Δt) that are necessary (and sufficient) to provide a very precise solution of Eq. 2 without performing unnecessarily costly simulations. The radius and time steps are clearly dependent on the proton flux and on the buffering capacity. Larger proton fluxes and smaller buffer concentrations necessitate a higher precision. Tables 2 and 3 show the results for oocytes and small cells, respectively. These tables are particularly useful if the numerical simulation shall be used for an exact comparison with experimental data, in cases where the linear approximation fails (see below). More efficient numerical methods may be developed that could allow a numerical integration of Eq. 2 using larger time and radius steps. However, two obstacles prevent a straightforward improvement of the numerical methods using, e.g., predictor corrector schemes: first, Eq. 2 is highly nonlinear; second, the boundary conditions are also highly nonlinear because the change in free proton concentration depends on the (nonlinear) depletion of buffer. Because of these principal difficulties, and because the Crank-Nicolson algorithm is in general efficient and robust for diffusional problems (20), we believe that our numerical implementation with the time and radius steps provided in Tables 2 and 3 are useful for an accurate, robust, and reasonably efficient solution of Eq. 2.

FIGURE 2.

Determination of the accuracy of the numerical solution of Eq. 2. The numerical algorithm was applied to integrate Eq. 2 for 10 s for an oocyte, assuming a current of 1 μA and a total buffer concentration of 0.2 mM (pK of buffer is 7). The different curves correspond to (Δr, Δt) values (in meters and seconds, respectively) of: (dash-dotted black) 10⁻⁸, 10⁻⁷; (solid black) 10⁻⁷, 10⁻⁶; (dashed black) 2 × 10⁻⁷, 2 × 10⁻⁶; (dotted black) 10⁻⁷, 10⁻⁵; (dotted gray) 2 × 10⁻⁷, 10⁻³; (dashed gray) 10⁻⁶, 2 × 10⁻⁶; (solid gray) 5 × 10⁻⁷, 10⁻³.

TABLE 2.

Maximal time and radius steps for large cells (Xenopus oocytes)

TABLE 3.

Maximal time and radius steps for small cells

Test of the fast buffering assumption

A basic assumption used in Eq. 2 and for the linear approximation (Eq. 4) is that the buffering reaction is so fast that the buffer is in local equilibrium with the free proton concentration. Fast proton buffers reach a diffusion limited association rate of the order of 10¹²–10¹³ M⁻¹s⁻¹ (22). For buffers with pK < 8 an association rate of λ = 10¹² M⁻¹ s⁻¹ means that the mean lifetime of the protonated buffer is <0.1 ms. For most situations considered here, this is probably fast enough to justify the fast buffering assumption. However, since for most practically used buffers no reliable reaction rates are available to fully justify that assumption, we sought to test the range of validity of the fast buffering assumption. To this end we simulated the full diffusion equation containing the buffering term (Eq. 1) for various assumed values of the association rate λ, keeping the pK of the buffer fixed (at 7) and compared the solution with that of the simplified Eq. 2. Results for an oocyte are shown in Fig. 3. For association rate constants ≥10¹⁰ M⁻¹ s⁻¹, the full solution (dashed and long-dashed black curves for λ = 10¹⁰ M⁻¹ s⁻¹ and λ = 10¹¹ M⁻¹ s⁻¹, respectively) is practically identical to the solution of the simplified Eq. 2 (black curve, superimposed with the long-dashed black curve). For λ = 10⁹ M⁻¹ s⁻¹ (dotted curve) a slight deviation can be seen close to the oocyte surface, whereas for λ = 10⁸ M⁻¹ s⁻¹ (gray curve) and for λ = 10⁷ M⁻¹ s⁻¹ (long dashed gray curve) gross deviations are visible. Very similar results were obtained for simulations around small cells (data not shown). Thus, for a buffer with pK = 7 and λ ≥ 10⁹ M⁻¹ s⁻¹, the fast buffering assumption is justified. Most likely, true association rates of realistic buffers are of the order of λ = 10¹⁰ M⁻¹ s⁻¹ or larger (22). However, possible limitations of this assumption have to be kept in mind. In particular, if diffusion is considered in the alkaline pH range, proton association and dissociation become drastically slower.

FIGURE 3.

Test of the fast buffering assumption. The full diffusion equation (Eq. 1) or the approximate Eq. 2 assuming an infinitely fast buffer was solved numerically at high precision. The solution of Eq. 2 (solid black) overlaps fully with the long-dashed line. The association rate constant, λ, was chosen as (in s⁻¹ M⁻¹) 10¹¹ (long-dashed black), 10¹⁰ (short-dashed black), 10⁹ (dotted black), 10⁸ (solid gray), 10⁷ (dashed gray).

Predictions

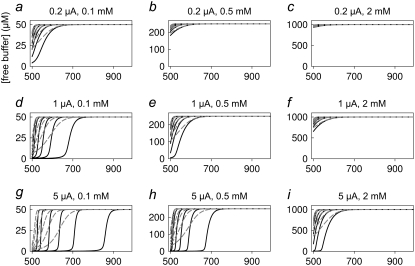
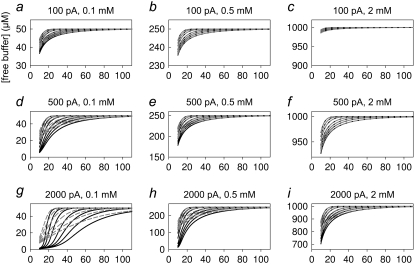
Using the above-determined values for (Δr, Δt) that are necessary to obtain accurate numerical results, we compare in Figs. 4 and 5 and in Figs. 6 and 7 the predictions of the exact numerical solution (Eq. 2) (solid black curves) with the solutions provided by the linearized Eq. 4 (dashed gray curves) for oocytes and small cells, respectively. The current values and total buffer concentrations are indicated in the panels. We plotted the pH (Figs. 4 and 6) as well as the free buffer concentration (Figs. 5 and 7) as a function of the distance from the cell center. The various curves in each graph represent different time steps after onset of the current (i.e., 0.1, 0.2, 0.5, 1, 2, 5, and 10 s for the oocyte and 0.05, 0.1, 0.2, 0.5, 1, 2, and 5 s for the small cell; see legends).

FIGURE 4.

Predictions for the diffusion around an oocyte: results for pH. Each panel shows the pH obtained from the numerical solution of Eq. 2 (solid black curves) and from the evaluation of the solution of the linearized system (Eq. 4) (dashed gray curves) at the indicated current values and total buffer concentrations. The traces correspond to time steps of 0.1, 0.2, 0.5, 1, 2, and 5 s. The x axis gives the distance from the oocyte center in micrometers. The complementary error function used in Eq. 4 was evaluated using code from Press et al. (27) implemented in double precision.

FIGURE 5.

Predictions for the diffusion around an oocyte: results for the free buffer concentration. In correspondence to the panels in Fig. 4, the free buffer concentration is plotted as a function of the distance from the oocyte center.

FIGURE 6.

Predictions for the diffusion around a small cell: results for pH. Each panel shows the pH obtained from the numerical solution of Eq. 2 (solid black curves) and from the evaluation of the solution of the linearized system (Eq. 4) (dashed gray curves) at the indicated current values and total buffer concentrations. The traces correspond to time steps of 0.05, 0.1, 0.2, 0.5, 1, 2, and 5 s. The x axis gives the distance from the cell center in micrometers.

FIGURE 7.

Predictions for the diffusion around a small cell: results for the free buffer concentration. In correspondence to the panels in Fig. 6, the free buffer concentration is plotted as a function of the distance from the cell center.

A first clear result is that, under all conditions, the explicit solution of the linearized equation converges to the full exact solution at sufficiently large distances from the cell. This fact is a very good indication that our implementation of the numerical approximation is accurate. It is, however, quite clear that for large currents and small total buffer concentrations the linearized equation is completely inadequate to describe the pH dependence close to the cell. In fact, the results of Figs. 4–7 can be used as a guide to decide if the application of the linearized solution is adequate for the analysis of specific experimental results.

Another important guide for the design of specific experiments resulting from our simulations regards the choice of the total buffer concentration for a given level of expression. For example, the relatively small whole-cell current of 100 pA combined with an extracellular buffer concentration of 0.5 mM leads only to very small changes of pH (Fig. 6 b) that may be difficult to detect.

Comparing the results shown in Figs. 4 and 6 it is obvious that comparable flux densities lead to much more profound extracellular pH changes in the large oocytes compared to the small cells. This is simply caused by the smaller dimension of the system: the relative volume increase of successive shells at distances Δr (see Fig. 1) is much larger starting from a small initial radius than starting from a large radius. In fact, if Δr ≪ a (a is cell radius), the relative volume increase of successive shells is given 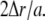For oocytes, the relative volume increase is practically zero, corresponding to the situation of diffusion away from an infinitely large plane source. In contrast, a small cell is more similar to a point source.

Fig. 5 shows that even moderate proton fluxes lead to complete buffer depletion if the buffer concentration is below 0.5 mM. This is, of course, an experimental situation that has to be avoided to guarantee a defined system with a stable pH. In fact, it is experimentally desirable to keep the acidification <∼0.8 pH units to allow efficient buffering.

DISCUSSION

We have performed an extensive analysis of buffered proton diffusion around a proton pumping cell. The study was motivated by the desire to quantitatively estimate proton fluxes from measured proton gradients in the extracellular medium. We developed an efficient computer program to simulate the full diffusion equation under the assumption of fast buffering. However, the full solution is only necessary for elevated proton fluxes and low buffering capacity. For smaller fluxes and/or larger buffering capacity the explicit solution of the linearized equation is fully adequate, in particular at some distance from the cell surface. This solution can be computed directly allowing a rapid fit to experimentally obtained data.

The solution of the linearized equation has a further advantage. In Eq. 4 the change in proton concentration, h, is directly proportional to 1/β, the inverse of the buffer capacity. In fact, Eq. 4 can be rewritten as

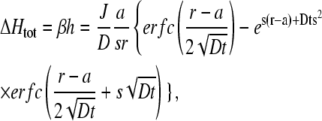where ΔH_tot is the total concentration of protons added. This expression is useful if a fluorescent indicator is used to measure the changes in proton concentration. The fluorescence signal can be directly calibrated in terms of fluorescence change per added (total) proton concentration, instead of a calibration in terms of pH. In this way, the fluorescence signal reports directly the change in total proton concentration and the gradients can be directly fitted with the above equation and the two parameters, J and D.

On the other hand, if pH sensitive microelectrodes are used to obtain spatiotemporal information on [H⁺], using for example self-referencing oscillating ion-sensitive microelectrodes (28), the buffering capacity of the solution has to be determined separately to use the theory of this article.

A critical assumption underlying our modeling study is that the H⁺ transporting protein under consideration is uniformly distributed over the membrane surface. Without this assumption the mathematical treatment of the diffusion problem would be much more complicated. This is an oversimplification because it is known that membrane proteins are often clustered. However, even in the case of clustering our analysis may still be valid in various conditions. If clustering occurs on a micrometer scale (see, e.g., Wang and Thompson (29)) the resulting inhomogeneity of the H⁺ concentration will be smeared out by diffusion at micrometer distances, allowing a straightforward application of the equations developed here. Large-scale clustering is exemplified by a polarized expression for example in Xenopus oocytes (see, e.g., Gomez-Hernandez et al. (19)). In such a case, the analysis should be restricted to a conical zone in which expression is homogeneous. The worst case is clustering at a spatial scale that leads to macroscopic inhomogeneities of the proton concentration at macroscopic distances from the cell. Nevertheless, even in this case, at least at moderate proton fluxes in the linear regime, the average proton concentration (averaged over spatial angle at a fixed radius) is expected to be well described by Eq. 4, because of the additive nature of the linearized diffusion problem. In either case, it is advisable to test the assumption of spherical homogeneity for a given experimental situation.

In several other studies, measurements of ion gradients have been used to obtain quantitative estimates for absolute fluxes. For example, Kang et al. have used ion sensitive microelectrodes to quantify ion fluxes across giant membrane patches expressing the Na-K-ATPase (30). Their approach is based on the simple equation

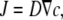that relates the ion flux density, J, to the concentration gradient. This relationship is valid, however, only when a stationary gradient is achieved. This condition is not satisfied under the circumstances considered in this article. In particular, for the diffusion around oocytes, a steady state is not reached even after 5 s of proton pumping (see Fig. 4). For the case of ClC-5 that necessitates the application of very positive voltages to activate transport, much longer times cannot be easily sustained experimentally without the activation of unspecific conductances. Thus, it is impractical to wait for the establishment of a steady-state gradient. Furthermore, the pH decrease obtained after very long activation of ClC-5 affects the function of the transporter (17). For these reasons, the solution of the nonstationary diffusion equation, as provided in this article, is necessary to obtain quantitative information about the absolute proton flux.

In summary, this modeling study provides the theoretical basis for the determination of absolute proton fluxes from extracellular, nonequilibrium pH gradients, and provides a guide for the amount of buffer needed for a given experimental proton current. The method may become useful to determine stoichiometry coefficients for transporters that involve H⁺ movements, for which more direct methods are not applicable.