Sampling the Cell with Anomalous Diffusion—The Discovery of Slowness

Abstract

Diffusion-mediated searching for interaction partners is an ubiquitous process in cell biology. Transcription factors, for example, search specific DNA sequences, signaling proteins aim at interacting with specific cofactors, and peripheral membrane proteins try to dock to membrane domains. Brownian motion, however, is affected by molecular crowding that induces anomalous diffusion (so-called subdiffusion) of proteins and larger structures, thereby compromising diffusive transport and the associated sampling processes. Contrary to the naive expectation that subdiffusion obstructs cellular processes, we show here by computer simulations that subdiffusion rather increases the probability of finding a nearby target. Consequently, important events like protein complex formation and signal propagation are enhanced as compared to normal diffusion. Hence, cells indeed benefit from their crowded internal state and the associated anomalous diffusion.

INTRODUCTION

Searching for a specific target is an ubiquitous process in biology ranging from the macroscopic prey-predator level in zoology to the binding of macromolecules in living cells. Commonly, the nondirected encounter rate of two interacting entities, be it on the macro or micro scale, is assumed to be determined by Brownian motion. This view is justified when bearing in mind that the thermally driven motion of a molecule is as much a random walk as the dispersal of insects in a forest (1). Searching a target by means of a random walk (i.e., Brownian motion) is fully characterized by the following features. The average position does not change in time, but the quadratic length of the excursions, i.e., the mean-square displacement (MSD) 〈r²(t)〉, grows linear in time with a prefactor that depends on the dimension (d) of the search space and the diffusion coefficient (D): 〈r²(t)〉 = 2dDt. For diffusion in bulk solution, one obtains the familiar expression 〈r²(t)〉 = 6Dt.

On the macroscopic level also enhanced diffusion, i.e., superdiffusion, with a MSD 〈r²(t)〉 ∼ t^β, β > 1, plays an important role, e.g., in the traveling behavior of humans and the associated spreading of infectious diseases (2). Indeed, superdiffusion has been shown to be a very efficient way to search for targets (3), e.g., in the context of gaze shifts (4). Most of the searching events inside a living cell, however, are governed by normal diffusion or its qualitatively slower companion subdiffusion. Subdiffusion is characterized by a MSD that grows like 〈r²(t)〉 ∼ t^α, α < 1, i.e., a qualitatively slower spreading than for normal diffusion is observed due to the exponent α < 1 (see, e.g., (5) and (6) for a more detailed introduction to subdiffusion). In fact, we have recently shown that diffusion in the cytoplasm and the nucleus of eukaryotic cells is generically subdiffusive due to molecular crowding (7,8), with 0.5 < α < 0.85; the same holds true for bacteria (9). The emergence of subdiffusion appears to be a consequence of the crowding-induced viscoelasticity of the cytoplasm and nucleoplasm (8). The poor spreading associated with subdiffusion (particles stay longer at their original position and return slower when having escaped to a far-away distance) implies a slow sampling process. One may ask whether the cell would not be better off when diluting its intracellular fluids. Or does the cell actually benefit from the crowding-induced subdiffusion?

Here we have investigated the efficiency of (sub)diffusion as a sampling strategy in the context of a diffuse-to-capture scenario. In particular, we asked how many particles (e.g., proteins) starting in a distance R from the target with radius a (e.g., a piece of DNA) are captured by the target within a given time t_max. For normal diffusion in bulk solution, the probability of capturing can be calculated to decrease as P(R) ∼ a/R (10). Using computer simulations, we demonstrate here that subdiffusion can massively enhance this probability, thus making the crowding-induced subdiffusion a slow but more reliable search algorithm. The increased reliability translates directly into facilitated intracellular signal propagation and complex formation, i.e., cells indeed benefit from their crowded internal state.

MATERIALS AND METHODS

Simulations

To record the probability of getting captured at the target, we started N individual, noninteracting particles on a sphere with radius R around the target's center, followed their (subdiffusive) random walk up to a time t_max, and monitored the fraction of captured particles. The target's radius a was used as an intrinsic length scale, which we have set to unity for simplicity. The erratic motion of the particles was simulated using the forward integration of the Langevin equation, i.e., the positions at times t = 1, 2, … , t_max were obtained via x_i(t + 1) = x_i(t) + ξ_i with i = 1, 2, 3. As a model for subdiffusive motion we have chosen to calculate the spatial increments ξ_i in each spatial direction i = 1, 2, 3 via the Weierstrass-Mandelbrot function (11,12):

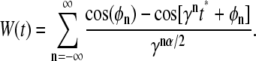(1)

Here, φ_n are random phases in the interval [0, 2π], γ > 1 is an irrational number, t_max is the length of the desired time series, and α is the degree of anomality that appears in the MSD (〈r²(t)〉 ∼ t^α). In accordance with Saxton (12), we have chosen 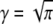and restricted the sum to the terms 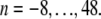The increments ξ_i = W(t + 1) − W(t) were chosen in such a way that the MSD for all α-values coincided at t = 1. By this approach, we took into account that in the realm of anomalous diffusion random motion in a viscoelastic fluid, (α < 1) will be hampered by elastic restoring forces with respect to a purely viscous fluid with normal diffusion (α = 1). Thus, anomalous diffusion should be subordinated with respect to the normal diffusion.

Conversion to SI units

To convert the simulation data to SI units, we took the following approach. The target radius a was the unit of length in our simulations, i.e., defining the respective targets as 1), a DNA operon (a = 2 nm) and 2), a Golgi membrane patch (a = 100 nm), automatically fixed the length scale. For gauging the timescale, we first note that anomalous diffusion may not be observed for very small timescales at which the moving particle essentially experiences a thin layer of a homogenous, viscous fluid; periods in which the entity moves less than its own radius may thus be regarded as governed by normal diffusion. We therefore assumed that normal diffusion governed the motion on timescales smaller than a single (sub)diffusion step in the simulations (t < 1) while anomalous diffusion emerged for t > 1. The associated crossover time t = 1, i.e., a single diffusive time step in our simulations, was translated to real time via the time a diffusing entity needs to move about its own radius. This time can be calculated via the Einstein-Stokes equation as

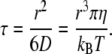(2)

Here, k_BT is the thermal energy, r denotes the radius of the diffusing entity (e.g., a protein), and η is the viscosity of the fluid. Assuming η = 3 × 10⁻³ Pa s, which is a reasonable value for the cytoplasm (13), a single time step of the simulation corresponded to (1) τ = 0.02 μs and (2) τ = 0.3 μs when assuming that LacI and the coatomer complex have radii r = 2 nm and r = 10 nm, respectively.

RESULTS AND DISCUSSION

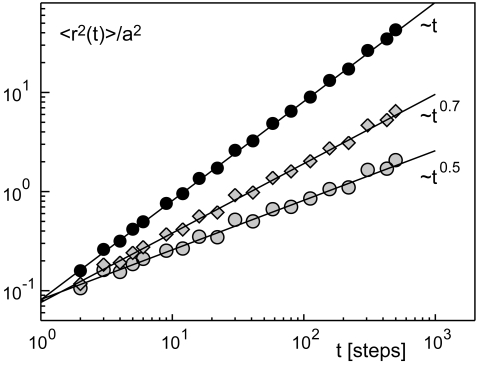
To determine the probability of finding a binding target by (anomalous) diffusion, we have used a diffuse-to-capture scenario. We started N noninteracting point particles (representing, for example, proteins) on the surface of a sphere with radius R. The particles were allowed to move in three-dimensional space by (anomalous) diffusion for t_max time steps, thereby showing the typical MSD of the associated (sub)diffusive random walk (Fig. 1). When a particle hit the target (having radius a) in the sphere's center, it was absorbed. After t_max time steps, we recorded the fraction of absorbed particles as P(R) and repeated the approach for another radius R. To ensure a fair competition between the different random walks, the MSD for a single time step, 〈r²(t = 1)〉, was chosen equal for all simulations (compare to Fig. 1 and Methods). For reporting our data, we have taken the target radius a as the unit of length and measured the time in number of diffusion steps. A conversion to SI units is performed below in the context of biological examples. For the sake of simplicity, we have neglected that virtually all subdiffusive processes are transient and converge toward a normal diffusive behavior at asymptotically large times (see, e.g., (14,15) for discussion).

FIGURE 1.

Representative MSD curves 〈r²(t)〉 for normal and anomalous diffusion as used in the simulations (solid circles, α = 1; shaded diamonds, α = 0.7; shaded circles, α = 0.5). Dashed lines highlight the respective scaling behavior 〈r²(t)〉 ∼ t^α. To ensure a fair competition between the different random walks, the MSD for a single time step r²(t = 1) was chosen equal for all simulations.

To mimic the subdiffusion of particles in crowded intracellular fluids like the cytoplasm, we have determined the diffusive steps according to the Weierstrass-Mandelbrot function (WMF; see Eq. 1). The WMF yields a path with the characteristics of fractional Brownian motion (11,16), i.e., the individual step sizes are not independent but correlated. The choice of a non-Markovian process seemed appropriate as the experimentally observed subdiffusion is a consequence of the viscoelasticity of the intracellular fluids (8), i.e., the WMF models the fluid's memory that is reflected in a nontrivial creep function (17). Due to its Markovian character we refrained from using a continuous time random walk (CTRW) where subdiffusion is achieved by assigning power-law distributed resting times to particles between periods of free diffusion (see (5) for a detailed introduction). In particular, the CTRW induces subdiffusion by altering the timing between two diffusional steps yielding a diffusion equation with a fractional time derivative (5). In contrast, the WMF rather affects the spatial increments and is thus similar in spirit to the porous media equation that describes percolation in disordered media.

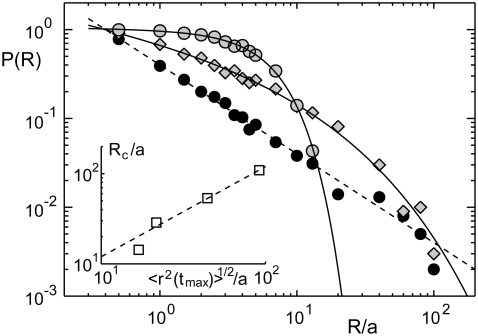
As a result of the simulations, we observed for normal diffusion the well-known relation P(R) ∼ a/R (Fig. 2), i.e., the probability to find the target decreased quite rapidly and became <1% when starting in a distance that exceeded the target's 10-fold radius. It is noteworthy that the statistics in P(R) may become limiting in two ways for very large radii: 1), to retain a smooth curve beyond P(R) = 0.1% the number of particles N needs to be larger; and 2), to maintain the scaling P(R) ∼ a/R for large radii R, the imposed search time t_max has to be larger than the mean time T = R²/(6D) needed to travel a distance R (where D is the diffusion coefficient). We have chosen N = 1000 and t_max = 2 × 10⁶ (unless stated otherwise) for which a proper scaling in the range R/a ≤ 100 was guaranteed (compare to Fig. 2).

FIGURE 2.

For normal diffusion, the probability P(R) to find a target within t_max = 2 × 10⁶ time steps, when starting off in a distance R, decays as P(R) ∼ 1/R (solid circles and dashed line). The probability is strongly increased when using subdiffusion, e.g., with α = 0.7 (shaded diamonds) or α = 0.5 (shaded circles). Full lines are guides to the eye. (Inset) The crossover distance R_c at which the anomalous diffusion becomes worse than normal diffusion (determined as the intersection of the full lines and the dashed line) increases linearly with the average excursion length. Please note the double logarithmic plot style.

In contrast to the nice power law P(R) ∼ a/R for normal diffusion, subdiffusion with different degrees of anomality α < 1 resulted in significantly different curves (compare to Fig. 2). For small radii, P(R) was considerably larger than for normal diffusion, while for large radii, a sudden drop below the efficiency of normal diffusion was observed. This drop is not a consequence of the limited number of particles in the simulation but can be well understood when comparing the crossover radius R_c (i.e., the intersection of P(R) for normal and anomalous diffusion) with the average maximum excursion length of a population of particles (as determined from the MSD in Fig. 1). Essentially, we find 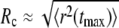for all anomalities α (Fig. 2, inset). Thus, when starting beyond this critical radius, the majority of particles have no chance to reach the target by (sub)diffusion (except a few fast particles) and consequently the probability P(R) massively decreases. Still, the probability of finding the target from a nearby position, say within a range of some multiple target radii, is up to 10-fold higher as compared to normal diffusion.

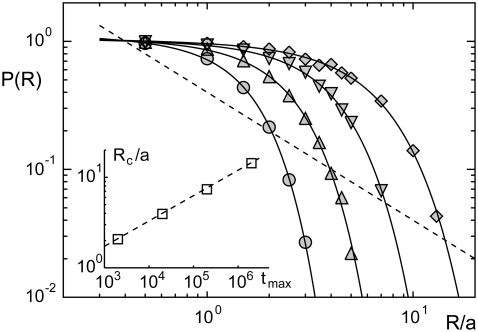
Increasing the search time t_max improves the probability to find the target by subdiffusion even for larger radii (Fig. 3). From the above result 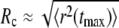and the scaling of the MSD 〈r²(t)〉 ∼ a²t^α, we predicted 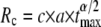with some constant c, i.e., extending the search time t_max increases the range of radii for which anomalous diffusion provides a better sampling strategy. The predicted scaling is confirmed by our numerical data with c ≈ 3 (Fig. 3, inset), i.e., the critical radius R_c below which subdiffusion finds the target with a higher probability increases algebraically with t_max. Therefore, for an infinite search time, subdiffusion would always be the better search strategy for finding a binding partner.

FIGURE 3.

The probability P(R) to find a target with subdiffusion (α = 0.5) when starting off in a distance R is enhanced when the search time is prolonged (t_max = 2 × 10³, 2 × 10⁴, 2 × 10⁵, 2 × 10⁶ time steps: circles, up-triangles, down-triangles, and diamonds, respectively). Full lines are guides to the eye, dashed lines highlight the behavior P(R) ∼ 1/R for normal diffusion. (Inset) The crossover distance R_c at which anomalous diffusion (α = 0.5) becomes worse than normal diffusion (determined as the intersection of the full lines and the dashed line) increases algebraically with the maximum search time t_max. Please note the double logarithmic plot style.

Given that molecular crowding is a major cause for the emergence of subdiffusion (7,8,18), our results strengthen the previous physico-chemical considerations (based solely on the free energy of a reaction) that crowding enhances the rate and extent of macromolecular associations (19). Also, the previously observed higher yield in binary reactions on a percolation cluster (20) and the weak ergodicity breaking in the presence of a reactive boundary (21) fit well to our results.

Having demonstrated the basic features of subdiffusion as a powerful strategy to enhance the encounter probability, we would like to translate our findings now to the biological context. Let us first consider the sequential events that underlie signaling cascades and complex formation (e.g., the assembly of the ribosomal complex). In both cases, the sequence of events may be represented by a symbolic chain A₁ → A₂ → A₃ →…, where the indices of the states A_i may describe the number of proteins in the complex or the number of already activated submodules in the signaling cascade, respectively. Transition from one state to another occurs with a probability p_i that basically depends on the (diffusion-mediated) encountering probability of two involved reaction partners. Assuming a typical distance R = 10a between the reaction partners and restricting the number of states to i ≤ 3, normal diffusion yields a very low probability (p = 0.043³ ≈ 6 × 10⁻⁵) for assuming the terminal state A₃. In contrast, subdiffusion with α = 0.5 and a search time t_max = 2 × 10⁶ yields a roughly 100-fold higher probability to reach the terminal state A₃ (p = 0.133³ ≈ 2 × 10⁻³), i.e., signal propagation and complex formation become much more reliable. Subdiffusion performs even better when considering more intermediate states before the terminal state: Using i ≤ 8, subdiffusion yields a 10⁴-fold higher probability to assume the terminal state A₈.

We next want to give two particular cell-biological examples that are likely to benefit from subdiffusion as a search strategy. We consider 1), the search of the transcription factor LacI for its operon (22) as a typical problem in gene regulation; and 2), the binding of the coatomer complex to Golgi cisternae (23). In both cases, we will assume an anomality α = 0.5, which has been measured for diffusion in the cytoplasm and the nucleus of eukaryotes (8); gauging the simulation units to SI units was done as described in Materials and Methods.

For LacI (radius roughly 2 nm), the time frame for completing the search for its target operon (a = 2 nm) may be estimated to be ∼1 s via the tumbling frequency of the bacterium (24). This corresponds to t_max = 5 × 10⁷ and via 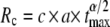(see above) transfers to a critical radius of R_c ≈ 500 nm. Given that only ∼10 LacI copies are present in a bacterium (volume 1 μm³), the typical distance of 450 nm between a LacI protein and the operon of interest is smaller than R_c, i.e., subdiffusion is the most advantageous strategy for LacI to search for the operon. If the nucleoplasm would be diluted, thereby allowing normal instead of anomalous diffusion, LacI may not bind the operon with a sufficient probability, thus compromising the cell's gene expression pattern.

For coatomer (radius 5 nm), the typical search time for a membrane patch on Golgi cisternae (a = 100 nm) is given by the turnover time of its adaptor protein ARF-1 (10 s, i.e., t_max = 3.4 × 10⁷) (13). This transfers to R_c ≈ 13 μm, which is approximately the radius of the entire cell, i.e., also here subdiffusion yields the most favorable searching strategy.

While subdiffusion alone already provides an improved efficiency of finding the respective binding target, we would like to emphasize here that, of course, also other mechanisms, e.g., reduction-of-dimension (25) in the case of LacI, may contribute to an advanced search in the considered examples.

Given the numerical observations and biological implications, what is actually the fundamental reason for subdiffusion performing so much better in finding a target? The answer to this is hidden in the geometric properties of the (subdiffusive) random walk—its fractal dimension. The fractal dimension of a random walk essentially determines how complete a given space will be explored for infinitely large times (see, e.g., (26) for a more thorough definition). Simple Brownian motion and a CTRW, for example, have a fractal dimension d_f = 2, i.e., the random walker explores a surface completely but will only visit a negligible subspace when moving in three-dimensional bulk solution. Subdiffusion in a viscoelastic fluid as modeled via the WMF on the other hand explores more than just a surface as its fractal dimension is given by d_f = 2/α (16). Thus, for the physiological range 0.5 ≤ α ≤ 0.85, the sampled subspace is considerably larger than a surface (d_f = 2) and may even exceed the dimension of the bulk (d_f = 3). Cells therefore are not hampered by the crowding-induced subdiffusion but can use it to enhance their performance.

A strong anomality (low α) not only is associated with an increasing probability of eventually finding the target but also with a long search time. For fractional Brownian motion the best trade-off appears to be given at α = 2/3. At this value, the three-dimensional space is fully explored while the subdiffusive spreading is not too slow. A generalized optimal α based only on the observation of subdiffusion may not be derived without considering the details of the random walk, i.e., its fractal dimension d_f. It is interesting, however, that intracellular fluids have just the right amount of crowding to induce an anomalous diffusion near to the critical α predicted by the fractional Brownian motion model (7–9).