Abstract
Sphingosine 1-phosphate (S1P) is a potent chemokinetic agent for endothelial cells that is released by activated platelets. We previously developed Arg-Gly-Asp (RGD)-containing polyethylene glycol biomaterials for the controlled delivery of S1P to promote endothelialization. Here, we studied the effects of cell adhesion strength on S1P-stimulated endothelial cell migration in the presence of arterial levels of fluid shear stress, since an upward shift in optimal cell adhesion strengths may be beneficial for promoting long-term cell adhesion to materials. Two RGD peptides with different integrin-binding specificities were added to the polyethylene glycol hydrogels. A linear RGD bound primarily to β3 integrins, whereas a cyclic RGD bound through both β1 and β3 integrins. We observed increased focal adhesion formation and better long-term adhesion in flow with endothelial cells on linear RGD peptide, versus cyclic RGD, even though initial adhesion strengths were higher for cells on cyclic RGD. Addition of 100 nM S1P increased cell speed and random motility coefficients on both RGD peptides, with the largest increases found on cyclic RGD. For both peptides, much of the increase in cell migration speed was found for smaller cells (<1522 μm2 projected area), although the large increases on cyclic RGD were also due to medium-sized cells (2288–3519 μm2). Overall, a compromise between high cell migration rates and long-term adhesion will be important in the design of materials that endothelialize after implantation.
INTRODUCTION
Endothelial cells provide a thrombosis-resistant interface with the blood, thereby inhibiting pathological cardiovascular events (1,2). The endothelium can be damaged during cardiovascular surgical procedures, such as balloon angioplasty, however (3). Exposure of the matrix underlying the endothelial monolayer causes remodeling of the matrix and resulting smooth muscle cell migration that may lead to restenosis (4,5). Implantation of a stent decreases restenosis rates (6,7), but failure of the implant due to in-stent restenosis may still occur (8), and late-term thrombosis rates may be significantly higher (9,10). Quick restoration of an intact endothelium may improve the long-term patency of the stents (11,12). Previous investigations have shown that promoters of endothelial cell migration accelerated endothelialization of stents, leading to a reduction in thrombosis (13).
Sphingosine 1-phosphate (S1P) is a potent chemokinetic factor (14), and we have shown that controlled release of S1P promotes endothelial cell migration on biomaterials (15). S1P is a vital regulator of endothelial layer barrier integrity and vascular stabilization (16–18) and inhibits smooth muscle cell migration at physiological concentrations (19). However, the rate of endothelialization will also depend on the interactions of endothelial cells with the biomaterial substrate, which influence cell adhesion and motility. Currently, the dependence of S1P-induced migration on adhesive properties of a substrate is not known.
The strength of interaction of endothelial cells with a substrate is critical for motility of the cells. Previous results from both experiments and mathematical modeling have shown that cell migration rates have a biphasic dependence on the concentration of adhesive ligands and the cell attachment strength (20–23). Migration requires sufficient attachment strength to allow traction for the cells to pull themselves forward, but not so much strength that the rear edge of the cells can not release. Even when changing the cell/substrate interactions via ligand type, ligand density, ligand affinity, or integrin expression, a major controlling factor of cell migration has been found to be the strength of cell adhesion to the surface (21,24).
We wished to produce polyethylene glycol (PEG) hydrogels with an Arg-Gly-Asp (RGD) concentration that allowed for maximal endothelial cell migration and adhesion in the presence of S1P and maximal adhesion in the absence of S1P. S1P increases endothelial cell migration on a number of substrates (14,25–33), but the relationship of this molecule to the adhesiveness of the substrate has not been systematically explored. In other cell types, growth factors such as EGF greatly affect the biphasic relationship between cell migration and strength of cell adhesion to the surface (34). S1P promotes FAK phosphorylation (29,35) and induces intracellular calcium release (36,37). FAK activation and calcium have been linked to an increase in adhesion disassembly and higher focal adhesion turnover (38,39). Because high adhesion strengths may reduce migration rates by preventing the release of the rear edge of the cell (20), we hypothesized that S1P enhances migration even on surfaces with high adhesion strength. If S1P allowed rapid cell migration at high adhesion strengths, this might allow for rapid wound healing on a device, at the same time promoting stable attachment of both the migrating cells and the final endothelial cell monolayer.
We tested linear (40) and cyclic (41) RGD peptides at various concentrations in the presence of fluid flow and a constant concentration of S1P. First, we showed that cell adhesion strength increased with RGD concentration and was stronger on the cyclic RGD peptide, as expected. We used single-cell tracking to demonstrate that maximal endothelial cell migration speeds were obtained with S1P on the cyclic RGD peptide. A biphasic response was demonstrated for migration speeds on linear RGD in the absence of S1P. On linear RGD in the presence of S1P, the highest migration speeds were observed at the highest RGD concentrations, with no indication of the onset of a decrease in migration speed at these high RGD concentrations. This may have indicated that the downslope of the biphasic response was at a higher RGD concentration than could be practically added to the gels, although a biphasic response may also not be present. For cyclic RGD, a relatively flat response was observed in the absence of S1P, whereas dramatic increases in cell migration speed were observed in the presence of S1P. Although we again could not practically add enough cyclic RGD to observe a downward slope in cell migration speed, we did observe a dramatic decrease in the mean random motility coefficient at the highest adhesion strength versus at intermediate adhesion strengths. Examining migration speeds as a function of initial cell adhesion strength, the largest increases in cell migration speed upon addition of S1P were observed at the higher initial cell adhesion strengths, effectively shifting the peak in the curve, even if a true biphasic response was absent. However, high initial cell adhesion strengths on the cyclic RGD peptide did not lead to higher rates of retention on the surface over 12 h in the presence of 20 dyn/cm2 fluid shear stress, indicating a tradeoff between cell migration speeds and long-term adhesion.
MATERIALS AND METHODS
PEG vinyl sulfone synthesis
PEG-octavinyl sulfone (PEG-OVS) was synthesized from eight-arm PEG (molecular weight 10,000, Shearwater Polymers, Huntsville, AL) in four steps, as described previously (15). Briefly, PEG dissolved in toluene was reacted with methane sulfonyl chloride in the presence of triethylamine (TEA) to form PEG-mesylate. The PEG-mesylate was dissolved in a sodium borate buffer and reacted with β-mercaptoethanol at reflux in nitrogen to form PEG-hydroxyethyl sulfide. The sulfide was oxidized by reaction at 0°C with hydrogen peroxide in distilled water containing sodium tungstate. PEG-hydroxyethyl sulfone was converted to PEG-vinyl sulfone by reaction with methane sulfonyl chloride in the presence of TEA. End-group conversion as shown by NMR was 83%.
Linear RGD peptide preparation
A linear RGD peptide with a single cysteine for coupling to PEG-OVS (Ac-GCGYGRGDSPG) was synthesized on an ABI 433A peptide synthesizer (Applied Biosystems, Foster City, CA) using Fmoc chemistry. The peptide was cleaved for 2 h under nitrogen in 5-mL cleavage cocktail (95% trifluoroacetic acid (TFA), 2.5% triisopropylsilane, 2.5% water) with mixing every 30 min. The resin was removed by filtration through glass wool packed in a glass pipette, and the peptide was precipitated in 200 mL ice cold ether. The peptide was collected by vacuum filtration through a polytetrafluoroethylene membrane and dried under vacuum. The RGD peptide was dissolved in 0.1% TFA in water and purified by high-performance liquid chromatography (HPLC) on a C18 column using a gradient of acetonitrile from 5% to 30% over 30 min. MALDI-TOF mass spectrometry was used to identify the HPLC fractions containing the product. The peptide fractions with molecular weight 1067.0 were dried by lyophilization.
Cyclic RGD preparation
The cyclic RGD (Ac-GCNAC*RGDGWC*G) was synthesized on an ABI 433A peptide synthesizer. The second and third cysteines (*) were p-methoxytrityl (Mmt)-protected, whereas the first cysteine was protected by a trityl (Trt) group. The Mmt protecting groups were selectively removed with 1% TFA while the peptide remained attached to the resin. The peptide was mixed with 94:1:5 dichloromethane/TFA/triisopropylsilane while bubbling nitrogen through the solution for 5 min. The solvent was removed and the selective cleavage was repeated two more times. The peptide was cyclized by air oxidation, bubbling air through the resin in N-methyl pyrrolidone with 0.1 M TEA. After 3 days of reaction, the solvent was removed by filtration. Cyclization of the peptide on the resin was confirmed using Ellman's reagent, testing for the presence of free thiol groups on the resin. The peptide was cleaved, purified, and collected as described for linear RGD above. After HPLC separation, pure cyclic peptide fractions were identified using MALDI to show the reduction of the molecular mass by 2 u from that of the noncyclized peptide, demonstrating the loss of two protons during the disulfide reaction (see Supplementary Materials, Fig. 1S.) The cyclic RG peptide has a molecular weight of 1238.3.
Hydrogel functionalization
The linear RGD peptide was dissolved at 0.2 mg/5 μL Dulbecco's phosphate-buffered saline (DPBS) and the cyclic RGD peptide at 0.232 mg/5 μL DPBS (137 mM NaCl, 8 mM Na2HPO4·7 H2O, 0.7 mM CaCl2, 2.7 mM KCl, 1.5 mM KH2PO4, and 0.5 mM MgCl2, pH 7.4). The RGD peptide was reacted with various fractions of the vinyl sulfone endgroups ranging from 1/10 to 1/160 (final RGD concentrations in the hydrogel of 0.32 mM to 5.5 mM) via the cysteine thiol on the peptide for 30 min at 37°C before cross-linking the PEG hydrogel. Using an Ellman's assay to detect unreacted cysteine groups on the RGD peptide, we found complete reaction of thiol within 5 min, even at the highest RGD concentration, as previously described (42).
Hydrogel formation
Hydrogels were formed by a conjugate addition reaction between PEG-OVS and fatty acid-free bovine serum albumin (FAF-BSA) (Sigma, St. Louis, MO). PEG-OVS and FAF-BSA were dissolved in DPBS by adding 10 mg solid to 50 μL PBS at pH 8.0. All precursors were sterile-filtered. PEG-OVS was then mixed with FAF-BSA. The optimal ratio of PEG-OVS to FAF-BSA was determined previously to be 20 μL PEG-OVS (∼3.3 mg) to 30 μL albumin (∼5.0 mg) (15).
Cell culture
All cell culture reagents were purchased from Sigma unless otherwise noted. Human aortic endothelial cells (HAEC) were purchased from Clonetics (Walkersville, MD) and cultured in endothelial growth medium (EGM) (MCDB 131 medium) supplemented with 2% fetal bovine serum, 10 ng/mL epidermal growth factor, 10 μg/mL heparin, 1.0 μg/mL hydrocortisone, 1% antibiotic-antimycotic (ABAM, 100×) solution (Invitrogen, Carlsbad, CA), and 6 mg/L bovine brain extract (Clonetics). HAEC were cultured in EGM in six-well tissue culture plates and cells from passages 4–9 were used for experiments.
Setup for tracking of endothelial cells under flow
Glass microscope slides (24 × 60 mm) were cleaned with 1 mM HCl in a 110°C oven overnight. The slides were washed with water and allowed to dry. Then the slides were silanated in 5% 3-mercaptopropyltrimethoxy silane (Gelest, Morrisville, PA) in 95% acetone for 1 h. The slides were washed with acetone and then cured at 110°C overnight. The slides were sterilized with 70% ethanol, and then a thin layer of PEG hydrogel solution (150 μL) with linear or cyclic RGD peptide was added, evenly covering the surface. The hydrogels were allowed to cross-link overnight in a humidified 37°C incubator and then were washed in excess PBS for 24 h. Cells seeded onto RGD/PEG-OVS/albumin hydrogels at 1000–2000 cells/cm2 were allowed to spread for 6 h in complete growth medium. The slides were placed into a flow chamber, with attention to minimizing any time without medium on the cells. The flow chamber consisted of two optically clear acrylic sheets. Before assembly, the flow chamber was sterilized with 70% ethanol, and the tubing and medium reservoirs were autoclaved. The PEG-coated slide was placed into the center of the bottom acrylic sheet. A silicone gasket was placed on the top acrylic sheet aligned with the glass slide. The two halves were then screwed together. Each end of the flow area defined by the silicone gasket had an inlet/outlet hole in the top acrylic sheet. The flow through the chamber was gravity-driven, and a peristaltic pump was used to recirculate the medium to the reservoir of the closed system. Fifteen milliliters of HEPES-buffered low serum medium (MCDB 131 with 0.4% FAF-BSA, 0.1% fetal bovine serum, 1% ABAM, and 10 mM HEPES, pH 7.4) with or without 100 nM S1P was added to the flow chamber and to the reservoir. The cells were tracked while exposed to 20 dyn/cm2 fluid shear stress using time-lapse microscopy for 12 h, recording images every 2 min. Individual cell migration speeds were analyzed manually using ImageJ to trace the path of each cell over time. The time increment between analyses was increased to 6 min if cells maintained a straight path in the three consecutive images. Data was analyzed by analysis of variance (ANOVA) with Tukey HSD for unequal N post hoc.
Determination of integrin specificity of RGD peptides
Fibronectin, serum protein, linear RGD, and cyclic RGD substrates were tested for integrin specificity. Fibronectin (1.5 μg/cm2 at 6 μg/mL in PBS) and serum (150 μL) were coated onto 48-well plates for 2 h at 37°C, followed by two PBS washes. Nonspecific adhesion was blocked with 1% BSA for 1 h at 37°C, followed by two PBS washes. PEG-OVS/albumin hydrogels containing 4.12 mM linear RGD or 0.69 mM cyclic RGD were also coated onto the bottom of 48-well plates. All wells were seeded with HAEC at 3500 cells/cm2 for 6 h. At the time of plating, the cells were mixed with blocking antibodies to the β1 (5 μg/mL, mAb13, BD Biosciences, Franklin Lakes, NJ) and β3 (5 μg/mL, BD Biosciences, VI-PL2) integrin subunits. The density of cell adhesion on each substrate with the blocking antibodies was compared to a control without antibodies.
Assay for initial substratum attachment strength
Cell adhesion strengths to linear and cyclic RGD containing hydrogels were assessed using a centrifugation assay (43,44). PEG hydrogels (75 μL) with various concentrations of RGD were formed on the bottom of a 48-well nontreated culture plate. After cross-linking for 24 h, HAEC were seeded onto the gels at 10,000 cells/cm2 in 500 μL EGM. After allowing the cells to attach and spread for 6 h, the gels were washed with DPBS. The wells were filled to their tops with DPBS and then covered with adhesive sealing tape. Images were obtained at 4× to quantify the number of cells initially attached to the hydrogel. The sealed plates were inverted in the centrifuge and spun at a specified rotational speed for 5 min to remove the cells from the hydrogels. The applied detachment force was calculated with the equation F = Vc × (σc – σm) × RCF, where Vc is the volume of the cell (∼5000 μm3, estimated from the diameters of spherically shaped cells of ∼20 μm), RCF is the relative centrifugal force, σc is the density of the cell (∼1.07 g/mL), and σm is the density of the DPBS (1.02 g/mL). The wells were washed with DPBS to remove the floating cells, and then images were acquired at the same locations as before the centrifugation. The force required to remove 50% of cells (F50) was interpolated from the data as 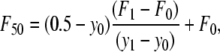 where y0 and y1 are the percent cell detachments that bracket 50% detachment and F0 and F1 are the corresponding forces on the cells. The standard deviation was calculated by propagation of error, i.e.,
where y0 and y1 are the percent cell detachments that bracket 50% detachment and F0 and F1 are the corresponding forces on the cells. The standard deviation was calculated by propagation of error, i.e., 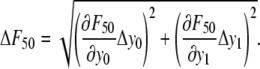
Calculation of motility parameters
Time-lapse microscopy images were obtained every 2 min for 12 h of endothelial cell migration on the surface of RGD-containing PEG hydrogels. The percent of cells remaining on the gels during the course of the experiment was recorded for each RGD concentration. The projected cell areas of all cells were determined by manually outlining the cells after 3 h under 20-dyn/cm2 shear stress. Isolated, spread endothelial cells were manually tracked for 12 h to obtain xy-coordinate data for the center of each cell (cells were excluded during cell division). Coordinate data recorded every 6 min (Δt = 6 min) for all cells in each experiment were saved as variables for analysis in MATLAB (MathWorks, Natick, MA). At each time point i, ti = iΔt, the mean-squared displacement was calculated using the overlapping interval method (45). The root mean-square speed of each individual cell was calculated by dividing the root mean-square displacement for the smallest tracking interval by the length of the smallest tracking interval (i.e., 6 min). Each cell's persistence time was determined by fitting the persistent random walk model given by:
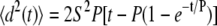 |
by nonlinear least-squares regression analysis, as previously described, using the manually measured root mean-square speed (45–47). Path lengths were calculated as the product of speed and persistence time. Random motility coefficients were calculated as half the product of the squared speed and persistence time. Data was analyzed by ANOVA with Tukey HSD for unequal N post hoc.
Directional index of migration
The directional index of migration (DIM) can be used to indicate the extent of migration in the direction of the flow relative to the speed of the migrating cell (48). The path length, s, of each cell, and the distance moved in the direction of flow, xf, were determined at each time point and then summed for the duration of the experiment (N time points). The DIM was calculated by dividing the total distance moved in the direction of flow by the total path length of the cell,
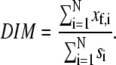 |
If a cell migrated against the flow, the DIM was negative. A mean DIM of zero would indicate no preference in the direction of migration for the cell population. Data was analyzed by ANOVA with Tukey HSD for unequal N post hoc.
Parameter estimation using a stochastic model
Cell migration was also analyzed as an Ornstein-Uhlenbeck process to account for the movement of cells due to fluid shear stress, similar to previously described methods for chemotaxis (49). Simulated cell migration is defined by three parameters in a stochastic differential equation, α, β, and γ, which describe the magnitude of random fluctuation, the susceptibility of the cell to random fluctuations, and a directional bias, respectively. The cell velocity is calculated from the stochastic differential equation 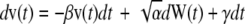 (49). The continuous-time white noise process, dW(t), adds random fluctuations in cell velocity to the model. The directional bias γ was set to zero in the direction perpendicular to the flow. The stochastic equation was solved using a second-order accurate finite difference method in MATLAB. The average cell displacements as a function of time were calculated for 100 solutions to the stochastic equation. The calculated displacements were optimized to fit the experimental cell displacement data using the subplex optimization algorithm (50) implemented in MATLAB by Bruce Lowekamp (“subplexm”), downloaded from http://www.netlib.org. The optimized parameters α, β, and γ were converted to speed (S), persistence time (P), and DIM for comparison to the values calculated from the cell tracking experiments using the equations
(49). The continuous-time white noise process, dW(t), adds random fluctuations in cell velocity to the model. The directional bias γ was set to zero in the direction perpendicular to the flow. The stochastic equation was solved using a second-order accurate finite difference method in MATLAB. The average cell displacements as a function of time were calculated for 100 solutions to the stochastic equation. The calculated displacements were optimized to fit the experimental cell displacement data using the subplex optimization algorithm (50) implemented in MATLAB by Bruce Lowekamp (“subplexm”), downloaded from http://www.netlib.org. The optimized parameters α, β, and γ were converted to speed (S), persistence time (P), and DIM for comparison to the values calculated from the cell tracking experiments using the equations 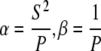 (49), and
(49), and 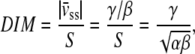 where
where 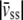 is the cell drift velocity due to fluid shear stress. For initial values, we calculated α, β, and γ using the values for speed, persistence time, and DIM calculated by the methods described above.
is the cell drift velocity due to fluid shear stress. For initial values, we calculated α, β, and γ using the values for speed, persistence time, and DIM calculated by the methods described above.
Immunofluorescent imaging
Round glass coverslips were cleaned with 1 M HCl overnight at 110°C and silanated with 3-mercaptopropyltrimethoxysilane. The slides were sterilized with 70% ethanol and a thin layer of PEG hydrogel solution (20 μL) containing 4.12 mM linear RGD or 0.69 mM cyclic RGD was coated onto the slides. After polymerization, the slides were seeded with HAEC and grown for 18 h at 37°C in low serum medium, with or without 100 nM S1P. The cells were fixed in 4% paraformaldehyde in PBS for 30 min at room temperature. After rinsing three times with PBS for 5 min each, blocking buffer (1% w/v IgG-free BSA and 3% normal goat serum in PBS) was added to the cells for 20 min at room temperature. The cells were incubated with primary antibody for vinculin (Sigma) or pY397-FAK (BioSource International, Camarillo, CA) at 1:250 dilution in blocking buffer overnight at 4°C. Slides were washed four times in PBS, and then incubated with the secondary antibody (Molecular Probes, Eugene, OR) at 1:400 dilution in PBS for 1 h at room temperature. Slides were imaged by confocal microscopy.
RESULTS
Cell migration is expected to have a biphasic dependence on the adhesion strength of cells to the substrate (21,24). We have previously shown that S1P promotes endothelial cell migration on PEG hydrogels containing linear RGD peptide (15). However, it is not known how S1P-induced increases in endothelial cell migration depend on the adhesiveness of the substrate. We examined cell adhesion strength and migration with and without 100 nM S1P in solution on PEG-OVS/albumin hydrogels that contained various concentrations of two different RGD-containing peptides. The concentration of S1P in serum is ∼1 μM (51), but the presence of high-density lipoproteins in plasma reduces the ability of S1P to interact with its receptors (52). Although it has been shown previously that endothelial cell migration continues to increase with higher S1P concentrations, e.g., up to 1–5 μM (14,27,53), concentrations in this range are likely to be nonphysiological. Thus, 100 nM S1P in low serum medium was used for the experiments, a concentration that is sufficient to increase endothelial cell migration and FAK phosphorylation (29,33,54–56).
Integrin specificity of RGD peptides
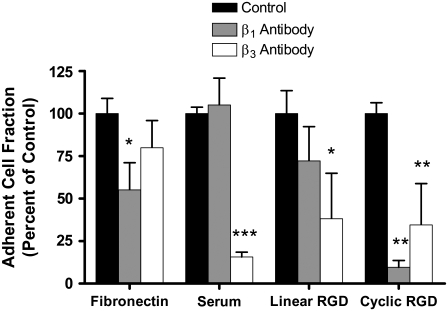
The two peptides used were a linear RGD peptide (Ac-GCGYGRGDSPG) and a cyclic RGD peptide (Ac-GCNAC*RGDWGC*G). The linear RGD peptide has a binding preference for the αvβ3 integrin over the α5β1 integrin (41,43). Use of integrin-specific function-blocking antibodies against β3 and β1 subunits confirmed that cell adhesion to the linear RGD peptide was mostly dependent on the αvβ3 integrin (Fig. 1). The cyclic RGD peptide was originally selected by Koivunen et al. from a phage display library for its binding to α5β1 integrin (41). Cell adhesion to PEG hydrogels containing the cyclic RGD peptide was significantly reduced by antibodies to both the β1 and β3 integrin subunits, with cell adhesion nearly eliminated with the anti-β1 antibody. Without RGD in the PEG hydrogels, cell adhesion was quite low, with <6 cells/cm2 remaining on the hydrogel after PBS washing, and these cells did not spread on the surface.
FIGURE 1.
RGD peptides show different integrin specificity. On the control surfaces, anti-β1 antibody significantly inhibited endothelial cell adhesion to fibronectin, whereas anti-β3 antibody inhibited endothelial cell adhesion to a serum-protein-coated well. On the PEG/albumin hydrogels, adhesion to the linear RGD peptide was inhibited by anti-β3 antibody, whereas adhesion to the cyclic RGD peptide was significantly inhibited by both the anti-β3 antibody and anti-β1 antibody. *p < 0.05 versus control on same substrate. **p < 0.005 versus control on same substrate. ***p < 0.0005 versus control on same substrate.
Cyclic RGD provides stronger cell adhesion
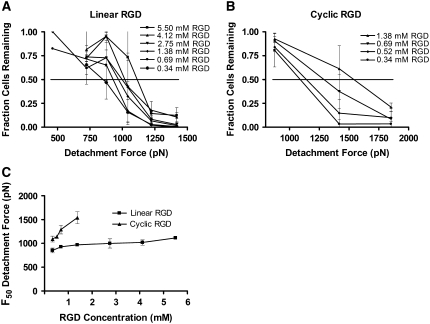
The initial adhesion strengths of endothelial cells to hydrogels containing linear or cyclic RGD were determined using a centrifugation assay. HAEC were allowed to adhere to and spread on the hydrogel surfaces for 6 h. The plates were inverted and centrifuged to apply a detachment force to the cells. The percent of cells remaining adhered to the hydrogels after centrifugation for 5 min was measured for various centrifugal forces (Fig. 2, A and B). The F50 for each RGD concentration was interpolated from the averaged data at each centrifugal force (Fig. 2 C). As the concentration of linear RGD was increased, the F50 increased from ∼850 to 1120 pN. Even though lower concentrations of cyclic RGD were added to the PEG hydrogels, the values of F50 for cyclic-RGD-containing hydrogels were higher, ranging from ∼1090 to 1550 pN. For example, at a concentration of 0.69 mM RGD, the F50 adhesion strength was 928 pN on linear RGD peptide and 1290 pN on cyclic RGD peptide.
FIGURE 2.
Centrifugal detachment force increases with RGD concentration in PEG hydrogels. The percent of endothelial cells remaining on PEG hydrogels after 5 min of centrifugal force was measured. The PEG hydrogels contained (A) linear RGD, or (B) cyclic RGD. Data are means ± standard deviations. (C) The detachment forces for removal of 50% of the cells (F50) from the RGD-containing PEG gels was interpolated from the data in A and B. The F50 increased as the RGD peptide concentration increased. The attachment strength to cyclic RGD was higher than on linear RGD at similar concentrations.
Cell adherence under shear stress is decreased on cyclic RGD
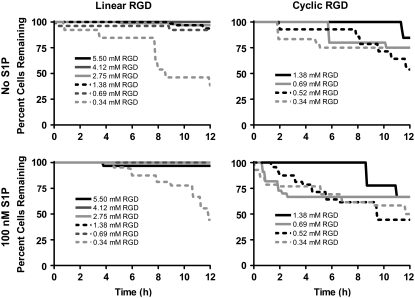
Human aortic endothelial cell migration was tracked by time-lapse microscopy on PEG-OVS/albumin hydrogels containing various concentrations of RGD peptide in a gravity-driven flow chamber. During the course of the 12-h experiment, some cells were removed from the hydrogel due to the fluid shear stress (20 dyn/cm2). For linear RGD, a significant loss of cells from the hydrogel surface was only seen on the lowest linear RGD concentrations (Fig. 3). Surprisingly, a significant loss of cells from the hydrogel surface was observed on all cyclic RGD concentrations. Even at the highest cyclic RGD concentration, a loss of ∼20% of the cells was seen over 12 h, whereas <5% of the cells were lost at the same concentration of linear RGD. Although cell division did occur during the 12 h, cell division was not coincident with cell detachment (data not shown).
FIGURE 3.
Cell adherence to RGD-containing PEG hydrogels under shear stress. The percent of endothelial cells remaining on the gels during the 12-h flow experiment increased with increasing peptide concentration. Greater than 50% cell loss was found for the lowest (0.34 mM) linear and cyclic RGD concentrations. Cell loss was 25–30% on 0.69 mM cyclic RGD, where the maximum migration speed was observed.
Presence of focal adhesions or focal contacts most prominent on linear RGD
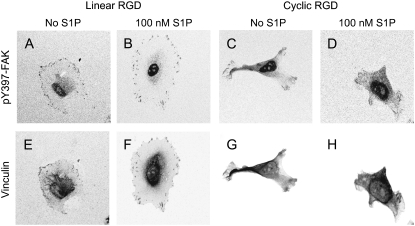
We observed larger, more spread cells that contained more focal adhesions and focal contacts in cells grown on 4.12-mM linear RGD (Fig. 4) (the RGD concentration that led to a maximum cell speed in the absence of S1P) compared with cells grown on 0.69 mM cyclic RGD (the RGD concentration that led to the highest cell speed in the presence of S1P). Although the staining was performed with cells in static conditions, the size difference was also apparent in the projected cell areas measured after 3 h in flow. On linear RGD peptide, the mean projected cell area was 3420 ± 2878 μm2 without S1P and 3450 ± 1900 μm2 with 100 nM S1P. On 0.69 mM cyclic RGD, projected cell areas were 1444 ± 613 μm2 without S1P and 1471 ± 697 μm2 with 100 nM S1P. The addition of S1P did not change cell size or the size and number of focal contacts and focal adhesions on either surface.
FIGURE 4.
RGD peptide effects on focal adhesion/focal contact formation. The extent of focal adhesion formation on 4.12-mM linear and 0.69-mM cyclic RGD was measured by immunofluorescence staining for pY397-FAK (A–D) and vinculin (E–H). On 4.12-mM linear RGD, staining was localized to sites of adhesion in the absence (A and E) and presence (B and F) of 100 nM S1P. On 0.69-mM cyclic RGD, vinculin and pY397-FAK staining was weak at the cell periphery and cells were generally smaller than on linear RGD (C and G, no S1P; D and H, 100 nM S1P). Black and white images were inverted in Image J to highlight staining. A color version of this figure containing additional cells is included in Supplementary Materials, Fig. S2.
S1P-induced cell migration is greatest at higher adhesion strengths on cyclic RGD
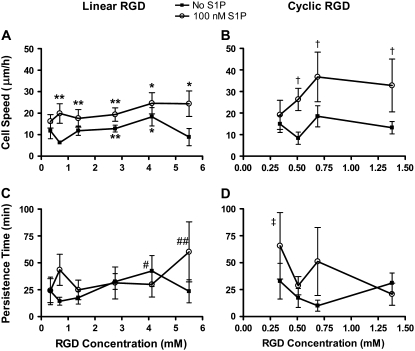
Cell positions recorded at each time interval were used to determine the mean speed for each cell over the 12-h tracking period. Without S1P, the migration speed of cells on the hydrogels had a biphasic dependence on the linear RGD concentration, with maximum cell speed at 4.12 mM linear RGD (a biphasic response is defined here as a statistically significant increase at a peptide concentration versus both a higher and lower peptide concentration). This biphasic dependence was expected from past research by DiMilla et al. (20,21). When 100 nM S1P was added to the medium, a significant increase in cell speed was seen with increasing RGD concentration, but a drop in migration speed was not observed at the highest linear RGD concentrations, 5.5 mM linear RGD (Fig. 5 A). At the highest linear RGD concentrations, endothelial cell migration speed more than doubled with the addition of 100 nM S1P. On cyclic RGD-containing hydrogels without S1P, the migration speed on the hydrogels did not have a statistically significant dependence on the peptide concentration (Fig. 5 B). The addition of 100 nM S1P dramatically increased the endothelial cell migration speed, particularly at the higher cyclic RGD concentrations. Migration speed with S1P peaked at 0.69 mM cyclic RGD. At this cyclic RGD concentration with S1P, the cell migration speed was more than twice the speed of cells without S1P, and 44% greater than the highest migration speed seen on linear RGD with 100 nM S1P.
FIGURE 5.
Cell speed and persistence time on PEG hydrogels with linear and cyclic RGD peptides in the presence of fluid flow. Individual cell speeds were found by dividing the displacement at the shortest time interval by the length of the time interval (i.e., 6 min). (A) Cell speed was biphasic on linear RGD without S1P, and was increased by S1P, particularly with 5.5 mM RGD *p < 0.05 versus no S1P, 0.69, 1.38, 2.75, and 5.5 mM linear RGD. **p < 0.05 versus no S1P, 0.69 mM linear RGD. (B) S1P increased cell speed for all cyclic RGD concentrations and a maximum cell speed was found for 0.69 mM RGD. †p < 0.05 versus no S1P, 0.52 and 1.38 mM RGD. (C) Persistence time was not strongly dependent on linear RGD concentration. #p < 0.05 versus no S1P, 0.69 and 1.38 mM linear RGD. ##p < 0.05 versus no S1P, 0.69 and 1.38 mM linear RGD and 100 nM S1P, 1.38 and 4.12 mM linear RGD. (D) S1P may increase the persistence time at low concentrations of cyclic RGD. ‡p < 0.05 versus no S1P, 0.52 mM cyclic RGD and 100 nM S1P, 1.38 mM cyclic RGD. Data are means ± 95% confidence interval based on the mean ± SE. Please confirm. Analysis by ANOVA with Tukey HSD for unequal N post hoc.
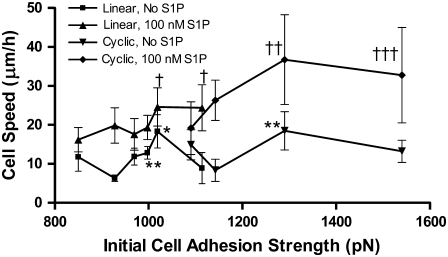
Cell attachment strengths at the lowest concentrations of cyclic RGD were comparable to the highest concentration of linear RGD peptide, allowing us to combine the data into a plot of cell speed over a wide range of cell adhesion strengths (Fig. 6). The relatively good agreement between cell migration speeds found for linear and cyclic RGD peptides with similar adhesion strengths is surprising given the tremendous difference in morphology and focal adhesion density between the cells on the different peptides.
FIGURE 6.
Cell speed related to initial attachment strength on linear and cyclic RGD in the presence of fluid flow. Cell speed on PEG hydrogels with linear and cyclic RGD peptides was affected by the initial strength of cell attachment to each gel. The linear and cyclic RGD results from Fig. 5 seem to overlap, indicating the importance of cell adhesion strength in determining cell speed. Without S1P, two maxima in migration speed are present, at 1020 and 1290 pN attachment strength. In the presence of 100 nM S1P, migration speed continues to increase from the linear RGD to the cyclic RGD attachment strength ranges. †p < 0.05 versus linear RGD without S1P, 930 pN. ††p < 0.05 versus linear RGD with S1P, 850 and 970 pN, linear RGD without S1P, 930, 970, 1000, and 1110 pN, and cyclic RGD without S1P, 1140 pN. †††p < 0.05 versus linear RGD with S1P, 850 and 970 pN, linear RGD without S1P, 930, 970, 1000, and 1110 pN, and cyclic RGD without S1P, 1140 and 1540 pN. *p < 0.05 versus linear RGD without S1P, 930, 970, and 1110 pN, and cyclic RGD without S1P, 1140 pN. **p < 0.05 versus linear RGD without S1P, 930 pN. Data are means ± 95% confidence interval based on mean ± SE. Analysis by ANOVA with Tukey HSD for unequal N post hoc.
Persistence time weakly affected by S1P or RGD concentration
The persistence time was determined for each cell by fitting the calculated root mean-squared speed to the persistent random-walk displacement equation. The persistence times were greater on 4.12 mM linear RGD than on 0.69 or 1.38 mM linear RGD in the absence of S1P (Fig. 5 C). With 100 nM S1P, persistence time was not significantly changed by RGD peptide concentrations except at the highest linear RGD concentration tested (5.5 mM). On the cyclic-RGD-containing hydrogels in the absence of S1P, the persistence time did not depend on RGD concentration (Fig. 5 D). With 100 nM S1P, persistence times showed an increase at the lowest cyclic RGD concentration tested (0.34 mM).
S1P may increase the directional index of migration
High levels of fluid shear stress, as would be present in arteries, have been shown to promote endothelial cell migration in the direction of flow (57–61). The DIM was calculated by dividing the total distance moved in the direction of flow by the total path length of the cell. The DIM can be used to indicate the extent of migration in the direction of the flow relative to the speed of the migrating cell. A negative value would indicate cell migration against the flow, whereas a value of zero indicates random motility, as would be expected without directional stimuli such as flow.
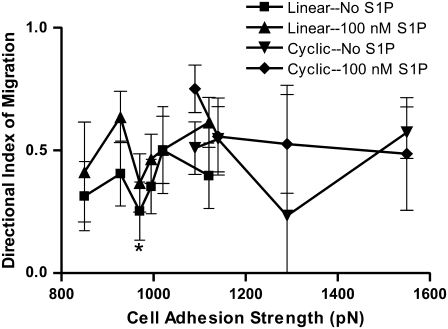
The DIM was calculated for endothelial cell migration on both linear and cyclic RGD, with and without 100 nM S1P under 20 dyn/cm2 of shear stress. Endothelial cells preferentially migrated in the direction of flow under all conditions. On linear RGD, the mean DIM ranged from 0.24 to 0.64 (Fig. 7). Although no significant increase due to S1P was observed at any single linear RGD concentration, S1P did cause a significant increase in the directional migration of the endothelial cells, combining data for all linear RGD concentrations. On cyclic RGD, the DIM ranged from 0.23 to 0.75. The addition of S1P did not significantly alter the DIM on cyclic RGD (Fig. 7).
FIGURE 7.
Directional index of migration of PEG hydrogels with RGD peptides in the presence of fluid flow. The DIM represents the fraction of cell displacement that is in the direction of flow. DIM does not strongly depend on the adhesion strength for either linear or cyclic RGD. *p < 0.05 versus linear RGD with S1P, 1110 pN initial adhesion strength. However, combining data for all concentrations of each RGD peptide, S1P caused a significant increase in DIM on linear RGD. Data are means ± 95% confidence interval based on mean ± SE. Analysis by ANOVA with Tukey HSD for unequal N post hoc.
Biphasic random motility coefficient in the absence of S1P
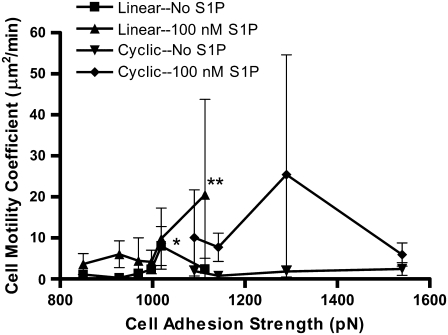
Together, cell speed and persistence time determine the motility characteristics of individual cells. A random motility coefficient, μ, can be calculated from the speed and persistence time using the equation 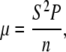 where n is the dimension of migration. The random motility coefficient, corresponding to the coefficient of molecular diffusion, quantitatively describes the random migration of the cell population. Without S1P, μ shows a biphasic dependence on the initial adhesion strength, displaying a single maximum at 1020 pN with linear RGD (Fig. 8). The random motility coefficient increased with the addition of 100 nM S1P to the medium, in some cases dramatically, but was associated with large variances. At an adhesion strength of 1290 pN, the mean random motility coefficient increased 13.8-fold upon addition of S1P.
where n is the dimension of migration. The random motility coefficient, corresponding to the coefficient of molecular diffusion, quantitatively describes the random migration of the cell population. Without S1P, μ shows a biphasic dependence on the initial adhesion strength, displaying a single maximum at 1020 pN with linear RGD (Fig. 8). The random motility coefficient increased with the addition of 100 nM S1P to the medium, in some cases dramatically, but was associated with large variances. At an adhesion strength of 1290 pN, the mean random motility coefficient increased 13.8-fold upon addition of S1P.
FIGURE 8.
The cell random motility coefficient is highest in the presence of 100 nM S1P. Random motility coefficients were calculated from the cell speeds and persistence times in Fig. 5. The random motility coefficient increased with 100 nM S1P and peaked at a higher adhesion strength when S1P was added. *p < 0.05 for linear RGD without S1P, 1020 pN versus 930, 970, and 1000 pN, and cyclic RGD without S1P, 1140 and 1540 pN. **p < 0.05 versus linear RGD without S1P, 930 and 970 pN. Data are means ± 95% confidence interval based on mean ± SE. Analysis by ANOVA with Tukey HSD for unequal N post hoc.
Cell speed related to projected cell area
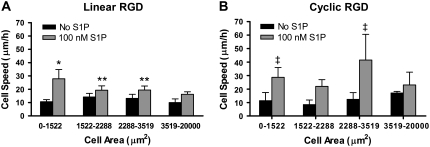
The projected area of each spread cell was measured after 3 h under 20 dyn/cm2 of shear stress. Without S1P, the mean cell area increased as the linear RGD concentration increased, but with the addition of 100 nM S1P, the mean cell areas were not significantly influenced by RGD concentration (data not shown). Examining the mean cell speeds as a function of the mean cell areas on linear RGD revealed no obvious relationship, with or without S1P. To further dissect how the cell area is related to cell speed, we split the cell areas into quartiles. The cell area quartiles were determined using cells on all linear RGD gels without S1P, to examine the full range of cell areas. In the absence of S1P, the cell speeds were not significantly different for cells in different cell-area quartiles (Fig. 9 A). When the cells were supplied 100 nM S1P, cell speeds were significantly greater for smaller cells compared to larger cells. Small cells also demonstrated a significantly greater migration speed in the presence of S1P than without it.
FIGURE 9.
Higher cell speeds across a range of cell areas on cyclic RGD in the presence of 100 nM S1P. Mean cell speeds by cell area quartiles are shown for endothelial cells migrating on: (A) linear or (B) cyclic RGD peptide. *p < 0.05 versus all other cell area quartiles on linear RGD with and without S1P. **p < 0.05 versus no S1P, 0-1522 and 3519–20000 μm2 cells on linear RGD. ‡p < 0.05 versus no S1P, 0–1522, 1522–2288, and 2288–3519 μm2 cells on cyclic RGD. Data are means ± 95% confidence interval based on mean ± SE. Analysis by ANOVA with Tukey HSD for unequal N post hoc.
For PEG hydrogels with cyclic RGD peptide, a trend toward larger projected cell areas at higher RGD concentrations was observed, although the difference was not significant. S1P did not change this trend. We examined the relationship between cell speed and cell area on the cyclic RGD gels. In the absence of S1P, no significant differences were observed (Fig. 9 B). When 100 nM S1P was added to the cells, the cell speed was significantly increased for cells with areas 0–1522 and 2288–3519 μm2.
Stochastic modeling analysis
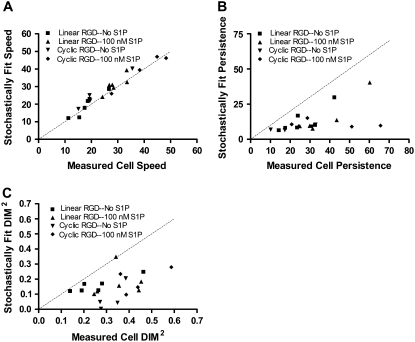
An alternative method of analyzing cell migration is to fit experimental cell displacements to simulated cell displacements over different time intervals, which allows a straightforward accounting of biased cell migration in the presence of flow. Stochastic cell migration is modeled here by three parameters, α, β, and γ, which describe the magnitude of random fluctuations, susceptibility of the cell to random fluctuations, and a directional bias, respectively (49). Random fluctuations in migration were modeled as a continuous white-noise process, and the stochastic differential equation was solved numerically, varying α, β, and γ to achieve a nonlinear least-squares fit with the cell displacement data. The parameters α, β, and γ were converted to speed, persistence, and directional index of migration for comparison to values calculated from the cell tracking experiments using the persistent random walk method (Fig. 10). We found an excellent agreement for the two methods in calculating the root mean-square cell speed (r = 0.97) and marginal agreement with persistence time and the squared DIM (r = 0.54 and 0.47, respectively). The squared DIMs were compared because positive and negative values for γ are equivalent by this method.
FIGURE 10.
Quantifying cell migration parameters using a stochastic model. Cell displacements on PEG hydrogels containing linear or cyclic RGD peptides were nonlinear least-squares fit to numerical solutions of an Ornstein-Uhlenbeck equation, as described in Methods. The RMS cell speeds, persistence times, and DIMs were determined. Each of the values derived from the stochastic model was compared to the manually measured values (speed and DIM) or least-squares fit (persistence time). (A) The stochastically measured cell speed had a Pearson correlation coefficient of 0.97 with the measured RMS cell speed. (B) The correlation coefficient for cell persistence time was 0.54. (C) The DIM squared had a correlation coefficient of 0.46.
DISCUSSION
Our PEG hydrogel materials are formed by cross-linking PEG-OVS with BSA. We have previously demonstrated that due to the lipid-binding abilities of albumin, S1P can be trapped in these hydrogels and delivered in a controlled manner (15). These S1P-releasing materials produced a strong angiogenic response in the chick chorioallantoic membrane assay and increased the migration speeds of human umbilical vein endothelial cells attached to the S1P-releasing hydrogels containing linear RGD peptides. Given the clinical utility of PEG materials as compared with other hydrogel materials used in cell adhesion and migration studies, we believe that the results generated with this system may be more readily applied to the development of coatings for endovascular stents and vascular grafts. As such, all of the migration experiments in this study were performed with human aortic endothelial cells in the presence of arterial levels of fluid shear stress.
The migration rates of endothelial cells are greatly influenced by chemical and physical interactions with the substrate. Experimental and theoretical results suggest that the migration rates of cells have a biphasic dependence on the strength of the cell's attachment to the substrate (20–23). Yet the circumstances under which cell adhesivity can be used to predict migration speeds are limited (21,24,34). Adhesion strength may control migration if other factors are kept constant, but if other stimuli are added, such as growth factors that affect signaling processes of the cell, the migration/adhesion relationship can be dramatically altered (34). More recent research from Waterman-Storer et al. has suggested that a balance between the activities of actin, myosin II, and focal adhesion dynamics determine cell migration speeds, and that cell adhesion strength is only one factor that contributes to the dynamic interactions between these proteins (63).
Our data demonstrated that initial cell attachment strengths at the lowest concentrations of cyclic RGD were comparable to those at the highest concentrations of linear RGD. Comparing the cell migration speeds on cyclic and linear RGD surfaces as a function of initial cell attachment strength (Fig. 6), the cyclic RGD migration speeds in the presence of S1P appeared to be a relatively smooth extension of the linear RGD migration speeds. However, the combined results in the absence of S1P seem to show two peaks in migration speed, one for each peptide. In principle, very low migration speeds should have been observed at all cyclic RGD concentrations in the absence of S1P due to the high strength of adhesion to this peptide. Although this was not observed for cell migration speeds, this pattern was observed for the random motility coefficient in the absence of S1P. This resulted from the presence of what appeared to be a biphasic persistence time on linear RGD in the absence of S1P, and an inverted biphasic persistence time on cyclic RGD in the absence of S1P. Staining for vinculin and focal adhesion kinase demonstrated differences in the organization of focal adhesions and in cell spreading between linear and cyclic RGD surfaces. If the same underlying machinery for cell locomotion is present in cells on both surfaces, then focal adhesions and focal contacts might be seen as a hindrance to the most rapid rates of cell migration. On cyclic RGD, cells may migrate more rapidly because they are not limited by the presence of focal adhesions, whose disassembly is necessary for cell migration. An Ezrin-mediated migration mode has been observed with cells in 3D culture (64), but we did not determine if cell migration on the cyclic RGD was noncanonical.
Long-term adhesion of endothelial cells to the cyclic RGD peptides in the presence of arterial levels of wall shear stress (20 dyn/cm2) was worse compared to that with linear RGD peptides. This was despite higher initial attachment strengths to the cyclic RGD hydrogels. This effect may be biomechanical, due to the higher profile in the flow and fewer focal adhesions. Cells growing on 1.38 mM cyclic RGD peptide had similar projected cell areas to cells growing on 1.38 mM linear RGD. However, projected cell areas were reduced at lower cyclic RGD concentrations. A less spread cell could have a greater contact angle with the surface that would alter the hemodynamic force applied to the cell (65).
Both the αvβ3 and α5β1 integrin are highly expressed in endothelial cells (66–69). Although integrin surface densities have not been reported for HAEC, α5β1 expression in HUVEC has been reported to be ∼7.5 × 105 receptors per cell (68). The expression of αvβ3 and α5β1 has been reported to be altered by shear stress. In HUVEC, mRNA and cell surface expression of α5β1 was reportedly increased by shear stress, whereas αvβ3 expression was unchanged (70). In bovine aortic endothelial cells, αvβ3 and α5β1 integrin cell surface density were both increased by exposure to shear stress, although upregulation required the engagement of the respective integrin on the substrate (71). However, in HAEC, it was reported that α5β1 mRNA expression was decreased by laminar shear stress after 24 h, whereas αvβ3 mRNA expression was unchanged (72). If α5β1 expression were decreased by shear stress in HAEC in our 12-h experiments, this could explain the loss of cells on the cyclic RGD during tracking, presuming that the β1 integrin binding was primarily associated with α5β1.
In addition to changes in the cell surface expression of integrins, the affinities of integrins are also dynamic (73). Both αvβ3 and α5β1 integrins can undergo affinity maturation, causing the recruitment of αvβ3 to focal adhesion in the cell periphery and lamellipodia (74,75), whereas α5β1 remains in fibrillar adhesions with no change in localization (74). Shear stress induces high-affinity αvβ3 in endothelial cells and focal adhesion formation (71,76). High-affinity α5β1 binding to fibronectin creates fibrillar adhesion, which requires a synergistic syndecan PHSRN binding site for maturation (77–79). The induction of high-affinity αvβ3 integrin and focal adhesions on the linear RGD, and the absence of maturation on the cyclic RGD due to absence of binding to the synergy site on α5β1 could also explain the differences in long-term cell adherence between the two peptides in the presence of fluid shear stress. However, we did not specifically identify the β3 integrin as αvβ3 nor the β1 integrin as α5β1, so other integrin α-subunits may also contribute to the observed results.
Many factors other than adhesion strength could play a role in the cell migration speed. As noted earlier, it has been suggested that focal adhesion and cytoskeletal dynamics could change the relationship of migration to cell attachment strength (63). Shear stress has been shown to affect endothelial cell migration through a variety of mechanisms involving integrins (70,80–82). The increase in cell migration speed induced by shear stress has been attributed entirely to the α5β1 integrin (83). S1P has been shown to stimulate the phosphorylation of focal adhesion kinase (29) and cause remodeling of focal adhesions in endothelial cells (35,84). This could alter cytoskeletal dynamics and change the effect of cell adhesion strength on migration speed.
Growth factors and other chemotactic/chemokinetic agents also affect the dynamics of actin and myosin in the cell. Activation of Rac by S1P, vascular endothelial growth factor (VEGF), or basic fibroblast growth factor (bFGF) results in increased lamellipodia formation and subsequent localization of Rac activity to the leading edge of the cell (75,85,86). Rac promotes lamellipodia extension via actin polymerization induced by activating WAVE proteins (85,87). High-affinity αvβ3 integrin is recruited to the leading edge by Rac, promoting the formation of new adhesions that stabilize the lamellipodia (75). Rac activation by VEGF and bFGF is PP2-sensitive and thus Src-dependent (86,88). S1P-induced migration does not require Src, but does depend on the on Akt-mediated phosphorylation of its S1P1 receptor (88). Lamellipodia extension promoted by S1P or VEGF requires phosphatidylinositol-3 kinase activity, whereas bFGF-induced lamellipodia formation does not (88). This suggests that although the chemotactic factors promote migration via Rac activation, cytoskeletal dynamics are altered through several independent pathways.
The results of the stochastic model generally agreed with the manual measurements, but highlight some of the difficulties in calculating two or three parameters using mean-squared displacement data. For least-squares fitting of the data to the stochastic model, we used as initial values the speed and persistence times previously calculated without considering cell drift. Considering the sensitivity of the mean-squared displacement to cell speed and persistence time (∂〈d2〉/∂S and ∂〈d2〉/∂P, respectively, of the equation 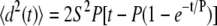 ), the mean-squared displacement is ∼100 times more sensitive to changes in the persistence time at values of the variables relevant to our system (e.g., S = 30 μm/h, P = 10 min with 1-h time steps). Therefore, it is not surprising that the minimization routine reduced the persistence time and not the cell speed to account for the cell drift. However, values of the absolute value of DIM calculated with the stochastic model were lower than the manual measurement. Given the reduction in persistence time with the stochastic model, it is possible that cell turning was present at time steps <6 min, increasing the cell speed and path length and decreasing the actual DIM. This should not affect the trends observed in the data but would impact the reported magnitudes.
), the mean-squared displacement is ∼100 times more sensitive to changes in the persistence time at values of the variables relevant to our system (e.g., S = 30 μm/h, P = 10 min with 1-h time steps). Therefore, it is not surprising that the minimization routine reduced the persistence time and not the cell speed to account for the cell drift. However, values of the absolute value of DIM calculated with the stochastic model were lower than the manual measurement. Given the reduction in persistence time with the stochastic model, it is possible that cell turning was present at time steps <6 min, increasing the cell speed and path length and decreasing the actual DIM. This should not affect the trends observed in the data but would impact the reported magnitudes.
Overall, our results indicate that the peak in cell migration speed and random motility coefficient is either eliminated or shifted to higher adhesion strengths in the presence of S1P. The magnitude of the maximum cell migration speed is increased by as much as 13.8-fold with the addition of 100 nM S1P. These effects may be due to more efficient lamellipodia formation via enhanced Rac activation and an increase in cell contractility due to localized RhoA activation in the trailing edge of the cell. Using the terms in the model by Dimilla et al. (20), we propose that Ψ, the ratio of uropodal to lamellipodal adhesiveness, is decreased, whereas fc, the intracellular contractile force, is increased with the addition of 100 nM S1P. We suggest that experimental perturbations of S1P1 phosphorylation, Rac activation, and myosin contractility may differentiate between lamellipodal adhesiveness and intracellular contractility in S1P-enhanced migration on RGD peptides.
CONCLUSIONS
Using single-cell tracking, we showed that S1P caused a significant increase in endothelial cell migration speeds on PEG hydrogels with linear and cyclic RGD peptides in the presence of fluid flow. The fastest migration speeds with S1P were found on the cyclic RGD peptide-containing hydrogels. S1P promoted rapid cell migration at RGD peptide concentrations that restricted cell migration without S1P. With S1P altering the biphasic relationship between cell adhesion and migration, a cyclic RGD concentration was found that promoted high rates of endothelial cell migration and high initial cell adhesion to the hydrogels. However, the endothelial cells on the cyclic RGD displayed a decrease in cell adherence in flow compared to linear RGD. To achieve firm adhesion in the presence of flow similar to that in in vivo conditions, it is possible that mixtures of different adhesion peptides will be beneficial, binding multiple integrins to allow both rapid cell migration in the presence of S1P and high long-term adhesion strengths in flow.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
We gratefully acknowledge funding from the Center for Materials Innovation at Washington University in St. Louis, from National Institutes of Health (NIH) training grant 5T32HL07916-05 (B.K.W., E.A.S., and S.K.A.), NIH R01CA85839 (G.D.L.), and NIH R01HL085364 (D.L.E.).
Editor: Michael Edidin.
References
- 1.Bjornsson, T. D., M. Dryjski, J. Tluczek, R. Mennie, J. Ronan, T. N. Mellin, and K. A. Thomas. 1991. Acidic fibroblast growth factor promotes vascular repair. Proc. Natl. Acad. Sci. USA. 88:8651–8655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Luscher, T. F., F. C. Tanner, M. R. Tschudi, and G. Noll. 1993. Endothelial dysfunction in coronary artery disease. Annu. Rev. Med. 44:395–418. [DOI] [PubMed] [Google Scholar]
- 3.Strauss, B. H., R. J. Chisholm, F. W. Keeley, A. I. Gotlieb, R. A. Logan, and P. W. Armstrong. 1994. Extracellular matrix remodeling after balloon angioplasty injury in a rabbit model of restenosis. Circ. Res. 75:650–658. [DOI] [PubMed] [Google Scholar]
- 4.Okura, H., S. Shimodozono, M. Hayase, H. N. Bonneau, P. G. Yock, and P. J. Fitzgerald. 2002. Impact of deep vessel wall injury and vessel stretching on subsequent arterial remodeling after balloon angioplasty: a serial intravascular ultrasound study. Am. Heart J. 144:323–328. [DOI] [PubMed] [Google Scholar]
- 5.Wilensky, R. L., K. L. March, I. Gradus-Pizlo, G. Sandusky, N. Fineberg, and D. R. Hathaway. 1995. Vascular injury, repair, and restenosis after percutaneous transluminal angioplasty in the atherosclerotic rabbit. Circulation. 92:2995–3005. [DOI] [PubMed] [Google Scholar]
- 6.Fischman, D. L., M. B. Leon, D. S. Baim, R. A. Schatz, M. P. Savage, I. Penn, K. Detre, L. Veltri, D. Ricci, M. Nobuyoshi, M. Cleman, R. Heuser, B. Almond, P. S. Teirstein, R. D. Fish, A. Colombo, J. Brinker, J. Moses, A. Shaknovich, J. Hirshfeld, S. Bailey, S. Ellis, R. Rake, and S. Goldberg. 1994. A randomized comparison of coronary-stent placement and balloon angioplasty in the treatment of coronary artery disease. N. Engl. J. Med. 331:496–501. [DOI] [PubMed] [Google Scholar]
- 7.Serruys, P. W., P. de Jaegere, F. Kiemeneij, C. Macaya, W. Rutsch, G. Heyndrickx, H. Emanuelsson, J. Marco, V. Legrand, P. Materne, J. Belardi, U. Sigwart, A. Colombo, J. J. Goy, P. V. D. Heuvel, J. Delcan, and M. Morel. 1994. A comparison of balloon-expandable-stent implantation with balloon angioplasty in patients with coronary artery disease. N. Engl. J. Med. 331:489–495. [DOI] [PubMed] [Google Scholar]
- 8.Chen, M. S., J. M. John, D. P. Chew, D. S. Lee, S. G. Ellis, and D. L. Bhatt. 2006. Bare metal stent restenosis is not a benign clinical entity. Am. Heart J. 151:1260–1264. [DOI] [PubMed] [Google Scholar]
- 9.Liistro, F., G. Falsini, P. Angioli, K. Ducci, and L. Bolognese. 2006. Late acute thrombosis after implantation of sirolimus-eluting stent to treat in-stent restenosis. Acute Card. Care. 8:116–118. [DOI] [PubMed] [Google Scholar]
- 10.Shuchman, M. 2006. Trading restenosis for thrombosis? New questions about drug-eluting stents. N. Engl. J. Med. 355:1949–1952. [DOI] [PubMed] [Google Scholar]
- 11.Brewster, L., E. M. Brey, M. Addis, L. Xue, V. Husak, J. Ellinger, C. C. Haudenschild, and H. P. Greisler. 2006. Improving endothelial healing with novel chimeric mitogens. Am. J. Surg. 192:589–593. [DOI] [PubMed] [Google Scholar]
- 12.Carnevale, K., K. Ouriel, Y. Gabriel, D. Clair, J. F. Bena, M. B. Silva, and T. P. Sarac. 2006. Biological coating for arterial stents: the next evolutionary change in stents. J. Endovasc. Ther. 13:164–174. [DOI] [PubMed] [Google Scholar]
- 13.Van Belle, E., L. Maillard, F. O. Tio, and J. M. Isner. 1997. Accelerated endothelialization by local delivery of recombinant human vascular endothelial growth factor reduces in-stent intimal formation. Biochem. Biophys. Res. Commun. 235:311–316. [DOI] [PubMed] [Google Scholar]
- 14.English, D., Z. Welch, A. T. Kovala, K. Harvey, O. V. Volpert, D. N. Brindley, and J. G. Garcia. 2000. Sphingosine 1-phosphate released from platelets during clotting accounts for the potent endothelial cell chemotactic activity of blood serum and provides a novel link between hemostasis and angiogenesis. FASEB J. 14:2255–2265. [DOI] [PubMed] [Google Scholar]
- 15.Wacker, B. K., E. A. Scott, M. M. Kaneda, S. K. Alford, and D. L. Elbert. 2006. Delivery of sphingosine 1-phosphate from poly(ethylene glycol) hydrogels. Biomacromolecules. 7:1335–1343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.McVerry, B. J., and J. G. Garcia. 2005. In vitro and in vivo modulation of vascular barrier integrity by sphingosine 1-phosphate: mechanistic insights. Cell. Signal. 17:131–139. [DOI] [PubMed] [Google Scholar]
- 17.Allende, M. L., T. Yamashita, and R. L. Proia. 2003. G-protein-coupled receptor S1P1 acts within endothelial cells to regulate vascular maturation. Blood. 102:3665–3667. [DOI] [PubMed] [Google Scholar]
- 18.Paik, J. H., A. Skoura, S. S. Chae, A. E. Cowan, D. K. Han, R. L. Proia, and T. Hla. 2004. Sphingosine 1-phosphate receptor regulation of N-cadherin mediates vascular stabilization. Genes Dev. 18:2392–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tamama, K., H. Tomura, K. Sato, E. Malchinkhuu, A. Damirin, T. Kimura, A. Kuwabara, M. Murakami, and F. Okajima. 2005. High-density lipoprotein inhibits migration of vascular smooth muscle cells through its sphingosine 1-phosphate component. Atherosclerosis. 178:19–23. [DOI] [PubMed] [Google Scholar]
- 20.DiMilla, P. A., K. Barbee, and D. A. Lauffenburger. 1991. Mathematical model for the effects of adhesion and mechanics on cell migration speed. Biophys. J. 60:15–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.DiMilla, P. A., J. A. Stone, J. A. Quinn, S. M. Albelda, and D. A. Lauffenburger. 1993. Maximal migration of human smooth muscle cells on fibronectin and type IV collagen occurs at an intermediate attachment strength. J. Cell Biol. 122:729–737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Goodman, S. L., G. Risse, and K. von der Mark. 1989. The E8 subfragment of laminin promotes locomotion of myoblasts over extracellular matrix. J. Cell Biol. 109:799–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huttenlocher, A., M. H. Ginsberg, and A. F. Horwitz. 1996. Modulation of cell migration by integrin-mediated cytoskeletal linkages and ligand-binding affinity. J. Cell Biol. 134:1551–1562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Palecek, S. P., J. C. Loftus, M. H. Ginsberg, D. A. Lauffenburger, and A. F. Horwitz. 1997. Integrin-ligand binding properties govern cell migration speed through cell-substratum adhesiveness. Nature. 385:537–540. [DOI] [PubMed] [Google Scholar]
- 25.Bayless, K. J., and G. E. Davis. 2003. Sphingosine-1-phosphate markedly induces matrix metalloproteinase and integrin-dependent human endothelial cell invasion and lumen formation in three-dimensional collagen and fibrin matrices. Biochem. Biophys. Res. Commun. 312:903–913. [DOI] [PubMed] [Google Scholar]
- 26.Endo, A., K. Nagashima, H. Kurose, S. Mochizuki, M. Matsuda, and N. Mochizuki. 2002. Sphingosine 1-phosphate induces membrane ruffling and increases motility of human umbilical vein endothelial cells via vascular endothelial growth factor receptor and CrkII. J. Biol. Chem. 277:23747–23754. [DOI] [PubMed] [Google Scholar]
- 27.Kimura, T., T. Watanabe, K. Sato, J. Kon, H. Tomura, K. Tamama, A. Kuwabara, T. Kanda, I. Kobayashi, H. Ohta, M. Ui, and F. Okajima. 2000. Sphingosine 1-phosphate stimulates proliferation and migration of human endothelial cells possibly through the lipid receptors, Edg-1 and Edg-3. Biochem. J. 348:71–76. [PMC free article] [PubMed] [Google Scholar]
- 28.Lee, H., E. J. Goetzl, and S. An. 2000. Lysophosphatidic acid and sphingosine 1-phosphate stimulate endothelial cell wound healing. Am. J. Physiol. Cell Physiol. 278:C612–C618. [DOI] [PubMed] [Google Scholar]
- 29.Lee, O. H., D. J. Lee, Y. M. Kim, Y. S. Kim, H. J. Kwon, K. W. Kim, and Y. G. Kwon. 2000. Sphingosine 1-phosphate stimulates tyrosine phosphorylation of focal adhesion kinase and chemotactic motility of endothelial cells via the G(i) protein-linked phospholipase C pathway. Biochem. Biophys. Res. Commun. 268:47–53. [DOI] [PubMed] [Google Scholar]
- 30.Morales-Ruiz, M., M. J. Lee, S. Zollner, J. P. Gratton, R. Scotland, I. Shiojima, K. Walsh, T. Hla, and W. C. Sessa. 2001. Sphingosine 1-phosphate activates Akt, nitric oxide production, and chemotaxis through a Gi protein/phosphoinositide 3-kinase pathway in endothelial cells. J. Biol. Chem. 276:19672–19677. [DOI] [PubMed] [Google Scholar]
- 31.Paik, J. H., S. Chae, M. J. Lee, S. Thangada, and T. Hla. 2001. Sphingosine 1-phosphate-induced endothelial cell migration requires the expression of EDG-1 and EDG-3 receptors and Rho-dependent activation of αvβ3- and β1-containing integrins. J. Biol. Chem. 276:11830–11837. [DOI] [PubMed] [Google Scholar]
- 32.Panetti, T. S. 2002. Differential effects of sphingosine 1-phosphate and lysophosphatidic acid on endothelial cells. Biochim. Biophys. Acta. 1582:190–196. [DOI] [PubMed] [Google Scholar]
- 33.Wang, F., J. R. Van Brocklyn, J. P. Hobson, S. Movafagh, Z. Zukowska-Grojec, S. Milstien, and S. Spiegel. 1999. Sphingosine 1-phosphate stimulates cell migration through a G(i)-coupled cell surface receptor. Potential involvement in angiogenesis. J. Biol. Chem. 274:35343–35350. [DOI] [PubMed] [Google Scholar]
- 34.Maheshwari, G., A. Wells, L. G. Griffith, and D. A. Lauffenburger. 1999. Biophysical integration of effects of epidermal growth factor and fibronectin on fibroblast migration. Biophys. J. 76:2814–2823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shikata, Y., K. G. Birukov, A. A. Birukova, A. Verin, and J. G. Garcia. 2003. Involvement of site-specific FAK phosphorylation in sphingosine-1 phosphate- and thrombin-induced focal adhesion remodeling: role of Src and GIT. FASEB J. 17:2240–2249. [DOI] [PubMed] [Google Scholar]
- 36.Mattie, M., G. Brooker, and S. Spiegel. 1994. Sphingosine-1-phosphate, a putative second messenger, mobilizes calcium from internal stores via an inositol trisphosphate-independent pathway. J. Biol. Chem. 269:3181–3188. [PubMed] [Google Scholar]
- 37.Mehta, D., M. Konstantoulaki, G. U. Ahmmed, and A. B. Malik. 2005. Sphingosine 1-phosphate-induced mobilization of intracellular Ca2+ mediates rac activation and adherens junction assembly in endothelial cells. J. Biol. Chem. 280:17320–17328. [DOI] [PubMed] [Google Scholar]
- 38.Giannone, G., P. Ronde, M. Gaire, J. Beaudouin, J. Haiech, J. Ellenberg, and K. Takeda. 2004. Calcium rises locally trigger focal adhesion disassembly and enhance residency of focal adhesion kinase at focal adhesions. J. Biol. Chem. 279:28715–28723. [DOI] [PubMed] [Google Scholar]
- 39.Ren, X. D., W. B. Kiosses, D. J. Sieg, C. A. Otey, D. D. Schlaepfer, and M. A. Schwartz. 2000. Focal adhesion kinase suppresses Rho activity to promote focal adhesion turnover. J. Cell Sci. 113:3673–3678. [DOI] [PubMed] [Google Scholar]
- 40.Pierschbacher, M. D., and E. Ruoslahti. 1984. Cell attachment activity of fibronectin can be duplicated by small synthetic fragments of the molecule. Nature. 309:30–33. [DOI] [PubMed] [Google Scholar]
- 41.Koivunen, E., B. Wang, and E. Ruoslahti. 1995. Phage libraries displaying cyclic peptides with different ring sizes: ligand specificities of the RGD-directed integrins. Biotechnology (N. Y.). 13:265–270. [DOI] [PubMed] [Google Scholar]
- 42.Elbert, D. L., and J. A. Hubbell. 2001. Conjugate addition reactions combined with free-radical cross-linking for the design of materials for tissue engineering. Biomacromolecules. 2:430–441. [DOI] [PubMed] [Google Scholar]
- 43.Liu, J. C., S. C. Heilshorn, and D. A. Tirrell. 2004. Comparative cell response to artificial extracellular matrix proteins containing the RGD and CS5 cell-binding domains. Biomacromolecules. 5:497–504. [DOI] [PubMed] [Google Scholar]
- 44.Reyes, C. D., and A. J. Garcia. 2003. A centrifugation cell adhesion assay for high-throughput screening of biomaterial surfaces. J. Biomed. Mater. Res. A. 67:328–333. [DOI] [PubMed] [Google Scholar]
- 45.Dunn, G. A. 1983. Characterising a kinesis response: time averaged measures of cell speed and directional persistence. Agents Actions Suppl. 12:14–33. [DOI] [PubMed] [Google Scholar]
- 46.Harms, B. D., G. M. Bassi, A. R. Horwitz, and D. A. Lauffenburger. 2005. Directional persistence of EGF-induced cell migration is associated with stabilization of lamellipodial protrusions. Biophys. J. 88:1479–1488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Othmer, H. G., S. R. Dunbar, and W. Alt. 1988. Models of dispersal in biological systems. J. Math. Biol. 26:263–298. [DOI] [PubMed] [Google Scholar]
- 48.Smith, L. A., H. Aranda-Espinoza, J. B. Haun, and D. A. Hammer. 2007. Interplay between shear stress and adhesion on neutrophil locomotion. Biophys. J. 92:632–640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Stokes, C. L., D. A. Lauffenburger, and S. K. Williams. 1991. Migration of individual microvessel endothelial cells: stochastic model and parameter measurement. J. Cell Sci. 99:419–430. [DOI] [PubMed] [Google Scholar]
- 50.Rowan, T. H. 1990. Functional Stability Analysis of Numerical Algorithms. University of Texas at Austin, Austin, TX.
- 51.Deutschman, D. H., J. S. Carstens, R. L. Klepper, W. S. Smith, M. T. Page, T. R. Young, L. A. Gleason, N. Nakajima, and R. A. Sabbadini. 2003. Predicting obstructive coronary artery disease with serum sphingosine-1-phosphate. Am. Heart J. 146:62–68. [DOI] [PubMed] [Google Scholar]
- 52.Murata, N., K. Sato, J. Kon, H. Tomura, M. Yanagita, A. Kuwabara, M. Ui, and F. Okajima. 2000. Interaction of sphingosine 1-phosphate with plasma components, including lipoproteins, regulates the lipid receptor-mediated actions. Biochem. J. 352:809–815. [PMC free article] [PubMed] [Google Scholar]
- 53.Lee, O. H., Y. M. Kim, Y. M. Lee, E. J. Moon, D. J. Lee, J. H. Kim, K. W. Kim, and Y. G. Kwon. 1999. Sphingosine 1-phosphate induces angiogenesis: its angiogenic action and signaling mechanism in human umbilical vein endothelial cells. Biochem. Biophys. Res. Commun. 264:743–750. [DOI] [PubMed] [Google Scholar]
- 54.Okamoto, H., Y. Yatomi, T. Ohmori, K. Satoh, Y. Matsumoto, and Y. Ozaki. 2000. Sphingosine 1-phosphate stimulates G(i)- and Rho-mediated vascular endothelial cell spreading and migration. Thromb. Res. 99:259–265. [DOI] [PubMed] [Google Scholar]
- 55.Yatomi, Y., T. Ohmori, G. Rile, F. Kazama, H. Okamoto, T. Sano, K. Satoh, S. Kume, G. Tigyi, Y. Igarashi, and Y. Ozaki. 2000. Sphingosine 1-phosphate as a major bioactive lysophospholipid that is released from platelets and interacts with endothelial cells. Blood. 96:3431–3438. [PubMed] [Google Scholar]
- 56.Hughes, S. K., B. K. Wacker, M. M. Kaneda, and D. L. Elbert. 2005. Fluid shear stress modulates cell migration induced by sphingosine 1-phosphate and vascular endothelial growth factor. Ann. Biomed. Eng. 33:1003–1014. [DOI] [PubMed] [Google Scholar]
- 57.Hsu, S., R. Thakar, D. Liepmann, and S. Li. 2005. Effects of shear stress on endothelial cell haptotaxis on micropatterned surfaces. Biochem. Biophys. Res. Commun. 337:401–409. [DOI] [PubMed] [Google Scholar]
- 58.Li, S., N. F. Huang, and S. Hsu. 2005. Mechanotransduction in endothelial cell migration. J. Cell. Biochem. 96:1110–1126. [DOI] [PubMed] [Google Scholar]
- 59.Sprague, E. A., J. Luo, and J. C. Palmaz. 2000. Endothelial cell migration onto metal stent surfaces under static and flow conditions. J. Long Term Eff. Med. Implants. 10:97–110. [PubMed] [Google Scholar]
- 60.Sprague, E. A., J. Luo, and J. C. Palmaz. 1997. Human aortic endothelial cell migration onto stent surfaces under static and flow conditions. J. Vasc. Interv. Radiol. 8:83–92. [DOI] [PubMed] [Google Scholar]
- 61.Wojciak-Stothard, B., and A. J. Ridley. 2003. Shear stress-induced endothelial cell polarization is mediated by Rho and Rac but not Cdc42 or PI 3-kinases. J. Cell Biol. 161:429–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Reference deleted in proof.
- 63.Gupton, S. L., and C. M. Waterman-Storer. 2006. Spatiotemporal feedback between actomyosin and focal-adhesion systems optimizes rapid cell migration. Cell. 125:1361–1374. [DOI] [PubMed] [Google Scholar]
- 64.Sahai, E., and C. J. Marshall. 2003. Differing modes of tumour cell invasion have distinct requirements for Rho/ROCK signalling and extracellular proteolysis. Nat. Cell Biol. 5:711–719. [DOI] [PubMed] [Google Scholar]
- 65.Wang, Y., and P. Dimitrakopoulos. 2006. Nature of the hemodynamic forces exerted on vascular endothelial cells or leukocytes adhering to the surface of blood vessels. Phys. Fluids.:18:087107. [Google Scholar]
- 66.Hoshiga, M., C. E. Alpers, L. L. Smith, C. M. Giachelli, and S. M. Schwartz. 1995. αvβ3 integrin expression in normal and atherosclerotic artery. Circ. Res. 77:1129–1135. [DOI] [PubMed] [Google Scholar]
- 67.Murphy, J. F., J. C. Bordet, B. Wyler, M. C. Rissoan, P. Chomarat, T. Defrance, P. Miossec, and J. L. McGregor. 1994. The vitronectin receptor (αvβ3) is implicated, in cooperation with P-selectin and platelet-activating factor, in the adhesion of monocytes to activated endothelial cells. Biochem. J. 304:537–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Conforti, G., A. Zanetti, S. Colella, M. Abbadini, P. C. Marchisio, R. Pytela, F. Giancotti, G. Tarone, L. R. Languino, and E. Dejana. 1989. Interaction of fibronectin with cultured human endothelial cells: characterization of the specific receptor. Blood. 73:1576–1585. [PubMed] [Google Scholar]
- 69.Suzuki, S., W. S. Argraves, H. Arai, L. R. Languino, M. D. Pierschbacher, and E. Ruoslahti. 1987. Amino acid sequence of the vitronectin receptor alpha subunit and comparative expression of adhesion receptor mRNAs. J. Biol. Chem. 262:14080–14085. [PubMed] [Google Scholar]
- 70.Urbich, C., D. H. Walter, A. M. Zeiher, and S. Dimmeler. 2000. Laminar shear stress upregulates integrin expression: role in endothelial cell adhesion and apoptosis. Circ. Res. 87:683–689. [DOI] [PubMed] [Google Scholar]
- 71.Tzima, E., M. A. del Pozo, S. J. Shattil, S. Chien, and M. A. Schwartz. 2001. Activation of integrins in endothelial cells by fluid shear stress mediates Rho-dependent cytoskeletal alignment. EMBO J. 20:4639–4647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Brooks, A. R., P. I. Lelkes, and G. M. Rubanyi. 2002. Gene expression profiling of human aortic endothelial cells exposed to disturbed flow and steady laminar flow. Physiol. Genomics. 9:27–41. [DOI] [PubMed] [Google Scholar]
- 73.Diamond, M. S., and T. A. Springer. 1994. The dynamic regulation of integrin adhesiveness. Curr. Biol. 4:506–517. [DOI] [PubMed] [Google Scholar]
- 74.Dormond, O., L. Ponsonnet, M. Hasmim, A. Foletti, and C. Ruegg. 2004. Manganese-induced integrin affinity maturation promotes recruitment of αvβ3 integrin to focal adhesions in endothelial cells: evidence for a role of phosphatidylinositol 3-kinase and Src. Thromb. Haemost. 92:151–161. [DOI] [PubMed] [Google Scholar]
- 75.Kiosses, W. B., S. J. Shattil, N. Pampori, and M. A. Schwartz. 2001. Rac recruits high-affinity integrin αvβ3 to lamellipodia in endothelial cell migration. Nat. Cell Biol. 3:316–320. [DOI] [PubMed] [Google Scholar]
- 76.Moon, J. J., M. Matsumoto, S. Patel, L. Lee, J. L. Guan, and S. Li. 2005. Role of cell surface heparan sulfate proteoglycans in endothelial cell migration and mechanotransduction. J. Cell. Physiol. 203:166–176. [DOI] [PubMed] [Google Scholar]
- 77.Burrows, L., K. Clark, A. P. Mould, and M. J. Humphries. 1999. Fine mapping of inhibitory anti-α5 monoclonal antibody epitopes that differentially affect integrin-ligand binding. Biochem. J. 344:527–533. [PMC free article] [PubMed] [Google Scholar]
- 78.Geiger, B., A. Bershadsky, R. Pankov, and K. M. Yamada. 2001. Transmembrane crosstalk between the extracellular matrix—cytoskeleton crosstalk. Nat. Rev. Mol. Cell Biol. 2:793–805. [DOI] [PubMed] [Google Scholar]
- 79.Humphries, M. J., M. A. Travis, K. Clark, and A. P. Mould. 2004. Mechanisms of integration of cells and extracellular matrices by integrins. Biochem. Soc. Trans. 32:822–825. [DOI] [PubMed] [Google Scholar]
- 80.Jin, Z. G., H. Ueba, T. Tanimoto, A. O. Lungu, M. D. Frame, and B. C. Berk. 2003. Ligand-independent activation of vascular endothelial growth factor receptor 2 by fluid shear stress regulates activation of endothelial nitric oxide synthase. Circ. Res. 93:354–363. [DOI] [PubMed] [Google Scholar]
- 81.Gloe, T., and U. Pohl. 2002. Laminin binding conveys mechanosensing in endothelial cells. News Physiol. Sci. 17:166–169. [DOI] [PubMed] [Google Scholar]
- 82.Gloe, T., H. Y. Sohn, G. A. Meininger, and U. Pohl. 2002. Shear stress-induced release of basic fibroblast growth factor from endothelial cells is mediated by matrix interaction via integrin αvβ3. J. Biol. Chem. 277:23453–23458. [DOI] [PubMed] [Google Scholar]
- 83.Urbich, C., E. Dernbach, A. Reissner, M. Vasa, A. M. Zeiher, and S. Dimmeler. 2002. Shear stress-induced endothelial cell migration involves integrin signaling via the fibronectin receptor subunits α5 and β1. Arterioscler. Thromb. Vasc. Biol. 22:69–75. [DOI] [PubMed] [Google Scholar]
- 84.Shikata, Y., K. G. Birukov, and J. G. Garcia. 2003. S1P induces FA remodeling in human pulmonary endothelial cells: role of Rac, GIT1, FAK, and paxillin. J. Appl. Physiol. 94:1193–1203. [DOI] [PubMed] [Google Scholar]
- 85.Ridley, A. J., M. A. Schwartz, K. Burridge, R. A. Firtel, M. H. Ginsberg, G. Borisy, J. T. Parsons, and A. R. Horwitz. 2003. Cell migration: integrating signals from front to back. Science. 302:1704–1709. [DOI] [PubMed] [Google Scholar]
- 86.Zhan, X., X. Hu, B. Hampton, W. H. Burgess, R. Friesel, and T. Maciag. 1993. Murine cortactin is phosphorylated in response to fibroblast growth factor-1 on tyrosine residues late in the G1 phase of the BALB/c 3T3 cell cycle. J. Biol. Chem. 268:24427–24431. [PubMed] [Google Scholar]
- 87.Cory, G. O., and A. J. Ridley. 2002. Cell motility: braking WAVEs. Nature. 418:732–733. [DOI] [PubMed] [Google Scholar]
- 88.Lee, J. F., H. Ozaki, X. Zhan, E. Wang, T. Hla, and M. J. Lee. 2006. Sphingosine-1-phosphate signaling regulates lamellipodia localization of cortactin complexes in endothelial cells. Histochem. Cell Biol. 126:297–304. [DOI] [PubMed] [Google Scholar]