Abstract
We explore the potential of a supercritical angle (SA) objective for fluorescence correlation spectroscopy (FCS). This novel microscope objective combines tight focusing by an aspheric lens with strong axial confinement of supercritical angle fluorescence collection by a parabolic mirror lens, resulting in a small detection volume. The tiny axial extent of the detection volume features an excellent surface sensitivity, as is demonstrated by diffusion measurements in model membranes with an excess of free dye in solution. All SA-FCS measurements are directly compared to standard confocal FCS, demonstrating a clear advantage of SA-FCS, especially for diffusion measurements in membranes. We present an extensive theoretical framework that allows for accurate and quantitative evaluation of the SA-FCS correlation curves.
INTRODUCTION
Fluorescence correlation spectroscopy (FCS) was introduced in the early 70s (1). But only its integration with confocal microscopes (2,3), leading to a small detection volume, low background, and therefore single molecule sensitivity, turned FCS into a widely used and now well-established method. It is used for the determination of local concentrations, molecular weights, translational and rotational diffusion coefficients, chemical rate constants, association and dissociation constants, and photodynamics in vitro as well as in vivo. An overview about recent developments in FCS can be found in Petrov and Schwille (4).
In confocal microscopy, detection volumes below 1 fL (= 10−15 L) can be reached, resulting in a useful concentration range of ∼100 pM to 100 nM. In vivo the typical concentration of biomolecules is often in the micro- to millimolar range, requiring smaller detection volumes. Techniques for further reduction of the detection volume in fluorescence fluctuation spectroscopy, reviewed in Blom et al. (5), include total internal reflection (TIR) (6–9), zero mode wave guides (10), and stimulated emission depletion (11). Further, it has been demonstrated that surface plasmon-coupled emission through thin metallic films confines the detection volume of FCS to the vicinity of the substrate (12).
To apply FCS on biological membranes, a high surface selectivity is important, since a certain concentration of fluorophores in solution can often not be avoided. In scanning FCS (13,14), the elongated detection volume is aligned parallel to the surface, leading to an approximately fivefold increase of membrane selectivity compared to standard confocal FCS.
TIR-FCS offers an even higher surface selectivity, probing a slice of ∼100 nm above the coverslip. This approach is especially suitable to study ligand-receptor kinetics (15), but has also been applied for diffusion measurements in membranes (16). Although the axial confinement in TIR-FCS is excellent, it is difficult to sufficiently confine the lateral excitation profile. A pinhole in the image plane can reduce the lateral extension of the detection profile to less than a micrometer, but further reduction also leads to a significant loss in signal. A substantial problem for diffusion measurements is out-of-focus photobleaching, which leads to a depletion of fluorophores in the membrane, limiting the accuracy of concentration measurements.
At TIRF, the difference between the refractive indexes of aqueous analyte (n = 1.33) and glass coverslip (n = 1.52) is used to illuminate the interface above the critical angle of TIR and obtain the well-known evanescent field that selectively excites fluorophores at the surface. The leap of the refractive index also has a strong impact on the emission properties of surface-generated fluorescence and leads to substantial emission above the critical angle (17–21).
Supercritical angle fluorescence (SAF) only occurs from emitters located in direct vicinity to the interface. Consequently, a high surface selectivity of the detection volume is obtained by collecting light exclusively above the critical angle, which can efficiently be done with a solid parabolic element (21–23).
The SAF collection method circumvents the need to illuminate at large angles as with TIRF and achieves an excellent axial confinement in combination with a small lateral excitation spot of a customized confocal microscope (24,25).
In this work, we accomplish SAF collection on a standard microscope platform with a prototype SAF-objective. The objective is used to explore the potential of SAF collection for FCS. All measurements are directly compared to standard confocal FCS, demonstrating that indeed small detection volumes are achieved with supercritical angle FCS (SA-FCS). Measurements on model membranes, also in presence of excessive free dye, demonstrate the excellent surface sensitivity, clearly better than obtainable with conventional microscope objectives. An extensive theoretical framework for accurate and quantitative evaluation of the SA-FCS curves is developed.
THEORY
Confocal FCS
To evaluate the confocal FCS curves, a standard three-dimensional Gaussian model (26) has been applied,
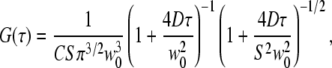 |
(1) |
where C is the concentration of fluorophores, w0 is the 1/e2-radius of the laser focus, D is the diffusion coefficient, and the structure parameter S = wz/w0 describes the axial extension of the detection volume. For membrane diffusion, the two-dimensional diffusion model is
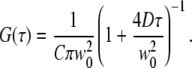 |
(2) |
SA-FCS
The molecule detection function (MDF) is the product of the collection efficiency function with the excitation intensity distribution. For the SAF-objective, it can be described by the lateral Gaussian excitation profile of the laser focus and the axial SAF collection profile. The latter is discussed in detail in Enderlein et al. (21). Here we will just point out some important features (see Eq. 11): Each supercritical collection angle θ of the SAF-objective is connected with a specific exponential decay exp(–2w(θ)z) along the optical axis with
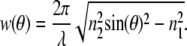 |
(3) |
It is noteworthy that the exponential decays associated with SAF collection and evanescent wave TIRF excitations are identical for each supercritical angle. Higher collection angles lead to a steeper decay of the detection efficiency (Fig. 1 a). The axial extent of SAF detection volume can be reduced with an aperture that increases the lower limit of collected supercritical angles (Fig. 1 b). The critical angle
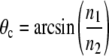 |
(4) |
depends on the refractive index of the coverslip (n2 = 1.52) and of the solution above (n1). For water (n = 1.33) θc amounts to 61°. Note that for biological samples, n1 and θc can be significantly higher (e.g., cytoplasm n1 ≈ 1.38 and θc ≈ 65°).
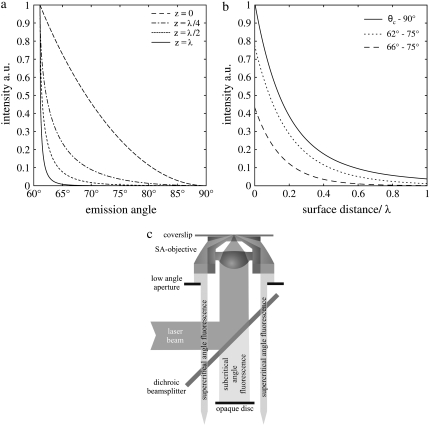
FIGURE 1.
(a) Dependence of the collection efficiency of the SAF-objective on the detection angle for randomly oriented fluorophores at different distances from the interface. The collection efficiency shifts toward lower detection angles and is reduced with increasing distance. (b) Axial detection profile for several ranges of acceptance angles. A circular diaphragm can be used to increase the minimum detection angle. This results in a faster decay of the detection profile but also in a reduced collection efficiency. (c) Beam path of the SAF-microscope: The collimated laser beam is focused by an aspheric lens onto the coverslip surface. Supercritical emission is collected by a parabolic mirror. Subcritical angle fluorescence is blocked by an opaque disk, the lower angle limit of SAF collection is set by a circular aperture below the objective.
For randomly oriented fluorophores at the water/glass interface, 74% of the overall emission is sent into the glass (vertical, 78%; horizontal, 72%). Thereof, 46% is supercritical (vertical, 60%; horizontal, 41%).
Despite the complex shape of the MDF in SA-FCS, an exact solution for the correlation curve could be derived (see Appendix). For randomly oriented dye molecules in solution, we find for the nonnormalized correlation curve,
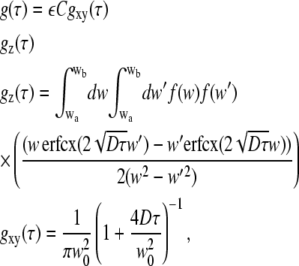 |
(5) |
with erfcx(x) = exp(x2)erfc(x). The value ε = κQI0 is the product of the detection efficiency, the molecular brightness of the fluorophore, and the excitation intensity. The value wa,b = w(θa,b) can be evaluated with Eq. 3 and the maximum (minimum) acceptance angle θa(b) of the parabola. The value f(w1) is given in Eq. 14. The resulting double integral can be evaluated numerically on a rather coarse grid.
To calculate the normalized correlation function G(τ) = g(τ)/I2, the average detection intensity I (Eq. 16) has to be evaluated.
Triplet contribution, background, and several components
Triplet contributions can be taken into account by an additional exponential factor in the correlation curve:
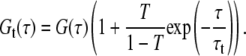 |
(6) |
A noncorrelated background leads to a reduction of the correlation amplitude and, if not corrected for, to an overestimation of the concentration. The connections between measured and true values are
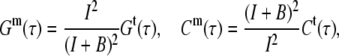 |
(7) |
where I is the signal and B the background count rate.
If two noninteracting species are present (i.e., fluorophores bound to the membrane and in solution), their normalized correlation curves can be added, weighted with their corresponding intensities:
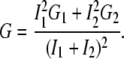 |
(8) |
For a one-component curve, the effective detection volume is defined here as
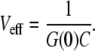 |
(9) |
The values G(0) and C can be obtained by fitting the measured correlation curves to the appropriate model; G(0) is inferred from the part of the correlation curve without triplet contributions. This definition of Veff has the advantage that it can be inferred directly from the experiment and that it is independent of an uncorrelated background.
MATERIALS AND METHODS
Confocal FCS
Confocal FCS measurements were performed on a LSM Meta 510 system (Carl Zeiss, Jena, Germany) using a 40 × N.A. 1.2 UV-VIS-IR C-Apochromat water immersion objective and a home-built detection unit at the fiber output channel as described in Ries and Schwille (14): A bandpass filter HQ525/50 (AHF Analyze Technik, Tübingen, Germany) was used behind a collimating Achromat to reject the residual laser and background light. Another Achromat (LINOS Photonics, Göttingen, Germany) with a shorter focal length was used to image the internal pinhole onto the aperture of the fiber-coupled avalanche photo diode (APD, PerkinElmer, Boston, MA). The correlation curves were recorded with the hardware correlator Flex 02-01D (correlator.com, Bridgewater, NJ). For measurements in solution, a 50:50 beamsplitter, placed behind the bandpass filter, was used to split the emission onto two APDs. Cross-correlation of the two channels allows for the measurement of FCS curves without the afterpulsing artifact, increasing the quality of the curves especially for small lag times.
SA-FCS
The custom-made SAF-objective used here is similar to that described in Ruckstuhl and Verdes (24), but it is of more compact dimensions allowing for its use in a standard microscope turret. It is composed of a polymer parabolic reflector with a focal length of 1.79 mm and an embedded aspheric lens with a focal length of 4 mm and a N.A. of 0.62 (Lens Code 350610, LightPath Technologies, Orlando, FL). This lens is designed to produce a diffraction limited focus through a 1.2 mm glass slide at a wavelength of 410 nm.
The setup is realized with an model No. IX70 microscope (Olympus, Melville, NY). The optical path is as follows: The laser (Sapphire 488-25; Coherent Laser, Santa Clara, CA) passes through a single mode fiber and is collimated to a beam waist of w0 = 4.1 mm. As shown in Fig. 1 c, the beam is then coupled into the aspheric lens via a dichroic beam-splitter to produce a nearly diffraction-limited focus on the surface. The plasma-cleaned coverslip is optically connected to the SAF-objective by immersion oil with a refractive index of n = 1.523. An opaque disk below the dichroic beam splitter blocks the fluorescence collected by the aspheric lens and lets pass the SAF collected by the parabola. The parabola collects the fluorescence up to surface angles of 75°. The lower angle limit of SAF collection is set by a circular aperture below the objective to 65.5°. This permits SA-FCS measurements also in cells, where the higher refractive index (n ≈ 1.38) (27) leads to an increased critical angle of θc ≈ 65°. The tube lens of the microscope focuses the SAF through a bandpass filter HQ535/70 (AHF Analyze Technik) onto the aperture of the fiber-coupled avalanche photo diode. APD and hardware correlator are the same as used for confocal FCS. A charge-coupled device camera (Cool Snap HQ; Photometrics, Tucson, AZ) is used to align the laser focus onto the focal spot of the parabola.
Correlation curves were evaluated with software written in MatLab (The MathWorks, Natick, MA). Numerical integration of the double integral (Eq. 5) was performed on a 30 × 30 grid. With a standard personal computer (1.8 GHz), one fit takes ∼10 s. To remove afterpulsing artifacts from the correlation curves, calibration correlation curves were obtained using a current stabilized LED as a light source, and were subtracted from the correlation curves according to (28). Analytical calculations were performed with the help of Mathematica (Wolfram Research, Champaign, IL).
Preparation of model membranes
Planar-supported bilayers were prepared as follows (29): 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC, Avanti Polar Lipids, Alabaster, AL), 0.002% BODIPY FL C5-ganglioside GM1 (BP-GM1, Molecular Probes, Eugene, OR), and when indicated, 0.02% 1,1′-dioctadecyl-3,3,3,3-tetramethylindodicarbocyanine perchlorate (DiD, Molecular Probes) were dissolved in chloroform and evaporated under nitrogen flux and then under vacuum for 1 h. The lipids were then rehydrated with 150 mM NaCl, 10 mM HEPES buffer (pH 7.4) and resuspended by vigorous vortexing. The suspension was bath-sonicated at 60°C for 1 h to obtain small unilamellar vesicles. As a support a roughly 10-μm-thin and freshly cleaved disk of mica was fixed with a small drop of immersion oil onto a cover slide. A plastic ring was glued directly onto the mica. A small aliquot of the suspension was diluted with a 3 mM CaCl2, 150 mM NaCl, and 10 mM HEPES buffer, and then placed on the support for 20 min. After that, the sample was rinsed several times to remove unfused vesicles.
RESULTS
SA-FCS in solution
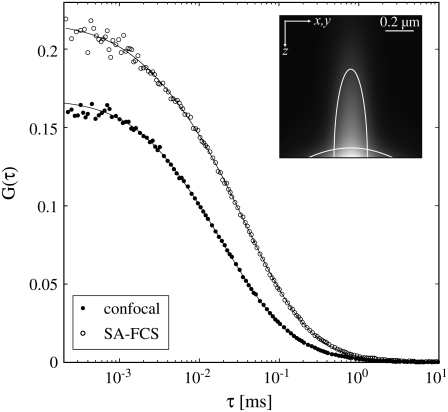
Fig. 2 shows confocal FCS and SA-FCS curves obtained in the same sample of free dye. The laser powers were chosen such that the maximum of the excitation intensity was approximately the same. The curves were fitted to Eq. 1 for confocal FCS and to Eq. 5 for SA-FCS. The results from this fit can be found in Table 1. To determine the geometric parameters of the detection volumes, the diffusion coefficient of the free Alexa488 (30) was fixed to DA488 = 410 μm2/s. For the SA-FCS curve the fit resulted in a 1/e2-radius of the laser focus of w0 = 0.485 μm. This size is still above the diffraction limit (w0 = 0.43λ/N.A. = 0.338 μm) (31), which is a consequence of the aberration introduced by not using the aspheric lens at its design wavelength of 410 nm.
FIGURE 2.
FCS curves obtained in a solution of 50 nM Alexa 488 and fits to Eq. 1 and Eq. 5, respectively. Confocal FCS: laser power 14 μW, acquisition with two APDs, 5 × 15 s. SA-FCS: laser power 87 μW, acquisition times: 5 × 15 s, corrected for after pulsing. (Inset) Comparison of confocal and SAF detection volume. The lines denote the half maximum isolines. See Table 1.
TABLE 1.
Results from fit
| Conf. FCS | SA-FCS | |
|---|---|---|
| c (μm−3) | 32.2 | 42 |
| w0 (μm) | 0.195 | 0.485 |
| T | 0.149 | 0.065 |
| τt (μs) | 3.7 | 2.3 |
| S | 5.3 | — |
| η (kHz) | 2 × 21.4 | 25.9 |
| Veff (fL) | 0.21 | 0.12 |
The SA-FCS curve has a higher amplitude G(0) because of the smaller size of the effective detection volume Veff (Eq. 9) compared to confocal FCS. However, the difference is relatively small as the larger beam waist of the prototype objective nearly counterbalances the smaller axial extension of the detection volume.
The apparent concentrations inferred by fitting the SA-FCS curves are higher than those measured with confocal FCS. This indicates the presence of a significant noncorrelated background (Eq. 7): Aberrations in the aspheric lens and scattering of the excitation light can lead to off-axis fluorescence excitation with low intensity. Fluorophores exited off-axis are too dim to contribute to the correlation amplitude but they have a significant contribution to the noncorrelated background. Assuming that confocal FCS curves give a good estimate for the true concentration, the signal/background ratio can be estimated (Eq. 7) to  Correlation curves can be corrected with Eq. 7, once the background characteristics are determined.
Correlation curves can be corrected with Eq. 7, once the background characteristics are determined.
The molecular brightness measured by SA-FCS is smaller than in confocal FCS. One cause is the background mentioned above. Correcting for this background leads to a molecular brightness of ηcorr = 34.0 kHz. Another cause is the rejection of undercritical light, which is not fully compensated by additional detection of supercritical emission. The lower triplet amplitude in SA-FCS could be due to surface effects.
In SA-FCS, the axial shape of the MDF is solely defined by the physical parameters of the objective and is not altered by artifacts such as saturation or coverslip thickness variations (32). Therefore, the model for a SA-FCS-curve includes one fitting parameter less than the standard Gaussian model where the axial extension is described by the rather ambiguous structure parameter S. Note that artifacts can still lead to a lateral enlargement of the detection volume.
SA-FCS on membranes
For measurements on membranes, a significant concentration of fluorophores in solution can often not be avoided—which can impede the extraction of accurate diffusion coefficients. Compared to the detection volume of a confocal microscope focused onto the glass/analyte interface, the detection volume of SA-FCS penetrates approximately an order-of-magnitude less into the analyte. This confinement makes SA-FCS well suited for the investigation of processes that occur in direct surface vicinity even in presence of fluorescent molecules in the adjacent solution.
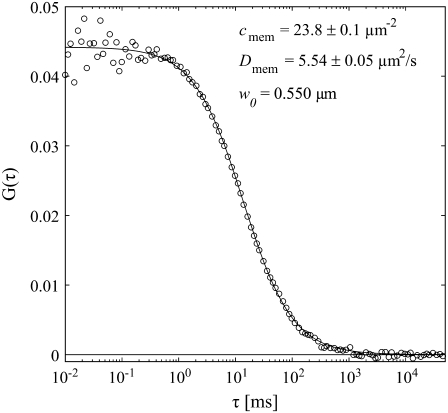
Fig. 3 shows a SA-FCS correlation curve obtained on a supported lipid bilayer composed of DOPC and 0.003% BP-GM1 with a fit to Eq. 2. The waist w0 has been determined by a calibration measurement as described in the previous section. The diffusion coefficient of D = 5.54 ± 0.05 μm2/s and the concentration of c = 23.8 ± 0.1μm−2 are in reasonable agreement with values of D = 4.6 ± 0.5 μm2/s and c = 20 ± 2 μm−2 obtained with the confocal z-scan method (33) (data not shown).
FIGURE 3.
SA-FCS curve obtained on a supported lipid bilayer composed of DOPC with 0.003% BP-GM1 and fit to Eq. 2. The value w0 was calibrated with free solution of Alexa 488. Acquisition time: 3 × 60 s, laser power 2.5 μW.
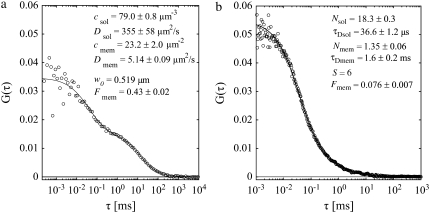
To demonstrate the excellent membrane selectivity of SA-FCS, free Alexa 488 (≈150 nM) was added to the solution above a bilayer composed of DOPC, 0.02% DiD, and 0.003% BP-GM1. The resulting additional fast diffusing component is clearly visible in the corresponding correlation curve (Fig. 4 a). The orientation of the transition dipoles of BP-GM1 can be assumed mainly perpendicular to the membrane. Therefore the curve was fitted to Eq. 8 with Eq. 28. The membrane fraction Fm = 0.43 ± 0.02 was determined from the relative contributions of free and membrane-bound dye to the overall correlation curve.
FIGURE 4.
Discrimination between membrane and solution. (a) SA-FCS and (b) confocal FCS on a supported lipid bilayer composed of DOPC with 0.003% BP-GM1 and free Alexa 488 in solution above. (a) Laser power 5 μW, acquisition time 3 × 60 s. (b) Laser power 1 μW, acquisition time 5 × 20 s.
As a comparison, Fig. 4 b shows a confocal FCS curve on the same sample. The correct vertical position was found by maximizing the emission of the red DiD in a second spectral channel and minimizing its diffusion time. Because of the much larger axial dimension of the detection volume, the contribution from membrane-bound fluorophores to the correlation curve is only Fm = 0.076 ± 0.007 and therefore significantly less than in SA-FCS. The free dye almost completely conceals the membrane-bound fluorophores, rendering a meaningful determination of membrane dynamics impossible.
DISCUSSION
The fluorescence collection above the critical angle is a powerful approach for applications where a surface-confined detection volume is important and can be a worthwhile alternative to the widely used TIRF excitation method. To use the SAF collection method, a microscope objective is required that captures the fluorescence at angles substantially beyond the critical angle. For standard coverslips, the highest available numerical aperture is 1.45, allowing for fluorescence collection up to 72° and captures SAF to some extent. However, the SAF collection efficiency is rather modest, especially for cell measurements where the critical angle lies at ≈65°. Further, the small beam diameter of the collected fluorescence makes it technically intricate to select the supercritical angles for the detection exclusively.
We have developed a new type of objective that collects fluorescence at very high surface angles and have demonstrated that the element can overcome the limitations of conventional microscopy optics. A practical advantage of the SAF-objective is that the fluorescence captured by the parabola exits the element in reversed order, i.e., the lowest collected angle lies at the outer margin of the collimated beam. By means of an iris aperture below the objective it is straightforward to set the low limit of collected angles to the desired value above the critical angle. This is advantageous when switching between samples of different refractive indexes, e.g., between solution/glass and cell/glass. Moreover, a variable low angle limit allows for successive measurements with different axial confinement (compare Fig. 1 b).
The presented SA-FCS curves point out a key advantage of SAF collection: the small axial extent of the detection volume. The efficient rejection of solution contributions enables accurate diffusion measurements on model membranes even in presence of high bulk concentrations. Consequently, the new objective is suitable for studying diffusion in membranes of cells expressing FP-tagged proteins since it largely excludes cytoplasmic background.
Recently, TIR-FCS has been introduced to generate comparably thin detection volumes to study membrane dynamics. The requirement to illuminate the sample at supercritical angles makes it impossible to obtain a small excitation spot of Gaussian shape. Therefore one is forced to use another approach to obtain a suitably small detection volume with TIR-FCS: a relatively large surface area is illuminated with nearly homogeneous intensity and the lateral confinement is obtained by a pinhole located in the image plane. With this approach, however, strong photobleaching outside the detection area cannot be avoided, rendering concentration and diffusion measurements on membranes difficult. In SA-FCS, on the other hand, out-of-focus photobleaching above the detection volume cannot be avoided, but the effects are small due to the faster diffusion and larger reservoir of fluorophores. It can be neglected if only membrane dynamics are of interest.
For most of the techniques used to produce small detection volumes (6–10), an exact model to fit the correlation curves has not been published. For SA-FCS, such a model could be derived. In addition, the axial extension of the detection volume is not altered by the known artifacts such as saturation or coverslip thickness variations (32). SA-FCS therefore facilitates accurate and quantitative FCS measurements, an important precondition for quantitative studies of receptor/ligand binding. Weak binding affinities are extremely difficult to detect as high ligand concentrations have to be used to obtain a certain amount of receptors/ligand complexes at the surface. Without surface confined-detection, as with SAF, the signal can easily be covered by the fluorescence of the unbound bulk.
We have demonstrated that the SAF-objective prototype achieves with 0.12 fL a nearly twofold smaller detection volume than a microscope objective of 1.2 N.A. but we emphasize that this reduction is not close to the potential of our approach. A straightforward technical improvement that can lead to a further dramatic reduction is the enhancement of the N.A. of the inner excitation optics. By replacing the simple aspheric lens with an elaborate multilens system it should be possible to obtain a N.A. of at least 1.0, which would reduce the detection volume by another factor of 10. A multilens system would also make it possible to chromatically correct the optics and achieve diffraction limited performance at several different wavelengths, rendering SA-FCS a suitable technique for measurements of highly concentrated fluorophores as can often not be avoided in biological samples or in binding studies using dual-color cross correlation. An appropriate numerical aperture of ≈1.0 will increase the collection efficiency significantly and achieve single molecule sensitivity of the inner optics. Most biological reactions occur at rather high concentrations. Techniques such as direct single molecule observation or fluorescence fluctuation spectroscopy are limited to rather low concentrations. By reducing the detection volume the SAF objective can help to extend single molecule detection to the range of natural concentrations.
As demonstrated recently (25), near and far field microscopy can be combined by measuring SAF collected by a parabolic element and fluorescence collected by the inner optics independently using two detectors. Consequently, confocal FCS and SA-FCS could be performed simultaneously, a powerful combination for the study of various dynamic processes occurring at interfaces and on membranes. Combined near and far field microscopy is also a promising noninvasive approach to measure cell topographies with a resolution of few nanometers.
Further, a combination with specially engineered excitation beams is conceivable due to the standard excitation optics. Axially polarized light (34) very efficiently excites membrane-bound fluorophores with vertical dipole moments; the combination of stimulated emission depletion (11) with SAF gives the prospect of nanoscopic optical FCS detection volumes.
Acknowledgments
We thank Salvatore Chiantia and Christoph Herold for help with the preparation of the planar-supported bilayers.
This work was supported by Europäischer Fonds für Regionale Entwicklung grant No. 4212/04-02.
APPENDIX: CORRELATION FUNCTION FOR SAF-DETECTION
Molecule detection function for SAF-detection
The molecule detection function Ω is the product of the excitation profile with the collection efficiency function. Since the Rayleigh length zR of the excitation beam can be expected to be much larger than the thickness of the SAF detection slice, the molecule detection function Ω(x, y, z) = εB(x, y)S(z) can be written as the product of the lateral excitation profile B(x, y) and the axial SAF detection profile S(z). The factor ε = κQI0 takes into account the detection efficiency, the molecular brightness of the fluorophore, and the excitation intensity. The lateral excitation profile is given by the Gaussian of a focused laser beam:
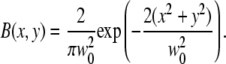 |
(10) |
The derivation of S(z) follows Enderlein et al. (21). There the Weyl representation of an oscillating dipole is used to calculate its emission profile close to a dielectric surface. The wave vector of the incident light is 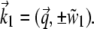 For supercritical emission
For supercritical emission 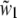 is imaginary, so here it is substituted by the real and positive w1:
is imaginary, so here it is substituted by the real and positive w1: 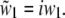 The supercritical emission profile of a fluorophore at a distance z0 from the interface can then be written as (21)
The supercritical emission profile of a fluorophore at a distance z0 from the interface can then be written as (21)
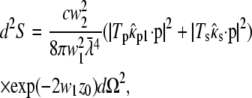 |
(11) |
where c is the speed of light, 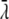 = λ/2π is the reduced wavelength, n1 and n2 are the refractive indices above and below the phase boundary, and w2 = (
= λ/2π is the reduced wavelength, n1 and n2 are the refractive indices above and below the phase boundary, and w2 = (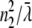 2 – q2)1/2. Tp and Ts are the transmission coefficients for plane p and s waves:
2 – q2)1/2. Tp and Ts are the transmission coefficients for plane p and s waves:
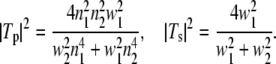 |
(12) |
Here we consider the case of randomly oriented molecules in solution. In this case, 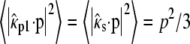 and the emission profile becomes rotationally symmetric. Using
and the emission profile becomes rotationally symmetric. Using 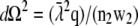 (Eq. 22 in (21)) the integration over the detection angle can be substituted by an integration over q and one integration can be carried out:
(Eq. 22 in (21)) the integration over the detection angle can be substituted by an integration over q and one integration can be carried out: 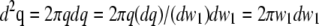 since q = (
since q = (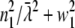 )1/2.
)1/2.
With 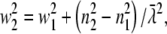 Eq. 11 can be written as
Eq. 11 can be written as
 |
(13) |
with
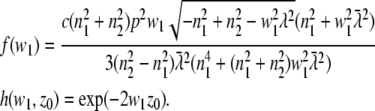 |
(14) |
For the vertical SAF detection profile, we therefore find
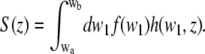 |
(15) |
The values wa and wb can be calculated from the acceptance angles of the parabola θa and θb with Eq. 3: wa,b = w(θa,b).
Integrated molecule detection function
To normalize the correlation curves, the intensity and therefore the integrated MDF has to be known:
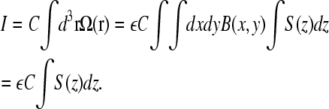 |
(16) |
C is the concentration of the molecules. The integration over z is straightforward:
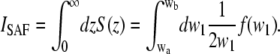 |
(17) |
The integration over w1 leads to a rather long expression,
 |
(18) |
using
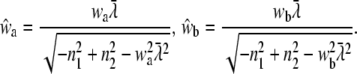 |
(19) |
SA-FCS correlation curve
The nonnormalized correlation curve can be calculated as usual (26):
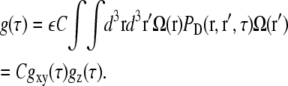 |
(20) |
The concentration correlation functions for free diffusion (7,26) can be written in the form:
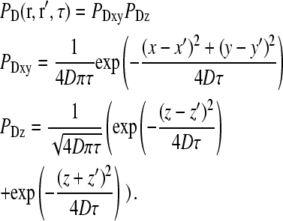 |
(21) |
Assuming a Gaussian excitation profile, gxy(τ) can be readily evaluated and gives the usual two-dimensional correlation curve:
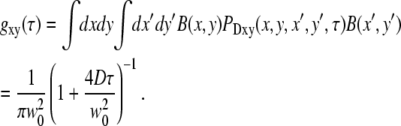 |
(22) |
For gz(τ), the double integral over z can easily be evaluated as
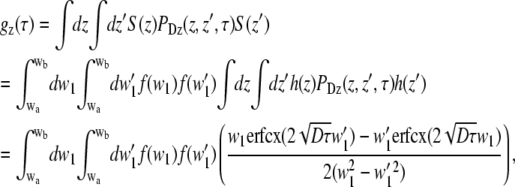 |
(23) |
with erfcx(x) = exp(x2)erfc(x), 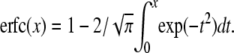
A closed solution to Eq. 23 could not be found but it can be integrated numerically.
SA-FCS on membranes
The correlation function for membrane diffusion is the usual two-dimensional Gaussian correlation function (Eq. 2). In presence of free dye in solution, the intensities for the free molecules (Eq. 18) and for the membrane-bound molecules have to be calculated to evaluate Eq. 8. The intensity of the membrane-bound molecules Im with the concentration Cm is
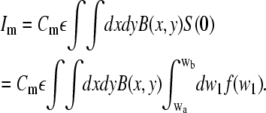 |
(24) |
For randomly oriented molecules in the membrane, Eq. 15 can be used. The integral over w1 yields the expression
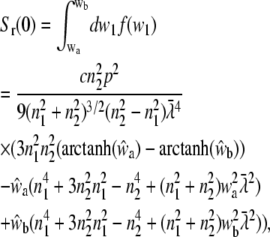 |
(25) |
with
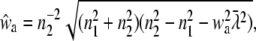 |
(26) |
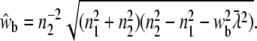 |
(27) |
Often membrane dyes exhibit a preferred orientation in the membrane. This can be taken into account by using the correct orientation factors in Eq. 2. For a vertical dipole, 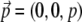 and
and 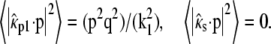 Equivalent to the derivation of Eq. 14 from Eq. 11, we find
Equivalent to the derivation of Eq. 14 from Eq. 11, we find
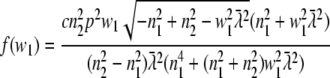 |
(28) |
and
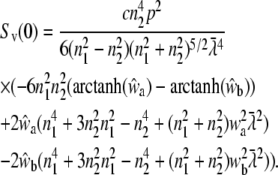 |
(29) |
For a random horizontal dipole 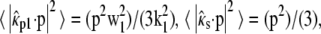
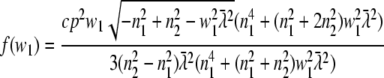 |
(30) |
and
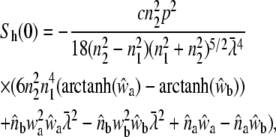 |
(31) |
with 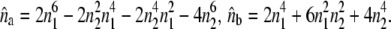
Editor: Gerard Marriott.
References
- 1.Magde, D., W. W. Webb, and E. Elson. 1972. Thermodynamic fluctuations in a reacting system—measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. 29:705. [Google Scholar]
- 2.Rigler, R., U. Mets, J. Widengren, and P. Kask. 1993. fluorescence correlation spectroscopy with high count rate and low background: analysis of translational diffusion. Eur. Biophys. J. 22:169–175. [Google Scholar]
- 3.Eigen, M., and R. Rigler. 1994. Sorting single molecules—application to diagnostics and evolutionary biotechnology. Proc. Natl. Acad. Sci. USA. 91:5740–5747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Petrov, E. P., and P. Schwille. 2007. State of the art and novel trends in fluorescence correlation spectroscopy. In Standardization in Fluorometry: State of the Art and Future Challenges. Springer, Berlin, Heidelberg, New York (2007).
- 5.Blom, H., L. Kastrup, and C. Eggeling. 2006. fluorescence fluctuation spectroscopy in reduced detection volumes. Curr. Pharm. Biotechnol. 7:51–66. [DOI] [PubMed] [Google Scholar]
- 6.Thompson, N. L., T. P. Burghardt, and D. Axelrod. 1981. Measuring surface dynamics of biomolecules by total internal reflection fluorescence with photobleaching recovery or correlation spectroscopy. Biophys. J. 33:435–454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Starr, T. E., and N. L. Thompson. 2001. Total internal reflection with fluorescence correlation spectroscopy: combined surface reaction and solution diffusion. Biophys. J. 80:1575–1584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hassler, K., T. Anhut, R. Rigler, M. Gösch, and T. Lasser. 2005. High count rates with total internal reflection fluorescence correlation spectroscopy. Biophys. J. 88:L01–L03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ruckstuhl, T., and S. Seeger. 2004. Attoliter detection volumes by confocal total-internal-reflection fluorescence microscopy. Opt. Lett. 29:569–571. [DOI] [PubMed] [Google Scholar]
- 10.Levene, M. J., J. Korlach, S. W. Turner, M. Foquet, H. G. Craighead, and W. W. Webb. 2003. Zero-mode waveguides for single-molecule analysis at high concentrations. Science. 299:682–686. [DOI] [PubMed] [Google Scholar]
- 11.Kastrup, L., H. Blom, C. Eggeling, and S. W. Hell. 2005. fluorescence fluctuation spectroscopy in subdiffraction focal volumes. Phys. Rev. Lett. 94:178104. [DOI] [PubMed] [Google Scholar]
- 12.Borejdo, J., N. Calander, Z. Gryczynski, and I. Gryczynski. 2006. fluorescence correlation spectroscopy in surface plasmon coupled emission microscope. Opt. Express. 14:7878–7888. [DOI] [PubMed] [Google Scholar]
- 13.Ruan, Q. Q., M. A. Cheng, M. Levi, E. Gratton, and W. W. Mantulin. 2004. Spatial-temporal studies of membrane dynamics: scanning fluorescence correlation spectroscopy (SFCS). Biophys. J. 87:1260–1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ries, J., and P. Schwille. 2006. Studying slow membrane dynamics with continuous wave scanning fluorescence correlation spectroscopy. Biophys. J. 91:1915–1924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lieto, A. M., R. C. Cush, and N. L. Thompson. 2003. Ligand-receptor kinetics measured by total internal reflection with fluorescence correlation spectroscopy. Biophys. J. 85:3294–3302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ohsugi, Y., K. Saito, M. Tamura, and M. Kinjo. 2006. Lateral mobility of membrane-binding proteins in living cells measured by total internal reflection fluorescence correlation spectroscopy. Biophys. J. 91:3456–3464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lukosz, W., and R. Kunz. 1977. fluorescence lifetime of magnetic and electric dipoles near a dielectric interface. Opt. Commun. 20:195–199. [Google Scholar]
- 18.Lukosz, W., and R. Kunz. 1977. Light emission by magnetic and electric dipoles close to a plane dielectric interface. II. Radiation patterns of perpendicular oriented dipoles. J. Opt. Soc. Am. 67:1615–1619. [Google Scholar]
- 19.Lukosz, W., and R. Kunz. 1977. Light emission by magnetic and electric dipoles close to a plane interface. I. Total radiated power. J. Opt. Soc. Am. 67:1607–1614. [Google Scholar]
- 20.Hellen, E., and D. Axelrod. 1987. fluorescence emission at dielectric and metal-film interfaces. J. Opt. Soc. Am. B. 4:337–350. [Google Scholar]
- 21.Enderlein, J., T. Ruckstuhl, and S. Seeger. 1999. Highly efficient optical detection of surface-generated fluorescence. Appl. Opt. 38:724–732. [DOI] [PubMed] [Google Scholar]
- 22.Ruckstuhl, T., and S. Seeger. 1999. Light detecting optical device. PCT Gazette, WIPO, WO 99/46596. http://www.wipo.int/pct/en/gazette/year.jsp.
- 23.Ruckstuhl, T., M. Rankl, and S. Seeger. 2003. Highly sensitive biosensing using a supercritical angle fluorescence (SAF) instrument. Biosens. Bioelectron. 18:1193–1199. [DOI] [PubMed] [Google Scholar]
- 24.Ruckstuhl, T., and D. Verdes. 2004. Supercritical angle fluorescence (SAF) microscopy. Opt. Express. 12:4246–4254. [DOI] [PubMed] [Google Scholar]
- 25.Verdes, D., T. Ruckstuhl, and S. Seeger. 2007. Parallel two-channel near and far field fluorescence microscopy. J. Biomed. Opt. In press. [DOI] [PubMed]
- 26.Elson, E. L., and D. Magde. 1974. fluorescence correlation spectroscopy. I. Conceptual basis and theory. Biopolymers. 13:1–27. [DOI] [PubMed] [Google Scholar]
- 27.Farinas, J., and A. Verkman. 1996. Cell volume and plasma membrane osmotic water permeability in epithelial cell layers measured by interferometry. Biophys. J. 71:3511–3522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhao, M., L. Jin, B. Chen, Y. Ding, H. Ma, and D. Chen. 2003. Afterpulsing and its correction in fluorescence correlation spectroscopy experiments. Appl. Opt. 42:4031–4036. [DOI] [PubMed] [Google Scholar]
- 29.Chiantia, S., J. Ries, N. Kahya, and P. Schwille. 2006. Combined AFM and two-focus SFCS study of raft-exhibiting model membranes. ChemPhysChem. 7:2409–2418. [DOI] [PubMed] [Google Scholar]
- 30.Dertinger, T., V. Pacheco, I. von der Hocht, R. Hartmann, I. Gregor, and J. Enderlein. 2007. Two-focus fluorescence correlation spectroscopy: a new tool for accurate and absolute diffusion measurements. ChemPhysChem. 8:433–443. [DOI] [PubMed] [Google Scholar]
- 31.Zhang, B., J. Zerubia, and J.-C. Olivo-Marin. 2007. Gaussian approximations of fluorescence microscope point-spread function models. Appl. Opt. 46:1819–1829. [DOI] [PubMed] [Google Scholar]
- 32.Enderlein, J., I. Gregor, D. Patra, T. Dertinger, and U. B. Kaupp. 2005. Performance of fluorescence correlation spectroscopy for measuring diffusion and concentration. ChemPhysChem. 6:2324–2336. [DOI] [PubMed] [Google Scholar]
- 33.Benda, A., M. Benes, V. Marecek, A. Lhotsky, W. Hermens, and M. Hof. 2003. How to determine diffusion coefficients in planar phospholipid systems by confocal fluorescence correlation spectroscopy. Langmuir. 19:4120–4126. [Google Scholar]
- 34.Wilson, T., F. Massoumian, and R. Jukaitis. 2003. Generation and focusing of radially polarized electric fields. Opt. Eng. 42:3088. [Google Scholar]