Cell Shape Dynamics in Escherichia coli

Abstract

Bacteria are the simplest living organisms. In particular, Escherichia coli has been extensively studied and it has become one of the standard model systems in microbiology. However, optical microscopy studies of single E. coli have been limited by its small size, ∼1 × 3 μm, not much larger than the optical resolution, ∼0.25 μm. As a result, not enough quantitative dynamical information on the life cycle of single E. coli is presently available. We suggest that, by careful analysis of images from phase contrast and fluorescence time-lapse microscopy, this limitation can be bypassed. For example, we show that applying this approach to monitoring morphogenesis in individual E. coli leads to a simple, quantitative description of this process. First, we find the time when the formation of the septum starts, τ_c. It occurs much earlier than the time when the constriction can be directly observed by phase contrast. Second, we find that the growth law of single cells is more likely bilinear/trilinear than exponential. This is further supported by the relations that hold between the corresponding growth rates. These methods could be further extended to study the dynamics of cell components, e.g., the nucleoid and the Z-ring.

INTRODUCTION

One of the fundamental problems in biology is the nature of cell cycle regulation. For this, Escherichia coli represents the ideal system since it is relatively simple, easily grown and manipulated, and its genome has been sequenced. Hundreds of genes that are involved in the cell cycle have been identified. Despite this, our understanding of the regulation of the E. coli cell cycle is incomplete. The processes leading to bacterial cell division are regulated at two levels, temporal and spatial. Temporal control ensures that chromosome duplication and segregation occur before cell division such that each of the daughters inherits all the components required for a normal cell cycle. In addition, spatial regulation is also necessary, forbidding assembly of FtsZ rings (the first step in cell septation) on the surface surrounding the replicating/segregating nucleoid and beyond, toward cell poles (1–4).

Using molecular biology and microscopy, detailed information has been obtained about the way E. coli grows and divides. Mutant strains allow identifying the function of specific proteins in the bacterial networks. Fluorophores that stain particular cell elements and GFP-proteins are used to map intracellular dynamics in both space and time. These approaches allowed drawing the present-day picture of the spatial organization of bacterial cell and its dynamics. This includes the high accuracy of the Z-ring placement at the cell center (5), positioning and dynamics of the replisome (6), and regular organization of the chromosome in the tightly packed nucleoid (7).

Initiation of division—FtsZ ring

Division in rod-shaped cells, e.g., E. coli, takes place via the formation of a constriction at the cell center. The constriction is driven by a large complex of proteins encoded by the filamentous temperature-sensitive genes (fts). This complex, known as the divisome, assembles on a cytoskeletal toroidal structure, the Z-ring, which is made of FtsZ oligomers. The Z-ring was visualized using electron (8) and fluorescence microscopy (9–11). The Fts proteins, FtsA, FtsK, FtsQ, FtsB, FtsL, FtsW, FtsI, and FtsN, attach to the Z-ring in a defined order and each plays a distinctive role in the division process. While for some of the Fts proteins this role is known, e.g., FtsA together with ZipA connect the Z-ring to the cytoplasmic membrane and FtsW together with FtsI participate in the synthesis of new peptidoglycan that forms the new caps, for others it remains to be resolved. After the divisome assembly is completed, it is activated by a putative additional signal that leads to the shrinking of the Z-ring until closure and the separation of the two daughter cells (1–4,12–14). Experiments using immunostaining suggest that the Z-ring disperses before the end of division (15).

Selection of the division site

E. coli locate the division septum with 4% accuracy around midcell (16,17). The position of the septum is restricted to midcell by the combined action of two mechanisms, namely, nucleoid occlusion and the MinCDE oscillations. Nucleoid occlusion prevents the formation of the Z-ring in the range adjacent to the nonsegregated chromosome (18,19). It was recently found that in Bacillus subtilis the nonspecific DNA binding protein, Noc (YyaA), mediates the inhibitory action of the nucleoid (20). On the other hand, the independent function of Min system is to preclude Z-ring formation in the nucleoid free areas at cell poles (21,22). It consists of three proteins, MinC, MinD, and MinE, of which the first inhibits the polymerization of FtsZ, the second recruits MinC to the membrane, and MinE drives the MinC-MinD to oscillate between the two poles (23–32). Due to these oscillations, on average the concentration of MinC is minimal at the cell center localizing the Z-ring to its neighborhood.

It was shown that when the Min system is impaired the nucleoid occlusion is still able to localize the Z-ring around midcell but with much less accuracy (33). In addition, Z-rings are also found near the poles leading to the formation of minicells (34,35). In the reverse situation, when enucleated cells where studied, Z-rings were observed in the range of the cell center with much higher dispersion than in normal cells (36).

Strikingly, Min proteins oscillate on a membranal helical structure, extending from one pole to the other (37). Moreover, FtsZ, not engaged in the Z-ring, also oscillates in a helical pattern in a manner similar to Min proteins (38). Neither Min nor FtsZ helices seem related to those of MreB, a cytoskeletal-like element. The mechanism leading to these helices is unclear.

The envelope

E. coli is Gram-negative and its envelope has three layers: cytoplasmic membrane, peptidoglycan, and outer membrane. The peptidoglycan is rigid determining the rod shape. To a good approximation, the E. coli cell has hemispherical caps and a cylindrical section in between. The peptidoglycan factories that are responsible for the growth of the cylinder are different from those that generate the new caps (39,40). While the former depends on PBP2 alone the latter depend on both PBP2 and PBP3 (FtsI) (41,42). The function of PBP2 is inhibited by mecillinam leading to spherical cells and that of PBP3 is inhibited by cephalexin-forming filaments. On the cylindrical section, the peptidoglycan factories are localized in a spotlike pattern (42). It has been proposed that they work by a three-for-one mechanism (40) although, at present, there is not enough experimental evidence to support this scenario. On the other hand, the PBP3 of the septum-forming factories is embedded in the Z-ring in a fixed number of copies (43). In E. coli there are 12 different enzymes that participate in peptidoglycan formation. Their role in this process has been recently reviewed by Scheffers and Pinho (44).

In the bacterial cell cycle three major processes may be distinguished, leading to formation of two daughter cells: mass growth, chromosome replication, and division. While the first process is continuous, the last two are discontinuous and have a clearly distinguished start and end, timing of which is dependent on the growth rate. These processes underlie the main morphological changes in the bacterial cell-cell elongation, nucleoid segregation, and septum formation. This implies, even within this extreme simplification, the existence of a control mechanism that coordinates these three processes in space and time to produce equal daughter cells. Comprehension of this control mechanism requires detailed information not only on specific molecular events and processes involved, but also on the accompanying morphological changes.

However, optical microscopy studies of single E. coli have been limited by its small size, ∼1 × 3 μm, not much larger than the optical resolution, ∼0.25 μm. As a result, not enough quantitative dynamical information on the life cycle of single E. coli is presently available. In particular, one of the implicit assumptions of the division process is that the nucleoid starts to separate before the Z-ring is formed. This was not yet explicitly verified. In fact, no clear definition of separation time was proposed. On the other hand, it was shown that, DNA replication ends slightly after formation of the Z-ring (15,45,46). These events were compared with the start of septum formation determined as the time when a visible constriction appears in the envelope. A large delay between the Z-ring formation and constriction posed the question whether this is the time required for assembling of the other proteins forming the divisome, or the divisome formed concurrently with the Z-ring awaits for another, yet unknown, signal to start the constriction. Moreover, these results were measured on populations of fixed E. coli and therefore represent averaged values. Not much is known about their corresponding distributions. This is an example where the biochemistry is known while the morphological data is partially lacking.

We show that, by careful analysis of images from phase contrast and fluorescence time-lapse microscopy of live single cells, the limitation due to optical resolution can be bypassed. This approach involves the calibration of pixel intensities to obtain accurate threshold values for the edge. Such threshold together with interpolation between neighboring pixels leads to subpixel precision in locating the contour of the cell. A similar approach was used by Kaplan and Gollub (47) to monitor the formation of dendrites in crystal growth. Applying our approach to monitoring morphogenesis in individual E. coli leads to a simple, quantitative description of this process. First, we find the time when the formation of the septum starts, τ_c. It occurs much earlier than the time when the constriction can be observed in a phase contrast image, τ_cv. Second, we find that the growth law of single cells is more likely bilinear/trilinear than exponential. This is further supported by the relations that hold between the corresponding growth rates.

METHODS

Microscopy

Imaging experiments are performed on an inverted microscope (model No. IX70, Olympus, Melville, NY) with a Micromax 512 camera (Roper, Princeton Instruments, Trenton, NJ) and two computer-controlled shutters (Uniblitz, Vincent Associates, Rochester, NY). One shutter blocks the mercury lamp and the other the halogen lamp. To minimize bleaching, the appropriate shutter opens only for the duration of the exposure time. Time-lapse movies were recorded at 6 frames/min. Exposure time was fixed to 0.5 s. In our optical system, the pixel size corresponds to a length of 87 nm. The sample is heated by a resistor wrapped around the objective. A feedback system stabilizes the temperature within ∼0.5°. All experiments were performed at 37°. The drift of the focus is manually corrected throughout the experiment.

We have measured the fluorescence point spread function (PSF) in our system using fluorescent microbeads of 0.1 μm diameter. To reduce fluctuations, the PSF was averaged over seven bead images.

Microbiology

We use a strain of E. coli (K-12) MW162, carrying a plasmid pBAD24-hupB-gfp encoding GFP attached to HU, a histonelike protein that participates in the packing of the nucleoid (courtesy of J. Rouviere-Yaniv (48)). The expression of HU-GFP is induced by 0.2% arabinose. Cells were grown in Luria Broth (LB) medium with ampicillin up to OD₆₀₀ = 0.2 in the exponential growth regime. For microscopy we pipette 10 μl bacterial culture on a thin layer of 2% agar with LB (Sigma, St. Louis, MO). We have verified that cells grow at steady state in the agar. This was done by monitoring approximately nine generations of a microcolony that has a single parent and counting the number of cells, N, as a function of time. We find that, up to five generations, the growth of N is exponential. To image the cytoplasmic membrane (CM) we stain E. coli with FM4-64 (Molecular Probes) after fixation with 0.2% formaldehyde. Alternatively, the CM is visualized in live E. coli cells XL1-Blue MRF using Tar(1-279)-YFP expressed from the plasmid pAV28 (courtesy of A. Vaknin (49)).

The cell cycle of a total of 33 bacteria was monitored during 10 experiments. The behavior of six cells out of the 33 was not appropriate for the analysis that we present in what follows. For example, one of the cells (see Figs. 6, 8, and 9) started dividing only 1.5 min after birth. Other cells spent a significant fraction of their cycle closely attached to their sister in a configuration that prevented us from performing the size measurements. Therefore, unless otherwise specified, averages will be computed over the remaining 27 cells.

FIGURE 6.

Variation of the normalized phase-contrast intensity at the center of the constriction, 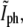as a function of time for an individual bacterium (solid circles). Time is measured from its birth that, in turn, is determined using the corresponding 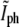for the parent cell (open circles). Using the division criterion obtained from the tip of the triangle in Fig. 5 b (solid line), τ_g = 19.4 ± 0.7 min.

FIGURE 8.

Behavior of the relative width of the constriction, W, as a function of time for the bacterium of Fig. 6. The measured W (solid circles) is compared to the prediction of Eq. 5 (solid line).

FIGURE 9.

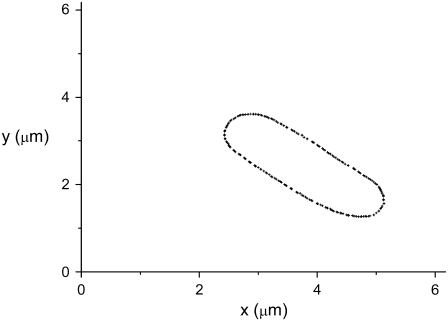
Phase contrast images of the bacterium of Figs. 6 and 8 at (a) τ_c, the daughters are still attached to each other and no constriction is visible; (b) τ_cv, the constriction is barely visible at the cell center; and (c) τ_g. Bar = 1 μm.

Finding the edge of the bacterium

To monitor the dynamics of septum formation in E. coli we need first to determine the location of the bacterial contour. In phase-contrast images, edges are smeared by the corresponding point spread function (PSF) (see Fig. 1). The intensity profile in the direction perpendicular to the edge varies over more than five pixels from the interior value to that of the background. Moreover, the additional interference halo also contributes to smearing the edge. To obtain the intensity threshold that corresponds to the edge we stain the fixed E. coli with FM4-64, a fluorescent dye that is known to accumulate in the CM. We then compare the fluorescence images with those in phase-contrast for individual bacteria that have not yet started to divide.

FIGURE 1.

Behavior of the intensity in phase-contrast images. We show an intensity profile taken perpendicularly to the orientation of a fixed E. coli at τ < τ_cv. (a) Phase-contrast image. Bar = 1 μm. (b) Intensity profile taken along the line shown in panel a. Each data point gives the measured light intensity in one of the pixels neighboring this line.

Fluorescence images of bacteria stained with FM4-64 also display a smeared view of the CM. However, in this case the perpendicular intensity profile is maximal in the neighborhood of the CM (see Fig. 2). In each such profile one can use interpolation to find the position of the maximum with subpixel precision. However, our aim is using the information from the fluorescence to calibrate the phase-contrast images, namely, to find an intensity threshold that corresponds to the position of the CM. We first normalize the phase-contrast intensity scale such that the average intensity in the interior of the bacterium corresponds to 0 and the average value of the background to unity. This is done separately for each individual cell. Next, we average the intensity of the normalized phase-contrast image in the pixels along the contour of the bacterium where the fluorescence is maximal (see Fig. 2). Averaging over the contours of 25 E. coli we obtain a threshold value, 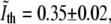where the “∼” sign indicates that this is a normalized intensity. In this procedure, we have made two simplifying assumptions: 1), the intensity of the edge in phase-contrast is on average constant all along the contour of the bacterium; and 2), this intensity when normalized is on average the same for different bacteria.

FIGURE 2.

Behavior of the intensity in fluorescence images of the CM for the same bacterium as in Fig. 1. (a) Fluorescence image of the CM. The region of the sample and the scale are the same as in Fig. 1. Bar = 1 μm. (b) Intensity distribution of the measured light intensity. The origin corresponds to the lower-left corner of the image in panel a.

Using the threshold value that was found we determine the corresponding contour of nondividing bacteria. To obtain subpixel precision we use linear interpolation on the normalized phase-contrast intensity values. The interpolation is performed between pixels that bracket the threshold value. The center of each interior pixel is connected with straight segments to the centers of its exterior neighboring pixels. The location of the edge along these segments is obtained by linearly interpolating between the corresponding intensity values. The result of this approach is shown in Fig. 3.

FIGURE 3.

The contour of the bacterium from Figs. 1 and 2. It was obtained using 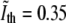and the interpolation procedure described in the text. The origin corresponds to the lower-left corner of the image in Fig. 2 a.

The error of the contour points

The error in the contour points that we measure (see Fig. 3) is due to: 1), the fluctuations of the phase contrast intensity along the ridge of maximal fluorescence intensity, Δ₁; 2), the drift of the focus, Δ₂; 3), the linear interpolation, Δ₃; 4), camera noise (read-out, photon counting, and dark noise), Δ₄; 5), background noise (not subtracted in our analysis), Δ₅; and 6), the projection of the three-dimensional cell on a two-dimensional image, Δ₆. We have measured the first five errors and obtained that the first two are dominant. We did not obtain the projection error, Δ₆. Unlike the others, it is a systematic error that slightly deflates the contours that we find. This effect would require us to add a small constant to our length and width measurements. Such correction would not modify our results and therefore we ignore Δ₆ in what follows.

To obtain Δ₁ we have measured the standard deviation of the phase contrast intensity in the pixels where the fluorescence intensity is maximal. We find that 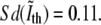Moreover, computing the average value of the derivative of the phase contrast intensity along the contour allows us to translate the error in intensity into the error in position, Δ₁ = 38 nm. This seems to be a conservative estimate of Δ₁ and should be regarded as an upper bound.

The error due to imprecise focusing, Δ₂, is the second most significant one. We have measured it using bacteria that were fixed. The corresponding standard deviation in the position of the contour points gives Δ₂ = 15 nm. In fact, this measurement includes the error due to the camera noise and background, Δ₄ and Δ₅. However, these were independently found to be much smaller than Δ₂ and will be ignored in what follows.

Finally, the linear interpolation error was measured by comparing the phase contrast intensity in a contour pixel with that obtained by linear interpolation between the two neighboring pixels. This measurement represents an overestimation of the actual Δ₃. This is because it performs the interpolation over three pixels while in our calculation of the contour points we only interpolate between neighboring pixels. We obtain that Δ₃ < 6 nm.

The errors Δ₃, Δ₄, and Δ₅ are negligible relative to the dominant ones, Δ₁ and Δ₂. Therefore, we use 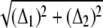as the error for the position of the contour points. Notice that it corresponds to 47% of the pixel size.

Measuring the generation time, τ_g

The edge threshold, that we found in the previous section, is expected to be accurate for nondividing bacteria. In the septal region, however, the membrane folds up such that the contribution to the phase-contrast intensity from the two folds adds up. As the constriction becomes deeper, the error in the contour obtained with the 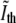threshold grows. Therefore, this approach cannot be used to deduce the time when the bacterium divides (see Fig. 4). Instead, we compare the values of the normalized phase-contrast intensity at the center of the constriction, 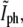with a correspondingly normalized value of the fluorescence intensity at the same location. The fluorescence at the center of the constriction, I_fl, is normalized by dividing it to the average fluorescence along the membrane in the two quarters of the E. coli next to the old poles. In Fig. 5 b we plot 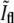as a function of 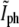for bacteria fixed and stained with FM4-64 at different stages of the division including pairs that have recently finished dividing but are still close enough to each other such that in the phase-contrast image they appear as one. As the septum becomes gradually thinner, the phase-contrast intensity at the center of the constriction keeps on growing. It will keep on growing even after division is completed, approaching the value of the background as the overlap between the intensity tails of the bacterial tips decreases. On the other hand, the normalized intensity of the fluorescence, 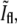grows as the two sides of the septal membrane approach each other, but then decreases after the end of division as the tails of the bacterial tips move apart. The 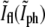data changes roughly linearly and at the intersection of the two best fitting lines one expects to find the values of 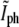and 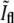that correspond to the division event. The intersection is obtained at 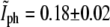and 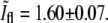The data points that lie above the intersection point in Fig. 5 are either due to daughter cells that are at an angle with respect to each other, 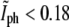or that have grown on top of each other,

FIGURE 4.

Examples of fixed E. coli at times around τ_g. Phase contrast images, a–c, are compared with the corresponding fluorescence images of the CM, d–f. Bar = 1 μm.

FIGURE 5.

Behavior of the fluorescence intensity at the center of the constriction, 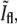as a function of the phase-contrast intensity at the same location, 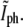(a) Schematic description of the expected behavior. While before division, τ < τ_g (solid circles), 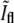grows, for τ > τ_g it decreases (pluses). (b) The corresponding data for 48 fixed E. coli. The solid circles and the pluses were separated arbitrarily according to whether they appear to belong to the raising part or to the decreasing part of the graph. The corresponding linear regressions are also shown (lines).

One would expect that the large fluctuations in the data of Fig. 5 b are due to using different bacteria and that these could be significantly reduced if the data were obtained from a single bacterium as it divides. However, similar fluctuations were also found when we measure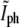d and 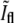for single bacteria using Tar-YFP to label the membrane (data not shown). On the other hand, only a small number of data points can be obtained for each bacterium due to rapid bleaching.

The value of 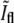at division is lower than what one would naively expect. In a one-dimensional situation where two PSFs corresponding to the bacterial tips precisely overlap, one should obtain that 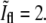However, this picture ignores the contributions from the rest of the membrane around the bacterial tips. Since these additional contributions are equally important at both caps, the relative ratio is smaller than in the one-dimensional case. To verify the value of 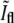we have used the measured PSF in the focal plane and convoluted it with a contour built from a bacterial contour and its reflection with respect to a line that is perpendicular to its orientation and is passing through its tip. The resulting value of 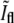for this calculation was 1.67 ± 0.03 in agreement with the value obtained from experiment.

The results from Fig. 5 b can be used to determine the timing of division from a phase-contrast time-lapse movie without the need for fluorescence. The behavior of 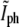for a single bacterium is shown in Fig. 6. It was computed only at times when the constriction is visible. It is constant up to a point and then starts growing linearly. Using linear regression for the growing regime we can find its intersection with the critical value of 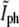to determine the generation time. For the bacterium of Fig. 6 we find that τ_g = 19.4 ± 0.7 min, which should be compared with the generation time for the corresponding population measured from the optical density at 600 nm, 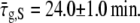We use the notation 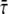to denote the average of τ over the bacterial population in a particular experiment. The value of τ_g can be further averaged over bacterial populations from different experiments that were performed under the same conditions. We denote such averaging by brackets, 〈…〉. Measuring τ_g for 27 different bacteria that belong to 10 different populations, 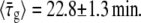The corresponding standard deviation is Sd(τ_g) = 6.6 min, that represents 29% of the average. From the rate of change of the culture turbidity at 600 nm, we obtain 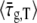22.7 ± 0.2 min in agreement with the value measured by microscopy.

RESULTS

The dynamics of the constriction—experiment

The ability to track the edge of the cell in phase-contrast can be used to monitor the dynamics of the width of the constriction, 2r, during septum formation. It is defined as the minimal distance between two points on the CM located on opposite sides of the E. coli and in its central part. However, as already discussed, when the membrane folds, the behavior of the phase contrast profile is modified by the overlapping contributions from the two folds. At what stage in the folding process does this error become significant? To answer this question we use again the comparison with the FM4-64 fluorescence images of the fixed E. coli. We use the profiles of the fluorescence intensity taken through the center of the constriction and determine the width of the constriction as the distance between the two maxima. Comparing the value of 2r obtained in this way with that obtained from the phase-contrast images using the edge threshold, 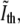we find that the two coincide up to where the width of the constriction is 59% of the total width of the cell, 2R. We therefore use phase-contrast time-lapse movies of live bacteria to track the constriction only up to this time. For this regime, we measure 2r using contours similar to that of Fig. 3. We also measure the corresponding value of 2R in each frame. The latter is obtained by averaging the width of the cylindrical sections of the dividing bacterium. The behavior of the normalized width, W ≡ r/R, as a function of time, is shown in Fig. 8 together with the prediction of a simple geometrical model that we discuss in the next section.

The dynamics of the constriction—model

To describe the behavior of the width of the constriction, r(t), we propose a geometrical model. It relies on four assumptions that are established in the literature as good approximations:

1. The shape of the nondividing bacterium is a cylinder with hemispherical caps.

2. The new caps are formed by gradually completing the missing parts of hemispheres (see Fig. 7).

3. The surface of the peptidoglycan membrane, S, in the septal region grows at a constant rate and it determines the rate at which the septum is formed,

   (1)
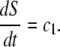
4. The radius of the cylindrical part of the bacterium is constant in time

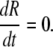
   (2)

Both Eqs. 1 and 2 are implied by this view of peptidoglycan formation mechanisms in the septum and the cylindrical wall, respectively. In the septum, the peptidoglycan factory is embedded in the cell division ring, the Z-ring. The Z-ring proteins that are required for peptidoglycan formation, FtsW and FtsI (PBP3), are immobilized and thus, appear in a fixed number of copies. Assuming that all peptidoglycan-forming complexes work at the same rate leads to Eq. 1. In the next section, we show that our measurements confirm the assumption of Eq. 1 (see Eq. 3, Figs. 11 and 13). On the other hand, in the cylindrical region peptidoglycan formation depends on the PBP2 protein. The corresponding peptidoglycan factories are believed to simply insert new glycan strands (39,40). This suggests a purely elongational process leading to Eq. 2. On the other hand, it was shown that the cell radius does slightly vary during the cell cycle (50). However, most of this variation takes place in the beginning and the end of the cell cycle. During the middle of cycle, Eq. 2 represents a good approximation and in fact, this is the relevant range for our model.

FIGURE 7.

The geometry of the model that leads to Eq. 5.

FIGURE 11.

Behavior of h(t) (squares) for bacterium A. The best fitting line to the data is also shown (line).

FIGURE 13.

Behavior of h(t) (solid circles) for bacterium B. Notice that the linear behavior shows no change in the slope at τ₂.

The assumed geometry of the dividing bacterium is shown in Fig. 7. It leads to S = 4π (R² − Rh), where R is the radius of the cylindrical part and h is the height of the missing section of the new cap. Using Eqs. 1 and 2

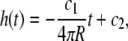(3)

where c₁ and c₂ are constants that can be determined from the boundary conditions

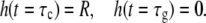(4)

Then, from geometry,

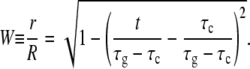(5)

For the bacterium of Figs. 6 and 8, the function of Eq. 5 provides a good fit to the data with τ_c and τ_g as the corresponding fitting parameters. The best fitting curve corresponds to τ_c = 1.5 ± 1.1 min and τ_g = 20.2 ± 1.8 min. Similar agreement was also found for the other 27 bacteria that were analyzed .

Note that the value of τ_g can now be determined in two ways:

1. From the fit of Eq. 5 to the data for the width of the constriction, W(t), τ_g,1;

2. Using the value of the phase-contrast intensity deduced from Fig. 5, τ_g.

The two methods use data that differ both in the quantity that is measured and in the time ranges used for the analysis. For example, for the bacterium of Figs. 6 and 8, τ_{g, 1} is computed from data for W(t) where t ∈ (8.5, 17.0) min while τ_g is obtained from a linear fit of the 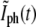of Fig. 6 for t ∈ (16.3, 20.2) min. Therefore, the two methods of determining τ_g are practically independent and comparing τ_g,1 and τ_g represents a test of consistency. Plotting τ_g,1 versus τ_g for the 27 bacteria that we analyzed, we find that data fluctuates slightly around a straight line, τ_g,1 = aτ_g + b, where the best fit corresponds to a = 1.03 ± 0.10 and b = −0.2 ± 1.9. The values of a and b are consistent with 1 and 0, respectively, which correspond to exact equivalence. Moreover, 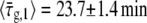in agreement with the value of 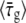found before.

The value of τ_c obtained from Fig. 8 is among the smallest that we got for the group of bacteria that was analyzed. It represents only 8% of τ_g (see Fig. 9). Moreover, it is much smaller than the time when the constriction becomes visible, τ_cv = 8.5 min—which corresponds to 44% of τ_g and the first data point in Fig. 8. However, the latter, τ_c ≪ τ_cv, was found to be the case for all of our 27 bacteria. We find that 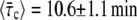while 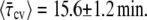The difference between τ_cv and τ_c is mainly due to optics and therefore does not significantly vary in a given experimental system. The relatively large difference between the two, 22% of is due to the shape of W(t), namely, it slows down as it approaches unity (see Fig. 8).

The dynamics of the length

The method we used in the previous section to find τ_c relies on a few assumptions. It is therefore important to verify its prediction. Another quantity that will change its behavior when division starts is the length of the cell. This is simply because at τ_c a new growth mechanism starts, namely, that for the new caps. As a result, one expects that the rate of growth will change at this time. Therefore, we use the bacterial contours, e.g., that of Fig. 3, to deduce the length of the E. coli, L, and monitor its variation as a function of time. We define the length as the largest distance between two contour points. Although this definition is somewhat arbitrary it leads to similar behavior to that obtained when this definition is slightly modified. On the other hand, using our approach to find the contour of E. coli we are limited to times that are not too small, that is, close to t = 0. As was discussed in Methods, finding the contour in the region around the new poles fails if the bacterium is still closely attached to its sister. We can, however, extend the definition of the length to hold in this regime using the point at the center of the constriction to represent the new edge of the newborn bacterium. In some cases, this approach also fails temporarily when one of the newly born sisters undergoes a sudden sidewise shift of its new pole relative to the pole of its sister. This shift opens new space for the young bacteria to grow into.

Another difficulty that we encountered is that the time dependence of the length, L(t), is influenced by changes in the radius of the bacterium, R(t). To separate, as much as possible, the behavior of L(t) from that of R(t), we define the length of the bacterium without the contribution from the old caps, 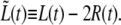Before the start of septum formation, t < τ_c, 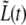is determined by the growth rate of the peptidoglycan in the cylindrical part of the cell. Later, for t > τ_c, there will be an additional contribution to 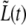due to the formation of the new caps.

Two elongation regimes in a single bacterium

We find that, for approximately half of the bacteria (12 out of 27), 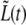apparently grows in two different linear regimes. In Fig. 10, we show the case of a cell, bacterium A, for which the two regimes are well separated (a different one than in Figs. 6, 8, and 9). The slopes of the best fitting lines to the 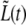data in the two regimes of Fig. 10 were found to be a₁ = 0.123 ± 0.004 μm/min and a₂ = 0.203 ± 0.004 μm/min, where a₁ corresponds to 0 < t < τ_c and a₂ to τ_c < t < τ_g.

FIGURE 10.

Behavior of the distance between the old caps, 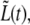for bacterium A. The symbols (squares and open circles) represent data points measured in the different time regimes. In each such regime, the best-fitting line is also shown (lines). Regimes 1 and 2 are separated by the value of τ_c that is obtained by fitting Eq. 5 to the corresponding data (as in Fig. 8). The gaps in the sequence of data points are due to either: 1), failure of the contour algorithm; 2), manual focusing; or 3), frames that were dedicated to viewing the fluorescence of the nucleoids.

An important observation regarding the two slopes of Fig. 10 is that these should be simply related to each other. In particular, we expect that

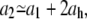(6)

where a_h is the absolute value of the slope for the best fitting line to the measured h(t) (see Eq. 3 and Figs. 7 and 11) and h(t) is obtained from the geometry of Fig. 7 using the measured values of the radiuses, r(t) and R(t). This relation between the slopes should hold because the growth of the cylindrical part takes place by a different mechanism than that of the new caps and continues during septum formation at the same rate, a₁, as before. Therefore, here the growth of 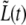is faster because in addition to the growth of the cylindrical part it contains the contribution from the growth of the two new caps. Each of these grows at an elongation rate a_h, leading to the value of a₂. We find that a₁ + 2a_h = 0.231 ± 0.019 μm/min, where a_h = 0.050 ± 0.006 μm/min. This result is not far from the value of a₂ but it is not quite equal to it either. In what follows, we show that the mismatch between the two sides of Eq. 6 could be due to the absence of a third growth regime in the case of bacterium A.

Three elongation regimes in a single bacterium

However, not all bacteria behave as the one of Fig. 10. For approximately half of the bacteria that we analyzed (15 out of 27), the septum-forming regime, τ_c < t < τ_g splits in two different linearly growing ranges (see Fig. 12). While for τ_c < t < τ₂, 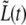grows as before at a rate, a₂, that satisfies Eq. 6, for τ₂ < t < τ_g, it grows at a faster rate, a₃. For the bacterium of Fig. 12, bacterium B, a₁ = 0.049 ± 0.002 μm/min, a₂ = 0.097 ± 0.003 μm/min, and a₃ = 0.151 ± 0.005 μm/min. In addition to the relation of Eq. 6, a₁ + 2a_h = 0.099 ± 0.008 μm/min, here we find that also

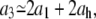(7)

where 2a₁ + 2a_h = 0.148 ± 0.008 μm/min. The elongational growth rate of the caps, a_h = 0.025 ± 0.004, is found as before in Fig. 11 (see Fig. 13). Note that the linear behavior of h(t) does not change at τ₂, indicating that the corresponding rate increase is not related to the peptidoglycan formation in the caps. This new relation between a₁, a₃, and a_h is satisfied by all the bacteria that display growth of 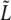in three regimes.

FIGURE 12.

Behavior of the distance between the old caps, 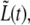for bacterium B. Same as in Fig. 10 only that here there are three regimes. The separation point between regimes 2 and 3 was qualitatively chosen at the time when an apparent change of slope occurs.

The value of the slope of 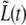in the third regime, a₃, suggests that while the new caps continue to grow at the same rate as in the second regime, here the cylindrical part grows two-times faster than before. A possible explanation for this observation is that the doubling of the cylindrical growth rate at τ₂ is due to the doubling of the number of peptidoglycan factories for the cylindrical section. This doubling occurs at τ₂ when the new PBP2-dependent peptidoglycan factories become functional after being expressed, synthesized, and transported to the neighborhood of the membrane. Moreover, this event may represent a preparation for the next generation. Assuming that growth in the cylindrical sections is continuous at τ_g, then for 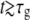Eq. 7 becomes

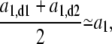(8)

where a_1,d1 and a_1,d2 are the growth rates of the daughters in the first regime. This relation, Eq. 8, would ensure the maintenance of the steady state.

Elongation regimes in the analyzed population

In the previous sections, we have discussed the behavior of individual bacteria. We now proceed to analyze the way that the observed behavior varies over a restricted sample of the bacterial population. We focus on the relations between the four growth rates, a₁, a₂, a₃, and a_h and the three corresponding times τ_c, τ₂, and τ_g. Together with 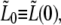these parameters determine the normalized length at all times,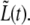

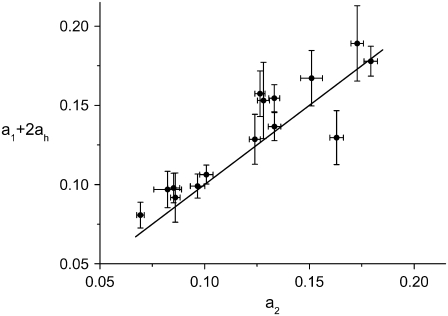
First, we test the validity of Eqs. 6 and 7 plotting the left side of the equations versus their right side. In Fig. 14 we show the plot of Eq. 6 for all the bacteria that grow in three regimes. The corresponding linear regression gives a₁ + 2a_h = a × a₂ + b where a = 0.92 ± 0.09 and b = 0.017 ± 0.010 μm/min. Although b is slightly larger than 0, Fig. 14 indicates that Eq. 6 represents a good approximation.

FIGURE 14.

Verifying the validity of Eq. 6 over the population of bacteria with three regimes (solid circles). The y = x line is also shown (line). All the growth rates are in units of μm/min. Large error bars correspond to cells for which the length could not be measured during part of the cell cycle.

To verify Eq. 7, a similar plot to that of Fig. 14 is shown in Fig. 15 for the bacteria that display elongation in three regimes. Here, the linear regression gives 2a₁ + 2a_h = a × a₃ + b where a = 1.09 ± 0.11 and b = −0.001 ± 0.018 μm/min. Thus, both the equalities of Eqs. 6 and 7 hold with similar accuracies.

FIGURE 15.

Same as in Fig. 14, only that here we test Eq. 7. For some of the cells the third regime is relatively short leading to large errors in the corresponding growth rate, a₃.

The fourth growth rate, namely that of the caps, a_h, represents the main ingredient in the description of the septum formation. It is related to the constant c₁ of Eq. 3. Using the boundary conditions for h(t), Eq. 4, we obtain that

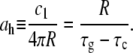(9)

Since R(t) is constant to first approximation, we find that a_h is inversely proportional to τ_g – τ_c (see Fig. 16). The corresponding linear regression gives where a = 0.48 ± 0.07 μm and b = 0.00002 ± 0.005 μm/min. On the other hand, averaging R(t) both over time and over the population of 27 bacteria we obtain 〈R〉 = 0.491 ± 0.005 μm in agreement with Eq. 9.

FIGURE 16.

Verifying Eq. 9 for all the 27 bacteria that had well-defined first and second regimes. a_h in units of μm/min.

Equations 6, 7, and 9 leave only one growth rate that is truly independent, namely, a₁. However, since the E. coli are in their steady-state regime, L_g ≡ L(τ_g) ≈ 2L₀. This steady-state relation will significantly restrict the possible values of a₁. We find that the relation between L_g and L₀ is accurately satisfied when averaged over the population of 27 bacteria, namely, 〈L_g〉 = 5.13 ± 0.14 μm and 〈L₀〉 = 2.54 ± 0.08 μm. However, the ratio L_g/L₀ for the individual bacteria fluctuates widely such that while its average is 2.07, its standard deviation equals 0.43. Correspondingly, this leads to large fluctuations in the values of a₁, such that 〈a₁〉 = 0.08 μm/min and Sd(a₁) = 0.03 μm/min.

The remaining mystery is the reason that some bacteria display two growth regimes while others grow in three regimes. The fact that the cylindrical growth rate, a₁, is on average larger for the bacteria with two regimes, 〈a₁〉 = 0.099 ± 0.006 μm/min than for those with three regimes, 〈a₁〉 = 0.067 ± 0.007 μm/min provides a hint to the solution. Another indication comes from the relation between τ₂ and τ_c. One expects that the slower bacteria, those with longer life times will also, on average, have larger values for τ_c and τ₂. Indeed we find that τ₂ is to a good approximation linearly dependent on both τ_c (see Fig. 17) and τ_g (not shown). The linear regression gives τ₂ = a × τ_c + b where a = 0.91 ± 0.33 and b = 10.6 ± 3.9 min. This relation allows us to estimate the values of τ₂ also for the bacteria that display only two growth regimes. We find that in all those cases the estimated value of τ₂, τ_2a, is either very close to τ_g or larger than τ_g. Therefore, the cells with two growth regimes are those for which the third regime is either indistinguishable from the end of the division or alternatively, it has been postponed for the next generation. For example, in the case of the bacterium A (see Figs. 10 and 11), τ_c = 8.1 ± 0.9 min, τ_g = 15.7 ± 0.3 min, and τ_2a = 17.9 ± 4.8 min. Since here τ_2a > τ_g, the activation of the new PBP2-dependent peptidoglycan factories may be expected to take place at the beginning of the life cycles of the daughter cells. Alternatively, it is possible that τ_g is the upper limit for τ₂. That is, whenever the activation of the new PBP2 factories does not take place before τ_g, the activation is suppressed. As it stands, our approach is unable to distinguish between the two scenarios. This is because when τ_2a exceeds τ_g it is only by a few minutes. In this range, the daughters are closely attached to each other and cannot be separated by our contour-finding algorithm.

FIGURE 17.

τ₂ is linearly related to τ_c for the bacteria that, like B, show three regimes.

DISCUSSION

We have monitored the morphological dynamics of individual E. coli throughout their life cycle. In particular, we have followed the formation of the septum and the rate of growth. Our main result is that the constriction starts forming on average 0.22τ_g earlier than previously believed. The difference between τ_c and τ_cv is due to the limitations of optical resolution in phase contrast microscopy. To obtain the value of τ_c we used a simple model that accurately reproduces the experimental data. The predictions of the model were further tested by measuring the growth rate. We find that apparently bacteria display either bilinear or trilinear growth whereby the first two growth regimes are separated by τ_c. The growth rate in the second regime, τ_c < t < τ₂, is to a good approximation the sum of the cylindrical growth rate with twice that of the new caps. A third linear growth regime was also observed in approximately half of the bacteria, τ₂ < t < τ_g, where the growth rate of the cylindrical section has approximatively doubled while the new caps continue growing at the same rate as in the second regime. It is possible that in the third growth regime a new generation of PBP2-dependent peptidoglycan synthesis factories have been activated and function together with those from the previous generation.

Growth law of single cells

Our findings provide further support to the view that the length growth in E. coli is, in fact, bilinear or trilinear rather than exponential (51). This has been the subject of a long dispute that started over forty years ago. Because of limited precision, single cell studies at that time led to contradictory results showing either exponential (52), bilinear (51), or interrupted (53) growth of L. With the advent of synchronized cultures, it became the main approach to the study of cell growth (54–59). Once again, different experiments led to different observations. Our results suggest that using synchronized cultures cannot alone determine the growth law of single bacterial cells. While in such experiments the time of birth is approximatively uniform, the other growth parameters are not synchronized. For example, we find that the coefficient of variation (CV) of τ_c is 53.4% corresponding to a spread of 0.248τ_g (see Table 1). In a synchronous population, the growth law is averaged over this variation leading to a widely smeared transition between the first two linear regimes.

TABLE 1.

Growth parameters for the 15 bacteria that display three growth regimes

Parameter	Mean	Sd	CV
τc	11.42	6.78	59.4%
τ2	21.15	6.02	28.5%
τg	25.08	7.97	31.8%
τg – τc	14.94	2.70	18.1%
Ac	0.428	0.107	25.0%
A2	0.854	0.077	9.1%
a1	0.067	0.027	40.2%
a2	0.122	0.035	28.4%
a3	0.174	0.049	28.3%
ah	0.032	0.005	15.6%
L0	2.50	0.35	14.0%
L(τc)	3.23	0.46	14.2%
L(τg)	5.08	0.85	16.7%
R	0.481	0.024	4.9%

A_c and A₂ are the ages, A ≡ t/τ_g, at τ_c and τ₂, respectively. Times are in minutes, growth rates in μm/min, and lengths in μm.

A third approach, introduced by Collins and Richmond (16,60–63) uses steady-state population distributions to obtain cell kinetics. They use the length distributions at birth and at division together with the steady state length distribution to obtain the growth law. This method suffers from a similar limitation as that of using synchronous cultures. That is, it ignores the variability of the growth law between individual bacteria during their life cycle.

A related controversy has emerged in the study of the growth of Schizosaccharomyces pombe, a rod-shaped, symmetrically dividing yeast (64–69). Monitoring the length of single cells during their life cycle led to data that was described as bilinear growth (64). This claim was further supported by showing that the derivative of the length data displayed two plateaus connected by a relatively smooth transition (66).

An exponential growth law implies that cell growth is a free-running process. On the other hand, bilinear/trilinear growth indicates that there is an underlying control mechanism that remains to be uncovered. Since during their life cycle, cells grow only by a factor of approximately two, distinguishing between exponential and bilinear/trilinear growth requires both precise measurements of the cell length throughout the cell cycle and control over the corresponding experimental error. Our experiments represent a significant step toward satisfying both these criteria.

Using the error estimate for 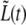(see Methods) we can use the standard χ² test to verify whether the bilinear/trilinear model is better or worse than the exponential one for our data. For the 15 bacteria that display trilinear growth we find that the average confidence level, CL, is 0.84 for the trilinear model while only 0.68 for the exponential one. Despite the advantage of the trilinear scenario, our data does not allow us to exclude the possibility of exponential growth.

Although the χ² test cannot exclude exponential growth, this scenario contradicts our findings regarding the change in the rate of growth at τ_c and τ₂. However, both these events are necessary components of the cell cycle. Since the mechanisms that generate peptidoglycan in the new caps and in the cylindrical section are different, a change in the rate of longitudinal growth will typically take place at τ_c. Moreover, on average, a doubling in the cylindrical rate of growth is required in each cell cycle to maintain the steady-state growth of the population. In individual cells, the change in the rate of cylindrical length growth at τ₂ (see Eq. 6) may vary around the factor of 2. We also found cell cycles that apparently lack the τ₂ event altogether, displaying only two growth regimes. In these cells, τ₂ has either been postponed to the next generation, τ₂ > τ_g or took place in the previous generation, τ₂ < 0. This behavior of τ₂ indicates that its variability is larger than τ_g and to obtain its true value requires monitoring several consecutive cell cycles.

Relying on our findings one may conjecture with respect to the limiting factor for bacterial growth. If cell mass is limiting then one would expect to observe exponential growth (70–72). On the other hand, growth in linear regimes suggests that it is the peptidoglycan layer that controls the cell elongation process. It also implies that at the growth loci along the sidewall, insertion of new material occurs at constant rates. Our results lead us to believe that the second scenario is more likely to be correct than the first one. Monitoring the growth of the single cell volume may further clarify this dilemma. However, at present our volume measurements are significantly less precise than those of the length. This is both due to the limited accuracy in measuring the cell radius and the deviations of cell shapes from that of a cylinder with hemispherical caps (unpublished data).

The picture on peptidoglycan growth emerging from this work is consistent with the results from the group of de Pedro (41,74). In particular, two of the modes of growth they found correspond to either mixed insertion of peptidoglycan in the cylindrical section or to the formation of new poles from entirely new material. While the first may correspond to our first regime where the growth rate is a₁, the second is linked to our second regime where 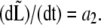On the other hand, it is not clear whether the patchiness emphasized by de Pedro as the third growth mode bears any relation to our third regime where 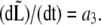Timing the appearance of the patches will shed light on this presently open question. Nevertheless, the existence of these patches is supportive of a limited number of peptidoglycan-forming factories. Similar patches were also observed in studies of PBP2 localization in both E. coli (42) and B. subtilis (75). Moreover, the number of these patches is qualitatively correlated to the measured number of PBP2 copies per cell (76).

Single cell parameters—correlations and variability

Studying the E. coli in rich medium (LB) might not be the best choice. The growth rate is faster than that of DNA replication leading to the coexistence of three different DNA replication cycles. On the other hand, it is reasonable to expect that in this limit the peptidoglycan factories function at their maximal rate. In this case, the growth rates, a₁ and a_h, are determined by the number of peptidoglycan factories in the cylindrical and septal sectors, N₁ and N_h, respectively. Then our data may allow us to measure the values of N₁ and N_h in individual cells. Moreover, it may allow us to determine the rate of peptidoglycan synthesis of a single factory.

The extent of the T-period, τ_g – τ_c, is determined by the radius, R, and the septal growth rate, a_h (see Eq. 9). Two possible scenarios for the formation of the new caps can be envisioned. In the first, the number of PBP3-dependent peptidoglycan factories, N_h, depends on the width of the cell, namely, for thick cells there will be more factories allowing us to maintain a constant T-period. In the second scenario, N_h is independent of the radius and is controlled by a different mechanism. We find no apparent correlation between a_h and R and therefore are inclined toward the second scenario. Moreover, we find that on average a_h is approximately one-half a₁, 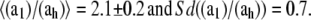Since each cell forms two new caps, this suggests that the rate of expression for the rate-limiting components of the PBP2-dependent and the PBP3-dependent peptidoglycan synthesizing networks are similar. The fact that this relation only holds on average may be due to PBP2 and PBP3 belonging to different operons (77).

Various control mechanisms have been proposed in the literature for the onset of division, τ_c. In particular, there has been a debate between those that claimed that division is initiated at a certain cell length (17) while others proposed that it is the cell volume that determines τ_c (78). We have tested whether length and volume are constant at τ_c for our bacterial population. We found that the confidence level for the assumption that either of them is constant is practically zero. A similar test has shown that age as well, A ≡ τ_c/τ_g, is not constant at τ_c (see Table 1) indicating that it also cannot be the factor that initiates division. This may indicate that one should look to the chromosome replication cycle for the division signal (79–81).

In Table 1 we compare the variabilities of the different cell growth parameters for the cells that elongate in three regimes. While the largest are the CVs of τ_c and a₁, the CVs of A_c and A₂ are significantly smaller than those of τ_c and τ₂, respectively. Moreover, no apparent correlations were found between τ_c and a₁. It is therefore interesting to note that the cell life time, τ_g, has a smaller CV than the factors that determined it. This suggests that there might be a compensation mechanism at work that limits the variability of the bacterial population.