A Comparison of Step-Detection Methods: How Well Can You Do?

Abstract

Many biological machines function in discrete steps, and detection of such steps can provide insight into the machines' dynamics. It is therefore crucial to develop an automated method to detect steps, and determine how its success is impaired by the significant noise usually present. A number of step detection methods have been used in previous studies, but their robustness and relative success rate have not been evaluated. Here, we compare the performance of four step detection methods on artificial benchmark data (simulating different data acquisition and stepping rates, as well as varying amounts of Gaussian noise). For each of the methods we investigate how to optimize performance both via parameter selection and via prefiltering of the data. While our analysis reveals that many of the tested methods have similar performance when optimized, we find that the method based on a chi-squared optimization procedure is simplest to optimize, and has excellent temporal resolution. Finally, we apply these step detection methods to the question of observed step sizes for cargoes moved by multiple kinesin motors in vitro. We conclude there is strong evidence for sub-8-nm steps of the cargo's center of mass in our multiple motor records.

INTRODUCTION

Biological machines frequently move in a stepwise fashion along a substrate. Such machines include the microtubule-based motors kinesin and dynein, the actin-based myosin motors, proteins involved in DNA replication and RNA transcription (which proceed in a stepwise fashion along a DNA strand), and ribosomal transcription of RNA into protein.

Since the determination of step size of the kinesin protein under in vitro conditions (1), similar methods have been used to examine the step size of other motor proteins including Myosin-V and RNA Polymerase (2). More recently, experiments have begun to look at new situations where the step-size of cargoes may not be constant. This includes single motors such as cytoplasmic dynein (3) and also multiple motors moving a single cargo. In multiple motor experiments, there exists a possibility of the motors moving at different times, resulting in the center of mass of the cargo moving with observed step sizes smaller than the usual 8-nm for kinesin. Alternatively, the motors may move in lock-step. Thus, details of the stepping behavior of the center of mass of the cargo can provide insight into the way the motors work together.

Detection of steps can also serve to provide kinematic and thermodynamic information about the individual motor. Information on the distribution of step sizes and step times can be used to differentiate between different theoretical models of how motors work. For instance, by detecting the distribution of step sizes, we can test the hypothesis that dynein works the same in vivo (4) as it does in vitro (3,5). Similar studies can compare kinesin or myosin function in vivo (4,6) to that established in vitro. Finally, as we start to investigate in vitro how motor function is altered/regulated by additional factors (e.g., the addition of other motors, the effect of load, the effect of MAPS bound to microtubules on motor function, or proteins that directly regulate motor function), such measurements can help understand how the combined system is functioning.

Given the utility of such step detection, what are the challenges? As the standard deviation of the noise increases to match the step size observed, detection of steps becomes progressively more difficult. While averaging can theoretically help, there are limits to how much it improves such studies. One popular method (7) has been picking out steps by eye. The human eye is quite good at pattern recognition (including step detection), but there are two issues which make it troublesome for step detection. First, this approach is subject to user bias. Second, high speed camera or quadrant photodiode detectors observing physiological speeds of motion can easily produce data sets containing potentially hundreds of steps, leading to extremely prohibitive times for manual analysis. Finally, it is important to either keep or ignore entire records rather than cherry-picking portions. Picking only the steps that are clearest for deeper analysis can skew the observed distribution of sizes in either direction depending on the observer: larger, because the clearest steps will often be the largest (as they rise the highest above the background noise) or smaller, because large steps are often assumed to be multiples and are therefore ignored.

Thus, we are interested in methods that can analyze long records of processive stepwise motion, detect stepping events, and determine their magnitude. As such, this article is not concerned with various methods which are intended to deal mostly with changes between two states. A survey of some of these methods may be found in Knight et al. (8). The pairwise distribution function (9) has been much used in this field (1,4,10–12), but is not suitable for applications where a variable step size is expected, particularly when we seek to know the distribution of step sizes found. Pairwise distances will always include a large number of double step (and higher) magnitude events, meaning that the strength of a particular peak is not proportional to the number of steps that have that size. For this reason, we excluded the pairwise distribution function from our analysis. We have also excluded methods that make assumptions about the underlying process (e.g., Markovian). See Milescu et al. (13,14) for information on a Markovian-based method of step detection.

The methods we considered here are:

• Velocity calculation and thresholding (specifically as described in (15)).

• Two sample student's t-test (similar to that described in (16)).

• Wavelet transform multiscale products (as described in (17,18)).

• A χ²-reduction method (described in (19)).

This analysis would be incomplete without consideration of various filtering techniques which has been applied to step detection in the past. We thus examine the effect of mean filtering and median filtering as well as the nonlinear filter described by Chung and Kennedy (20) and used by Nan et al. (4).

Much of this analysis was motivated by the study of transport along filaments with known repeat size. Since motors move along these filaments, repeatedly binding at identical sites along the filament, we expect step sizes of single motors to be integral multiples of the typical repeat length. For the case of microtubules, the tubulin dimer size is 8 nm. Thus, much of our analysis was not focused on differentiating between steps that are very closely separated, but rather on differentiating between steps that are different multiples of the expected lattice spacing. The simulated data used here to test the methods focused predominantly on determining the ability of the different methods to detect the relative frequency of the expected 8-, 16-, and 24-nm steps of dynein. We also considered the case of two motors functioning together, when the center of mass of a cargo could move in smaller steps. For instance, if two kinesin motors are moving a cargo, and do not move in lock-step, one might expect the cargo's center of mass to move 4 nm, half of the step-size of the individual motors 8-nm steps. We discuss the challenges to 4-nm step detection stemming from the high stepping rate and the high noise in the real system. We show that even in the presence of significant noise, we can infer the presence of such steps by examining the shape and peak location of the histogram of step sizes.

While we focused specifically on relative performance of the step-detection algorithms against a staircase type function (processive motors), these results may hold for the situation of transitions between two states, and so may be applicable to two-state (on/off) results as observed in single-channel and some myosin experiments.

By comparing several methods, we hope to establish a base for making informed decisions when considering the issue of step detection, particularly in those situations where steps are not expected to be of uniform size. In our comparison, we seek the answers to these questions:

• How do the methods respond to variations in key parameters: levels of noise, velocities, and step magnitudes?

• What are the limitations of current methods?

• Is any one method significantly better?

• Do different approaches excel at different aspects of the problem?

MATERIALS AND METHODS

Taxol-stabilized microtubules were prepared as previously described (3). Kinesin assay was prepared as previously described (21). Data was acquired as described in Vershinin et al. (21) with custom software and procedures as described in main text.

Filters

Windowed mean filter (mean filter)

The window consists of the current point of interest and r (rank) points before and r points after the current point. The value at the current point is replaced with the mean value of the points in the current window.

Windowed median filter (median filter)

The window consists of the current point of interest and r (rank) points before and r points after the current point. The value at the current point is replaced with the median value of the points in the current window.

Chung and Kennedy nonlinear filter (CK filter)

The method (20) has three parameters, K, M, and p. We attempted to optimize these settings for our datasets. Overall, best performance was achieved with K = 5, M = 5, p = 3. These optimized settings and the settings used by Nan et al. (4) (K = 5, M = 10, p = 10) as well as values in between were tested. Our values were found to perform best on our benchmark datasets, and appear throughout this article.

Step detection methods

Two sample students' t-test

As described by Carter and Cross (16). For each data point, N points before and after the point are compared by the two sample Student's t-test,

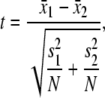where N is the number of points in each sample, s₁, s₂ are sample variances, and x₁ and x₂ are the sample means. Unlike Carter and Cross, we calculate the probability of observing a particular t-value for a given degree of freedom (P(t,df), calculated using the built-in LabVIEW function) with the degrees of freedom determined by

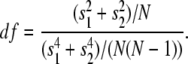Steps are found as downward peaks (forward step) or upward peaks (backward step) in the P(t) record. Periods between steps are scored as pauses and the difference between the means of successive pauses are recorded as the step size. We compare this approach with the Carter-Cross approach in the Supplementary Material (Supplementary Fig. 1). To summarize, we found the two implementations of the t-test method had similar performance, provided filters were used with the Carter-Cross t-test method.

Velocity threshold (VT)

A number of velocity thresholding methods have been described; we use a method described in Hua et al. (15). In the original description, a median filter is used before any other calculations. In our implementation, we have considered a wider range of prefiltering approaches (see above). The first derivative by quadratic convolute (the velocity) is found by first using a Savitzky-Golay filter of order 2 to fit the data and then dividing by the time between frames. The specific implementation of the Savitzky-Golay filter used here is a LabVIEW (National Instruments, Austin, TX) implementation of the one found in Teukolsky et al. (23). The number of points used by the Savitzky-Golay filter we refer to as the window size and is equal to 2N+1 where N is the number of points used to either side of our central point of interest. Beginnings and endings of steps are identified by the crossing of a velocity threshold. Periods between steps are identified as pauses, and the difference between mean positions during the pauses give the step sizes.

Chi-squared minimization method (χ² method)

This method created by Kerssemakers et al. (19) is based on a χ² minimization. To summarize, the method identifies the most prominent step in the record and partitions the data at the identified location. The algorithm proceeds iteratively until the specified number of steps is identified. The authors of the method also introduced a parameter S which is the ratio of the χ² of a counter fit (where all the steps are selected to occur in the plateaus of the best fit) to the χ² of the best fit. In effect, S is a measure of quality of step identification. Low values of S occur either when the fit is not close enough or when the algorithm fits the data too closely (mistaking noise for steps). A peak in S parameter occurs when the number of steps identified is close to the number of steps occurring in the data. Details on its implementation may be found in Appendix 3 of Kerssemakers et al. (19). Here we use their MatLab (The MathWorks, Natick, MA) implementation.

Derivative of Gaussian wavelet (dG wavelet)

Discrete wavelet transform is calculated using the derivative of Gaussian wavelet. The method used is the MZ-DWT as implemented by Sadler et al. (17,18).

Generation of benchmark data

The testing methodology used in this article is to use artificial data sets which closely mirror typical experimentally obtained records. The advantage of such an artificial benchmark is that we know all underlying parameters (temporal position and size of steps) and therefore can quantitatively compare this a priori knowledge with the output of step detection algorithms (a posteriori results).

The simplest behavior of kinesin, observed under condition of low ATP, is that there is a single rate-determining step leading to simple Poisson stepping behavior (10). Under conditions where ATP is not limiting the stepping rate, the motion of kinesin has two rate-determining steps. In principle, the more rate-limiting steps there are, the more “regular” the stepping, so that there is a decreased likelihood of two steps occurring within a very short time. In practice, the effect turns out to be small; noise and other factors such a frame rate and averaging have a much larger effect. A brief investigation of the difference in performance for simulated data with one and two rate-limiting steps is provided in the Supplementary Material (Table S1 and Fig. S2). As expected, the performance does improve slightly when there are two rate-determining steps, since this reduces the incidence of very short times between steps. We therefore believe that the single rate-determining step represents worst-case method performance.

In general, we must account for the fact that for low data acquisition rates, multiple steps may occur in a single low-speed data sample. Therefore we first constructed a high-speed data stream for a simple Poisson stepper. Times between steps are randomly chosen from under a decaying exponential distribution (the decay constant of this distribution is equal to the mean velocity divided by the step size). The times between steps are rounded to 0.1 ms and then used to construct a 10,000 frame per second (FPS) position versus time record. To better emulate real stepping, our steps occur over an extended period of 0.2 ms. We chose this amount of time because it is on the order of the time reported for steps to occur in vitro (16). The resulting high speed position versus time record is then split into segments based on the desired frame rate. The positions within each segment are then averaged simulating the action of a camera (for instance, averaging 100-frame-long segments would produce 100 FPS final data stream). Finally, Gaussian white noise (25) with a selectable standard deviation was added to create noisy records, which were then analyzed with the different step detection algorithms. To indicate the amount of noise added, we refer to the size in nanometers of the standard deviation, i.e., SD5 (or SD 5 nm) means we have Gaussian noise with a standard deviation of 5 nm.

Determining performance with different amounts of noise

To gauge which methods in general perform best, we used several 30 FPS datasets with 200 8-nm steps and a mean velocity of 10 nm/s. Gaussian noise was varied between SD1 and SD5. We estimate the minimum noise observed in our single and multiple kinesin experiments to be ∼SD3 nm. Under conditions of low load, noise may be on the order of SD7 to SD8, with noise being reduced as the distance from the center of the trap increases. Note that we have used SD1 to SD5 levels of noise in step detection tests precisely to span the range between idealized low noise limit and realistic high noise data.

Determining performance with variable frames per step

To explore how frame rate and velocity affect step detection we generated datasets with 200 8-nm steps at variable mean velocity (between 10 nm/s and 600 nm/s) and fixed frame rate (1000 FPS). We also tested step detection for fixed velocity (50 nm/s) but variable frame rate (30–1000 FPS). Both datasets had a noise of SD3 added. If the velocity is raised at a fixed frame rate then fewer samples occur between steps. Lowering the frame rate at fixed velocity also results in fewer samples between steps. These parameters have similar effects, and it proves most sensible, therefore, to think about the mean number of samples (frames) between steps when examining the performance of step detection methods.

Determining performance for variable step size

For variable step size testing, some slight modifications were made to our general procedure. The size of each step was chosen randomly. The probability of a given step size being chosen is set in advance. For instance, to produce a record with roughly equal numbers of 8-nm and 16-nm steps we fix the chance of occurrence of each step size at 50%.

As mentioned above, the decay constant of the exponential distribution from which we choose times between steps is the ratio of mean velocity and the mean step size. Here, we use the effective mean step size, so that each step magnitude is weighed by the relative likelihood of its occurrence. In the example above (50% 8-nm, 50% 16-nm steps), the effective mean step size used for calculating velocity was 12 nm. All our mixed step datasets were 200 steps with a mean velocity of 10 nm/s and 30 FPS and a noise of SD5.

Metric

To compare the results for the different methods, we need a common set of criteria with which to judge them. Ideally, we are searching for a method that finds the maximum number of a priori steps with the minimum number of false positives. It is also important to minimize blurring nearby steps together particularly for extracting rate information from the stepping record. For our simulated records, we know exactly when each step occurred, and its size, and can therefore score a posteriori steps for accuracy in size as well as examining how often nearby steps are located together rather than singly.

When we look for steps, there are three concerns (illustrated in Supplementary Fig. 3): First, if a step occurred in the data record, did we in fact detect it (either as a standalone step or blurred together with other nearby steps)? The parameter that measures this is henceforth called “percent found.” Second, from our program, we are going to receive an output of putative steps. How many of those a posteriori steps are correct, that is, reflect a priori steps? The parameter that measures this is henceforth called “percent correct.” Third, our methods typically look for a step in a given temporal window, but in some cases multiple steps in the actual data occur in that window. For instance, consider a case where there were two a priori steps in the window. If the program reveals a single a posteriori step whose magnitude is the sum of those two individual a priori steps, it will be doing as well as can be expected, and these steps will be identified as correct as far as the “percent found” and “percent correct” measures. However, we would also like a measure of how many of the steps detected correspond to such “fused” steps. For our benchmark datasets that have only 8-nm steps, we can measure the fraction of correct a posteriori steps whose size is found to be 8 nm (±3 nm). This is reported as the third parameter, “percent 8's.” This parameter is thus a measure of a method's ability to individually resolve nearby steps.

The analysis of the χ² method is slightly more complicated as it is not intrinsically a windowed method, and its output format differs from the other three methods. Specifically, the χ² method does not report a time window for when a step occurred, but rather the exact time when the step happened. Directly comparing its reported step time and step size proves problematic as the step time may be off by a few frames from the correct time. Since the other methods are allowed to have the step time wrong by the size of their window, we decided to allow the χ² method a similar leeway. We construct windows around each a posteriori step, allowing two points to either side. Any windows which overlap are then combined. This results in a five-point window centered on each a posteriori step.

Stepping in vitro

The in vitro kinesin assay was prepared as described in Vershinin et al. (21) with an ATP concentration of 1 mM. Under these conditions ATP is not limiting the stepping rate. A custom LabVIEW program was used to bring a bead into contact with a microtubule and subsequently follow the beads motion by moving the piezoelectric stage to keep the bead within 150 nm of the trap center to allow detection of the bead's position using the quadrant photodiode. The linkage compliance for single and multiple motors were found separately as in Svoboda et al. (1). ATP-driven motion was captured at 20,000 samples per second, then decimated into 10 samples segments that were averaged to produce a final 2000 sample/s record.

RESULTS

Setting of user-chosen method parameters

Each of the methods examined has one or more parameters which must be set by the user. The χ² method has one parameter, the number of steps to be reported, and a built in graph (S versus number of steps) which provides guidance in setting the parameter (sample in Fig. 1 a). The wavelet method has two user-settable parameters—the number of dyadic scales to be examined and a threshold value. Similarly, the VT and t-test method have two parameters—window size and a threshold value. For wavelet, VT, and t-test, the parameters influence each other, so the threshold value is affected by window size (or dyadic scale size in the case of wavelet).

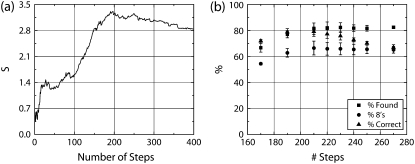
FIGURE 1.

Example of performance of the χ² method. (a) The curve of the S parameter versus number of steps at noise SD 3 provides guidance for the optimal pick for the number of steps in a record being analyzed. (b) Three performance characteristics are shown for various choices of the number of steps (SD 3 noise), combining steps as described in text. Note that the performance in panel b is fairly stable over a large region near the peak value of the S parameter found in panel a.

There is an inherent tradeoff between noise resistance (resulting from a greater number of points within the window) and decreasing ability to separately identify closely spaced steps. Ideally, we wanted to compare the best performance that each method had to offer so we used our a priori knowledge of step positions and sizes to optimize the window size parameter for each method. It also proved possible, for most methods under most conditions, to reproduce the ideal window sizes we determined with a priori knowledge by examination of the number of steps found versus threshold value. See below and Supplementary Fig. 4 for a description of the procedure we used.

The best window size was determined for VT, dG wavelet, and t-test by finding the window size that gave the highest mean of % found, % correct, and % 8's. Fig. 2 b, Supplementary Fig. 5 b, and Supplementary Fig. 6 b illustrate the results (mean and SD of results for measurements against three sets of 200 steps).

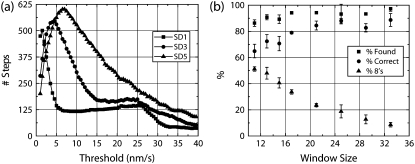
FIGURE 2.

Example of performance of the VT method. (a) The total steps found in the record being analyzed varies significantly as the threshold is increased. The graphs for VT method (window of 13) for SD1, 3, and 5 noise are shown. The plateau in the graphs is generally close to the optimal choice for the threshold. Note, however, that the plateau loses its definition at higher noise, making setting of the threshold difficult. (b) Three performance characteristics are shown for various choices of window size at SD3 noise for the VT method. For each window size, the threshold was found following rules described in the text for each of three runs and the mean and SD are plotted here. Percent Found and Correct remain stable across a wide variation in rank/window size. The Percent 8's decreases with increasing window size. As a result, mean performance (mean of all three parameters) also drops with increasing window size.

The Kerssemakers article (19) contains suggestions on using the graph of S versus number of steps (Fig. 1 a) to set the expected number of steps, recommending the value just beyond where the peak in S occurs. In our tests, little change in algorithm performance is observed for a fairly large range of expected number of steps near the peak S value (Fig. 1 b).

We attempted to find a repeatable “best” way of setting the threshold for t-test, VT, and wavelet methods, to be used when a priori information was lacking. If steps are typically distinct from noise fluctuations, then we expect that the number of a posteriori steps detected will vary only slightly near the “optimal” threshold value. We therefore swept the threshold value and determined the total number of a posteriori steps and looked for a plateau in the observed relation. One complication of this optimization procedure is that the best threshold value turns out to depend on window size.

Examples of this threshold sweep procedure at various noise levels are shown for the VT method in Fig. 2 a. For the VT method, the best threshold values are indeed found in the region where the total steps versus threshold flattens out. Best results are usually obtained closer to the minima of this flattened region. Note that this flat region is almost nonexistent for SD5 noise, making selection of a threshold value very difficult.

Similarly, for the wavelet algorithm whose total step versus threshold graph looks similar to the VT graph (Supplementary Fig. 5 a), the best threshold values are found where the plateau occurs in the graph of total steps versus threshold. The flat region erodes more quickly with noise for the wavelet method than it does for the VT method, making setting of the threshold level even more difficult.

Curiously, for t-test, the optimal threshold setting is slightly less restrictive than the value inferred from where the plateau occurs. The graph for t-test appears in the Supplementary Material (Supplementary Fig. 6 a, plotted so less restrictive thresholds appear on the left).

Comparison of methods with variable noise

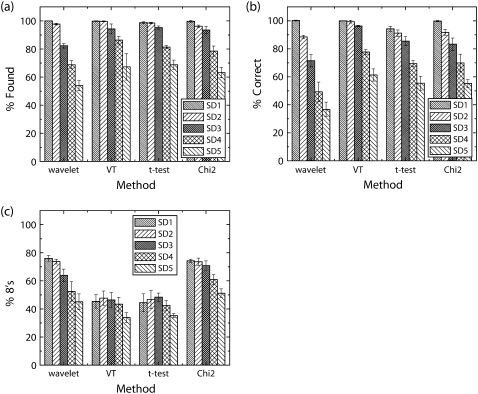
Each method was optimized as described above and tested against three separate datasets with increasing amounts of Gaussian white noise added. The mean and standard deviation of the % found, % correct, and % 8's were calculated and are plotted in Fig. 3.

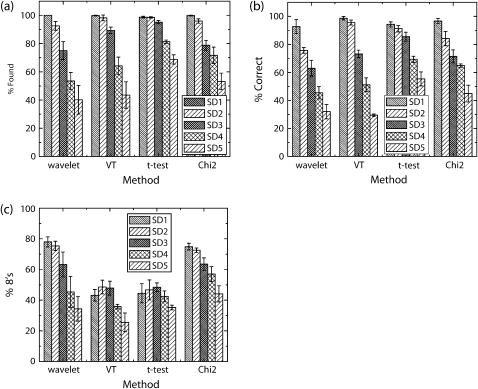
FIGURE 3.

Comparison of step detection performance. Three performance characteristics, Percent Found, Percent Correct, and Percent 8's are shown in a–c, respectively. Note that the dG wavelet method rapidly loses performance as noise level increases. The percent found and percent correct are similar for the other three methods (excluding VT at SD5). The t-test method, unlike the other methods, immediately finds a fair number of false steps as soon as noise appears in the signal.

First, let us investigate algorithm performance ignoring the temporal resolution (% found and % correct measures shown in Fig. 3, a and b, respectively). All methods show excellent performance at low noise levels. However, at the highest level of noise tested, t-test had the best overall response followed closely by χ² (VT and dG wavelet methods being the worst). Once we factor-in a measure of temporal resolution (% 8's shown in Fig. 3 c), the overall picture changes. Here, the methods break broadly into two categories: wavelet and χ², which do a better job discriminating nearby steps, and VT and t-test, which do distinctly worse.

A more detailed look at the distribution of step sizes found appears in Supplementary Table 2. In general, it bears out what Fig. 3 c implies: dG wavelet and χ² methods are more efficient at discriminating nearby steps. It also shows with greater detail that larger window sizes/dyadic scales cause decreased ability to discriminate nearby steps.

Results for test datasets with filters applied

As a next step, we examined if any additional factors could be used to improve method performance. Filtering is a traditional method of improving response in noisy conditions, and the VT method was originally described (15) with a median filter used before the derivative. We tested each of the four methods (using the best window size determined above, and with the threshold determined as described) with one of three filters in place (mean, median, and the Chung-Kennedy (CK) nonlinear filter) and the results, organized by step detection method, appear in Fig. 4.

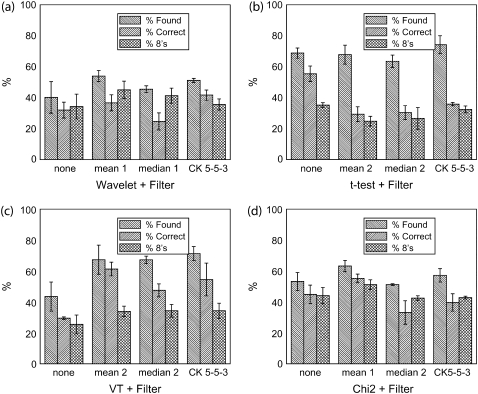
FIGURE 4.

Comparison of step detection performance after data filtering. Three performance characteristics are shown for (a) dG wavelet method, (b) t-test method, (c) VT method, and (d) χ² method. The filters used are indicated in each panel along with their settings (e.g., rank for mean and median filters). For the wavelet method, the best performance is found with the mean filter. The t-test is better off with no filter applied. The VT method benefits from filtering, with the best performance coming from mean filtering. Finally, the χ² method benefits modestly from filtering with the greatest improvement seen from mean filtering with nonlinear taking a close second. Noise level was SD5.

Most methods perform better with a mean filter applied. For t-test, filtering provides mixed results—percent correct rises, but the percent found drops. In the end, we decided to use no filter with t-test as any improvement is not statistically significant. It is interesting that the sophisticated CK nonlinear filter does not perform any better than the simple mean filter in our tests. It does not erode edges as much as a mean or median filter; however, it has a tendency to reinforce sudden large jumps resulting from noise, even as it eliminates the small jumps due to noise, making noise appear more steplike.

For methods positively affected by mean filtering (dG wavelet, χ², VT), the filter decreases the frequency with which noise is identified as steps. The VT method has the largest improvement (see Supplementary Fig. 7). The decrease in the number of false positives is immediately clear (Supplementary Fig. 7 a). There are no obvious changes to the histogram of steps identified as correct (Supplementary Fig. 7 b).

With the best performing filter in place we find that the χ² method has the best overall performance. We again compare the % Found, % Correct, and % 8's (Fig. 5). VT, t-test, and the χ² method have very similar % Found and % Correct values. The χ² method and dG wavelet do a better job finding individual 8-nm steps than t-test and VT. The χ² method performs the best for this reason—it has similar performance to the VT and t-test methods for % found and % correct, but its temporal resolution is better and it exceeds their performance on % 8's. Even with filters applied, dG wavelet is a poor performer, although its performance has improved considerably from the no filter case.

FIGURE 5.

Fig. 3 reprised with best filter in place. Here again, Percent Found, Percent Correct, and Percent 8's are shown in a–c, respectively. With best filter in place VT, t-test, and the χ² methods all have very similar percent found and correct. Wavelet is still a poor performer when noise gets large, although its performance has improved considerably.

For a more detailed examination of temporal resolution of various methods with filters in place, see Supplementary Table 3. Comparing Supplementary Table 3 to Supplementary Table 2 shows that filtering disturbs the step size distribution, moving it further from the ideal (as expected, larger filtering windows generally result in more blurring together of nearby steps). Here, the χ² and dG wavelet methods have better performance than the t-test and VT methods.

Best performers

Based on the above results, the χ² method (with data preprocessed by a mean filter) seems to be the best overall performer. Moving forward from here, we will focus on the performance of the χ²⁺ mean method. Results for the VT method appear in the Supplementary Material for comparison.

Velocity/frame rate effects

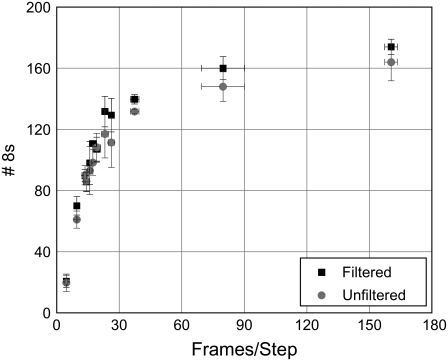
What happens to detection of steps as the velocity rises at a fixed frame rate? Conversely, what happens as the frame rate is increased for the same velocity? Are the changes in number of steps detected, linear? The first two questions are interrelated, and increasing the frame rate at a constant velocity is the same as lowering the velocity at a constant frame rate. By using a common measure, frames per step (which is the result of multiplying the frame rate by effective step size and dividing by the velocity), we get the results plotted in Fig. 6 (VT in Supplementary Fig. 8).

FIGURE 6.

Step detection performance changes as a function of frames per step. The χ² method was used to detect steps in three sample data sets with 200 total 8-nm steps each and SD3 noise. Step detection results with and without mean filter applied are shown. All data points represent the mean and SD of the results for the three data sets. Mean filter rank was chosen using a priori knowledge.

Fig. 6 shows the relative performance of the χ² method, with and without the mean filter, as the number of frames per step increases. We observe a rapid increase in detection of 8-nm steps with increasing frames per step followed by a plateau where the optimal result is approached. At 16.3 frames per step, the χ² method is able to identify nearly half of all steps as singles. Different filter strengths work best at different frames per step (see comparison in Table 1). Strangely, performance falls off at high (near 782 and above) frames/step. Close examination revealed that the χ² method was still detecting the steps, but was placing them more frames away from the correct position than our window would accept as correct. The exact cause is unclear, but seems to be related to the length of the record, as splitting of the 782 frame/step record into two parts improved method performance. Interestingly, this performance falloff was not observed for a long record with evenly spaced steps. We would therefore recommend keeping records under ∼100,000 frames in length, as this improved performance in the cases we have tested.

TABLE 1.

Low filter ranks are optimal for the χ² method

Frames/step	χ2 unfiltered rank	χ2 mean filter rank
800	NA	2
160	NA	1
80	NA	1
40	NA	1
26.7	NA	1
22.9	NA	1
20	NA	1
17.8	NA	1
16	NA	1
14.5	NA	1
13.3	NA	1
9.6	NA	1
4.8	NA	1

Mean filter rank was optimized using a priori knowledge for sample data sets (also used in Fig. 6), which had 200 total steps and SD3 noise.

Performance when the sample contains a mix of step sizes

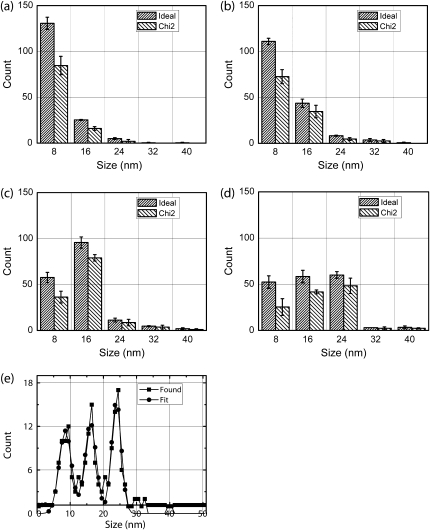
We created several records with mixes of 8- and 16-nm steps with SD5 noise (100% 8's, ∼80% 8's, ∼60% 8's, ∼40% 8's, ∼20% 8's, and 0% 8's) and examined the resulting distribution of correct a posteriori steps (Fig. 7, VT in Supplementary Fig. 9). For each case, we found expected performance (assuming four frames of separation between steps for clear detection). The change in step distribution is clearly observable. These changes do not result in a simple proportional change to the step distribution (that is, 40% 8's vs. 60% 8's does not result in a 20% drop in detected 8's and a 20% increase in detected 16's) due primarily to two factors: 1), the combination of nearby steps resulting from windowing; and 2), missed steps due to noise. A mix of 33% each of 8's, 16's, and 24's is also clearly distinguishable from mixes of 8's and 16's. For all of these data sets, velocity was 10-nm/s and frame rate was 30 FPS. This velocity to frame rate ratio was sufficient for good detection of single steps. Note that (per Fig. 6) this is equivalent to 300 FPS for a cargo moving at 100 nm/s; for a cargo moving 1000 nm/s we would need 3000 FPS.

FIGURE 7.

The χ² method detection of 8-16 and 8-16-24 nm mixed step distributions. We have used data sets with (a) 100% 8's, (b) ∼80% 8's, (c) ∼40% 8's, and (d) approximately even mix of 8-, 16-, and 24-nm steps and SD5 noise to test χ² performance. Panels a–d show the mean and SD of three datasets. (e) The results of the χ² method for a data set containing 60 8-nm steps, 56 16-nm steps, and 59 24-nm steps were binned to produce a histogram shown (squares). A fit of the histogram to a combination of three Gaussians is shown (circles). The fit suggests that ∼53 8-nm steps, ∼54 16-nm steps, and ∼57 24-nm steps were found by χ² method.

Up to this point, we have determined the step distribution using our a priori knowledge of where steps occurred. In a real situation, the distribution of step sizes would need to be determined by some other method, such as fitting of the peaks in the histogram of detected steps with multiple Gaussians. Fig. 7 e shows that this is feasible for an approximately even mix of 8-, 16-, and 24-nm steps (72 steps, 65 steps, and 63 steps, respectively). By estimating counts under each Gaussian, we find ∼53 8's, 54 16's, and 57 24's. Some of the missing steps may be found as higher order combinations.

A real-life example: steps observed for beads moved by multiple kinesin motors

Recently, our lab has been investigating how multiple motors work together (21,26). We have found that for low numbers of motors, stalling forces are approximately additive, and that the mean travel of a cargo moved by multiple motors is much larger than for a cargo moved by a single motor. As we try to understand the ensemble function of the multiple motors, one question is how they work together—do they step in unison, or independently? One way to approach this question is to look at displacements of the center of mass of a bead moved by two motors. If the motors step in unison, the center of mass should move 8 nm at each step, whereas if the motors step independently, we might expect the center of mass to move 4 nm (when one motor steps 8 nm, and the second does not). In particular, we want to know how the motors step under approximately physiological conditions—that is, at ∼1 mM ATP, and not heavily loaded down, so that the cargo's mean travel speed is >100 nm/s. To achieve this, we cannot use strong opposing load to slow down the motors or to damp their thermal noise. Because of this, we are faced with the technically challenging question of investigating 4 nm vs. 8 nm steps at high stepping rate, in the presence of high thermal noise.

To gather experimental data, we performed experiments on beads moved along a microtubule by either a single kinesin (as determined by having a binding fraction of <0.4) or by multiple kinesins (all beads can bind to microtubules and move multiple microns). For the particular kinesin concentration used, our past studies (21) indicate that moving cargos are most often moved by two motors, so we believe that a significant fraction of the stepping events we observe correspond to the movement of a cargo driven by two motors. We do expect that the cargos will occasionally be moved by either one or three motors and the resulting displacements are present in our datasets. Because of the high rate of stepping, we needed to use the quadrant photodiode to detect the bead's position (with a 2 kHz temporal resolution) instead of using video microscopy. To do this, we implemented a crude repositioning system, moving the piezo-controlled stage to follow a moving bead, and keep it in the trap. The bead was kept between ∼30 and ∼130 nm from the center of the trap; this resulted in the load experienced by the beads varying from ∼1 pN to a single kinesin stall force of 5 pN.

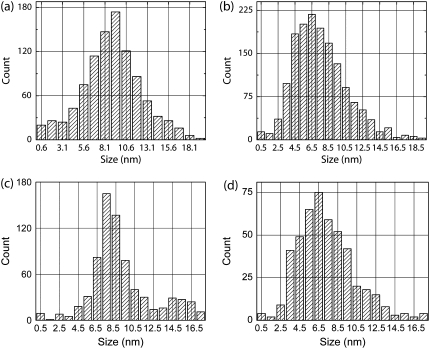
We then examined the position record produced by the beam position detector for steps in each case (Fig. 8). Since we were trying to distinguish between close step sizes, accuracy in step location was critical. This requirement favors χ² and dG wavelet methods (Fig. 5 c). We also estimate that the noise in our data was at least SD3 (see below). In this case, the χ² method is preferable to the wavelet method since it is less sensitive to noise (Fig. 5 b). Moreover, in this case no a priori knowledge was available so that setting thresholds for the wavelet, VT, and t-test methods was far more difficult, time consuming, and ultimately ambiguous than setting the number of steps in each record based on the S parameter guidance (Table 2).

FIGURE 8.

Detection of steps in experimental and simulated data. Experimentally measured cargo motion in single motor and multi-motor assays was analyzed using the χ² method and histograms of detected steps are shown in panels a and b, respectively. Note the skewed appearance of the multimotor step histogram. Additionally, 18 simulated runs of 50 steps each with all 8-nm steps and all 4-nm steps and SD6 level noise were also analyzed with the χ² method. Two rate-limiting steps were assumed when generating the stepping datasets. Aggregate histograms of detected steps for all 8-nm steps and all 4-nm are shown in panels c and d, respectively. Methods: Taxol-stabilized microtubules were prepared as previously described (3). Kinesin assay was prepared as previously described (21). Data was acquired as described in Vershinin et al. (21) with custom software and procedures as described in main text.

TABLE 2.

Comparison of parameters used needed for different methods

Wavelet	VT	T-test	χ2
Prefilter rank	Prefilter rank		Prefilter rank
Dyadic scale range	Window size	Window size	Step joining range
Threshold level	Threshold level	Threshold level	Number of steps

For rough guidance, the ease with which a given parameter can be optimally set is represented by shading (darker shading represents parameters which are harder to set). The more sensitive the method to a given parameter, the harder it is to set optimally. Note that the easiest parameters to set are the number of steps for the χ² method (where robust guidance for setting the parameter is available) and the dyadic scale range for the wavelet method (since the method is not very sensitive to this setting). On the other hand, optimally setting thresholds for the wavelet, VT, and t-test methods is difficult, especially when little a priori knowledge about the data is available.

The average step sizes obtained via the χ² step detection method were statistically distinct: 7.6 ± 3.3 nm for multimotor and 9.0 ± 3.6 nm for single motor (mean ± SD; either the two-sample t-test or skewness insensitive two-sample rank-sum test give p < 0.0005). We calculated the skewness of the single and multiple motor distributions to be −0.02 and 0.12, respectively (Bowley skewness (27), zero for normal distribution). These findings lead us to conclude that beads moved by single and multiple kinesin motors move in different ways. For the multiple-motor driven beads, the steps were smaller than the expected 8 nm, but there was no clear peak of 4 nm steps. Sample tracks with χ² fits appear in Supplementary Fig. 10 (adjusting position for linkage compliance).

To interpret this difference, we looked at a variety of simulated data under different assumptions, to determine which classes of models could give rise to what we observed. To effectively compare experiments and theory, we needed to evaluate the amount of noise present. The effective noise was not constant. The noise is difficult to exactly measure for moving beads close to the center of the trap, but we estimate it to be ∼SD7 for single motor case and ∼SD5 for multiple motor case. At high load (examining portions of the record where the bead was apparently stationary), we measure the noise to be ∼SD 4.4 nm for a single motor beads, and ∼SD 3.6 nm for the multiple motor beads. The average noise is therefore above SD3, and below SD7.

We generated simulated data consisting of all 8-nm steps, various combinations of 4- and 8-nm steps, and all 4-nm steps, added different amounts of noise (noise levels from SD4 to SD6), and then analyzed the resulting data sets exactly as we had analyzed the real experimental data. As expected, regardless of the noise used (up to SD6), the simulated 8-nm only histogram matched the experimental single-motor bead data quite well (compare Fig. 8, a–c). However, almost all combinations of 4- and 8-nm, regardless of the added noise, did not match the multiple-motor experimental histogram—in each case, either the distribution peaked at 8-nm, was double peaked at ∼4- and 8-nm, or was flat from 4- to-8 nm, instead of showing a sharp rise at ∼3.5-nm, peaking at 6.5-nm, and then a gradual decline (some examples in Supplementary Fig. 11).

The only simulated scenario we tried that generated a histogram similar to the experimentally measured one was to assume all 4-nm steps, in the presence of ∼SD6 noise (compare Fig. 8, panel b to panel d). Both histograms are skewed, have the same sharp rise starting at ∼3.5-nm, peak at about the same location (∼6.5-nm), and then gradually decline. The key observation then is that the experimentally observed histogram is not consistent with the all 8-nm steps hypothesis but can arise if the cargo center of mass moves in 4-nm steps. We note that the magnitude of noise used above (SD6) is higher than typically observed in multiple motor assays, suggesting that our experimental data may reflect a more complex scenario. For instance, the center of mass of the bead may be moving with variable sub-8-nm steps centered on 4 nm, with occasional 8-nm steps. Crucially, these more complex assumptions are generally consistent with the hypothesis that the activity of individual motors is uncorrelated. We can thus safely conclude that when kinesin motors move at saturating ATP under low to moderate load, they do not move in lock-step.

DISCUSSION

On selecting parameters for best performance

Proper setting of the parameters is a difficult problem. For the VT and dG wavelet methods we have three parameters (two for t-test, since filtering does not improve performance) to determine window size, threshold, and filter rank. All of these parameters are linked; raising filter rank can lower the window size needed for best performance, which may cause the best threshold level to change. Given a selection of filter rank and window size, it may be possible to select the best threshold using a graph of total steps detected versus threshold (see Fig. 2 and Supplementary Figs. 5 and 6), although this becomes impossible at higher noise levels.

We have developed a “sweep” method that makes it possible to select a best window size, using either plots of number of steps versus threshold for multiple windows (selecting the one where the plateau is most clear, see Supplementary Fig. 4) or the use of a simulated dataset with similar properties to the dataset to be analyzed as options for setting these parameters. Generalizing our choices made here using simulated data, larger windows work better for datasets with lower mean velocity and filtering allows the use of smaller step-location windows than would be optimal with no filter.

Relative to these other methods, the χ² method has a distinct advantage: it has only two parameters to set—the expected number of steps and filter rank—and there is a straightforward way of deciding what value should be used for the expected number of steps. Additionally, while the χ² method benefits from filtering, it appears (Fig. 6) that high levels of filtering are generally undesirable, somewhat simplifying decisions on what filter rank to use. For the χ² method we can show that with modest (SD3) noise, if one selects more steps than are actually present but then combines nearby steps, one gets good step detection results. This indicates that the method has a tendency to split steps that are actually there when ordered to find too many steps. So, provided we expect most steps to be well separated, we can combine close steps to get a better record. Therefore, our process for adding a window (five frames for all but the kinesin analysis, where we used 11 frames, based upon testing with a stuck bead moved in 8-nm steps by a piezoelectric stage) has a practical value beyond allowing us to compare it with the other methods. With this low “window size” the χ² method was still as good at resisting noise and finding steps as the VT and t-test methods using larger window sizes. This smaller window size is partly responsible for the χ² method's superior performance in finding single steps. We note that for extremely long records (>100,000 frames), the χ² method has decreased performance. Specifically, there appears to be increased “jitter” in the temporal location of steps. This performance dropoff can be compensated for by increasing the window size. However, it may be advisable to split the data sets into smaller segments instead, since no analytical method has been found to aid in setting window size.

From our sample data we see a few trends. The VT and t-test methods % found and % correct were fairly insensitive to the window size, as measured by overall performance, although larger windows will lead to loss of temporal sensitivity (see Fig. 2 and Supplementary Fig. 6). For these two methods there is a balance point where improvement to % found and % correct due to larger window size is offset by the decreased temporal sensitivity. For the dG wavelet method (Supplementary Fig. 5), there was an optimal dyadic scale—on either side of which performance slowly falls off (particularly % correct and % 8's, indicating a loss of temporal sensitivity and a greater vulnerability to detecting noise as steps). Finally, the χ² method performance is fairly flat, given that nearby steps are combined as described above and that the number of steps it is ordered to find is within ∼10% over the peak value in the S versus number of steps graph (see Fig. 1).

Choice of filter and positives and negatives involved with their use

The performance of the examined methods is often improved by applying some form of prefiltering (t-test method is the notable exception). The mean filter was found to be most beneficial with the CK nonlinear filter usually being a close second. Filters do have one negative effect—they decrease the ability of methods to separately identify closely spaced steps (see Supplementary Tables 2 and 3). In general, when there are, on average, more frames between steps, higher filter rank is beneficial (e.g., for the VT method, mean filter of rank 2 is best at low frames/step, but at 782 frames/step a mean filter of rank 6 is more appropriate; data not shown). The exception is the χ² method, for which it is generally best to keep the filter power low, even at high numbers of frames between steps.

Finding individual steps: what can realistically be expected?

The simplest model of molecular motor function assumes a single rate-limiting step, and thus motor stepping can be described by a Poisson process,

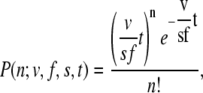where P is the probability that n steps occur in t frames, v is velocity, f is the number of frames per second, and s is the step size (28). For a Poisson process, the distribution of wait times will be a decaying exponential (28). This means that the probability of very short times between steps can be fairly high. For this reason, there is some real, finite probability of finding more than one step in the time necessary for step detection (several frames), or even a single frame. This probability can be reduced to near zero for slowly moving motors or for very high frame rates (frames per step becomes large), which is hinted at in Fig. 6.

Below, and in the Supplementary Material, we develop a theoretical description of what can be expected. The average number of steps per frame is calculated by dividing the velocity by the product of the step size and the frame rate. Since we are not capable of detecting events that occur faster than our sample time (time per frame), the equation above is set up to measure time in number of frames. If we take t = 1 frame we can calculate the probability of 0, 1, or more steps occurring in any single frame. If we had perfect step detection (able to differentiate steps that occurred in adjacent frames), this would give the approximate step size distribution observed.

In the Supplementary Material, this type of approach is extended to more realistic cases where several frames with no motion are necessary to allow differentiation of two steps. Doing so allows us to make some quantitative predictions about the step distribution we expect from step detection. For instance, as measured directly from the dataset a record with 200 total steps made at 30 FPS, 10 nm/s with 8-nm steps has a step distribution of 140 single, 25 double, two triple, and one quadruple (when steps within four frames of another step are merged). The predicted distribution for these conditions would be 137.5 singles, 23.5 doubles, 4.0 triples, and 0.7 quadruple. Reporting only steps determined to be correct, the χ² method at SD3 finds 130 singles, 20 doubles, and one triple (at this noise level, the χ² method should find ∼90% of steps).

This is the reason why “cherry picking” of data is dangerous. If only especially clear steps are analyzed we would expect enrichment in double steps, as they will be more likely to rise above the noise. Even for relatively high frame/step rates we may still observe 10% (∼80 frames/step) or more of all steps as multiples, possibly significantly more if we have already biased our search by only looking at the best. Even at that 10% rate, we may expect to see adjacent doubles 1% of the time. Two possible approaches can be taken to appropriately investigate the presence or absence of steps with a magnitude different from 8 nm. First, we perform step detection on as much of our dataset as possible, with unanalyzed portions being rejected following simple rules (e.g., remove regions where the detector is not well calibrated and portions where the motor is stalled, etc.). Second, we can predict based on mean velocity and record duration how many 16-nm steps we would expect to observe if the motor only takes 8-nm steps. Then, if the observations lead to a count for 16-nm steps dramatically exceeding these expectations (exact amount would depend on the number expected since the process is stochastic), it may be valid to say the motor is taking 16-nm steps.

Naturally, we can use this approach in reverse to plan experiments, and also to help interpret observations. For instance, if we believe we are dealing with a single motor which acts as a simple Poisson stepper, then given the maximum velocity typically reported for in vivo motors (1000–1500 nm/s (29), 1500 nm/s used here), an assumed step size (constant 8 nm used here) and presuming we want at least 67% of all steps to be ideally detectable as singles, we can predict we would need a frame rate of ∼1500 FPS. Similarly, to detect 80% singles requires ∼2500 FPS. We would need ∼10,000 FPS before we would reasonably expect to be able to detect 95% of all steps as singles. It is therefore perfectly natural that in any realistic data set some multiples of the motor step size will be observed. The significance they have is entirely in the relative percentages.

Detecting variable step size

Generally, if the number of detected (a posteriori) 16-nm steps changes between an experiment and a control by some percentage, this does not imply an equal percentage change in the number of a priori steps (misdetection due to noise and blurring together of nearby steps is mostly to blame). Fig. 7 reveals, however, that it is indeed possible to detect the presence of 16-nm steps in a background of 8's, or even of 16-nm and 24-nm alongside 8-nm steps. While differences between, e.g., ∼40% and ∼60% 16's may be difficult to quantify, the difference between 0% 16 and as little as 20% 16's is very clear.

Detection of steps other than 8-nm multiples in multi-kinesin data

The ability of all methods surveyed here to detect 8-nm steps falls off dramatically as noise level rises close to SD 4 nm (Figs. 3 and 5). Therefore, for good detection of a step, we desire the standard deviation of the noise be half the step size or less. This also extends to detection of different step sizes—we would need the noise to be at most half the difference in step sizes for robust detection. Experimentally, under small to moderate load, our actual noise levels observed are approximately SD 5-nm, which makes detection of 4 nm steps extremely challenging. We do, however, expect the step size distribution to be disturbed if 4-nm steps are present in sufficient numbers.

There was indeed a striking difference between single kinesin and multiple-kinesin driven beads. In the former case, clear 8 nm steps could be clearly and frequently observed. In the latter case, we observed long stretches of time when motion appeared smooth, presumably because the stepwise motion of the bead's center of mass was too fine to be distinguished from noise. Note that the asynchronous stepping of two kinesins is expected to displace the bead's center of mass 4 nm at a time. This is close to the noise level in our recordings, which makes clean detection of these and smaller steps difficult. Nonetheless, a key difference between the two cases is revealed by the histogram of detected step sizes. Histograms for both cases show a single peak but the shape of the peak is different and the peak for the multiple motor case is shifted to lower average value. Therefore, one clear conclusion from this study is that when the cargo is not close to stall, the motors frequently do not step synchronously. We created simulated data sets with 4-nm and 8-nm steps and examined the histogram of steps identified (Fig. 8). We see a significant similarity between the measured multiple motor stepping size histogram and the histogram of found steps for data simulated to have 4-nm steps and SD6 noise. Additionally, the measured single motor histogram and the histogram of found steps for simulated data with 8-nm steps and SD6 noise appear similar. Thus, for all possible noise levels in our experiments, the distribution of steps found experimentally cannot be explained due to 8 nm steps with high noise, but instead reflects the predominant presence of sub-8 nm steps.

While further work will be required to determine the details of how multiple motors function together, the small step behavior of the bead's center of mass observed in vitro already has ramifications for in vivo studies of stepping cargos—if the cargo is moved by multiple motors, the steps observed in cargo motion records may be smaller than the displacements of each individual motor. Therefore, without knowing the number of motors moving a cargo, simply observing a cargo moving in 8-nm steps (7,30,31) only establishes that each underlying motor is taking at least 8-nm steps. The steps of individual motors may well be larger than 8 nm.

CONCLUSION

Most step detection methods examined had similar performance levels. The VT, t-test, and χ² methods had almost identical % found and % correct. The χ² method was superior for temporal resolution, however (greater % 8's than VT and t-test, similar to dG wavelet). The χ² method is easier to set. It only had one parameter (two if a filter is used), the other methods each have two parameters (three if a filter is used). Filters help, but they also tend to add some degree of blur between nearby steps, decreasing temporal resolution. A high FPS to velocity ratio (frames per step) is important if one is trying to determine if 8- and 16-nm steps are both present in a single record (provided certain assumptions about the motor kinematics are met). Given this is taken into account, it should be possible to identify when a significant percentage of 16 nm steps are present. We also find clear evidence that multiple kinesin motors driving a single bead are not forced into lock step under the observed range of forces (<5 pN), and future work will be required to more fully investigate how multiple motors function together.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.