Spatially discordant voltage alternans cause wavebreaks in ventricular fibrillation

Abstract

BACKGROUND

Ventricular fibrillation (VF) is characterized by complex ECG patterns emanating from multiple, short-lived, reentrant electrical waves. The incessant breakup and creation of new daughter waves (wavebreaks) perpetuate VF. Dispersion of refractoriness (static or dynamic) has been implicated as a mechanism underlying wavebreaks.

OBJECTIVE

The purpose of this study was to investigate the mechanisms underlying wavefront instability in VF by localizing wave fractionation sites (the appearance of multiple waves) and their relationship to local spatial dispersion of voltage (V_m) oscillations.

METHODS

Wave fractionations were identified by tracking V_m oscillations optically at unprecedented spatial (100 × 100 pixels) and temporal (2,000 frames per second) resolution using a CMOS camera viewing the surface (1 × 1 cm²) of perfused guinea pig hearts (n = 6). VF was induced by burst stimulation, and wavefront dynamics were highlighted using region-based image analysis to automatically detect wavebreaks. Direct detection of wavebreak locations by image analysis was more reliable than the phase reconstruction method because baseline noise obstructed the correct identification of phase singularities by detecting false-positives.

RESULTS

Wave fractionations (34 ± 4 splits/s·cm²) fell into three categories: decremental conduction (49% ± 7%), wave collisions (32% ± 8%), and wavebreaks (17 ± 2%). Wavebreaks occurred at a frequency of 5.8 ± 1 splits/s·cm² and did not preferentially occur at anatomic obstacles (i.e., coronary vessels) but coincided with discordant alternans where V_m amplitudes and durations shifted from high to low to from low to high on opposite sides of wavebreak sites.

CONCLUSION

Spatial discordant alternans cause wavebreaks most likely because they are sites of abrupt dispersion of refractoriness.

Introduction

The complex patterns of electrical activity recorded in ventricular fibrillation (VF) are caused by multiple, short-lived, reentrant circuits that are continuously created and annihilated.^1,2 The splitting of wavefronts into daughter waves (i.e., wavebreaks) that perpetuate VF may occur when wavefronts meet anatomic and/or functional obstacles that cause unidirectional conduction blocks that form new reentrant circuits. For this reason, in order to understand VF one first must understand the mechanism(s) that cause wavebreaks.

Anatomic obstacles or structural barrier have been studied mostly in diseased heart. For example in hearts with augmented fibrosis, the severity of fibrosis has been linked to enhanced vulnerability for fibrillation.^3,4 In general, anatomic obstacles tend to enhance arrhythmia vulnerability by altering tissue excitability, which can either anchor reentrant circuits and rotors about a pivot point or promote wavefront instabilities that lead to wavebreaks.⁵ Anatomic obstacles also may act by slowing down conduction velocity, particularly at short cycle lengths or following a premature beat, which links restitution of conduction velocity to arrhythmia vulnerability. For instance, patients with cardiomyopathy exhibit prolonged conduction delays during premature beats.⁶ Optical mapping studies on structurally normal hearts⁷ suggested that the cores of reentrant circuits are not randomly located but tend to be clustered on anatomic landmarks such as the large coronary vessels. However, little is known regarding the conditions whereby anatomic obstacles promote the anchoring of a reentrant circuit or wavebreaks in the fibrillating heart.

Besides anatomic obstacles, enhanced dispersion of refractoriness has been implicated as a mechanism responsible for unidirectional conduction blocks that lead to the formation of reentry and complex activation patterns in VF. Gradients of repolarization can result from intrinsic spatial heterogeneities of ionic channel expression,^8,9 alterations of ion channel expression elicited by hormones, or remodeling caused by an infarct.^10,11 In addition, dynamic changes in refractoriness (restitution kinetics) have been extensively investigated as a potential factor promoting wavefront instability and creation of new rotating waves.^12–14 Premature cardiac contractions lead to shortening of action potential (AP) durations (APDs), and the slopes of restitution curves are often used as a predictor of VF (restitution hypothesis). However, the causal relationship between APD restitution and wavebreaks in VF has not been clearly demonstrated and often is disputed.^15,16

The purpose of this study was to apply digital image analysis to detect wavebreaks using a combination of exceptionally high spatial and temporal resolution and to correlate the location of wave fractionations to local dispersion of repolarization, anatomic landmarks (e.g., large coronary vessels), and other obstacles. It is important to point out that a fast sampling rate (≥1,000 frames per second), high spatial resolution (~100 × 100 μm²), and sufficiently high signal-to-noise ratio all are critical to identifying wave fractionation sites accurately and measuring the electrical properties of the myocardium at adjacent sites. We recorded transmembrane potentials (V_m) using a voltage-sensitive dye and a high-speed CMOS camera at an unprecedented combination of spatial and temporal resolution: 2,000 frames per second with 100 × 100 pixels (100 × 100 μm² of tissue per pixel). Wave fractionations were automatically detected during VF, and their locations were correlated to anatomic features, fiber orientation, and spatial alternations of V_m at the wave fractionation sites.

Methods

Heart preparations

Guinea pigs (all male, >450 g) were anesthetized with pentobarbital 45 mg/kg intraperitoneally and injected with heparin 200 U/kg. Hearts were excised, cannulated, placed in a chamber designed to abate movement artifacts, and retrogradely perfused through the aorta with a solution of the following composition (in mM): 130 NaCl, 24 NaHCO₃, 1.25 CaCl_2, 1.0 MgCl₂, 4.0 KCl, 1.2 NaH₂PO₄, 5 dextrose, and 20 mannitol; pH 7.4, gassed with 95% O₂ and 5% CO₂. The investigation conformed to the current Guide for Care and Use of Laboratory Animals published by the National Institutes of Health.

Temperature was maintained at 37.0°C ± 0.2°C, and perfusion pressure was adjusted to 65–70 mmHg with a peristaltic pump (AD Instruments, Colorado Springs, CO, USA). Hearts were stained with the voltage-sensitive dye di-4 ANEPPS (40 μL of 1 mg/mL dimethylsulfoxide [DMSO]) and were not exposed to chemical uncouplers to block contractions. VF was induced by a burst of stimuli (120 pulses, 35-ms intervals) delivered through Ag⁺/AgCl electrodes located on the left ventricle. Once VF was induced, stimulation was stopped, and data were collected with the camera a few minutes after onset of VF.

Optical apparatus

The optical apparatus was previously described.¹⁷ In brief, light from two 100-W tungsten-halogen lamps was collimated, passed through 520 ± 30 nm interference filters, and illuminated the heart from two sides for uniform illumination. Fluorescence emitted from the stained heart was collected with two camera lenses (50 mm f/1.2 mm Nikon and 50 mm f/0.95 Navitar, Figure 1A). Fluorescence emission was passed through 610-nm cutoff filter (Omega Optical, Brattleboro, VT, USA) and focused on a 100 × 100 pixel CMOS camera (Ultima, Scimedia, Ltd., Tokyo, Japan) scanned at 2,000 frames per second. Pixel resolution was 100 × 100 μm², and data were recorded and stored in intervals of 4 – 8 second. Typical optical recordings of V_m during VF are shown in Figure 1. The signal-to-noise ratio was calculated from the ratio of the maximum V_m amplitude divided by the standard deviation of the noise level. Because the V_m fluorescence recordings in VF show continuous oscillations, the noise level was calculated from a short period of time typically in a 20-ms time interval during stable phases of V_m.

Figure 1.

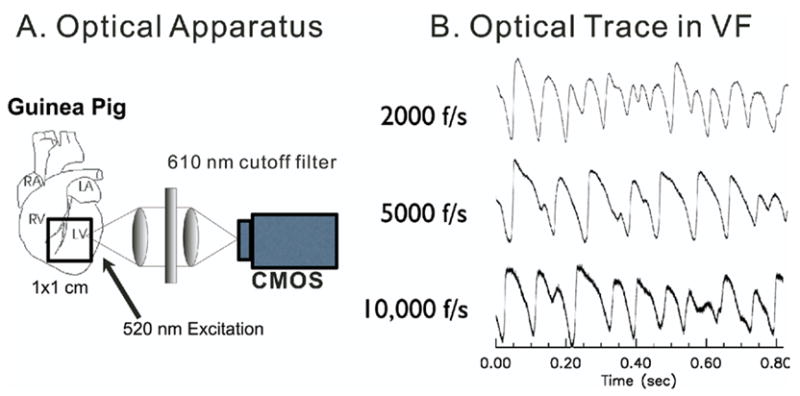
Optical apparatus. Transmembrane potentials were imaged optically using a 100 × 100 CMOS camera at up to 10,000 frames per second (0.1-ms resolution). A: Orientation of field of view and schematics of optical apparatus. B: Sample traces at 2,000, 5,000, and 10,000 frames per second. Signal-to-noise ratio was 81:1, 47:1, and 21:1 respectively.

Phase reconstruction analysis

Phase reconstruction analysis was performed as previously reported.¹⁸ Time delay τ was chosen to be 12 ms where autocorrelation crosses the zero line.¹⁸ Fluorescence signals (F(t)) were filtered using a gaussian filter (11-ms window), and F(t) vs F(t+τ) was plotted to visualize the trajectory of reconstructed phases. The phase angle was calculated using θ(t) = arctan(F(t+τ) − F*, F(t) − F*), where F* is the origin. F* was set to the mean values of F(t).¹⁸ In contrast with previous reports,¹⁸ the angles of trajectories calculated from our data did not always increase but often decreased mostly during small V_m oscillations. During a 4-second interval of VF, we quantified the ratio of the trajectory with positive to negative angles by taking the cross-product between sequential time points to determine positive vs negative values of the cross-products, which were counted and represented as percentages.

Detection of wavebreaks

Wavefronts were tracked in time and wavebreaks were detected by locating sites where a single wavefront splits into multiple wavelets, using a modified version of a method previously described by Rogers et al¹⁹ for multiple electrode recordings. Wavefronts can be readily tracked using digital image analysis routines because the fluorescence from voltage-sensitive dyes represents the actual transmembrane potential in that region of the heart. Detection of wavebreaks was based on a three-step protocol: (1) segmentation of individual waves, (2) detection of waves that split into multiple daughter wavelets, and (3) identification of wavebreak locations (Figure 2).

Figure 2.

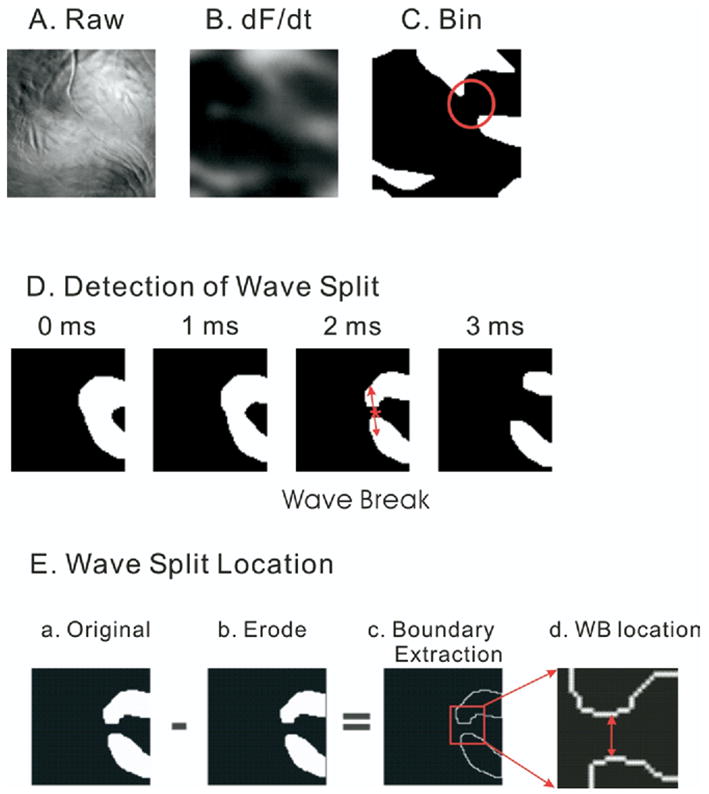
Wave split detection. Wavelets were isolated from the first derivatives of transmembrane potentials, and the split of single wave into multiple wavelets was automatically detected (see Methods). A: Raw image. B: First derivatives. C: Binary image. D: Split of wavefronts. A sequence of wavefront images is shown in a 1-ms interval. Here, a single wavefront splits into two wavefronts. Note that once the split occurs at the 2-ms time frame, the waves spread apart rapidly and are more than 15 pixels apart within 1 ms (see 3-ms frame). This highlights the need for a frame rate of 2,000 frames per second. E: Detection of wave split location. The original wavefront image (panel a) is subtracted by the same image after applying the erode operator (panel b) to produce an image of the edges of the wavefronts (panel c). The boundary pixel extraction (panel c) generated by subtracting the eroded image (panel c) from the original image (panel a) was used to determine the wave split location by selecting the midpoint between the edges of the daughter wavelets (panel d, see Methods).

Segmentations of individual waves

To isolate wavefronts in VF from fluorescence images (Figure 2A), the first derivative of each trace was calculated by convolution of 13-point polynomials. The first derivative of fluorescence images (Figure 2B) then were converted into binary images to enhance the contrast between each wavefront and the adjacent background (Figure 2C). To reduce false-positives where background noise can be incorrectly detected as a wavefront, a probability at the given pixel was calculated by applying a gaussian kernel to 3 × 3 neighboring pixels, and the threshold was set to a level three times the standard deviation of the background noise. Individual wavefronts were identified by a blob-coloring algorithm.²⁰ The dimensions of each blob or reentrant circuit were estimated by calculating the number of pixels in that contiguous region. Reentrant waves encompassing fewer than nine pixels were considered as noise and removed from the analysis. In addition, wavefronts were tracked in at least three consecutive images (i.e., 1.5 ms), and the wavefronts that lasted for fewer than four consecutive images were removed from the analysis.

Wave split detection

Wavebreak is defined as the separation of one propagating wave into multiple waves in the next image (Figure 2D). Even at sampling rates of 2,000 frames per second, daughter waves emanating from a common wave spread apart by >0.1 mm in 0.5 ms. Thus, it was important to sample at 2,000 frames to accurately identify the locations of wavebreaks that were taken to be the midpoint between the two new “daughter” wavefronts, at the earliest time when the daughter wavefronts were closest to each other. Figure 2E delineates the steps used to automate the calculation of the midpoint between daughter waves. The edge of wavefronts was identified by applying an “erode” operator (shrinking image, Figure 2E, panel b) then subtracting the eroded region from the original region (Figure 2E, panel a), resulting in a boundary extraction (Figure 2E, panel c). As shown in Figure 2E, panel c and d, the smaller subset of edge pixels makes possible the accurate determination of the midpoint pixel between two waves where the distance from the midpoint to the edge of wavefronts is the shortest. The accuracy of the midpoint or wavebreak location is within a region of 3 × 3 pixels or 300 × 300 μm². A detailed discussion of the morphologic operator including erosion and dilation operators was given by Gonzales and Woods.²⁰

Categorization of wave fractionation

Wave fractionations fell in one of three categories: (1) collisions, when two waves were annihilated in the middle due to collision of two waves— detected by existence of two waves propagating toward the fractionation point in the previous frame, (2) decremental conduction, when the amplitude of action potentials or V_m signals became gradually smaller after a split then disappeared— detected by gradual decay of dF/dt amplitude in the following three frames, or (3) wavebreaks, when the wavefront encountered a zone of nonexcitable tissue, resulting in wave annihilation and the creation of two wavelets.

Comparison of digital image and phase singularity algorithms

The wavebreak detection algorithm was compared to the detection of phase singularities by applying the two algorithms on computer-simulated VF data to avoid possible complications due to camera noise and motion artifact. The computer simulation was based on a canine ventricular myocyte model.¹⁴ Simulations were performed on a two-dimensional sheet of 500 × 500 nodes, the integration time step was set to 0.025 ms, and V_m distribution was saved at every 1-ms interval.²¹ Calculations were performed using optimized C routines compiled by an IBM XLC compiler on a dual G5 Macintosh and the result visualized by Yorick (http://yorick.sourceforge.net).

Figure 3 shows an example of wavebreak detection using the two methods. First V_m is simulated during VF to yield a “Raw Image” (Figure 3, panel A), then first-derivative and high-contrast binary images are generated to identify wavefronts (panels B and C, respectively). The red arrows point at the location of a wavebreak. Panels C and D show the detection of a wave splitting into two waves using digital image analysis routines. Panel E shows the phase map reconstructed from the time embedded method with a time delay of 3 ms. The locations of phase singularities were marked with asterisks, detected by the curl of the spatial phase gradient.²² As expected, the wavebreak forms two phase singularities with opposite chirality (panel E).

Figure 3.

Comparison of wavebreak (WB) detection algorithms. WB locations were detected by digital image analysis routines and compared to detection of WBs by the time-embedding phase reconstruction method³⁵ by applying the two algorithms to the computer simulation data based on a canine ventricular model.²⁵ A: Snapshot of V_m from computer-simulated ventricular fibrillation (VF) data (black to white represents the range of V_m from polarized to depolarized). B: Map of the first derivative of V_m (dF/dt), which is used to identify activation time points and visualize wavefronts during VF. C: Binary image of dF/dt taken from panel B. D: WB location detected by digital image analysis routines. E: Phase map. Phase singularities are marked with asterisk. Red arrow indicates an example of a WB that created two phase singularities with opposite chirality. F: Superimposed traces of V_m from neighboring pixels surrounding the WB point shown in panel D. G: Map of WB locations. WBs detected with phase singularity algorithm are marked with asterisks. WBs detected by digital image routines are marked with open triangles. H: Histogram of distance between WBs detected by the two methods. Average distance was 2.8 ± 2.1 pixels (n = 185 WBs).

Panel G is the cumulative plot of wavebreaks detected by the two methods: phase singularities (*) and wavebreaks by image analysis routines (Δ). In general, the two methods were in agreement with respect to the distribution of wavebreak locations (see Supplementary Video 1 for detection of wavebreaks using the two methods). Small differences that occurred were mostly due to (1) false-positive detection of wavebreaks by the phase singularity method as previously reported by another group²³ and (2) ability of the wave split method to detect wavebreaks located near the edges of the field of view because of ambiguities in determining the direction of wave propagation. Despite these limitations, the average error between the two methods was within three pixels (see histogram in Figure 3, panel H).

Data analysis and statistical analysis

Activation and APD maps were generated using (dF/dt)_max and (d²F/dt²)_max as described previously.²⁴ Typically, several waves coexisted and meandered in complicated patterns, which made it difficult to track their propagation pathways continuously. Therefore, wave propagations were followed and mapped for 400-ms intervals, which is ~10 times the average lifespan of reentrant circuits in guinea pig hearts.¹⁷ VF frequency maps were generated by calculating the power spectral density at each pixel, and the maximum frequency was mapped at 1-Hz intervals. VF maps were displayed such that the darker the gray area, the higher the VF frequency. The bandwidth of power spectral density was estimated by calculating the standard deviation of the power spectrum from each pixel and displayed as a contour map where the darker the area, the larger the VF frequency bandwidth.

Wave splits that occurred near the outer edge of the field of view were disregarded and removed from the analysis because of the difficulty in distinguishing waves that propagated out of view from true wave splits. Data points that corresponded to wavebreak sites were analyzed for statistical significance using Ripley’s K function.²⁵ The neighbors of a wavebreak point i, K_i(r) are all the points located at a distance less than or equal to a given distance r. When the process is spatially homogeneous, K(r) is proportional to πr². Ripley’s K function is defined as follows:

$$L(r)=\sqrt{K(r)/\pi r^2}.$$

If L(r) is linear, this suggests a random spatial distribution of wavebreaks with no clustering.

The angles of wavefronts were considered as axial data. Circular mean and dispersion were calculated from 2θ, then divided by 2 as previously described for axial data analysis.²⁶ To test the uniformity of axial data, the Rayleigh test was performed. The Rayleigh test is a likelihood ratio test when alternative hypothesis is a unimodal distribution with unknown mean direction and unknown mean resultant length ||R||, that is, Fisher distribution. Here, R is the resultant vector:

$$R=(\sum _{i}cos{\alpha }_i,\sum _{i}sin{\alpha }_i),$$

where α_i is an axial data point.

Because the uniform distribution can be viewed as a special case of the Fisher distribution, a test of uniformity is equivalent to checking if the precision constant in the Fisher distribution is zero. The critical region of the likelihood ratio test can be written as follows:

$$\text{R}>\text{K\hspace{0.17em}for\hspace{0.17em}some\hspace{0.17em}constant\hspace{0.17em}K}.$$

Ripley’s K function and the Rayleigh tests were performed using a statistical package R available online (www.r-project.org).

Results

Patterns of wave propagation in VF

Figure 1 shows the schematics of our optical apparatus and typical examples of transmembrane potentials (V_m) recorded optically using di-4 ANEPPS and a high-speed CMOS camera. Figure 1B shows examples of raw traces that were recorded at 2,000, 5,000, and 10,000 frames per second from the anterior region of the heart. Such traces were recorded routinely with excellent signal-to-noise ratio throughout the epicardium. At 2,000 frames per second and a field-of view of 100 × 100 μm² of tissue, V_m oscillations were recorded with a signal-to-noise ratio >70:1 (Figure 1B).

We previously had shown that activation maps in VF were highly complex, varying from beat to beat with no apparent repetitive patterns, but we were criticized because of the low spatial resolution of our 16 × 16 element photodiode array (Hamamatsu Inc.).²⁷ Here, we reexamined activation maps in VF at higher spatial and temporal resolution of 100 × 100 μm² and 0.5 ms, respectively (Figure 4). Again, activation patterns were seemingly random, with no discernible repetitive sequence between consecutive propagations waves (panel C), which is in agreement with our earlier observation.²⁸

Figure 4.

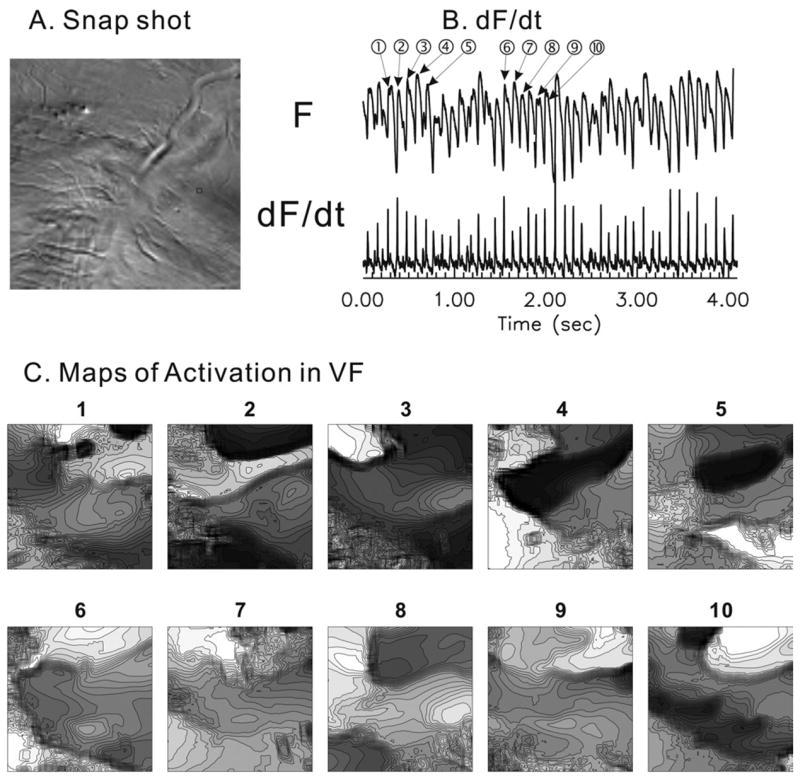
High-resolution activation maps in ventricular fibrillation (VF). A: Raw image. B: Typical example of fluorescence signal and its first derivatives. C: Consecutive activation maps. Lines are drawn every 1 ms. Brighter color means earlier activation. No clear repetitive activation patterns were observed, as previously described in this animal model of VF.¹⁷,²⁸

Comparison of wavebreak detection by image analysis vs phase reconstruction algorithms

In previous reports, the location of wavebreaks was correlated to the location of phase singularities detected using time-embedded phase reconstruction methods.²⁹ The direct detection of wavebreaks by image analysis was in agreement with the detection of phase singularities (Figure 3 and Supplemental Video 1) when the two methods were compared using idealized simulated V_m oscillation in VF. However, the phase reconstruction algorithm was considerably less accurate when applied to experimental data where the signal-to-noise ratio and baseline drift (due to fluctuations of light intensity, dye washout, and motion artifacts) can influence the identification of phase singularities. Figure 5 shows typical examples of phase trajectory in reconstructed phase state space in [F(t), F(t+τ)]. The time delay of τ was chosen when autocorrelation of F(t) first crosses zero (zero autocorrelation method).¹⁸ Note that phase loops often formed outside of the origin. We further examined how often the phase trajectory formed a loop outside the origin by calculating the phase angle and the ratio of time during which the angle increased/decreased (see Methods). Most of the time (91% ± 2%, n = 4 hearts), the phase trajectory rotated clockwise around the origin (phase decreased); however, during a significant portion of time (9% ± 2%), the trajectory rotated counterclockwise (phase increased). The apparent increase of phase (opposite direction) was not due to actual counterclockwise rotation around the origin but occurred because the origin was outside of the phase loop. Figure 5 (panels B and C) illustrates the cause of apparent clockwise rotation of phase loop. Panel B shows phase loops from relatively regular AP oscillations, and loops are formed around the origin (red Δ). However, when AP oscillations are irregular with numerous small depolarizations, the phase loops often formed below or above the origin (panel C), resulting in incorrect phase values.

Figure 5.

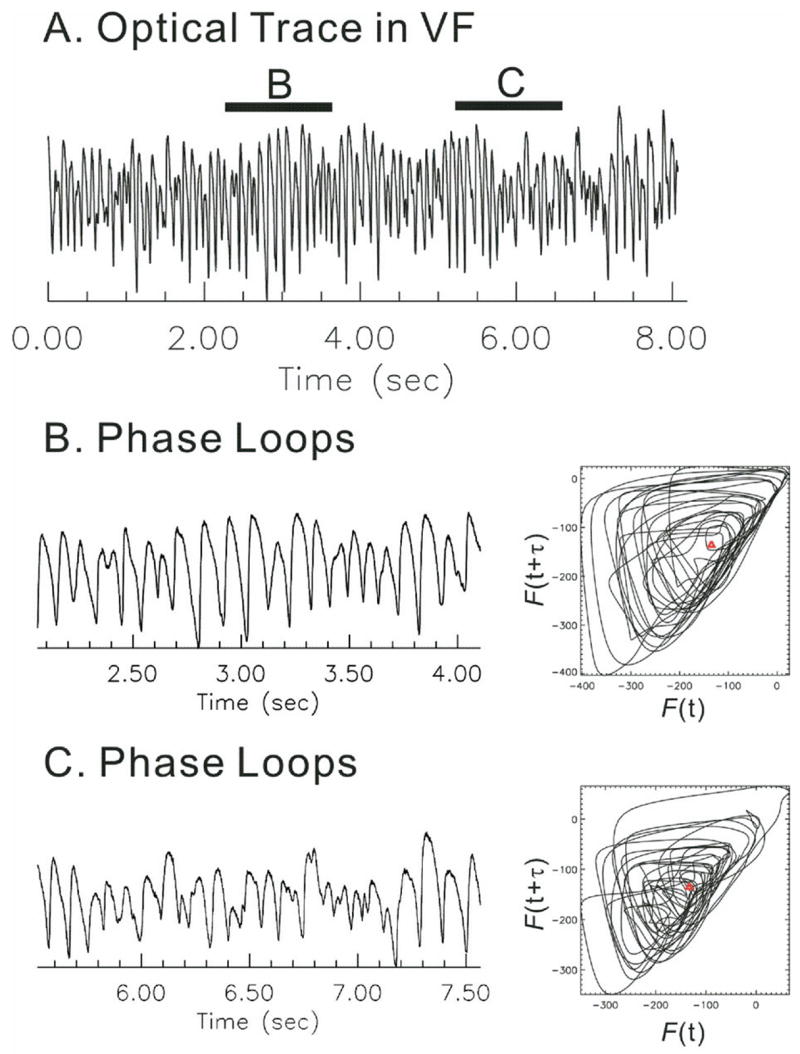
Phase loops and calculation of phase angle. Calculation of phase was performed using time-embedding methods. A two-dimensional state space was reconstructed from [F(t), F(t+τ)].¹⁸ A: Sample trace of a fluorescence V_m signal recorded during ventricular fibrillation (VF). B: Phase loops derived from an interval of VF with large-amplitude V_m oscillations. Phase trajectory consisted of loops rotating clockwise around the origin (red ρ). C: Phase loops derived from an interval of V_m oscillations with small, irregular amplitudes. Note that phase loops fell often outside the origin (red ρ). Time delay (τ) was set to 12 ms.¹⁸

Another potential source of errors for the phase reconstruction algorithm is the calculation of phase angles in the presence of baseline drift. To test the influence of baseline drift on the detection of phase singularities, a sinusoidal oscillation was injected (20-mV peak amplitude and 0.5-Hz frequency) in simulated V_m data during VF, and detection of wavebreaks was repeated using image analysis and phase reconstruction algorithms. Insertion of baseline drift increased the number of false wavebreaks detected by the phase reconstruction method to 13% of total WBs (Supplementary Video 2 and Supplementary Figure 1) compared to the analysis without drift (Supplementary Video 1), whereas image routines detected a 4% increase in false-positives (compare Supplementary Videos 1 and 2).

Mechanisms underlying wavebreaks

Instead of detecting phase singularities, we used digital image analysis to track wavefronts in VF and to detect wavebreaks because this method does not require phase calculations and can be used to investigate wavefront instabilities without the uncertainties of phase reconstruction analysis. Wave fractionations were frequently observed (34 ± 4 splits/s · cm²) and fell in one of three categories: (1) collisions, (2) decremental conduction, or (3) wavebreaks. These three types of events were associated with markedly different features at neighboring pixels, adjacent to the sites of wave fractionation. Figure 6 shows examples of these three categories: collision (panel A), decremental conduction (panel B), and wavebreaks (panel C; Supplementary Video 3). In panel A, wave fractionation was caused by a wave collision where all V_m signals from the neighboring pixels were similar and had large amplitudes and durations, like normal action potentials (red arrow). In panel B, wave fractionation was caused by decremental conduction, where V_m depolarizations at all the neighboring sites had small V_m amplitudes, in sharp contrast with wave collisions (compare panels A and B). In decremental conduction, newly formed wavelets failed to propagate past the fractionation site and were annihilated rapidly. This decremental conduction mechanism may correspond to “fibrillatory” conduction as described for the “mother rotor” hypothesis.³⁰ In panel C, wave fractionation was caused by wavebreak, where the wavefront encountered a heterogeneous recovery of excitability caused by a spatially discordant dispersion of V_m oscillations at adjacent sites. The new waves arising from the wave fractionation exhibited a gradual dispersion of depolarization amplitudes (panel C, red arrow). In the latter case, the daughter waves had a longer lifespan and propagated more effectively to the rest of the heart. From an analysis of 12 seconds of VF per heart (n = 6 hearts), the most common mechanism was “decremental conduction,” composing 49% ± 7% of all forms of wave fractionations, followed by “collisions” (32% ± 8%) and lastly by “wavebreaks by dispersion of V_m” (17% ± 2%).

Figure 6.

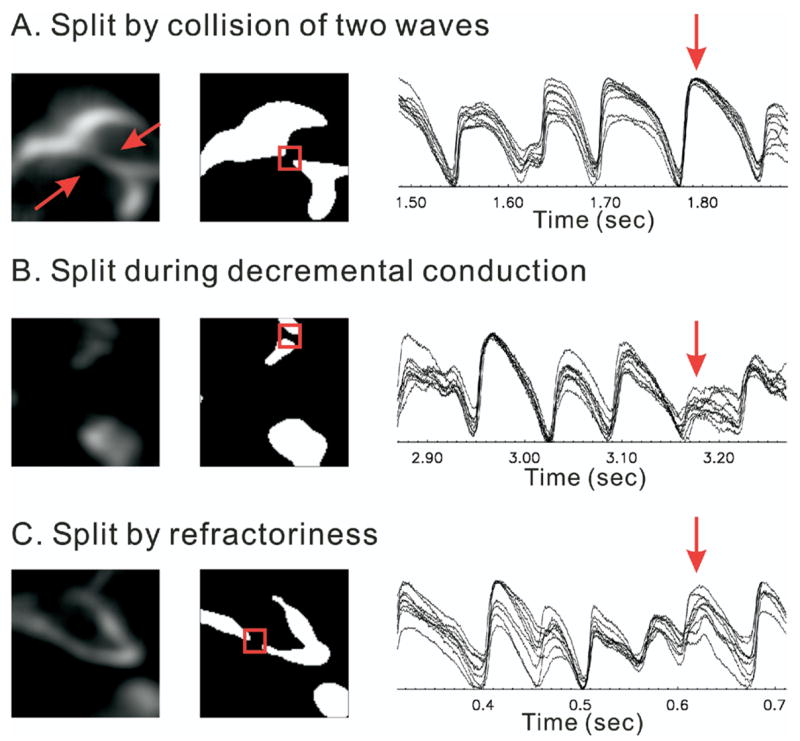
Types of wave splits. Splits of waves are observed when two waves collide, a propagating wave meets heterogeneous refractoriness, or during decremental conduction. Neighboring pixels show different action potential amplitudes and recoveries in different types of wave splits. A: Wave collisions. The action potentials show full amplitude in all the neighboring pixels. B: Decremental conduction. All the neighboring pixels show very small depolarizations. C: Heterogeneous repolarization. In this case, recovery from the previous depolarization is different in the neighbors, causing various amplitudes of action potentials.

Spatial distribution of wave fractionations

We previously reported that VF frequencies are higher at the apex than at the base and that the frequency distribution on the epicardium was statistically correlated to the gradient of AP durations recorded in the same guinea pig hearts under sinus rhythm.^17,28 The latter study used an imaging system with suitable temporal resolution, but the findings were questioned because of the low spatial resolution (16 × 16 photodiode array). We reexamined VF frequency distribution at high spatial and temporal resolution using the CMOS camera. Figure 7 shows the results from a single heart analyzed for three episodes of VF, each lasting 4 seconds for a total of 12 seconds of VF. Panel A shows an image of the anterior surface of the heart recorded by the CMOS camera. Panels B and C are maps of power spectral density and their bandwidth. Note that VF frequencies detected at the apex are higher than at the base, which is in agreement with the photodiode array data.²⁸

Figure 7.

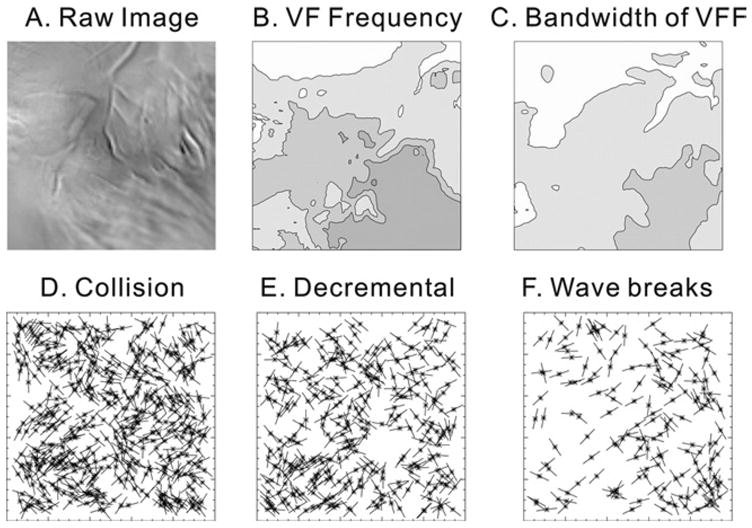
Wavebreak locations. A: Raw image. B: Power spectral density map. Power spectral density was calculated from all the pixels and mapped as described in the Methods. Contour lines are drawn every 1 Hz from 11–16 Hz. C: Bandwidth map of power spectral density (1-Hz isolines, 4–6 Hz). D: Sites of collision. Locations are marked with an asterisk and line for the tangent angles of wavefronts. E: Sites of wave split during decremental conduction. F: Sites of wavebreaks due to dispersion of repolarization at the site of wavebreaks. None of the cases showed possible relationship with Fast Fourier Transformation (FFT) distribution in panel B.

To determine if wave splits (or fractionations) occurred preferentially at anatomic obstacles or correlated with a particular range of frequencies, the x-y position and angle of each wavefront were extracted and their distribution patterns analyzed as described in the Methods. Figure 7, panels D, E, and F mapped the sites of wave splits caused by collision, decremental conduction, or, wavebreaks associated with V_m dispersion, respectively. There was no apparent visual correlation between the locations of wave fractionations and coronary vessels or correlation with high versus low VF frequencies. A more rigorous mathematical analysis using Ripley’s K function failed to expose a clustering of wave splits for all three categories. Thus, the wave split locations did not show evidence of reproducible or recurring patterns for >5 minutes of VF, indicating that wavebreaks did not preferentially occur in a specific region. To test the possibility of a preferential angle of wavefront propagation at the time of wave splits, the Rayleigh test of uniformity was performed on angular data of wavefront (see Methods). Only wavebreaks caused by “V_m dispersion” exhibited a statistically significant nonuniformity, with a preferential direction at a mean angle of 15.44° and a mean vector length of 0.22, which were aligned parallel to the longitudinal axis of epicardial fibers (panel D, collision: P = 0.31, panel E decremental conduction: P = 0.40, and panel F dispersion: P = 0.01, n = 6 hearts, 4 seconds of VF each).

Dispersion of AP recovery and wavebreaks

Spatial dispersions of V_m, (i.e., as in Figure 6C) that were associated with wavebreaks displayed a range of characteristics with respect to gradient of AP amplitudes and/or durations in the pixels adjacent to the wavebreak sites. To determine how spatial gradients of V_m influenced the occurrence and location of wavebreaks, we characterized V_m in adjacent regions of myocardium immediately before the occurrence of a wavebreak. From a visual inspection of 113 episodes of wavebreaks related to V_m dispersion, three types of V_m dispersions were identified in the eight neighboring pixels (Figure 8). Panel A shows an example of spatially discordant AP alternations, where neighboring pixels started “in phase” with similar shapes and amplitudes of AP (at the beginning of the trace), then small depolarizations (black arrow) caused spatially discordant alternations of AP amplitude, immediately before the wavebreak (red arrow). Panel B shows an example of wavebreaks where the previous depolarizations had no evidence of V_m dispersion among the eight neighboring pixels (black arrow), then there was an abrupt spatial dispersion of AP durations immediately prior to the wavebreak. The abrupt depolarization gradient at the time of wavebreak may have been due to the earlier “out-of-phase” AP alternations at the 7.2- to 7.3-second time points. Note that the blue trace in panel B exhibited an increase in the amplitude of AP alternations, and again V_m oscillations were “out of phase” with respect to the red trace, as in panel A. Wavebreak in panel C did not exhibit obvious discordant/out-of-phase alternations, yet small (most likely electrotonic) depolarization (black arrow) immediately before the occurrence of wavebreak may have produced an APD gradient on opposite sides of the wavebreak site, causing unidirectional conduction block.

Figure 8.

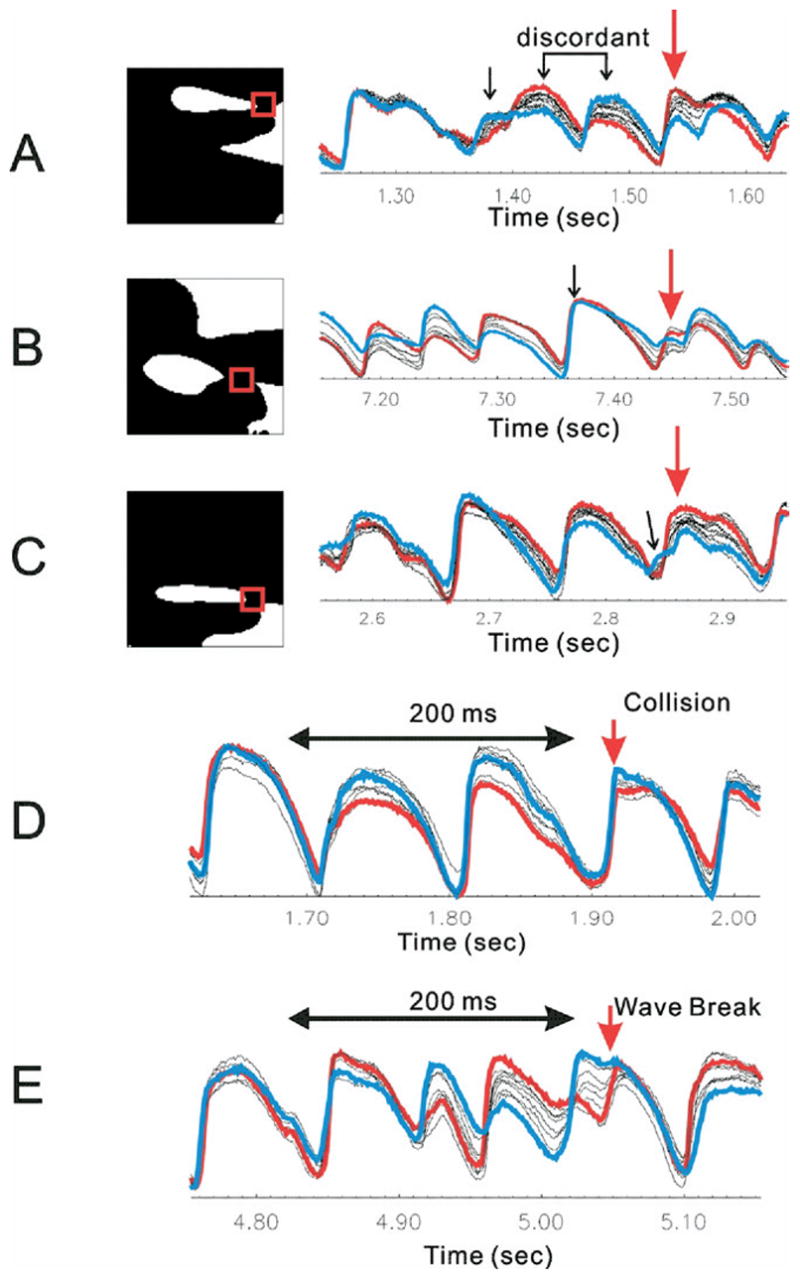
Traces from neighboring pixels of wavebreak location. Binary images of wavebreaks are shown in the left column, and traces from eight pixels around the wavebreak location (red box) are superimposed in the right column to show dispersion of repolarization at the site and time of wavebreaks. Blue lines are traces from the front of wavebreaks. Red lines are traces from the back of wavebreaks. A: V_m depolarizations started with approximately similar amplitudes but progressed into heterogeneous alternation of amplitude (spatially discordant) and eventually conduction blocks (red arrow). B: V_m recovery at the time of wavebreaks is heterogeneous, causing wavebreaks. Note that the blue trace oscillates large- and small-amplitude V_m depolarizations, and the final beat came under the refractoriness. C: Traces did not show alternations of amplitude. Instead, small V_m depolarization (black arrow) causes refractoriness at the site of wavebreak. The degree of local synchronization was calculated using cross-correlation among neighboring pixels. Cross-correlations from 200-ms traces were calculated from all possible pairs of eight neighboring pixels, and minimum correlation was chosen to represent dispersion of V_m oscillations. Traces in blue and red represent the pair of minimum correlation. D: In the case of collisions, V_m traces were synchronized before the wave split. Minimum correlation was 0.59 ± 0.05 (n= 5). E: In the case of wavebreaks. V_m traces were highly asynchronous, with out-of-phase alternation. Minimum correlation was 0.47 ± 0.05, which was significantly lower than for collisions (n = 5, P = .012).

The relationship between spatially discordant or asynchronous oscillations of V_m and the occurrence of wavebreaks was investigated further by statistical analysis to determine if the occurrence of discordant V_m oscillations at wavebreak sites were coincidental events or mechanistically linked processes. The link between these two processes was assessed by calculating the correlation of V_m oscillations between neighboring pixels with that of wavebreaks or collisions (Figure 8, panel D and E). V_m signals recorded during 200-ms intervals of VF were extracted from the eight neighboring pixels at the site of wavebreak, and cross-correlations of all the possible pairs of traces were calculated (₈C₂ = 28 pairs from eight neighboring pixels). The minimum correlation among pairs of traces was chosen to represent the degree of asynchrony of V_m oscillations, which is equivalent to the maximum spatial dispersion of V_m. Figure 8 (panels D and E) illustrates a segment of traces and calculations of cross-correlation. A time window of 200 ms was chosen because it would be sufficient to include at least two or three previous V_m depolarizations or AP upstrokes. The minimum correlation was observed from pairs of traces with the most different V_m amplitudes and phases (see red and blue traces in panels D and E). Note that V_m oscillations are more asynchronous at the site of wavebreak (panel E) compared with collision (panel D). Summary data from five hearts (4 seconds of VF for each heart) showed that the minimum correlation among pixels was 0.59 ± 0.05 at sites of wave collision (as in Figure 8D) and 0.47 ± 0.06 at sites of wavebreaks (as in Figure 8E, paired t test: P = .012).

To determine if dispersions of V_m cause wavebreaks, we tested whether or not dispersions of V_m occurred only at times and sites where wavebreaks occurred. The minimum correlation (i.e., the maximum dispersion of V_m) was calculated at random time points for the eight neighboring pixels surrounding wavebreak sites. The minimum correlation measured for five random time points per wavebreak was 0.59 ± 0.03 (n = 5 hearts), which is larger in value than the correlation for wavebreaks and closer to the correlation for collision sites. The analysis provides compelling evidence that asynchronous V_m oscillations or spatially discordant V_m alternans cause wavebreaks.

Discussion

The complexity of ECG pattern in VF has been attributed to the instability of wavefronts and subsequent wavebreaks. As a result, considerable attention has been given to the identification of wavebreak sites, the potential mechanisms that promote wavebreaks, and their correlation with anatomic landmarks or dynamic changes of refractoriness (restitution). In this study, V_m oscillations in VF were recorded using a high-speed CMOS camera (100 × 100 pixels, 2,000 frames per second) with high signal-to-noise ratio (>70:1). All the traces shown here are raw traces without spatial or temporal filtering, such that the high signal-to-noise ratio made it possible to examine the shape and time course of AP at and near wavebreak sites.

Detection of wavebreaks

Complex electrical waves in VF were thought to be due to the continuous creation and annihilation of waves. Therefore, it is critical to first detect and quantify wavebreaks to examine the electrical properties of the myocardium before the occurrence of wavebreaks in an attempt to elucidate the mechanisms leading to the creation of new waves and maintenance of VF. In some studies, wavebreaks were identified by detecting the point where the activation (i.e., wavefront) of a wave joined with the repolarization (i.e., wave back) of another wave.³¹ In this algorithm, wavefronts and wave backs were determined by 50% cutoff value. Another approach applied more sophisticated phase analysis based on time-embedding methods.²⁹ The locations of wavebreaks were found to be well correlated to the locations of phase singularities, which has provided the rationale to use a phase singularity algorithm as a surrogate for detecting wavebreaks.²⁹

However, such a method was not applicable to our data (Figure 5) because our recordings had numerous intervals of small V_m oscillations, and assigning a phase to such small depolarizations would often be incorrect. It could be that our recordings contained more small-amplitude V_m oscillations compared with other studies that reported a high degree of correlation between phase singularities and wavebvreaks.²⁹ Several possibilities could account for small V_m oscillations in our VF recordings: (1) the recordings were not entirely free of motion artifacts, which may have caused slow baseline drifts; (2) the high spatial resolution images had detailed texture of the heart, which may have enhanced V_m errors caused by motion; (3) small depolarizations could be due to wavefronts coming from deeper layers of tissue; and (4) fluorescence signals were not from a single cell, but the sum of several cells and small depolarization can be due to three-dimensional scrolls that subsequently could hinder phase calculation. Alternatively, one can reasonably argue that motion artifacts tend to increase, not decrease, fluorescence signals and that intervals of small V_m oscillations are important components of VF dynamics, not an artifact. In that case, it would be important to include them correctly in an analysis of wavebreaks.

An alternative approach to phase singularities is detection of fractionation of wavefronts. Rogers et al¹⁹ isolated individual wavefronts from an array of unipolar electrodes by grouping together adjacent active electrogram recordings and checking whether or not a single wavefront split into multiple wavefronts. Here, we applied a similar algorithm to high-resolution optical maps where the signals are proportional to the actual V_m changes. Wavefronts were isolated from the maximum first derivatives of optical signals (dF/dt)_max, which offers several advantages: (1) the texture of the heart, such as vessels and fiber orientation, diminishes V_m amplitudes but has no effect on activation times; (2) distortions of signals by photobleaching, dye washout, or motion artifacts have minimal effect on (dF/dt)_max; and (3) the wavefront and the sharp edge of local (dF/dt)_max can be detected automatically to obtain the angle or curvature of each wavefront. The sites of wave splits were automatically detected using a digital image analysis algorithm. As a result, the exact location of wave collision and fractionation could be determined within ±100 μm and an accuracy of 0.5 ms, making possible the application of more detailed analyses.

Mechanisms underlying wavebreaks

Wavebreaks can occur when wavefronts collide with an obstacle, but the occurrence of such events depends on the excitability of tissue, the size of the obstacle, and the curvature of the wavefronts. Obstacles can be either anatomic or functional. In the present study, wavebreaks in the heart seem to occur when wavefronts encounter zones of refractoriness created by passage of the previous activation. Traces near the site of wavebreaks (within 600 μm) showed markedly different recovery phases compared with the previous activation, which suggests that wavebreaks are caused by dynamic changes of refractoriness. These results are in excellent agreement with an earlier study by Lee et al,³¹ who investigated wavebreak mechanisms using optical mapping technique (300 × 300 μm² spatial and 3.75-ms temporal resolution) and found that the majority of wavebreaks (~80%) were caused by head-to-tail interactions when propagating wavefront encounters residual refractoriness.³¹

There was no clear relationship between wavebreak locations and VF frequency distributions or coronary vessels, reinforcing the interpretation that the majority of wavebreaks occurred due to refractoriness. By inspecting neighboring traces near wavebreak sites, it appears that dispersion of refractoriness was caused by oscillations of AP amplitude with dynamic changes in APD. Correlation analysis showed that V_m oscillations were highly asynchronous right before wavebreaks occurred. Moreover, spatially discordant (out-of-phase) alternation of AP amplitudes was frequently observed, leading to enhanced dispersion of refractoriness and a higher propensity to conduction blocks.

The restitution hypothesis predicts that a small perturbation in APD can result in larger APD changes on a beat-to-beat basis (i.e., alternans), which would increase the vulnerability to unidirectional conduction block and wave breakups.^2,32 Alternans can be spatially discordant, where the phase of alternation can be out of phase with different region of heart.^33,34 Such discordant alternans increases the dispersion of refractoriness and the propensity to conduction blocks. Our data provide robust evidence that spatially discordant dispersion of V_m oscillations or AP amplitudes causes wavebreaks in VF.

Watanabe et al³⁵ proposed two other mechanisms of generation of discordant alternans: (1) conduction velocity oscillations or (2) enhanced dispersion of diastolic intervals produced by ectopic foci. Our data suggest that small depolarizations (Figure 8C) often precede the onset of alternation or conduction blocks, which may be related to the dispersion of diastolic interval mechanism, as suggested by Watanabe et al.³⁵ Of note, the traces shown in Figure 8 have not been filtered (neither spatially nor temporally) so that the small depolarization signals can be detected and can be relied upon to represent an actual shift in V_m.

Although local dispersion of refractoriness and discordant alternation clearly precede most wavebreaks in our experiments, the role of restitution kinetics in influencing discordant alternans remains uncertain. Huang et al³⁶ investigated APD restitution kinetics using multiple autoregression analysis of APD as a function of previous diastolic intervals and APDs and found that the correlation drops to 0.39 in VF, suggesting the existence of other important modulation mechanisms in VF. In the present study, we tested AP amplitude analysis because of uncertainties in measurements of APD in VF and obtained a low correlation coefficient of 0.52 ± 0.17 (n = 4 hearts) compared with pacing, in agreement with Huang et al.³⁶ The low correlation in VF probably is due to the more substantial influence of electrotonic effects during collisions (Figure 6A) and small depolarizations (Figure 8, panels A and C) that have not been incorporated in the multiple regression analysis.

VF frequency distribution

Spatial organization of VF has been the subject of intense investigation to better understand the mechanisms underlying maintenance of VF. Based on the assumption that rotating waves can be detected as a periodic source, VFs were often analyzed in the frequency domain to investigate their spatial distributions.^17,37 VF frequency distributions can be discrete, with large regions of hearts sharing a single stable frequency.³⁷ Other investigators, including our group, found that a VF frequency does not remain pinned to a certain region of the heart but instead changes rapidly, within 1 second.^17,38 Spatial and temporal resolution of the optical instruments have been raised as a possible explanation for these discrepancies. In this study, power spectral density maps obtained with the CMOS camera, which so far has the best combination of high spatial and temporal resolution (Figure 7B), produced similar patterns as those obtained using photodiode arrays.²⁸ These findings suggest that the different spatial resolutions of the CMOS and the diode arrays were a negligible factor in studying VF frequencies. A possible explanation for the discrepancies in VF frequencies and distributions could be the different types of VF analyzed by various groups.³⁹ In addition, species differences may exhibit different VF dynamics; for example, guinea pig cardiac myocyte lack I_to, which may influence VF frequencies. Additional studies are required to identify the differences in experimental conditions and their impact on modifying the mechanisms leading to different types of VFs.

Study limitations

In this study, optical recordings were limited to the anterior region of heart, and this region was chosen because it allows us to view simultaneously the right and left ventricles while providing a relatively flat region of ventricle that can be more easily focused across the surface of the CMOS sensor. As with all current optical mapping studies, deeper layers of myocardium could not be examined for possible preferential locations of wavebreaks. All experiments were performed in continuously perfused small heart (guinea pigs), and mechanisms underlying wavebreaks may differ in different species, in ischemia, in failing hearts, or in hearts with chronic infarcts. V_m recordings were limited to 4 seconds of continuous recordings because of the memory size of the apparatus. As a result of brief recording times, the number of wavebreaks detected in each time interval was small and may reduce the statistical power of an analysis carried over long uninterrupted periods of recordings in VF.

Appendix

Supplementary Video 1

Supplementary data associated with this article can be found, in the online version, at doi: 10.1016/j.hrthm.2007.03.037.