Cross-correlation of instantaneous phase increments in pressure-flow fluctuations: Applications to cerebral autoregulation

Abstract

We investigate the relationship between the blood flow velocities (BFV) in the middle cerebral arteries and beat-to-beat blood pressure (BP) recorded from a finger in healthy and post-stroke subjects during the quasisteady state after perturbation for four different physiologic conditions: supine rest, head-up tilt, hyperventilation, and CO₂ rebreathing in upright position. To evaluate whether instantaneous BP changes in the steady state are coupled with instantaneous changes in the BFV, we compare dynamical patterns in the instantaneous phases of these signals, obtained from the Hilbert transform, as a function of time. We find that in post-stroke subjects the instantaneous phase increments of BP and BFV exhibit well-pronounced patterns that remain stable in time for all four physiologic conditions, while in healthy subjects these patterns are different, less pronounced, and more variable. We propose an approach based on the cross-correlation of the instantaneous phase increments to quantify the coupling between BP and BFV signals. We find that the maximum correlation strength is different for the two groups and for the different conditions. For healthy subjects the amplitude of the cross-correlation between the instantaneous phase increments of BP and BFV is small and attenuates within 3−5 heartbeats. In contrast, for post-stroke subjects, this amplitude is significantly larger and cross-correlations persist up to 20 heartbeats. Further, we show that the instantaneous phase increments of BP and BFV are cross-correlated even within a single heartbeat cycle. We compare the results of our approach with three complementary methods: direct BP-BFV cross-correlation, transfer function analysis, and phase synchronization analysis. Our findings provide insight into the mechanism of cerebral vascular control in healthy subjects, suggesting that this control mechanism may involve rapid adjustments (within a heartbeat) of the cerebral vessels, so that BFV remains steady in response to changes in peripheral BP.

I. INTRODUCTION

Cerebral autoregulation (CA) is the ability of cerebral blood vessels to maintain steady cerebral perfusion in response to fluctuations of systemic blood pressure (BP), postural changes, or metabolic demands. This regulatory mechanism is known to operate over a range of blood pressure values (e.g., 80−150 mm Hg) [1] and on time scales of a few heartbeats [2]. The long-term CA compensates for chronic BP elevations and metabolic demands [3]. Ischemic stroke is associated with an impairment of autoregulation [4,5], which may permanently affect cerebrovascular reactivity to chemical and blood pressure stimuli [6,7]. With impaired CA, the cerebral blood flow follows BP fluctuations, posing a risk of insufficient blood supply to the brain during transient reductions in peripheral BP. Therefore, evaluating the effectiveness of CA is of great interest, given the clinical implications.

Traditional experimental methods evaluating the mechanism of CA require time-consuming invasive procedures [8,9] and are focused on long-term BP and blood flow velocity (BFV) characteristics such as the mean, lacking descriptors of the temporal BP-BFV relationship. To address this problem, an alternative “dynamic” approach has been proposed [10] to quantify CA using transcranial Doppler ultrasound during the transient responses in cerebral BFV to the rapid BP changes induced experimentally by thigh cuff inflation, Valsalva maneuver, tilt-up, or a change in posture [3,11]. The autoregulation indices derived from this approach may be more sensitive to indicators of hypoperfusion after stroke [12].

The analytic methods evaluating the dynamics of cerebral autoregulation are currently based on mathematical modeling and Fourier transform analysis [13]. The Fourier-transform-based transfer function method has been widely used [2]. This method estimates the relative cross spectrum between BP and BFV signals in the frequency domain. The dynamic indices of autoregulation, based on Fourier transform methods, presume (i) signal stationarity (i.e., the mean and standard deviation of the signal are stable and remain invariant under a time shift) and (ii) a linear BP-BFV relationship. However, physiologic signals are often nonstationary, reflecting transient responses to physiologic stimuli [14]. The effect of this nonstationarity on the results obtained from the transfer function analysis has not been carefully assessed in previous studies.

Here we investigate the dynamics of the BP-BFV relationship when the system reaches a quasisteady state after an initial perturbation. While studies traditionally have focused on the response in BFV to transient changes in BP [3], we hypothesize that spontaneous physiologic fluctuations during the quasisteady state, which is characterized by the absence of physiologic stimuli or constant level of stimulation, may also contain important information about the CA mechanism.

Our focus on fluctuations in the BP and BFV is motivated by previous work which has demonstrated that physiologic fluctuations contain important information about the underlying mechanisms of physiologic control. Robust temporal organization was reported for the fluctuations characterizing cardiac dynamics (interbeat intervals) [15−22], respiratory dynamics (interbreath intervals) [23−27], locomotion (gait, fore-arm motion) [28−33], and brain dynamics [34−36]. Moreover, it has been demonstrated that physiologic fluctuations carry information reflecting the coupling between different physiologic systems; e.g., correlations in the heartbeat change with physical activity [37,38], with wake and sleep [39], during different sleep stages [40−43], and even different circadian phases [44]. BP and BFV signals are impacted by the heartbeat, and thus one can expect that fluctuations in BP and BFV may reflect modulation in the underlying mechanisms of control. Previous studies have focused on the transitional changes in BP and BFV in response to abrupt perturbation of the physiologic state—e.g., rapid switch from supine to tilt. In contrast, we focus on the dynamical characteristics of BP and BFV signals after the initial perturbation, when the system has reached a quasisteady state during which there is no change in physiologic stimuli. Further, we hypothesize that certain dynamical characteristics of the fluctuations in BP and BFV at the steady state, and how these characteristics change for different physiologic conditions, may reflect aspects of the underlying mechanism of CA. For example, under normal CA the fluctuations of the BFV in healthy subjects at the steady state may relate to high-frequency adjustments (even within a single heartbeat) of the diameter of the cerebral blood vessels, while loss of CA after stroke may lead to impaired vascular dilation or contraction associated with reduced fluctuations in BFV.

To test this hypothesis, we measure BP and BFV signals from healthy and post-stroke subjects during four physiologic conditions: supine, tilt, hyperventilation, and CO₂ rebreathing in upright position. We apply several complementary methods to quantify the dynamical BP-BFV relationship in these quasisteady conditions—transfer function analysis and cross-correlation and phase synchronization analyses—and we compare these methods with our method of cross-correlation between the instantaneous phase increments of BP and BFV signals. Interactions between peripheral circulation (beat-to-beat BP) and cerebral vasoregulation [BFV in the middle cerebral artery (MCA)] can be modeled as the dynamic synchronization of two coupled nonlinear systems. Specifically, we hypothesize that the CA mechanism may also involve adjustments in the cerebral vascular tone to spontaneous changes in BP that may be present within a single heartbeat even when the system is in the steady state and there are no significant changes in the mean blood pressure.

The synchronization phenomenon was first observed by Huygens for two coupled pendulum clocks [45], and since then, it has been found in many physical and biological systems where two or more coupled subsystems interact [46−52]. Alternatively, synchronization may also be triggered by the influence of external noisy or regular fields [53,54]. In recent years, the concept of synchronization has been widely used to study the coupling of oscillating systems, leading to the discovery of phase synchronization in nonidentical coupled systems in which the instantaneous phases are synchronized, while their instantaneous amplitudes remain uncorrelated [55−58]. Such phase synchronization has been empirically discovered in a range of physical and physiological systems [59,60]. Specifically, studies have found coupling between the cardiac rhythm and other systems: phase synchronization was observed between the heartbeat and respiration during normal conditions [61] and during respiratory sinus arrhythmia [62,63], change of cardiorespiratory phase synchronization with newborns’ age [64], and with the level of anaesthesia [65]. Phase analysis methods have been used to probe spatial synchronization of oscillations in blood distribution systems [66], between cortical centers during migraine [67], as well as between certain brain areas and muscle activity of the limbs [68].

In this study we evaluate the time-domain characteristics of both the amplitudes and instantaneous phases of the BP and BFV, which can be considered as two interacting subsystems within the CA mechanism. To determine the characteristics of the coupling between BP and BFV in healthy subjects, and how they change with stroke, we analyze the cross-correlation between the instantaneous phase increments of these two signals. We find that this cross-correlation is much stronger for post-stroke subjects, indicating increased synchronization between BP and BFV, which suggests an impaired mechanism of the CA. We compare the results of the instantaneous phase increment cross-correlation analysis with those obtained from several complementary methods including the transfer function, cross-correlation, and phase synchronization analyses.

II. METHODS

A. Study groups

We obtain data from the Autonomic Nervous System Laboratory at the Department of Neurology at The Ohio State University and from the SAFE (Syncope and Falls in the Elderly) Laboratory at the Beth Israel Deaconess Medical Center at Harvard Medical School. All subjects have signed informed consent, approved by the Institutional Review Boards. Demographic characteristics are summarized in Table I. Control group: 11 healthy subjects (age 48.2±8.7 years). Stroke group: 13 subjects with a first minor ischemic stroke (>2 months after acute onset) (age 52.8±7.1 years). Post-stroke subjects have a documented infarct affecting <1/3 of the vascular territory as determined by MRI or CT with a minor neurological deficit (modified Rankin score scale <3). The side of the lesion is determined by neurological evaluation and confirmed with MRI and CT. The lesion is in the right hemisphere in five of the subjects and in the left hemisphere in eight of the subjects. Normal carotid Doppler ultrasound study is required for participation. Patients with hemorrhagic strokes, clinically important cardiac disease including major arrhythmias, diabetes, and any other systemic illness are excluded. All subjects are carefully screened with a medical history and physical and laboratory examination.

TABLE I.

Demographic characteristics.

Variable	Demographic characteristics
				Control			Stroke
Men/women				4/7			7/6
Age
(mean±SD)				48.2±8.7			52.8±7.1
Race W/AA				10/1			12/1
Stroke side							5/8
(Right/left)

Group (mean±SD)	Supine		Tilt		Hyperventilation		CO2 rebreathing		Statistics (P values)
	Control	Stroke	Control	Stroke	Control	Stroke	Control	Stroke
BP (mm Hg)	96.4±20.9	101.0±20.6	93.1±20.1	105.9±22.5	94.2±19.7	105.4±22.0	97.6±21.7	108.8±22.7	0.66a	0.0005b
BFV-MCAR/Normal side (cm/s)	66.0±18.7	55.2±18.0	57.3±18.1	49.7±18.5	40.3±15.7	39.8±14.9	54.7±21.9	56.3±21.5	<0.0001a	0.77b
BFV-MCAL/Stroke side (cm/s)	63.5±19.6	51.1±19.0	54.8±17.1	51.5±19.3	40.8±14.9	41.0±17.9	54.6±21.5	57.4±23.3	<0.0001a	0.008b
CO2 (mm Hg)	33.5±6.0	37.7±4.9	32.0±3.6	32.5±2.5	21.0±4.5	23.5±8.0	34.6±7.2	33.2±6.5	<0.0001a	0.28b
CVRc-MCAR/Normal side	1.54±0.45	1.96±0.54	1.75±0.53	2.28±0.93	2.68±1.10	3.00±1.28	1.97±0.61	2.17±0.83	0.0001a	0.007b
CVR-MCAL/Stroke side	1.59±0.56	1.97±0.65	1.79±0.61	2.29±0.83	2.57±0.90	3.04±1.60	1.96±0.56	2.19±0.94	0.0001a	0.01b

^aP value between physiologic conditions comparisons.

^bP value between groups comparisons.

^cCVR (cerebral vascular resistance) is defined as mean BP/BFV.

B. Experimental protocol

All subjects have participated in the following experimental protocol.

1. Base-line supine rest—normal breathing (normocapnia): Subject rests in supine position for 5 min on a tilt table.

2. Head-up tilt—upright normocapnia: The tilt table is moved upright to an 80° angle. The subject remains in upright position for 5 min and is breathing spontaneously.

3. Hyperventilation—upright hypocapnia: The subject is asked to breathe rapidly at ≈1 Hz frequency for 3 min in an upright position. Hyperventilation induces hypocapnia (reduced carbon dioxide), which is associated with cerebral vasoconstriction.

4. CO₂ rebreathing—upright hypercapnia: The subject is asked to breath a mixture of air and 5% CO₂ from rebreathing circuit at a comfortable frequency for 3 min in an upright position. CO₂ rebreathing increases carbon dioxide above normal levels and induces hypercapnia, which is associated with vasodilatation.

The mechanism of CA is at least partially related to the coupling between metabolic demands and oxygen supply to the brain [3]. Carbon dioxide (CO₂) is one of the most potent chemical regulators of cerebral vasoreactivity. Head-up tilt provides both pressure and chemical stimulus—BFV and CO₂ decline in upright position, reflecting the change in intracranial pressure and shifting autoregulatory curve towards lower BP values. There is a linear relationship between CO₂ values and cerebral blood flow: hypocapnia (through hyper-ventilation) causes vasoconstriction and thus decreases the blood flow, and hypercapnia (through CO₂ rebreathing) causes vasodilatation and increases the blood flow in the brain [3].

C. Data acquisition

We perform experiments in the morning or more than 2 h after the last meal. We measure the electrocardiogram from a modified standard lead II or III using a SpaceLab Monitor (SpaceLab Medical Inc., Issaquah, WA). We record beat-to-beat BP from a finger with a Finapres device (Ohmeda Monitoring Systems, Englewood, CO), which is based on a photoplethysmographic volume clamp method. During the study protocol, we verify BP by arterial tonometry. With finger position at the heart level and temperature kept constant, the Finapres device can reliably track intraarterial BP changes over prolonged periods of time. We measure the respiratory wave forms with a nasal thermistor. We measure CO₂ from a mask using an infrared end tidal volume CO₂ monitor (Datex Ohmeda, Madison, WI). We insonate the right and left MCA’s from the temporal windows, by placing the 2-MHz probe in the temporal area above the zygomatic arch using a transcranial Doppler ultrasonography system (MultiDop X4, DWL Neuroscan Inc, Sterling, VA). Each probe is positioned to record the maximal BFV and is fixed at a desired angle using a three-dimensional positioning system attached to the light-metal probe holder. Special attention is given to stabilizing the probes, since their steady position is crucial for reliable, continuous BFV recordings. BFV and all cardiovascular analog signals are continuously acquired on a beat-to-beat basis and stored for off-line post-processing. We visually inspect the data and remove occasional extrasystoles and outlier data points using linear interpolation. We use the Fourier transform of the Doppler shift (the difference between the frequency of the emitted signal and the echo frequency of the reflected signal) to calculate BFV. BFV’s in the MCA correlate with invasive measurements of blood flow with xenon clearance, laser Doppler flux, and positron emission tomography [69−71]. Since the MCA diameter is relatively constant under physiological conditions [72], BFV can be used for blood flow estimates.

D. Statistical analyses

We use the multiple analysis of variance (MANOVA) with 2×4 design for the two groups (control and stroke) and for four physiologic conditions (supine, tilt, hyperventilation, and CO₂ rebreathing) with subjects as nested random effects (JMP version 5 software analysis package, SAS Institute, Cary, NC). For each group and condition, we calculate (i) the mean BP, BFV, cerebral vascular resistance (CVR, calculated by mean BP/BFV) from the right and the left MCA’s, and CO₂ (see Table I); (ii) gain, phase, and coherence from transfer function analysis (see Table II); and (iii) the direct cross-correlation, the phase synchronization, and the cross-correlation of instantaneous phase increments of BP and BFV (see Table III). We analyze BFV on the stroke side in the right MCA in five patients and on the stroke side in the left MCA in eight patients (see Sec. II A for details). In our comparative tests, we consider the side opposite to the stroke side as the “normal” side, as we did not a priori know whether the side opposite to the stroke side would exhibit normal or perturbed behavior. In the group comparison, we compare the stroke side BFV for the stroke group to the BFV in the left side MCA for the control group because the majority of post-stroke subjects had stroke on their left side. We note that our comparative tests between the stroke side BFV for post-stroke subjects and the right side BFV for the control group show similar results. We compare the normal side (opposite to the stroke side) BFV for the stroke group to the BFV in the right side MCA for the control group.

TABLE II.

Gain, coherence, and phase in the low-frequency (LF, 0.05−0.2 Hz) range and in the heartbeat frequency (HBF, 0.7−1.4 Hz) range for the control and stroke groups during different physiologic conditions. We compare data from BFV in the right MCA (BFV-MCAR) in healthy subjects with data from BFV in the normal side MCA in post-stroke subjects (mean±standard deviation values are presented in the left column for each condition). We compare data from BFV in the left MCA (BFV-MCAL) in healthy subjects with data from BFV in the stroke side MCA in post-stroke subjects (mean±standard deviation values are presented in the right column for each condition). The p values from 2×4 MANOVA are calculated for comparing differences between groups and conditions.

		Supine		Tilt		Hyperventilation		CO2 rebreathing		Statistics
Variable		BFV-MCAR/Normal side	BFV-MCAL/Stroke side	BFV-MCAR/Normal side	BFV-MCAL/Stroke side	BFV-MCAR/Normal side	BFV-MCAL Stroke side	BFV-MCAR/Normal side	BFV-MCAL/Stroke side	BFV-MCAR/Normal side	BFV-MCAL/Stroke side
Low frequency 0.05−0.2 Hz
Gain	Control	0.94±0.30	0.97±0.27	1.06±0.21	0.97±0.21	0.95±0.41	1.02±0.43	1.03±0.15	1.03±0.15	0.38a	0.11a
Gain	Stroke	0.84±0.42	0.72±0.37	0.95±0.27	0.95±0.25	1.09±0.36	1.08±0.38	0.92±0.20	0.95±0.21	0.48b	0.26b
Coherence	Control	0.65±0.15	0.59±0.21	0.75±0.08	0.66±0.19	0.58±0.18	0.62±0.19	0.82±0.09	0.84±0.08	0.0006a	0.0004a
Coherence	Stroke	0.53±0.19	0.44±0.24	0.70±0.20	0.66±0.27	0.62±0.17	0.61±0.19	0.69±0.19	0.70±0.20	0.07b	0.07b
Phase (rad)	Control	0.56±0.27	0.63±0.26	0.62±0.32	0.63±0.30	0.92±0.33	0.94±0.39	0.63±0.23	0.63±0.20	0.0002a	0.0001a
Phase (rad)	Stroke	0.79±0.27	0.56±0.38	0.58±0.24	0.60±0.25	0.86±0.32	0.94±0.47	0.42±0.25	0.49±0.23	0.74b	0.37b
Heartbeat frequency 0.7−1.4 Hz
Gain	Control	0.92±0.18	0.93±0.24	0.91±0.15	0.91±0.21	0.88±0.23	0.94±0.23	0.89±0.16	0.91±0.18	0.50a	0.73a
Gain	Stroke	0.77±0.29	0.82±0.28	0.88±0.27	0.97±0.43	0.97±0.24	0.98±0.28	0.96±0.28	0.97±0.31	0.96b	0.84b
Coherence	Control	0.76±0.15	0.75±0.18	0.75±0.13	0.71±0.18	0.58±0.16	0.58±0.18	0.68±0.23	0.70±0.22	0.15a	0.27a
Coherence	Stroke	0.64±0.24	0.63±0.25	0.57±0.23	0.56±0.21	0.55±0.20	0.56±0.21	0.64±0.25	0.63±0.27	0.035b	0.05b
Phase (rad)	Control	0.32±0.13	0.27±0.14	0.38±0.18	0.38±0.20	0.46±0.27	0.46±0.26	0.46±0.26	0.42±0.24	0.16a	0.03a
Phase (rad)	Stroke	0.35±0.31	0.31±0.24	0.36±0.14	0.36±0.21	0.47±0.20	0.49±0.28	0.42±0.21	0.42±0.15	0.95b	0.81b

^aP value between physiologic conditions comparisons.

^bP value between groups comparisons.

TABLE III.

The maximum correlation strength C_max and the characteristic lag τ₀ obtained from the direct cross-correlation of the BP and BFV signals and from the cross-correlation of the instantaneous phase increments in the BP and BFV signals, as well as the entropy index ρ obtained from the synchronization analysis for the control and stroke groups during different physiologic conditions. We compare data from BFV in the right MCA (BFV-MCAR) in healthy subjects with data from BFV in the normal side MCA in post-stroke subjects (mean±standard deviation values are presented in the left column for each condition). We compare data from BFV in the left MCA (BFV-MCAL) in healthy subjects with data from BFV in the stroke side MCA in post-stroke subjects (mean±standard deviation values are presented in the right column for each condition). The p values from 2×4 MANOVA are calculated for comparing groups and conditions difference.

	Supine		Tilt		Hyperventilation		CO2 rebreathing		Statistics
	BFV-MCAR/Normal side	BFV-MCAL/stroke side	BFV-MCAR/Normal side	BFV-MCAL/Stroke side	BFV-MCAR/Normal side	BFV-MCAL/stroke side	BFV-MCAR/Normal side	BFV-MCAL/Stroke side	BFV-MCAR/Normal side	BFV-MCAL/Stroke side
Direct cross-correlation Cmax
Control	0.91±0.02	0.89±0.06	0.88±0.05	0.84±0.06	0.88±0.13	0.87±0.12	0.91±0.03	0.91±0.03	0.066a	0.069a
Stroke	0.92±0.03	0.92±0.03	0.88±0.09	0.89±0.06	0.91±0.06	0.90±0.09	0.92±0.04	0.93±0.04	0.33b	0.024b
Direct cross-correlation τ0
Control	6.5±4.1	6.6±4.1	3.3±1.4	3.5±1.3	3.2±1.2	3.2±1.3	4.8±3.2	5.0±3.4	0.008a	0.01a
Stroke	11.4±6.6	11.2±6.9	6.5±5.6	6.4±5.6	6.2±5.8	6.2±5.7	9.8±7.2	9.6±7.2	0.0001b	0.0004b
Phase synchronization index ρ for τ=0
Control	0.32±0.07	0.31±0.06	0.25±0.07	0.23±0.07	0.21±0.08	0.20±0.08	0.27±0.06	0.26±0.06	<0.0001a	0.0002a
Stroke	0.35±0.07	0.34±0.07	0.26±0.09	0.27±0.09	0.25±0.09	0.25±0.10	0.32±0.09	0.32±0.09	0.047b	0.008b
Phase synchronization index ρ for τ=0.4 s
Control	0.18±0.05	0.17±0.05	0.11±0.05	0.11±0.06	0.11±0.06	0.11±0.06	0.12±0.05	0.12±0.04	<0.0001a	<0.0001a
Stroke	0.21±0.05	0.21±0.05	0.11±0.05	0.12±0.06	0.11±0.06	0.11±0.06	0.13±0.05	0.13±0.05	0.43b	0.18b
Phase cross-correlation Cmax
Control	0.55±0.17	0.49±0.22	0.39±0.16	0.33±0.17	0.47±0.17	0.43±0.16	0.45±0.13	0.41±0.13	0.006a	0.07a
Stroke	0.62±0.12	0.58±0.14	0.43±0.21	0.47±0.20	0.51±0.19	0.52±0.20	0.57±0.20	0.58±0.21	0.049b	0.001b
Phase cross-correlation τ0
Control	2.0±2.0	2.0±1.7	2.2±1.3	2.5±1.5	2.0±0.9	2.0±0.9	2.6±1.5	2.6±1.5	0.6a	0.7a
Stroke	6.6±6.7	5.9±5.3	3.8±3.4	3.6±3.5	5.3±5.6	5.7±5.9	5.9±5.4	5.8±5.6	0.0003b	0.0004b

^aP value between physiologic conditions comparisons.

^bP value between groups comparisons.

1. Method 1: Transfer function analysis

We first normalize the BP and BFV signals to unit standard deviation to obtain the respective signals P(t) and V(t). We then calculate their respective Fourier transforms V(f) and P(f). In the frequency domain, the coherence function γ²(f) is defined as

$${\gamma }^2\left(f\right)\equiv \frac{{\mid S_{PV}\left(f\right)\mid }^2}{S_{PP}\left(f\right)S_{VV}\left(f\right)},$$ (1)

where S_VV(f)=|V(f)|², S_PP(f)=|P(f)|², and S_PV(f)=P^*(f)V(f) are the power spectra of V(t), P(t), and the cross spectrum of V(t) and P(t), respectively. The value of the coherence function γ²(f) varies between 0 and 1. The transfer function H(f) is defined as

$$H\left(f\right)\equiv \frac{S_{PV}\left(f\right)}{S_{PP}\left(f\right)}.$$ (2)

From the real part H_R(f) and imaginary part H_I(f) of the transfer function, we can obtain its amplitude (also called gain)

$$\mid H\left(f\right)\mid \equiv {[H_R^2\left(f\right)+H_I^2\left(f\right)]}^{1∕2}$$ (3)

and its phase

$$\Phi \left(f\right)\equiv \arctan [H_I\left(f\right)∕H_R\left(f\right)].$$ (4)

We note that the phase Φ(f) is a frequency domain characteristic of the cross spectrum between two signals and is different from the instantaneous phase in the time domain we discuss in Secs. II D 3 and II D 4 (methods 3 and 4).

2. Method 2: Cross-correlation analysis

To test dynamical aspects of the mechanism of CA, we investigate the cross-correlation between BP and BFV signals and how this cross-correlation changes under stroke. Although we consider segments of the BP and BFV recordings during the quasisteady state, where we have constant level (or absence) of physiologic stimuli, these signals may still exhibit certain trends in the mean value. So, to eliminate these trends, we first preprocess the BP and BFV signals applying a bandpass filter (10 Hz>f>0.05 Hz) in the frequency domain. To be able to compare signals with different amplitude, we next normalize the bandpassed signals to unit standard deviation (Fig. 1). Finally, we perform a cross-correlation analysis estimating the cross-correlation function C(τ) for a broad range of values for the time lag τ, where C(τ) is defined as

$$C\left(\tau \right)\equiv \frac{\langle (P\left(t\right)-\langle P\rangle )[V(t+\tau )-\langle V\rangle ]\rangle }{{\sigma }_P{\sigma }_V},$$ (5)

where 〈···〉 and σ denote the mean and standard deviation of a signal, respectively.

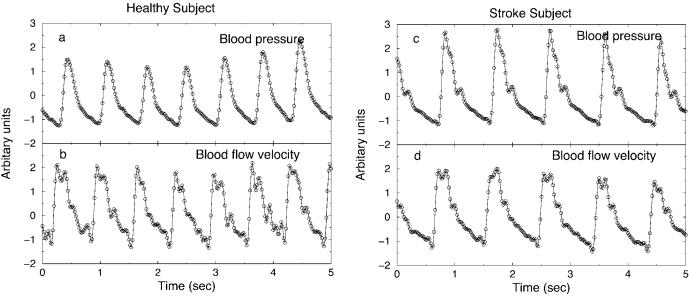
FIG. 1.

BP and BFV signals during CO₂ rebreathing after a bandpass Fourier filter in the range [0.05 Hz, 10 Hz] and normalization to unit standard deviation: (a), (b) for a healthy subject, (c), (d) for a post-stroke subject.

Results of our cross-correlation analysis for one healthy subject and one post-stroke subject during all four physiologic conditions are shown in Fig. 2 and are discussed in Sec. III C.

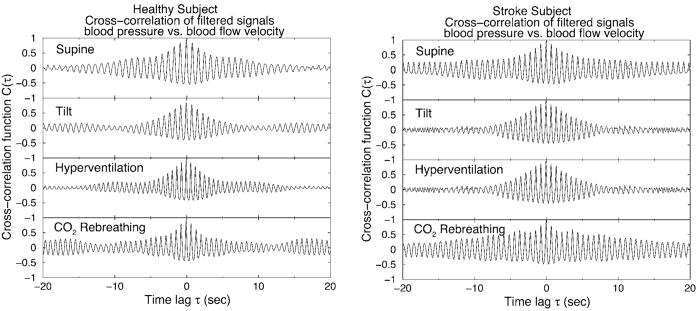
FIG. 2.

Cross-correlation function C(τ) for the BP and BFV signals during four physiologic conditions: (a) for the same healthy subject and (b) for the same post-stroke subject as shown in Fig. 1. BP and BFV signals are preprocessed using a bandpass Fourier filter in the range [0.05 Hz, 10 Hz] and are normalized to unit standard deviation before the analysis. Since BFV precedes BP, the maximum value C_max in the cross-correlation function C(τ) is located not at zero lag but at τ≈−0.1 sec.

3. Method 3: Phase synchronization analysis

We study the beat-to-beat BP-BFV interaction during quasisteady-state conditions (supine rest, upright tilt, upright hyperventilation, and CO₂rebreathing) employing a phase synchronization method. We first apply a high-pass (f > 0.05 Hz) and a low-pass (f < 10 Hz) Fourier filter to the BP and BFV signals. The high-pass filter is used to reduce nonstationarity related to slow trends in the mean of the signals. The low-pass filter is used to remove high-frequency random fluctuations in the signals. Next we perform a Hilbert transform which for a time series s(t) is defined as [55,56,73−76]

$$\tilde{s}\left(t\right)\equiv \frac{1}{\pi }P{\int }_{-\infty }^{\infty }\frac{s\left(\tau \right)}{t-\tau }d\tau ,$$ (6)

where P denotes the Cauchy principal value.$\tilde{s}$(t) has an apparent physical meaning in Fourier space: for any positive (negative) frequency f, the Fourier component of the Hilbert transform $\tilde{s}$(t) at this frequency f can be obtained from the Fourier component of the original signal s(t) at the same frequency f after a 90° clockwise (anticlockwise) rotation in the complex plane. For example, if the original signal is sin(ωt), its Hilbert transform will become cos(ωt). For any signal s(t) one can always construct its “analytic signal” S [55,56,73,74,76], which is defined as

$$S\equiv s\left(t\right)+i\tilde{s}\left(t\right)=A\left(t\right)e^{i\phi \left(t\right)},$$ (7)

where A(t) and φ(t) are the instantaneous amplitude and instantaneous phase of s(t), respectively. Application of the analytic signal approach to heartbeat dynamics has been shown in [15,75]. The instantaneous amplitude A(t) and the instantaneous phase φ(t) are instantaneous characteristics of a time series s(t) and present different aspects of the signal. For a pure sinusoid, A(t) is a constant and φ(t) increases linearly in time: the amplitude quantifies the strength of the oscillation and the slope of the straight line formed by the increasing phase quantifies how fast the oscillation is. For more complex signals, both A(t) and φ(t) may display complicated forms. Further, we note that the instantaneous phase φ(t) is different from the transfer function phase Φ(f): φ(t) is a time-domain characteristic of a single signal, while Φ(f) is a cross-spectrum characteristic of two signals in the frequency domain.

From the definition of the Fourier transform one can find that the mean of a given signal s(t) is proportional to the Fourier component of s(t) at the frequency f=0. After applying the high-pass filter (f>0.05 Hz), the Fourier component of s(t) at f=0 is filtered out, and correspondingly, the mean of the filtered signal becomes zero. Furthermore, from the definition of the Hilbert transform, one can find that the Hilbert transforms of two signals s(t) and s(t)+c (where c ≠0 is a constant) are identical, although the two original signals have obviously different means due to the constant c. Since both the instantaneous phase φ(t) and amplitude A(t) depend on the original signal as well as on the Hilbert transform of the original signal [see Eq. (7)], the instantaneous phase and amplitude for s(t) and s(t)+c will be also different. However, when we let both signals s(t) and s(t)+c pass a high-pass filter (f>0.05 Hz), the mean of both signals becomes zero, and both signals will have identical phases and amplitudes. Thus, the phase and amplitude of a signal does not depend on its mean and is uniquely defined after the signal is processed with a high-pass filter.

Following [55], we estimate the difference between the instantaneous phases of the BFV and BP signals φ_BFV(t)–φ_BP(t) at the same time t. We then obtain the probability density p for the quantity

$${\Psi }_{1,1}\equiv {\left(2\pi \right)}^{-1}[{\phi }_{BFV}\left(t\right)-{\phi }_{BP}\left(t\right)]\mathrm{mod}1,$$ (8)

following the approach presented in [68]. To quantify the shape of the probability density p, which can be very broad (uniform) for nonsynchronized signals and very narrow (peaked) for strongly synchronized signals, we utilize the index ρ [68]. The index ρ is based on the Shannon entropy and is defined as

$$\rho \equiv (S_{\max }-S)∕S_{\max },$$ (9)

where $S=-{\sum }_{k=1}^N{p}_k\ln p_k$ is the Shannon entropy of the distribution of Ψ_1,1 and S_max=ln N corresponds to the uniform distribution, where N is the number of bins. In our calculations, we choose N=40. For the normalized index ρ, we have 0≤ρ≤1, where ρ=0 corresponds to a uniform distribution (no synchronization) and ρ=1 corresponds to a Dirac-like distribution (perfect synchronization).

Results of our synchronization analysis for several healthy and post-stroke subjects are shown in Figs. 3 and 4 and are discussed in Sec. III D.

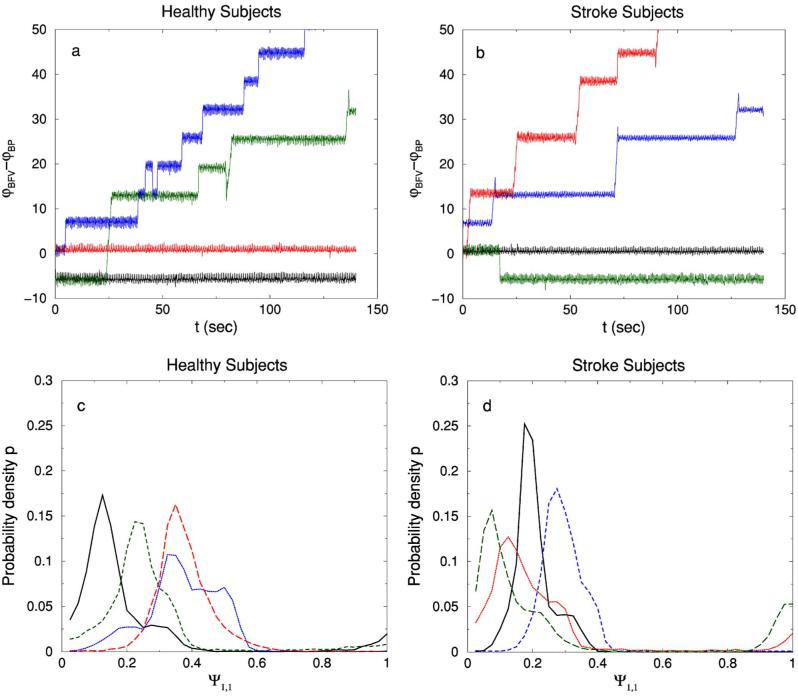
FIG. 3.

(Color online) (a) The relative phases φ_BFV(t)–φ_BP(t) for healthy subjects (a) and post-stroke subjects (b), where φ(t) is the instantaneous phase of a signal. The phase difference of BFV and BP for both groups may fluctuate around a constant value or jump between different constant values. These jumps are always a multiple of 2π and occur due to (1) artifacts in the BP signals related to machine calibration during the process of recording which do not occur in the simultaneously recorded BFV signals or (2) difference in the morphology of the BP and BFV waves (see Fig. 1) which on certain occasions exhibit a more strongerly pronounced bump on the right shoulder of the wave for one of these two signals. The distributions of Ψ_1,1≡(2π)⁻¹[φ_BFV(t)–φ_BP(t)] mod 1 for healthy subjects and for post-stroke subjects are shown in (c) and (d), respectively. Employing this definition for Ψ_1,1 eliminates the effect which jumps of multiple of 2π may have on the synchronization analysis. The number of bins in the histogram is N=40.

FIG. 4.

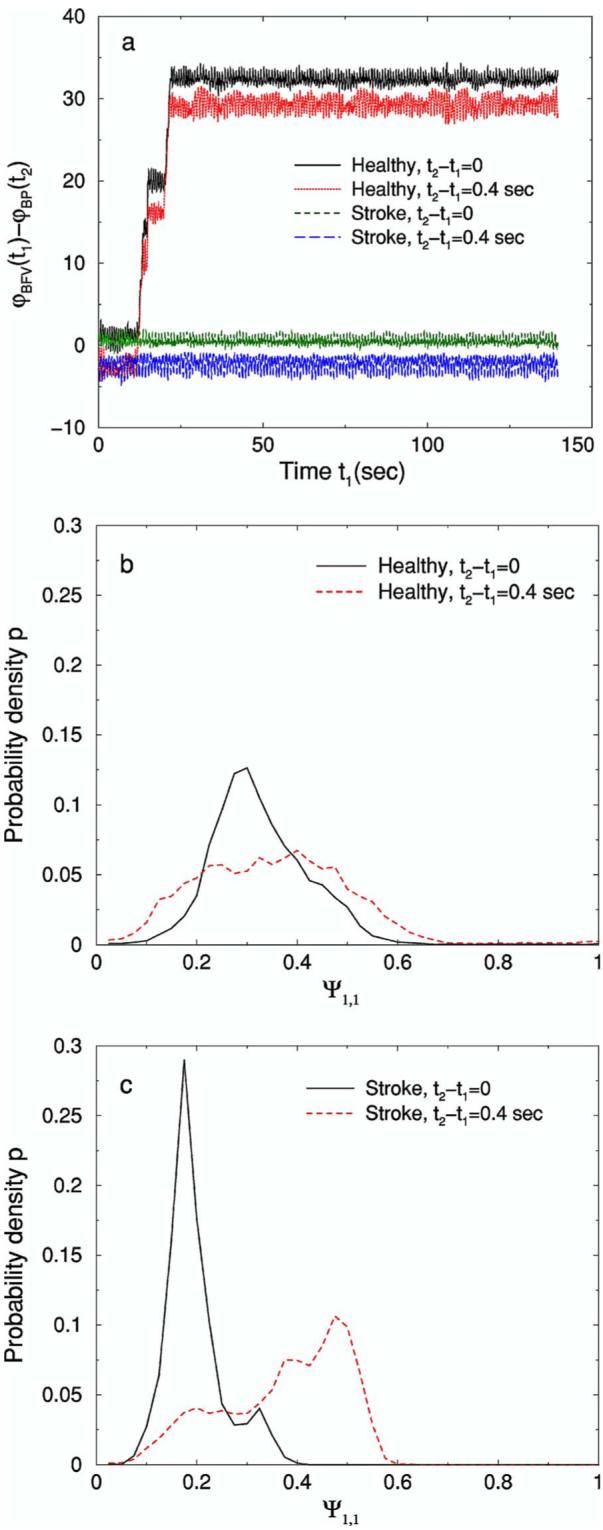
(Color online) (a) The relative phases φ_BFV(t₁)–φ_BP(t₂) for a healthy subject and a post-stroke subject. We find that the relative phases between BFV and BP depend on the time difference t₂–t₁ between these two signals. Accordingly, the distributions of Ψ_1,1≡(2π)⁻¹[φ_BFV(t₁)–φ_BP(t₂)] mod 1, shown in (b) and (c) for a healthy subject and a post-stroke subject, respectively, also depend on the time difference between BFV and BP. We note that our choice of time difference t₂–t₁=0.4 sec is arbitrary and does not carry any specific physiologic meaning. The number of bins in the histogram is N=40.

4. Method 4: Cross-correlation of instantaneous phase increments

The instantaneous phase φ(t) for both BP and BFV is a nonstationary signal and can be decomposed into two parts: a linear trend and fluctuations along the trend. The trend is mainly driven by the periodic heart rate at a frequency ≈1 Hz. However, the fluctuations are of specific interest, since they may be affected by the cerebral autoregulation. To remove the trend, we consider the increments in the consecutive values of the instantaneous phase, defined as

$$\Delta \phi \left(t_i\right)\equiv \phi \left(t_i\right)-\phi \left(t_{i-1}\right),$$ (10)

where t_i and t_i–1 are the times corresponding to two successive recordings (in our case we have t_i–t_i–1=0.02 sec). The instantaneous phase increment signal Δφ is stationary in the sense that it has fixed mean and fixed standard deviation and fluctuates in the range (–π,π]. In Figs. 5(c) and 5(d) we show examples of Δφ for healthy subjects and in Figs. 5(g) and 5(h) for post-stroke subjects.

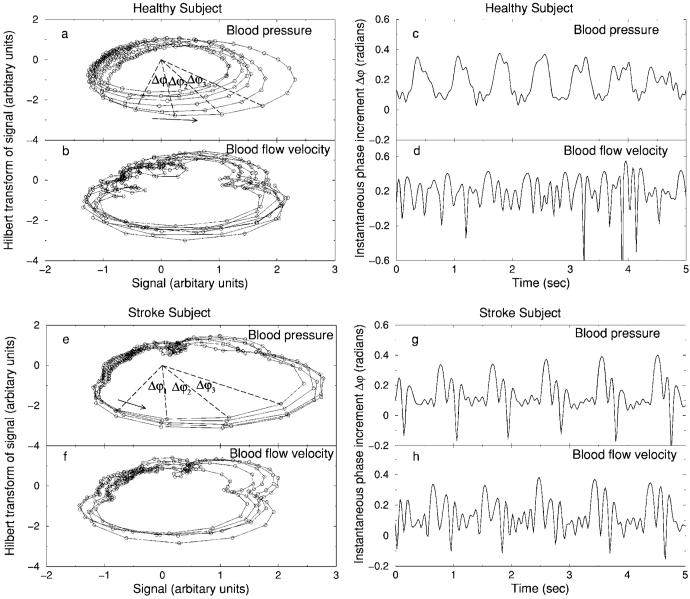
FIG. 5.

Presentation of the BP and BFV signals vs their Hilbert transforms (a), (b) and their corresponding instantaneous phase increment Δφ during the CO₂ rebreathing condition (c), (d) for the same data from a healthy subject as shown in Figs. 1(a) and 1(b). BP and BFV signals vs their Hilbert transforms (e), (f) and their corresponding instantaneous phase increment Δφ during the CO₂ rebreathing condition (g), (h) for the same data from a post-stroke subject as shown in Figs. 1(c) and 1(d). Repetitive temporal patterns associated with each heartbeat in Δφ for the peripheral BP signal from a healthy subject (c) are not matched by corresponding patterns in the cerebral BFV signal (d), reflecting active cerebral vascular regulation. In contrast, periodic patterns in Δφ of the peripheral BP signal from a post-stroke subject (g) are matched by practically identical patterns in Δφ of the cerebral BFV signal (h), indicating dramatic impairment of cerebral vascular tone with higher vascular resistance after minor ischemic stroke.

We then apply a cross-correlation analysis to quantify the dynamical relationship between the stationary phase increments Δφ of the BP and BFV signals. For each subject, during each physiologic condition we calculate the correlation coefficient C(τ) versus the time lag τ between the BP and BFV signals. To quantitatively distinguish the control group and the stroke group, we further analyze the characteristics of the correlation function C(τ). Specifically, we investigate the maximum value of C(τ), denoted as C_max, which represents the strength of the cross-correlation between the instantaneous phases of the BP and BFV signals. Another important characteristic of the cross-correlation function is how fast the correlation between two signals decreases for increasing values of the time lag τ. To quantify this aspect, we choose a fixed threshold value r=0.3, which is the same for all subjects and for which we obtain a good separation between the control and the stroke group. Since C(τ) is a periodiclike function of the time lag τ with a decreasing amplitude for increasing τ (Fig. 6), we first record all maxima of |C(τ)| during each heartbeat period (∼1 sec); then, we determine the two maxima with largest positive and negative time lags τ at which the correlation function C(τ) is above rC_max. The average of the absolute values for these two time lags is marked as a characteristic time lag τ₀.

FIG. 6.

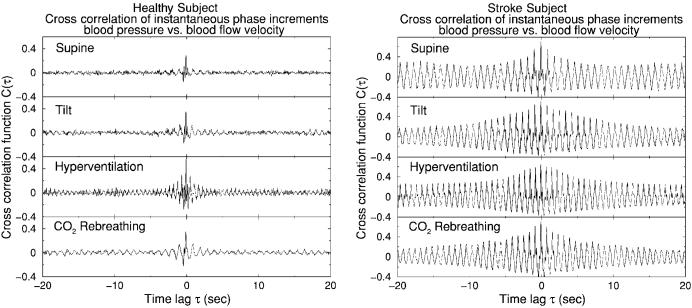
Cross-correlation function C(τ) of the instantaneous phase increment Δφ for the BP and BFV signals during four physiologic conditions. We find that the cross-correlation function for all healthy subjects exhibits a very distinct type of behavior compared to post-stroke subjects. Two typical examples are shown. Left: a healthy subject: C(τ) has a small amplitude at τ=0 and is close to zero at time lags τ<5 seconds during all four conditions. Right: a post-stroke subject: C(τ) has a much larger amplitude at τ=0 which lasts for lags τ up to 20 seconds, indicating a strong coupling between the BP and BFV signals—i.e., loss of cerebral autoregulation.

In summary, we note that, to avoid problems with the nonstationarity when applying the cross-correlation analysis between instantaneous phase increments, we have performed the following steps: (1) We have considered BFV and BP at the steady state for all four physiologic conditions, and we have analyzed only short segments (≈2.3 min) of data during which the heart rate remains approximately stable. (2) We have performed cross-correlation analysis after preprocessing BFV and BP signals by a high-pass filter, thus removing low-frequency trends. (3) The phase increment signals Δφ are stationary at least according to the definition of weak stationarity. For the data segments we consider, Δφ has a constant mean value and fluctuates within a fixed range (–π,π].

III. RESULTS

A. Mean values

We compare the mean values of all signals for both control and stroke groups and for all four physiologic conditions (baseline supine rest, upright tilt, tilt-hyperventilation, and CO₂ rebreathing) using the MANOVA method. Our results are shown in Table I. We see that the mean values of the BFV and CO₂ signals are significantly different for the four different conditions while the BP mean values are similar. For control and stroke group comparison, we find that BFV’s from the left (stroke side) MCA were significantly different and that the mean value of BP for the stroke group is significantly higher than that for the control group. Furthermore, we observe that the cerebral vascular resistance (CVR) is significantly higher for the stroke group.

B. Transfer function analysis

We apply transfer function analysis of the original BP and BFV signals under different physiologic conditions in both the low-frequency (LF) (0.05−0.2 Hz) and heartbeat-frequency (HBF) (0.7−1.4 Hz) ranges. Gain, phase, and coherence are calculated for each subject and for all four physiologic conditions (Table II). We use MANOVA to compare our results for the two groups and for the four conditions. In both frequency ranges, we do not find a significant difference in the gain. In the LF range, the phase Φ(f) and coherence γ²(f) are significantly different between the physiologic conditions, but are not different between the groups. In the HBF range, we find that the phase Φ(f) for the MCAL-BFV is significantly different between the conditions (p=0.03). The coherence in the HBF range shows no significant difference in the physiologic conditions comparison; however, it is significantly higher for the control group.

C. Cross-correlation analysis

We have performed a cross-correlation analysis directly between the BP and BFV signals, after first preprocessing these signals by a high-pass filter as shown in Fig. 1. Representative examples for the cross-correlation function over a broad range of time lags τ for one healthy and one post-stroke subject during the four physiologic conditions (supine, tilt, hyperventilation, CO₂ rebreathing) are shown in Fig. 2. Group statistics and comparative tests are included in Table III.

The BFV data show more random fluctuations for healthy subjects compared to post-stroke subjects (one example is shown in Fig. 1), leading to a slightly reduced cross-correlation amplitude between BP and BFV for healthy subjects. However, the difference in the maximum cross-correlation value C_max is not significant (see Table III), the reason being that the general shape of the BP and BFV oscillations at each heartbeat is very similar for both healthy and post-stroke subjects, and in addition, the amplitude of BP and BFV oscillations is much larger relative to the small random fluctuations on top of these oscillations. In contrast, the shape of the oscillations observed in the phase increments of the BP and BFV signals at every heartbeat is very different for healthy subjects [see Figs. 5(c) and 5(d)] but very similar for post-stroke subjects [see Figs. 5(g) and 5(h)]. Thus, the instantaneous phase cross-correlation between BP and BFV for healthy subjects is significantly different from post-stroke subjects, as one can see by comparing Figs. 2 and 6. This difference is also shown in Table III. Comparative statistical tests indicate significant differences between the control and stroke group based on the instantaneous phase cross-correlation parameter C_max when we compare both the stroke side and the normal side of post-stroke subjects with healthy subjects. There is no significant difference in C_max obtained from the direct cross-correlation between BP and BFV signals when we compare the normal side of post-stroke subjects with healthy subjects (see also results in Sec. III E).

We also note that healthy subjects exhibit higher variability in the intervals between consecutive heartbeats, leading to higher variability in the intervals between consecutive peaks in the BP and BFV waves (Fig. 1). As a result, both the direct cross-correlation and instantaneous phase cross-correlation between the BP and BFV signals decay faster with increasing time lag τ for healthy subjects compared to post-stroke subjects. For both methods we show that the parameter τ₀, which characterizes the decay in the cross-correlations, separates equally well the stroke group from the control group (see Table III).

D. Phase synchronization analysis

In Fig. 3 we present the results of the phase synchronization analysis for four healthy and four post-stroke subjects. The statistics for all four physiologic conditions (supine rest, tilt, hyperventilation, CO₂ rebreathing) in our database and over the entire control and stroke groups are summarized in Table III. We find a statistically significant difference between the control and stroke group based on the entropy index ρ.

Since both BP and BFV are driven by the heartbeat, one would expect that these signals would be synchronized. However, the mechanism of the cerebral autoregulation which influences the BFV may alter this synchronization. Our results (Table III) show that the phase synchronization index ρ has smaller values for healthy subjects for which the cerebral autoregulation is intact, so that the cerebral BFV is not well synchronized with the peripheral BP. In contrast, we obtain larger values for the synchronization index ρ for the post-stroke subjects in our database for which the mechanism of the cerebral autoregulation is impaired, and thus the synchronization between the cerebral BFV and the peripheral BP is stronger.

In the traditional phase synchronization method one estimates the difference between the instantaneous phases of two signals at the same time, and thus it does not reflect possible time delays between the two studied signals and, correspondingly, between their instantaneous phases. However, such time delays have been recently observed in coupled physical and physiological systems [51,77−79] and have been analytically investigated [56,59,80]. To demonstrate the effect of the time delays in the context of the system we study, we consider the difference between the instantaneous phases of BP and BFV, when the phase of BFV is taken at time t₁ and the phase of BP is taken at time t₂=t₁+τ. As we show in Fig. 4, the result of the phase synchronization analysis is very different when considering instantaneous phase difference with a time delay—the histogram of the phase difference becomes much broader (the entropy index ρ much smaller) compared to the case when no time delay is introduced.

Statistics for the groups and physiologic conditions are presented in Table III and indicate a very different result no statistically significant difference between the control and stroke group for the entropy index ρ estimated for an arbitrary chosen time delay of τ=0.4 sec. This is in contrast to the results obtained for the entropy index ρ from the synchronization analysis when one does not consider a time delay. Thus, the results of the traditional phase synchronization method strongly depend on the time at which the instantaneous phases of two signals are compared [51,80]. This motivates our approach to investigate the cross-correlation between the instantaneous phases of two coupled systems at different time lag τ, as presented in Sec. III E.

E. Cross-correlation of instantaneous phase increments

We apply the instantaneous phase increment cross-correlation analysis to all four conditions and both study groups. We find that the patterns of the cross-correlation function C(τ) of the instantaneous phase increments Δφ of the BP and BFV signals are very different for the stroke group compared to the control group. In general, the cross-correlation function C(τ) for the control group is characterized by smaller amplitude and faster decay (time lag τ less than 10 sec)(Fig. 6). In contrast, for post-stroke subjects, the amplitude of the cross-correlation function C(τ) is much larger and decays much slower (over time lags larger than 10 sec) (Fig. 6). This stronger cross-correlation results from the fact that for post-stroke subjects the patterns found in the instantaneous phase increments Δφ of the cerebral BFV are matched and are aligned in time by very similar patterns in Δφ of the peripheral BP signals [see Figs. 5(g) and 5(h)], indicating a strong synchronization.

The cross-correlations at short time scales (less than 10 sec) may be partially attributed to the effect of heart rate (∼1 sec) and respiration (∼5 sec)—i.e., they may reflect the effect of other body regulations (similar to “background noise”) on both BP and BFV signals. When cerebral auto-regulation is effective in healthy subjects during the quasisteady state, it weakens significantly the cross-correlations between the instantaneous phase increments Δφ of the BP and BFV at short time scales, even within a heartbeat (Fig. 6), due to the fast-acting mechanism of CA [3]. The effect of cerebral autoregulation (and of heart rate and respiration) on the cross-correlation of Δφ decreases rapidly with increasing time lag τ. Thus, the significantly stronger cross-correlations at long time scales (>10 sec) observed for post-stroke subjects (Fig. 6) cannot be attributed to the influence from cerebral autoregulation during the quasisteady state. Instead, the existence of such strong and sustained cross-correlations over a broad range of time scales may imply that cerebral BFV passively follows changes in peripheral BP, indicating the absence of cerebral vascular dilation or constriction due to impaired cerebral autoregulation for the post-stroke subjects.

To quantitatively distinguish the control group from the stroke group, we study the characteristics of the correlation function C(τ) for all subjects. For each correlation function C(τ), we first find C_max, the maximal value of C(τ), which indicates the strength of the correlation. Then we choose a threshold value r=0.3 and search for the maximum of |C(τ)| during each heart beat period along both positive and negative lags τ. Next, we find two maximum points corresponding to the positive and negative largest time lags at which the correlation are still above rC_max. The average of absolute values of these two time lags gives the characteristic time lag τ₀. For all subjects and during all physiologic conditions, we find that subjects in the stroke group exhibit larger C_max and longer time lag τ₀ compared to those in the control group.

We apply MANOVA to demonstrate whether τ₀ and C_max are different for healthy and post-stroke subjects. The results are shown in Table III. We find that during tilt and hyperventilation, the control and stroke groups are not significantly different (p values >0.05). In contrast, during supine rest and CO₂ rebreathing, the difference between the control group and the stroke group becomes significant (p values <0.05).

To explain the above difference in τ₀ and C_max during supine rest, we note that post-stroke subjects exhibit higher BP and CO₂ mean values in base line (see Table I). Therefore, the BP-BFV autoregulatory curve for post-stroke subjects is shifted to the right, to higher BP values, while at the same time the plateau of this curve is narrowed due to the higher level of CO₂ [3]. CO₂ rebreathing increases the level of the CO₂ after the period of hyperventilation (hypocapnia), thus further testing the reactivity of the CA which shows impaired vasodilatatory responses in post-stroke subjects. In contrast, vasoconstrictor responses to tilt-up hyperventilation are preserved.

IV. DISCUSSION AND CONCLUSIONS

In this study we investigate dynamics of cerebral autoregulation from the relationship between the peripheral BP in the finger and the cerebral BFV for a group of healthy and post-stroke subjects during the four different physiologic conditions of supine, tilt, hyperventilation, and CO₂ rebreathing. The mechanism of cerebral autoregulation is traditionally accessed through the response of the average cerebral BFV to abrupt perturbation in the average BP (e.g., upright tilt from supine position) and is typically characterized by the ability of the cerebral blood vessels to restore equilibrium and a steady cerebral blood flow after such perturbation—a process which is known to operate on time scales above several heartbeats. In contrast, we focus on the dynamical characteristics of the pressure-flow fluctuation around average values. We show that in healthy subjects the CA mechanism is active even during the steady equilibrium state. Moreover, we find that on top of the BFV wave forms associated with each heartbeat there are robust fluctuations which are reduced in the post-stroke subjects, indicating an active cerebral vascular regulation in healthy subjects on time scales within a single heartbeat even under steady BP.

To test for the dynamical patterns in the BP-BFV fluctuations we use four different methods, and we compare the results of the analyses by evaluating the combined effects of pressure autoregulation (upright tilt) and metabolic autoregulation (hyperventilation and CO₂ rebreathing) in healthy and post-stroke subjects. We find that the gain and phase obtained from the traditional transfer function analysis do not provide a significant difference between healthy and post-stroke subjects. In contrast, the coherence is significantly different in the heartbeat frequency range (0.7−1.4 Hz) when we compare both the normal side and the stroke side of post-stroke subjects with healthy subjects.

Further, we find that the amplitude of the direct cross-correlation between the BP and BFV signals does not separate the control from the stroke group or reveal differences between different physiologic conditions when we compare the normal side of post-stroke subjects with healthy subjects. However, comparing the stroke side of post-stroke subjects with healthy subjects, we find a statistically significant difference, suggesting that the direct cross-correlation method is sensitive to detect abnormalities in CA only for the stroke side. In addition, we observe a significantly faster decay in the BP-BFV cross-correlation function for healthy subjects, reflecting higher beat-to-beat variability in the BP and BFV signals, compared to post-stroke subjects.

Since both BP and BFV are driven by the heartbeat, we also test the coupling between these two signals applying the phase synchronization method. For healthy subjects we observe a weaker synchronization between BP and BFV characterized by a significantly smaller value of the synchronization index ρ compared to post-stroke subjects, indicating that the CA mechanism modulates the cerebral BFV waves so that they are not completely synchronized with peripheral BP waves driven by the heartbeat. We find a significantly stronger BP-BFV synchronization in post-stroke subjects, characterized by a larger value of the index ρ, indicating the loss of cerebral autoregulation.

To probe how the CA mechanism modulates the BFV we investigate the dynamical patterns in the instantaneous phase increments of the BP signals, Δφ_BP, and compare them with the patterns we find in the instantaneous phase increments of the BFV signals, Δφ_BFV. Remarkably, we find that for post-stroke subjects Δφ_BP and Δφ_BFV exhibit practically identical patterns in time, leading to very high degree of cross-correlation between Δφ_BP and Δφ_BFV. In contrast, for healthy subjects Δφ_BFV exhibits robust random fluctuations very different from the structured oscillatory patterns we find in Δφ_BP. This leads to a significantly reduced cross-correlation between Δφ_BP and Δφ_BFV for healthy subjects compared to post-stroke subjects. Our results indicate a statistically significant separation between the stroke and control groups when we compare both the normal and stroke sides in post-stroke subjects with healthy subjects. This suggests that our approach based on cross-correlation of the instantaneous phase increments of BP and BFV is sensitive to detect impairment of cerebral vascular autoregulation in both hemispheres for subjects with minor ischemic stroke.

Our findings of robust fluctuations in Δφ_BFV, which do not synchronize with periodic patterns in Δφ_BP, clearly indicate that the mechanism of cerebral autoregulation impacts the dynamics not only on scales longer than several heartbeats but is also active within a single heartbeat—i.e., much shorter time scales than previously known. Since these fluctuations are present in the data after we have truncated the part of BP and BFV signals corresponding to the initial perturbation related to changes in the physiologic condition, our results also suggest that the cerebral autoregulation plays an important role even in the quasisteady state.