Cooperation and self-interest: Pareto-inefficiency of Nash equilibria in finite random games

Abstract

The relative merits of cooperation and self-interest in an ensemble of strategic interactions can be investigated by using finite random games. In finite random games, finitely many players have finite numbers of actions and independently and identically distributed (iid) random payoffs with continuous distribution functions. In each realization, players are shown the values of all payoffs and then choose their strategies simultaneously. Noncooperative self-interest is modeled by Nash equilibrium (NE). Cooperation is advantageous when a NE is Pareto-inefficient. In ordinal games, the numerical value of the payoff function gives each player’s ordinal ranking of payoffs. For a fixed number of players, as the number of actions of any player increases, the conditional probability that a pure strategic profile is not pure Pareto-optimal, given that it is a pure NE, apparently increases, but is bounded above strictly below 1. In games with transferable utility, the numerical payoff values may be averaged across actions (so that mixed NEs are meaningful) and added across players. In simulations of two-player games when both players have small, equal numbers of actions, as the number of actions increases, the probability that a NE (pure and mixed) attains the cooperative maximum declines rapidly; the gain from cooperation relative to the Nash high value decreases; and the gain from cooperation relative to the Nash low value rises dramatically. In the cases studied here, with an increasing number of actions, cooperation is increasingly likely to become advantageous compared with pure self-interest, but self-interest can achieve all that cooperation could achieve in a nonnegligible fraction of cases. These results can be interpreted in terms of cooperation in societies and mutualism in biology.

When agents act on the basis of individual self-interest alone, to what extent can they attain all the gains they could obtain in the same situation if they were to act cooperatively? Two examples, one from business and one from ecology, suggest that cooperation may be advantageous under some conditions.

In the 1970s, “Silicon Valley,” in northern California, and “Route 128,” in eastern Massachusetts, led innovation in electronics and software, stimulated by university research and military spending. In the early 1980s, international competition in the manufacture of semiconductor memory and the rise of workstations and personal computers challenged both regions and slowed their growth. During the 1980s, in Silicon Valley, new companies emerged and flowered along with large high-technology companies, and high-technology employment and production surged. Along Route 128, by contrast, layoffs at minicomputer companies overbalanced startups and the so-called “Massachusetts Miracle” ground to a halt. A careful comparison (ref. 1, pp. 2–6) suggests that the firms interacted with one another in substantially different ways in the two regions, and that the different forms of interaction were at least partially responsible for the regions’ differing success in meeting external challenges. In Silicon Valley, “a regional network-based industrial system [promoted] collective learning and flexible adjustment among specialist producers of a complex of related technologies, … informal communication and collaborative practices … The Route 128 region, in contrast, [was] dominated by a small number of relatively integrated[,] … independent firms that internalize[d] a wide range of productive activities. Practices of secrecy and corporate loyalty govern[ed] relations between firms and their customers, suppliers, and competitors. … Their differences in performance cannot be explained by approaches that view firms as separate from the social structures and institutions of a local economy.”

A second example comes from Lake Tanganyika, one of the African Great Lakes and home to at least 165 species of fishes in the family Cichlidae. Most Tanganyikan cichlids live on or near the lake bottom. There they find food, breeding sites, and areas for foraging and mating. Cichlids interact in different ways in different places. Detailed studies (2) compared cichlid communities in two patches of lake bottom at the northwest end of Lake Tanganyika: a sandy-bottom habitat of area 7 × 10 m at a depth 4 m, and a rocky–sandy bottom habitat of area 8 × 9 m at a depth of 5 m. In the sandy-bottom patch, there was an abundance of aggressive, exclusive behavior. In the rocky–sandy bottom habitat, the majority of the 26 rock-dwelling cichlid species were passive and tolerant of one another and of aggression. The rocky bottom supported many more cichlid species and more individuals of these species than did the sandy bottom. Intricate commensal and mutualistic behavioral interactions enabled many cichlids to coexist on the rocky bottom. For example, fry-eaters and piscivores had higher rates of success in feeding when other cichlids with similar food habits were present, apparently because the variety of attack methods confused the prey. Overall, “a community on a sandy bottom is characterized by fewer species, fewer threats by predators, and fewer co-operative relationships, while a community on [a] rocky bottom has more species, more threats by predators, and more co-operative relationships …” (ref. 2, p. 224).

Neither the comparison between Silicon Valley and Route 128 nor that between sandy- and rocky-bottom habitats in Lake Tanganyika is a controlled experiment. Therefore inferences can be only weakly tested by these observations. Nevertheless, the examples suggest that economic growth and technological advance, as well as richness of species and abundance of individuals, are both associated with cooperative, or at least tolerant, interactions and with a diversity of modes of interaction. This weak claim does not exclude the possibility that background factors (intellectual property law and regulatory practices in the high-technology communities; primary productivity and substrate complexity in the fish communities) play a role in the differences between communities.

This paper reports results about Nash equilibria and Pareto-optimality in finite random games which suggest that examples such as these illustrate a coherent pattern: cooperation becomes advantageous increasingly often, compared to self-interest alone, in increasingly complex situations when actors have increasingly numerous possible responses to the strategic actions of others.

GAME THEORETIC BACKGROUND

Game theory provides a mathematical way to compare the benefits of self-interest with those of cooperation when individuals interact with others (3, 4). In game theory, a game consists of a set of at least two players, a set of at least two actions for each player, and a set of payoff functions, one per player. This paper is limited to single-period or one-shot games, and all players are assumed here to have complete information about the payoff functions of every player. Each player chooses his or her own action on the basis of all the payoff functions without knowing the actions chosen by other players. A player’s payoff function assigns to that player a payoff (a real number) that depends on the actions chosen by all players. When there are n players and n is finite, the game is called n-player. When each player’s set of actions is finite, the game is called finite.

A mixed strategy for a player is a probability distribution over the player’s set of actions. An action is sometimes called a pure strategy. The term “strategy” without qualification refers to a pure or mixed strategy.

A strategic profile specifies one strategy for each player. A pure strategic profile specifies an action for each player. When a strategic profile includes a mixed strategy, each player’s payoff is the average of the payoffs of the corresponding actions, with weights given by the mixed strategies, assuming that the probability distributions of different players are independent.

A Nash equilibrium (NE) (5, 6) is a strategic profile in which each player’s strategy is a best response to the strategies chosen by the other players. The concept of NE is a standard game-theoretic formalization of noncooperative self-interest on the part of all players. A pure Nash equilibrium (PNE) is a NE and a pure strategic profile. A mixed Nash equilibrium (MNE) is a NE in which at least one player’s strategy is mixed.

Two strategic profiles may be partially ordered by Pareto-dominance. As no other kind of dominance will be discussed here, henceforth “dominance” will refer to Pareto-dominance. If the respective payoffs from the second profile are at least as large as those from the first profile for every player and are strictly larger for some player, then the second profile is said to dominate the first. A strategic profile is said to be Pareto-inefficient if some strategic profile dominates it.

A strategic profile is said to be Pareto-optimal if it is not Pareto-inefficient. A strategic profile is said to be pure Pareto-optimal (PPO) if no pure strategic profile dominates it. A pure strategic profile that is PPO may be Pareto-optimal or may not, according as there does not exist, or does exist, a mixed strategic profile that dominates it. A pure strategic profile that is not PPO is Pareto-inefficient by definition.

Game theory can formalize the question, “to what extent could interacting agents do as well by self-interest alone as they could through cooperation?” to clearer but narrower questions: “to what extent are Nash equilibria not Pareto-optimal?” or “to what extent are pure Nash equilibria not pure Pareto-optimal?” Here “cooperation” may be defined as any binding and enforceable commitment that makes it rational for players to choose a strategic profile that is not a given NE. When a given NE is Pareto-inefficient, then cooperation is required for players to choose a profile that dominates that NE (even if the dominating profile is another NE, as may occur in so-called coordination games).

Here we consider n-player finite random games. Player p is assumed to have m_p actions, 1 < m_p < ∞, p = 1, … , n. The payoff function of an n-player finite game is specified by an (n + 1)-dimensional m₁ × ⋯ × m_n × n payoff array A. The last dimension of this array corresponds to the set of players: the payoff function of player p is the m₁ × ⋯ × m_n subarray A(⋅, … , ⋅, p). If a PNE i* = (i^*₁, … , i^*_n) exists, define its degree d(i*) to be the number of pure strategic profiles i = (i₁, … , i_n) that dominate it. When the degree of a PNE is 0, that PNE is PPO. When the degree is positive, then the PNE is Pareto-inefficient. The degree measures how Pareto-inefficient the PNE is (though this measure ignores the existence of any MNE that may dominate the PNE).

The M = ∏_p=1ⁿ m_p numerical values in the payoff function of each player are generated in one of two ways: discretely or continuously. In discrete n-player finite random games, the M values are a random permutation of the integers {1, 2, … , M}. In continuous n-player finite random games, the M values are independently and identically distributed (iid) from a continuous distribution function. The continuity of the distribution function ensures that all values in all the payoff functions are distinct with probability 1. The payoff functions of distinct players are assumed to be mutually independent.

Whether discrete or continuous, n-player finite random games may be ordinal or cardinal. In ordinal games, a player’s payoffs are interpreted as specifying only a rank ordering over the set of all possible strategic profiles: the smallest payoff is least preferred and the largest is most preferred, but no averaging or adding of different payoffs is meaningful, even for one player. Mixed strategies are not meaningful in ordinal games. The probability of any preference rank ordering over any set of strategic profiles, for any player or set of players, is exactly the same in an ordinal discrete n-player finite random game as it is in an ordinal continuous n-player finite random game.

In cardinal games, a player’s payoffs are interpreted as specifying a quantity that can be added and averaged for that player. Then mixed strategies are meaningful, and the particular continuous real-valued distribution function that is used to generate the payoffs is important (unlike the ordinal case). A cardinal game in which payoffs are measured on the same scale for all players is called a game with transferable utilities. A game with transferable utilities need not have a medium of exchange; all that is required is that it be meaningful to add different payoffs of a given player and of different players.

In each realization of a finite random game, all players are shown the values of all players’ payoffs (which are randomly determined for each realization). Then all players simultaneously choose their strategies as if those payoffs specified a usual deterministic (single-shot normal-form) game. The infinite ensemble of such realizations, and players’ choices, constitutes the finite random game.

Prior Comparisons of NEs and Pareto-optima.

General results on the Pareto-inefficiency of NEs in well defined classes of games are recent. In games induced by market mechanisms, NEs are Pareto-optimal if there is a continuum of traders (players) and other conditions are satisfied (7). When the number of traders is finite, NEs are generically not Pareto-optimal (8). In n-player noncooperative games with smooth payoff functions, where each player’s set of actions is a finite-dimensional simplex, NEs are generically not Pareto-optimal (9).

Stanford (10) found that the average payoffs from randomly chosen PNEs (always conditional on the existence of at least one PNE) exceed the average payoffs from randomly chosen PPOs in two-player finite discrete cardinal random games. However, in a generic game, for every k PNEs, there are at least k − 1 MNEs (11). Limiting the analysis to PNEs in contexts where averaging of payoffs has meaning leaves open the question of how the MNEs would behave.

Prior Results on Ordinal Games with No PNEs.

As our results for ordinal games are conditional on the existence of a PNE, it is important to know what fraction of ordinal random games have no PNE.

In two-person ordinal finite random games, as the number of actions of both players gets large, the probability of no PNE converges to 1/e (12), and the probability distribution of the number of PNEs in two-player ordinal finite random games is known explicitly (13). In n-person ordinal finite random games, as the number of actions of at least two players gets large, the probability of no PNE converges to 1/e (14) and the limiting distribution of the number of PNEs is Poisson with mean 1 (15). If the number of actions of only one player, say, player 1, gets large, then the limiting distribution of the number of PNEs is binomial with parameters ∏_p=2ⁿ m_p and 1/∏_p=2ⁿ m_p (ref. 15, p. 280).

In an n-player ordinal finite random game, if by definition lim_{mp→∞,∀p} P₀(m₁, … , m_n) = P_0,n is the limiting probability of no PNE when all n players have many actions, then P_0,2 = 1/e and P_0,n+1 = exp(−1 + P_0,n) for n ≥ 2, a sequence that increases monotonically with the number n of players and converges to 1 (16, 17). When every player has the same fixed finite number of actions and the number of players becomes large, the probability of having no PNE again approaches 1.

In the light of these findings, results conditional on the existence of a PNE are most relevant to games with finite numbers of players, whether the number of their actions be small or large.

ORDINAL FINITE RANDOM GAMES

Exact Results for n ≥ 2 Players.

As before, define m_p to be the number of actions of player p. Let m⃗ = (m₁, … , m_n), M = ∏_p=1ⁿ m_p. A strategic profile i = (i₁, … , i_n), 1 ≤ i_p ≤ m_p, specifies that player p chooses action i_p, for p = 1, … , n. Also define

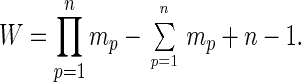1

Assume that {a(i₁, … , i_n, p) : i_p = 1, … , m_p, for p = 1, … , n} is a family of M × n independent random variables uniformly distributed on (0, 1).

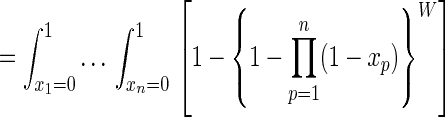
Proposition 1. For any pure strategic profile i* = (i^*₁, … , i^*_n), 1 ≤ i^*_p ≤ m_p, for p = 1, … , n, the conditional probability P(m⃗) that i* is not PPO, given that i* is a PNE, is

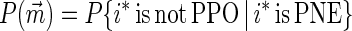2

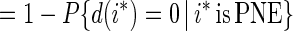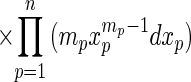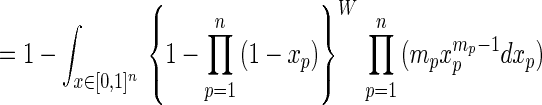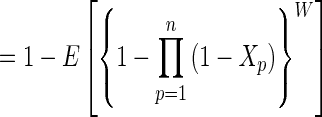where, under the last integral, x = (x₁, … , x_n), and in the last line X_p is the maximum of m_p iid random variables uniformly distributed on (0, 1).

Proof: Because all inequalities between elements of A are strict with probability 1, I shall write strict inequalities without further comment. Define (i_−p, j) to mean that player p chooses action j while every other player q ≠ p chooses the action i_q specified by the profile i. Thus, by definition, (i_−p, i_p) ≡ i. This notation (i_−p, j) describes a situation in which player p varies her choice of action from that specified by i while all other players persist in the choice specified in i. If i* is a PNE, then by definition no dominating pure strategic profile can have the form (i^*_−p, j) for any j and for any p. Hence the number of pure strategic profiles that could possibly dominate a PNE i* is W defined by Eq. 1. W is the number of cells that remain in the payoff subarray of any player, say player 1, after striking out all the “rows” and “columns,” one for each player, that pass through the PNE i*. For example, if n = 2 and (2, 3) is a PNE, then W is the number of pure strategic profiles that remain after striking out the second row and third column of both players’ payoff matrices. These remaining pure strategic profiles are all and only the pure strategic profiles that could dominate (2, 3) if (2, 3) is a PNE.

The complement of the conditional probability that a PNE is not PPO is the conditional probability that the PNE has degree 0. The latter conditional probability, given that player p’s payoff at the PNE i* is x_p, is

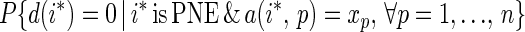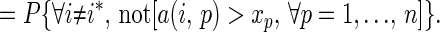For a single pure strategic profile i among the W pure profiles that could possibly dominate i*, P{a(i, p) > x_p} = 1 − x_p for each player p. Because the payoff functions of the players are mutually independent,

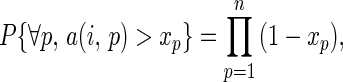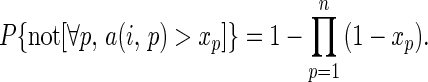Because the distinct entries in each player’s payoff function are mutually independent, and because there are W pure strategic profiles that could dominate i*,

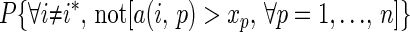3

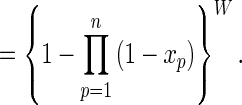To remove the conditioning on a(i*, p) = x_p, ∀p = 1, … , n, integrate over all x = (x₁, … , x_n) ∈ [0, 1]ⁿ with respect to the probability density of this event. Because x_p is the maximum of m_p iid uniform random variables for each player p, the probability density of x given that i* is PNE is ∏_p=1ⁿ (m_px_p^m_p−1 dx_p) (ref. 18, pp. 60–61). □

If each payoff for player p has the continuous distribution function F_p(.) instead of a uniform distribution, and if the assumptions of independence are retained, then reasoning identical to that used to establish Eq. 2 yields

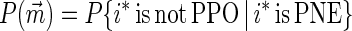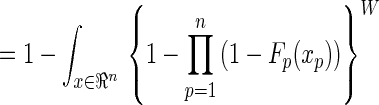4

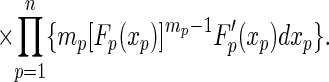Alternatively, Eq. 4 follows immediately from Eq. 2 because if the random variable X has continuous distribution function F, then the random variable F(X) is uniform on [0, 1]. Because Eq. 2 is the special case of Eq. 4 in which F_p(x) = x, x ∈ [0, 1], it follows that Eqs. 2 and 4 are equivalent.

In ordinal games, the probability distribution over orderings of the elements of the payoff function for each player does not depend on the distribution (always assumed continuous) of each element. Hence it is possible to express P{i* is not PPO | i* is PNE} without reference to the distribution of each element. Define

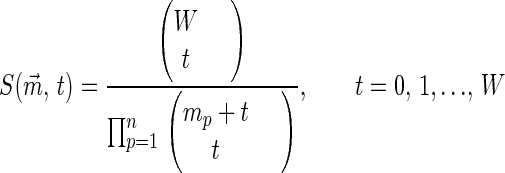5

so that S(m⃗, 0) = 1.

Proposition 2.

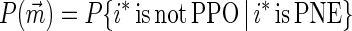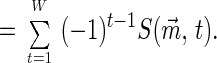6

Proof: We calculate the probabilities that the PNE i* is dominated by t or more pure strategic profiles (has degree t or more), for each t = 1, … , W, and then use the theorem of inclusion and exclusion (ref. 19, vol. 1, p. 106, equation 3.1) to obtain the probability that the PNE is dominated by 0 pure strategic profiles. It will simplify notation, and entails no loss of generality, to suppose that i^*_p = 1, for all p. Then given that (1, … , 1) is a PNE, any pure strategic profiles that dominate (1, … , 1) must be drawn from the set D of W pure strategic profiles that remain after striking out the first “column,” the first “row,” and every other first “straight line” of each player’s payoff subarray.

Consider pure strategic profiles that dominate (1, … , 1) from the point of view of player 1. For any fixed t ∈ {1, … , W}, consider the m₁ + t pure strategic profiles (1, 1, … , 1), (2, 1, … , 1), … , (m₁, 1, … , 1), i⁽¹⁾, … , i^(t) where i^(s) ∈ D for all s = 1, … , t. Given that a(1, 1, … , 1) > a(r, 1, … , 1), ∀r = 2, … , m₁ (because (1, … , 1) is a PNE), what is the conditional probability that a(1, 1, … , 1) < a(i^(s)), ∀s = 1, … , t? For each ordering (from smallest to largest) of the m₁ elements of “column” 1 of A(⋅, … , ⋅, 1) such that a(1, 1, … , 1) > a(r, 1, … , 1), ∀r = 2, … , m₁ and for each ordering of the t payoffs a(i⁽¹⁾, 1), … , a(i^(t), 1), there is only one ordering of the union of these two sets such that all m₁ elements of the former set are smaller than all t elements of the latter set, whereas the elements of the former and latter sets (considered one set at a time, without regard to the other set) retain their chosen order. However, for each ordering of the m₁ elements of “column” 1 of A(⋅, … , ⋅, 1) such that a(1, 1, … , 1) > a(r, 1, … , 1), ∀r = 2, … , m₁ and for each ordering of the t payoffs a(i⁽¹⁾, 1), … , a(i^(t), 1), if the elements of the former and latter sets retain their chosen order but there is no constraint on the ordering between the sets (so that elements of the latter set may occur anywhere between elements of the former set when the elements of both sets are ordered from smallest to largest), then there are

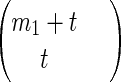orderings of the union of the two sets such that the elements of the former and latter sets (considered one set at a time, without regard to the other set) retain their chosen order. Hence

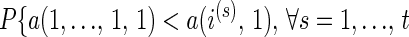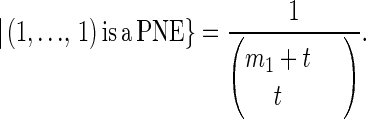An identical argument works for every player. Because payoffs to different players are mutually independent,

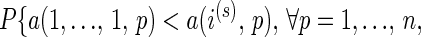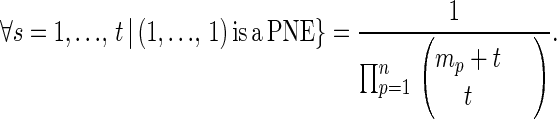There are (_t^W) choices of the t pure strategic profiles i⁽¹⁾, … , i^(t) from the set D. Hence,

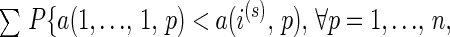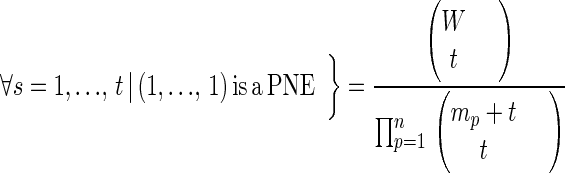where the sum extends over all subsets of t pure strategic profiles from D. Direct application of the theorem of inclusion and exclusion yields Eq. 6. □

More generally, for a pure strategic profile i*, define the conditional probability that i* has degree d, given that i* is a PNE, as Q(m⃗, d). Thus P(m⃗) = 1 − Q(m⃗, 0). Then again using inclusion and exclusion and the previous results, we find

7

Comparing Eqs. 2 and 6 gives an identity:

Proposition 3.

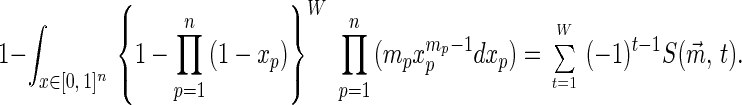8

Proof: To prove identity 8 directly, use the binomial expansion and the Beta integral ∫₀¹ x^a(1 − x)^bdx = a!b!/(a + b + 1)! for nonnegative integers a, b. Then

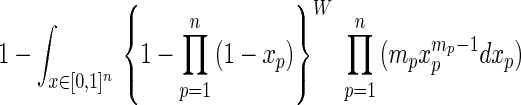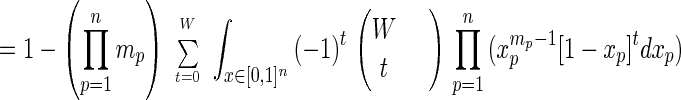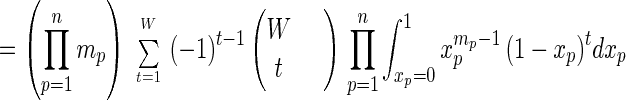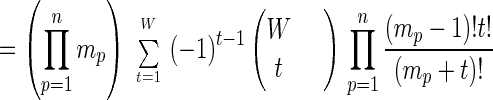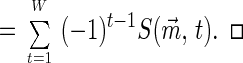Inequalities.

Proposition 4. Let X_p be the maximum of m_p iid random variables uniformly distributed on (0, 1), for p = 1, … , n, as before. Then

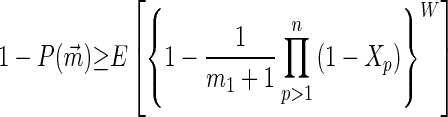9

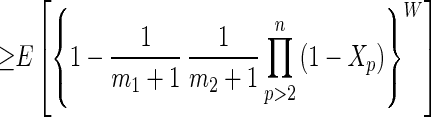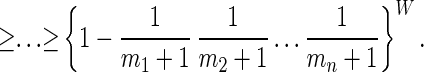Proof: Holding x₂, … , x_n constant, {1 − ∏_p=1ⁿ (1 − x_p)}^W is easily seen to be a convex function of x₁. Consequently, Jensen’s inequality for conditional expected values (ref. 20, p. 449) applies. Because E[X_p] = m_p/(m_p + 1) and E[1 − X_p] = 1/(m_p + 1) for each p, Eq. 2 gives

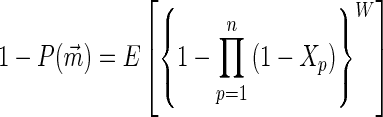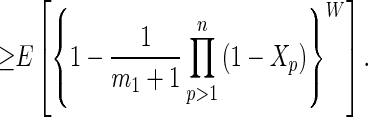The same argument applies successively to p = 2, 3, … , n. □

Limiting Behavior.

Proposition 5. Suppose there are n = 2 players. Then

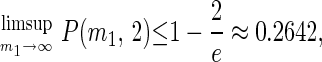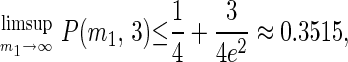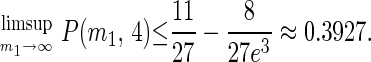Proof: When n = 2, W = (m₁ − 1)(m₂ − 1) and when m⃗ = (m₁, 2), W = m₁ − 1. Hence

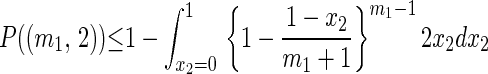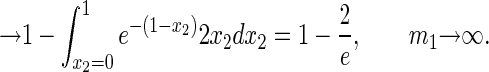The same method proves the other cases. □

Proposition 6. Suppose n is fixed and the number of actions of each player increases without bound. Then

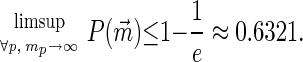Proof: From the definition 1, lim_{∀p,mp→∞} W/∏_p=1ⁿ(m_p + 1) = 1. Then from the last member of inequalities 9,

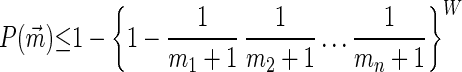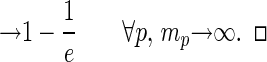Proposition 7. Suppose that every player has the same fixed number m ≥ 2 of actions and that the number of players n increases without bound. Then, in the limit, the probability that a PNE is not PPO vanishes:

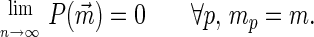Proof: In this case, W = mⁿ − mn + n − 1, so lim_n→∞ W/(m + 1)ⁿ = 0. Hence

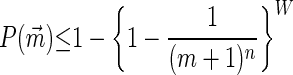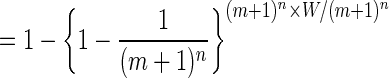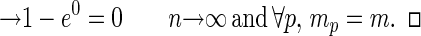Numeric Computations and Results.

Numerical computations indicate that increasing the number of actions available to any player increases the conditional probability that a PNE is not PPO. That is, for all 1 ≤ p ≤ n,

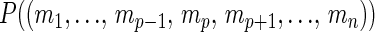10

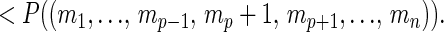However, I have no general proof of this inequality. A sufficient condition for inequality 10 is that for every q such that 0 ≤ q ≤ 1, for r = 1 − q, and for positive integers m ≥ 2, a ≥ 1, b ≥ 1 such that am − b ≥ 1,

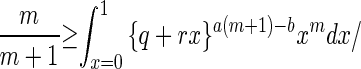11

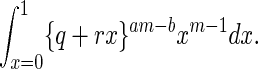It is easily proved that if r = 0, then 11 is an equality, while if r = 1, then 11 is a strict inequality, because then the right side equals (am − b + m)/(am + a − b + m + 1) < m/(m + 1). For r in a sufficiently small open neighborhood (0, ɛ), ɛ > 0, the inequality 11 is strict. If inequality 10 could be proved in general, then all the limsups above would actually be limits.

For very small numbers of players and few actions per player, the finite sum 6 is an easy way to calculate P(m⃗). Fixing the number of players at n = 2, the formula gives for 2 × 2 games P((2, 2)) = S((2, 2), 1) = 1/9, as W = 1; that is, self-interest will not attain a PPO outcome in only 1/9 of games. As the number of actions per player increases, we find P(3, 3) = 244/1,225; P(4, 4) = 229,301/920,205; P(5, 5) = 4,021,593,943/14,354,835,768. A few decimal approximations based on sum 6 are shown in Table 1, labelled F for finite sum.

Table 1.

Conditional probability that a PNE is not PPO in an n-player game where each player has m actions

Actions per player m	Numbers of players n
	2	3	4	5	6
2	S 0.1098	S 0.1257	S 0.1080	S 0.0814	S 0.0544
	I 0.1111	I 0.1211
	F 0.1111	F 0.1241	F 0.1051	F 0.0803	F 0.0582
3	S 0.1911	S 0.2057	S 0.1688	S 0.1102*
	I 0.1992	I 0.1976
	F 0.1992	F 0.2021	F 0.1662
4	S 0.2376	S 0.2531	S 0.1951
	I 0.2492	I 0.2341
	F 0.2492	F 0.2401
5	S 0.2760	S 0.2654	S 0.2168
	I 0.2802	I 0.2541
	F 0.2802
6	S 0.3063	S 0.2837	S 0.2352
	I 0.3010
	F 0.3010

S, based on 2,500 simulations; I, based on numerical integration of Eq. 2, F, based on summation of the finite series 6. 

^*Only 500 simulations. 

An unexpected feature of the results in Table 1 is that, when each player has 2 actions, P(m⃗) is not monotonic in the number of players:

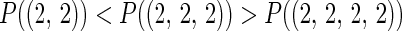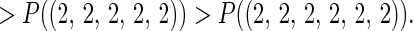Similarly,

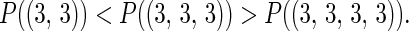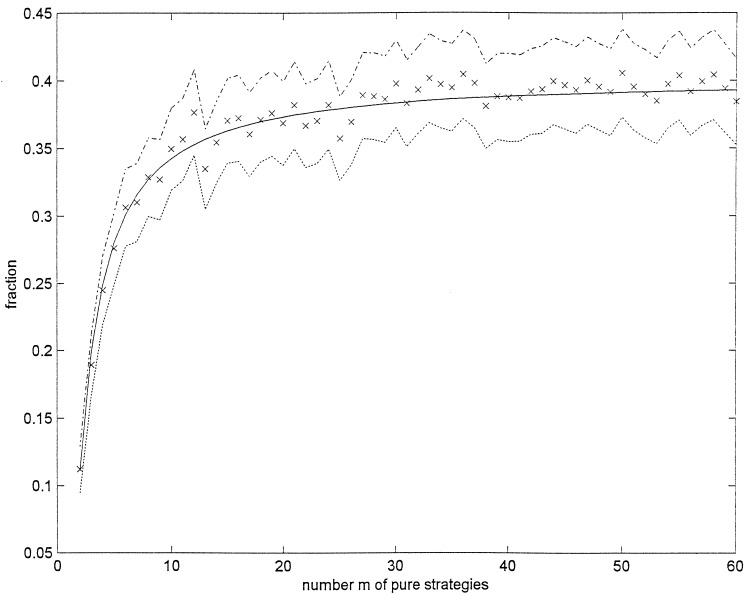
To compute P(m⃗) by Eq. 2 requires an n-fold integral for n-players. For 2 players, the double integral required is readily computed numerically. Table 1 gives a few numeric values (labeled I for integral) for 2 and 3 players. These values agree to the precision shown with those obtained from the finite sum for 2 players, but there are small discrepancies (not exceeding 0.006) between I and F for 3 players. Fig. 1 plots P(m⃗) when both of 2 players have from 2 to 60 actions.

Figure 1.

Probability that a PNE is not PPO in two-player ordinal finite random games where each player has m actions. Solid line, probability computed by numerical quadrature of Eq. 2; ×, fraction estimated from 2,500 simulations for each m; dotted and dash–dotted lines, lower and upper limits of 99% confidence intervals (±2.57 standard deviations) around ×.

To check these results, I simulated 2,500 random games for each combination of the parameter values shown in Table 1 and Fig. 1 and recorded the fraction f of PNEs that were PPO. The denominator of the fraction f is the number N of the 2,500 simulated pairs of payoff matrices that had one or more PNEs. The first PNE encountered in each simulation was checked to see if it was PPO. Only one PNE was examined per simulation. The numerator of the fraction f is the number of PNEs checked that were not PPO. The estimated standard deviation of f is [f(1 − f)/N]^1/2. The simulated values (labeled S for simulated) in Table 1 are generally within 2 or 3 standard deviations of the values calculated by the other methods. When all players have 2 or 3 actions, the simulated values display the same nonmonotonicity with increasing numbers of players as the F estimates of P(m⃗) based on the finite sum 6 (Table 1).

TRANSFERABLE PAYOFFS IN TWO-PLAYER FINITE RANDOM GAMES

We now shift attention to two-player finite games (often called bimatrix games) with transferable utilities, and we give full attention to mixed strategies. Player 1’s pure or mixed strategies may be represented as probability vectors [each denoted x = (x₁, … , x_m1)], that is, vectors with nonnegative elements that sum to 1. (This notation has no connection with the notation x in the previous section.) Each element x_i is the probability of the action i (namely, choosing row i). Player 2’s strategies may be represented as probability vectors [each denoted y = (y₁, … , y_m2)]. If player 1 chooses strategy x and player 2 chooses strategy y, the payoff to player p is v_p(x, y) = Σ_i Σ_j x_ia(i, j, p)y_j, p = 1, 2. As before, a strategic profile (x*, y*) is a NE if and only if, for all strategies x and y, v₁(x*, y*) ≥ v₁(x, y*) and v₂(x*, y*) ≥ v₂(x*, y). Nash (5, 6) showed that every bimatrix game has a NE.

Assuming that payoffs are transferable, the combined value of a strategic profile (x, y) is defined as the sum of the payoffs to each player v(x, y) = v₁(x, y) + v₂(x, y). The Nash high value v_H is the maximum of v(x*, y*) for any NE (x*, y*). The Nash low value v_L is the minimum of v(x*, y*) for any NE (x*, y*).

The Pangloss value (“the best of all possible worlds,” as Voltaire put it) is the highest combined payoff that the two players can obtain by cooperative action: v_P = max_i max_j Σ_p a(i, j, p). Fudenberg and Maskin (21) call a pair of payoffs “strongly efficient” if their sum equals the maximal sum of payoffs. When all payoffs (to individual players and combined) resulting from pure strategic profiles are distinct (as occurs with probability 1 in the random games considered here), a unique pair of payoffs is strongly efficient; a unique strategic profile (called the Pangloss profile) yields the Pangloss value. The Pangloss profile is PPO.

In the following simulations, the elements of the payoff array A are drawn from one of four probability distributions: uniform from 0 to 1 (denoted U); exponential from 0 to infinity with mean 1, denoted X = −log U; normal with mean 0 and variance 1, denoted N; and lognormal, with log-mean 0 and log-variance 1, denoted L = exp(N).

If player 1 chose action i at random and player 2 chose action j at random, without regard to payoffs, then the average combined payoff E(v₁ + v₂) attained by the two players would be 2E(U) = 1, 2E(X) = 2, 2E(N) = 0, and 2E(L) = 2exp(1/2) = 3.2974, where E denotes expectation or average. Letting R denote any one of the random variables U, X, N, and L, the constants k_R = 2E(R) are the average combined value that the players could attain by random choice of a pure strategic profile.

The average improvements in combined payoff, compared to the random baseline, that the players could attain by reaching the Nash low value, the Nash high value, and the Pangloss value are, respectively, E(v_L) − k_R, E(v_H) − k_R, and E(v_P) − k_R. Hence the gain from cooperation relative to the Nash high value is

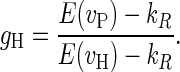The gain from cooperation relative to the Nash low value is

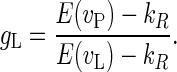Explicit formulas for E(v_H) and E(v_L) appear to be unknown. I estimated these values and the gains from cooperation by simulation. The number of actions available to each player was set in turn at m₁ = m₂ = 2, 3, 4, 5, 6, 7, 8, and 10. For each m₁ = m₂, 100 payoff arrays were sampled numerically from each probability distribution. In total, 8 (game sizes) × 100 (simulations) × 4 (probability distributions) = 3,200 bimatrix games were generated.

For each game, I computed all Nash equilibria (pure and mixed) by using the algorithm of Vorobjev (22), Kuhn (23), and Jansen (24). In this algorithm, for s = 1, … , m₁, each s × s submatrix of A(⋅, ⋅, 1) and the corresponding s × s submatrix of A(⋅, ⋅, 2) are checked to see if the pair of submatrices generates a NE. Each such check requires inverting both s × s submatrices. Because the matrices are sampled from smooth probability distributions, each s × s submatrix is nonsingular with probability 1 so inversion is well defined.

To verify the correctness of my encoding of this algorithm, I checked computational results against numerous textbook examples and hand computations. In addition, I tabulated the numbers of PNE and MNE computed for each simulated game and compared the numbers with known results: nondegenerate bimatrix games have an odd number of NEs (25); if a nondegenerate bimatrix game has T NEs (T odd), at most (T + 1)/2 of them are pure (11); the average number of PNE in a random bimatrix game with smoothly distributed payoffs is 1, regardless of the payoff distribution or the number of actions (ref. 15, p. 280). Numerical results were completely consistent with these theorems.

To check the pseudorandom variates used in the simulations, I compared the average Pangloss values E(v_P) from the simulations using normal random elements against the theoretical expectation of the maximum of m₁m₂ samples from a normal distribution with mean 0 and standard deviation 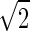. For m₁ = m₂ = 2, 4, 6, the sample average Pangloss values E(v_P) ± one standard deviation of the mean were 1.55 ± 0.10, 2.40 ± 0.08, and 3.09 ± 0.07 (Table 2), none of which differed significantly from the theoretical expectations (based on normal order statistics) of 1.46, 2.50, and 3.00, respectively.

Table 2.

Means and standard deviations (SD) of the Pangloss value (v_P), Nash high value (v_H), Nash low value (v_L), gains from cooperation (g_H and g_L), and frequencies of advantages to cooperation, in simulated two-person games with random payoffs independently distributed according to the uniform, exponential, normal, and lognormal distributions

m	νP		vH		vL		gH	gL	Frequency νP > vH	SD of frequency	Frequency νP > vL	SD of frequency
	Mean	SD	Mean	SD	Mean	SD
	Uniform random elements
2	1.4157	0.0284	1.3122	0.0342	1.2398	0.0359	1.3318	1.7339	0.36	0.0480	0.50	0.0500
3	1.5907	0.0199	1.4449	0.0298	1.2970	0.0286	1.3277	1.9884	0.55	0.0497	0.77	0.0421
4	1.7056	0.0148	1.5828	0.0262	1.3279	0.0269	1.2107	2.1520	0.47	0.0499	0.84	0.0367
5	1.7384	0.0130	1.5813	0.0245	1.2922	0.0258	1.2703	2.5273	0.63	0.0483	0.92	0.0271
6	1.8118	0.0098	1.6977	0.0192	1.3148	0.0247	1.1636	2.5791	0.55	0.0497	0.90	0.0300
7	1.8202	0.0094	1.6810	0.0205	1.2892	0.0219	1.2046	2.8366	0.64	0.0480	0.98	0.0140
8	1.8319	0.0088	1.7138	0.0174	1.2739	0.0199	1.1654	3.0367	0.59	0.0492	0.98	0.0140
10	1.8823	0.0066	1.7725	0.0176	1.2199	0.0172	1.1421	4.0125	0.60	0.0490	0.98	0.0140
	Exponential random elements
2	3.4815	0.1411	2.8728	0.1618	2.5108	0.1507	1.6974	2.9002	0.48	0.05	0.65	0.0477
3	4.7606	0.1677	3.8955	0.1855	3.0581	0.1689	1.4564	2.6091	0.50	0.05	0.72	0.0449
4	4.9592	0.1407	3.7552	0.1705	3.0805	0.1635	1.6859	2.7387	0.61	0.0488	0.79	0.0407
5	5.9810	0.1700	4.4791	0.1953	3.1167	0.1402	1.6058	3.5650	0.63	0.0483	0.87	0.0336
6	5.8790	0.1225	4.3161	0.1577	3.0923	0.1501	1.6748	3.5514	0.73	0.0444	0.94	0.0237
7	6.4515	0.1321	4.7634	0.1978	2.9706	0.1177	1.6109	4.5863	0.67	0.0470	0.95	0.0218
8	6.9736	0.1598	5.2178	0.1906	2.9158	0.1196	1.5457	5.4306	0.79	0.0407	0.98	0.0140
10	7.2419	0.1339	5.5513	0.1757	2.7568	0.0965	1.4761	6.9264	0.71	0.0454	0.98	0.0140
	Normal random elements
2	1.5460	0.0990	1.0982	0.1328	0.9580	0.1306	1.4078	1.6138	0.44	0.0496	0.53	0.0499
3	2.1637	0.0875	1.6321	0.1144	0.9772	0.1128	1.3257	2.2142	0.46	0.0498	0.72	0.0449
4	2.4020	0.0785	1.8329	0.1044	1.1692	0.1096	1.3105	2.0543	0.58	0.0494	0.82	0.0384
5	2.7643	0.0747	2.2084	0.1143	1.0749	0.1055	1.2517	2.5717	0.51	0.0500	0.85	0.0357
6	3.0859	0.0705	2.2795	0.1112	0.9262	0.0784	1.3538	3.3319	0.64	0.0480	0.95	0.0218
7	3.2937	0.0635	2.6162	0.1093	0.8942	0.0789	1.2589	3.6832	0.59	0.0492	0.98	0.0140
8	3.5375	0.0562	2.8731	0.1012	0.9247	0.0713	1.2312	3.8256	0.65	0.0477	1	0
10	3.6397	0.0667	2.8989	0.1110	0.6496	0.0574	1.2556	5.6031	0.66	0.0474	0.99	0.0099
	Lognormal random elements
2	5.7816	0.2759	4.7429	0.2839	4.2310	0.2557	1.7186	2.6609	0.38	0.0485	0.51	0.0500
3	7.9461	0.3982	5.9691	0.4053	4.9034	0.3698	1.7400	2.8946	0.58	0.0494	0.74	0.0439
4	12.1749	0.6061	7.3961	0.5582	4.9426	0.3738	2.1660	5.3960	0.71	0.0454	0.90	0.0300
5	13.6882	0.6132	7.7887	0.5528	4.5540	0.2558	2.3135	8.2694	0.73	0.0444	0.95	0.0218
6	15.2887	0.8331	9.1590	0.6870	5.0921	0.3389	2.0458	6.6815	0.73	0.0444	0.94	0.0237
7	16.1433	0.8001	8.6974	0.6402	5.0961	0.3438	2.3789	7.1421	0.80	0.0400	0.96	0.0196
8	16.6446	0.8053	10.1846	0.6489	4.9593	0.2922	1.9380	8.0315	0.74	0.0439	0.96	0.0196
10	19.4218	0.8089	11.2659	0.7444	5.6061	0.6422	2.0235	6.9842	0.79	0.0407	0.94	0.0237

For payoff matrices with uniformly distributed random elements and two actions for each player (Table 2), the Pangloss value v_P exceeded the Nash high value v_H with frequency 0.36 (that is, in 36 of 100 simulated cases) and exceeded the Nash low value v_L with frequency 0.50. In half of these simulated interactions, two players would have attained the best that cooperation could attain even if they reached the worst outcome attainable by pure self-interest. On the other hand, in 0.36 of the simulations, the two players would have done better through cooperation than they could have done under the most favorable noncooperative NE. The gains from cooperation relative to self-interest ranged from 33% if the average Nash high value were attained (g_H = 1.33), to 73% if the average Nash low value were attained (g_L = 1.73).

As the number of actions available to each player increased from 2 to 10, the estimated probabilities rose to 98% and 60%, respectively, that the Pangloss value would exceed the Nash low value or the Nash high value. The average Pangloss values and the average Nash high values increased steadily and nearly in parallel, but the average Nash low values changed relatively little. Consequently, the gain from cooperation over the average Nash low values rose from 1.73 to 4.01, while the gain from cooperation over the average Nash high values fell from 1.33 to 1.14. Thus the relative gain from cooperation rose or fell with increasing numbers of actions depending on whether the average Nash low value or the average Nash high value was attained.

The results for exponential, normal, and lognormal payoffs were qualitatively similar to those for the uniformly distributed payoffs (Table 2). When players had 10 choices, the Pangloss value exceeded the Nash low value (v_P > v_L) from 94% to 99% of the time; the gain from cooperation (relative to the average Nash low value) ranged from 5.6 to 7.0. When players had 10 choices, the Pangloss value exceeded the Nash high value from 66% to 79% of the time (more frequently than when payoffs were uniformly distributed) and the relative gain from cooperation ranged from 26% to 102% (higher than the 14% gain in the uniform case).

Some simple conclusions emerge from these computations. In two-player finite random games with transferable payoffs and very small numbers of actions, as the number of actions increases, the fraction of cases where a NE attains the maximal combined payoff declines rapidly. Cooperation always yields an average combined payoff that is larger than the average Nash high value, but the relative gain from cooperation decreases as the number of actions increases. The gain from cooperation over the average Nash low value rises dramatically as the number of actions increases.

DISCUSSION

This paper addresses the question: in an ensemble of strategic interactions, how likely is it that noncooperative self-interest alone would yield a Pareto-optimal outcome? Alternatively, how likely is it that cooperation could be advantageous to the participants? Present results suggest an increasing selective advantage to cooperative institutions and behaviors in increasingly complex social and biological interactions.

Here finite random games model an ensemble of interactions. Calculations show that in finite random games with limited numbers of actions, self-interested players can often achieve the best that could be attained by cooperation. As the number of actions increases, it becomes increasingly likely that cooperation enables, or is required for, players to capture payoffs beyond those accessible to self-interest alone. If Pareto-optimal outcomes are desired, then the policy implication is that complex situations are more likely than simple situations to require mechanisms for cooperation, but if cooperation seems unattainable, the set of available actions should be kept small if possible.

Understanding the relative merits of self-interest and cooperation is a central task of the social and biological sciences. In economics, Adam Smith’s parable of the Invisible Hand (ref. 26, p. 423) has been formalized in a so-called Fundamental Welfare Theorem: If all relevant goods are traded in a market at publicly known prices and if firms and households are all price takers, then the outcome of the market is Pareto-optimal. However, markets frequently fail to satisfy all the theoretical conditions required to perform Pareto-optimally (ref. 27, p. 308). Externalities and public goods are among the principal (though not the only) reasons for market failures. For example, self-interested users of road networks (28, 29), queuing networks (30–32), and the Internet (33) experience congestion avoidable by proper pricing or cooperation; common-pool natural resources are often exhausted in the absence of cooperation or rational pricing (34, 35); self-interested rates of savings are suboptimal (36, 37); individual decisions regarding fertility do not take account of all externalities (38–40); independent national decisions regarding monetary and fiscal policy are likely to be less effective than internationally coordinated policy (41); and self-interested national decisions regarding emissions of greenhouse gases reduce welfare compared to those attainable by cooperation (42, 43). Thus there are abundant examples of complex strategic interactions where agents must cooperate to attain Pareto-optimal outcomes.

In terms of biological evolution (44), some evolutionists “argue that the fundamental unit of selection, and therefore of self-interest, … is the gene, the unit of heredity” (ref. 45, p. 11). Others argue that natural selection acts simultaneously at multiple levels (46), for example, on genomes (47, 48), kinships, colonies and communities (49), to produce behaviors that appear sometimes to be cooperative (50), mutualistic (51, 52), or altruistic (53) from the point of view of the individual.

Further Research.

These results have important limitations and leave open many questions.

For ordinal finite random games, mathematical proof is required that increasing the number of actions available to any player increases the conditional probability that a PNE is not PPO.

For two-player finite random games with transferable utility, and with iid payoffs distributed according to a sufficiently smooth probability distribution, where each player has m₁ = m₂ actions, mathematical analysis of the quantities estimated by simulation is needed. Does lim_m1→∞ P{v_P > v_H} exist, and if so what is its value? Can it be proved (for some probability distributions of payoff elements) that g_L, the gain from cooperation relative to the Nash low value, is an increasing function of the number of actions available to each of two players, whereas g_H, the gain from cooperation relative to the Nash high value, is a decreasing function of the number of actions available, as the simulations suggest? Supposing each NE were considered equally likely, the average NE payoff could be simulated. How would the average NE payoff behave, and can its behavior be analyzed mathematically?

Additional technical questions include: What are the analogous results for evolutionarily stable strategies (54)? In finite random games with cardinal payoffs, what is the conditional probability that a PNE is not Pareto-optimal? What is the probability that a MNE is not PPO? is not Pareto-optimal? Do these probabilities depend on whether the game has a PNE?

ABBREVIATIONS

iid

independently and identically distributed

MNE

mixed Nash equilibrium

NE

Nash equilibrium

PNE

pure Nash equilibrium

PPO

pure Pareto-optimum