The relative importance of directional change, random walks, and stasis in the evolution of fossil lineages

Abstract

The nature of evolutionary changes recorded by the fossil record has long been controversial, with particular disagreement concerning the relative frequency of gradual change versus stasis within lineages. Here, I present a large-scale, statistical survey of evolutionary mode in fossil lineages. Over 250 sequences of evolving traits were fit by using maximum likelihood to three evolutionary models: directional change, random walk, and stasis. Evolution in these traits was rarely directional; in only 5% of fossil sequences was directional evolution the most strongly supported of the three modes of change. The remaining 95% of sequences were divided nearly equally between random walks and stasis. Variables related to body size were significantly less likely than shape traits to experience stasis. This finding is in accord with previous suggestions that size may be more evolutionarily labile than shape and is consistent with some but not all of the mechanisms proposed to explain evolutionary stasis. In general, similar evolutionary patterns are observed across other variables, such as clade membership and temporal resolution, but there is some evidence that directional change in planktonic organisms is more frequent than in benthic organisms. The rarity with which directional evolution was observed in this study corroborates a key claim of punctuated equilibria and suggests that truly directional evolution is infrequent or, perhaps more importantly, of short enough duration so as to rarely register in paleontological sampling.

First proposed more than 30 years ago, the model of punctuated equilibria (1) claimed that gradual, directional changes are rare in the fossil record, and instead most traits show little net change except for geologically rapid punctuations associated with speciation. Many aspects of this claim were contentious, with especially heated debate concerning what novel evolutionary processes, if any, are required to account for this pattern (2, 3). More fundamentally, even whether punctuated equilibria accurately describes the empirical fossil record has been disputed. Specific evolutionary sequences interpreted as gradual by some were seen as representing stasis and/or punctuation by others (4). These disagreements are reflected in published overviews of the subject, which have come to rather disparate conclusions about the preponderance of stasis and gradual transformation within lineages (5–9).

These conflicting views linger unresolved for two primary reasons. First, stasis and gradual change were initially identified subjectively, and, although several quantitative approaches have been developed in the interceding years (10–12), none readily permit comparison of the statistical support for competing evolutionary interpretations (13). Second, because it is generally agreed that no pattern is universal, robust estimates of the relative frequency of different evolutionary modes require data from many traits and lineages. Although previous reviews have surveyed many prominent case studies (5–9), these reviews are all qualitative, and none have individually assessed more than a few dozen evolving traits.

In this paper, I present analyses that address both of these limitations. Recent analytical developments (13) permit the measurement of statistical support for different hypothesized modes of evolution in fossil sequences. I apply this approach to a large sample of >250 documented cases of phenotypic traits evolving within fossil lineages. This large dataset allows for much greater confidence in assessing the relative frequency with which different evolutionary modes occur. In addition, comparisons of different traits, lineages, and depositional environments within this database can be used to test various biological and geological factors that have been suggested to shape phenotypic divergence.

In recent years, three models have become standard in attempts to understand the nature of evolutionary divergence in fossil lineages: directional change, unbiased random walk, and stasis (10–13). Although simplified, these modes of change are useful abstractions that distinguish fundamentally different kinds of evolutionary dynamics. Directional evolution generates trends within lineages and, traditionally at least, was thought to be common in the fossil record (14). When operating in directional mode, evolutionary divergence accrues steadily, and descendants are readily discriminated from ancestral populations of the same lineage (Fig. 1A). At the opposite extreme, stasis allows for fluctuations between populations but predicts no net change within evolutionary sequences (Fig. 1C). Unbiased random walks are intermediate in pattern; they are not inherently directional, but phenotypic differences accumulate so that expected divergence increases with elapsed time (Fig. 1B). Quantitatively, the behavior of each of these modes is governed by just a few parameters, and their relative success at accounting for real paleontological data can be unambiguously measured by using likelihood-based procedures (see Methods).

Fig. 1.

Examples of fossil trait sequences that are best fit by each of the three evolutionary models. (A) Directional evolution: shell shape in the planktonic foraminifera Contusotruncana from DSDP site 384 (45). (B) Unbiased random walk: shell width in the land snail Mandarina (46). (C) Stasis: shell shape (convexity) in the bivalve Chesapecten nefrens (34).

Results

In fitting the three standard modes of evolution to a large sample of paleontological sequences, three main findings emerge.

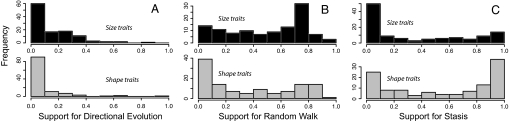
1. Directional evolution is rarely observed within lineages traced through the fossil record. Only ≈5% of cases (13 of 251) are best fit by the directional evolution model, with the remaining sequences split approximately evenly between the unbiased random walk and stasis models (Table 1). Akaike weights for directional evolution are mostly quite low (median = 6%) (Table 1), and very few sequences provide unequivocal support for this model (Fig. 2A).

2. Size traits are significantly less likely than shape traits to experience stasis (Fig. 2C). Approximately 37% of size-related trait sequences are best fit by the stasis model; this proportion is nearly 60% for shape traits (G = 11.59, df = 2, P = 0.003) (Table 1). On average, stasis receives substantially more support in size traits compared with shape traits (W = 4285, P < 0.0001) (Fig. 2C), with the opposite pattern holding true for the random walk model (W = 8164, P = 0.001) (Fig. 2B). Because this contrast holds separately over the three broad categories of fossils (Fig. 3), it is not likely to result from the idiosyncrasies of any particular study or clade.

3. Other factors, including depositional environment, clade membership, and temporal span of the sequences, have mixed or relatively minor influence on evolutionary mode. It has been suggested on geological and biological grounds that planktonic fossils should be especially liable to exhibit gradual transformation (8, 15). There is some support for this proposal. Directional sequences are more common in planktonic microfossils than in either benthic microfossils (12% vs. 3%; G = 3.92, df = 1, P = 0.048) or benthic macrofossils (12% vs. 2%; G = 4.30, df = 1, P = 0.038). Additionally, size traits show less support for stasis in planktonic microfossils than in benthic microfossils (W = 304, P = 0.034), but the same difference does not hold for shape traits (W = 358, P = 0.88) (Fig. 3). There is mixed evidence for evolutionary differences between micro- and macrofossils. These two fossil groups do not differ in their support for stasis in size traits (W = 1,400, P = 0.24), but macrofossil shape sequences appear to be even more prone to stasis than their microfossil counterparts (W = 984, P = 0.0002) (Fig. 3), although this difference should be interpreted cautiously because much of the macrofossil shape data are from just a few studies [supporting information (SI) Table 3]. The situation is more straightforward with regard to the temporal scope of the studies—neither the total temporal span of a sequence nor the median elapsed time between adjacent sampled populations had any significant influence on the support for the various evolutionary models (duration: G = 2.43, df = 4, P = 0.66; resolution: G = 4.77, df = 4, P = 0.31).

In summary, although there is strong evidence for different evolutionary dynamics in size versus shape traits, the full range of evolutionary dynamics are observed more equally across different fossil groups, depositional environments, and temporal windows of observation.

Table 1.

Summary of the empirical support for the three evolutionary models

Model	Median model support	Frequency with which each model is best supported
		All	By trait type			By fossil group
			Size	Shape	Other	Plank micro	Benth micro	Macro
Directional change	0.06 (0.04, 0.08)	13	5	4	4	5	3	5
Random walk	0.47 (0.39, 0.56)	123	67	43	13	24	57	42
Stasis	0.34 (0.20, 0.50)	115	42	68	5	12	37	66

The first column indicates the median model support, measured as Akaike weight, with 95% confidence intervals generated by bootstrap resampling the observed weights 10,000 times. The remaining columns give the frequencies for which each of the indicated models is the best supported of the three, first tabulated over all sequences, then split across trait types and taxonomic categories. ″Other″ traits are mostly meristic (count) variables, with a few multivariate descriptors that include aspects of both size and shape. The fossil groups are listed in order of planktonic microfossils (Plank micro), benthic microfossils (Benth micro), and macrofossils (Macro).

Fig. 2.

Frequency distribution of statistical support, measured as Akaike weights, for three evolutionary models: directional evolution (A), unbiased random walk (B), and stasis (C). For each model, size traits (black bars, Upper) are shown separately from shape traits (gray bars, Lower).

Fig. 3.

Mean and approximate 95% confidence interval of support for the stasis model, computed separately by both taxonomic categories (benthic microfossils, planktonic microfossils, and macrofossils) and trait types (black circles, size traits; gray squares, shape traits).

Beyond summarizing the overall success of the models, Akaike weights allow for more nuanced exploration of the strength of evidence for different models. For example, the shell shape trend in the foraminifera Contusotruncana (Fig. 1A) is very robust; the directional evolution model accounts for nearly all (96%) of the Akaike weight for this sequence. However, most sequences cannot be so unambiguously assigned to evolutionary modes. On average, the best-supported model accounts for 77% of the available Akaike weight, with the second and third best models accounting for 20% and 3%, respectively. It is common (78%) for the worst of the three models to achieve only negligible support (weight <5%), but in only 20% of sequences can both suboptimal models be confidently dismissed. This capacity to quantify shades of support is invaluable for analyzing real paleontological data, which do not always conform to idealized models.

Discussion

The paucity of trait sequences best described by the directional change model supports one of the central claims of punctuated equilibria, namely that gradual and directional transformations are rarely observed in the fossil record. Although not exhaustive, the large database of evolutionary sequences analyzed here is likely to be representative of the published paleontological literature (see Methods). Moreover, because researchers have preferentially studied traits and lineages with prior evidence for gradual change (9, 16), the 5% incidence of directionality is likely to be an overestimate.

Some previous paleontological studies have used a model of directional change in which evolutionary changes proceed at an absolutely constant rate in the same direction indefinitely (11). Although of heuristic value, most would agree that this model is not realistic over paleontological time scales. In contrast, directional evolution as modeled here assumes only that the average evolutionary increment differs from zero. As a result, this model can be strongly supported even when there is only a slight excess of microevolutionary changes in one direction over the other. For example, test shape in Contusotruncana shows a robust increasing trend (Fig. 1A), yet the parameter estimates of this model imply only a trivial excess of increases on generational time scales: On average, this trait should increase in only 50.1% of years. From a genetic standpoint, there is little reason to believe that this dynamic could not be sustained indefinitely. In fact, the net rate of divergence for this trait is substantially slower than the expectation from mutation–drift balance (17), indicating that variation generated by mutation would be more than capable of keeping pace with this trend. The rarity in the fossil record of lineages with this degree of directionality is therefore meaningful, and it requires explanation.

Some perspective may be gained by considering population dynamics in terms of phenotypic adaptive landscapes (14, 18, 19). Assuming that the relevant traits are genetically variable and that genetic drift is unimportant, the location of a population on this landscape is determined by the position of selective optima of relatively well adapted phenotypes. When these peaks move in response to changes in the selective conditions, populations follow with a lag that is generally negligible on geological time scales (20). When net divergence occurs within a clade, evolution is very likely to be directional, at least in part, and at some temporal scale. Within this framework, the results of the present study can be accommodated if directional adaptive shifts are typically rare, too brief to resolve in the paleontological record (<10⁴ years in most depositional environments), or both. The minority of sequences that do exhibit morphological trends over geological time would then correspond to the relatively rare instances in which selective conditions trend directionally for an unusually long period. This general explanation could hold whether or not periods of directional change are associated with speciation, as postulated by the punctuated equilibria model.

As modeled here, evolutionary dynamics were assumed to be uniform throughout the observed duration of each fossil sequence. It is possible that directional change could be limited to a subset of samples within a sequence; at the extreme, this could be expressed as a single punctuated burst between two consecutive samples. I have developed extensions of the methods used in this paper that allow for a shift in evolutionary dynamics within a sequence (unpublished data). I have used these methods to analyze many fossil sequences, but even the most promising examples (e.g., refs. 21 and 22) do not support models of sustained directional change, although single interval punctuations are sometimes implied (unpublished data). Thus, even relaxing the assumption that evolutionary mode is uniform within lineages, we are still led to the conclusion that directional change is rarely observed over paleontologically significant time scales.

Whereas directional trends are rare, random walks appear to be at least as frequent as stasis in these fossil lineages. At times, the term stasis has been applied more widely to describe any evolutionary pattern that is not strongly directional. Such an overly broad definition is at odds with most recent accounts of stasis (9, 23) and obscures real differences between the fluctuating but stationary trajectories of stasis and the unbounded meandering of random walks.

Despite the commonness of stasis, there is little consensus about its cause or causes. Various forms of stabilizing natural selection have been invoked (2, 8, 20, 24, 25), and early suggestions of constraint (1, 26) have been resuscitated by more sophisticated genetic perspectives (27). One factor recently advocated is spatially heterogeneous natural selection across semiisolated populations (9, 23, 28). This is thought to induce stasis because local adaptive divergences are potentially nullified by gene flow between demes. However, because this explanation relies on properties of populations, it should affect all traits equally. As such, it cannot account for a prominent feature of the present dataset: the preponderance of stasis in shape more so than size traits. This difference suggests that the population structure argument is incomplete and that at least part of the explanation for stasis must involve properties of traits. One possibility is that body size may be a more frequent target of directional natural selection than shape traits. This suggestion has been advanced previously on the basis of differences in genetic architecture between size and shape features (29) and measured selection coefficients in natural populations (30). Regardless of mechanism, the current finding is consistent with several previous paleontological studies suggesting that body size may be more evolutionarily labile than aspects of shape (16, 31, 32), and this size–shape contrast may be a valid macroevolutionary generalization.

Punctuated equilibria sparked an intense debate within the paleontological and biological communities about the nature of phenotypic evolution as revealed by the fossil record. On the whole, this debate was tremendously productive. In addition to prompting paleontologists to scrutinize the limits of sedimentological resolution and completeness (33), it also generated a wave of important studies that carefully documented patterns of morphological evolution in fossil lineages. To the extent that this debate was unprofitable, however, much of the fruitless back and forth can be traced to the ambiguity of verbal descriptions of evolutionary mode. The use of explicit, statistical models of evolution can reconfigure discussions about evolutionary mode into a form that better allows for the resolution of outstanding evolutionary issues.

Methods

Datasets.

The database of empirical datasets, drawn mostly from the published literature, includes 251 traits from 53 different evolutionary lineages (SI Table 3). I included in this database all published case studies for which the requisite data were published, regardless of the evolutionary interpretations of the original authors. I generally did not seek unpublished data directly from authors of particular case studies so as to reduce the possibility of biasing the frequencies of evolutionary modes. The one exception to this was Kelley's (34) study of Neogene mollusks, which was included because it exhaustively analyzed all mollusk species that were adequately represented in the sampled deposits and, thus, represented an unbiased sample of lineages. Although some well known case studies, including celebrated examples of both stasis (35) and gradualism (36), could not be included because the necessary data were not available, the resulting database is likely to be relatively representative of the published paleontological literature. Many microfossil sequences were analyzed, especially for benthic foraminifera, planktonic foraminifera, and ostracodes (Table 2). The distribution of macrofossils is more uneven, but two important fossil groups, mollusks and mammals, are well represented by many sequences from multiple studies. Several different kinds of traits were analyzed, including those related to body size (dimensions of organisms or parts of organisms), shape variables (ratios, angles, landmark positions, and outlines), meristic traits, and multivariate descriptors.

Table 2.

Taxonomic distribution of analyzed fossil sequences

Taxonomic category	No. of sequences	N
Planktonic microfossils
Foraminifera	23 (8, 6)	48
Radiolaria	9 (3, 1)	9
Conodonts	9 (1, 1)	6
Benthic microfossils
Foraminifera	37 (5, 4)	19
Ostracodes	60 (12, 3)	7
Macrofossils
Mollusks	70 (10, 6)	10
Mammals	40 (11, 7)	7
Teleost fish	2 (2, 2)	17.5
Trilobites	1 (1, 1)	22

The second column indicates how many sequences were analyzed in each taxonomic category, followed in parentheses by the number of different lineages and studies, respectively, represented. N is the median number of sampling horizons per sequence for each taxon.

Evolutionary Modes.

Each mode of evolution was expressed as a statistical model. Directional evolution was modeled as a general (also called biased) random walk, an approach that has proven useful in previous paleobiological studies (10, 13, 37, 38). In this model, time occurs in discrete intervals, during each of which evolutionary transitions are drawn at random from a distribution of “steps.” Long-term dynamics under this model are determined by the mean (μ_s) and variance (σ_s²) of this step distribution; μ_s governs the directionality of trait evolution, whereas σ_s² determines the volatility of evolutionary changes around the directional trend (13). According to this model, the expected change between ancestor and descendant populations separated by t time steps is normally distributed with a mean of tμ_s and a variance of tσ_s².

An unbiased random walk is a special case of this model in which trait evolution is not directional (μ_s = 0). In this situation, the expected difference between ancestor and descendant is normally distributed with a zero mean and a variance of tσ_s². In modeling stasis, I followed a recent parameterization (39) that invokes a central phenotype (θ), around which populations fluctuate with a variance (ω). Regardless of the ancestral phenotype, the expected descendant value is normally distributed with a mean of θ and variance ω. Thus, for each model, the expected difference between successively sampled populations in an evolving lineage is a normally distributed variate, with mean and variance that depend on the specific evolutionary parameter values. For real paleontological sequences, sampling error must also be incorporated (see ref. 13). The expected distribution of ancestor–descendant difference allows one to compute the likelihood of empirical sequences for each evolutionary model (13).

For each dataset, three evolutionary models—directional change, unbiased random walk and stasis—were fit by maximum likelihood using the package paleoTS in the freely available statistical programming environment R (40). Model support was assessed by using the bias-corrected Akaike Information Criterion (AIC_C) (41), which balances goodness of fit (log-likelihood) with model complexity (the number of model parameters). The model with the lowest AIC_C value is best supported, with the degree of support quantified by Akaike weights. These weights are a simple transformation of AIC_C values that sum to one and are interpreted as approximate probabilities that each model is the best of those considered (41). An important advantage of this model-based approach is that no evolutionary mode is granted privileged null status; all models are compared on an equal footing based on their empirical support. Because the parsimony penalty term of the AIC_C is particularly severe at low sample sizes, the unbiased random walk model (which has one parameter) might be at an advantage over the two-parameter models (directional change and stasis) for very short sequences. However, this effect appears to be minor because many of the shortest sequences (fewer than eight samples) favor stasis or directional change despite the parsimony advantage of the random walk model.

As in previous paleontological studies, these evolutionary models are based on patterns rather than on explicit microevolutionary processes. Nevertheless, each model can be related to microevolutionary mechanisms; for example, stabilizing selection can produce stasis (20) and unbiased random walks can result from neutral genetic drift or wandering adaptive optima (42). However, each evolutionary mode is consistent with a plurality of microevolutionary scenarios, and there persists considerable disagreement about how best to link pattern and process in evolving lineages (for differing explanations of stasis alone, see, for example, refs. 23, 25–28, 43, and 44). Until such time that this pattern–process divide can be better bridged, pattern-based models, such as stasis and random walks, offer a fruitful means by which different kinds of evolutionary trajectories can be explored.

A summary with information about the traits, lineages, and model fits for all analyzed sequences is available as SI Table 3.

Testing for Differences Across Evolutionary Mode.

Nonparametric statistics were used to test whether evolutionary mode differed systematically with respect to trait type (size and shape), life habit (planktonic and benthic), broad fossil groups (microfossils and macrofossils), and the temporal duration/resolution of the fossil sequence. G tests assessed whether counts of the best-supported evolutionary mode were independent of categorical variables (trait type, life habit, and fossil group), and Wilcoxon rank sum tests were used to test for differences in median Akaike weight for particular models across groups. For temporal duration (total time span of the sequence) and resolution (the median elapsed time between adjacent samples), the distributions of these variables were divided into empirical thirds at the 33rd and 67th percentiles, and G tests were used to test whether the distribution of best-supported models was independent of the temporal duration and resolution of the samples (duration cutoffs: 1.4 and 4.5 Ma; resolution cutoffs: 0.08 and 0.34 Ma). Empirical thirds were chosen as a compromise between the number of temporal bins and sample sizes within bins; other similar divisions of these distributions (halves, quartile, and quintiles) yielded similar results.