Attosecond electron pulses for 4D diffraction and microscopy

Abstract

In this contribution, we consider the advancement of ultrafast electron diffraction and microscopy to cover the attosecond time domain. The concept is centered on the compression of femtosecond electron packets to trains of 15-attosecond pulses by the use of the ponderomotive force in synthesized gratings of optical fields. Such attosecond electron pulses are significantly shorter than those achievable with extreme UV light sources near 25 nm (≈50 eV) and have the potential for applications in the visualization of ultrafast electron dynamics, especially of atomic structures, clusters of atoms, and some materials.

Structural dynamics of complex systems with many atoms, such as those of chemical reactions and phase transitions, involve intermediates and transition states on a multidimensional energy landscape (see refs. 1 and 2). Likewise, when more than one electron is involved, electron dynamics are expected to define a landscape, because electrons are correlated by Coulomb forces that may result in sequential or concerted interactions (see refs. 3 and 4). However, because of the difference in time scales, femtoseconds for nuclear motions and attoseconds for electron motions, consideration of the energy uncertainty must be addressed (5, 6). For chemical and biological structures, the femtosecond resolution is ideal, because on this time scale the energy uncertainty is only a small fraction of the intrinsic energy and the average photon energy can be made in resonance with molecular or material transitions, from the infrared to the UV. In addition, spatial localization of the nuclear wave packet is nearly complete (7).

Because electron dynamics are on the time scale of attoseconds, the applications become that of atoms near or above ionization or in environments such as clusters or special materials. The pioneering work (see ref. 8) in the generation of attosecond pulses at wavelengths of 15–40 nm (30–100 eV) and bandwidths of 10–30 eV (9–14) has shown applications so far in the spectroscopy of Auger processes (15), tunneling in atoms (16), and reconstruction of diatom charge distributions (17). The dynamics resolved is that of a few femtoseconds (18–20).

Here, we focus on the possibility of generating near-15-attosecond free electron pulses and their utilization to extend the domain of electron microscopy and diffraction to the subfemtosecond and attosecond scales. This direct visualization of structures in space and in time has been termed 4D imaging (21–23) and provides the necessary picometer spatial and ultrafast temporal resolution (21, 24). From the uncertainty relation, we derive the general requisites for reaching the attosecond time scale with electrons. A compression methodology for electron packets in synthesized optical fields of intensity gratings is discussed, and the reported numerical simulations show the feasibility of such approach under realistic experimental conditions.

Attosecond Pulse Generation and Characteristics

The generation of optical attosecond pulses during the interaction of intense femtosecond pulses with atoms (or small molecules) can be described as follows (8, 9, 25). By ionization at the field maxima of the optical cycles, electrons are released and accelerated back and forth in the time-dependent electric field of the laser pulse. A large fraction of the electrons returns to the ion core within a few femtoseconds with kinetic energies that are significantly increased by the trajectories in the laser field. Recombination then generates extreme UV electromagnetic radiation with the time structure of an attosecond pulse train (11). Isolated attosecond pulses are obtained by applying few-cycle laser pulses, polarization modulations, or multicolor fields, which restrict attosecond pulse generation to a single optical cycle (9, 10, 12, 14, 15, 26). To date, pulses as short as 130 as have been achieved (14).

Applications in spectroscopy make use of such attosecond pulses or the recolliding electrons. The decay of inner-shell electrons by an Auger mechanism (15) and electron tunneling in the presence of an optical field (16) were studied by using attosecond pulses to initiate the dynamics and by following the secondary electron emission processes by attosecond streaking (12). Timing of the electron recollision by using different wavelengths allowed for the nuclear oscillation in diatomic molecules to be investigated on the femtosecond time scale (18). The recollision process involves interference between the outgoing free electron and the residual electron wave packet, and the interference for a set of recollision directions mirrors the original orbital (17). Quantum interference, depending on molecular symmetry, was found in rotationally aligned molecules (19) and recollision of a chirped electron wave packet was used to probe molecular dissociation (20). When resolved, these methodologies provide dynamics on a few-femtosecond time scale, but recently some attosecond fine-structures were reported (16).

Several characteristics of attosecond optical pulses and their applications are worth mentioning. First, attosecond dynamics is linked to broadband excitation. Similar to the launch of nuclear wave packets by femtosecond lasers, attosecond electron dynamics can only be initiated by an excitation process that reaches a sufficiently large ensemble of states to spatially localize an electronic wave packet. Applications in the attosecond regime with pulses of 30–100 eV involve electronic transitions near or above the ionization limit of atoms. Second, the generation of attosecond optical pulses is only possible at central energies high enough to support one optical cycle. Current technology has reached such a limit, and the recently demonstrated 130-attosecond pulses (λ ≈ 35 nm) are almost fully compressed to the Fourier limit (14); progress toward significantly shorter pulses will require soft x-ray energies (8). Strategies for initiating and probing attosecond electron dynamics must therefore take such energy range and the required wave packet localization into account.

Our interest here is focused on the development of attosecond free electron pulses for 4D diffraction and microscopy, as mentioned above. In contrast to extreme UV and x-ray radiation, electrons offer a much shorter de Broglie wavelength (for example, λ_el = 7 pm at 30 keV and λ_el = 2.5 pm at 200 keV), readily attainable electron energy scaling from electron volts to megaelectron volts, and a large cross-section for elastic and inelastic interaction with matter. Central to attosecond clocking is impulsive activation and attosecond imaging. In what follows, we consider the generation of attosecond electron pulses for such domain of experiments, especially in view of recent developments in this laboratory (21) of 4D ultrafast electron microscopy (22, 27–29) and diffraction (2, 30–32).

Results and Discussion

Three challenges have to be addressed to advance imaging by electron diffraction and microscopy into the attosecond time domain. First, the relevant time scale should be below 100 attoseconds to initiate and freeze the relevant transient electronic configurations in time. Second, nonrelativistic electron pulses with appropriate energy are needed to obtain a good scattering cross-section and detectable diffraction angles. Third, the attosecond electron pulses must be well synchronized with an optical field, or a second electron/x-ray pulse, to initiate the dynamics. These three requirements are met in the approach presented here. Specifically, we illustrate how 15-attosecond electron pulses at 31-keV energy can be generated in full synchronization to the phase of a laser wave, and these pulses may be used as pump and probe or only for probing in imaging and other applications.

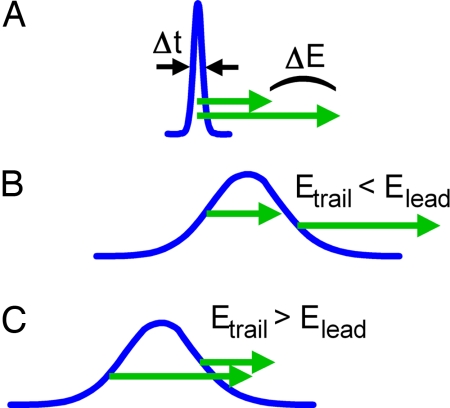
Fig. 1 depicts the physical conception underlying the approach. Fig. 1A shows an extremely short electron pulse of duration Δt. According to the uncertainty relation, such a pulse must have a significant energy bandwidth ΔE and at nonrelativistic energies different parts of the electron packet therefore travel with significantly different velocities. For example, a 15-attosecond pulse at 30-keV central energy will disperse to a duration of many femtoseconds after just 10 mm of propagation. Such a pulse is then chirped, in the sense that its fast parts lead its slow parts by a well defined (and in principle reversible) relationship of energy versus time (see Fig. 1B). The generation of free-space attosecond electron pulses with nonrelativistic energies must therefore begin with a temporally extended and negatively chirped electron packet such that the lower-energy parts initially lead the higher-energy parts (see Fig. 1C). For a suitable primary distribution of energies and speeds, the packet will then self-compress to an extremely short duration after some propagation in free space.

Fig. 1.

Propagation dynamics of an attosecond electron pulse (blue). (A) An attosecond electron packet, because of the uncertainty relation, must have a large energy bandwidth, ΔE, corresponding to a distribution of speeds (green arrows). (B) The packet acquires dispersion while propagating in free space such that its trailing parts have less energy and speed than its leading parts. (C) The pulse compression concept used to generate an attosecond electron packet. The trailing parts must initially have a higher energy and speed than the leading parts (green arrows). After some propagation in free space, this difference leads to self-compression with attosecond duration (see A).

For the femtosecond regime, we recently proposed a spatially tilted electron generation, making use of such concept for generating self-compressing electron packets with a high electron density (24). Likewise, recompression of long electron pulses was suggested with THz fields or radio-frequency cavities acting as time-varying acceleration elements (33, 34). With such schemes, subfemtosecond pulse durations could in principle be reached, but the resulting electron pulses are not well synchronized to the optical field required to initiate the ultrafast dynamics to be investigated; the temporal jitter degrades the effective time resolution. Other proposals for the generation of attosecond electron pulses rely on relativistic laser intensities for direct electron acceleration to megaelectron volt energies (35, 36). However, such high-energy electrons are not favorable for our diffraction and imaging experiments, because of their low scattering cross section and low diffraction angles.

In the present approach, the starting point is the use of an electron packet of ∼30 keV energy and 300 fs duration. The pulses can be generated from photo-emitted electrons accelerated in static fields (21, 37, 38). The electron packet is first considered to be monoenergetic in the sense that ΔE ≪ E_central, and of low electron density, i.e., space-charge-free; such effects will be discussed later. Central to the present approach is the use of synthesized optical fields to compress a long electron packet to pulses of subwavelength duration. The 30-keV electron packet travels at ≈0.33 c and has therefore a large velocity mismatch compared with the phase velocity of light. The direct interaction with an optical electric or magnetic field will therefore average to zero and cannot be readily used to achieve the macroscopic acceleration and retardation that are necessary for self-compression. We therefore invoke the ponderomotive force, which is proportional to the intensity gradient of the optical field and accelerates charged particles out of regions with high optical intensity (39–41). The intensity distribution of an optical field can move with a velocity of less than the speed of light, and its movement can therefore be matched to the speed of nonrelativistic electrons. In consequence, the ponderomotive force can accumulate over an extended period with sufficient effect on propagation. By synthesizing a suitable optical intensity distribution, the ponderomotive force can be tailored to control and steer an electron packet in space and time.

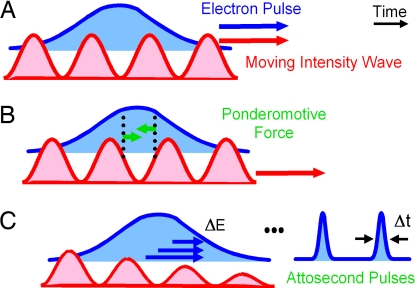
For the generation of attosecond electron pulses, we invoke the concept of a moving intensity grating. Fig. 2A depicts a standing wave (red), in which the intensity maxima and minima travel with the same group velocity as the electron packet. Such a wave can be generated from two colliding laser pulses of different frequencies, as shown below. Within a copropagating electron packet (blue), those parts located at a rising slope feel an accelerating ponderomotive force, and those parts that travel along a falling slope feel a retarding ponderomotive force (Fig. 2B, green arrows). Over time, these forces accumulate to a macroscopic momentum and velocity distribution that is directly correlated with the original electron position. After the laser intensity fades away, this momentum distribution (shown as ΔE in Fig. 2C) leads to self-compression after some propagation in free space. The originally extended electron packet compresses to ultrashort pulses of duration Δt, with an interpulse spacing given by the wavelength of the intensity wave.

Fig. 2.

Concept of optical compression in a moving intensity grating. (A) An electron packet (blue) copropagates at a velocity of less than the speed of light with the maxima and minima of a moving intensity wave (red), synthesized from two counterpropagating laser pulses of different frequencies (see text). (B) The ponderomotive forces (green arrows) push electrons out of regions with high intensity. Within every optical cycle, the parts of the electron packets that are located at a falling slope are accelerated (left green arrow) and the parts located at a rising slope are retarded (right green arrow). (C) The resultant momentum and velocity distribution Δp leads into self-compression to the final attosecond duration (Δt) within every optical cycle (see text).

The synthesis of the moving intensity grating is made through the superposition of two colliding waves of different frequencies ω₁ and ω₂. The fields are laser pulses with durations of 300 fs, which is long enough to cover the entire initial femtosecond electron packet during the temporal overlap of the two laser pulses. Such interferences were considered for transversal deflection of electrons in oscillating fields with interest in diffraction and quantum effects (40, 42). Here, our focus is on the compression of electron pulses to reach the attosecond regime. The higher frequency pulse (ω₁) is chosen to copropagate with the electron packet, and the lower frequency pulse (ω₂) to come from the opposite direction. From the perspective of an electron moving with v_el, both laser waves are subject to the Doppler shift. For a suitable ratio of ω₁ and ω₂, the two Doppler-shifted frequencies become equal and the electron, in its rest frame, is statically located on a standing wave. For the Doppler-shifted frequencies ω̃₁ and ω̃₂ we obtain

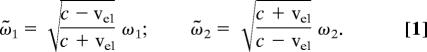To yield a standing wave in the electron packet's rest frame, ω̃₁ must be equal to ω̃₂, and it is straightforward to find:

For example, the laser frequency ω₁ can conveniently be chosen to be the second harmonic of ω₂. As such ω₁ = 2ω₂ and the matching electron velocity becomes v_el = (1/3)c, corresponding to E_el ≈ 31 keV. Table 1 gives other combinations of laser harmonics that match the group velocity of various electron energies. Other electron velocities in such range can be matched with tunable laser sources (43).

Table 1.

Speed of a moving intensity wave, together with the matching electron speed and energy, for different combinations of laser harmonics

Laser harmonics	Electron speed, c	Electron energy, keV
2ω, 3ω	0.2	10
ω, 2ω	0.33	31
ω, 3ω	0.5	79
ω, 4ω	0.6	128

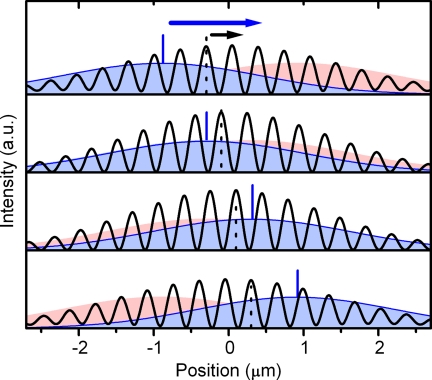
Fig. 3 depicts a moving intensity wave as observed in the laboratory frame. The two colliding laser pulses are shown in red (ω₂) and blue (ω₁), with the position of intensity maximum marked in blue. Both pulses interfere, and the resulting intensity (averaged over one optical oscillation period) is shown as the black line. Note that the two laser pulses travel with the speed of light, but the maximum of the interference pattern (marked by the dotted lines) moves with only 0.33 c. We also note that the position of maximum intensity (blue line) is moving much faster than that of the interference. Nonrelativistic electrons with v_el = 0.33 c can therefore copropagate with matched speed, and effective ponderomotive compression takes place.

Fig. 3.

Synthesis of a moving intensity grating. Two laser pulses of different frequencies (blue and red) interfere in a colliding geometry. Both pulses travel with the speed of light (see blue mark). The intensity of the resulting interference pattern (averaged over one temporal optical cycle) is shown as oscillating pattern (black). Because of the two different optical frequencies, the maxima and minima of such an intensity wave travel with less than the speed of light (see dotted black mark). The propagation of the interference pattern can therefore be matched to the speed of nonrelativistic electrons. Supporting information (SI) Movie 1 shows the intensity wave.

The following considerations provide an estimate of the achievable electron pulse duration and necessary laser power. For electrons of 31 keV energy (v_el = 0.33 c), with an initial packet duration of τ ≈ 300 fs, and laser pulses having wavelengths of 1,040 nm (ω₂) and 520 nm (ω₁), the pulse energy is in the range of E_pulse = 5 μJ each. Such laser pulses are realistic with repetition rates of up to megahertz. The optical pulse durations are also easy to obtain as they need to be 300 fs, with the focal diameter of 50 μm (radius r = 25 μm). The intensity I_pulse of a single laser pulse becomes I_pulse ≈ E_pulse/πr²τ ≈ 8·10¹¹ W·cm⁻², which can be treated nonrelativistically because the oscillatory speed of the electrons is ≪c. Therefore, the classical ponderomotive approach can be used to describe the forces on electrons (39, 40).

For simplicity, we consider the description in the rest frame of the electron packet. The relativistic effects associated with v_el = 0.33 c, such as length contraction and time dilation, are not significant because $\gamma =c/\sqrt{c^2-{\text{v}}_{\text{el}}^{\text{2}}}=1.06\approx 1$. The wavelength λ̃ of the standing wave is twice the wavelength of the constituting Doppler-shifted waves:

When both laser pulses interfere constructively, and thus form a maximum, we estimate the optical intensity to be I ≈ 4I_pulse ≈ 3·10¹² W·cm⁻², corresponding to a ponderomotive potential of U_p ≈ 0.2 eV. At the middle of a rising or falling slope of the standing wave, the ponderomotive force F_p is approximately

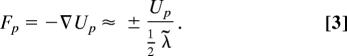This ponderomotive force is continuously effective during all of the time τ that the two laser pulses overlap (τ ≈ 300 fs). An electron located in the middle of a falling slope gains a velocity of

and an electron at a rising slope acquires the same amount of speed in the opposite direction. Note that this velocity is small so that the electrons do not slip along the intensity grating. After the laser pulses have passed, the packet begins to self-compress. The maximum compression is reached when parts of the initial electron packet initially located at the maximum gradient (middle of a slope) coincide with those initially located at a minimum. This occurs after time of

The quality of the compression depends on the linearity of the induced velocity distribution and on the initial energy bandwidth of the long electron packet. Because the ponderomotive force is the gradient of the sinusoidal wave intensity, the induced velocity distribution is approximately linear at a large range around the minima, where the individual packets compress. In principle, this leads to a perfect compression. In practice, the achievable electron pulse duration is primarily limited by the initial statistical velocity distribution within the electron packet. Such a distribution can originate from the photoemission process that is used for the femtosecond electron packet generation. Assuming a bandwidth of ΔE_spread ≈ 0.4 eV, typical for photoactivated electron sources in imaging, we obtain a velocity distribution of Δv_spread ≈ 2·10⁻⁶ c intrinsic to each single electron traveling at v_el. At the coincidence time T_coin, this leads to a temporal broadening of about

This is the order of magnitude that can be expected for the final electron pulse duration. We note that, to satisfy the uncertainty principle, such compression must be associated with a significant energy spread of ΔE ≈ (1/2)–h/Δt ≈ 30 eV. For the discussed case, this is fulfilled by the induced velocity distribution Δv (see simulations below).

Electrons repel each other because of the Coulomb force. In a multielectron packet, space charge effects dynamically change the velocity distribution (chirp) during propagation. This would perturb the introduction of a controlled chirp by the presented compression scheme and reduce the quality of the pulses. Fortunately, ultrafast electron diffraction and microscopy are effectively possible with electron packets consisting of very few or even single electrons, when the experiment is repeated with a higher repetition rate (21–23). The original femtosecond electron packet may therefore have a low electron density such that space-charge effects are negligible. As estimated above, rather low laser pulse energies on the order of 10 μJ are sufficient for optical compression, and a high laser repetition rate is therefore experimentally feasible. In addition, we believe that a limited amount of space charge can be tolerated in the presented scheme. For favorable packet shapes and sufficient electron density, the space charge repulsion induces an almost linear momentum distribution (44), which means that the electron packet is locally monoenergetic within every optical cycle, as discussed above.

Two points are worth mentioning. First, for single-electron packets, the initial temporal extend of the electron must be large enough to include about half a cycle of the intensity wave, to introduce the energy bandwidth necessary for attosecond times (≈30 eV for 15 attoseconds) (see Fig. 1). In imaging and diffraction, the electrons have a coherence length of hundreds of nanometers (27), comparable to λ̃/2, and the discussed compression is therefore possible for packets consisting of single electrons. Second, acceleration and retardation in the moving intensity grating act on the electron density, and phase effects within the matter wave are not significant. Single-electron or multielectron packets can therefore be treated semiclassically as an electron density.

Simulations and Experimental Time Scales

In this section, simulations of trajectories of electrons under the ponderomotive force of the moving intensity wave are presented. A Gaussian distribution of electrons at 31-keV energy with a duration of 300 fs and a transversal diameter of 10 μm is the initial condition outlined earlier. The laser parameters also are set at the values mentioned above. For 50,000 single electrons, each trajectory is numerically integrated in the ponderomotive force of the laser field and, for confirmation, directly in the electric and magnetic fields with time steps of 50 attoseconds.

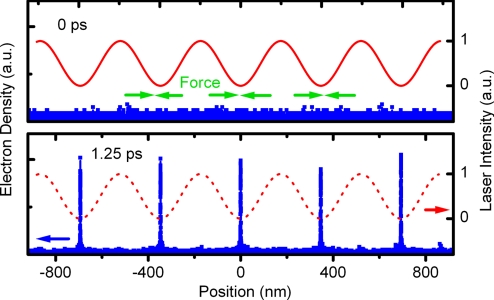
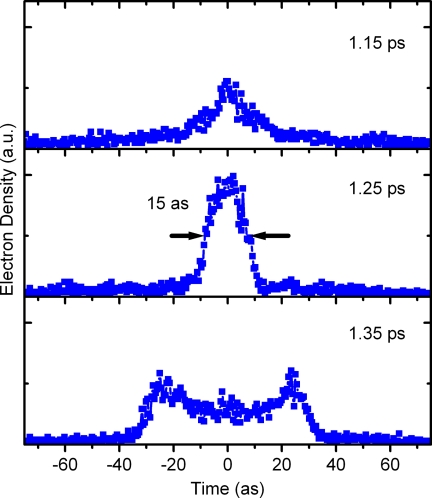
Fig. 4 shows a section of the electron density (blue) and the intensity wave (red) at time zero (when the two laser pulses overlap) and after 1.25 ps. Note that at 1.25 ps the laser intensity has faded; the dotted line (red) depicts where the optical wave would be. Clearly, the electron density shows the expected self-compression at the minima of the intensity wave. The energy bandwidth increases to ≈50 eV, such as is required to reach attosecond times (see Fig. 1). The compression dynamics for one of the pulses is given in detail in Fig. 5, for just before T_coin, at T_coin = 1.25 ps, and after T_coin. The electron pulse duration at T_coin is 15 attoseconds, evaluated as the full width at half maximum. After T_coin, the electron density disperses with the shown characteristic shape, which is the result of nonlinear contributions to the velocity distribution induced by the sinusoidal intensity grating. After multiples of T_coin, several recurrences of compression to longer attosecond pulse durations are observed.

Fig. 4.

Trajectory calculations showing the compression. (Upper) A long electron packet (blue) is overlapped with a moving intensity wave (red wave). Over time, the ponderomotive force (green arrows) accumulates and initiates self-compression. (Lower) At later times, when the intensity wave has faded (red, dotted wave), the electron density shows marked peaks of attosecond duration, which are located at the minima of the intensity wave. Note that the position scale is relative to the electron packet center.

Fig. 5.

Compression dynamics for attosecond electron pulses. After initiating self-compression by an optical intensity wave, the electron density (blue) starts accumulating (1.15 ps), peaks up to a 15-attosecond duration (1.25 ps), and disperses again (1.35 ps). The times are given relative to the laser pulse overlap (see text). SI Movie 2 shows the compression dynamics.

As evident from Fig. 5, there is a limited time window during which the electron pulses have the desired attosecond duration. Conceptually, this cannot be avoided, because the energy bandwidth associated with the attosecond pulse duration must lead to a temporal spread at nonrelativistic energies, as explained above (see Fig. 1). The window time ΔT_coin of compression is

In an experimental arrangement, the depth of the probed region must therefore be limited to ≈3 μm to avoid diffraction contributions from partially compressed electron pulses. In electron diffraction and microcopy, samples with 10–100 nm thickness are routinely used to match the penetration depth of the electrons. The mentioned micrometer requirement from the optical compression scheme therefore constitutes no major limitation in the desired application of the attosecond electron pulses.

The performance of the presented compression scheme does not significantly depend on the optical pulse duration. An increase in the optical pulse duration not only leads to a decrease in the ponderomotive force because longer optical pulses of the same energy have less intensity but also to an increase of the interaction time during which the ponderomotive force is effective. These two effects cancel for a wide range of pulse durations. Fluctuations in the optical pulse length will therefore not be critical for the stability of the electron pulse compression. In addition, the optical pulses do not need to be particularly short, which reduces demand on the applied laser system.

To characterize the attosecond pulses in time, streaking in an optical field can be used (12). Alternatively, a second moving intensity wave can be applied at the region of compression. Information about the electron pulses can be obtained by observing the energy spectrum or spatial deflection, which will change differently depending on whether or not the pulses are compressed.

The self-compressed attosecond electron packets are precisely located at the minima of the moving intensity wave and are therefore synchronized to the optical phase of the involved laser pulses. The time T_coin of free propagation (picoseconds) is short enough to prevent dephasing effects. The phase of the intensity grating and, therefore, the location of the attosecond electron pulses in time are determined by the relative phases between the two colliding laser pulses. The electron pulse train can therefore be temporally shifted with attosecond precision by adjusting the phase between the two colliding laser pulses, for example, by moving refractive elements such as glass wedges into one of the optical beams to introduce a controlled phase delay. For a pump–probe-type experiment, the strong electric field of a laser pulse or second electron/x-ray pulses can be used to initiate the dynamics to be studied. The attosecond electron pulses can then be used with the discussed adjustable attosecond delay to follow the investigated electron motion in space and time by elastic or inelastic scattering, diffraction, energy-loss spectroscopy, or real-space atomic-scale imaging (27). The spacing ΔT between the attosecond pulses is ΔT ≈ λ̃/v_el ≈ 3.5 fs, which is long enough to follow the relevant electron dynamics from the attosecond to the few-femtosecond scale in pump–probe or streaking-type experiments.

Summary and Outlook

The study presented here indicates that femtosecond electron packets can be effectively compressed to a train of attosecond electron pulses by the copropagation of a moving intensity gradient from a low-power laser. The achievable pulse duration of 15 attoseconds would be significantly shorter than the optical pulses generated from high laser harmonics, which at present are typically ≈250 attoseconds and recently reached 130 attoseconds, limited by the duration of an optical cycle. The few-attosecond free electron pulses are most promising for extending our domains of 4D imaging to the studies of ultrafast electronic motions and transitions that proceed on so-far-unexplored time scales with a table-top apparatus. The methodology discussed here also offers the following unique features: the exact synchronization of pump and probe pulses, the resolution of the problem of group velocity mismatch by proper choice of the interfering optical grating fields (which move at controllable sublight speed), and the reach for imaging and diffraction under realistic experimental conditions. Defocusing of electrons is minimal because the initial electron packet of ≈300 fs has ΔE ≪ E_central. Naturally, combinations of accelerating potentials and laser fields will be determined by the experimental applications.

The ponderomotive compression scheme offers the possibility of achieving even shorter electron pulses with more intense laser pulses. With the same settings as above, but with still nonrelativistic optical pulse energies of E_pulse ≈ 100 μJ, subattosecond (zeptosecond) electron pulses are in principle possible to generate with self-compression in ≈100 fs. This is still within or close to the optical overlap time and not in a field-free region, as in the case described above. Nevertheless, subattosecond electron pulses are conceptually feasible and have potential to achieve subattosecond time resolution for time-resolved investigations of inner-nuclear processes. If the laser intensity or the interaction time is further increased, individual electrons will slip down the intensity gradient and will oscillate back and forth within the potential provided by an optical cycle. The motion will lead to temporal quantum interference of single electrons with themselves, provided the initial coherence length is comparable to the optical wavelength (40).

The concept of velocity-matched ponderomotive interaction is more general, beyond its use for generating attosecond electron pulses. Tailored intensity gradients created by optical-field synthesis allow for a flexible shaping of nonrelativistic electron packets in space and time. Although the ponderomotive force is weak compared with direct electric-field interactions, the possible creation of slowly moving intensity gradients gives rise to macroscopic force accumulation controlled by the optical field. The concept could perhaps be useful for laser-induced particle acceleration and for the generation of temporally and spatially shaped electron packets for the investigation of some quantum effects of interferences. But of most interest to us is the potential for visualizing the dynamics of electrons, especially those of atoms, clusters, and surfaces, with diffraction and microscopy.