Natural stimuli evoke dynamic sequences of states in sensory cortical ensembles

Abstract

Although temporal coding is a frequent topic of neurophysiology research, trial-to-trial variability in temporal codes is typically dismissed as noise and thought to play no role in sensory function. Here, we show that much of this supposed “noise” faithfully reflects stimulus-related processes carried out in coherent neural networks. Cortical neurons responded to sensory stimuli by progressing through sequences of states, identifiable only in examinations of simultaneously recorded ensembles. The specific times at which ensembles transitioned from state to state varied from trial to trial, but the state sequences were reliable and stimulus-specific. Thus, the characterization of ensemble responses in terms of state sequences captured facets of sensory processing that are missing from, and obscured in, other analyses. This work provides evidence that sensory neurons act as parts of a systems-level dynamic process, the nature of which can best be appreciated through observation of distributed ensembles.

The time courses of sensory neural responses are rich with structure. Taking time into consideration increases the amount of information that can be extracted from neural codes (1–5) and changes the nature of that information (6–8). Such temporal complexity is the natural result of interactions among neural populations (9–11), a concept recently illustrated in studies of olfactory antennal lobe responses in insects (12–14).

The behavior of mammalian sensory systems has proven more difficult to characterize, due in part to the relative complexity of these networks and of the behaviors and neural activity that they subtend. Feedback and convergence found in mammalian brains are extensive and diffuse (15), a fact that contributes to high trial-to-trial variability of mammalian cortical sensory responses (16). This variability is usually dismissed as noise, a decision formalized by the use of across-trial averages such as peristimulus time histograms (PSTHs) (8) and compilations of sequentially recorded neurons (13) to characterize temporal codes.

If the variability in neural responses is not noise, however [if, for instance, it reflects network processes evolving at different speeds from trial to trial (17, 18)], then trial-averaging techniques will obscure features of the underlying neural processes. Recent evidence indirectly suggests that this possibility may be the case: repeating multineuronal temporal patterns that are not reflected in PSTHs follow application of sensory stimuli (19, 20) and precede initiation of motor behaviors (21–23), although the search algorithms used to identify such patterns are controversial (24, 25); furthermore, the speed of perceptual identification itself varies from trial to trial (26, 27) in a manner linked to the dynamics of network activity (27–30).

Here, we provide direct evidence that trial-to-trial variability is a reliable, information-rich part of ensemble sensory processing in awake rats, by using hidden Markov models [HMM (31)] to detect coherent rate patterning in populations of simultaneously recorded neurons. This method, which has been successfully used to study decision making (32), reveals that taste processing can be characterized as a progression of reliably stimulus-specific sequences of ensemble firing rate states. The specific times at which ensembles transition between states vary from trial to trial, but the sequences remain the same. Because trial-specific information is obscured in across-trial averages, stimuli are identified more successfully by using state sequences than trial-averaging techniques. This simple, dynamic characterization of primary sensory activity captures important facets of sensory codes that are missing from most classical analyses, suggesting that the variability between trials represents an important part of the structure of perceptual processing (33) and that the sense of taste makes use of true distributed codes (34).

Results

Sensory Responses Are Reliably Characterized as Sequences of Ensemble Firing Rate States.

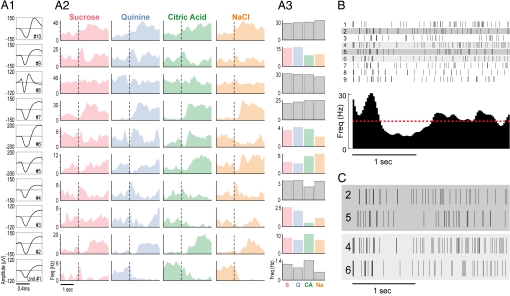
We implanted 32 electrodes into the gustatory cortex (GC) of four attentive rats (28) and recorded bilateral ensemble sensory responses in 13 separate sessions (9.3 neurons per session). By standard analysis, 38% of the neurons were classified as “taste-responsive” (Fig. 1A). Such responses were typically noisy from trial to trial, however (Fig. 1B). The coefficient of variation for response magnitudes was 0.76 ± 0.59 (average ± SD). Even in pairs of trials with similar response magnitudes, variability was high (Fig. 1C).

Fig. 1.

Taste responses in GC neurons. (A1) Waveforms representing the average action potential shapes for the 10 neurons (each numbered in bottom right) of one simultaneously recorded ensemble; x axis, time; y axis, amplitude (μV). (A2) PSTHs of the response of each neuron to the four basic taste stimuli (top); x axis, time; y axis, firing rate (Hz); dashed vertical line, stimulus onset. (A3) Responses of each neuron to the four tastes, averaged across trials and across 2.5 sec of poststimulus time; color panels are taste-specific by classic analysis (28). (B) (Upper) Raster plots of a neuron response on individual trials (rows). Each tick mark is an action potential. (Lower) Resultant PSTH; the red dashed line indicates the spontaneous firing rate. (C) Two pairs of trials from B, each matched for number of action potentials.

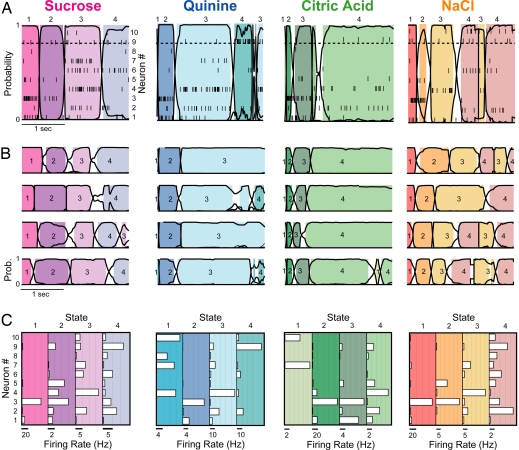
When the display was reorganized such that the responses of all simultaneously recorded neurons were aligned in time (Fig. 2A), coherence in the ensemble firing response to each stimulus was revealed: the firing rates of several neurons changed simultaneously at certain times. HMM confirmed and extended this characterization, showing that ensembles progressed through a series of three or four firing rate states (shaded regions of each panel) across 2.5 sec of poststimulus time. State sequences were punctuated by brief transitions during which HMM could not identify a state as most likely (<80% likelihood, denoted by the lack of shading).

Fig. 2.

Coherent state sequences in GC ensembles. (A) Representative single trials of the response of one GC ensemble to each basic taste stimulus (top) reveal simultaneous changes in firing rates in several neurons. Overlaying the population raster plots (each tick mark is an action potential, and each row is a different simultaneously recorded neuron; right y axis) is the HMM output: black continuous lines show the likelihood (left y axis) of each state through time (x axis), and shaded regions are periods during which one particular state (each shade represents specific states, numbered above the panel) exceeds 0.8 likelihood (horizontal dashed line). In nonshaded periods, no state was dominant. (B) Four more trials of the response of the same ensemble to each taste, showing reliability of state sequence and trial-to-trial variability of transition time. Numbers within each colored region label the state number. (C) Histograms showing firing rates of each neuron (open horizontal bars) in each state for each taste. Each box summarizes the states for the above taste, and each shaded panel within each box corresponds to a state (color-coded as above); the number of the state is listed above. [Scale bars (below each shaded panel): spikes per sec; y axis, neuron (numbered from 1 to 10).]

Fig. 2B shows four more trials of each taste delivered in this session. In every case, the ensemble switched through a sequence of states, each stable for an order of magnitude longer than between-state transitions. The timing of the transitions changed from trial to trial, but the sequence itself was conserved. The ensemble patterns of firing rates (Fig. 2C) for a subset of states in each sequence were clearly stimulus-specific (i.e., were significantly different from all states specified by HMM of other tastes, P < 0.01, ANOVA interaction term for two-state comparisons).

To test how well the HMM characterized spike trains across the 13-ensemble dataset, we performed a post hoc probability analysis [see supporting information (SI) Methods]. This analysis, which specifically examined how likely particular spike trains were to have come from particular rate functions, confirmed that the HMM fit the data well; across 309 neuron–taste pairs, the mean log ratio of probabilities comparing fits of HMM and PSTH with spike trains was 2.44 (±0.77) in favor of HMM, a highly significant difference (P < 0.001) even though the smoothed PSTH uses more than twice as many parameters to describe an average trial than HMM (200 compared with 68).

State-to-state transitions involved the coordinated activity of many neurons. Fifty-one percent of the neurons in each ensemble changed their firing rates (P < 0.01 by paired t test comparing firing rates in pairs of states) at transitions, including similar percentages of putative interneurons (58%) and pyramidal neurons (49%; see SI Fig. 5). An implication of this high percentage is that some neurons involved in state transitions are not recognized as taste-responsive in across-trial averaging (19, 28).

State Sequences Reflect Coherent Network Processing.

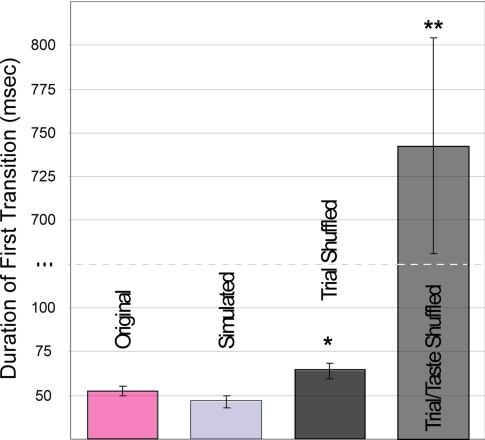
To evaluate further the above characterization of sensory processing, we first asked whether transitions truly reflected coherent shifts in neural ensemble rates. We compared the data-derived results with those calculated on the basis of ideal simulated datasets, constructed to progress instantaneously from one underlying state to another. Inhomogenous Poisson spike trains were generated directly from the HMMs of the datasets but with periods of uncertainty removed; e.g., for one simulation, neurons fired at rates specified in Fig. 2C, with changes occurring at the midpoints of the transitions shown in Fig. 2B (see SI Methods). Fig. 3 demonstrates that these ideal transitions, which by design were as fast as could be achieved, were no faster than those in the actual data (48 ± 4 vs. 53 ± 3 msec, P > 0.05, t test). Thus, coherent GC ensembles transition between stable states as quickly as is theoretically possible.

Fig. 3.

State transitions are rapid in simultaneously recorded neural ensembles. The average duration of transitions between states (±SEM) for the real data (pink bar) was equivalent to that for simulated data with instantaneously changing underlying states (light gray bar) and faster than that for both trial-shuffled (dark gray bar) and trial/taste-shuffled (medium gray bar) data. *, P < 0.05; **, P < 0.001.

Further, these rapid transitions are not an artifact of applying HMM to this kind of dataset; even subtle data perturbations significantly increase the length of transitions. We constructed trial-shuffled datasets, in which trials of the responses of each neuron to a particular taste were randomly swapped with other trials of the same neuron's response to the same taste. This procedure disrupts within-trial coherence in the dataset but leaves intact all temporal information available in the PSTH. If the true rate changes are gradual (as they look in PSTHs; see Fig. 2) or unrelated to interneuronal coherence, trial shuffling should not increase transition durations.

In fact, when HMM is fit to such datasets, state-to-state transitions are significantly less well defined (Fig. 3); trial-shuffled data consistently switched from state to state more slowly (64 ± 5 msec) than unshuffled data (P < 0.01). Note that the difference between the original and trial-shuffled data is more than twice the size of the difference between the original and simulated data (which, again, transitions from state to state as quickly as possible); the small-seeming absolute increase in transition duration caused by trial-shuffling is, in relative terms, large. When spike trains were randomly swapped without regard to taste (taste/trial-shuffling), transition durations increased further; in fact, transitions become more prominent (742 ± 61 msec) than states after this shuffle. Rapid switches between states in a sequence are therefore a true feature of the ensemble sensory responses and not an artifact of HMM analysis.

State Sequences Are Centrally Generated.

It is highly unlikely that observed state sequences represent either a reflection of orofacial behaviors (26, 33) or of reliable taste receptor activation sequence caused by such behaviors. For one thing, stimulus-specific state sequences routinely began within the first 200 msec of the responses, whereas stimulus-specific behaviors do not emerge until much later (26). Furthermore, analysis of video, captured simultaneously with ensemble recordings, reveals that even the time series of nondistinctive oral movements that are produced during the 1st sec of stimulus processing differ across trials and are not time-locked to states or state transitions in any appreciable way (SI Fig. 6; see also refs. 26 and 33). We found no significant Pearson correlations between behavioral latencies and the latencies of the first three neural state transitions (average R² = 0.15 ± 0.04).

As one further test of this possibility, we examined the degree to which somatomotor neurons account for rate changes at transitions. Because much of the rat's oral behavior is rhythmic (35, 36), the across-session power spectra of neurons with oral somatomotor receptive fields tend to be strongly modulated at 6–9 Hz (8). Such neurons were plentiful in our ensembles (n = 21), but they were no more likely to be involved in transitions than were other GC neurons (in fact, 51% of each subsample changed firing rates between successive states). In summary, several analyses all fail to show any evidence for any peripheral sensory or motor explanation for state sequences (8, 37).

State Sequences Provide Information Greater Than That Available in Averaged Temporal Codes.

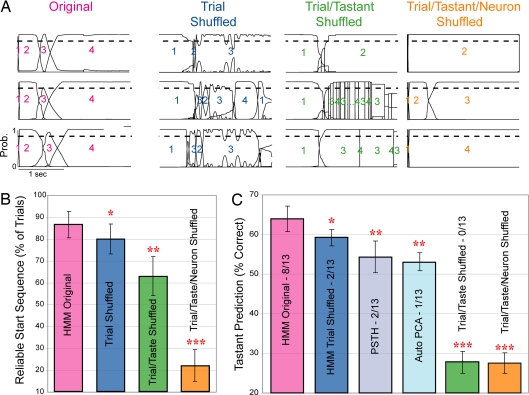
Fig. 4A shows three trials from the original dataset (Left, pink label); all three contain the identical state sequences (the assigned numbers of the states are overlain on each trial), with trial-specific timing of transitions. Right columns show that the reliability of the calculated sequence is lower for trial-shuffled data (blue), lower still for trial/taste-shuffled data (green), and nonexistent for randomly shuffled (trial/taste/neuron shuffling) data (orange). Across 13 sessions (Fig. 4B), the dominant state sequence was observed in 87 ± 6% of normal trials, 80 ± 7% of trial-shuffled trials, 63 ± 9% in trial/taste-shuffled trials, and 22 ± 7% (i.e., chance) of trial/taste/neuron-shuffled trials. All shuffled percentages were significantly different from the original data (P < 0.05 by paired t test).

Fig. 4.

State sequences predict sensory stimuli better than other techniques. (A) State sequences were more consistent for original (unshuffled) trials than after trial-shuffling, trial/taste-shuffling, or trial/taste/neuron-shuffling. Shown are three representative trials per dataset; as in Fig. 2, continuous lines represent the probability of a specific state (y axis), numbers label the dominant states, and the dashed line is 0.8 probability. (B) Across ensembles, the percentage of trials beginning with the same three-state sequence (y axis) is higher for the original data (pink bar) than for trial-shuffled (blue bar), trial/taste-shuffled (green bar), or trial/taste/neuron-shuffled data (orange bar). (C) The percentage of trials in which the taste was correctly predicted is higher for the original data (pink bar) than for trial-shuffled (dark blue bar), trial/taste-shuffled (green bar), or trial/taste/neuron-shuffled data (orange bar). HMM also performed better than ensembles of PSTHs (gray bar) and better than PCA (light blue bar). *, P < 0.05; **, P < 0.01; ***, P < 0.001, all paired t tests.

If reliable sequences demonstrate trial specificity of transition timing, then they should transmit stimulus-related information more cleanly than across-trial averages. We tested this possibility directly, by using a jackknife cross-validation procedure to quantify stimulus prediction in single trials. The analysis revealed that HMM correctly identified stimuli in 64 ± 3% of the individual trials (Fig. 4C), despite the use of as few as five trials to construct the model. This percentage was only modestly related to the number of neurons and taste neurons in an ensemble (SI Fig. 7). Trial shuffling significantly reduced the percentage of trials that could be correctly identified (59 ± 2%, P < 0.02); both trial/taste and trial/taste/neuron shuffling reduced stimulus identification to chance levels (both 28 ± 3%).

We also compared directly the predictive efficacy of HMM with that of more commonly used approaches. First, we evaluated predictions based on jackknifed ensembles of PSTHs, which proved to be significantly less successful than HMM-based predictions (54 ± 4%, P < 0.01), despite using more parameters (see SI Methods). Next, we used principal components analysis (PCA) to classify jackknifed sets of trials by means of automatic and manual clustering techniques (see Methods) in low-dimensional space. This technique is the same one used to describe and classify temporal codes in insect olfactory responses (13, 38), here restricted to simultaneously recorded ensembles. Using automatic clustering, we were able to identify successfully 53 ± 3% of the trials (Fig. 4C), 11% fewer than HMM (P < 0.01); discrete clusters were difficult to discern in our sets of simultaneously recorded neurons (SI Fig. 8). Even when classification was optimized by using manually defined clusters, PCA performed significantly worse (54 ± 6%, Fig. 4C) than HMM (P < 0.05). The similarity in performance of the unsupervised PCA, manual PCA, and PSTH analyses likely reflects the fact that all assume trial-to-trial variability to be noise (38).

Discussion

GC neurons produce temporally complex sensory responses (8, 28), as do neurons in other systems (1–8). Although sensory dynamics have been extensively characterized in systems with highly reliable responses (12), our understanding of inherently noisy awake mammalian cortical sensory responses (39) has progressed more slowly. Here, we show that sensory responses are coherent across ensembles of mammalian cortical neurons, which respond to tastes with reliable, taste-specific sequences of relatively stable firing-rate states. The information accessible in the state sequences is degraded by any shuffling of the data and thus reflects a genuine network property of sensory responses. It is unrelated to ongoing sensorimotor sequences and thus reflects central rather than peripheral mechanisms.

Our work takes its cue from the success of theoretical work treating neural activity as a function of coherent (40, 41) underlying states with minimal assumptions. Our results are consistent with previous findings showing that variability in the response of one neuron may predict variability in others (4, 19, 42, 43) in a way that carries information efficiently (44, 45) and with evidence that ensemble rate changes accompany “up/down” states in visual (46) and somatosensory cortex (47). It is clear that the use of averaged neuronal responses misses perceptually meaningful interactions between neurons. The slow changes in firing rate observed in PSTHs (Fig. 1) in fact create a false impression of taste information accumulating gradually in single neurons, obscuring the rapid transitions that are cleanly observed in ensemble analysis. Recent modeling efforts have suggested that transient olfactory dynamics (13) also vary from trial to trial (17, 18), but here, we provide an empirical demonstration that sensory information available in single-trial ensemble codes exceeds that available in across-trial averages (see also ref. 48).

Although the significant differences between the performance of HMM and PSTH/PCA classifiers are not large in terms of absolute numbers (Fig. 4 B and C), this subtlety is to be expected; PSTHs are used because they do carry a great deal of information. The value of the conceptual advance offered here goes far beyond raw effect size. Coherent ensemble codes take into account the basic fact that neurons interact within networks, whereas other characterizations do not. In addition, such codes offer a plausible synchronization signal whereby an animal might determine the actual onset times of important stimuli within constant, ever-varying streams of action potentials; the zero time point used to construct PSTHs is something that the experimenter knows but that the animal does not. Finally, our state-sequence characterization is consistent in important ways with the nature of perception itself, which is reliable but variable in latency from trial to trial.

Coherent state sequences are likely the result of coordinated action in distributed, massively recursive neural systems (15, 46, 49). As such, they probably do not represent pure “sensory codes” to be interpreted by downstream “grandmother neurons.” Rather, we suspect that we are observing a process in which sensory input is being transformed into motor output through neuron–neuron interactions (perhaps underlain by asynchronous convergence upon GC of inputs from multiple brain regions; see ref. 15). Single-neuron analyses have suggested that information in GC taste responses progresses from being sensory- to action-related within the first 1.5 sec after stimulus (8, 28). The three coherent ensemble states that we observe unfolding across this same period may reflect, in much sharper relief, explicit temporal multiplexing in sensory responses: rather than sensory coding, decision making, and motor coding being handled by separate regions in a spatial hierarchy, the distributed system may be processing sensory stimuli through a temporal hierarchy. As such, these data go beyond extant theories of taste function (15), which propose that the roles of neurons in the sensory neuroaxis are spatially determined, and beyond theories of sensory function that dismiss trial-to-trial variability.

Methods

Experimental Preparation.

Methods conform to the Brandeis University Institutional Animal Care and Use Committee guidelines. Female Long–Evans rats (250–300 g) were anesthetized and implanted with bilateral GC-drivable microelectrode assemblies (16 wires per bundle) and intraoral cannulae (for stimulus delivery). After recovery, rats were trained to wait patiently in restraint for 40-μl aliquots of 100 mM NaCl, 100 mM sucrose, 100 mM citric acid, or 1 mM quinine HCl (tastes selected randomly without replacement).

Electrophysiology.

Recordings were amplified (1,000–2,000), filtered (300–800 Hz), and digitized. Single neurons of >3:1 signal-to-noise ratio were isolated by using a waveform template, augmented with offline cluster cutting software (Plexon, Dallas, TX) (50). Resultant taste responses are similar to those observed with sharp 5-MΩ electrode penetrations (51, 52).

Taste Profile Analysis.

A neuron was deemed a taste neuron if it responded differently to at least one taste than to others (53); the significance of the difference was established by using ANOVA and a subsequent post hoc test (Tukey's HSD, P < 0.01). This is a relatively conservative measurement: a neuron producing strong but similar responses to all tastes will not be deemed taste-responsive.

HMM.

HMMs reveal the degree to which data can be described as reflecting a sequence of stable “hidden states” (41). Trained on neural ensemble data containing neurons from both left and right GC (coherent firing rate changes are similar for uni- and bilateral GC neuron pairs; see ref. 19), the Baum–Welch algorithm (54) returns the set of underlying states, each defined as a vector of firing rates, one for each neuron, and the probability of transitioning from any one state to any other. We produced three- to seven-state solutions for a subset of the data, but higher-state solutions resembled the four-state solution; added states occurred only very briefly and once (data not shown). Hence, we chose five states as our upper limit.

For an extensive description of the procedure, assumptions, and robustness, see SI Methods.

Comparison of States.

ANOVAs were used to compare ensembles of firing rates between states. States were considered significantly different only when the interaction P < 0.01 (which meant that states were deemed different when the shape of the neuron × rate distributions differed) and to be the same when the interaction P value exceeded 0.2. Few P values fell between 0.01 and 0.2. Tukey's HSD (P < 0.01) revealed which neurons had different firing rates in each pair of significantly different states.

Data Shuffling.

Three control datasets, each identical in size to the original dataset, were constructed for each session, by randomizing the trial ordering within groups of 2.5-sec spike trains. For trial shuffling, shuffling was done independently on 6–12 trial sets of the response of each neuron to a specific taste; when this procedure is applied to each neuron in the ensemble, the resultant “trials” (e.g., “trial 1” consisting of trial 3 of neuron 1, trial 5 of neuron 2, trial 1 of neuron 3, etc.) contain no information specific to simultaneous recordings but leave all information available in across-trial averages (e.g., PSTH) intact. For trial/taste shuffling, the set of trials encompassing the responses of a single neuron to all tastes was randomized, destroying the information in PSTHs but leaving any “cell-specific” information intact. For trial/taste/neuron shuffling, an entire dataset was randomized.

All analyses performed on the original dataset were performed anew on shuffled datasets.

Simulated Datasets.

Ideal simulated datasets contained ensembles of inhomogenous Poisson spike trains generated from the HMM solutions for the real datasets. Spike trains in these simulations changed rates coherently at transitions, and periods of uncertainty concerning the dominant underlying state were eliminated (for more detail, see SI Methods). Subsequent HMMs of these datasets revealed the lower limit on detectable transition times for datasets with the same numbers of neurons (at similar firing rates) to be those empirically recorded.

Prediction of Stimuli in Single Trials with HMM.

Using the Baum–Welch algorithm (11), we determined the likelihood that “held-out” ensemble spike trains came from each of the four taste models constructed on n−1 trials. The model that yielded the highest likelihood for each spike train was chosen as the taste prediction for that trial. This procedure was repeated such that each trial was held out once (jackknife cross-validation).

Prediction of Stimuli in Single Trials with PSTH Ensembles.

PSTHs were computed (100-msec bins) for the response of each neuron to each taste, in n − 1 trials. Euclidean distances between single-trial responses and the four taste-specific firing rate models were then computed; the model with the smallest Euclidean distance was chosen as the taste prediction. The procedure was repeated such that each trial was held out once (jackknife).

Prediction of Stimuli in Single Trials with PCA.

Single trials were represented as the time course of an ensemble response. For each trial, PCA was performed on a vector of length n × b (where n is the number of neurons in the ensemble and b is the number of time bins). As shown in ref. 38, bin size = 50 msec, thus, b = 50. The first six principal components (describing 39% of the variability) were used for clustering and classification on the basis of examination of scree plots.

We calculated the PCA on n − 1 trials of each taste (see SI Fig. 8) and then performed both an automated classification of trial types (k means clustering) and a jackknife cross-validation on manually determined clustering for each taste. For the latter, cluster centers were defined as the mean of all used responses to that taste for that ensemble. Each held-out trial was classified as belonging to the nearest cluster based on the Euclidean distance in PC space.

Abbreviations

GC

gustatory cortex

HMM

hidden Markov model

PCA

principal components analysis

PSTH

peristimulus time histogram.