Protein anisotropy turns solubility on its head

In the effort to understand living cells, knowledge about molecular details competes with knowledge of collective properties of large systems of molecules. On the one hand, molecular structures and interactions strongly suggest how the cell's molecular machines work and give rise to rich metabolic diagrams. On the other hand, subtle collective properties such as the entropy and free energy represent driving forces for chemical reactions, self-assembly, and phase transitions within cells. In a recent issue of PNAS, McManus et al. (1) report a dramatic advance in understanding the differing consequences of protein structure for crystallization and solution clouding. Their work straddles the structural and collective viewpoints and has implications for several current scientific efforts.

Just as clouds in the sky reflect attractions between water molecules, forces between proteins lead to phase transitions of clouding and crystallization in solutions. Indeed, analogs of both liquid and ice clouds occur in protein solutions in cataract, the leading cause of blindness (2, 3). However, the complicated surfaces of proteins make for a richer repertoire of transitions than occur for small molecules, and small changes in a protein surface can easily tilt the balance from one transition to another.

The dew point of air has an analog in solution called the cloud point. As temperature or other conditions reach the cloud point, droplets of dense or dilute liquid form spontaneously and scatter light, as in clouds. This liquid–liquid coexistence occurs in the oil and water of salad dressing, in molten liquid metal alloys and rocks, in protein solutions (2, 4), in membrane lipids (5), and even in supercooled pure water. It has been extensively analyzed, starting with Van der Waals before 1900 (6).

Protein phase transitions, including the liquid–liquid transition and many others, are central to cataract disease (2), sickle-cell disease (7), as well as Alzheimer's disease and numerous other neurodegenerative diseases (8) and are important in crystal growth (9), cell physiology (10), and industry (11). The work of McManus et al. (1), in the laboratory of George B. Benedek in the Department of Physics at the Massachusetts Institute of Technology, grew out of findings that several single-site mutations alter phase boundaries so as to cause cataract (3, 12–14). To understand the relevant driving forces is challenging because the transitions are sensitive to weak, noncovalent interactions and are affected by the crowded, multicomponent cytoplasm (15–17).

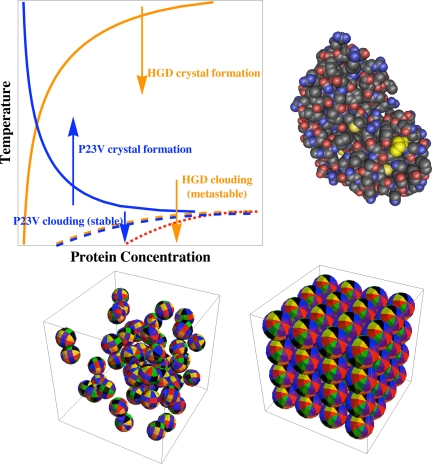
Imagine turning a dial to change some water molecules so as to make them freeze when you raised their temperature above the boiling point. Outlandish as that may be, an individual amino acid change does just the analog for the human eye lens protein γD-crystallin (HGD). McManus et al. (1) changed proline 23 to valine, which turned the new P23V protein's crystallization boundary upside down, so that it crystallized upon raising the temperature instead of upon lowering the temperature (1, 14) (Fig. 1 Upper Left). However, they also found the cloud point boundary for liquid–liquid coexistence to be essentially unchanged (Fig. 1) and set out to discover why.

Fig. 1.

Protein anisotropy has different effects on crystal formation and liquid–liquid separation. (Upper) McManus et al. (1) show that, in human HGD (Protein Data Bank ID Code 1hk0) (13) (Right), replacing proline 23 (residue in yellow) with valine (P23V) switches solid-phase solubility from normal (orange line) (Left) to retrograde temperature dependence (blue line) but leaves liquid–liquid cloud points unchanged (dashed orange and blue lines). The red dotted line indicates the spinodal boundary for thermodynamic instability. (Lower Left) Snapshot from Monte-Carlo simulation of square-well attraction between globular proteins in liquid solution, with varying orientations essential for averaging of interactions (18) added for illustration (see text). (Lower Right) Specific orientations in the crystal, in comparison with varying orientations in the liquid (Lower Left), give rise to contrasting influences of mutation on the crystallization and cloud boundaries (1, 18).

To understand their approach, it is important to recognize that, just as temperature differences drive heat flow, chemical potentials are the collective properties that drive flows of molecules in phase changes, diffusion, and chemical reactions. McManus et al. (1) measured the chemical potentials relevant for clouding and crystallization. They found that only the crystal chemical potentials changed substantially in response to the mutation, not those of the liquid solution.

An essential aspect of their analysis stems from the work of Lomakin et al. (18) on aeolotopic, or orientation-dependent, interactions of globular proteins. Lomakin et al. addressed a key question: Under what circumstances can net protein interactions be adequately represented with a Boltzmann-weighted average over individual molecular orientations? That work provides a basis for chemical potential models for analyzing the competition between transitions for which an angular average may be appropriate, such as liquid–liquid phase separation and nonspecific aggregation (Fig. 1 Lower Left), and other transitions involving more specific relative orientation, including fibril and crystal formation (Fig. 1 Lower Right).

The contrasting sensitivities of the liquid–liquid and liquid–solid phase boundaries to the P23V mutation (Fig. 1 Upper Left) (1) are consistent with the analysis of Lomakin et al. (1, 18). In the liquid, varying protein orientation makes different subsets of patches adjacent between neighboring proteins (Fig. 1 Lower Left), making an orientational average useful and reducing the consequences of changes in a single patch, such as that made by a mutation. In contrast, orientational ordering in the crystal brings specific patch interactions to the fore (Fig. 1 Lower Right). Consequently, the crystal formation boundary can be more sensitive to a mutation, and its temperature dependence can change dramatically, reflecting that of the selected interactions.

Another unusual feature of protein solutions provides important background for the present work. Protein crystallization boundaries, such as those for HGD, can occur at temperatures above the cloud-point curve (Fig. 1 Upper Left) (19). This phenomenon is as if water were to freeze at temperatures above its boiling point as one lowered the temperature. In fact, the protein cloud-point boundary can be entirely evanescent, or metastable, in that after days or weeks, clear liquid will surround

Analogs of both liquid and ice clouds occur in protein solutions in cataract, the leading cause of blindness.

the crystals and no cloud droplets will remain, as for HGD (Fig. 1 Upper Left).

Simulation and analysis have shown that the short range of protein attractions, relative to protein size, can indeed make cloud points evanescent with respect to crystal formation (20, 21). However, the present work shows that the short range of the attractions can be just part of the needed rationale for metastability, because the dilute cloud points of the P23V protein are stable with respect to the observed crystallization (Fig. 1 Upper Left).

The work of McManus et al. (1) informs several other areas of research. First, measuring the relevant chemical potential changes is an important step toward quantifying conditions needed to control phase transitions in normal physiology and in phase transition diseases. It is important to note that it is hardly conceivable that the chemical potentials could have been so deeply analyzed without using temperatures that ranged well away from physiological.

Second, the close proximity of many protein cloud-point and crystallization curves helped inspire the use of cloud points to help search for protein crystallization conditions needed for x-ray structure determination (refs. 4 and 9 and references therein). This work exhibits a new relationship between a protein's cloud-point and crystallization boundaries, important for such a strategy.

Third, that protein solution transitions have differing sensitivities to mutation informs efforts to understand the evolution of compartment formation and other spontaneous ordering within cells (22). In this connection, it will be interesting to compare the mutation sensitivities of related phase transitions of importance in cells (10).

That a change in a single amino acid of the 174 amino acids in this protein can switch its solubility from normal to retrograde temperature dependence illustrates the extreme sensitivity of cellular macromolecular phase transitions. The chemical potential changes measured by McManus et al. (1), associated with the dramatic crystallization boundary change between the HGD and P23V, are comparable in magnitude to the strength of an interaction as weak as a single hydrogen bond. Such sensitivity has long been familiar in other contexts, including sickle-cell disease (7). Because such small changes can make the difference between health and disease, it is very important to continue the needed development of accurate theories for all of the relevant types of noncovalent interactions in aqueous electrolyte solutions (23).

By integrating mutagenesis with thermodynamic measurements and modeling, McManus et al. (1) provide a key insight into protein phase boundaries and a beautiful example of biology-inspired advances in statistical physics.